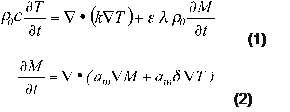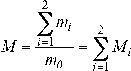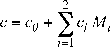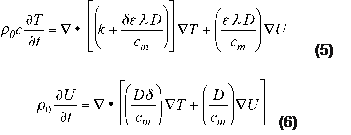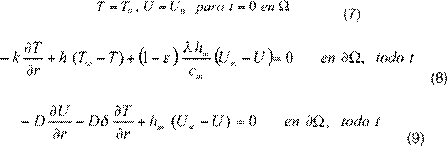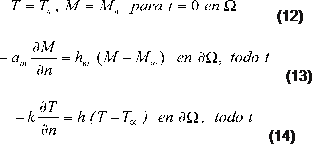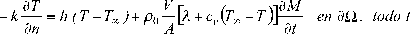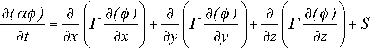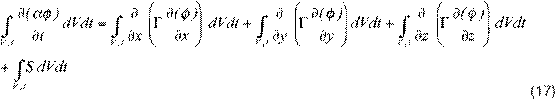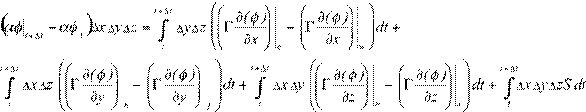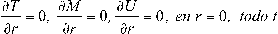Introducción
El secado es uno de los métodos más importantes para la preservación de los productos agrícolas, como, por ejemplo, los granos de cereales, café, los productos comestibles y la madera. El comportamiento del material durante el secado depende de la transferencia de calor y masa en el producto sometido a este proceso. Por lo tanto, es fundamental conocer la distribución de temperatura y humedad en el sistema cuando se requiere diseñar procesos y equipos, así como también para controlar la calidad y la selección de las operaciones de manejo y almacenamiento de estos productos. Para el proceso físico del secado industrial de granos, o en general de elementos granulares, se consideran dos fenómenos fundamentales: i) la humedad del grano se evapora y sucesivamente se difunde fuera del kernel o del conjunto de granos; ii) la energía necesaria para la evaporación de la humedad fluye en dirección opuesta a la difusión y causa que la masa húmeda cambie del estado líquido al gaseoso. La resultante de estos dos procesos brinda así las características cinéticas del proceso de secado; los dos fenómenos de transporte que ocurren son la transferencia de calor y el transporte de masa. Las fuerzas motoras que causan el transporte y aquellas que provocan la resistencia a este movimiento determinan la velocidad del secado. Normalmente, en el proceso de secado se puede asumir que los granos forman un medio poroso con los poros con comportamiento capilar, es decir, el potencial capilar es más grande que el potencial gravitacional, pudiéndose despreciar así las fuerzas gravitacionales.
Para el fenómeno de transporte de calor y masa en un medio poroso capilar, Luikov (1975) propone un modelo fenomenológico basado en un sistema de ecuaciones de difusión de calor y masa acopladas, que considera los efectos del gradiente de temperatura sobre el transporte de la masa húmeda. Sanderson (1986), en cambio, considera un modelo de un lecho de material granular poroso e higroscópico con un flujo de aire uniforme y en el lecho tres zonas distintas con temperatura y humedad relativa constantes. Un modelo más simple es el de secado de granos en capas delgadas, con espesores de capa del orden del tamaño del grano, de tal manera que todos los granos son sujetos a las mismas condiciones de secado por aire. En este caso, un trabajo muy relevante se debe a Sokhansanj y Bruce (1987), que usan las ecuaciones de transporte difusivo y una condición de borde que acopla el contenido de humedad y la temperatura.
Para la modelación computacional del proceso de secado existen varios trabajos científicos publicados (véase, por ejemplo, la revisión de Parry, 1985). Aplicando el modelo de Luikov, Liu y Cheng (1991) describen el secado de un bloque de madera usando la función potencial de humedadU y ecuaciones diferenciales en una sola variable. Irudayaraj et al. (1992) usan dos modelos diferentes, el de Luikov y el de Sokhansanj y Bruce e incorporan algunas correlaciones para representar el cambio de algunos parámetros físicos en función de la temperatura T y del contenido de humedad M. Comparando los resultados numéricos de T y M con valores experimentales y computacionales de literatura para el proceso de secado de soya, maíz y cebada, los autores concluyen que las predicciones del modelo de Sokhansanj y Bruce son más eficaces que las del modelo de Luikov. Yang et al. (2002) aplican el método de los elementos finitos para predecir los valores de M en el interior de granos de arroz. El modelo de Yang et al. analiza el calor perdido por la evaporación del agua en la superficie de los granos y usa una ecuación similar a la de Sokhansanj y Bruce, incluyendo otras dos ecuaciones diferenciales de transporte.
Otra solución analítica del modelo de Luikov la obtienen los investigadores Kulasiri y Woodhead (2005), que estudian el proceso de secado de la madera de la especie Pinus radiata, usando una técnica de resolución para el caso unidimensional, basada en el método de los valores propios y funciones propias. Para el secado de granos de café pergamino, Ciro-Velásquez et al. (2010) utilizan el modelo de Sokhansanj y Bruce y aplican el método de volúmenes finitos para el transporte de masa y calor, en régimen transitorio, en un grano esférico de radio equivalente. Los autores encuentran que las predicciones de humedad del modelo son muy sensibles al coeficiente de masa convectivo, que es del orden de 10-7 m/s. Khatchatourian (2012) aplica el modelo de Luikov al secado de granos de soya en capas delgadas y considera la variación radial del coeficiente de transporte, usando dos coeficientes de difusión distintos para dos regiones esféricas del grano. Silva et al. (2013) extienden las ecuaciones de Luikov mediante una generalización de las ecuaciones de transporte difusivo y consideran un proceso no Markoviano con difusión anómala, obtienendo soluciones analíticas de M y T para un caso unidimensional. Más recientemente, para estudiar la eficiencia energética del proceso de secado, Golmohammadi et al. (2015) desarrollan un modelo basado en la ley de difusión de Fick para calcular la distribución de humedad en granos esféricos de arroz con cáscara.
Un aspecto de la modelación del proceso de secado se relaciona con los valores de los parámetros físicos de las ecuaciones de transporte. En el caso de la transferencia difusiva de calor en arroz, Yang et al. (2002) usan una correlación cuadrática de la conductividad térmica k como función de M. Irudayaraj et al. (1992) emplean valores iguales respectivamente a 0.10 W/ (m K) para la soya, 0.15÷0.24 W/(m K) para el maíz y una función linear creciente con M en el caso de la cebada, siendo k siempre inferior a 1 W/(m K). Para el coeficiente de transferencia de calor convectivo h, Irudayaraj et al. usan valores iguales respectivamente a 60 W/(m2 K) para la soya, 56.7 W/(m2 K) para el maíz y en el caso de la cebada un valor de 110 W/(m2 K). Por otro lado, Yang et al. (2002) usan una correlación donde h se relaciona a la velocidad de la corriente de aire mediante una función de potencias.
Una propiedad que depende de k y del calor específico c es el coeficiente de difusión térmica o difusividad térmica a, el cual es pequeño en estos tipos de productos. Por ejemplo, usando densidades ρ para soya y maíz de 1180 kg/m3 y 1275 kg/m3, respectivamente, se obtendrán valores de a del orden de 10-8 m2/s. En cambio, los fenómenos asociados a la transferencia de masa son controlados por el coeficiente de difusión de masa del material a m que depende fuertemente de T. Existen diversas ecuaciones que representan esta dependencia, entre otras la de Arrhenius y la de Stokes- Einstein. En el caso del secado de trigo, Sokhansanj y Cenkowsky (1987) brindan valores de a m mediante una función de T y M donde a m aumenta con T y presenta un valor máximo con un valor determinado de M, variando entre 5x10-12 m2/s y 50x10-12 m2/s. En el caso del secado de arroz, Yang et al. (2002) usan una expresión tipo Arrhenius, con coeficientes diferentes para las regiones del casco, salvado y endospermo; lo mismo que Golmohammadi et al. (2015) para el secado de arroz con cáscara. Para la transferencia de masa convectiva, Yang et al. emplean un coeficiente de transferencia de masa convectivo h m como función tipo potencia de la velocidad de la corriente de aire, y Ciro-Velásquez et al. (2010) consideran un valor constante. Finalmente, otro parámetro de los modelos del proceso de secado es el coeficiente de gradiente térmico δ, que se define como la relación entre el gradiente ∇M y el gradiente ∇T en estado estacionario y en ausencia de transferencia de masa. Como ejemplo para el secado de granos de cereal, Irudayaraj et al. (1992) usan valores de δ en el rango 0.01 ÷0.03 [1/K].
Modelación físico-matemática del proceso de secado de granos
Las ecuaciones del modelo físico matemático del presente trabajo se basan en la teoría del proceso de secado desarrollada por el ruso Luikov (1975) y en el trabajo de Sokhansanj y Bruce (1987). En el trabajo pionero de Luikov las hipótesis consideradas son:
el agua (en su fase líquida y vapor) y el aire llenan completamente los poros del cuerpo capilar poroso;
el flujo de masa en el cuerpo es extremadamente lento, así que la temperatura de los fluidos intersticiales y de la matriz porosa son localmente iguales, es decir, existe un equilibrio termodinámico;
en la transición de fase participan solamente el líquido y el vapor;
no hay reacciones químicas en el medio;
la masa de aire y la masa de vapor de agua son despreciables con respecto a la masa de agua líquida dentro de los poros;
las variaciones de volumen y porosidad del cuerpo provocadas por cambios en la humedad son despreciables;
el medio se considera isotrópico.
De manera sucesiva se considera un proceso difusivo puro y difusión de humedad, debido simultáneamente a los gradientes de humedad y temperatura, con flujo de calor q[W/m2] y flujo de masa de la fase i J i [kg/(m2 s)], donde i = 0 se refiere al cuerpo seco, i = 1 al vapor de agua e i = 2 al agua líquida. Luego las ecuaciones del transporte de energía y masa son:
donde ρ 0 es la densidad del cuerpo seco, T[°C ] la temperatura y M[kg/kg cuerpo seco] es el contenido de masa (humedad), definido como la concentración de agua relativa:
Aquí m i [kg] y M i [kg/kg cuerpo seco] son, respectivamente, la masa y el contenido de masa de la fase i. Con λ[J/kg] se expresa el calor latente de evaporación y con c [J/kg °C] el calor específico reducido:
(4)
donde c i es el calor especifico de la fase i. Finalmente, ε representa la cantidad de cambio de fase (0 ≤ ε ≤ 1), siendo que: ε = 0 implica que no ocurre cambio de fase en el medio poroso, la humedad se transporta como líquido y el cambio de fase se realiza en la superficie del medio poroso; ε = 1 significa que todo el líquido cambia de fase y la humedad se transporta como vapor en el medio. Las ecuaciones 1 y 2, con apropiadas condiciones iniciales y de borde, constituyen el modelo matemático de Luikov para el análisis de la transferencia simultánea no estacionaria de masa y calor en un medio poroso de volumen Ω y frontera ∂Ω. Si se usa el potencial de humedad U[°M], siendo M=c m U , se tiene:
en términos de T y de U, donde c m [ kg /kg cuerpo seco] es la capacidad de humedad específica y D[kg/(m s)] es la conductividad de la humedad en el medio. Los modelos anteriores se completan con las siguientes condiciones iniciales y de borde:
Aquí T ∞ y U ∞ representan la temperatura constante y el potencial constante del ambiente externo, respectivamente. Si las difusiones de calor y masa son desacopladas, las ecuaciones 1 y 2 se simplifican en la ley de Fourier y la segunda ley de Fick, es decir:
Las condiciones iniciales para T y M y las condiciones de borde para los flujos de masa y calor en la frontera ∂Ω de dirección normal n son ahora:
El modelo del secado propuesto en este trabajo incorpora además las ecuaciones de Sokhansanj y Bruce, representadas por las ecuaciones 10 y 11, con mecanismos de transporte acoplados mediante una condición de borde en la ecuación de Fourier. Con este propósito, se introduce el flujo de calor necesario para la evaporación del agua en la superficie de grano o conjunto de granos de volumen V y área exterior A. Luego, si c v es el calor específico a volumen constante, la condición de balance de energía térmica en la frontera es:
Modelo computacional
En el trabajo de modelación computacional se consideran las ecuaciones diferenciales de Luikov (ecuaciones 5-9) definidas como modelo 1 y las de Sokhansanj y Bruce (ecuaciones 10-13 y 15) que representan el modelo 2. Para la solución numérica se usa el método de volúmenes finitos, técnica computacional muy robusta y de alto nivel. Como las ecuaciones de ambos modelos describen el fenómeno de difusión en ausencia de transporte convectivo, la ecuación diferencial general de transporte en coordenadas cartesianas x, y, z es:
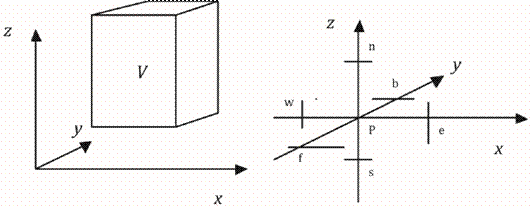
donde φ es la variable dependiente, α y Γ magnitudes que pueden variar en el tiempo y en el espacio y S un término fuente o sumidero. Dividiendo la región de cálculo Ω en elementos discretos de volúmenes V (figura 1), la ecuación 16 se integra en el tiempo y en el espacio, obteniéndose:
Definiendo P el punto central del volumen finito y e, w, f, b, n y s las intersecciones del volumen, respectivamente con los ejes x, y y z como se indica en Figura 1, la integración de la ecuación 17 en el volumen finito V y en el intervalo de tiempo ∆t brinda:
(18)
con ∆x, ∆y y ∆z las longitudes del volumen finito respectivamente en las direcciones x, y y z. A partir de la ecuación 18, usando funciones de interpolación lineal, propiedades físicas constantes en el grano y formulación totalmente implícita para la integración en el tiempo, se obtiene una ecuación algebraica lineal para cada volumen finito de la región de cálculo Ω. Los volúmenes finitos de frontera, es decir, los que forman ∂Ω, introducen las condiciones de borde, a través de un valor puntual φ P o la derivada (∂φ/∂n) e . Considerando un grano genérico con geometría esférica (Figura 2) de radio R, las derivadas de las ecuaciones diferenciales de tipo difusivo son nulas en las direcciones ξ y ϕ y las ecuaciones diferenciales presentan términos que son función solo de la coordenada r. Luego, existiendo simetría radial, el problema se estudia para 0 ≤ r ≤ R. Adicionalmente a las condiciones de borde en la frontera del grano, se introducen las condiciones en r = 0, iguales en ambos modelos, siendo que por simetría se tiene:
(19)
Dividiendo R en n intervalos de longitud ∆r se obtienen n volúmenes finitos de centro P i , como se indica en Figura 3. De manera similar, para integrar las ecuaciones en el dominio de tiempo t, se consideran K subintervalos de magnitud ∆t. Finalmente, los algoritmos del modelo computacional anterior se desarrollan en lenguaje de programación Fortran 95 (Lahey, 2002) y se obtienen las soluciones numéricas de las ecuaciones diferenciales del proceso de secado.
Resultados numéricos y análisis
A continuación, se presentan los resultados de las simulaciones numéricas efectuadas en el caso de secado industrial de granos de soya, para los cuales se disponía de datos de literatura (Cuadro 1, Irudayaraj et al., 1992). Los granos se consideran esféricos de radio R = 3.5 mm, la malla de cálculo espacial consta de 10 volúmenes finitos iguales de longitud ∆r = 0.35 mm y la integración en el tiempo se realiza usando un intervalo ∆t = 10 s. En la figura. 4 se muestran los resultados numéricos de humedad M para r = R/2, obtenidos con el modelo 2. En este caso, el modelo 1 brinda resultados similares, siendo posible identificar un periodo de secado con tasa constante para los tiempos iniciales y un periodo de secado con tasa cayente para los tiempos finales. Se observa que después de unos 900 minutos (15 horas), M es muy cercano al valor ambiental de equilibrio M ∞ = 0.11. En la misma Figura 4 se trazan los valores experimentales del contenido medio de humedad de Overhults et al. (1973) y numéricos de Irudayaraj et al. (1992), en las mismas condiciones simuladas. Se evidencia como estos datos se comparan satisfactoriamente con los valores calculados en este trabajo, con excepción de la región con tasa constante. En la Figura 5 se reportan solamente los valores de temperatura T para r = R/2 obtenidos con el modelo 1, conjuntamente con los valores de temperatura media obtenidos por Irudayaraj et al. mediante los mismos modelos. Se observa que T aumenta rápidamente del valor inicial de 20 °C hasta el valor de equilibrio T ∞ de 35 °C, siguiendo un patrón similar al modelo 1 de Irudayaraj et al. En el caso de las simulaciones del modelo 2, que no se trazan, aunque la temperatura del grano converge velozmente a T ∞ , los resultados brindan valores de temperaturas muy bajos en los tiempos iniciales del proceso de secado. Esto se debe al acoplamiento de la difusión de masa y energía dado por la ecuación 15, donde en caso de fuerte evaporación se requiere que el calor necesario sea suplido por el mismo grano, disminuyendo el valor de T. En la Figura 6 se proporciona el valor de M después de 960 minutos (16 horas) en el interior del grano para el caso del modelo 1, siendo que el modelo 2 arroja resultados muy similares. El valor de M en el centro del grano (r=0) es el mayor, aproximadamente igual a 0.140 kg/kg cuerpo seco, mientras que para radios mayores M disminuye hasta alcanzar un valor en la periferia (r=R) próximo al valor ambiental M ∞ de0.11 kg/kg cuerpo seco. Finalmente, en la Figura 7 se presentan los valores de temperatura en el interior del grano para el caso del modelo 2, para un tiempo de 960 minutos, donde se evidencia que todo el grano está prácticamente en equilibrio con el aire a 35 °C.
Cuadro 1 Datos de Irudayaraj et al. (1992) usados para la simulación del secado de soya.
| ρ[kg/m3] | 1180 |
| c[J/kg K] | 1884 |
| k[W/m K] | 0.10 |
| δ[1/K] | 0.015 |
| ε | 0.7 |
| λ[J/kg] | 2.257x106 |
| D[kg/m s] | 2.478x10-10 |
| a m [m2/s] | 7.0x10-11 |
| c m [kg/kg cuerpo seco] | 0.003 |
| h[W/m2 K] | 60 |
| h m [m/s] | 0.282x10-6 |
| T ∞[°C] | 35 |
| U ∞[°M] | 36.7 |
| M ∞[kg/kg cuerpo seco] | 0.11 |
| T 0[°C] | 20 |
| U 0[°M] | 110 |
| M 0 [kg/kg cuerpo seco] | 0.33 |
| R[m] | 3.5x10-3 |
| n | 10 |
| ∆r [m] | 3.5x10-4 |
| ∆t[s] | 10 |
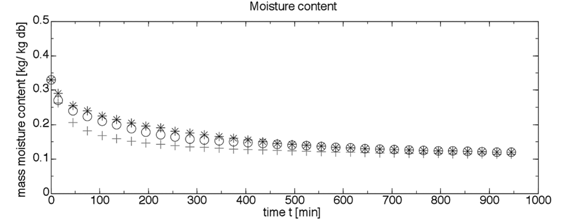
Figura 4 Resultados numéricos de M para r = R/2 usando el modelo 2, comparados con datos experimentales y otros resultados numéricos del contenido medio de humedad (+ modelo 2, o datos experimentales de Overhults et al. (1973), * datos numéricos de Irudayaraj et al. (1992).
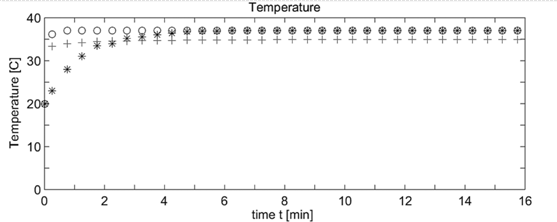
Figura 5 Resultados numéricos de T para r = R/2 usando el modelo 1, comparados con otros resultados numéricos de la temperatura media (+ modelo 1, o modelo 1 de Irudayaraj et al. (1992), * modelo 2 de Irudayaraj et al. (1992).
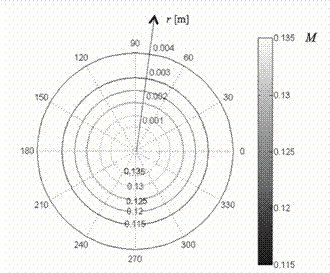
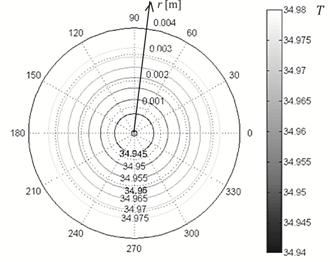
Figura 6 Resultados numéricos de M en el grano después de 16 horas usando el modelo 1; los valores se brindan en [kg/kg cuerpo seco] en función del radio r[m] y del ángulo azimutal [grados].
Conclusiones
Se desarrolló un trabajo de modelación del proceso de secado industrial y una solución computacional en el caso del secado de granos de soya, mediante el método de volúmenes finitos. El modelo se basa en los trabajos del investigador ruso Luikov (1975) en el área de los fenómenos de transporte en medios porosos y de Sokhansanj y Bruce (1987), este último con acoplamiento del transporte difusivo de masa y calor a través de una condición de borde en la superficie del grano. Las soluciones numéricas del modelo computacional se compararon con datos experimentales y numéricos disponibles en la literatura científica, demostrándose que los resultados de los valores de masa y temperatura obtenidos con el método de volúmenes finitos son satisfactorios, para ambos modelos desarrollados. En el caso de las ecuaciones de Sokhansanj y Bruce, los resultados numéricos de temperatura, en los tiempos iniciales del proceso de secado, se ven influenciados por la modelación de la evaporación de la humedad en el borde del grano.