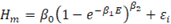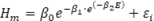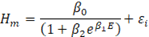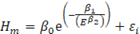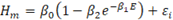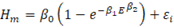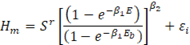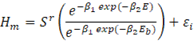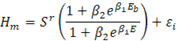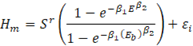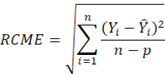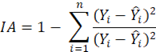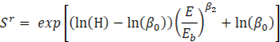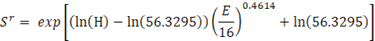Introducción
Uno de los aspectos más importantes en el establecimiento y manejo de las plantaciones forestales es el desarrollo de sistemas de clasificación de terrenos de acuerdo con su capacidad productiva (Mora & Meza, 2003), en función de las especies utilizadas. Desde el punto de vista de la producción maderable, se dice que los terrenos difieren en su calidad de sitio; definido este como el potencial para la producción de madera que ofrece una localidad, para una determinada especie. Se supone que, entre mayor sea la calidad de los terrenos, mayor será la producción de madera que se puede esperar (Clutter et al., 1983).
Existen diversos métodos para expresar la calidad de sitio, ya sea tomando en cuenta las propiedades de la masa forestal, o bien, las características del sitio (p.ej.; clima, suelos, fisiografía) en el que crecen los árboles (Skovsgaard & Vanclay, 2008). Sin embargo, la forma más aceptada de evaluar la calidad de sitio es a través de curvas de índice de sitio, las cuales permiten clasificar el crecimiento de la altura dominante, en los lugares donde se encuentra creciendo la especie, a una edad de referencia. El índice de sitio (IS) se define como la altura promedio de los 100 árboles más altos por hectárea a una edad base definida y, en el caso de los rodales monoespecíficos y coetáneos se asume que, 1) la altura dominante de un rodal es poco afectada por la densidad de la masa; 2) el crecimiento en altura dominante del rodal debe seguir un patrón determinado; y 3) la altura dominante presenta una buena correlación con la producción en volumen (Clutter et al., 1983).
En los últimos años, con el advenimiento de la teca (Tectona grandis L. f.) como una de las especies tropicales de mayor importancia económica a nivel mundial y con el establecimiento de plantaciones en Asia, América, África y Oceanía (Kollert & Kleine, 2017), el interés por el desarrollo de curvas de índice de sitio para esta especie se ha traducido en un considerable número de investigaciones y publicaciones en varios países y bajo diferentes enfoques. Cabe destacar, para América los trabajos de Keogh (1982) para la región del Caribe, Centro América, Venezuela y Colombia; Friday (1987) en Puerto Rico; Mora & Meza (2003 a) para el Pacífico de Costa Rica; Pereira da Cruz et al., (2008) en Matto-Grosso, Brasil; Jerez-Rico et al., (2011) para los Llanos Occidentales de Venezuela; Torres et al., (2012) para la Región Caribe de Colombia, y, en México, Tamarit-Urías et al., (2014) y Minoche et al., (2017) para plantaciones de teca en los estados de Campeche y Tabasco, respectivamente. Adicionalmente, podemos mencionar a Miller (1969) en Trinidad y Henao (1982) en el departamento de Córdoba, Colombia; citados por Mora y Meza (2003 b). Dichos trabajos han abarcado no solo una gran variedad de modelos matemáticos, sino también diferentes técnicas de ajuste, incluyendo los modelos clásicos de regresión lineal y no lineal con efectos fijos y efectos mixtos, también se han utilizado ambos enfoques de la diferencia algebraica (clásico ADA y generalizado GADA) y algunos modelos basados en ecuaciones diferenciales.
Los modelos y enfoques empleados dependen en gran parte de las características de los datos recopilados. Así, el uso de cronosecuencias, es decir, mediciones puntuales para una misma especie, obtenidas en diferentes sitios y para diferentes edades, trabajando con parcelas temporales, determina que solo se pueden obtener curvas mediante el método de la curva guía (Clutter et al., 1983); mientras que los otros enfoques requieren datos provenientes de al menos dos pares de mediciones altura-edad, separadas en el tiempo, medidas sobre un mismo sujeto o parcela; lo cual solo se puede obtener a través de mediciones sucesivas de parcelas permanentes, o bien, de análisis fustal (Prodan et al., 1997).
En general, los parámetros estadísticos son estimados mediante modelos de regresión lineal o no lineal, pero dadas las características de los datos de crecimiento, la estructura de la matriz de varianzas y covarianzas de los residuos contraviene los supuestos de la regresión clásica, esto es ɛ~I (0, σ2), debido a las desviaciones de la normalidad y la heteroscedasticidad. En el caso de los datos de mediciones repetidas, como ocurre con las parcelas permanentes, es imposible aleatorizar el factor temporal o espacial, lo que provoca que se incumpla el supuesto de independencia de los errores, y por lo tanto, las estimaciones que se realicen de los parámetros por mínimos cuadrados ordinarios, y sus errores estándar, pueden resultar seriamente distorsionadas (Schabenberger & Pierce, 2002). En varios casos se dispone de juegos de datos de diferente naturaleza, como, por ejemplo, información de parcelas permanentes y de análisis fustal, o bien, información de parcelas temporales y de parcelas permanentes; por esto, García (2005) analizó algunos métodos para combinar este tipo de datos.
1.1 Técnicas empleadas para analizar la información en estudios de calidad de sitio y aspectos a tomar en cuenta al momento de construir las curvas
Las mediciones repetidas y los datos tomados a lo largo del tiempo son comunes en el sector forestal (Linnell Nemec, 1996), pues se requiere estudiar el crecimiento de los árboles en períodos de tiempo, ya sean estos largos o cortos. Esto involucra procesos de obtención de datos en series de tiempo, lo cual hace que el problema se torne aún más complejo, ya que los datos suelen estar correlacionados serialmente, es decir, que las mediciones actuales están correlacionadas con las anteriores. Por esto, se hace necesario aplicar métodos especiales de análisis estadístico, debido a las características particulares de este tipo de información (Linnell Nemec, 1996).
La estimación de los parámetros utilizados en la construcción de las curvas de índice de sitio, tradicionalmente se ha realizado con modelos de regresión lineal y no líneal ordinarios (de efectos fijos) que asumen que los residuos (o errores) se distribuyen normalmente, con varianzas iguales, y con total independencia. Tales supuestos pueden ser violados cuando se analizan datos longitudinales (en series de tiempo), ya que el término de error no resulta ser independiente de la variable tiempo y, por lo tanto, los errores resultan autocorrelacionados, causando que las estimaciones de los parámetros por medio de cuadrados mínimos ordinarios se vean afectadas, y las estimaciones del error estándar pueden resultar seriamente distorsionadas (Souza, 1998, citado por Floriano et al., 2006). Por lo tanto, no es recomendable utilizar el análisis de regresión ordinario para procesar los datos de series de tiempo porque, por lo general, se violan los supuestos en los cuales está basado el modelo clásico de regresión lineal (SAS Institute, 2010). Por un lado, si los datos provienen de mediciones repetidas en el tiempo, o en el espacio, sobre las mismas unidades de muestreo, como es el caso de las parcelas permanentes y del análisis troncal, la estructura de la matriz de varianzas y covarianzas (() de los residuos no corresponde con los supuestos de los modelos de regresión clásicos, ya que no es posible aleatorizar el factor temporal, o espacial, violando de esta manera el supuesto de independencia de los errores (Schabenberger & Pierce, 2002).
Por otro lado, los modelos tradicionales de efectos fijos que se utilizan para trabajar con la relación altura-edad, se caracterizan por aumentar la varianza de los residuos conforme aumenta la edad (heteroscedasticidad). Los modelos de efectos mixtos, por su parte, permiten representar apropiadamente la estructura de la matriz de varianzas y covarianzas asociada con mediciones repetidas en el tiempo (Littell et al., 2006), ya que estos incorporan efectos aleatorios, diferentes de los asociados con los términos de error. Tales modelos mixtos han sido poco utilizados en nuestro medio, a pesar de que permiten modelar la estructura de varianzas y covarianzas cuando se trabaja con series de tiempo, y realizar inferencias más precisas; razón por la cual vale la pena experimentar con ellos. El objetivo de este estudio fue evaluar el desempeño relativo de modelos no lineales mixtos reparametrizados en función de la altura dominante a la edad base (S), utilizando datos combinados de parcelas permanentes y de análisis fustal, con el fin de generar curvas de índice de sitio para las plantaciones de teca en la vertiente del Pacífico de Costa Rica.
Metodología
2.1 Área de estudio
En el estudio de análisis fustal el área de trabajo incluyó las provincias de Guanacaste y Puntarenas y abarcó terrenos comprendidos entre los 0 y los 600 m.s.n.m. En el caso de la provincia de Guanacaste, se presentó una mayor concentración de los sitios de muestreo en la parte central de la Península de Nicoya, entre los cantones de Santa Cruz al norte y Nandayure al sur (Figura 1). Esto se da debido a una mayor concentración de plantaciones en la parte central de la península, por lo tanto, el muestreo se dio en forma proporcional a la frecuencia de aparición de las áreas plantadas (Mora & Meza, 2003). Unos pocos puntos de muestreo se presentan cerca de la costa del Pacífico y en la margen opuesta del río Tempisque, en los cantones de Abangares y Bagaces. En el caso de la provincia de Puntarenas, se presentan tres áreas de concentración, correspondiendo la primera al área de Paquera y Cóbano, al sur de la Península de Nicoya; la segunda, a la zona de Parrita y Quepos, en el Pacífico Central; y la tercera, en el cantón de Buenos Aires, en la Zona Sur de nuestro país. Algunos pocos sitios se presentan al sur de este último cantón (en Palmar Norte y Río Claro).
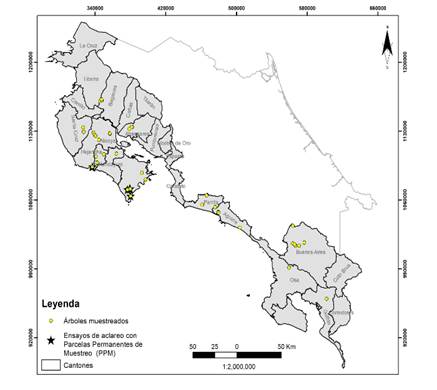
Figura 1 Ubicación de los sitios de medición para plantaciones de Tectona grandis, Vertiente del Pacífico, Costa Rica.
En Carrillo, Cóbano y Cabuya los suelos son alfisoles, con suelo principal Typic Haplustalf y suelos asociados Typic Ustropept y Vertic Ustropept, de relieve plano a casi plano, profundos, texturas moderadamente finas a finas, colores pardo muy oscuro, rojo oscuro, rojo, rojo amarillento a pardo fuerte, de drenaje bueno a moderado, fertilidad media (Acon y Asociados, 1991). El pH promedio varía entre 5.2 y 6.2, el Al es de 0.20 meq/100 ml suelo y el K es bajo. En general, las condiciones de suelo no son limitantes para el buen desarrollo de esta especie. El clima se caracteriza por lluvias estacionales de mayo a octubre, con un periodo seco de diciembre a abril; precipitación promedio de 2 896.8 mm, temperatura media anual de 26°C, con una máxima anual de 33.1°C. (Instituto Meteorológico Nacional, 1988).
2.2 Descripción de las plantaciones
Los datos de análisis fustal provienen de árboles de parcelas temporales circulares, de 400 m2 (r = 11.28 m), con un número entre 11 y 37 árboles/parcela (275-925 árboles/ha); las densidades menores corresponden a las masas más viejas. Las mediciones de árboles dominantes en pie provienen de 38 parcelas permanentes rectangulares establecidas en ensayos de aclareo y rendimiento. Las edades al momento de establecer las parcelas variaron entre 3 y 7 años (Cuadro 1). El período de medición va desde los 10 hasta los 32 años con hasta 22 años de remediciones anuales consecutivas. El período total de los ensayos de aclareo y rendimiento se extiende desde 1984 hasta el año 2018, para un total de 34 años acumulados de mediciones sucesivas en parcelas permanentes de teca, en la Vertiente del Pacífico de Costa Rica.
Cuadro 1 Edad de las plantaciones y cantidad de parcelas permanentes por ensayo de Tectona grandis. Vertiente del Pacífico, Costa Rica.
| Nombre del ensayo | Año de instalación | Edad de instalación del ensayo (años) | Edad de la última medición (años) | Período de evaluación (años) | Cantidad de parcelas |
|---|---|---|---|---|---|
| Festejos | 1984 | 5 | 26 | 21 | 4 |
| Río Negro | 1984 | 4 | 25 | 21 | 5 |
| Cóbano centro | 1984 | 3 | 17 | 14 | 2 |
| Cabuya | 1989 | 7 | 29 | 22 | 9 |
| Pto. Carrillo | 1995 | 4 | 14 | 10 | 10 |
| Norman Quirós | 1995 | 4 | 14 | 10 | 8 |
2.3 Selección y procesamiento de datos del análisis fustal para los árboles dominantes
Se seleccionaron uno o dos árboles dominantes a derribar en cada parcela circular, según el procedimiento descrito en Mora y Meza (2003). Se empleó la metodología de “análisis fustal para reconstruir el crecimiento de la altura” de los árboles apeados. Se contaron los anillos presentes en cada sección, para calcular, por medio de la diferencia en el número de anillos entre dos cortes consecutivos, el total de años transcurridos en cada uno de los “períodos de crecimiento” (estos últimos definidos por la distancia entre dos cortes sucesivos). A partir del conteo de anillos, se reconstruyó el crecimiento de la altura total para cada año de vida de los árboles analizados. Para esto, fue necesario calcular cada una de las “alturas intermedias” (o, ápices ocultos del árbol), correspondientes a las “edades intermedias” (diferentes de la edad de corta). Para estimar el valor de dichas alturas se utilizó una fórmula desarrollada con este fin, a partir de un algoritmo propuesto por Carmean (1972).
Selección de modelos matemáticos y técnicas de ajuste
Se seleccionó un conjunto de modelos no lineales para ajustar los pares de observaciones de altura dominante en metros y edad en años (Cuadro 2). Se seleccionaron los modelos de Richards, Gompertz, Logístico, Korf, Mitscherlich y Weibull. Dichos modelos fueron desarrollados con base en consideraciones teóricas sobre los fenómenos del crecimiento biológico, a partir de la ecuación de von Bertalanffy (1957), por lo cual es posible dar una interpretación biológica a sus parámetros (Zeide, 1993). En todos los modelos, el parámetro β 0 representa la altura máxima que en teoría puede alcanzar un árbol o una masa forestal; β 1 y β 2 se relacionan con el punto de inflexión de la curva de crecimiento y la escala. En el caso de las curvas de índice de sitio, estos parámetros también pueden considerarse como parámetros “globales”, comunes a todos los “sujetos” (es decir, sitios, rodales, parcelas o árboles), o como parámetros “específicos” particulares para cada sujeto (Carrero et al., 2008).
Cuadro 2 Modelos no lineales seleccionados para ajustar los pares de observaciones de altura dominante (metros) y la edad (años) en las plantaciones de Tectona grandis. Vertiente del Pacifico, Costa Rica.
Los modelos se reparametrizaron en función de S, β 0 y β 1, asociando un efecto aleatorio con la altura dominante S a la edad base t 0 , siguiendo el procedimiento propuesto por Carrero et al. (2008). En este trabajo, se empleó S para t o = 16 años, lo que permitió obtener una buena estimación inicial para S. La generalización de este enfoque fue propuesta por Fang y Bailey (2001) y aplicada a plantaciones de teca en Colombia por Torres et al. (2012). Se ajustaron dos grupos de modelos mixtos no lineales a) reparametrizados en función de β 0 y S r = S+u, y b) reparametrizados en función β 1 y S r = S+u (Cuadro 3). El primer grupo de modelos genera una familia de curvas anamórficas, mientras que el segundo grupo genera una familia de curvas polimórficas en la estructura de medias. Los modelos reparametrizados dan origen a familias de curvas si se asignan valores fijos para S a t o; S = (15, 18, 21, 24, 27 y 30). Los modelos se ajustaron utilizando el método de máxima verosimilitud con el procedimiento NLMIXED de SAS 9.2.
Cuadro 3 Modelos no lineales reparametrizados para ajustar los pares de observaciones de altura dominante (metros) y la edad (años) de plantaciones de Tectona grandis. Vertiente del Pacifico, Costa Rica. H m = altura dominante (m); e = base de los logaritmos naturales; E = edad (años); β 0 , β 1 , β 2 (efectos fijos) y µ (efecto aleatorio) a ser estimados.
Buenos valores iniciales fueron obtenidos de acuerdo con los procedimientos sugeridos por Schabenberger y Pierce (2002). Para identificar el mejor modelo se utilizó los criterios de información de Akaike (AIC) y Bayesiano (BIC) (Carrero et al., 2008; Schabenberger & Pierce, 2002). A menor valor de estos criterios, mejor es el modelo. Estos criterios son indicadores relativos de ajuste, es decir, nos dicen cuál modelo es mejor con respecto a otro, pero no nos dicen qué tan buena es la calidad del ajuste. Por otra parte, no permiten comparar modelos que incluyan variables dependientes en una escala diferente (Jerez-Rico et al., 2011). De igual manera, se consideró la significancia estadística de los estimados de los parámetros.
Para tener información sobre la calidad del ajuste de los modelos en términos de sesgo y precisión se utilizaron los siguientes métodos de bondad de ajuste y análisis de residuos.
Para medir el sesgo, se calculó la media de las desviaciones o residuos (MD):
Donde:
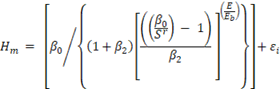 y
y 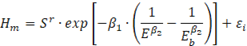 son valores observados y predichos respectivamente para cada parcela y n es el número observaciones y;
son valores observados y predichos respectivamente para cada parcela y n es el número observaciones y;la media de las desviaciones absolutas (MDA) que es similar a MD excepto que se toma
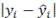 . Mientras más cerca se encuentren los valores de MD y MDA de cero, menor será el sesgo del modelo.
. Mientras más cerca se encuentren los valores de MD y MDA de cero, menor será el sesgo del modelo.Como indicadores de la precisión y la calidad del ajuste se emplearon:
la raíz del Cuadrado Medio del Error (RCME):
Donde:
n - p son los grados de libertad (n = sujetos y p = número de parámetros del modelo). El RCME tiene las mismas unidades de la variable dependiente, es decir metros, y es mejor mientras menor sea su valor.
el Índice de Ajuste (Mayer & Butler, 1993)
El IA es análogo al coeficiente de determinación R 2, pero varía entre -∞ y 1, con 1 indicando un ajuste perfecto (Kvälseth, 1985).
Finalmente, se presentan los gráficos de los residuos y alturas predichas respecto a la edad. Estos gráficos permiten ver los efectos de dispersión de los residuos, la heteroscedasticidad, la autocorrelación y el sesgo de los modelos ajustados.
Para obtener las curvas de índices de sitio (IS), se debe escoger una edad base y definir las categorías que se desean trabajar para la variable de clasificación, el IS, luego se deberá hacer el despeje usual para ( 0 (curvas anamórficas, pendiente común), o, ( 1 (curvas polimórficas, asíntota común).
Dado que la calidad del ajuste no refleja necesariamente la calidad de las predicciones futuras, los modelos deberían ser validados usando un conjunto de datos independientes, o bien, ajustando los modelos a una serie más corta de observaciones (datos de calibración) y dejando la última porción de la serie observada como datos de validación. En general, se asume que la incorporación de efectos mixtos reduce los inconvenientes generados por la violación de los supuestos del modelo de regresión, principalmente la autocorrelación, debida a las mediciones repetitivas, y la heteroscedasticidad, pero este no es necesariamente el caso (Fang & Bailey, 2001).
Resultados
3.1 Comparación de los datos de crecimiento producidos por análisis fustal y los datos de las mediciones sucesivas realizadas en parcelas permanentes
En las Figuras 2a y 2b se presentan las gráficas para los datos de análisis fustal y parcelas permanentes. Nótese que, a pesar de que se incluyeron datos de árboles reconstruidos mediante análisis fustal, que provienen de calidades de sitio diferentes a los de las parcelas, la tendencia en el patrón de crecimiento de la altura es muy similar para ambos conjuntos de datos.
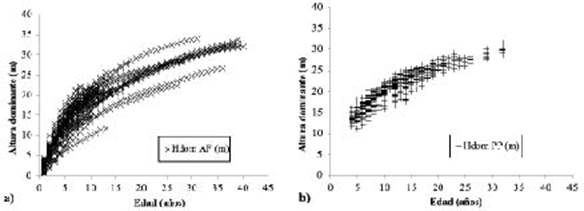
Figura 2 Datos a) Mediciones de análisis fustal (AF), b) Mediciones de parcelas permanentes (PP) en plantaciones de Tectona grandis. Vertiente del Pacífico, Costa Rica.
En la Figura 3 se puede observar la comparación gráfica de las curvas de crecimiento, al sobreponer el crecimiento en altura de los 55 árboles dominantes (producidas mediante análisis fustal) y el crecimiento de las 38 parcelas permanentes de muestreo (medidas durante un período de 34 años). Es necesario destacar que, en general, las curvas de crecimiento en altura de los árboles dominantes, construidas a través de la técnica de análisis fustal, presentan un patrón de crecimiento muy similar al que evidencian los datos provenientes de los promedios de las parcelas permanentes, lo que refuerza la posibilidad de usar la técnica de análisis fustal en la construcción de las curvas de índice de sitio. Se aprecia que la información producida por los análisis fustales complementa muy bien los datos provenientes de las mediciones sucesivas de parcelas permanentes.
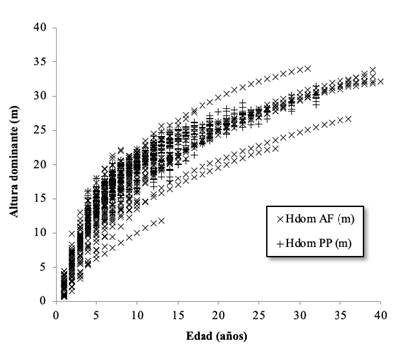
Figura 3 Datos combinados de análisis fustal (AF) y mediciones sucesivas en parcelas permanentes (PP), superpuestos para mostrar el ajuste óptimo de los mismos, en plantaciones de Tectona grandis. Vertiente del Pacífico, Costa Rica.
3.2 Comparación del ajuste relativo de los modelos anamórficos y polimórficos para Índice de Sitio
Desde el punto de vista de los criterios de información (AIC y BIC) el mejor modelo fue el de Korf, tanto para las curvas anamórficas como para las polimórficas con un AIC de 2 681 y 2 573, respectivamente (Cuadro 4). El segundo mejor modelo fue el de Richards, en ambos tipos de curvas, con un AIC de 2 851 para las anamórficas y 2 744 para las polimórficas; y el tercer mejor modelo es el de Weibull con 2 728 en curvas anamórficas y de 2 779 en las curvas polimórficas. Los de peor comportamiento fueron el modelo de Gompertz y el Logístico.
En términos generales, el AIC por modelo para las curvas polimórficas es mejor que el AIC por modelo en las curvas anamórficas. Al menos esta tendencia se da para los modelos de Richards, Logístico, Korf y Mitscherlich; caso contrario se da para Gompertz y Weibull que presentaron mejores valores del AIC en las curvas anamórficas.
Cuadro 4 Valores de los criterios de información de Akaike (AIC) y criterio de información Bayesiano (BIC) para los modelos anamórficos y polimórficos seleccionados. Menor valor indica el mejor modelo.
| Tipo de curvas | Modelo | AIC | BIC | |
|---|---|---|---|---|
| Anamórficas | Richards | 2851 | 2871 | |
| Gompertz | 3360 | 3380 | ||
| Logístico | 3626 | 3646 | ||
| Korf | 2681 | 2701 | mejor anamórfico | |
| Mitscherlich | 2921 | 2941 | ||
| Weibull | 2728 | 2748 | ||
| Polimórficas | Richards | 2744 | 2764 | |
| Gompertz | 3603 | 3623 | ||
| Logístico | 3521 | 3541 | ||
| Korf | 2573 | 2593 | mejor polimórfico | |
| Mitscherlich | 2784 | 2804 | ||
| Weibull | 2779 | 2799 |
Los parámetros estimados, sus errores estándar y Límites de Confianza se presentan en el Cuadro 5 para los modelos anamórficos y en el Cuadro 6 para los polimórficos. Para los modelos anamórficos, los modelos de Gompertz y Weibull, muestran valores más elevados y con mayor error estándar para S. El modelo de Korf, presenta un valor asíntótico considerablemente mayor que para los demás modelos.
Cuadro 5 Parámetros estimados para los modelos anamórficos (Todos significativos p < 0.0001). Vertiente del Pacífico, Costa Rica. EE = error estándar, LIC y LSC, límites de confianza superior e inferior (α = 0.05); β 0 , β 1 , β 2 , su, se = parámetros estimados, con su, se = desviación estándar de los efectos aleatorios.
| Modelo | Parámetro | Estimado | EE | LIC | LSC |
|---|---|---|---|---|---|
| Richards | β 1 | 0.0694 | 0.0030 | 0.0637 | 0.0751 |
| S | 22.9191 | 0.2850 | 22.3533 | 23.4849 | |
| β 2 | 0.7748 | 0.0150 | 0.7457 | 0.8040 | |
| su | 2.6938 | 0.2060 | 2.2849 | 3.1027 | |
| se | 1.3355 | 0.0270 | 1.2820 | 1.3890 | |
| Gompertz | β 1 | -1.9021 | 0.0290 | -1.9590 | -1.8452 |
| S | 25.7669 | 0.7750 | 24.2292 | 27.3046 | |
| β 2 | 0.1577 | 0.0040 | 0.1503 | 0.1651 | |
| su | 4.1313 | 0.3400 | 3.4561 | 4.8064 | |
| se | 1.7529 | 0.0350 | 1.6826 | 1.8232 | |
| Logístico | β 1 | -0.2160 | 0.0060 | -0.2274 | -0.2046 |
| S | 23.6318 | 0.3000 | 23.0367 | 24.2270 | |
| β 2 | 3.8698 | 0.1060 | 3.6599 | 4.0797 | |
| su | 2.6657 | 0.2200 | 2.2292 | 3.1021 | |
| se | 2.0060 | 0.0410 | 1.9256 | 2.0865 | |
| Korf | β 1 | -3.0571 | 0.0240 | -3.1044 | -3.0098 |
| S | 22.6833 | 0.2780 | 22.1317 | 23.2348 | |
| β 2 | 0.4502 | 0.0140 | 0.4227 | 0.4776 | |
| su | 2.6603 | 0.2010 | 2.2621 | 3.0584 | |
| se | 1.1765 | 0.0240 | 1.1294 | 1.2237 | |
| Mitscherlich | β 1 | 0.0969 | 0.0020 | 0.0928 | 0.1011 |
| S | 23.2950 | 0.2910 | 22.7169 | 23.8732 | |
| β 2 | 0.9667 | 0.0060 | 0.9555 | 0.9780 | |
| su | 2.7587 | 0.2130 | 2.3364 | 3.1811 | |
| se | 1.4083 | 0.0280 | 1.3518 | 1.4647 | |
| Weibull | β 1 | -0.1251 | 0.0020 | -0.1293 | -0.1209 |
| S | 24.3499 | 0.6700 | 23.0202 | 25.6796 | |
| β 2 | 0.8215 | 0.0120 | 0.7983 | 0.8447 | |
| su | -4.0307 | 0.3140 | -4.6539 | -3.4075 | |
| se | -1.3113 | 0.0260 | -1.3638 | -1.2587 |
Cuadro 6 Parámetros estimados para los modelos polimórficos (Todos significativos p < 0.0001). Vertiente del Pacífico, Costa Rica. EE = error estándar, LIC y LSC, límites de confianza superior e inferior (α = 0.05); β 0, β 1, β 2, su, se = parámetros estimados, con su, se = desviación estándar de los efectos aleatorios.
| Modelo | Parámetro | Estimado | EE | LIC | LSC |
|---|---|---|---|---|---|
| Richards | β 0 | 32.42306 | 0.282 | 31.86338 | 32.98274 |
| S | 22.9071 | 0.246 | 22.41976 | 23.3944 | |
| β 2 | 0.807006 | 0.014 | 0.779451 | 0.83456 | |
| Log(su) | 2.341135 | 0.175 | 1.994088 | 2.688181 | |
| Log(se) | 1.231632 | 0.025 | 1.182302 | 1.280963 | |
| Gompertz | β 0 | 29.44567 | 0.205 | 29.03909 | 29.85226 |
| S | 22.9659 | 0.165 | 22.6376 | 23.29412 | |
| β 2 | 0.139544 | 0.003 | 0.133247 | 0.145841 | |
| Log(su) | 1.415407 | 0.114 | 1.189841 | 1.640973 | |
| Log(se) | 1.782048 | 0.036 | 1.710601 | 1.853494 | |
| Logístico | β 0 | 28.47712 | 0.182 | 28.11636 | 28.83789 |
| S | 23.6834 | 0.276 | 23.13634 | 24.23053 | |
| β 2 | 4.129235 | 0.097 | 3.935938 | 4.322532 | |
| su | 2.552242 | 0.202 | 2.150988 | 2.953497 | |
| se | 1.902714 | 0.038 | 1.826353 | 1.979074 | |
| Korf | β 0 | 56.3295 | 1.5945 | 53.1643 | 59.4946 |
| S | 23.9305 | 0.0121 | 0.4373 | 0.4854 | |
| β 2 | 0.4614 | 0.2239 | 23.4860 | 24.3750 | |
| su | 2.1413 | 0.1592 | 1.8253 | 2.4573 | |
| se | 1.0888 | 0.0220 | 1.0452 | 1.1324 | |
| Mitscherlich | β 0 | 30.90179 | 0.186 | 30.53305 | 31.27053 |
| S | 23.2115 | 0.242 | 22.73174 | 23.69126 | |
| β 2 | 0.973236 | 0.005 | 0.963301 | 0.98317 | |
| su | 2.315257 | 0.173 | 1.971054 | 2.65946 | |
| se | 1.289016 | 0.026 | 1.237383 | 1.34065 | |
| Weibull | β 0 | 33.38766 | 0.364 | 32.66541 | 34.1099 |
| S | 22.8364 | 0.243 | 22.35341 | 23.31932 | |
| β 2 | 0.847425 | 0.011 | 0.826227 | 0.868623 | |
| Log(su) | 2.320629 | 0.173 | 1.976982 | 2.664276 | |
| Log(se) | 1.211839 | 0.024 | 1.163302 | 1.260376 |
En términos del Índice de Ajuste (IA), los modelos de Korf y Mitscherlich se comportaron bastante bien, seguidos por los modelos de Richards y Weibull, superando al modelo de Gompertz y a la función Logística por un buen margen (Cuadro 7).
Cuadro 7 . Estadisticos de las medidas de bondad de ajuste para los modelos parametrizados por tipo de curva. Vertiente del Pacifico, Costa Rica.
| Forma | Modelo | MD | MDA | RCME | IA |
|---|---|---|---|---|---|
| Anamórficos | Richards | -0.051 | 0.794 | 0.362 | 0.996 |
| Gompertz | -0.054 | 1.434 | 0.362 | 0.988 | |
| Logístico | -0.083 | 2.116 | 0.363 | 0.974 | |
| Korf | -0.022 | 0.155 | 0.362 | 1.000 | |
| Mitscherlich | -0.008 | 0.509 | 0.361 | 0.999 | |
| Weibull | -0.057 | 0.778 | 0.363 | 0.996 | |
| Polimórficos | Richards | -0.043 | 0.554 | 0.362 | 0.998 |
| Gompertz | -0.045 | 1.258 | 0.362 | 0.991 | |
| Logístico | -0.111 | 2.295 | 0.364 | 0.969 | |
| Korf | -0.009 | 0.272 | 0.361 | 1.000 | |
| Mitscherlich | -0.005 | 0.329 | 0.361 | 0.999 | |
| Weibull | -0.048 | 0.529 | 0.362 | 0.998 |
Entre todos los modelos no lineales utilizados en el presente estudio sobresale el modelo de Korf, el cual demostró ser el que mejor ajustó la información. Sin embargo, todos los modelos presentaron buenos estadísticos para la bondad de ajuste; no obstante, en términos puntuales, el modelo de Mitscherlich fue el segundo mejor, sobre todo en términos de sesgo (MDA), respecto al de Korf, tanto en su versión anamórfica como polimórfica.
3.3 Construcción de las curvas de Índice de Sitio
La dispersión de los residuos, en ambos gráficos, parece aceptable ya que no se aprecian ni patrones ni tendencias claras que pudieran indicar que existe algún problema serio con los residuales (Figuras 4a y 4b). Exceptuando algunos picos o cimas de poca monta, se observa un comportamiento bastante razonable de los errores, especialmente en la Figura 4a.
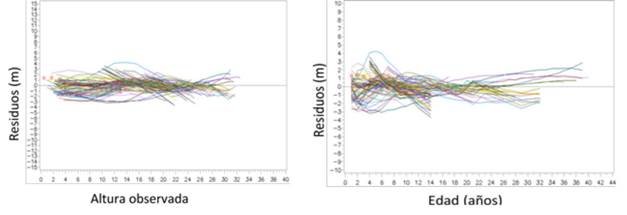
Figura 4 Gráficos de residuales para el mejor modelo (Korf polimórfico) reparametrizado en S y b 1. a) Residuos entre la altura predicha y la observada, b) Residuos entre la edad predicha y la observada. Vertiente del Pacífico, Costa Rica.
En la Figura 5 se observa que, al graficar las curvas de índice de sitio contra la muestra de alturas dominantes, producidas por análisis fustal y por mediciones sucesivas en parcelas permanentes, fue necesario construir las curvas para los índices de sitio del 15 al 30 (a una edad base de 16 años), con el objetivo de abarcar todo el intervalo de sitios registrado; donde, IS = 15 representa el sitio de calidad más baja observado. Seguidamente se construyeron curvas de índice de sitio cada tres metros hasta alcanzar el IS = 30, el cual es el mejor sitio registrado por los datos.
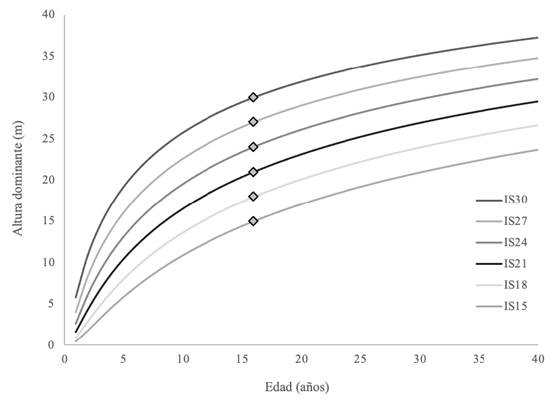
Figura 5 Curvas de índice de sitio polimórficas para 30, 27, 24, 21, 18 y 15 m de altura a la edad base de 16 años (Korf polimórfico) reparametrizado en S y b1. Vertiente del Pacífico, Costa Rica.
Aplicación de las curvas de índice de sitio
Supongamos que se desea calcular el índice de sitio para una parcela, o un grupo de parcelas; entonces, será necesario despejar el índice de sitio (Sr) del modelo polimórfico que se presenta en el Cuadro 3, el cual se representa de la siguiente manera:
En este modelo, la altura dominante es una función del índice de sitio (S r ) y de la edad (E), siendo la edad base (Eb) una constante.
Hecha la transformación de seis pasos que se requiere para lograr la conversión del modelo, podemos representar el índice de sitio (S r ) como una función de la altura dominante (H) y de la edad (E).
Donde H y E son la altura dominante promedio (m) y la edad (años) de la parcela o rodal (m), S r = S+u es el índice de sitio a la edad base E b , y β0, β2 son los estimados de los parámetros obtenidos para el modelo, según el Cuadro 6. Utilizando estos valores, podemos construir la ecuación que tenemos que usar para calcular el índice de sitio, de cualquier masa plantada de teca en la Vertiente del Pacífico de Costa Rica.
Utilizando otro enfoque más conservador, podemos obtener una estimación del índice de sitio para una parcela, o rodal, en las poblaciones representadas en el presente trabajo, determinando “bandas de confianza” (α = 0.5, t α/2.96 gl = 0.7) para cada clase de índice de sitio seleccionada. Estas bandas fueron construidas utilizando la desviación estándar del coeficiente de efecto aleatorio u (u = 0, Su = 2.14763) y los coeficientes de los efectos fijos para el modelo de Korf polimórfico. Las bandas para cada calidad de sitio se muestran en el Cuadro 8.
Cuadro 8 Límites para las clases de Índice de sitio y porcentaje de distribución de los sitios por clase de sitio, para las plantaciones de teca en la vertiente del Pacífico de Costa Rica.
| Curva | Límites | |||||
|---|---|---|---|---|---|---|
| Categoría de sitios | Clase de sitio | IS | Inferior (m) | Superior(m) | Número de sitios | Porcentaje de sitios (%) |
| Muy buenos | I | 30 | 28.5 | 31.49 | 1 | 1.04 |
| II | 27 | 25.5 | 28.49 | 13 | 13.54 | |
| Buenos | III | 24 | 22.5 | 25.49 | 52 | 54.17 |
| IV | 21 | 19.5 | 22.49 | 21 | 21.88 | |
| Malos | V | 18 | 16.5 | 19.49 | 8 | 8.33 |
| VI | 15 | 13.5 | 16.49 | 1 | 1.04 | |
Con la intención de determinar la distribución de las plantaciones, se procedió a utilizar la ecuación que ajusta los índices de sitio para asignarle un valor de clasificación a cada una de las parcelas que conforman la muestra. De esta manera, se logró clasificar la muestra, con base en el índice de sitio, y ubicar cada sitio muestreado, dentro de una clase de calidad de sitio. Se observa en el Cuadro 8 que la distribución adoptada por los terrenos ocupados por las plantaciones de teca, a lo largo de la Vertiente del Pacífico, corresponde a una distribución típicamente normal, con una mayor concentración de plantaciones en los sitios intermedios (Clases II, III y IV). Aproximadamente, un 76 % de los terrenos que participaron en el estudio se ubican en sitios Buenos (Clases III y IV); en contraste, solamente un 9.37 % de las plantaciones se localizan en sitios Malos (Clases V y VI). Los sitios Muy buenos están representados por un 14.58 % de los sitios estudiados (Clases I y II).
Discusión
4.1 Comparación de los datos de crecimiento producidos por análisis fustal y los datos de las mediciones sucesivas realizadas en parcelas permanentes
Mora y Meza (2003) lograron confirmar, en un análisis previo, la factibilidad de utilizar una muestra combinada de alturas dominantes, obtenidas por análisis fustal, con los promedios anuales de las parcelas permanentes en la construcción de curvas de índice de sitio. En dicha comparación, estos autores observaron que la forma de las curvas generadas mediante el análisis de los anillos de crecimiento mostraba un patrón análogo al de las parcelas. En esta oportunidad, se varió totalmente el enfoque y se confrontó la muestra total obtenida mediante la aplicación de ambos procedimientos de toma de datos. Aun cuando se hayan incluido, en este caso, árboles provenientes de calidades de sitio diferentes a los de las parcelas, el patrón de crecimiento en altura que exhiben los árboles reproduce fielmente la tendencia que muestran dichas parcelas. No hay duda de que ambas bases de datos se complementan perfectamente y al superponer unas curvas sobre las otras se obtiene un acople extremadamente bueno. No se observan mayores discrepancias, ni divergencias, que pudieran poner en duda la afinidad de ambos conjuntos de datos. Se confirma, de esta manera, las observaciones realizadas por Mora y Meza en el 2003, con respecto al comportamiento de los datos.
4.2 Comparación de los modelos por tipos de curvas (anamórficas y polimórficas) para Índice de Sitio
Al analizar la estimación de los modelos, tanto anamórficos como polimórficos, se observa, en términos generales, que todos obtuvieron muy buenos resultados. De hecho, todos los parámetros, en ambos grupos de datos, resultaron ser altamente significativos (p < 0.0001). Al trabajar con algunas pruebas de máxima verosimilitud, como el criterio de información de Akaike (AIC) y el criterio bayesiano de información (BIC), se pudo determinar que el modelo que tuvo mejor desempeño fue el de Korf, tanto para las curvas anamórficas como para las polimórficas, con un AIC de 2 681 y 2 573, respectivamente. El efecto beneficioso de estos criterios es reconocido porque logran compensar las diferencias en los grados de libertad que puedan surgir cuando se especifican los modelos con diferentes estructuras de errores. En el Cuadro 6 se observa que el modelo de Korf mostró un valor asintótico muy alto (56.33 m) con respecto a los otros modelos. Sin embargo, hay que tener presente que este modelo fue desarrollado por Korf en 1939 trabajando en condiciones de bosques templados con edades que sobrepasan los 100 años (Zeide, 1993), lo cual está fuera de las edades de interés para estas plantaciones.
Según Fang y Bailey (2001) y Torres et al. (2012), no cabe duda de que al incorporar los efectos mixtos al modelo se mejora la calidad de las estimaciones de los efectos fijos (β 0 , β 1 y β 2 ), que son los que nos interesa calcular para construir las curvas de índice de sitio, esto es, la estructura de medias. Sin embargo, las mejoras en las predicciones se logran visualizar mejor cuando se utilizan los estimados de los efectos mixtos para hacer predicciones en sitios individuales (Fang & Bailey 2001). En este caso, no se realizó dicha comparación con el fin de mantener la orientación del trabajo fiel al enfoque que nos habíamos propuesto.
4.3 Construcción de las curvas de Índice de Sitio
Cuando se graficaron las alturas predichas por el modelo de Korf versus las alturas observadas, provenientes de los análisis fustales y de las parcelas permanentes, se formó una nube compacta de datos que no mostró discrepancias ni desviaciones que hicieran suponer que podría existir alguna incompatibilidad entre ambos juegos de datos. Este resultado es muy edificante pues los datos estimados por el modelo se apegan sólidamente a los valores observados en las plantaciones.
Al trabajar con los residuos, se observa que la dispersión de estos, en ambos gráficos, es bastante aceptable ya que no se aprecian patrones, ni tendencias claras, que pudieran indicar que exista algún problema serio con los residuales. Exceptuando algunos picos o cimas de poca monta, se observa un comportamiento bastante razonable de los errores, especialmente cuando se grafican los residuos contra las alturas observadas.
Al concluir todos los análisis de la información y habiendo elegido el modelo de Korf como el de mejor ajuste se procedió a construir las curvas de índice de sitio. Comenzando con el IS = 15, se fueron adicionando curvas de índice de sitio, cada tres metros, hasta alcanzar el IS = 30, el cual se constituyó en el mejor sitio contemplado en este sistema de clasificación de sitios basado en el crecimiento de la altura dominante versus la edad. Fue necesario construir las curvas para los índices de sitio entre 15 y 30, con el fin de abarcar todo el intervalo de sitios registrados por la muestra, donde el IS = 15 representa al sitio de calidad más baja dentro de este sistema de clasificación de terrenos.
Conclusiones
Se determinó que el 90.6 % de los terrenos ocupados con plantaciones de teca se ubican en sitios Buenos y Muy buenos, los cuales son fuertemente recomendados para el cultivo de esta especie. Los terrenos ocupados con plantaciones de teca, en la Vertiente del Pacífico de Costa Rica, presentan una distribución típicamente normal, de acuerdo con el índice de sitio, mostrando una mayor concentración de plantaciones en los sitios Buenos (un 76 %). Solamente un 9.4 % de las plantaciones se localizan en la categoría de sitios Malos, los cuales son totalmente inapropiados para el cultivo de la especie.
A través de pruebas gráficas se pudo determinar que los datos de análisis fustal se complementan muy bien con los datos de las parcelas permanentes. Al sobreponer ambos conjuntos de datos el acople que se obtuvo fue óptimo.
Utilizando los criterios de información (AIC y BIC) se determinó que el mejor modelo para estos datos es el de Korf, tanto para las curvas anamórficas como para las polimórficas, con un AIC de 2 681 y 2 573, respectivamente. El segundo mejor modelo es el de Richards en ambos tipos de curvas; y el tercer mejor modelo es el de Weibull. Los de peor comportamiento fueron el modelo de Gompertz y la función Logística los cuales no lograron alcanzar el nivel logrado por los otros.
Los datos estimados por el modelo de Korf se apegan fuertemente a los valores observados en las plantaciones de T. grandis. Fue necesario construir las curvas entre los índices de sitio 15 y 30, con el fin de abarcar todo el intervalo de sitios registrado por la muestra, donde el IS = 15 se convirtió en el sitio de calidad más baja dentro de este sistema de clasificación de sitios. El sistema de clasificación de terrenos, construido durante el presente trabajo, cumple a cabalidad con los requisitos establecidos por Curtis (1964) para la construcción de un sistema ideal de curvas de índice de sitio.
Ética y conflicto de intereses
Las personas autoras declaran que han cumplido totalmente con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en la producción del manuscrito; que no hay conflictos de intereses de ningún tipo; que todas las fuentes financieras se mencionan completa y claramente en la sección de agradecimientos, y que están totalmente de acuerdo con la versión final editada del artículo.











 uBio
uBio