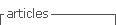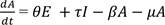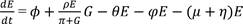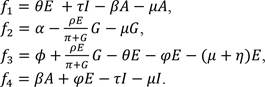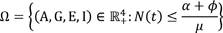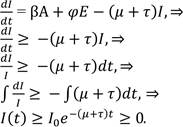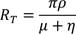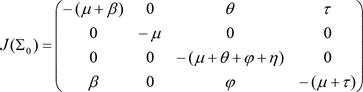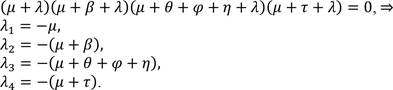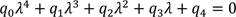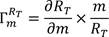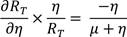1. Introduction
The importance of education in a society cannot be overemphasized. It is so necessary for development that the quality of people and the level of transformation are functions of the quality of education. The quality of education, however, is determined by its ability to meet the desires of society. Transformation is brought about by education only when education is functional. Functional education, therefore, is the education that places emphasis on the ability to carry out productive tasks rather than education that intends to produce ideological conformity (Maduegbunam & Okafor, 2014). Functional education highlights practice more than theory and stands for utility and practicality. It has brought about an unprecedented transformation in terms of the agricultural and industrial revolution in some countries of the world (Vries, 1994).
The Industrial Revolution is a complex set of economic, technological, and social changes that occurred over a substantial period. The first country to experience the industrial revolution was Britain in the eighteenth century (Mohajan, 2019). The emergence of the industrial revolution was attributed to British authority and wealth as an empire, stable government, and spirit of individual freedom and capitalism (Ferreira et al., 2015). Another important factor that led to the first industrial revolution in Britain was the agricultural revolution of the eighteenth century. The changes in the methods of farming and stock breeding that characterized the agricultural transformation led to a significant increase in food production. This implies that British agriculture could feed more people at lower prices with less labor (Groumpos, 2021).
Industrial Revolution had many advantages, and many nations that have not gone through it typically have a life expectancy below fifty years of age, infant mortality approaching 20%, a diet that cannot guarantee good health, and a per capita income of lower than the amount a high school student in America would spend on his/her prom (Digital History, n.d; Francks, 2021). Many people who reside in non-industrial nations such as Nigeria and Algeria, Bangladesh, or Haiti usually cannot read or write, never see a doctor, record at least a death of one child before the age of five, and rarely get enough to eat. On the contrary, people who reside in most industrial countries have far special lives that usually comprise homes with central heating, one or more computers, and cars with air conditioning, a dishwasher, and several televisions. Even most of the poorest people in industrialized nations like America eat meat quite a lot of time a week and have access to minimum health care, electricity, and indoor plumbing (Digital History, n.d; Wikipedia, n.d; Hoppit, 1987).
The industrial revolution is a function of the availability of natural resources such as fertile soil, an excess of money to invest, a significant working force, men and women of energy, ambition, and talent, with administrative abilities, and favorable government policy (Menon & Fink, 2019; Kapas, 2008). Nigeria boasts some of the conditions required for the industrial revolution. For instance, Nigeria is blessed with abundant natural resources and a significant workforce with men and women of energy, but its educational system is far from being functional to properly tap the resources and harness the potentials of the teeming working force (Ayoade & Farayola, 2021). The dream of the nation to join the league of industrialized countries after sixty years of independence becomes a mirage because of the state of its educational system.
The education sector is ill-funded to the extent that the UNESCO recommendation of 26% of the national budget to finance the education of the Third World has become a tall dream as less than 3% of the national budget is allocated to education in Nigeria (Thom-Otuya & Inko-tariah, 2016). Elites and educationists are becoming increasingly worried as no university in Nigeria is ranked among the top fifty universities in Africa, and none is among the top three thousand universities in the world (Thom-Otuya & Inko-tariah, 2016). The poor performance of the education sector eventually pushes other sectors of the economy to a state of inevitable collapse (Ayoade & Farayola, 2020a).
The place of education in national transformation has been studied over the years (Mpofu, 2013; Turkkahraman, 2012; Kayani et al., 2017). Furthermore, the roles of industries and agriculture in national development have also been the subject of intense study (Diao et al., 2010; Agarwal & Agarwal, 2017; Adenomon & Oyejola, 2013). However, much attention has not been paid to the impact of education on the growth of industry and agriculture. In particular, the use of mathematics to study the role of education in the growth of industry and agriculture is relatively new and rare in the literature. It is on this note that the present study attempts to examine a nexus between the industrial and agricultural revolutions in Nigeria in terms of functional education from the mathematical point of view.
Model Formulation
The study derived its theoretical foundation from the structural change theory.
This theory was developed by Arthur Lewis in 1954 and called it ''economic development with unlimited supplies of labor''(Lewis, 1954). The theory states that an economy is made up of two sectors. One is the traditional (agricultural or subsistence) sector, while the other is the modern (capitalist, industrial, or manufacturing) sector. This gives rise to the two-sector model. The theory also assumes that the development of an economy depends on the growth of the two sectors. Mathematically, y=f (AGRIC, IND), where; y=economic development, AGRIC = agricultural sector, and IND = industrial sector. The theory was recently adopted by Taiwo & Muftau (2018) to study the impact of agricultural financing schemes on agricultural output in Nigeria.
The structural change theory was able to simplify the complexity of the real world as the development truly depended on the growth of agriculture and industry in the short run. However, the theory failed to consider other sectors of the economy that enhanced the optimality of the agricultural and industrial sectors. These two sectors are interrelated. The agricultural sector employs capital inputs, labor expertise, and also a final consumer of the output of the industrial sector, while the industrial sector employs labor and output of the agricultural sector. The point of convergence or common denominator for the two sectors is labor because both employ labor in the production process. However, the quality of labor is a function of the quality of education, while the quality of education is a function of the quality of all the factors of education. Therefore, the revolution in agricultural and industrial sectors is a function of the performance of the education sector, and the performance of the education sector itself is a function of the policies of the government.
Hence, contrary to Lewis' view, development is not just a function but a function of a function or a composite function. The present work will, therefore, use a mathematical modeling approach as in Ayoade et al. (2019), Ayoade et al. (2020b), Ayoade & Farayola (2021), Adenuga et al. (2021), and Ayoade & Agboola (2022a) to examine a nexus between agricultural and industrial revolution in Nigeria in terms of a functional education by incorporating the education sector and government policies on education into the Lewis' model. The transfer diagram of the new model is in Figure1.
The model is made up of four compartments of levels of government G(t), education sector E(t), agricultural sector A(t), and industrial sector I(t). Politicians are recruited into the levels of government at the rate 𝛼, while individuals are recruited into the levels of education at the rate 𝜙. The government releases funds to the education sector, but since human beings are involved in the disbursement and management of the funds, part of them may be diverted, and the purpose for which they were released may be defeated before the they get to the sector. Therefore, the rate of influence of government on education may not be linear and is, thus, expressed as G. The education sector supplies labor to the agricultural and industrial sectors at the rates 𝜃 and 𝜑 respectively. The agricultural sector supplies
raw materials to the industries at the rate 𝛽, while the industrial sector supplies inputs to agriculture at the rate 𝜏. It is assumed that the following occurs at the same rate 𝜇: level of dropouts from the education compartment E(t) represented by 𝜇E, the level of retrenchment from the industrial compartment I(t) represented by 𝜇I, the level at which the able-bodied leave farming activities from the agricultural compartment A(t) represented by 𝜇A, and the rate at which changes in government put different politicians into governance at different times represented by 𝜇G since general elections hold every four years. Also, when the funds released by the government finally reaches the education sector, there is a tendency for misappropriation of the funds since human beings are involved in their management. This would constitute a leakage to the growth of the sector, and the rate of leakages is represented by 𝜂E. These assumptions and the transfer diagram are translated into the following set of first-order ordinary differential equations.
with initial conditions
A (0) = A0, G (0) = G0, E (0) = E0, I (0) = I0.
The nomenclatures for the parameters are displayed in Table 1.
Table 1 Definitions for the model parameters
| Parameters Description | Symbol |
| Rate of influx of politicians into political offices | 𝛼 |
| Rate of influx of individuals into schools | 𝜙 |
| Rate of embezzlement among the officials who handle fund disbursements to the education sector | 𝜋 |
| Rate of supply of labor to A(t) from E(t) | 𝜃 |
| Rate of supply of raw materials from A(t)to I(t) | 𝛽 |
| Rate of funding education sector | 𝜌 |
| Rate of supply of inputs from I(t)to A(t) | 𝜏 |
| Rate of supply of labor to I(t)from E(t) | 𝜑 |
| Rate of leakages in each of the compartments | 𝜇 |
| Rate of embezzlement in the education sector | 𝜂 |
Note: derived from research.
Basic Features
Existence of solutions
Well-posedness of a model is a function of the existence of solutions of the model. If there exist solutions, the dynamics of the model can be predicted by dealing with the model solutions or its approximate solutions. The popular Derrick and Grossman theorem, which has been used in numerous studies, for example, see Ayoade et al. (2020b) and Adenuga et al. (2021), shall be used to verify the existence of solutions for the proposed model.
Lemma 1 (Adenuga et al 2021). Let Ω represent a region 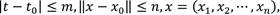
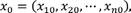 and assuming the Lipschitzian criterion
and assuming the Lipschitzian criterion 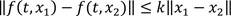 is fulfilled by ƒ(t, x), whenever (t, x1), and (t, x2) are in Ω where k is nonnegative. Then, there exists a unique continuous vector solution x (t) in the interval t - t0 ≤ 𝛿 such that 𝛿 > 0. It is necessary to consider that the condition is fulfilled based on the requirement that for i, j = 1, 2, 3, . . . are continuous and bounded in Ω.
is fulfilled by ƒ(t, x), whenever (t, x1), and (t, x2) are in Ω where k is nonnegative. Then, there exists a unique continuous vector solution x (t) in the interval t - t0 ≤ 𝛿 such that 𝛿 > 0. It is necessary to consider that the condition is fulfilled based on the requirement that for i, j = 1, 2, 3, . . . are continuous and bounded in Ω.
Theorem 1. The model solutions with initial conditions A(0)≥0, G(0) ≥0, E(0) ≥0, I(0) ≥0 exists as well as unique in for all t ≥ 0.
Proof. The RHS of the model can be written as:
It is straightforward to establish that 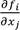 are continuous and deduce that
are continuous and deduce that 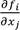 for i, j = 1, 2,..., 4, where x1 = A, x2 = G, x3 = E, and x4 = I. By Lemma 1, the model has unique solutions.
for i, j = 1, 2,..., 4, where x1 = A, x2 = G, x3 = E, and x4 = I. By Lemma 1, the model has unique solutions.
Invariant region
The boundedness property of the model shall be used to establish the invariant region. Here,
N (t) = A (t) + G (t) + E (t) + I (t) which follows that
The solution for the inequality can be generally expressed as
The initial value is N (0), i.e., N (t) =N (0) at t = 0.
Further, it is deduced that 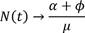 as t ⟶ ∞. Hence, N (t) remains bounded as
as t ⟶ ∞. Hence, N (t) remains bounded as 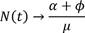 . Thus, the region of feasibility for the model is nonnegative and is given as
. Thus, the region of feasibility for the model is nonnegative and is given as
Positivity of solutions
The solutions of the model must be positive since it monitors real-life phenomena.
Theorem 2. The solutions of the system preserve positivity.
Proof. Suppose {A (t), G (t), E (t), I (t)} denotes the final solutions to the variables of the model for t ≥ 0 with positive initial conditions {A (0) > 0, G (0) > 0, E (0) > 0, I (0) > 0}.
From (1),
Also, consider (2),
In (3),
Lastly, in (4),
Since ek is nonnegative for all k then, the solutions for A (t), G (t), E (t), and I (t) are positive.
Qualitative Analysis
Equilibria
Two equilibria are associated with the epidemiological modeling - disease-free equilibrium (DFE) and the endemic equilibrium (EE). Equilibrium is at the DFE when the infection is virtually non-existence in the population, while it is at the EE when the population is plagued with the disease.
In the present analysis, transformation in agriculture and industry is anchored on functional education, while functional education itself is anchored on adequate funding by the government. Therefore, there exist two equilibria as well - education poor funding equilibrium (EPE) and education adequate funding equilibrium (EAE). It is assumed, as in epidemic modeling, that EPE exists when there is total neglect of the education sector to the degree that the rate of funding education is zero, i.e., 𝜌 = 0, while EAE exists when 𝜌 > 0. Hence, the system (1)-(4) allows an education poor funding equilibrium (EPE)
Σ0 = (A0, G0, E0, I0) with coordinates
and an education adequate funding equilibrium (EAE)
Σ* = (A*, G*, E*, I*) with coordinates
where
Transformation Ratio, R T
In epidemiology, the basic reproduction ratio R0 measures the average number of secondary infections that a typical infectious individual is able to produce in a completely susceptible population (Diekmann et al., 1990). If R0 > 1, they are able to infect at least one person, and the disease takes off in the population; but if R0 < 1, they are unable to infect a single individual, and the disease dies out or fails to take off in the population. In the present analysis, transformation ratio RT measures the functionality of education in terms of the transformation in agricultural and industrial sectors. Transformation in agricultural and industrial sectors is a function of functional education, while functional education itself is a function of government policies. Transformation in agriculture and industry in terms of functional education, therefore, depends on the rate of funding education (𝜌), the level of corruption among the officials who handle fund disbursements to the education sector (𝜋), the rate of dropouts (𝜇) and the rate of misappropriation of funds in the education sector (𝜂). Transformation ratio RT is therefore defined as the ratio of the product of the rates of funding education (𝜌) and the level of corruption among the officials who handle fund disbursements to the education sector (𝜋) to the sum of the rates of dropouts (𝜇) and the misappropriation of funds in the education sector (𝜂), i.e.,
In (9), the transformation ratio parameter (RT) is inversely related to the sum of the rates of dropouts (𝜇) and the misappropriation of funds in the education sector (𝜂), if the rate of funding education (𝜌) is constant. The implication is that education would be functional, and the functionality would translate into an agricultural and industrial revolution if there is a decrease in the rates of dropouts (𝜇) and misappropriation of funds in the education sector (𝜂), even if the rate of funding education (𝜌) is constant; otherwise, an injection of funds (𝜌) into the education sector might not result in functional education. So, a decrease in (𝜇) and (𝜂) with an increase in (𝜌) and a decrease in (𝜋) will guarantee functional education. On the other hand, an increase in (𝜇) and (𝜂) with a decrease in (𝜌) and an increase in (𝜋) will frustrate functional education. Following the epidemiological modeling principle as applied in Ayoade & Aliu (2022b), Ayoade & Farayola (2022c) and Ayoade & Agboola (2022a), education becomes functional, and the functionality informs the agricultural and industrial revolution if RT > 1; otherwise, education does not reach the level of revolutionizing agricultural and industrial sectors (i.e., RT < 1).
Stability of the Education Poor Funding Equilibrium, Σ 0
One of the equilibria that are identified with the model is education poor funding equilibrium (Σ0) which exists when there is total neglect of the education sector to the degree that the rate of funding education is assumed zero, i.e., 𝜌 = 0. Poor funding equilibrium in quantific terms means that the education sector is neglected, and it is measured in terms of the nondimensional quantity RT. It exists when RT < 1. We shall examine the stability of (Σ0) following the epidemiological modeling approach to establish the conditions that can instigate (Σ0). Theorem 3. The education poor funding equilibrium of the model is stable if RT < 1; otherwise, it is unstable.
Proof. The education poor funding equilibrium is stable, and RT < 1 if it is shown that all the eigenvalues of the Jacobian matrix of the system (1)-(4) are negative. If the system (1)-(4) is linearized, then, it becomes
Evaluating (10) about the education neglect equilibrium Σ0, i.e., when the rate of funding education is zero (𝜌 = 0), then, (10) becomes
In (11),
Since all the eigenvalues are negative, the education poor funding equilibrium (Σ0) of the model is stable. The stability of the education poor funding equilibrium (Σ0) implies that education would continue to be dysfunctional unless there are favorable perturbations in the values of the model parameters.
Stability of the Education Adequate Funding Equilibrium, Σ*
Education adequate funding equilibrium (Σ*) exists when the education sector is receiving the needed attention from the government, i.e., when 𝜌 > 0. It is measured in terms of RT and exists when RT > 1. We shall establish the conditions that can instigate (Σ*).
Theorem 4. The education adequate funding equilibrium of the model is stable if RT > 1; otherwise, it is unstable.
Proof. The education adequate funding equilibrium is stable, and RT > 1 if it is established that all the eigenvalues of the Jacobian matrix of the model are less than zero.
At EAE, when the rate of funding education is greater than zero, i.e., 𝜌 > 0, (10) becomes
where
In (13),
where
and
Going by the stability criterion of Routh-Hurtwitz in Ayoade et al. (2019), all the eigenvalues in (14) are less than zero if
Therefore, the education adequate funding equilibrium Σ* of the model is stable if the inequalities in (15) are true. The stability of Σ* implies that education would continue to be functional if the present state of the values of the model parameters that instigated functional education is sustained.
Sensitivity Analysis
The contribution of education to agricultural and industrial sectors is quantified theoretically by computing the relative effects of key parameters on functional education (i.e., transformation ratio), following the formula of normalized forward sensitivity index (Ayoade & Ibrahim, 2022d).
With (16), the indices of sensitivity for the key parameters with respect to the transformation ratio RT are derived in (17)-(20).
Quantitative Analysis and Discussion
Simulation is conducted to verify the analytical results in section 3 and to confirm the stability nature of the model. It is achieved via the Maple software as well as a set of logical parameter values. With simulations, the transformation in agriculture and industry based on functional education, which has been computed in (9), is studied numerically. Further, the relative effects of the key parameters on functional education are revealed via indices of sensitivity for the major parameters. In the system (1)-(4), set 𝛼 = 0.1, 𝜙 = 0.3, 𝜋 = 0.45, 𝜃 = 0.4, 𝛽 = 0.2, 𝜌 = 0.25, 𝜏 = 0.5, 𝜑 = 0.3, 𝜇 = 0.075, 𝜂 = 0.1. Then, from (9), RT = 0.64, and the indices of sensitivity for the major parameters in (17)-(20) are shown in Table 2.
Table 2 Indices of sensitivity for key parameters to transformation ratio RT
| Parameters | Sensitivity indices |
|---|---|
| 𝜋 | 1 |
| 𝜌 | 1 |
| 𝜇 | -0.43 |
| 𝜂 | -0.57 |
Note: derived from research.
According to the meaning for RT in subsection 3.2, the result RT = 0.64 implies that, within the values chosen for the parameters, the agricultural and industrial revolution remains a tall dream because education is not functional. The poor state of education based on the result for the transformation ratio (RT) could be linked to poor funding (𝜌), high rates of embezzlement by the government officials who disburse funds to the education sector (𝜋), misappropriation of funds in the education sector (𝜂) as well as a high rate of dropouts (𝜇).
On a serious note, the situation in Nigeria affirms the result RT = 0.64 which indicates the poor state of Nigerian education. In the first place, education is ill-funded in Nigeria to the degree that the UNESCO recommendation of 26% of the state budget to finance the education of the Third World has become a tall dream as less than 3% of the national budget is allocated to education in Nigeria (Thom-Otuya & Inko-tariah, 2016). Worst still, the little amount set aside for education is usually diverted, awfully misused, and unaccounted for (Ayoade & Farayola, 2020a).
Nigeria becomes the second most corrupt country in West Africa in 2021 (The Nairametrics, 2021). Given the current level of corruption in Nigeria, the amount of funds released for education might be cornered before disbursements, while the little that gets to the sector might even be used for the purposes for which those funds are not released. China is one country that has attained industrialization through purposeful investment in education.
Besides, the indiscriminate closure of schools due to incessant industrial actions has pushed education into a state of an inevitable collapse in Nigeria and forced many students out of schools. It is on record that university teachers in Nigeria embark on strikes 16 times in 23 years (The Punch, 2022). Public universities in Nigeria were closed down for 9 months in 2020 due to a strike by the university teachers (The Punch, 2022). Further, academic activities in Nigerian public universities have been suspended for more than 4 months in 2022 (since February 14, 2022) due to another industrial action by the university lecturers (The Punch, 2022).
As regards the sensitivity indices for some parameters in Table 2, parameters with positive indices are directly related to the transformation ratio (RT). For example, the index +1 for 𝜌 indicates that an increase in government spending on education increases the performance of Nigerian education by 100%. On the other hand, parameters with negative indices are inversely related to the transformation ratio (RT). For example, the index -0.57 for 𝜂 indicates that a 57% reduction in the misappropriation of funds in the education sector improves Nigerian education by 57%. It is therefore deduced from the sensitivity indices for the parameters that, to facilitate a revolution in industry and transformation in agriculture, the Nigerian government must invest heavily in education (𝜌) and fight corruption with all seriousness (𝜂).
To examine the stability properties of the system that were stated in subsections 3.3 and 3.4, the transformation ratio (RT) is evaluated at various values of the key parameters. The outcomes of the computation are shown in Table 3.
Table 3 Results of stability for functional education model
| S/No | 𝜋 | 𝜌 | 𝜇 | 𝜂 | RT | Nature of Stability |
| 1 | 0.45 | 0.25 | 0.075 | 0.10 | 0.64 | Unstable |
| 2 | 0.50 | 0.35 | 0.075 | 0.30 | 0.47 | Unstable |
| 3 | 0.55 | 0.45 | 0.075 | 0.50 | 0.43 | Unstable |
| 4 | 0.60 | 0.55 | 0.075 | 0.75 | 0.40 | Unstable |
| 5 | 0.20 | 0.60 | 0.075 | 0.01 | 1.41 | Stable |
| 6 | 0.19 | 0.65 | 0.075 | 0.009 | 1.47 | Stable |
| 7 | 0.18 | 0.70 | 0.075 | 0.008 | 1.52 | Stable |
| 8 | 0.10 | 0.65 | 0.075 | 0.30 | 0.17 | Unstable |
| 9 | 0.50 | 0.30 | 0.075 | 0.09 | 0.90 | Unstable |
Note: derived from research.
In Table 3, S/No. 1 is the base that gives the initial result for the transformation ratio (i.e., RT = 0.64). From S/No. 2 to S/No. 4, it is observed that, as an increase in government spending on education (𝜌) is accompanied by an increase in both (𝜋) and (𝜂), the embezzlement of funds allocated for education and misappropriation of funds in the education sector respectively, education remains dysfunctional. The model is unstable at these points (S/No. 2 - S/No. 4) as RT = <1. On the other hand, in S/No. 5 S/No. 7, as an increase in (𝜌) is matched with a decrease in both (𝜋) and (𝜂), education becomes functional as RT = >1. The model becomes stable in the region within S/No. 5 and S/No. 7.
Further, an increase in (𝜌) with a decrease in (𝜋) but an increase (𝜂) in S/No. 8 makes education dysfunctional as the model moves to unstable regions with RT = <1. In the same manner, an increase in (𝜌) with an increase in (𝜋) but a decrease in (𝜂) in S/No. 9 also makes education dysfunctional as the model remains in an unstable region with RT = <1.
The results of the stability analysis in Table 3 complement the result of the sensitivity analysis in Table 2. It is deduced from simulations in Table 3 that, to make education functional and to translate functionality in education to an agricultural and industrial revolution in Nigeria, the government must invest heavily in education (𝜌) and fight corruption not only among the people that disburse funds to the education sector (𝜋) but also among the school administrators (𝜂).
With the aid of the Maple software, we are able to generate plots to visualize the functionality of education in terms of agricultural and industrial transformation. In Figure 2, it is observed that an increase in the educational sector is accompanied by an increase in the agricultural and industrial sectors. This shows that the government is investing heavily in education, and the investment is impacting the sector positively which, in turn, instigates transformation in agricultural and industrial sectors. On the other hand, in Figure 3, a rise in the educational sector is accompanied by a fall in the agricultural and industrial sectors. The implication is that either the education sector is poorly funded or the funds released to the sector are diverted and embezzled, which is frustrating growth in the agricultural and industrial processes.
Conclusions
Agricultural transformation and industrial revolution are major indices of prosperity that have been fostered through functional education in some countries of the world. Given abundant natural resources and significant human capital, a model has been developed to characterize the necessary and sufficient conditions for revolution in industry and transformation in agriculture in Nigeria through functional education. Functional education is the education that highlights practice more than theory and stands for utility and practicality. It is education that places emphasis on the ability to carry out productive tasks rather than education that intends to produce ideological conformity. Ample mathematics theorems have been employed to show that the solutions for the model exist, and are positive and bounded. The model equilibria have been derived, and the analytic threshold for revolution in industry and agriculture through functional education has been computed and used to examine the stability nature of the system equilibria. The sensitivity study of some major parameters has been performed, and the simulations have been conducted to determine the region where the increase in government expenditure on education resulted in functional education and facilitated a revolution in industry and agriculture, and the region where expansion in government expenditure on education had no effect on education.
It was found from the results that transformation in agriculture and revolution in industry through functional education depend on massive investment in education and victory over corruption. The study found massive investment in education the necessary condition for functional education, and victory over corruption the sufficient condition. Nigeria can make a revolution in agriculture and industry happen through its education if the country could borrow a leaf from China. China is one country in the world that has achieved significant breakthroughs in technology by investing massively in education and by making corruption unattractive through severe penalties.