PSYCHOLOGY IN STUDENTS’ CHOICE OF A MATHEMATICAL CAREER
The reasons to study or not to study a career in the science, technology, engineering, or mathematics fields have been widely studied in international contexts. From the psychological point of view, research shows the influence of motivational forces such as interest, enjoyment, value, and perceived competence or self-efficacy beliefs in the choice of careers related to mathematics. Multiple contextual, social, cultural, and economical factors -such as gender, ethnic, or social classes - also influence these forces. Among all these motivational forces, self-efficacy beliefs in mathematics draw special attention as the immediate and strongest predictor of students’ choice of a mathematical career (Hackett, 1985, 1995; Hackett & Betz, 1995; Zeldin & Pajares, 2000). Self-efficacy is defined as people’s judgements of their capabilities to produce designated levels of performance in mathematics (Bandura, 1997). More widely, two psychological models have received much attention and have been extensively examined in relation to the choice of a mathematical career: the expectancy-value theory of motivation (e.g., Eccles et al., 1983; Wigfield & Eccles, 2000) and the social cognitive career theory (Lent & Brown, 2013; Lent, Brown, & Hackett, 1994). We suggest that recent research about students’ choice of career has been no study in-depth because this kind of study implies a combination of different aspects and theories that allow researchers to explain the reason o sources of the choice. In fact, this research combines students’ mathematical career choice, students’ motivations, narrative identity and self-efficacy beliefs in order to identify the motivations, the sources of those motivations and expectations associated with the choice of Mexican students’ mathematical career.
Social Cognitive Career Theory
Social cognitive career theory (Lent & Brown, 2013; Lent et al., 1994) is used to explain processes through which people develop interests, make choices, achieve and persist in performances, and experience satisfaction in educational and career-relevant contexts. According to Lent et al. (1994) the core concepts (Figure 1) in social cognitive career theory are: self-efficacy (perceived capabilities), outcome expectations (beliefs about the outcomes of certain efforts), and goals (determination to engage in a particular activity or to strive for a particular future outcome). This framework assumes self-efficacy influences outcome expectations. Interests are assumed to develop mainly based on self-efficacy beliefs and outcome expectations. Research based on social cognitive career theory shows that self-efficacy, outcome expectations, and interest are the major influences on career choice (Lent, Lopez, & Bieschke, 1991, 1993). So, for example, students who expressed strong efficacy beliefs and perceived positive outcomes as a result of success in mathematics and science courses were more likely than other students to choose a mathematical career.
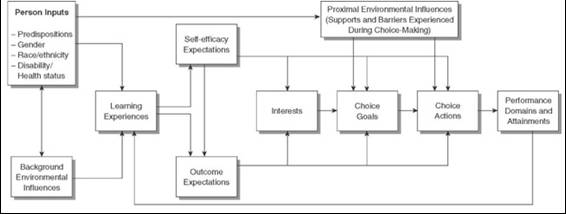
Figure 1. Influences on career choice behaviour according to social cognitive career theory (Lent et al., 1994)
Expectancy-Value Theory
Research based on Expectancy-Value theory have widely demonstrated the influences of mathematics expectancies and values on students’ choices to participate in mathematics in senior high school and college enrolments (Eccles et al., 1983; Meece, Wigfield, & Eccles, 1990; Watt, 2005, 2006; Wigfield, 1994). From the expectancy-value theory perspective, students planning to pursue mathematics-related careers are expected to cite reasons such as (Watt, 2005): (1) their expectations of being successful in mathematics (the definition of expectancies of success is, in fact, the same as self-efficacy), (2) their high mathematical abilities, (3) their interest in mathematics, (4) perceptions of mathematics as useful, (5) considering mathematics to be important to do, or (6) not having competing interests or costs. Students planning not to pursue mathematics-related careers were anticipated to give explanations such as: (1) expectations of not succeeding in mathematics, (2) their low mathematical abilities, (3) being uninterested in mathematics, (4) not perceiving mathematics as useful, (5) not needing mathematics or considering mathematics to be unimportant, or (6) having competing interests or costs.
Sources of Self-Efficacy Beliefs
Self-efficacy researchers have long theorized four distinct sources to instill people’s beliefs about their efficacy (Bandura, 1997; Lent et al., 1994; Usher, 2009; Usher & Pajares, 2009; Zeldin, Britner, & Pajares, 2008; Zeldin & Pajares, 2000). These investigations show that self-efficacy beliefs are developed as individuals interpret information from four sources: mastery experience, vicarious experience, social or verbal persuasion, and emotional or psychological state. The most powerful source is the interpreted result of one’s own previous attainments, or mastery experience: interpretation of results from past performance accomplishments can create a strong sense of efficacy to accomplish similar tasks in the future. The second source of self-efficacy information is the vicarious experience gained by observing task performance of others: observing successes and failures of others, people gather information that contributes to their judgements about their own capabilities. Social or verbal persuasion -messages from others about one’s ability to accomplish a task- are hypothesized to exert the most positive influence on those who already have a strong sense of self-efficacy. Finally, Bandura hypothesized that self-efficacy beliefs are informed by emotional and physiological states such as anxiety, stress, fatigue, and mood. Students learn to interpret their physiological arousal as an indicator of personal competence by evaluating their own performances under differing conditions. We used the notion of motivation “source” to refer to the experiences that participants cited as being the sources of their motivations and expectations in this research.
Purposes of the Research
Several facts emerged from the previous literature review: A lot of research in psychology focuses on the factors that influence the choice of a mathematical career. These are mainly quantitative studies that look for generalities; therefore, most of this knowledge does not consider the context or subjective processes that intervene in the choice. There are just a few qualitative studies that look for motivations or reasons why specific people under specific circumstances choose a mathematical career. In this sense, there is not much information about the ways young people integrate their motivations to study a mathematical career with their mathematical life experiences. Most research focused on the factors that influence the choice of a mathematical career in developed countries, specifically North America, Europe, and Oceania. Therefore, there is not much information in this area from other continents or countries.
We identify some qualitative research focused on the identification of factors favoring the choice of mathematics as a profession among women in Mexico (Carrasco & Sánchez, 2016; Manzano & Sánchez, 2017; Sánchez, Romo, Mendoza, Molina, & Castañeda, 2013). According to these investigations, the main factors choosing a mathematical career are being aware of the fact that they are good at mathematics, the influence of their mathematics teachers and relatives and that they like mathematics. This research starts filling these gaps by pursuing the goal to identify the experiences of young Mexican students choosing a mathematical career through their mathematical life histories.
NARRATIVE INQUIRY AND NARRATIVE IDENTITY
Narrative inquiry is an epistemological approach to research through which the knowledge of people’s lived experience is explored and interrogated. For Connelly and Clandinin (2006):
Arguments for the development and use of narrative inquiry come out of a view of human experience in which humans, individually and socially, lead storied lives. People shape their daily lives by stories of who they and others are and as they interpret their past in terms of these stories. Story, in the current idiom, is a portal through which a person enters the world and by which their experience of the world is interpreted and made personally meaningful. Viewed this way, narrative is the phenomenon studied in inquiry. Narrative inquiry, the study of experience as story, then, is first and foremost a way of thinking about experience. Narrative inquiry as a methodology entails a view of the phenomenon. To use narrative inquiry methodology is to adopt a particular narrative view of experience as phenomena under study (p. 477).
For McAdams and McLean (2013) the concept of narrative identity postulates that individuals form an identity by integrating their life experiences into “internalized and evolving life story, integrating the reconstructed past and imagined future to provide life with some degree of unity and purpose” (p. 233). From McAdams (2011):
Narrative identity is the internalized and evolving story of the self that a person constructs to make sense and meaning out of his or her life. The story is a selective reconstruction of the autobiographical past and a narrative anticipation of the imagined future that serves to explain, for the self and others, how the person came to be and where his or her life may be going (McAdams, 2011, p. 99).
Mathematical Narrative Identity
We adapted the narrative identity definition to our specific interest in mathematics and define mathematical narrative identity as a person’s internalized and evolving mathematics life story, integrating the reconstructed past and imagined future to provide mathematics life with some degree of unity and purpose.
In order to make our definition of mathematical narrative identity fully operational with the thematic analysis (Braun & Clarke, 2006, 2012), we divided the mathematics life story associated with the decision to choose a mathematical career into three narrative moments: The present time, corresponding with the moment when the choice of the mathematical career occurs. It is conceptualized as the motivations and explicit reasons that an individual expresses a choice of a mathematical career. The past time, corresponding to the preceding moment of the election of the mathematical career. It consists of significant positive and negative experiences. It is conceptualized as the sources of the actual individual motivations (in the sense of self-efficacy researches). An imagined future time, conceptualized as the hopes or future expectations associated with the choice of a mathematical career. As the narrative identity concept proposes, we assume these three moments will have a certain degree of unity and purpose in the group of students as a whole.
Research Questions
Taking into account the previous theoretical and methodological considerations, the main goal of this research can be broken down into three specific goals: (1) identify the motivations of Mexican students to choose a mathematical career, (2) identify the sources of those motivations in the past time, and (3) identify their future expectations associated with the choice of a mathematical career. These goals transform into the following research questions:
METHODOLOGY
We developed this study under a qualitative research approach, this approach allows us to understand the meaning of individuals ascribed to a social or human problem (Cresswell, 2014). In this research we focus on the students’ motivation to choose a mathematical career, to reach this aim we involved the process of emerging questions and procedures (e.g., thematic analysis), data collected in the participant’s setting, and analyzed it inductively in order to build themes from particulars to general. Beyond identifying themes, we used a case study in order to develop an in-depth analysis of multiple cases, these cases are bounded by time and activity, and provide detailed information that is shaped into a general description (Yin, 2009, 2012).
Context
The research was carried out in the Mathematics Academic Unit of the public Autonomous University of Zacatecas (MAU-Zacatecas). MAU-Zacatecas is in the city of Zacatecas, Zacatecas, a northern state of Mexico. The students admitted to this university come from middle to low socio-economic settings and the education received is free. MAU-Zacatecas offers four and a half years of mathematical degree organized into nine semesters with four possible specializations: basic mathematics, applied mathematics, mathematics education and statistics. From the sixth semester, students take a series of elective courses in the specialization they choose in addition to the required courses: two mathematical analysis courses, one ordinary differential equations course, and one complex variable course. After nine semesters, students obtain a mathematical degree with a specialty in the specific terminal line chosen.
The curriculum states that the mathematical career is designed for young students interested in improving the mathematical education of the country, solving problems that require the application of mathematics, and exploring mathematics investigation. The curriculum also states that graduates with mathematical education specialization are able to teach mathematics in high school and even major studies related to mathematics. According to the third author of this paper, insider and key informant of the research, the teachers of MAU-Zacatecas perceive that students enroll in this mathematical course because the Normal School (school that prepares teachers for basic levels in the city of Zacatecas) prepares teachers for only the basic levels and they want to teach in higher levels. Most of the high school teachers known by the students graduated from the Normal School or from MAU-Zacatecas.
Data Gathering and Participants
The first and third authors of this paper conducted interviews with 47 students, recently graduated from different high schools in the state of Zacatecas, who were admitted into the mathematical course at MAU-Zacatecas in August 2014. The participants volunteered to be videotaped for an educative investigation. Each interview lasted between 15 and 35 minutes. There were 23 women and 24 men between 17 and19 years old. The first author of this paper, an experienced researcher, conducted the first 10 interviews with the non-participative presence of the third author. At the end of each interview, they exchanged points of view about the interview. The third author conducted the next 10 interviews with the non-participative presence of the first author; they continued exchanging points of view at the end. The final interviews were conducted by the third author alone.
Interview Protocol
The aim of the interview was to encourage participants to describe their mathematical narrative identity focusing on three moments: past, present, and future time. There are three sets of questions: (1) questions around the explicit motivations or reasons to choose a mathematical career in the present time (Table 2), (2) questions around the mathematical life of the students to identify the sources of those motivations (Table 1), and (3) questions to identify the future expectations of the students associated with the choice of a mathematical career (Table 3). First, the students answered questions about their mathematical lives and later about their motivations and expectations.
Table 1 Questions about students’ mathematical life
| School life To what have you dedicated your life? Could you talk to me about your academic training? Where did you study? What did you study there? Why did you study in there? What did you like or dislike about the places where you studied? Tell me about your academic background. Which disciplines did you like? Why? What courses did you fail? Why did you fail those courses? What things did you like in high school? Why? What things did you dislike in high school? Why? Could you talk about your family? What do they do for living? What did they study? Mathematical life Tell me your story related to mathematics. Considering your whole life, tell me some positive experiences in mathematics. Why did you experience that? Considering your whole life, tell me some negative experiences with mathematics. Why did you experience that? Is there any other positive or negative experience you would like to talk about? |
Table 2 Questions about motivations to choose a mathematical career
| Motivation to study for a mathematical career Could you tell me your reasons and motivations to choose a mathematical career at MAU-Zacatecas? Is there any other reason or motivation to choose a mathematical career? What are your expectations of success or failure in this mathematical career? |
Table 3 Questions about expectations for choosing a mathematical career
| Expectations for choosing a mathematical career Could you explain me what do you expect to obtain for studying for a mathematical career? How do you imagine you will use mathematics in the future? What are your expectations of work when you graduate? Do you know any mathematician? Who? Do you think you will continue your studies after your graduation? Why would you like to keep studying? |
Data Analysis: Principles of Thematic Analysis
The purpose of thematic analysis is to identify “patterns of meaning” (themes) throughout a data set provided by the answers to the research question addressed (Braun & Clarke, 2006, p.82): “A theme captures something important about the data in relation to the research question and represents some level of patterned response or meaning within the data set” (emphasis in original). Patterns are identified through a rigorous process of data familiarization, data coding, and theme development and revision. Braun and Clarke (2012, p.57) explain that “thematic analysis allows the researcher to see and make sense of collective or shared meanings and experiences”, focusing on the meanings across a data set. Identifying unique or idiosyncratic meanings and experiences found only within a single data item is not the focus of thematic analysis. This method, then, is a way of identifying what is common in how a topic is talked or written about and of making sense of those commonalities. Themes or patterns within data can be identified in one of two primary ways in thematic analysis: in an inductive or “bottom-up” way, or in a theoretical or deductive or “top-down” way.
An inductive approach to data coding and analysis is a bottom-up approach and is driven by what is in the data. What this means is that the codes and themes derive from the content of the data themselves-so that what is mapped by the researcher during analysis closely matches the con-tent of the data. In contrast, a deductive approach to data coding and analysis is a top-down approach, where the researcher brings to the data a series of concepts, ideas, or topics that they use to code and interpret the data. What this means is that the codes and themes derive more from concepts and ideas the researcher brings to the data-here, what is mapped by the researcher during analysis does not necessarily closely link to the semantic data content (Braun & Clarke, 2012, p.58)
Phases of Data Analysis
Data analysis was carried out in three different stages using an inductive thematic analysis to identify: (1) motivations. (2) sources of these motivations, and (3) future expectations associated with the choice of a mathematical career. Each stage corresponds with a research question.
RQ1 Phase: Identification of the motivations
This stage focus on the identification of students’ motivations to study a mathematical career. The thematic analysis in this stage was carried out in an inductive way considering all data; however, answers to the questions in Table 2 were considered to be specifically important.
RQ2 Phase: Identification of the sources of motivations
The goal of this phase is to trace the sources of the motivations identified in the previous phase; it considered the testimonies about the participants’ mathematical lives (Table 1). We carried out two types of thematic analysis in this stage: (1) A deductive thematic analysis to identify the sources of self-efficacy beliefs, identified as the main motivation in RQ1 phase. We focus on the sources of beliefs found in the literature: mastery experience, vicarious experience, social persuasion and emotional and psychological states (Usher & Pajares, 2009); (2) an inductive thematic analysis to detect attributions (i.e. cause-effect relationships) expressed by the participants to identify the sources of other motivations.
Interpretations of the interviews about a motivation or source were conducted under the definition of Braun and Clarke (2006, 2012) of life story associated with the decision to choose a mathematical career. Excerpts of the interview corresponding with a present time when the choice of the mathematical career occurs, are conceptualized as the motivations and contain explicit reasons of the choice of a mathematical career. Significant positive and negative experiences in the past time corresponding to the preceding moment of the election of the mathematical career were conceptualized as the sources of the motivations.
RQ3 Phase: Identification of expectations
This stage focuses on the identification of the future expectations associated with the choice of a mathematical career. This thematic analysis was also carried out in an inductive way and considered mainly the answers to the questions in Table 3.
Thematic Analysis
We follow the steps mentioned Braun and Clarke (2006) for each thematic analysis: (1) become familiar with the data, (2) generate initial codes, (3) search for themes, (4) review themes, (5) define and name themes, and (6) produce a report. This procedure is summarized in Table 4.
Table 4 Procedure to conduct theme analysis
| Phase 1: Familiarizing yourself with the data | All the interviews were transcribed by a person outside the research. All authors of this paper repeatedly read the transcriptions to become familiar with the data. We periodically exchanged opinions. In those meetings, the third author of this paper (insider and key informant of the research) also explained the context of the participants. |
| Phase 2: Generating initial codes | Each interview was separately analysed. We properly coded each statement according to: Students’ motivations or reasons attributed to the choice of a mathematical career. Students’ attributions (cause-effect relationships) expressed as causes of their motivations. Students’ future expectations associated with the choice of a mathematical career. |
| Phase 3: Searching for themes | We had regular meetings to create, assign, and modify codes, as well as to understand their relationships and establish the family codes (potential themes). |
| Phase 4: Reviewing potential themes | We discussed the correspondence between the data and the potential themes identified in the former phase. We eliminated themes with no sufficient evidence and clustered initial themes, thus generating new themes. |
| Phase 5: Defining and naming themes | We named these new themes and checked that the codes were in accordance with them. Finally, the themes were interpreted as participants’ motivations, sources of motivations, and future expectations. |
| Phase 6: Producing the report | We wrote up the results. The whole process of analysis was done in Spanish and translated to English just for the purpose of writing this paper. |
Standards for the Presentation of Excerpts
We identify each excerpt presented in this paper with the number of the student participant who expressed it (S01, S02 … to S47); we also highlight in italics the parts of the text specifically referring to participants’ motivations, sources of motivations, and future expectations. Explanations and notes are presented in square brackets.
RESULTS
Table 5 shows different motivations, sources of motivations, and future expectations associated with the choice to study a mathematical career. Figure 2 shows the mathematical narrative identity participants’ in terms of motivations, sources of motivations, and expectations.
Table 5 Participants’ motivations, sources of motivations, and future expectations associated with the choice of a mathematical career.
| Motivations and expectations | Frequency | |
|---|---|---|
| Motivation 1 | Liking mathematics | 41 |
| Sources of motivation 1 | Good teachers | 19 |
| Self-efficacy beliefs | 15 | |
| Close relatives | 4 | |
| Motivation 2 | Self-efficacy beliefs | 37 |
| Sources of Motivation 2 | Mastery experience | 23 |
| Vicarious experience | 5 | |
| Motivation 3 | Want to become a good mathematics teacher | 24 |
| Sources of Motivation 3 | Good teachers and liking mathematics | 19 |
| Relatives who are teachers | 4 | |
| Motivation 4 | Personal recommendations | 9 |
| Motivation 5 | Free of charge | 3 |
| Expectations | Be a good mathematics teacher | 37 |
| Learn more mathematics | 20 | |
| Become a researcher | 13 | |
| Work in a company | 5 | |
We will now describe the most common motivations, sources of motivations, and future expectations identified. Titles in these sections correspond with the identified motivations and expectations; subtitles correspond with the sources of these motivations. We describe the motivation, source or expectation at the beginning of each section and then illustrate it with excerpts from the interviews. We highlight in italics the parts of the excerpts directly related to the description.
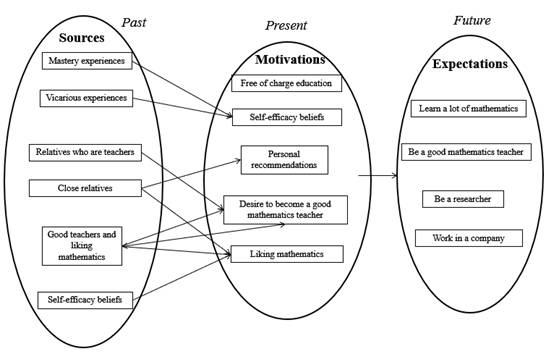
Figure 2 Mathematical narrative identity participants’ in terms of motivations, sources of motivations, and expectations. Note: Arrows denote attributions identified by at least one participant.
Motivation 1: “Liking mathematics”
Most participants explicitly expressed that their reason for studying mathematics was because they “like” mathematics. S07, S04, S13 and S22 expressed “liking mathematics” was a positive affective support for choosing a mathematical career.
S07: I chose a mathematical career because I like Mathematics, and I chose this university because I don’t have enough financial resources and I can afford this one.
S04: The main reason is because I like it, and someone told me to study what I like and not “torment myself”. I have liked mathematics since primary school, but this feeling increased in high school.
S13: It’s just because I like it; mathematics distracts me when I am hyperactive.
S22: I always liked mathematics and that’s what motivates me; it comes from deep inside of me.
Sources of “liking mathematics”
There are three types of sources for “liking” mathematics: (1) ‘good mathematical teachers’ who taught them to “like” mathematics, (2) being ‘good at mathematics’ (self-efficacy beliefs), and (3) ‘the interest’ experienced towards mathematics.
Good teachers
The participants described the positive experiences of having ‘good mathematics teachers’ who taught them to like mathematics as a source of ‘liking mathematics’. These are significant experiences that modified their relationships with mathematics, their source for liking mathematics.
S02: I chose mathematics because our high school teachers taught us to like it. They taught me how to work with it. Some of my classmates didn’t do it.
S33: But it was until high school that I decided to study mathematics. We had very good teachers there and they motivated me. This reinforced my love to mathematics, and the love to teach mathematics.
S36: I remember I liked mathematics since secondary school. I wanted to study a Mathematics Education career. There was a teacher named Arturo, who made us all feel comfortable in class; he had many teaching activities, his class was really entertaining. So, I wanted to become a mathematics teacher.
Self-efficacy beliefs
Another cause for liking mathematics is the perceived ability to solve mathematics tasks and the perception of being ‘good at mathematics’.
S22: Mathematics has been easy for me ever since I was a child; that influenced me to like it.
S29: I did not fail any [mathematics] course in primary school; this is when I started liking mathematics.
S32: There was a teacher in my first secondary grade who invited me to a contest to choose a student of each grade to represent our school in the mathematics Olympiad. This awakened my love for it.
S17: I studied high school in Bachilleres. It is a high-level school, and I liked it because I participated in the mathematics Olympiad. That’s when I started liking mathematics.
Close relatives
The participants perceived the experience of having a close relative who is a mathematician or mathematics teacher as the initial mediator for liking mathematics.
S02: My brother was a motivation; he spoke nicely about mathematics to me. Later, in high school, my teachers also did it. That is the way I started liking it. But it was also for me, mathematics sharpens your mind and I like to think a lot.
S31: It was really easy for me. And also, my uncle, a mathematics teacher; he challenged us with exercises and I liked it a lot.
S05: My dad has a PhD in mathematics from Spain. He teaches at Loreto Normal school. I remembered I have always liked fractions since I have memory.
S19: Yes (answered the question if he knows any mathematicians). My dad, he studied mathematics education; my calculus teacher. I want to become like him (his father), have the knowledge. I believe they overcome all challenges.
Motivation 2. Self-efficacy Beliefs
Many participants expressed that their decision to study a mathematics career came from their perception of how “easy” is mathematics for them and because they are ‘good at mathematics’.
S12: Operations are easy for me, they have always interested me: get the result, how to know it. I always wanted to be like my mother, be well prepared to get a good job, earn more.
S19: (I chose a mathematical career because) mathematics is easy for me and I like it; it is easy for me to use theorems, and I like it because I see problems as a personal challenge, and I also like the fact that I wouldn’t have much competition.
S45: I have an aunt who teaches physics. She keeps telling me how it was here: teachers interacting with students. I chose to study at MUA-Zacatecas because they have here a basketball team and you have the chance to play against other universities. Other motivation is that mathematics is easy for me.
Sources of Self-Efficacy Beliefs
Our data suggests there are two sources for self-efficacy beliefs: mastery experiences and vicarious experiences.
Mastery experiences
Participants narrated mastery experiences: positive experiences of success associated with mathematics. Some examples are getting good grades, winning first place prizes in mathematics at school, passing complex tests, and participating in mathematics competitions (local, regional, or municipal). These are personal experiences of success that, as a whole, form the source of belief in their abilities to solve mathematical tasks. Therefore, mastery experiences, a source of self-efficacy beliefs in mathematics, support the motivation of students to choose a mathematical career.
S09: I’ve done my mathematics tasks gladly since secondary school. In fact, the final test to finish eleventh grade consisted strictly of mathematics and it was not difficult for me.
S10: I was doing well in high school, tests also, so I was hoping “to be invited” (to a mathematics competition). The teacher chose the competitors through the tests, and I was selected.
S20: I hated mathematics in primary school. I became a student of 7 or 8 grades (she is referring to her mathematics grades, being 10 the top one and 1 the minimum) in secondary so I started liking mathematics. I raise my grades in high school to 9 or 10; I have good mathematics grades now.
In this way, mastery experiences are the source of self-efficacy beliefs in mathematics that support the students’ motivation to choose a mathematical career.
Vicarious experiences
Participants narrated vicarious experiences: positive experiences where they had higher mathematics achievement than their classmates; for example, they got better grades, won first prize, or completed their mathematics tasks first. These experiences are, from the point of view of the participants, successes achieved on a personal level that together form the source of belief in their abilities to solve mathematics tasks; these experiences also placed the participants at an advantage with respect to their classmates. The experiences of S19, S44 and S08 lead us to consider vicarious experiences as the source of self-efficacy beliefs in mathematics and support of the motivation to choose a mathematics career.
S19: What I liked about mathematics is that I always solved the exercises first. I used to go out for recess first. The next day, the teacher gave me more difficult problems than my classmates. It was odd to be treated differently. As the years passed, in secondary school, for example, I spoke about mathematics in class. Later, in high school, when mathematics courses started, I understand the teacher explanations and then I explain all in an easier way to my classmates.
S44: A friend and I were the only ones who understood derivatives and answered almost all in high school; everybody hated us for that. I think this is good.
S08: I remember a lot a positive experience with teacher Alcalá, my mathematics teacher in high school. My classmates felt happy if they got a 6 with him because it was really hard to pass his course, but I managed to get a 10.
Motivation 3. Desire “to become a good teacher”
A motivation to choose to study a mathematics career is the desire to become a teacher.
Sources of the Desire “to become a good teacher”
Good teachers and liking mathematics
The positive experiences of having ‘good mathematics teachers’ who taught them to like mathematics are not just sources for liking mathematics; they are also the source “to become good mathematics teachers”. Some participants considered a ‘good mathematics teacher’ to be one who teaches students ‘to like mathematics’ and, therefore, a personal and social model worthy of consideration. S36, S44 and Israel narrated how their positive experiences in class with their secondary teachers were their source to want to become a mathematics teacher.
S36: There was a teacher named Arturo Díaz, who made us all feel comfortable in class; he had many teaching activities, his class was really entertaining. So, I wanted to become a mathematics teacher.
S44: First of all because it is really easy for me, but it is also because I had a high school teacher who taught me really well and I want to be like him.
S33: It was in high school where I decided to study mathematics. I had really good teachers there, they motivated me, raised my love for mathematics and teaching.
S22 also expressed that the idea of teaching mathematics to children who do not like mathematics to help “future generations” emerged from watching his teachers in class. S14 used high intensity level words like “inspiration”, “passion”, “exciting” in her testimonies. Her experience with a good mathematics teacher is a key source for her desire to become a mathematics teacher.
S22: I was motivated by watching my teachers in class and telling myself how nice it would be to teach kids that don’t like mathematics. It is not necessary that everyone likes mathematics; they should discover it by their own means. I would like to help future generations.
S14: How exciting it is to imagine becoming like her (one of her teachers), such passion inspired me to become a teacher, to explain things. She teaches her students to like mathematics.
Teachers in family
Some participants considered that a source of their desire to become a mathematics teacher is the experience of having a teacher in their family. This relationship becomes a model to follow.
S12: I always wanted to be like my mother (university teacher), be well prepared to get a good job, earn more.
S19: Yes (answered the question if he knows any mathematician). My dad, he studied mathematics education, my calculus teachers. I want to become like him (his father), have the knowledge. I believe they put on challenges and overcome them.
S45: I have an aunt who teaches physics. She keeps telling me how it was here: teachers interact a lot with students.
S31: It was really easy for me. Besides, my uncle, a mathematics teacher, challenges us with exercises and I liked it a lot.
Expectation 1. “Be a good mathematics teacher”
Most of the participants explicitly expressed that they expected to work as high school or university teachers.
S23: I want to work as a teacher in high school or university … or training teachers.
S24: Being a high school or university teacher.
S27: Teaching, first of all, but I also like statistics. As I told you before, I also liked statistics in high school, so maybe I will focus on that.
S45: I think I am going to be a teacher. I imagine myself teaching math to other people.
We could also add the expectation to become a ‘good mathematics teacher’. This is a consequence of the positive experiences of having had “good teachers” who taught them to like mathematics and their perception that there are not many people who like mathematics.
S18: I will be successful if I become a good mathematics teacher in high school. I will fail if I don´t finish my career.
S25: Success is to become a good teacher, and teach good classes. Failure, I don’t know, I am a person who wouldn’t like to fail. I am afraid to fail because there are factors that could lead you to fail.
S36: For me, success would be to become a teacher who teaches well, and that everyone understands mathematics.
DISCUSSION AND CONCLUSIONS
Four thematic analyses of the data were conducted to explore the mathematical life of 47 Mexican students who chose to study a mathematical career. This analysis produced the following results: Motivations and sources of motivations of students’ choice to study a mathematical career are: (1) “liking mathematics”, which comes from positive experiences of having “good teachers”, self-efficacy beliefs, and positive experiences with close relatives, (2) self-efficacy beliefs, which stem from mastery and vicarious experiences, (3) the desire ‘to become a good mathematics teacher’, which comes from the experience of having “good teachers” who taught them to “like mathematics” and the experience of having relatives who are teachers, (4) personal recommendations, which are also vicarious experiences, and (5) free education. The future expectations of the participants are: (1) “to become a good mathematics teacher”, (2) ‘to learn a lot of mathematics’, (3) “to become a researcher” and (4) “to work in a company”.
Results as a Whole
Three motivations, two future expectations, and four sources of motivations stand out for their frequency of appearance in the testimonies. The motivations are ‘liking mathematics’, self-efficacy beliefs, and the desire to become “good teacher”. The expectations are “to become a good mathematics teacher” and “learn a lot of mathematics”. The sources of motivations are: self-efficacy beliefs, mastery experiences, vicarious experiences, and the experiences of having “good mathematics teachers”. Some implications of these results all together are:
The motivations identified in this research (self-efficacy beliefs, influence of mathematics teachers and relatives and liking mathematics( are consistent with the main factors favoring the choice of mathematics as a profession among Mexican women (Carrasco & Sánchez, 2016; Manzano & Sánchez, 2017; Sánchez et al., 2013). However, the identification of the sources of those motivations and expectations within the mathematical narrative identity concept allowed us to go beyond these investigations because it was possible to understand the moment when the choice of the mathematical career occurs within the context of their mathematical life histories.
The sources of motivations and future expectations are a group of significant experiences that participants consider positive. The sources that stand out are: (1) the experiences with “good teachers” are the source for their liking mathematics and (2) the source of their self-efficacy beliefs are vicarious and mastery experiences and, at the same time, the source for ‘liking mathematics’. Therefore, the motivations to choose a mathematical career are a combination of cognitive (self-efficacy beliefs) and affective (liking mathematics) aspects. This result reinforces the assumption that is at the heart of affective domain studies in mathematics education (McLeod, 1992): cognition and affect are complementary aspects. The “good teachers” or relatives who taught the participants to like mathematics are personal and professional models to follow. These experiences shaped the mathematical narrative identity of the participants.
Socio-Mathematical Context of the Participants
Even when we do not know the specific context of each participant, their motivations, future expectations, and their sources are coincident. Many components of their narrative identity share this characteristic. Why does this happen? What does this homogeneity in a potential heterogeneity mean? We venture the hypothesis of the existence of a socio-mathematical context (a social context linked to mathematics) in each of the participants’ individual contexts. We can even infer some characteristics of this socio-mathematical context:
“Liking mathematics” is highly appreciated and transmitted by “good teachers”. Liking mathematics is a fundamental highly appreciated characteristic and a complement of “being good at mathematics”. Liking mathematics and being good at mathematics distinguish any person who possess these traits. Therefore, ‘liking mathematics’ constitutes the affective source for choosing a mathematical career: a source of individual pleasure that students are willing to continue with their choice. The testimonies of the participants suggest that the main source for ‘liking mathematics’ is the experience of having “good teachers” who taught them to like mathematics. Taking into account the social characteristic of all human beings, we infer from the former argument that ‘liking mathematics’ is a consequence of social influence. The main agents of this influence are the teachers, who are the hosts of “liking mathematics”.
Being a mathematician is ‘being a mathematics teacher’. Most of the participants in this research wanted to become a mathematics teacher, even though MAU-Zacatecas is not a proper teacher training school. A possible explanation of this phenomenon is that there is no productive system that employs mathematicians in the state of Zacatecas; this is also the case in almost all states in Mexico. As a consequence, being a mathematics teacher is almost exclusively the only possible job after graduating as mathematician. This also explains the low frequency of the expectation of working in a company: almost all mathematicians they know are mathematics teachers and only those who know mathematicians working in companies, specifically in the area of statistics, expressed this expectation.
Studying a mathematics career is necessary to become a high school or university mathematics teacher. The choice of studying a mathematics career comes almost exclusively from the desire to become a mathematics teacher, even when there is a Mathematics Education specialization. One possible explanation is the fact that the professional training for mathematics teachers in Zacatecas, as in all the country, focuses only in primary and secondary school. These studies are attended in the Normal school at Zacatecas.
“Being good at mathematics” is highly appreciated. “Being good at mathematics” is highly appreciated among participants; it is considered an important component of the mathematical narrative identity. Therefore, “being good at mathematics” becomes a source of prestige, a positive characteristic that distinguishes them from their peers. From this point of view, the earned reputation of ‘being good at mathematics’ becomes the main motivation to choose a mathematical career. A possible source of this high appreciation of ‘being good at mathematics’ could be the fact that mathematics is considered to be “really difficult” and “being good in mathematics” is thus an expression of a superior intelligence in wide social sectors in Mexico, specifically in Zacatecas. This also explains the fact that many positive experiences are related to mathematics competitions. Competitions are perceived as settings for superior mathematical abilities.
On Psychological Models
Our results have similarities and differences from the psychological explanations of the choice of a mathematical career conducted under the theoretical frameworks of self-efficacy beliefs (Hackett, 1985, 1995; Hackett & Betz, 1995; Zeldin & Pajares, 2000), Expectancy-value theory (Eccles et al., 1983; Meece et al., 1990; Watt, 2005, 2006; Wigfield, 1994) and the social cognitive career theory (Lent & Brown, 2013; Lent et al., 1994). A similarity found with the expectancy-value theory is that self-efficacy beliefs and future expectations of success are the main motivational forces to choose a mathematical career. Like Bandura (1997) and Usher and Pajares (2009), we also found that self-efficacy beliefs are, at the same time, the source for ‘liking mathematics’ and for the expectation of ‘learning a lot of mathematics’. ‘Liking mathematics’ is also the source of the desire to become a “good mathematics teacher”. Therefore, we consider self-efficacy beliefs to be the central motivational force among participants in this research. Our results on the importance of future expectations of success as motivational forces to choose a mathematical career are consistent with the expectancy-value theory. Our results highlight the participants’ high appreciation for mathematics and for ‘being good at mathematics’.
There are two significant differences from the psychological explanations for the choice of a mathematical career: ‘liking mathematics’ and ‘the desire to become a good mathematics teacher’. We consider that the presence of these two motivational forces is the consequence of a socio-mathematical context among the participants; we described this earlier as a hypothesis. Another hypothesis, that could be investigated in future research, is that it is necessary to ‘like mathematics’ to choose a mathematical career.
In this sense, we also consider that the motivational force ‘the desire to become a good mathematics teacher’ reflects the social and cultural context of the participants because in Zacatecas, as in almost every state of Mexico, teaching mathematics is the only professional activity socially recognized for a mathematics professional. The former discussion highlights the importance of deepening understanding of the role of close and distant contexts of the students that influence their decision to choose a mathematics career. Results from these investigations could modify theories for further practical purposes.
AUTHOR CONTRIBUTION STATEMENT
The total contribution percentage for the conceptualization, preparation, and correction of this paper was as follows: G.M.S. 40 %., J.C.B. 30 % and L.J.S. 30 %.
DATA AVAILABILITY STATEMENT
Data sharing is not applicable since no new data was created or analyzed in this study. The data supporting the results of this study will be made available by the corresponding author, [G.M.S], upon reasonable request.