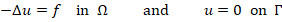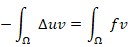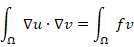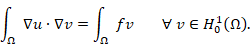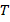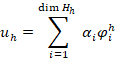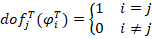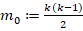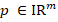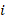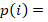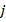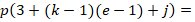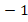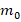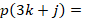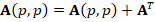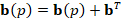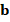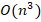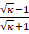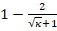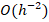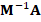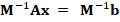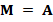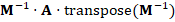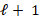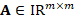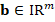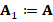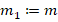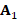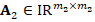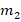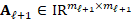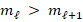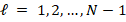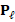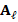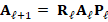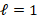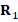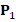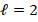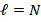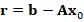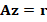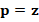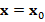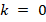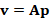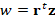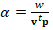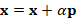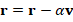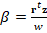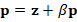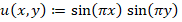Introduction
The main goal of this paper is to spread some computational aspects about the implementation of numerical methods for engineering, computer science and mathematics. The original contribution is not related to the mathematical analysis of the numerical methods for partial differential equations (PDE), but rather to explain the aspects about an efficient and clear computational implementation of a numerical method to approximate the solution of a PDE. We hope that the present work will be used for researchers and people interested in learning this kind of topics. It is important to note that there are papers and books which present in detail the methods that we discuss on this work. Nevertheless, there is not literature concerning to the explanation about the implementation of preconditioning techniques for linear systems associated to PDE.
In the first part of this article we discuss some general aspects related to the H1-conforming Finite Element Method (FEM). The FEM approach is considered as one of the well-established and useful technique for the numerical solution of problems in different fields, described with the use of partial differential equations with different types of boundary conditions. One of the most important aspects related to the success of FEM corresponds to the fact that it is based largely on the basic finite element procedures used: the formulation of the problem in variational form, the discretization of this formulation and the effective solution of the resulting finite element equations. These features do not change from different types of problems (see, e.g., Ciarlet (2002) and Johnson (2009), for details).
In general, the discrete problem for FEM requires to solve a linear system of the form 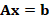 . This kind of systems are usually solved by iterative methods, which approximate the exact solution of the system with a certain number of accurate digits. The corresponding selection of the iterative solver depends on the properties of matrix
. This kind of systems are usually solved by iterative methods, which approximate the exact solution of the system with a certain number of accurate digits. The corresponding selection of the iterative solver depends on the properties of matrix 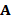 . For example, for symmetric and positive definite matrices the most popular method is the Conjugate Gradient (CG) method. However, in general, iterative solver depends on the condition number of the matrix of the system, which is related to the performance of the method. According to this, preconditioning techniques can be considered to accelerate convergence of the iterative methods. There are several types of preconditioning techniques, for example, one simple preconditioning technique of the system is to consider the equivalent system
. For example, for symmetric and positive definite matrices the most popular method is the Conjugate Gradient (CG) method. However, in general, iterative solver depends on the condition number of the matrix of the system, which is related to the performance of the method. According to this, preconditioning techniques can be considered to accelerate convergence of the iterative methods. There are several types of preconditioning techniques, for example, one simple preconditioning technique of the system is to consider the equivalent system 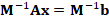 for some invertible matrix
for some invertible matrix 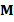 , which improve the conditioning of the system (see, e.g., Chen (2005)).
, which improve the conditioning of the system (see, e.g., Chen (2005)).
An important advance about preconditioning of large linear systems is given by multigrid techniques. The main idea in multigrid approaches is that any iterative solver works on a series of nested meshes, usually defined by a coarsening strategy, which depends on each mesh. Geometric grids are preferred for structured meshes, but algebraic multigrid (AMG) methods are better for unstructured meshes (see, e.g, Stüben (2001)). The AMG requires a simple relaxation process, usually Jacobi or Gauss-Seidel relaxation, and a suitable construction of the coarsening and interpolation operators. The goal of this kind of methods is to define the coarse level variables as a subset of the fine level variables. In other words, to split the fine level variables in two disjoint sets, one of them contains the coarse level variables, and the second one the remaining variables. In practice, the algorithms are usually based on heuristics. For example, for Beck’s algorithm, the coarsening strategy are constructed with the information of the graph associated to the matrix of the system (see Beck (1999)).
Finally, this paper is organized as follows. First, we present a classical FEM scheme for a Poisson equation with homogeneous boundary conditions and describe some aspects about its computational implementation. Next, we present an explanation about preconditioning techniques for primal-FEM formulations. In particular, we focus in the algebraic multigrid preconditioner from Beck (1999), since it is an efficient and simple preconditioner for our variational formulation. However, we include more details related to the construction of the meshes and the coarsening operators. In this way, we describe more aspects than Beck (1999) in order to allow more people to understand the main aspects of the computational implementation of multigrid approaches. In next section, we perform some numerical experiments and discuss the results, to describe the advantages and disadvantages of the preconditioner. Here, we present a complete MATLAB® code. Finally, we provide some conclusions and further work related to the preconditioning techniques for FEM schemes.
H1-conforming finite element method
In this section we present an example of a classical boundary value problem in order to justify the construction of the algebraic multigrid preconditioner. More precisely, given a bounded polygonal domain 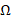 in
in 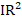 with boundary
with boundary 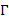 , we seek a scalar field
, we seek a scalar field 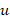 such that
such that
where 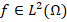 is a volume force, and as usual
is a volume force, and as usual 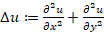 . Now, given
. Now, given 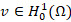 from the Poisson equation note that
from the Poisson equation note that
where, employing the Green’s formula in the left-hand side, we arrive at
for all 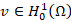 . In other words, we obtain a variational formulation of problem (1), which reads: Find
. In other words, we obtain a variational formulation of problem (1), which reads: Find 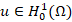 such that
such that
It is well known that this problem has a unique solution, which continuously depends of the source 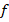 .
.
It is important to note from the new problem (2) that it only requires one order derivative and it establishes a function Hilbert space for the solution. On the other hand, the problem (1) does not allow us the explicit calculation of the solution 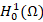 , because
, because 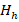 is an infinite dimensional space. A classical way of circumventing this drawback is the introduction of a finite dimensional subspace
is an infinite dimensional space. A classical way of circumventing this drawback is the introduction of a finite dimensional subspace 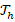 of the space
of the space 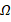 defined above consisting of piecewise polynomial continuous functions. More precisely, given
defined above consisting of piecewise polynomial continuous functions. More precisely, given 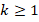 be a shape-regular triangulation of
be a shape-regular triangulation of 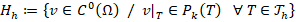 without the presence of hanging nodes, and an integer
without the presence of hanging nodes, and an integer 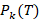 , it follows that
, it follows that
where, we let 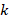 be the space of polynomials defined in
be the space of polynomials defined in 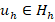 of total degree at most
of total degree at most 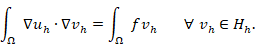 . Furthermore, we define a discrete variational formulation (i.e. Galerkin scheme) which reads: Find
. Furthermore, we define a discrete variational formulation (i.e. Galerkin scheme) which reads: Find 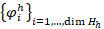 such that
such that
It is easy to check that the problem (3) has a unique solution 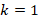 (see, for example, Ciarlet (2002)), which in fact is an approximation of the continuous solution
(see, for example, Ciarlet (2002)), which in fact is an approximation of the continuous solution 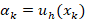 of problem (2). Furthermore, there is a basis
of problem (2). Furthermore, there is a basis 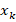 of
of 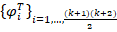 , and then
, and then
where, at least for 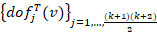 (low order),
(low order), 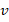 is called a Lagrange-type basis, because it holds that
is called a Lagrange-type basis, because it holds that 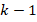 , for each vertex
, for each vertex 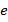 of
of 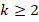 . In other words, the unknowns of the problem (3) correspond to the values of the solution at the vertices of the triangulation of
. In other words, the unknowns of the problem (3) correspond to the values of the solution at the vertices of the triangulation of 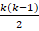 .
.
In general, the finite element method (FEM) for solving partial differential equations, is one of the high-order discretization schemes that has become a very active research area during the last decade. The main advantage of FEM approaches includes numerical solving of big partial differential systems through the analysis of small versions of the problem (on each element of 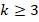 ). There are some variations of the FEM techniques, for example, the Galerkin scheme (3) is known as the classical finite element technique. On the other hand, there is a locally discontinuous version originally introduced in Cockburn (1998), and a virtual version presented in Beirão da Veiga (2013).
). There are some variations of the FEM techniques, for example, the Galerkin scheme (3) is known as the classical finite element technique. On the other hand, there is a locally discontinuous version originally introduced in Cockburn (1998), and a virtual version presented in Beirão da Veiga (2013).
Computational implementation
A fact of the development of FEM methods lies in the difficulty of its computational implementation. Actually, there is few literature detailing the computational implementation of FEM methods, for example, one of the most famous contribution was presented in Carstensen (2002). In the present paper, we do not present details of the implementation of FEM schemes, but in order to explain a preconditioning technique below, we consider some general aspects. Indeed, let 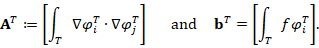 be an element of
be an element of 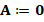 and define
and define 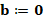 as the Lagrange basis on
as the Lagrange basis on 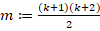 , which holds
, which holds
where 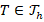 are the local degrees of freedom of
are the local degrees of freedom of 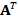 on
on 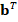 given by
given by
It is not difficult to see that the local basis 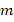 is a restriction of
is a restriction of 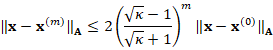 on
on 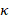 . Furthermore, the local discrete operators of
. Furthermore, the local discrete operators of 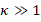 that contribute to the global linear system of problem (3) are given by
that contribute to the global linear system of problem (3) are given by
Using these discrete operators, we can assembly the global system of problem (3) following the algorithm:
Finally, for the incorporation of boundary conditions, we modify the matrix 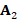 and the vector
and the vector 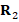 on the degrees of freedom corresponding to the boundary edges of
on the degrees of freedom corresponding to the boundary edges of 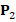 . The main idea here, is that each row of the linear system associated to the boundary degrees of freedom becomes exactly the boundary condition of problem (1). The incorporation can be done as we described before. However, in order to define a graph-strategy for the construction of an algebraic multigrid for the global linear system, we actually eliminate the degrees of freedom corresponding to the boundary edges of
. The main idea here, is that each row of the linear system associated to the boundary degrees of freedom becomes exactly the boundary condition of problem (1). The incorporation can be done as we described before. However, in order to define a graph-strategy for the construction of an algebraic multigrid for the global linear system, we actually eliminate the degrees of freedom corresponding to the boundary edges of  , and then the main unknowns of the system are the values of the solution in the interior nodes of
, and then the main unknowns of the system are the values of the solution in the interior nodes of 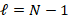 .
.
Preconditioning techniques
In practice, the linear system associated to problem (3) has a large number of unknowns, then, solving it by Gaussian elimination is quite slow, because this method has a complexity of 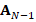 (see, for details, Saad (2003)). It is well-known (see, for example, Ciarlet (2002)) that
(see, for details, Saad (2003)). It is well-known (see, for example, Ciarlet (2002)) that 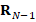 is a symmetric positive definite sparse matrix. Then, the Conjugate Gradient method (CG) is the most appropriate to approximate the system solution. However, for the
is a symmetric positive definite sparse matrix. Then, the Conjugate Gradient method (CG) is the most appropriate to approximate the system solution. However, for the 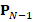 th iteration of CG holds that
th iteration of CG holds that
where 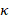 is the condition number of
is the condition number of 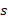 . It follows for
. It follows for 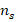 that the term
that the term 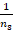 behaves like
behaves like 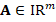 , which converges towards 1. Thus, inequality (4) predicts a slow convergence of the CG. On the other hand, the condition number of the matrix
, which converges towards 1. Thus, inequality (4) predicts a slow convergence of the CG. On the other hand, the condition number of the matrix 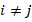 of linear system (3) has an asymptotic behavior of
of linear system (3) has an asymptotic behavior of 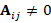 , which establishes that
, which establishes that  when we use very fine triangulations.
when we use very fine triangulations.
According to the previous discussion, it is necessary to use techniques that reduce the condition number of 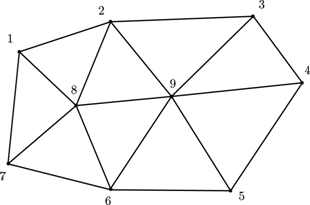 . In general, these techniques construct a nonsingular matrix
. In general, these techniques construct a nonsingular matrix 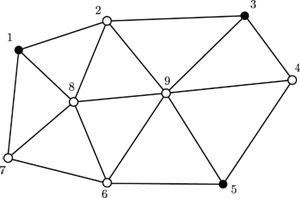 , which is called a preconditioner, such that the matrix
, which is called a preconditioner, such that the matrix 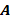 of the equivalent system
of the equivalent system 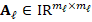 has a better condition number than the matrix
has a better condition number than the matrix 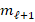 of the original system. Note that if
of the original system. Note that if 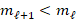 the system is solved immediately. In the case of CG, which requires symmetry in the matrix, the preconditioned system possess the matrix
the system is solved immediately. In the case of CG, which requires symmetry in the matrix, the preconditioned system possess the matrix 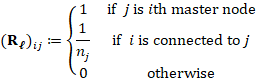 , which is symmetric. The method of solving a linear system by CG using some preconditioner, is known as a Preconditioned Conjugate Gradient (PCG). Some of the most common preconditioners for symmetric systems are Jacobi, Gauss-Seidel, Cholesky and multigrid techniques (see, for example, Saad (2003)).
, which is symmetric. The method of solving a linear system by CG using some preconditioner, is known as a Preconditioned Conjugate Gradient (PCG). Some of the most common preconditioners for symmetric systems are Jacobi, Gauss-Seidel, Cholesky and multigrid techniques (see, for example, Saad (2003)).
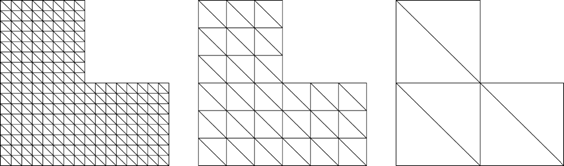
Multigrid techniques are the most attractive, because they reduce the size of the matrix of the linear system, by a sequence of nested meshes. Consequently, the number of iterations does not depend on the size of the matrix. More precisely, the matrix of the system is reduced by merging or deleting matrix entries. After the new matrix is generated, the corresponding new system is also recursively reduced with the help of the next mesh. Thus, this process is continued and stops when all meshes are used. This sequence of matrices is known as preconditioner levels. For example, in Figure 1 we show a sequence of meshes that satisfy the nested condition. This multigrid preconditioner is known as a geometric multigrid preconditioner (see Trottenberg (2000)).
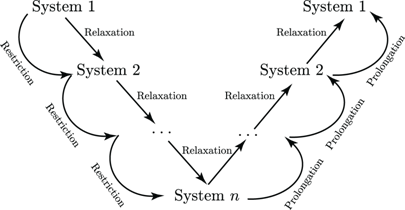
Once all the preconditioner levels have been generated, some steps of a relaxation method, such as Jacobi or Gauss-Seidel, are performed to solve the linear system. The approximation obtained is restricted to be used as the initial value of the auxiliary linear system given by the next lower level. In the same way this process is followed to the last level. Then, when the 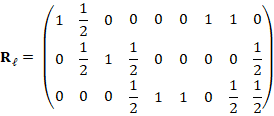 system is solved, the solution is prolonged to level
system is solved, the solution is prolonged to level  , where again some steps of a relaxation method are performed before moving on to the next level. This whole process is known as the V-cycle, which is illustrated in Figure 2.
, where again some steps of a relaxation method are performed before moving on to the next level. This whole process is known as the V-cycle, which is illustrated in Figure 2.
Unfortunately, in practice this sequence of nested meshes is not available, only the finest mesh. For this reason, it is necessary to generate this sequence through the fine mesh by agglomerating cells. In Cartesian meshes this process is simpler than in unstructured meshes, where in most cases the agglomeration of cells is not possible. For example, in the case of a triangle mesh, the agglomeration of triangles does not always result in another triangle. An alternative to solve this problem is to create the next level, using the graph that represents the matrix of the system and not by the graph that represents the mesh. This process is known as algebraic multilevel and was introduced by Ruge and Stüben (1987).
Methodology employed
The research proposed in this work considers a scientific approach to a particular problem in the area of Applied Mathematics. It is done under an exploratory quantitative approach. Also, the methods presented are commonly used in problems related to finding approximations for solutions of boundary problems in partial differential equations.
Protocol
A particular algebraic multigrid preconditioner is described in detail for the model problem, introduced in the previous section. We consider the method introduced by Beck (1999), which is an interesting work, but it does not show a clear description, making it not accessible for beginning readers. Thus, we intend to explain in more detail some relevant elements of the preconditioner.
A proposal for computational implementation for the Beck's preconditioner (see Beck (1999)) is presented in MATLAB. The code follows an object-oriented paradigm and, according to its organization, can even be used for the implementation of other multilevel preconditioners different than Beck's.
Once a code has been established in MATLAB for the Beck's preconditioner, it is shown its behavior, in order to demonstrate its usefulness. Thus, two model examples of the Poisson problem are considered, whose solution is approximated by FEM scheme. To study the behavior of the preconditioner, only the results related to the resolution of the associated linear systems will be reported. Essentially, the number of iterations performed by the Conjugated Gradient method is shown, when it is used without a preconditioner and with the Beck's preconditioner.
Additionally, the Incomplete Cholesky method will be considered to compare the behavior between preconditioners. For this purpose, we use meshes that do not exceed 800 000 degrees of freedom. Also, a maximum of 500 iterations and a tolerance relative to the first residue not exceeding 10-6, since these parameters are sufficient to illustrate the desired behavior. On the other hand, it is important to consider one of the examples with a high number of condition to observe that the AMG method retains adequate behavior, which will allow to demonstrate the robustness of this preconditioner.
The results are tabulated and plotted to show the good behavior of Beck's preconditioner over the other methods considered. In particular, the execution time will not be reported because its measurement depends on various factors that are not necessarily controlled by the authors. This should not be construed as a disadvantage of the AMG method, but as a consequence of implementation in software such as MATLAB and low performance computers.
Beckʼs algebraic multigrid preconditioner
In Ruge and Stüben (1987), Saad (1996), Beck (1999), Castillo and Sequeira (2013), the authors present several algebraic multigrid preconditioners. In particular, in this section we describe an algebraic multigrid technique proposed by Beck (1999), which take advantage of the characteristics of the finite element scheme (3). More precisely, the author identifies the geometric relations of the mesh in the sparse structure of the matrix.
The first algebraic multigrid preconditioner is presented in Ruge and Stüben (1987), which is based on partitioning the variables in each level of the multigrid in two sets by determining strong connection relations imposed by the structure of the matrix associated to the problem. The idea proposed in Beck's method is a simple coarsening strategy related to the Ruge-Stüben's method, which define a graph for the matrix using only the sparse structure and ignoring the strength of the connections, i.e. all connections are treated equally (the value of the entries of the matrix are not considered in each partition).
According to the previous discussion, we explain the algebraic multigrid approach using a general linear system:
where 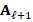 and
and 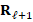 . Now we define
. Now we define 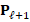 and
and 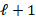 as the data of the first level, where the new right-hand side will be explained later. Thus, the main idea of this method is to reduce
as the data of the first level, where the new right-hand side will be explained later. Thus, the main idea of this method is to reduce 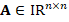 to a new matrix
to a new matrix 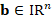 with
with 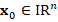 considerably smaller than
considerably smaller than 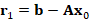 . Then, this process is repeated in order to generate
. Then, this process is repeated in order to generate 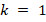 linear systems with associated matrices
linear systems with associated matrices 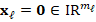 such that
such that 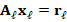 , for
, for 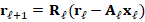 , where
, where 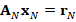 is the maximun number of levels selected such that the last linear system can be solved efficiently.
is the maximun number of levels selected such that the last linear system can be solved efficiently.
To perform this procedure for each level 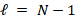 we construct matrices
we construct matrices 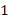 and
and 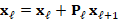 in order to compute
in order to compute 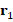 . The matrix
. The matrix 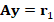 is known as the restriction operator, whereas the matrix
is known as the restriction operator, whereas the matrix 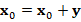 is the prolongation operator. Using these operators, we obtain the matrix
is the prolongation operator. Using these operators, we obtain the matrix 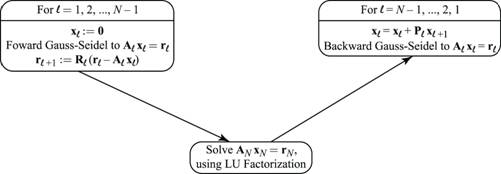 from the following algorithm, which define the matrices of each level of the algebraic multigrid preconditioner, summarized in Table 1.
from the following algorithm, which define the matrices of each level of the algebraic multigrid preconditioner, summarized in Table 1.
Table 1 Summary of matrices in each level of Beck’s algebraic multigrid preconditioner.
Note: derived from research.
Finally, in order to describe the construction of each level of the preconditioner (i.e.  and
and 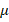 ), in the following section we analize a coarsening strategy for sparse matrices, which allow us to construct the restriction and prolongation operators. After that, we introduce the iterative solver based on the V-cycle approach.
), in the following section we analize a coarsening strategy for sparse matrices, which allow us to construct the restriction and prolongation operators. After that, we introduce the iterative solver based on the V-cycle approach.
Coarsening
We now explain the classical design of the coarsening technique briefly described in Section 3 of Beck (1999). In addition, we incorporate more explanations and examples, including a suggestion for a MATLAB® implementation.
The main idea of the coarsening algorithm is to select a favorably distributed subset of the matrix nodes (i.e. indexes of rows and columns), which are to become the nodes of the new matrix (coarse grid matrix). More precisely, the nodes for the new matrix are known as master nodes, whereas the remaining (which will be dropped) are known as slave nodes. In particular, this coarsening algorithm satisfies that the number of unknowns is reduced substantially in every coarsening step, and the coarse grid matrices preserve the sparsity pattern of the fine grid matrix, that is, coarse grid basis functions retain a local support and a restricted overlap with neighboring ones.
According to Section 3 in Beck (1999), there are three rules for the selection of master nodes. That is:
No master node may be directly connected to another master node.
There should be as many master nodes as possible.
The values of all master nodes are transferred with weight 1. The value for a slave node
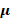 is interpolated from the
is interpolated from the 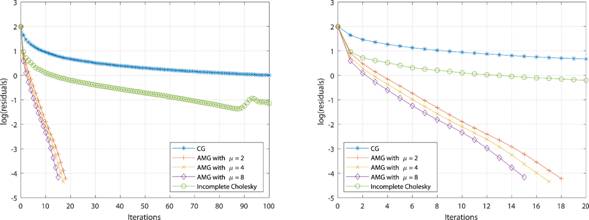 master nodes it is connected to, where each master node contributes with weight
master nodes it is connected to, where each master node contributes with weight 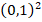 . This is used in the construction of the restriction operator below.
. This is used in the construction of the restriction operator below.
Here is important to remember that every Dirichlet node have been eliminated in order that the sparsity pattern of the matrix allows the separation of its nodes into two disjoint sets.
On the other hand, let 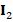 be a symmetric sparse matrix. Now consider the graph that represents this matrix. More precisely, letting
be a symmetric sparse matrix. Now consider the graph that represents this matrix. More precisely, letting 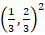 nodes (numbering from 1 to
nodes (numbering from 1 to 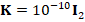 ), we say that node
), we say that node 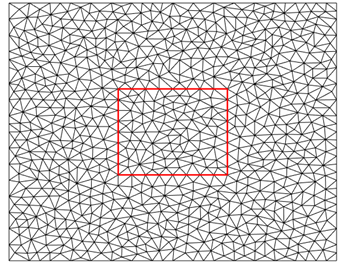 is connect to node
is connect to node 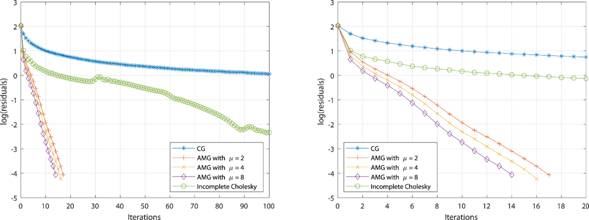 , with
, with 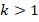 , if entry
, if entry 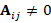 . For example, consider matrix
. For example, consider matrix
which graph is given in Figure 3.
Note: derived from research.
Note that the graph follows from the sparsity pattern of 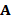 . Now, we select one node to be our first master node. For example, we take node 1 and then, every neighboring node of 1 will be mark as slave node (i.e. node 2, 7 and 8). From the remaining nodes (3, 4, 5, 6 and 9) take the next master node. We take node 3, and then its neighbors (2, 4 and 9) are now slave nodes. Following this procedure, we take node 5 as master node and mark its neighbors as slaves. In Figure 4, we summarize the previous classification strategy.
. Now, we select one node to be our first master node. For example, we take node 1 and then, every neighboring node of 1 will be mark as slave node (i.e. node 2, 7 and 8). From the remaining nodes (3, 4, 5, 6 and 9) take the next master node. We take node 3, and then its neighbors (2, 4 and 9) are now slave nodes. Following this procedure, we take node 5 as master node and mark its neighbors as slaves. In Figure 4, we summarize the previous classification strategy.
Note: derived from research.
Observe that the coarsening process operates in a geometric way by sequentially choosing a master node and eliminating the corresponding neighboring nodes of the graph. Moreover, a primary criterion for selecting the next master node is to take the node with the minimum number of connections (taking into account the eliminations). And a secondary criterion is to follow the original numbering. We use the first choice by listing the nodes in ascending order, according to the number of non-zero elements of each row of 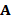 . We now present a MATLAB® implementation for previous coarsening strategy.
. We now present a MATLAB® implementation for previous coarsening strategy.
% --------------------------------------------------------
% This function marks the master and slave nodes for a
% given matrix A of order m.
% ---------------------------------------------------------
% marked: is a m-size vector which contains 0 on its ith
% component if node i is slave. Otherwise, node
% i is master, and the ith component of the vector
% contains a new numbering for node i.
% sizeM: is the number of master nodes.
% ---------------------------------------------------------
function (marked, sizeM) = coarsening(A)
m = length(A); % Order of the matrix
%
nnzRow = zeros(1, m); % Number of non-zero elements of
% A by row
for i = 1 : m
nzRow(i) = nnz( A(i,:) );
end
(~, idxRow) = sort(nnzRow); % Sort indices according to
% the number of non-zero elements
% -----------------------------------------------------
% First, every node is marked with a negative number,
% in order to indicate that the node is unmarked.
marked = -1 * ones(1, m);
sizeM = 0;
% Using the symmetry of A, we follow the columns of A:
for j = idxRow
c = A(:,j); % Define the jth column of A
I = find(c); % Find indices of non-zero elements
if marked(j) == -1 % Unmarked node
% Node j has not been marked yet. That's
% why it will be marked as master and its
% neighboring nodes will be slaves.
% ---------------------------------------------
% Mark its neighbors as slaves:
marked(I) = 0;
% Mark as master:
sizeM = sizeM + 1; % A master node was found
marked(j) = sizeM; % New numbering for node j
end
end
end
Using function coarsening() with the matrix defined in (5), we obtain the following results
marked = 1 0 2 0 3 0 0 0 0
sizeM = 3
which establish that the current node 1, 3 and 5 will be, respectively, the node 1, 2 and 3 of the matrix in the next level of the preconditioner.
Restriction and prolongation operators
After choosing master nodes, we can assemble the restriction matrix 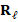 . Indeed, given
. Indeed, given 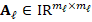 the matrix of level
the matrix of level 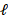 , let
, let 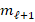 be the number of master nodes obtained by the previous coarsening algorithm, such that
be the number of master nodes obtained by the previous coarsening algorithm, such that 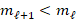 . Then, letting
. Then, letting 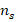 be the number of neighboring master nodes of slave node
be the number of neighboring master nodes of slave node 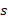 , we define
, we define 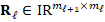 as
as
Observe that the values of all master nodes are transferred with weight 1, whereas the values of all slave nodes are interpolated from its neighboring master nodes. This selection is strongly related to the definition of the degrees of freedom of scheme (3), at least for 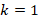 . For example, the restriction matrix for graph in Figure 4 is given by
. For example, the restriction matrix for graph in Figure 4 is given by
On the other hand, Beck (1999) suggests a similar construction for prolongation operator 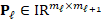 . However, in order to preserve symmetry in the matrix of the next level, we define
. However, in order to preserve symmetry in the matrix of the next level, we define
Finally, using the restriction and prolongation operators we define 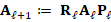 as the matrix of next level. Then, we continue the process employing
as the matrix of next level. Then, we continue the process employing 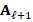 to construct
to construct 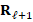 and
and 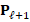 . The stopping criterion corresponds to a maximum order for the last matrix. In addition, the last matrix presents a considerably reduction in the order of the original matrix, then direct methods (for example LU factorization) can be used for solver effects.
. The stopping criterion corresponds to a maximum order for the last matrix. In addition, the last matrix presents a considerably reduction in the order of the original matrix, then direct methods (for example LU factorization) can be used for solver effects.
According to the above discussion, we now propose the following computational implementation for the construction of all the matrices required by the algebraic multigrid preconditioner.
% ---------------------------------------------------------
% This function constructs the levels of the algebraic
% multigrid preconditioner.
% ---------------------------------------------------------
% A: is a mxm symmetric positive definite sparse matrix.
% maxSize: is the maximum size of the matrix in the last
% level.
% MA: is a list of matrices for coarse matrices
% MR: is a list of matrices for restriction operators
% MP: is a list of matrices for prolongation operators
% L: is the lower triangular matrix of the LU factorization
% of the last matrix A
% U: is the upper triangular matrix of the LU factorization
% of the last matrix A
% steps: is a list of the Smoothing steps for Gauss-Seidel
% ---------------------------------------------------------
function (MA, MR, MP, L, U, steps) = createLevels(A, maxSize)
MA = {}; % List of matrices
MR = {}; % List of restriction operators
MP = {}; % List of prolongation operators
% ----------------- Create the levels -----------------
numLevels = 0; % Number of levels
m = length(A); % Order of the matrix
while m >= maxSize
% Mark nodes as Master and Slave
(marked, sizeM) = coarsening(A);
% Construct Restriction matrix
R = sparse(sizeM, m);
for j = 1 : m
if marked(j) == 0
% -------------- SLAVE NODE ---------------
c = A(:,j); % Define the jth column of A
I = find(c); % Find indices of non-zero
% elements of the jth column of A
(~, ~, I) = find( marked(I) ); % Find indices
% of master nodes
% arround node j
nnz = length(I); % Number of neighboring master
% nodes of node j
R(I, j) = 1 / nnz;
else
% -------------- MASTER NODE --------------
R(marked(j), j) = 1;
end
end
% Store matrices on lists
numLevels = numLevels + 1;
MR{numLevels} = R;
MA{numLevels} = A;
MP{numLevels} = R';
% Preparations for next level
A = R * A * R';
m = sizeM;
end
% ---- Compute LU Factorization for the last matrix ---
(L,U) = lu(A);
% ---------- Create list of smoothing steps -----------
steps = zeros(numLevels, 1);
for i = 1 : numLevels
steps(i) = i + 1;
end
end
The vector steps, defined by function createLevels(), contains the number of relaxation steps for the V-cycles of the preconditioner. For simplicity, we perform 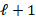 relaxation steps for level
relaxation steps for level 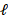 .
.
V-cycles iteration
According to the previous sections, we now aim to present an iterative solver for linear system 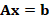 based on the iterative refinement method (see, e.g, Wilkinson (1994) or Burden, Faires and Burden (2015)). Indeed, given
based on the iterative refinement method (see, e.g, Wilkinson (1994) or Burden, Faires and Burden (2015)). Indeed, given 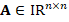 ,
, 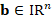 , and
, and 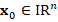 an initial guess, we consider the following algorithm
an initial guess, we consider the following algorithm
For 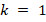 until number of V-cycles do
until number of V-cycles do
Perform some steps of a relaxation method to the system 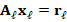
End For
Perform some steps of a relaxation method to the system 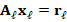
End For
End For
Here 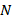 is the total number of levels defined by createLevels() in the previous section. Notice that, after the calculation of the first residual
is the total number of levels defined by createLevels() in the previous section. Notice that, after the calculation of the first residual 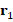 and according to the iterative refinement method, we need to solve alternative linear system
and according to the iterative refinement method, we need to solve alternative linear system 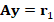 in order to make the correction
in order to make the correction 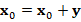 . Thus, for solving
. Thus, for solving 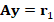 we perform some steps of a relaxation method, such as the Jacobi iteration or Gauss-Siedel iteration. Next, we restrict the new residual to the following level. We continue this process until level
we perform some steps of a relaxation method, such as the Jacobi iteration or Gauss-Siedel iteration. Next, we restrict the new residual to the following level. We continue this process until level 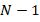 . In last level, we compute the solution of the corresponding system employing a direct solver. In particular, for simplicity we use LU Factorization, but Cholesky Factorization is also a good choice. Finally, through each level, the solution is prolonged and updated until a new approximation to the original system is obtained.
. In last level, we compute the solution of the corresponding system employing a direct solver. In particular, for simplicity we use LU Factorization, but Cholesky Factorization is also a good choice. Finally, through each level, the solution is prolonged and updated until a new approximation to the original system is obtained.
It is important to observe that the original residual 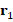 is not changed. In addition, in order to preverse symmetry (see, e.g., Chen (2005)), we utilize Forward Gauss-Seidel iteration when each residual is restricted. On the other hand, we use Backward Gauss-Seidel iteration when each residual is prolonged. We end this section by illustrating the definition of every V-cycle in Figure 5. The MATLAB® code for this solver will be presented in function apply() in a section below.
is not changed. In addition, in order to preverse symmetry (see, e.g., Chen (2005)), we utilize Forward Gauss-Seidel iteration when each residual is restricted. On the other hand, we use Backward Gauss-Seidel iteration when each residual is prolonged. We end this section by illustrating the definition of every V-cycle in Figure 5. The MATLAB® code for this solver will be presented in function apply() in a section below.
Note: derived from research.
Preconditioned Conjugate Gradient Method
The V-cycle iteration is a solver for the linear system 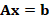 . However, this is used as a preconditioner for the usual preconditioned conjugate gradient (PCG) method. More precisely, consider the PCG method (see, e.g., Saad (2003)) given by
. However, this is used as a preconditioner for the usual preconditioned conjugate gradient (PCG) method. More precisely, consider the PCG method (see, e.g., Saad (2003)) given by
Next, note from steps 2 and 11 that it is necessary to solve linear systems for every preconditioner. In this case, we will use the iterative solver defined in previous section.
Complete MATLAB® code
In this section, we propose a simplified computational implementation for the algebraic multigrid preconditioner introduced by Beck (1999). All procedures described in the foregoing sections are unified in a MATLAB® class called amgBR, which is presents at end of this paper (see Annex 1).
On the other hand, consider the following implementation for PCG method:
% ---------------------------------------------------------
% Preconditioned conjugate gradient method.
% ---------------------------------------------------------
% P: is a preconditioner
% A: is the matrix of the linear system
% b: is the right-hand side of the linear system
% x: is an initial guess
% tol: tolerance
% iterMax: is the maximum number of iterations
% iterUsed: is the number of iterations used
% ---------------------------------------------------------
function (x, iterUsed) = pcg(P, A, b, x, tol, iterMax)
r = b - A*x;
z = P.apply(r);
p = z;
nrm0Tol = tol * norm(r);
iterUsed = 0;
while iterUsed < iterMax && norm(r) >= nrm0Tol
v = A * p;
w = r'*z;
alpha = w / (v'*p);
x = x + alpha * p;
r = r - alpha * v;
z = P.apply(r);
beta = (r'*z) / w;
p = z + beta * p;
iterUsed = iterUsed + 1;
end
end
Then, the class amgRB, defined at the beginning of this section, can be used as in the following example:
P = amgRB(A, maxSize, numVCycles); % Define preconditioner
x0 = zeros(length(A),1); % Define initial guess
(x, k) = pcg(P, A, b, x0, 1.0e-6, 1000)
where A, b, maxSize, and numVCycles must be previously defined.
Numerical experiments
In this section, we carry out two numerical experiments to validate our code and illustrate the behavior of the algebraic multigrid preconditioner proposed in Beck (1999) at least for 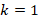 . For all the examples, triangular meshes were generated using the software TRIANGLE developed by Shewchuk (1996). In addition, we modify the continuous problem (1) to
. For all the examples, triangular meshes were generated using the software TRIANGLE developed by Shewchuk (1996). In addition, we modify the continuous problem (1) to
where 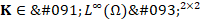 is a uniformly positive definite tensor describing the material properties of
is a uniformly positive definite tensor describing the material properties of 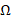 . The idea of introducing the tensor
. The idea of introducing the tensor 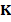 is to consider a problem with high condition number (see Example 2 below).
is to consider a problem with high condition number (see Example 2 below).
The numerical results were obtained using the MATLAB® code introduced in previous section. The corresponding linear systems are solved by the Conjugate-Gradient method with a tolerance of 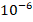 , 500 as the maximum number of iterations, and taking as initial guess the vector which each entry is equal to one. Here, we use ndofs for the number of unknown of each linear system, that is, the value of
, 500 as the maximum number of iterations, and taking as initial guess the vector which each entry is equal to one. Here, we use ndofs for the number of unknown of each linear system, that is, the value of 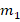 . In addition, we introduce the integer
. In addition, we introduce the integer 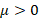 in order to define the number of smoothing steps used by Gauss-Seidel methods. More precisely, for a level
in order to define the number of smoothing steps used by Gauss-Seidel methods. More precisely, for a level 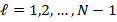 , the number of relaxation steps are given by
, the number of relaxation steps are given by 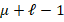 . Moreover, we only use one V-Cycle for the AMG preconditioner. Finally, we also consider the classical Incomplete Cholesky preconditioner (see, e.g, Saad (2003)) as an alternative solver.
. Moreover, we only use one V-Cycle for the AMG preconditioner. Finally, we also consider the classical Incomplete Cholesky preconditioner (see, e.g, Saad (2003)) as an alternative solver.
In Example 1, we consider 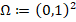 ,
, 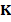 the identity matrix, and choose the data
the identity matrix, and choose the data 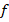 so that the exact solution is given by
so that the exact solution is given by
for all 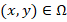 . In Figure 6, we show a triangular decomposition for our domain obtained with TRIANGLE, where it is important to note that only unstructured meshes are used.
. In Figure 6, we show a triangular decomposition for our domain obtained with TRIANGLE, where it is important to note that only unstructured meshes are used.
Note: derived from research.
In Table 2, the results of the AMG preconditioner studied in this work are presented and compared to the classical CG method. We also obtain results for the Incomplete Cholesky method. The AMG method shows an improvement with respect to the classical methods, in terms of the number of iterations and the obtained residuals. For instance, note that the CG method almost never converges after 500 iterations for any of the experiments, while the Incomplete Cholesky method, although converging, the number of iterations is significantly increasing compare to AMG. In fact, the most important aspect to observe is that the AMG method always converges, and its number of iterations does not exceed 22 (considering all experiments), which allow us to see the robustness of the preconditioner. In addition, these iterations decrease as the parameter 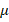 increases, which establishes that several relaxation steps carry out fewer iterations, but will require more execution time, which is not shown in this paper because the measurement of time depends on multiple reasons related to particular situations.
increases, which establishes that several relaxation steps carry out fewer iterations, but will require more execution time, which is not shown in this paper because the measurement of time depends on multiple reasons related to particular situations.
Table 2 Example 1: Number of iterations and last residual.
Note: derived from research.
On the other hand, for the last mesh of 782939 degrees of freedom, we show in Table 3 a description of each level created by the AMG preconditioner. There, it is possible to see a significant reduction in the unknowns of the system. Finally, in Figure 7, we show that the residuals of the AMG method decreases faster.
Table 3 Example 1: Description of the levels of the AMG preconditioner for the mesh of 782939 degrees of freedo m
| Level | Order of the matrix | Number of non-zero entries |
|---|---|---|
| 1 | 782939 | 5472891 |
| 2 | 207841 | 2001147 |
| 3 | 42911 | 478627 |
| 4 | 7873 | 94105 |
| 5 | 1364 | 16372 |
| 6 | 237 | 6010 |
Note: derived from research.
Note: derived from research.
In Example 2, we consider the model problem on a domain with two different materials and an isotropic diffusion. More precisely, 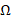 consists of two squares, the first one is the unit square
consists of two squares, the first one is the unit square 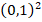 , which has diffusion
, which has diffusion 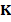 equal to the identity matrix
equal to the identity matrix 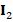 , and within this square, a second square
, and within this square, a second square 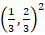 with diffusion
with diffusion 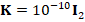 . An example of the meshes for this domain is shown in Figure 8. Here the source function
. An example of the meshes for this domain is shown in Figure 8. Here the source function 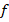 is equal to zero.
is equal to zero.
In Table 3, we note that the AMG method performs a behavior similar to the obtained in Example 1, although the condition number of the system matrix in Example 2 is 109 greater than the condition number of Example 1. Thus, the AMG preconditioner does not show a significant change by increasing the conditioning of the matrix. Finally, in Table 4, a level description is presented, whereas in Figure 9, we show the residuals history, all this for the last mesh used in Table 4.
Table 4 Example 2: Number of iterations and last residual.
Note: derived from research.
Table 5 Example 2: Description of the levels of the AMG preconditioner for the mesh of 781506 degrees of freedom.
| Level | Order of the matrix | Number of non-zero entries |
|---|---|---|
| 1 | 781506 | 5458246 |
| 2 | 208021 | 2003307 |
| 3 | 42978 | 477048 |
| 4 | 7909 | 93343 |
| 5 | 1404 | 16444 |
| 6 | 250 | 4927 |
Note: derived from research.
Conclusions and future directions
In this article, we have described an object oriented implementation of the algebraic multigrid preconditioner introduced in Beck (1999), applied to elliptic problems using unstructured triangular meshes. The numerical experiments presented illustrate the appropriate behavior of the preconditioner. In particular, there is not a considerable increase in the number of iterations of PCG method even when the mesh size is decreased.
Anexo en archivo pdf In the future we would like to consider a new coarsening strategy, which allow us a better selection for master nodes. In addition, in this work we used only H1-conforming elements in order to explain the preconditioner in a cleaner way. However, the results presented here can be extended to the case of H(div)-conforming elements. Finally, we are interesting to develop an extension of the Beck's preconditioner to polynomial bases of degree higher than one (that is, 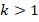 ), which implies that the degrees of freedom are not only in the vertices, and then the coarsening technique would not be accurate.
), which implies that the degrees of freedom are not only in the vertices, and then the coarsening technique would not be accurate.