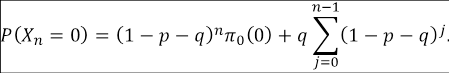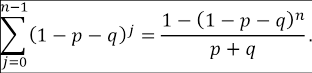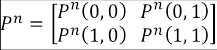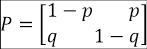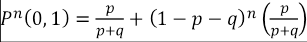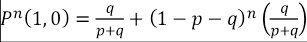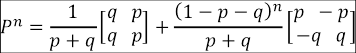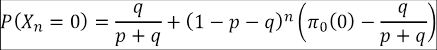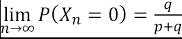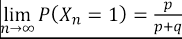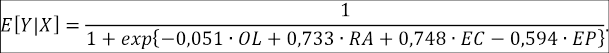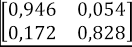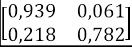Introducción
La masificación de la educación superior chilena de los últimos 20 años, dentro de un contexto de alta privatización, no ha redundado en mayores niveles de equidad educativa, especialmente si se toma en cuenta que solo el 3,4 % de las personas del primer quintil de ingreso per cápita (el 20 % de menores recursos) culmina la educación superior (Encuesta de Caracterización Socioeconómica Nacional (CASEN, 2013). Igualmente, el 64,4 % de quienes ingresan a la educación superior en Chile es primera generación en este nivel formativo; sin embargo, su egreso no está garantizado al presentar un mayor riesgo de deserción que estudiantado heredero de este nivel, con casi tres veces más posibilidad de desertar (Castillo & Cabezas, 2018). En efecto, uno de los principales problemas que ha venido enfrentando el sistema de educación superior chileno es el concerniente a la deserción. Este fenómeno alcanzó un 27,6 % para la cohorte 2016 (Servicio de Información de Educación Superior [SIES], 2017), cuyas consecuencias se hacen sentir en la reproducción de la pobreza o en la frustración profesional (González, 2006), entre otros factores.
A la luz de lo anterior y desde una perspectiva de responsabilidad social universitaria, Schmelkes (2001) establece que una educación de calidad tiene que ser eficaz, es decir, que se logren los objetivos propuestos para todo el alumnado, además de eficiente, es decir, que se atienda con responsabilidad la relación existente entre los resultados alcanzados y los costos consignados para obtenerlos. Ello pone de manifiesto la importancia que tiene el establecer políticas educativas destinadas a maximizar las tasas de retención, contrapunto de la deserción (Himmel, 2002), pues no basta con incrementar el acceso de estudiantes al sistema, es también necesario disminuir el número de estudiantes que lo abandonan.
Los estudios que abordan el problema de la deserción universitaria se sustentan, mayoritariamente, en los modelos teóricos desarrollados inicialmente por Bean (1980), Spady (1970) y Tinto (1975), modelos diferenciados en función de los factores que condicionan y precipitan la deserción estudiantil. Mientras que en los modelos de Bean y Spady los factores son externos a la universidad, en los modelos de Tinto depende de la integración que logre el estudiantado con el ambiente académico y social de la universidad (Castaño, Gallón, Gómez y Vásquez, 2004), aunque la evidencia indica que el modelo más realista necesariamente incorpora una combinación de elementos internos y externos a la institución (Larroucau, 2015). Incluso existen diferenciales que atienden el tipo de deserción detectada, ya sea deserción temporal, explicada principalmente por razones vocacionales, socioculturales y motivacionales, o deserción permanente, explicada por razones socioeconómicas (Canales & De los Ríos, 2018).
Considerando lo antepuesto, se ha acreditado que el rendimiento académico en la universidad es la variable más influyente en la permanencia del estudiantado en su institución (Esteban et al, 2017). En efecto, el 45 % de los abandonos en los primeros dos años de universidad se atribuyen al rendimiento académico, aunque dicho efecto se reduce al avanzar de los años (Stinebrickner, 2014). En el mismo sentido, estudiantes con mayores promedios de calificaciones en la escuela secundaria tienen más probabilidades de finalizar con éxito los estudios superiores, en comparación con quienes presentan promedios más bajos (Farmer & Hope, 2015), aunque dicho efecto es cuestionado por Santelices, Catalán, Horn y Venegas (2018), quienes sugieren que el efecto del ranking de egreso de la escuela secundaria, asociado al rendimiento comparado entre pares, es marginal para predecir la persistencia universitaria. Al rendimiento también se le adicionan factores como el sexo del estudiantado y el currículo académico de las carreras (Paura & Arhipova, 2014).
Por su parte, Roso, Jiménez y García (2016) sugieren que estudiantes con bajos niveles emocionales tienen mayor probabilidad de abandonar sus estudios. En efecto, el factor de proximidad o lejanía con la universidad, el desagrado con la carrera y los problemas de relaciones personales pesan al momento de desertar de la universidad (Pascual, 2017). Aquí destaca la vocación y la adaptación social y académica lograda por el estudiantado (Bernardo, Esteban, Fernández, Cervero, Tuero & Solano, 2016). Es más, fenómenos con incipientes estudios en América Latina, como el compromiso estudiantil (Aspeé, González & Cavieres, 2018), tienen una asociación con la disminución de la deserción evidenciada (Pineda-Báez et al. 2014). En Chile, el trabajo de Carvajal, González y Sarzoza (2018) mostró que el orden de lista, los ramos aprobados, el estado civil y la educación del padre, son variables que intervienen de forma directa en la deserción de estudiantes de primer año de una facultad de ciencias.
Adicional a los factores personales antes enunciados sucintamente, existen factores institucionales que condicionan y, en algunos casos, explican la deserción. Por ejemplo, se ha demostrado que el acceso a ayuda financiera, especialmente mediante préstamos para sustentar el costo de la educación, es sustantivo para mantenerse en el sistema y persistir en los estudios, esto con independencia del grupo socioeconómico al que se pertenezca, y que a su vez ciertos subsidios dirigidos a estudiantes de bajos ingresos tienen un alto efecto de retención en instituciones técnicas (Santelices, Catalán, Kruger & Horn, 2016). De esta manera, y teniendo presente el conjunto de factores que interviene en el fenómeno de la deserción, puede ser explicada por un conjunto de cuatro dimensiones: la dimensión individual del estudiantado, la dimensión socioeconómica, la dimensión característica del colegio de origen y finalmente la dimensión institucional (Larroucau, 2015).
En Chile, y luego de que Himmel (2002) estableciera que los estudios destinados a reconocer y cuantificar los motivos que llevan a estudiantes a desertar del sistema de educación superior fueran insuficientes y fundamentalmente centrados en cuantificar la magnitud del fenómeno, se dio un fuerte impulso a su análisis con trabajos de intenciones más explicativas (Díaz, 2008; Donoso y Schiefelbein, 2007; Canales y De los Ríos, 2007; Díaz, 2009), lo que ha permitido ir caracterizando este fenómeno. Tal es así, que el acervo desarrollado respecto de la deserción ha transitado desde el uso de modelos teóricos que explican la deserción, a modelos basados en evidencias (Carvajal et al. 2018; Pérez, Escobar, Toledo, Gutiérrez & Reyes, 2018). Un siguiente paso en este derrotero, y de lo cual intenta hacerse cargo este trabajo, es la construcción de un conjunto de herramientas estadísticas (indicadores) que ofrezcan información de utilidad social (Tejedor, 2018) a las instituciones, de manera que puedan implementar acciones destinadas a fortalecer la permanencia de sus estudiantes en el sistema de educación superior.
En consideración a los párrafos precedentes y teniendo en cuenta lo importante que es para las instituciones de educación superior contar con indicadores estandarizados que aborden el fenómeno de la deserción, se ha planteado como objetivo la construcción de un índice que permita estimar la probabilidad de deserción de estudiantes en un enésimo momento, esto es, detectar las probabilidades de deserción por períodos de avance curricular o semestres, lo que permite focalizar las acciones correctivas en aquellos periodos más críticos. Dicha estimación del riesgo a la deserción individual se basa en el uso de las cadenas de Markov. Las cadenas de Markov son una familia de procesos estocásticos, definidas como una secuencia de variables aleatorias en la que la dependencia de los eventos sucesivos está dada solo por una unidad de tiempo, es decir, que la probabilidad futura del proceso depende únicamente del estado actual del proceso y no está influenciada por su historia pasada, lo cual es denominado propiedad Markoviana (Tijms, 2003). En tal sentido, un importante número de investigaciones han mostrado que tanto la deserción estudiantil como el progreso académico son variables aleatorias que poseen importantes características estocásticas, necesarias para ser modeladas a través de las cadenas de Markov (Brezavšček, Bach & Baggia, 2017; Caicedo, Atuesta & Caicedo, 2016; Elsayed, Dawood & Karthikeyan, 2017).
En la bibliografía, existen trabajos que aplican las cadenas de Markov en el análisis de diversas problemáticas enmarcadas en el sistema de educación superior. Respecto de la deserción destacan los trabajos de Elsayed, Shaik y Karthikeyan (2017), quienes utilizaron una cadena absorbente de Markov para desarrollar un modelo de predicción de la retención de estudiantes en una facultad de ingeniería. También se destaca la propuesta realizada por Caicedo et al. (2016), quienes analizaron la intensión de estudiantes de desertar de su programa académico en ingeniería, basándose en el número de veces que reprueban una misma asignatura de su plan de estudio, modelaron el comportamiento de estudiantes por medio de cadenas de Markov discretas. Precedentemente, Symeonaki y Kalamatianou (2011) habían modelado el progreso educativo de estudiantes con la utilización de los sistemas markovianos no homogéneos (NHMS) con estados difusos (fuzzy). Es así como la utilización de las cadenas de Markov en este proceso de definición del índice se justifica ante la variedad de aplicaciones y la coherencia entre lo que modela y lo que se quiere modelar.
En consecuencia, se pretende avanzar desde la teorización y explicación de la deserción universitaria (y de la educación superior en general) hacia su prevención mediante indicadores que orienten el accionar de las instituciones. De tal manera que las siguientes líneas presentan una modelación de la deserción universitaria utilizando cadenas de Markov. Se detalla claramente el procedimiento de modelación, y se culmina en una aplicación a un conjunto de datos reales de una universidad regional de Chile.
Materiales y método
Modelación
Se identifica con la letra  a la probabilidad de que en el enésimo semestre (esta expresión representa un semestre cualquiera) se produzca la deserción; sin embargo, en el semestre siguiente o
a la probabilidad de que en el enésimo semestre (esta expresión representa un semestre cualquiera) se produzca la deserción; sin embargo, en el semestre siguiente o  se recupera la normalidad y el alumno prosigue sus estudios. Por otro lado, se dirá que q representa la probabilidad de que siendo un alumno regular en el enésimo semestre, este deserte al siguiente (n+1), observe que
se recupera la normalidad y el alumno prosigue sus estudios. Por otro lado, se dirá que q representa la probabilidad de que siendo un alumno regular en el enésimo semestre, este deserte al siguiente (n+1), observe que 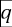 y
y  no son complementarios, por tanto
no son complementarios, por tanto 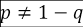 . La representación simbólica descrita permitirá modelar situaciones de estabilidad en la permanencia, es decir, dada la permanencia en el semestre
. La representación simbólica descrita permitirá modelar situaciones de estabilidad en la permanencia, es decir, dada la permanencia en el semestre 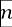 , al siguiente continúe en ello, esto es
, al siguiente continúe en ello, esto es  . También, se dirá que π
0(0) denota la probabilidad de que el alumno deserte de manera inicial o precoz, en el sentido de Castaño et al. (2004), es decir, al comienzo del día 0. Finalmente se caracteriza con el valor 0 al estado correspondiente a la deserción y 1 al estado de permanencia y éxito en la retención del estudiante. Así, la variable aleatoria X
n
representa el estado del alumno en el semestre o tiempo
. También, se dirá que π
0(0) denota la probabilidad de que el alumno deserte de manera inicial o precoz, en el sentido de Castaño et al. (2004), es decir, al comienzo del día 0. Finalmente se caracteriza con el valor 0 al estado correspondiente a la deserción y 1 al estado de permanencia y éxito en la retención del estudiante. Así, la variable aleatoria X
n
representa el estado del alumno en el semestre o tiempo 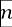 .
.
Formalizando las características descritas en el párrafo anterior, P (X
n+1
= 1|X
n
= 0) = p representará la probabilidad condicional de que, dado que un alumno deserta en un semestre particular, en el siguiente se integre y permanezca en la institución. La línea vertical representa la separación entre lo observado,  y lo que se espera ocurra en el semestre siguiente, X
n+1
= 1, es decir se observa deserción
y lo que se espera ocurra en el semestre siguiente, X
n+1
= 1, es decir se observa deserción  y se quiere cuantificar la probabilidad que se reintegre en el semestre siguiente X
n+1
= 1.
y se quiere cuantificar la probabilidad que se reintegre en el semestre siguiente X
n+1
= 1.
Por otro lado, P (X n+1 = 0|X n = 1) = q representa la probabilidad de que, dado que un alumno es regular (retención) en un semestre particular, este deserte al siguiente. Un estado de suma importancia que es necesario simbolizar para el proceso de modelación es la deserción precoz o deserción al día 0, la cual será simbolizada por P (X 0 = 0) = π 0(0).
Con base en la complementariedad de las probabilidades, es posible obtener representaciones para los siguientes estados: P (X n+1 = 0|X n = 0) = 1−p, en el cual se observa que la condicionalidad X n = 0 hace referencia a la deserción del alumno en un determinado semestre y lo esperado X n+1 = 0, dice relación con mantener esta condición al siguiente, por tanto, es complementario a P (X n+1 = 1|X n = 0). De esa manera su probabilidad de ocurrencia es representada por 1−p. Equivalentemente para P (X n+1 = 1|X n = 1) = 1−q, se observa que en un semestre cualquiera el alumno permanece o se retiene y al siguiente se mantiene igual.
A su vez, se dice que π 0(1) representa la probabilidad de éxito o retención inicial, simbólicamente podemos indicar que π 0(1) = P (X 0 = 1) = 1− π 0(0), esta relación se basa en la complementariedad de los eventos, recordando que π 0(0) representa la probabilidad de deserción precoz.
Por todo lo anterior, es posible proponer un índice de cálculo de probabilidades de retención o deserción en el enésimo semestre. Simbólicamente se presenta un índice que cuantifica P (X n = 0) y P (X n = 1).
Para la formalización de la propuesta, se tiene que la probabilidad de deserción en el semestre n y en el semestre n+1 es modelada por P (X n = 0 y X n+1 = 0), equivalentemente P (X n = 1 y X n+1 = 0) representa la probabilidad de retención en el semestre n, sin embargo, al semestre siguiente (n + 1) este deserta. De esta manera, la probabilidad de deserción puede ser expresada en términos de las dos situaciones antes descritas, esto es:
Esta relación se puede ver en la Figura 1.
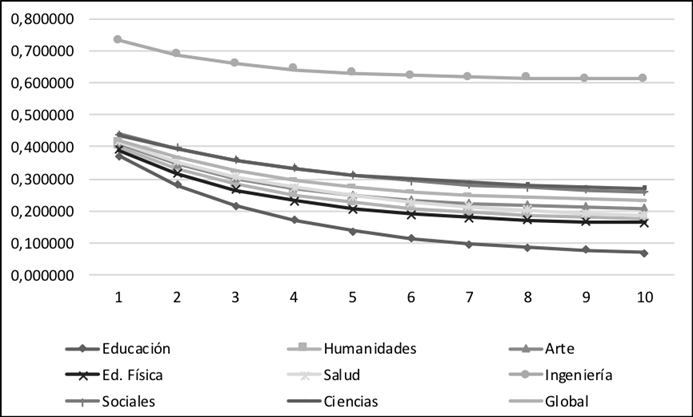
Figura 1 Relación de la deserción en el enésimo semestre, González, Carvajal, Aspeé (2019). Fuente propia de la investigación.
En el ámbito de las probabilidades, existe una serie de propiedades que permiten la descomposición y plantear expresiones más simples, en particular referidas a probabilidad condicional, que son las que se aplicarán en la siguiente expresión:
P (X n+1 = 0) = P (X n = 0)P (X n+1 = 0|X n = 0) + P (X n = 1)P (X n+1 = 0|X n = 1).
Según las definiciones y expresiones anteriores:
P (X n+1 = 0) = (1 − p)P (X n = 0) + qP (X n = 1),
P (X n+1 = 0) = (1 − p)P (X n = 0) + q (1 − P (X n = 0)),
P (X n+1 = 0) = (1 − p − q)P (X n = 0) + q.
Recordemos que la probabilidad de deserción precoz era representada por P (X 0 = 0) = π 0(0), así se puede decir que la probabilidad de deserción el primer semestre es:
P (X 1 = 0) = (1 − p − q)π 0(0) + q.
De manera equivalente para el segundo semestre:
P (X 2 = 0) = (1 − p − q)P (X 1 = 0) + q
= (1 − p − q)2 π 0(0) + q (1 + (1 − p − q)).
Buscando la generalización y repitiendo el proceso n veces es posible obtener la siguiente expresión:
Observemos que para la situación particular y trivial en la cual p = q = 0, se tiene para todo n, P (X n = 0) = π 0(0) y P (X n = 1) = π 0(1). Supongamos ahora que p+q > 0, luego es posible encontrar una expresión equivalente para la suma de la progresión geométrica finita, de la siguiente forma:
Esta importante relación permite dar respuesta al problema planteado, esto es, la probabilidad de deserción en el enésimo semestre es dado por P (X n = 0) que puede ser escrito como:
Finalmente, la probabilidad de retención:
Resumen matricial
Se observa que todos los elementos antes definidos permiten caracterizar a cada estudiante por medio de una matriz de estimaciones de probabilidad para cada enésimo tiempo. Cada componente de esta matriz se representa por P(i,j), que indica la probabilidad de pasar del estado i al estado j. En este contexto particular se ha indicado que 0 representa el estado de deserción y 1 el estado de retención. Esto es:
Esta notación es informativa y global, pues permite tener una visión de todos los posibles estados y sus respectivas probabilidades de transición. Se incorpora en esta matriz de transición el súper índice n para indicar el semestre que se está estudiando, esto es:
P n (0,0) simboliza la probabilidad de que, estando en el estado de deserción universitaria en el enésimo semestre, el alumnado se mantenga en ello al semestre siguiente. Se supone, entonces, que la matriz de transición inicial o momento 1 es dada por:
Luego, asumiendo que p + q > 0, es decir, descartando el caso obvio de que p = q = 0, el desafío es lograr establecer una forma general para la matriz de transición en el enésimo momento, lo que significa encontrar P n .
La probabilidad de pasar del estado 0 al estado 0 en el enésimo momento se representa por P
n
(0,0) equivalentemente se anotará P
n
(0,0) = P
0 (X
n
= 0). Se ha considerado que π
0(0) = 1 y reemplazando en  , se tiene:
, se tiene:
Equivalentemente para encontrar P n (0,1) = P 0 (X n = 1), se ha considerado que π 0(1) = 0, así reemplazando en:
Se obtiene:
De esta manera, se concluye que la matriz de transiciones para cada estudiante en el enésimo semestre o momento se da por:
Consistencia asintótica
Procurando la consistencia de los resultados anteriores, es natural preguntarse ¿qué sucede en situaciones límites?, por tal razón las siguientes observaciones se enmarcan en formalizar esas situaciones.
Supongamos que p y q son diferentes de 0 y de 1, luego 0 < p + q < 2, implicando que |1 − p − q| < 1. En este contexto es posible mostrar que:
Universo y muestra: Caso de aplicación
La población de estudio, en la presente aplicación, estuvo constituida por 5.700 estudiantes con matrícula entre los años 2012-2015, correspondientes a la Facultad de Ciencias de la Educación, Facultad de Humanidades, Facultad de Arte, Facultad de Ciencias de la Actividad Física y del Deporte, Facultad de Ciencias de la Salud, Facultad de Ingeniería, Facultad de Ciencias Sociales y Facultad de Ciencias Naturales y Exactas, todas ellas pertenecientes a una universidad pública y regional de Chile, cuyos tamaños de muestras por facultad se describen en la Tabla 1.
Tabla 1 Distribución por Facultad
| Facultad | Tamaño de muestra |
|---|---|
| Facultad de Ciencias de la Educación Facultad de Humanidades Facultad de Arte Facultad de Ciencias de la Actividad Física y del Deporte Facultad de Ciencias de la Salud Facultad de Ingeniería Facultad de Ciencias Sociales Facultad de Ciencias Naturales y Exactas | 636 1.342 745 452 910 643 512 460 |
| Total | 5.700 |
Nota: Fuente propia de la investigación.
Para la aplicación del índice de deserción Markoviano, aquí definido con el propósito de estimar la probabilidad de transición, se utiliza la raíz jerárquica de tercer orden, propuesta por Carvajal et al. (2018), en la cual se estima la probabilidad de desertar, utilizando un modelo de regresión logística, dada la naturaleza dicotómica de la variable respuesta. Como resultado de este proceso, el modelo estimado queda definido como:
Donde
OL: Orden de lista (Posición de ingreso a la carrera)
RA: Ramos aprobados
EC: Estado civil
EP: Educación del padre
Para la ilustración del funcionamiento del índice, se desarrollará de manera inicial la estimación de la probabilidad de transición, todo esto a partir de la media de las probabilidades de transición (ver Tabla 2). De esta forma se logrará la construcción de la matriz de transición inicial global, además de las matrices de transición de cada una de las facultades analizadas.
Tabla 2 Estadísticos iniciales
Nota: Fuente propia de la investigación.
Resultados
La Tabla 3 expresa los resultados del modelo descrito en las líneas anteriores, aplicado a la muestra señalada. La misma Tabla 3 detalla las diferentes matrices de transición para las diferentes facultades, permitiendo resumir las estimaciones de cada uno de los cambios de estados, condicionados a los contextos de deserción o permanencia.
Tabla 3 Matriz de transición inicial por Facultad y lobal
Nota: Fuente propia de la investigación.
A partir de las estimaciones anteriores, es posible establecer, de manera recursiva, una estimación de la probabilidad de desertar transcurrido el enésimo semestre en cada facultad del estudio (ver Tabla 4).
Tabla 4 Estimación de la probabilidad de desertar transcurrido el enésimo semestre
| Probabilidad de desertar por Facultad | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| N.° Semestre | Arte | Salud | Humanidades | Ed. Física | Ciencias | Ingeniería | Educación | Sociales | Global |
| 1 2 3 4 5 6 7 8 9 10 | 0,410 0,346 0,302 0,272 0,250 0,236 0,225 0,218 0,213 0,209 | 0,417 0,354 0,308 0,273 0,247 0,227 0,213 0,202 0,194 0,188 | 0,402 0,332 0,284 0,249 0,225 0,208 0,196 0,188 0,182 0,178 | 0,391 0,316 0,265 0,231 0,207 0,190 0,179 0,172 0,166 0,163 | 0,439 0,393 0,358 0,333 0,313 0,299 0,288 0,280 0,275 0,270 | 0,731 0,687 0,659 0,641 0,630 0,622 0,618 0,615 0,613 0,612 | 0,373 0,282 0,217 0,171 0,138 0,114 0,097 0,085 0,077 0,071 | 0,441 0,395 0,360 0,333 0,311 0,295 0,282 0,273 0,265 0,259 | 0,422 0,366 0,325 0,296 0,275 0,260 0,249 0,242 0,236 0,232 |
Nota: Fuente propia de la investigación.
Tomando los valores de la Tabla 3, y viendo como ejemplo la Facultad de Arte, los valores de p y q son 0,242 y 0,061, respectivamente. Entonces, el cálculo de probabilidad de desertar al enésimo semestre para esta facultad es obtenida como se muestra en la Tabla 5.
Tabla 5: Ejemplo de cálculo de la probabilidad de desertar al enésimo semestre
| Semestre | Probabilidad de desertar al enésimo semestre 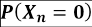
|
|---|---|
| Primer |
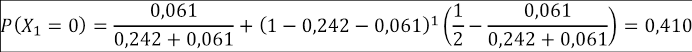
|
| Segundo |
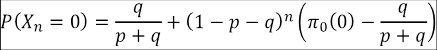
|
| Tercero |
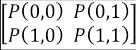
|
| Cuarto |
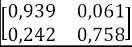
|
| Quinto |
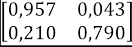
|
| Sexto |
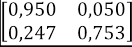
|
| Séptimo |
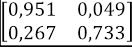
|
| Octavo |
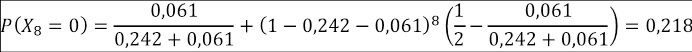
|
| Noveno |
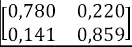
|
| Décimo |
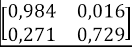
|
Nota: Fuente propia de la investigación.
Por su parte, la información entregada por la Gráfica 1 permite establecer que, con independencia de la facultad estudiada, las mayores probabilidades de deserción se concentran en los primeros semestres de la carrera, para luego mostrar un decrecimiento constante a lo largo de los diez semestres estimados. Ello es un comportamiento compartido por las ocho facultades de la Universidad. Sin embargo, las facultades de Ciencias Sociales, Ciencias Naturales y Exactas y de Ingeniería, son las que presentan una mayor tasa de deserción, superando la media institucional; destaca notoriamente la Facultad de Ingeniería, la cual duplica la tasa de la Universidad a todo lo largo del periodo estudiado.
Discusión
Durante las últimas décadas el número de jóvenes que han tenido acceso a la educación superior chilena ha crecido de manera significativa, sin embargo, este importante crecimiento no permite asegurar que estas nuevas generaciones de estudiantes, en su mayoría jóvenes provenientes de familias vulnerables, finalicen con éxito su proceso formativo, lo que se hace evidente en la importante tasa promedio de deserción universitaria (29,8 % entre los años 2011-2016).
En este trabajo, se ha desarrollado un indicador de la deserción utilizando un modelo de cadena de Markov, el cual estima la probabilidad de desertar al enésimo semestre. De esta manera, el modelo propuesto permite realizar un seguimiento continuo del comportamiento de deserción, insumo crucial a la hora de generar políticas destinadas a retener al estudiantado en el sistema de educación superior. Es decir, salta de la simple descripción de la magnitud del fenómeno a su intervención, tal como lo desafiara Himmel en el 2002.
Para ilustrar la utilidad del modelo, este fue aplicado a 5.700 estudiantes con matrícula entre los años 2012-2015, correspondientes a ocho facultades de una universidad regional de Chile. Los resultados obtenidos muestran que la investigación tiene importantes implicancias prácticas, no solo para las autoridades de la institución, sino también para aquellos organismos gubernamentales responsables de la generación y aplicación de políticas públicas destinadas a mejorar los indicadores de calidad del sistema de educación terciario. Entre estas implicancias, la investigación deja vislumbrar que las mayores probabilidades de deserción se presentan en los dos primeros semestres de estudios, con una probabilidad promedio superior al 39 %, resultado concordante con otras investigaciones como la de Stinebrickner (2014), lo cual hace suponer que una fuerte inversión, focalizada en este primer año, permitirá reducir estos indicadores.
Por otro lado, se pudo establecer que la Facultad de Ingeniería es aquella que presenta las mayores probabilidades de deserción promedio en los tres primeros semestres, alcanza una media del 69,1 % que supera en más de 84 % la tasa global. En esta misma línea, pero a menor escala, se encuentran la Facultad de Ciencias Sociales y la Facultad de Ciencias Naturales. Por su parte, la Facultad de Educación, Humanidades y la Facultad de Educación Física son las que presentan una menor tasa de deserción, con un 31 % bajo la media global. Esto rememora los factores institucionales que pueden estar jugando en la deserción tal como lo evidenciara Tinto (1975) y Castaño, Gallón, Gómez y Vásquez (2004) respecto de la integración académica y social a la universidad o, en su defecto, a la interacción de dichos factores con los que el mismo estudiantado lleva consigo, tal como lo sugiriera Larroucau (2015). Así, es posible aventurar que existen condicionantes de contexto educativo que precipitan, en mayor medida, la deserción universitaria; empero, ello debe ser objeto de otros estudios en profundidad en las facultades señaladas.
Todo lo anterior deja de manifiesto la necesidad de implementar acciones remediales que permitan reducir estos indicadores, pues el aletargamiento o la inmovilidad solo redundará en la generación de una capa social de jóvenes y familias que verán frustradas sus aspiraciones vitales. En este sentido, las acciones deben ser creadas, ejecutoriadas y monitoreadas, al menos en tres dimensiones, a saber: a) dimensión económica, que implica generar y potenciar un conjunto de acciones que alivianen la carga financiera que significa estudiar, tales como becas, gratuidad, subsidios de alimentación y movilización, entre otros; b) dimensión política institucional, que refiere a promover una potente articulación entre la enseñanza secundaria y la enseñanza terciaria, fomentando los procesos de orientación vocacional y diversificando los mecanismos de ingreso a las instituciones de educación superior, entre otros; y finalmente c) dimensión pedagógica, que incorpora la actualización de los currículos y promueva la creación de escuelas de ayudantes y personas tutoras pares, o la generación de estudios de nivelación, entre otros.
Finalmente, el modelo propuesto tiene la ventaja de poder estimar las probabilidades de desertar, tanto de estudiantes en particular como la de un conjunto de estudiantes pertenecientes a una carrera, departamento o facultad en general, todo esto al momento enésimo, lo que se diferencia de los trabajos de Giraldo, Zapato y Toro (2008); Caicedo R, Atuesta y Caicedo J (2016) y permite el monitoreo de la deserción, al detectar el mejor momento para su intervención, lo que se transforma en una potente herramienta de conocimiento y de gestión académica para las instituciones de educación superior en general.
Conclusión
Aplicado el modelo al conjunto de estudiantes analizados y considerando los resultados de la investigación, expuestos en las líneas precedentes, se puede concluir que:
Las mayores probabilidades de deserción se suceden dentro de los dos primeros semestres de estudios. Hecho que pudiera ser explicado atendido las razones vocacionales que afectan la deserción temprana o, en su defecto, las condicionantes de tipo formativa que traen consigo el estudiantado novel. Sin embargo, estos elementos y otros, que pueden ser los causales de que estudiantes de primer año tengan una mayor probabilidad de desertar, deben ser analizados en estudios posteriores.
A partir del tercer semestre dichas probabilidades van disminuyendo paulatinamente. Esto puede deberse a que el estudiantado ha tenido la posibilidad de generar lazos afectivos con sus pares, profesorado y la comunidad, lo que permite constituir un sentimiento de pertenencia. Por otro lado, los compromisos personales con sus propias metas académicas se van reafirmando a través del tiempo, todo esto supone una disminución en la probabilidad de desertar. No obstante, ello también debe ser objeto de un estudio en particular, que tome como base los hallazgos de la presente investigación.
Este comportamiento no se diferencia en función del contexto educativo o programa de estudio, pues las diferencias porcentuales entre facultades o carreras no son relevantes o significativas.
No obstante, existe un contexto educativo con mayores probabilidades de deserción que la media, lo que obliga a analizar, en profundidad, dicha realidad y estudios comparativos entre instituciones de manera de visualizar la ocurrencia o no de un patrón.