A notable characteristic of the mathematics teaching and learning process has been the low levels of student achievement, and various studies at all educational levels have been carried out to identify the causes of this problem. García (2013) points out that research carried out since 1980 shows that the problem of teaching and learning mathematics is one of the most significant themes in any educational model, as shown by the levels of passing and repetition in secondary and university mathematics courses.
At the university level, and specifically in the Universidad Nacional de Costa Rica, poor performance in mathematics courses is reflected in dropout and repetition rates in the various courses offered by the School of Mathematics ( Escuela de Matemática, 2011). Rates of course repetition produce delays in obtaining academic degrees, generating an additional problem in terms of the time for graduation and permanence of each student in the formal higher education system.
A lack of prior knowledge of students entering universities has been shown to be a factor that could be affecting performance at the university level (Escalona, 2011). In addition, Kajander and Lovri (2005) point out that the experiences of high school students in mathematics correlate with their success in college mathematics courses.
To determine the level of mathematical knowledge of students entering the Universidad Nacional, the Mathematics School has since 2008 applied a non-compulsory yearly test of mathematics knowledge and skills for students entering programs of study that include at least one mathematics course in their curricula.
This test is an element in a strategy that seeks to collect information about one of the most significant possible causes of the high dropout and failure rates that are usually present in mathematics courses: deficiencies in mathematical knowledge and skills among students entering college. Informing the university community of the results of the test is intended to assist students, professors and university authorities to propose and implement measures that contribute to overcome the possible deficiencies identified (Escuela de Matemática, 2016a, p.1).
According to the Report on the Mathematics Diagnostic Test: First-year students of 2016, in January of that year 1832 students participated in the programs of Business Administration, Office Administration, Biology, Cartography and Digital Design, Geographical Sciences, International Business and Trade, Aquaculture, Economics, Business Education, Mathematics Teaching, Science Teaching, Sustainable Tourism Management, Agronomic Engineering, Industrial Bioprocess Engineering, Forestry Science Engineering, Environmental Management Engineering, Information Systems Engineering, Surveying, Cadastre and Geodesy Engineering, English, Veterinary Medicine, Economic Planning and Social Promotion, Industrial Chemistry, and International Relations (Escuela de Matemática, 2016a). Although the target population is students entering programs of study that include at least one mathematics course in their curricula, students in programs that did not include any mathematics courses in their curricula also participated.
Among the results presented in the report, it is notable that less than 2.5% of those who took the test obtained a score above 60, while the majority of students (76.8%) scored between 20 and 40, and the average grade was 29.73 (Escuela de Matemática, 2016a).
The results for 2016 are similar to those obtained in previous years. In 2015, for example, 1760 students participated in this test and 76.53% (1347) scored between 20 and less than 40. Only 2.78% (49 students) had a grade higher than 60, and the average grade of the entire population was 29.2 (Escuela de Matemática, 2015).
In this context, it is relevant to enquire about academic performance in mathematics courses at the Mathematics School of the Universidad Nacional (EM-UNA) . However, there is only one relevant compilation of statistics, carried out in the year 2011 for the period 2007-2010, and updated data is clearly needed.
According to this data, the rate of students passing in this area is lower in first- and second-level courses, and the dropout rate is higher (Escuela de Matemática, 2011).
It should also be noted that in Costa Rica, in 2012, the Costa Rican Higher Council of Education approved new mathematics programs for all primary and secondary education in the country. These programs provide the basic knowledge with which the students enter the university, and should serve as a reference for introductory university mathematics courses. Kajander and Lovric (2005) point out that there has not been a single education reform that has not affected, in one way or another, the way in which mathematics is taught, and that curricular changes also influence student characteristics. It is therefore necessary to provide information that assists in determining how the reform carried out in 2012 in Costa Rica affected university education and the teaching of mathematics.
Institutions of higher education should take into account that entering students have a previous academic background and a social context that cannot be ignored, and with different, often unclear, views on mathematics and its role in their future careers and lives (Kajander and Lovric, 2005). These authors also point out that a large number of university teachers do not understand or want to accept the importance of these factors, in part because of the small amount of research on mathematics education at this level.
Given the foregoing, it is necessary to analyze academic performance in the introductory courses of mathematics offered by the EM-UNA and the congruence of the contents of these courses with the secondary mathematics curriculum that was approved in 2012, to make suggestions for the revision and updating of university-level programs.
Theoretical framework
Teaching mathematics in universities
Teaching mathematics at the university level is conceived of as a transmission of facts in which the majority of teachers think that a clear exposition of the subject is sufficient to make it understandable to students (Sarmiento and Sánchez-Quinzá, 2002). This leads to a permanent conflict that contributes to the feeling that mathematics learning is an end in itself, as opposed to seeing it as a language within the Knowledge Society and an instrument for many scientific and professional areas related to the development of scientific and technological competences (García, 2013).
When the student's understanding is not adequate, teachers tend to attribute this to lack of interest or poor prior training (Sarmiento and Sánchez-Quinzá, 2002). This has led to the addition of a new mathematics course in several institutions whose objective has been to solve the observed deficiencies in training.
In this sense it is important to consider that the relationships that students establish with mathematical objects are different in secondary education and in a university, and that the change of institutions generates specific problems that must be taken into account in a broader perspective on education (Sarmiento and Sánchez-Quinzá, 2002). The transition between secondary education and higher education is a complex phenomenon covering a wide range of situations and difficulties; in mathematics, in particular, this transition is often quite problematic (Kajander and Lovric, 2005).
It is therefore necessary to know what students know, how they know it, and the differences between students, as well as the individual, social, economic, and family factors that can affect students’ ability to learn. In this context, Escalona (2011) points out that mathematics teaching in higher education is characterized by the following:
Poor results and difficulties for students in the subject due to lack of mastery of basic concepts, few skills to analyze and solve problems, and poor ability to apply mathematical contents to solve problems related to their specialty.
An inadequate methodology in which the meaning of mathematics is not understood; for instance, where the concepts, theorems and formulas originate and how can they be useful.
A concept of the subject as an obstacle to graduation.
It is not always clear what the role of mathematics is, what its formative functions are, and its relationship to professional life, so students consider it to be very complex, abstract and unrelated to their future work.
There is a lack of knowledge of student characteristics, accompanied by a lack of contextualization of the course with regard to the essential processes and phenomena of program of study and students’ future professions.
The author emphasizes that there is a diversity of ways in which higher level mathematics teaching and learning process is organized and carried out, in which the majority of teachers imitate patterns of behavior assimilated from their former teachers. In addition, Escalona (2011) indicates:
There is a tendency for teaching by transmission of contents by an active subject (the teacher) and the passive reception of these contents by a passive subject (the student). Students’ "classroom participation" is in many cases limited to taking notes and being presented with algorithms that they later try to memorize when studying for their exams.
The style of classroom exposition by mathematics teachers is centered around the elaboration of the logical foundations of the subject: it begins with a definition of content that is devoid of meaning for students and completely removed from their experiences, after which operations are presented.
Deficiencies in the teaching staff’s methodology limit analysis of the contents or subjects in this discipline.
Teaching staff lacks knowledge about the relationships between mathematics and the other disciplines of each program of study.
There is limited use of information and communication technologies (ICT) in teaching.
It is possible to conclude, as García (2013) points out, that the learning and teaching of mathematics at the university level takes place at different levels that are opposed and even contradictory: while one proposes an ideal world that includes integral formation of students, formally promoting the generation of competences, the other proposes theoretical, axiomatic, decontextualized and meaningless learning that does not penetrate the students’ minds, nor facilitate the acquisition of knowledge and its relation to their chosen university program of study.
Sarmiento and Sánchez-Quinzá (2002) state that although university students are cognitively and emotionally mature enough to confront the study of more difficult mathematical content, in reality the current university methodology is possibly not the most appropriate, at least in the early years of study, since there is a growing educational failure and increasing concern by teachers about their teaching. This is, however, a subject which requires further investigation.
As previously indicated, this situation is not irrelevant to any mathematics course, but it is especially critical when considering introductory courses. Based on our experience as teachers, the description of the reality in which the student lives, provided by Busto, Calvo and Escribano (2002) in a study carried out at the Universidad Complutense de Madrid, can be equally applied to the Costa Rican university environment. The authors write:
It is only necessary to talk to some of the students in introductory Algebra or Calculus classes in most college programs of study to realize that something is failing. These students meet the established legal requirements to enter the University, have a high school diploma, and have passed the University’s entrance exam, which should be a guarantee that they have been sufficiently trained to successfully deal with higher education. (Busto, Calvo and Escribano, 2002, p.2).
Although the subject will not be covered in more detail in this document, it is important to note that the first year of university education represents a challenge for students, not only because of the change of educational level, but also because they must adapt to different teaching methods, methodologies and treatments, as well as greater freedom and the different nature of the courses that they enroll in (Busto, Calvo and Escribano, 2002).
There is growing concern among university professors, about the progressive increase of so-called university failure, as evidenced by a high rate of dropout in certain careers, repetition of courses, absence to take exams, absenteeism, and high levels of student passivity, especially in the early years, among others (Lentini, Martínez, Lentini, Tarifa and Crespo, 2003). According to the authors, this leads to a questioning of factors related to the quality of the curricula offered by the institution, the degree of preparation of its teachers, the use of different working methodologies, the degree of fulfillment of curricular requirements, their choice of career, and their socio-economic situation.
It is imperative to address this situation, since, as the Inter-University Development Center (CINDA) (2006) mentions, repetition and withdrawal, in particular, have personal, institutional, social and economic implications not only for students but also for their families and educational centers.
The High School Mathematics Curriculum in Costa Rica
In May 2012, the Costa Rican Higher Education Council approved new mathematics programs for all primary and secondary education in the country, which started to be distributed among teachers in 2013.
According to Ruiz (2013), a global element that strongly motivated the search for reform was an attitude of rejection and fear of mathematics, which negatively affects the social and emotional attitudes of students, parents and even teachers during the teaching and learning of mathematics. In addition, the author highlights other elements of the educational process and training of professionals which have influenced the teaching and learning of mathematics and motivated the drive for reform, including:
Students with poor cognitive abilities in mathematics.
Mathematical learning that does not explain the significance of the subject in modern society.
Cultural and family contexts that do not promote positive attitudes and beliefs about mathematics.
Negative school experiences with mathematics as one of the main causes of student dropout.
Passivity and lack of discipline as an expression of the dominant teaching style.
Very weak preparation of primary education mathematics teachers at the university level, with curricula that include only 1 or 2 courses on the subject and do not present a specific mathematical pedagogy.
A system of recruitment of teachers by the Ministry of Public Education (MEP) which is not based on quality, as no tests are required for their formalization as teachers or for promotions in their teaching careers.
Teaching practices that are characterized by the absence of curricular support, use of texts, inequality in the availability of resources, over-modification of curricula, and little preparation of teachers in the approaches to be used.
A short school year with many missed classroom days.
Significant inequalities between school preparedness and conditions for teaching between urban and rural areas, private and public institutions, daytime and nighttime education, and academic and technical high schools.
Uncertainty about education caused by the absence of medium and long-term government policies.
A divorce between curricula, teacher training programs, and classroom practice.
According to Ruiz (2013): "This curriculum seeks to achieve mastery of knowledge, skills generation, and especially, the simultaneous creation over the medium and long terms of transversal mathematical skills: reasoning and argumentation, representation, communication, problem solving, and connection " (Ruiz, 2013, p.31). See MEP (2012), for more information.
The study plan approved in 2012 was, according to Ruiz (2013), designed to provide a vertically integrated theoretical basis covering the entire mathematical curriculum from the first grade to the end of secondary education, with a similar theoretical foundation for all the mathematics-related areas in the curriculum. Referring to this plan, Alfaro, Alpízar, Morales, Ramírez and Salas (2013) state:
The curriculum is organized into five mathematical areas: numbers, measures, geometry, relations and algebra, and probability and statistics.
In each area, classroom activities are oriented towards the development of specific skills and capacities over short periods of time.
The development of mathematical competence is regarded as strengthening the ability to use mathematics in various situations in life.
Central mathematical processes include reasoning and arguing, formulating and solving problems, communication, connection and representation.
Pedagogical mediation plays a fundamental role.
In addition, Ruiz (2013) notes that five curricular axes are established: problem solving, active contextualization, reinforcing positive attitudes and beliefs, intelligent use of technologies, and use of the history of mathematics.
Skills are generated through gradual and integrated processes, where the curriculum is organized in the following areas: numbers, geometry, measures, relations and algebra, and statistics and probability, with the mathematical processes of reasoning and arguing, formulating and solving problems, communicating, connecting and representing are considered transversal actions (Ruiz, 2013).
Methodology
This research uses a mixed (quantitative - qualitative) model, primarily descriptive. A study was carried out on approval, failure, withdrawal and dropout percentages in the courses given by the EM-UNA from 2011 through the first Academic Cycle of 2016. (there are three Academic Cycles, or periods, in each school year, with the third corresponding to summer school studies).
Context
The first university-level math courses taught by the EM-UNA are General Mathematics MAT001, Calculus I MAT002, Financial Mathematics MAT020 and Mathematics for Information Sciences MAT030. These are the first university-level math courses that first-year students receive in the following programs of study:
A) MAT001 General Mathematics: Aquaculture, Business Administration, Biology, Cartography and Digital Design, Geographical Sciences, International Business and Commerce, Economics, Science Teaching, Agronomic Engineering, Forest Science Engineering, Environmental Management Engineering, Survey and Cadastre Engineering.
B) MAT002 Calculus I: Industrial Bioprocess Engineering, Industrial Chemistry.
C) MAT020 Financial Mathematics: Economic and Social Planning.
D) MAT030 Mathematics for Information Sciences: Information Systems Engineering.
Sources of information and protocol
The study was carried out based on the course results for all participants in these courses in this period. The following points were taken into consideration:
A change in course codes by the School of Mathematics was motivated by guidelines and administrative provisions, and did not reflect a change in the topics covered. This meant that the analysis included data from groups with the following codes
General Mathematics: MAT001 and MAX084.
Calculus I: MAT002 and MAY436.
Financial Mathematics: MAY43, MAY452 and MAT020.
Mathematics for Information Sciences I: MAY220, MAY230 and MAT030.
Withdrawing: Students who presented a justification for withdrawal (JW).
Passing: Students who had a final grade equal to or higher than 70.0.
Failing: Students who had a final grade equal to or higher than 20.0 and less than or equal to 67.5.
Dropping out: Students who had a final grade equal to or lower than 17.5 or did not participate in the class (DNP). A DNP was taken as a grade of 00.0. The grade-based criterion for classifying a student as a dropout was based on the argument used by the Department of Registration of the Universidad Nacional, although it is not formally specified in any document. It is assumed that a grade of less than or equal to 17.5 is due to the student not participating in all course evaluations (taking no more than two short tests or exams).
Grades lower than 70.0: all students who were as failing or dropping out, considering a DNP as a score of 00.0.
Incomplete: students who received an incomplete (I). An I is given when the student, for reasons justified before his teacher, cannot complete the course in the school cycle in which he is enrolled, but can take it back within a period indicated in the institutional regulations.
To analyze the relationship between the minimum contents that, according to the MEP should be studied in mathematics in secondary education and those studied in introductory mathematics courses in the Universidad Nacional, reviews were carried out of the contents of the secondary education mathematics curriculum and the Universidad Nacional’s General Mathematics, Calculus I, Mathematics for Information Sciences and Financial Mathematics courses.
In the case of the MEP curriculum, the review consisted of determining the content covered in secondary education in the areas of numbers, measures, geometry, relations and algebra, and probability and statistics, based on official definitions of knowledge, specific skills and specific indications. The results of this review were then compared with those of a similar review of MS-UNA courses aimed at first-year students.
Although the mathematics curriculum of the MEP consists of five mathematical areas, students in secondary education only receive courses in numbers, geometry, relations and algebra, and statistics and probability. The area of measures is covered only in primary education, but is considered to be a transversal element in all secondary mathematics content.
Analysis
Academic performance in introductory math courses
The data presented in Table 1 show that in the case of the General Mathematics course no more than 35% of students achieved a passing grade in the first and second Academic Cycles. There were significant variations in the results for courses in the third Academic Cycle (summer school), with more than 50% of students passing in some periods, while in others less than 37.0% passed. More than 60% of students received grades under 70 in most of the Academic Cycles in which the course was offered.
Figure 1 complements the discussion in the previous paragraph. It also shows that that failure and dropout percentages have in general increased in recent years. It is important to note that the percentage of withdrawals in the third Academic Cycle is always 0% because there is no initial period defined within which withdrawal is permitted.
Table 1 Percentage distributions of academic results for students enrolled in the General Mathematics course (MAX084-MAT001). Grade records of 2011- Academic Cycle I 2016
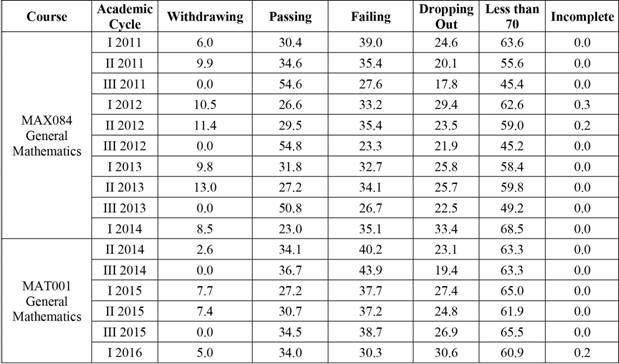
Note: Authors’ elaboration.
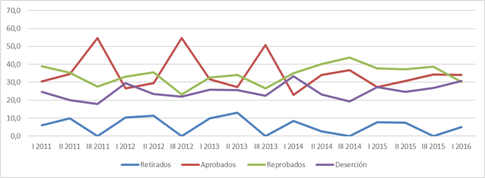
Figure 1 Percentage distributions of academic results for students enrolled in the General Mathematics course (MAX084-MAT001). Grade records of 2011- Academic Cycle I 2016. Authors’ elaboration.
The data in Table 2 and Figure 2 show that the percentage of students passing the Calculus I course in the first and second Academic Cycles has been, for the most part, lower than the percentage of students failing the course. As was the case for the General Mathematics course, when the Calculus I course has been offered in the second Academic Cycle, the percentage of students passing has been higher. The percentage of students passing the Calculus I course has varied widely between 2011 and the first Academic Cycle of 2016, from 18.2% to 50.0%.
Table 2 Percentage distributions of academic results for students enrolled in the Calculus I course (MAY436-MAT002). Grade records of 2011- Academic Cycle I 2016.
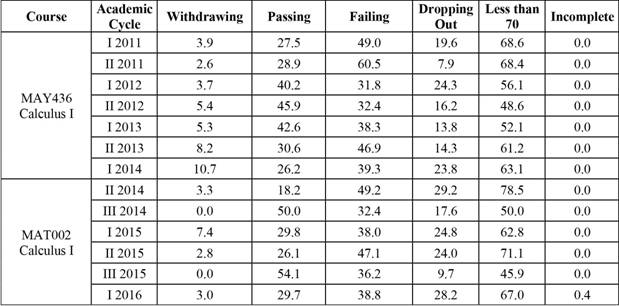
Note: Authors’ elaboration.
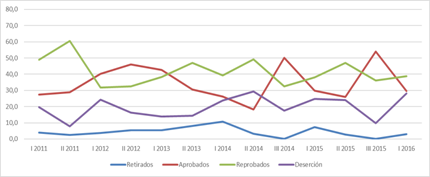
Figure 2 Percentage distributions of academic results for students enrolled in the Calculus I course (MAY436-MAT002). Grade records of 2011- Academic Cycle I 2016. Authors’ elaboration.
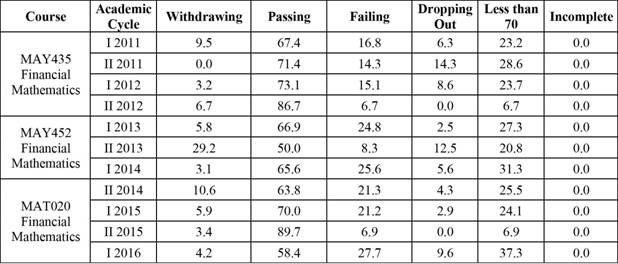
The data in Table 3 and Figure 3 show that the percentages of students passing the Financial Mathematics course are much higher than those for the courses discussed previously, reaching as high as 89.7%.
Table 3 Percentage distributions of academic results for students enrolled in the Financial Mathematics course (MAY435-MAY452-MAT020). Grade records of 2011- Academic Cycle I 2016.
Note: Authors’ elaboration.
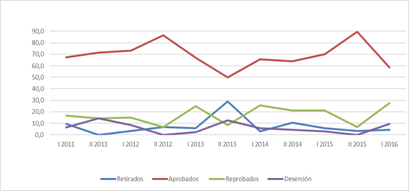
Figure 3 Percentage distributions of academic results for students enrolled in the Financial Mathematics course (MAY435-MAY452-MAT020). Grade records of 2011- Academic Cycle I 2016. Authors’ elaboration.
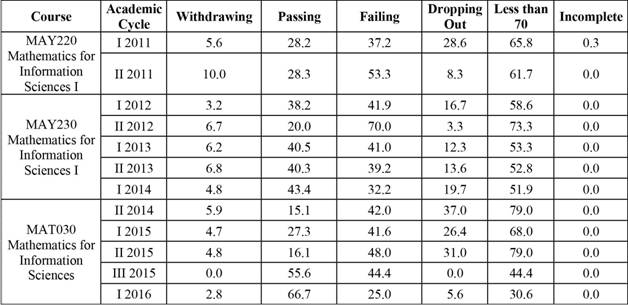
The percentage of students passing the Mathematics for Information Sciences course has been below 45.0% in most Academic Cycles, although 66.7% of students passed the course in the first Academic Cycle of 2016. The course also had a high dropout rate in some periods: in the second Academic Cycle of 2014, it reached 37.0%.
Table 4 Percentage distributions of academic results for students enrolled in the Mathematics for Information Sciences course (MAY220-MAT230-MAT030). Grade records of 2011- Academic Cycle I 2016.
Note: Authors’ elaboration.
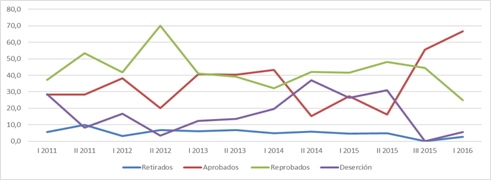
Figure 4 Percentage distributions of academic results for students enrolled in the Mathematics for Information Sciences course (MAY220-MAT230-MAT030). Grade records of 2011- Academic Cycle I 2016. Authors’ elaboration.
Table 5 presents the percentage distributions of average academic results for students in all introductory mathematics courses between 2011 and the first Academic Cycle of 2016.
Table 5 Percentage distributions of average academic results for students enrolled in introductory courses in Mathematics. Grade records of 2011- Academic Cycle I 2016
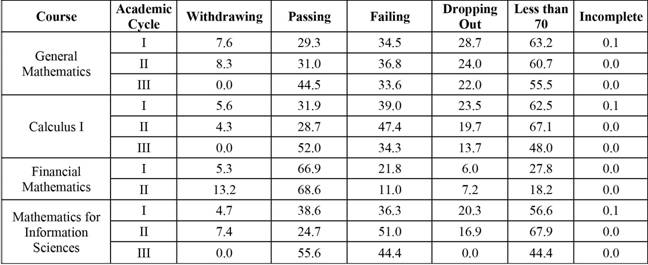
Note: Authors’ elaboration.
Various aspects of the data in Table 5 deserve mention:
In the first Academic Cycle, the lowest rate of students passing courses occurs in General Mathematics, as do the highest rates of dropouts and grades lower than 70.
The lowest rate of students passing the Calculus I course and the highest percentage of grades under 70 in that course occurs in the second Academic Cycle. The highest dropout rate in the course occurs in the first Academic Cycle.
The Financial Mathematics course has a high percentage of students passing the course (above 65.0%) and a low dropout rate.
In the Mathematics for Information Sciences course, the lowest passing percentage and the highest percentage of grades lower than 70 occur in the second Academic Cycle. However, the highest dropout rate in this course occurs in the first Academic Cycle.
In the third cycle, the highest rates of students passing and the lowest dropout rates occur in the third Academic Cycle (summer school).
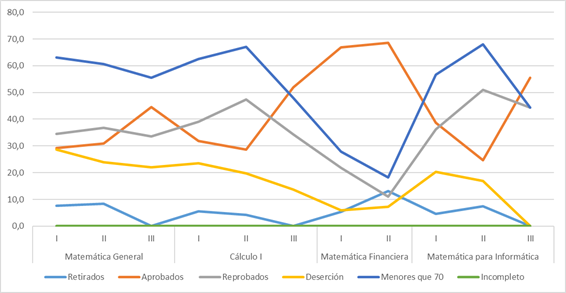
Figure 5. Average percentage distribution of students enrolled in introductory mathematics courses according to grade records and Academic Cycle, for the period 2011- Academic Cycle I 2016. Authors’ elaboration.
Figure 5 shows that, with the exception of the Financial Mathematics course, the remaining introductory university-level mathematics courses, which are the first contact students have with this discipline at college level, generally have low rates of passing and high dropout rates. This creates problems for planning academic offerings for the next academic year, as well as budgetary problems, since the majority of students who drop out of a course or fail it will require spaces when they re-enroll in it.
Contents considered in the MEP curriculum and the programs of the EM-UNA courses
When comparing the contents of mathematics courses in secondary education provided by the MEP with those of the mathematics courses of the EM-UNA for first-year university students, a number of subjects in the university courses that are unfamiliar to first-year students were encountered. These are presented in Table 6.
Table 6 New mathematical content for students in EM-UNA introductory mathematics courses
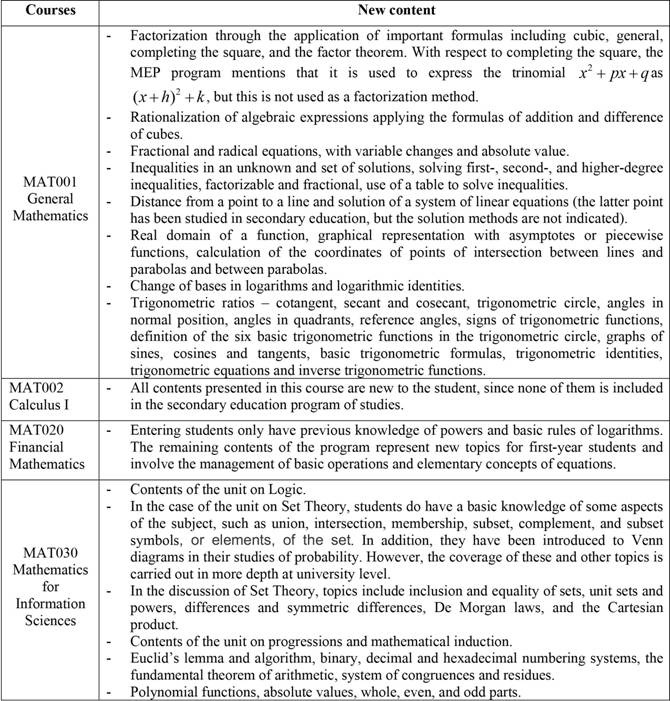
Note: Authors’ elaboration, based on data from theEscuela de Matemática (2016b,2016c,2016d,2016e).
As can be seen in the table above, there are various topics in university-level mathematics that are new to entering students that were educated in the programs of study approved in 2012. Therefore, coverage of these topics at the university level cannot be considered as a review of topics that students have already studied and it cannot be assumed that students already have a knowledge of these topics that can serve as the basis for the development of more complex content.
In addition, it is important to remember that, as mentioned in the theoretical framework section of this document, that in the mathematics curriculum five disciplinary axes have been adopted that cross-cut and strengthen the curriculum: solving problems as a principal methodological strategy, active contextualization as a special pedagogical element, intelligent and visionary use of digital technologies, the enhancement of positive attitudes and beliefs about mathematics, and the use of the history of mathematics. In this context, pedagogical mediation occupies a fundamental place and is based on five basic processes: reasoning and arguing, formulating and solving problems, connecting, establishing relations, representation in different forms (graphical, numerical, symbolic, tabular, etc.), and communicating and expressing mathematical ideas both formally and verbally.
Based on the above, a lesson model is proposed in which the introduction and learning of mathematics are promoted through four approaches: proposal of a problem, independent student work, interactive and communicative discussion, and closure. The participation of teachers is fundamental in all of this process, to provide guidance, counseling and assistance in problem formulation.
However, analysis of the programs for university-level mathematics courses found no reference to the approaches specified in programs for the study of mathematics in secondary education mathematics. There is rather a clear difference between methodological approaches: while the secondary education curricula encourage a more constructive approach, with a preponderant role for students and based on problem solving, university-level courses are developed through lectures and practical work.
It is important to note that in the MEP curricula evaluation is conceived of as an integral part of the teaching and learning process, the purpose of which is to collect valid and reliable information to determine the extent to which proposed skills, abilities, and competencies are achieved. Evaluation is therefore seen as a tool that assists teachers to make appropriate decisions oriented towards improvement of student performance. In addition to this, the evaluation of student work is based on several types of results, such as daily work, homework, exams, knowledge about the students according the teacher, and attendance.
In contrast, evaluation at university level is usually based on the results of three partial exams; only in the Financial Mathematics course, 15% of the final evaluation is based on short tests.
The data collected on program content and aspects related to methodology and evaluation indicate that there are important differences in the way mathematical contents are addressed at the secondary and university levels. Problems associated to the transition from secondary to university education, including non-academic factors, should also be considered.
Although university education builds on, and must be different from, secondary education because it requires specific competences and has a different purpose, the design of introductory university mathematics courses does not seem to consider previous student experiences. It is not a question of "equating" both levels of education, but rather one of assuring that university education assumes its responsibility to effectively facilitate student insertion at this educational level based on an understanding of students’ previous experiences.
Results
Students entering the UNA for the first time have mostly graduated from secondary education the year before they enter the university system. Although the interaction of different factors influences their academic performance, the data show that levels of prior knowledge play an important role in this regard.
If the majority of students are considered to have passed the baccalaureate examination in mathematics (which is a requirement for completing high school) at the end of the year prior to admission to the university, the results of this examination are relevant, even more so if it is assumed that the skills and knowledge evaluated in the baccalaureate examination should provide an adequate basis for introductory university mathematics courses. However, it would be a mistake to make this assumption, since the contents of mathematics courses in secondary education do not provide such a basis.
The results of the diagnostic test applied by the EM-UNA have provided indications that the students' mathematical knowledge is not satisfactory. However, the question arises, “satisfactory for whom?” Should the curriculum in high school mathematics prepare students for universities, or should universities train students at a "common level" to continue their studies? Although answering this question is not the purpose of this document, it is a question that we consider should be discussed between the MEP and universities.
The results of this research also suggest that it is necessary for the EM-UNA to review and, if relevant, to redefine its diagnostic test for entering students, since it is not possible to evaluate students in areas in which it is previously known that have not been covered in secondary education. This test should focus on determining the level of understanding of the content that is covered in secondary education. It is up to the EM-UNA, together with the programs of study that have mathematics courses in their curricula, to modify university mathematics programs to deepen the coverage of new content.
The EM-UNA has based its approach on the assumption that students have prior knowledge that is a sufficient basis for university courses to be structured as a review of this knowledge, or to immediately begin developing more complex knowledge based on this foundation. However, the results of comparing the mathematics curriculum of the MEP and the programs of the courses taught by the EM-UNA for first-year students show that the students do not have knowledge of some subjects that are considered to have been previously covered. In addition, the MAT001 General Mathematics course is considered by some teachers as a review of subjects covered in secondary education. However, evidence shows that there are various areas which have not been addressed at that level. This creates a gap between what the student body can achieve and what the course is intended to achieve.
The situation is more complex for students entering the MAT002 Calculus I course, in which it is assumed that they have studied and have an adequate knowledge of all the contents of the MAT001 General Mathematics course. If students do not have the previous knowledge required, it is not reasonable to think that the situation will be different in the MAT002 Calculus I course. For these groups, therefore, a consideration of knowledge gaps must not only include that which exists between secondary education and what is required in the MAT001 General Mathematics course, but also what is required in the MAT002 Calculus I course.
A similar situation exists with respect to the MAT030 Mathematics for Information Sciences course. However, the difference between this course and those mentioned in the last paragraph is that the contents that are covered are highly complex compared to the content presented in secondary education. It begins with topics which are new to the students, while functions, which they have some knowledge of, are only studied at the end of the course. The course program shows no recognition of the need to manage the transition between secondary and university content.
The situation is different in the case of the MAT020 Financial Mathematics course. This begins with a review of subjects which have been studied in secondary education, and introduces new topics which require competence in handling basic operations, solving equations, the laws of powers, logarithms and basic algebra (all of which have been covered in secondary education). This provides students with the basis needed to acquire new knowledge.
Summary
It is not the purpose of this paper to evaluate the quality and relevance of the mathematics curriculum for secondary education, or the manner in which students are being educated. Nor is it our objective to determine if graduates of secondary education have the profiles that are indicated in its theoretical foundations. What is important is that at the university level, the EM-UNA, along with those responsible for different careers, must lead a process aimed at carrying out a comprehensive review of the courses offered according to the needs of students in different programs of study and previous knowledge that students have.
The results of this study clearly indicate that there is a significant gap between what students graduating from secondary education know and what universities (at least in the case of the UNA in mathematics) assume they know, which can affect the achievement of the objectives of introductory university courses. Although there have been some short-term training actions aimed at creating the necessary bases for effective learning at the university level, these have not solved the problems previously discussed.
We will not deny the fact that university education requires of its students to have skills, abilities and behaviors which are not provided in secondary education, and that passing a university course requires a great deal of effort, study and dedication. However, we believe that the university should guarantee students the conditions necessary to succeed in their courses, one of which is a consideration of their previous levels of knowledge and, based on this consideration, taking the institutional actions that are necessary to guarantee the students at least the minimum of learning that they require.














