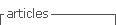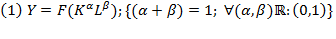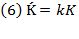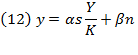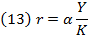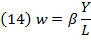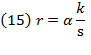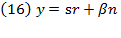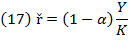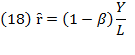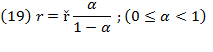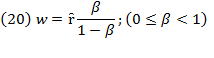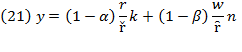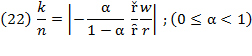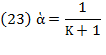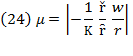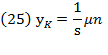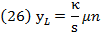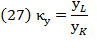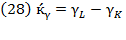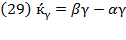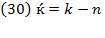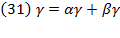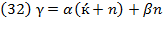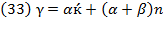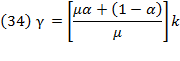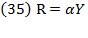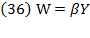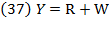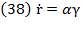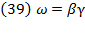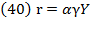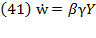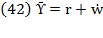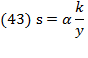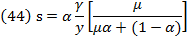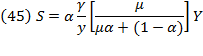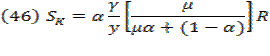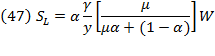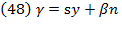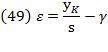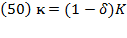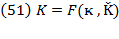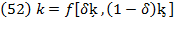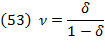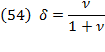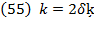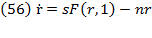Introduction
Trevor Swan’s (1956) contribution to the theory of economic growth has not received the attention it deserves. He theoretically worked on economic growth and capital accumulation “to illustrate…a theme common to Adam Smith, Mill, and Lewis, the theory of which is perhaps best seen in Ricardo: namely, the connexion between capital accumulation and the growth of the productive labour force,” and he also affirmed that “the neoclassical economists were in favour of productivity and thrift, but never found a way to make much use of them” (Swan, 1956, p. 334).
Based on Cobb-Douglas’s (1928) production function, Swan’s unclassical case attributes production growth to the combination of capital and labor force, and it professes to be an explanation of how saving and capital accumulation are related to production growth. It can be suggested that Swan tried to answer the five questions formulated by Cobb and Douglas (1928, p. 139-140) in “A Theory of Production,” adding the theme of thrift in relation to adding capital to stock in a given instant. The role of savings in the capital accumulation process was also a concern in Keynes (1936), Harrod (1939; 1960), Domar (1946; 1953), Solow (1956), and more recently in Piketty (2014) and Stiglitz (2015).
Using the Keynesian concept of effective demand, Swan (1956) formulated two basic assumptions. First, “effective demand is so regulated (via the rate of interest or otherwise) that all savings are profitably invested, productive capacity is fully utilized, and the level of employment can never be increased merely by raising the level of spending” (p. 335). In Keynes (1936), the substance of his theory is effective demand, which is summed up into eight propositions (p. 22-23); it is defined as “the expected proceeds” at each instant, where the level of employment is not predicted to be equal to full employment (p. 22). Secondly, “the forces of perfect competition drive the rate of profit or interest 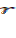 and the (real) wage rate w into equality with the marginal productivities of capital and labour” (Swan, 1956, p. 335).
and the (real) wage rate w into equality with the marginal productivities of capital and labour” (Swan, 1956, p. 335).
Swan’s arguments and crucial assumptions are useful in the present research to demonstrate how the rate of thrift and the rate of capital accumulation are related to the rate of labor and capital, and also capital and labor contribution to production growth. Swan’s model hopes to reveal a strong relationship between capital and labor in production processes through their contributions to production growth. A result of this research is providing formulas to compute relative, average, and gross product, aggregated by those resources to production growth and both capital return and labor income or wage could be determined; by applying the model we propose to Costa Rican data during 2010 - 2017, all these indicators were obtained.
The next section analyzes the model suggested by Swan (1956) and as a result, new formulas will be provided, which measure the elasticity of resource composition, capital and labor productivity, and contribution and share on production growth. Section three focuses on expanding Swan’s unclassical model, the fundamental challenge of this research, to reveal how Swan’s assumptions can be explained. In the subsequent section, formulas will be provided to measure resource share on production growth while the following section will deal with the relationship between thrifts, accumulation, and economic growth. As an addendum, section six suggests a hybrid Swan-Solow equation of economic growth. To evaluate the robustness of the model we propose in this research, we analysis the case of Costa Rica during 2010 - 2017 in section seven. Furthermore, conclusions, limitations, and possible contributions of this research are stated at the end, followed by the references.
Swan’s Unclassical Case: Resource Contribution
“In the first instance…in a given state of the arts, the annual output  depends on the stock of capital
depends on the stock of capital 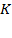 and the labour force
and the labour force  ” (Swan, 1956, p. 334).1 Swan’s case is based on Cobb-Douglas’s (1928) production function. Therefore:
” (Swan, 1956, p. 334).1 Swan’s case is based on Cobb-Douglas’s (1928) production function. Therefore:
Also, “the annual addition to the capital stock is the amount saved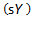 , where
, where 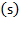 is a given ratio of saving to output (or income)” (Swan, 1956, p. 335).
is a given ratio of saving to output (or income)” (Swan, 1956, p. 335).
Thus, from the previous equation, the amount saved is:
This amount saved is equal to the annual addition to the capital stock.
Now, the annual addition to the capital stock is the amount in which capital stock changes. Let us call 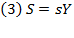 that addition and define it as follows:
that addition and define it as follows:
Here we derived 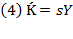 by equalizing equations (3) and (4). So, the annual relative growth of capital
by equalizing equations (3) and (4). So, the annual relative growth of capital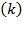 is:
is:
So that:
After replacing equation (4), we obtain:
Thus:
Differentiating equation (1) presumes “all variables are treated as continuous functions of time, which is measured in years…'annual output' is the instantaneous rate of output per annum” (Swan, 1956, p. 335). This is as a consequence of annual variations in 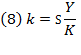 and the elasticity of production
and the elasticity of production 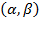 due to those changes:
due to those changes: 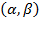 . From this result, the “instantaneous relative rates of growth per annum, subject to instantaneous compounding” (Swan, 1956, p. 335)
. From this result, the “instantaneous relative rates of growth per annum, subject to instantaneous compounding” (Swan, 1956, p. 335) 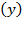 will emerge:2
will emerge:2
where 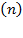 “stand(s) for the annual relative rate of growth” of labor (Swan, 1956, p. 335).
“stand(s) for the annual relative rate of growth” of labor (Swan, 1956, p. 335).
Furthermore, 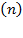 stand for capital and labor’s potential relative contribution to production growth. If
stand for capital and labor’s potential relative contribution to production growth. If 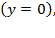 then
then 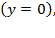 and
and 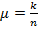 so that:
so that:
In this, 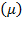 is the elasticity of resource composition, from which
is the elasticity of resource composition, from which 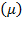 can be estimated as:
can be estimated as:
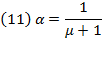 is the elasticity of capital contribution to production growth (Villalobos, 2019a). Inserting equation (8) into equation (9) will result in Swan’s basic formula for the relative rate of growth of output:
is the elasticity of capital contribution to production growth (Villalobos, 2019a). Inserting equation (8) into equation (9) will result in Swan’s basic formula for the relative rate of growth of output:
Swan’s rate of profit 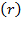 , also equivalent to the rate of interest driven by the forces of perfect competition, is:
, also equivalent to the rate of interest driven by the forces of perfect competition, is:
Hence, the rate of profit is a fraction 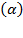 of the average output of capital, which defines the marginal productivity of capital. Thus, the rate of profit is an amount equal to the marginal productivity of capital, meaning profit is measured in terms of a certain amount of output. Also, the real wage rate
of the average output of capital, which defines the marginal productivity of capital. Thus, the rate of profit is an amount equal to the marginal productivity of capital, meaning profit is measured in terms of a certain amount of output. Also, the real wage rate 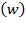 is supposed in such “forces of perfect competition” as equivalent to marginal productivity of labor:
is supposed in such “forces of perfect competition” as equivalent to marginal productivity of labor:
For this definition, a profit rate for capital invested in labor must be yielded, which was not suggested by Swan. From equation (8), 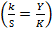 which when placed in equation (13) will give:
which when placed in equation (13) will give:
So, at a given 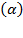 , the rate of profit will depend on the rate at which savings satisfy the augment on capital accumulation. In that equation,
, the rate of profit will depend on the rate at which savings satisfy the augment on capital accumulation. In that equation, 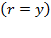 as
as 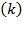 grows proportional to
grows proportional to 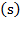 at instantaneous
at instantaneous . This brings Piketty’s fundamental force for divergence to mind:
. This brings Piketty’s fundamental force for divergence to mind: 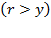 , which is his crucial assumption (Piketty, 2014, p. 25), but dubious (Krugman, 2015; Mankiw, 2015; Raval, 2017; Villalobos, 2019b; Galbraith, 2014). If
, which is his crucial assumption (Piketty, 2014, p. 25), but dubious (Krugman, 2015; Mankiw, 2015; Raval, 2017; Villalobos, 2019b; Galbraith, 2014). If 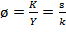 , the prior equation or (13) gives rise to Piketty’s tautological formulation
, the prior equation or (13) gives rise to Piketty’s tautological formulation 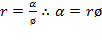 or his first fundamental law of capitalism (Piketty, 2014, p. 52). Equation (15) can be expressed as
or his first fundamental law of capitalism (Piketty, 2014, p. 52). Equation (15) can be expressed as 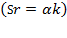 , and Swan’s basic formula given by equation (9) can be written as:
, and Swan’s basic formula given by equation (9) can be written as:
This is what Swan (1956, p. 335) suggested in footnote 5. Suppose 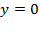 so that per equation (16),
so that per equation (16), 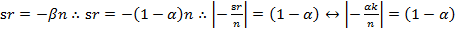 from which equation (10) will result.
from which equation (10) will result.
Expanding Swan’s Unclassical Case: Resource Productivity
Let 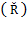 stand for the average rate of return on capital or capital income at a given instant;
stand for the average rate of return on capital or capital income at a given instant; 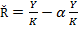 and thus:
and thus:
If 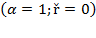 and
and 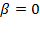 . Similar for the labor productivity,
. Similar for the labor productivity, 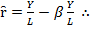
 denotes the average rate of return on labor alone. By inserting equation (17) into (13), and equation (18) into (14) and after some movements, we obtain respectively:
denotes the average rate of return on labor alone. By inserting equation (17) into (13), and equation (18) into (14) and after some movements, we obtain respectively:
Equation (19) depicts the curve of the rate of profit of capital alone, depending on capital return and capital productivity, whose slope is traced by 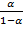 . Equation (20) delineates the curve of wage rate of labor alone with slope
. Equation (20) delineates the curve of wage rate of labor alone with slope 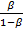
These two previous rates lead to a balance in capital and labor shares on production growth at each state of the arts. Replacing those equations and equation (8) into (9), we transform Swan’s basic formula given by equation (12) into the following:
This formula could explain oscillations in the share of income in the long run, provided that the state of the arts, market conditions, and government policies change. Assuming 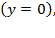 the level of output will remain constant, and so
the level of output will remain constant, and so 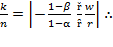
Resource composition plays its role in tracing the line in which production growth, cost growth, and profit lie (Villalobos, 2019a). Equalizing equations (17) and (18) will result in 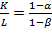 . Let
. Let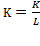 stand for resource composition, so that
stand for resource composition, so that 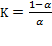 and thus,
and thus, 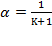 ; but in this case,
; but in this case,  measures capital contribution to the cost growth of production, for which we label it
measures capital contribution to the cost growth of production, for which we label it  so that:
so that:
which with respect to equation (11), 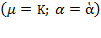 , that is, relative capital contribution to production growth equals relative capital contribution to the cost growth (Villalobos, 2019a).
, that is, relative capital contribution to production growth equals relative capital contribution to the cost growth (Villalobos, 2019a).
Once 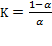 is placed into equation (22), it will yield:
is placed into equation (22), it will yield:
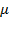 stands for resource composition elasticity composited by resource composition and capital and labor relative rates of profit. After inserting
stands for resource composition elasticity composited by resource composition and capital and labor relative rates of profit. After inserting 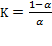 and equation (24) into (21) and making
and equation (24) into (21) and making 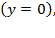 we have
we have 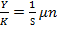 so that the average productivity of capital is:3
so that the average productivity of capital is:3
Due to 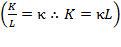 , average labor productivity will be computed after being replaced in
, average labor productivity will be computed after being replaced in 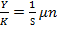 . Thus:
. Thus:
There is no surprise in these results; the same can be concluded from equation (12), which is Swan’s equation, after replacing 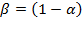 and making
and making 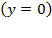 . By the ratio of equations (25) and (26), the composition of potential resource productivity is:
. By the ratio of equations (25) and (26), the composition of potential resource productivity is:
After differentiating this equation, we will unveil the potential resource productivity effect attributed to changes in the state of the arts as Swan (1956) suggested, or by capital and labor exploitation, complemented by government policies. This is:
So, 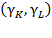 identify the relative average rates of capital and labor potential productivity.4 If in equation (28) we suppose
identify the relative average rates of capital and labor potential productivity.4 If in equation (28) we suppose 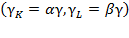 , it can transform into:
, it can transform into:
By the derivative of 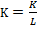 , the relative rate of resource composition
, the relative rate of resource composition  is found, denoting any fluctuations on resource composition. So,
is found, denoting any fluctuations on resource composition. So, 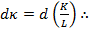
If 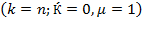 , then
, then 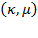 remains the same at each instant, but not necessarily the state of the arts. Equation (28) shows that if
remains the same at each instant, but not necessarily the state of the arts. Equation (28) shows that if 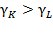 , then
, then 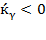 . However, equation (30) denotes that at
. However, equation (30) denotes that at 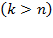 ,
, 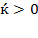 . As a hypothesis, the economy could promote increments in
. As a hypothesis, the economy could promote increments in 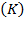 provided that it entails a greater productivity of labor, which could reveal technological changes. These results explain that technological productivity
provided that it entails a greater productivity of labor, which could reveal technological changes. These results explain that technological productivity 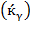 is implicit in resource productivity. It is a net result in economic growth: neither a simple “beyond the contribution of capital and labour” as Swan (1956, p. 337) wrote nor just a residual factor as Solow M. R. (1957) and Arrow, Chenery, Minhas, and Solow (1961) fruitlessly advocated.
is implicit in resource productivity. It is a net result in economic growth: neither a simple “beyond the contribution of capital and labour” as Swan (1956, p. 337) wrote nor just a residual factor as Solow M. R. (1957) and Arrow, Chenery, Minhas, and Solow (1961) fruitlessly advocated.
If 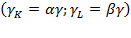 , a function of resource productivity growth can be defined as:
, a function of resource productivity growth can be defined as:
With respect to equation (9), 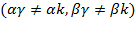 , implying that resource contribution could differ from resource productivity along time; it is what we call residue
, implying that resource contribution could differ from resource productivity along time; it is what we call residue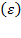 . This result provides evidence that technological and exploitation effects on production growth could result from the changes in the state of the arts, market conditions, and government policies. To highlight this,
. This result provides evidence that technological and exploitation effects on production growth could result from the changes in the state of the arts, market conditions, and government policies. To highlight this, 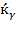 is the relative net rate of productivity, which could be attributed to technological changes in capital and labor or exploitation productivity effects on the relative rate of economic growth. However, it could also be a sign of inefficient and ineffective resource allocation in the economy, unfair production growth distribution, or even a result of imperfect statistics. This tentative hypothesis could be supported by
is the relative net rate of productivity, which could be attributed to technological changes in capital and labor or exploitation productivity effects on the relative rate of economic growth. However, it could also be a sign of inefficient and ineffective resource allocation in the economy, unfair production growth distribution, or even a result of imperfect statistics. This tentative hypothesis could be supported by  differing from
differing from 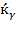 and thus equation (29) does not reveal
and thus equation (29) does not reveal 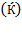 , the technological productivity of resource composition.
, the technological productivity of resource composition.
So, 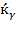 could explain the deviations around
could explain the deviations around  , ceteris paribus, denoting how resource productivity can differ with respect to their contributions; at
, ceteris paribus, denoting how resource productivity can differ with respect to their contributions; at 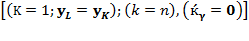 ,
, 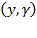 keeps its pace, but if
keeps its pace, but if 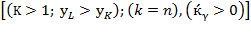 ,
, 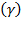 growth must occur. Nevertheless, its distribution between capital and labor might be unequal, which will be reflected by a fall in
growth must occur. Nevertheless, its distribution between capital and labor might be unequal, which will be reflected by a fall in 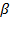 . When equations (31) and (9) are matched,
. When equations (31) and (9) are matched, 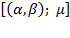 remains, revealing that no fraction of production growth will evaporate, and resource contribution could disclose convergence with divergence and, conceivably, resource share inequality. As it must be clear in the preceding analysis,
remains, revealing that no fraction of production growth will evaporate, and resource contribution could disclose convergence with divergence and, conceivably, resource share inequality. As it must be clear in the preceding analysis, 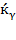 could differ from
could differ from  , which could explain how and why resource contribution could create distance from resource share.5 It is so because “the rate of technical progress” (and) “the rate of growth of labor may not be independent of the rate of accumulation” (Swan, 1956, p. 338).
, which could explain how and why resource contribution could create distance from resource share.5 It is so because “the rate of technical progress” (and) “the rate of growth of labor may not be independent of the rate of accumulation” (Swan, 1956, p. 338).
The formula that simplifies those processes of the previous analysis can be obtained by replacing 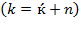 from equation (30) into equation (9) as follows:
from equation (30) into equation (9) as follows:
This is equivalent to Swan’s basic formula given in equation (12), and after simplifying will result in:
Due to 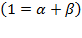 ,
, 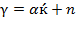 and by equation (30) and the fact that
and by equation (30) and the fact that 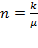 , we obtain
, we obtain 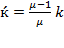 so that:
so that:
This is our fundamental equation, equivalent to those given in equations (9) and (16) as long as 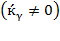 , which shows the essential long-term dynamics of economic growth and its cycles and trends. Thus, it could depict the convergence-divergence problem prevailing in economic growth theory (Villalobos, 2019b).
, which shows the essential long-term dynamics of economic growth and its cycles and trends. Thus, it could depict the convergence-divergence problem prevailing in economic growth theory (Villalobos, 2019b).
Measuring Resource Share on Production Growth
Partial derivative of equation (1) in terms of capital is 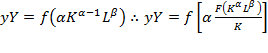 and letting
and letting 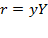 be the rate of capital income or profit, we get equation (13). Defining
be the rate of capital income or profit, we get equation (13). Defining 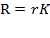 as the total capital income, we will obtain the following from the prior equation:
as the total capital income, we will obtain the following from the prior equation:
In the case of labor, 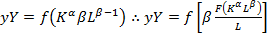 and making
and making 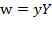 to express the rate of labor income or wage, we get equation (14). If
to express the rate of labor income or wage, we get equation (14). If 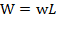 is the total income (wage) for labor, then:
is the total income (wage) for labor, then:
In terms of distribution of production as capital and labor income, we obtain:
The same results can be derived from equation (9) due to 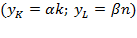 where
where 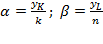 are, respectively, the elasticity of capital and labor productivity. By multiplying both sides of these expressions by
are, respectively, the elasticity of capital and labor productivity. By multiplying both sides of these expressions by 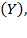 we compute the amount of product or income that those resource contributions generate, as defined by equations (35) and (36).
we compute the amount of product or income that those resource contributions generate, as defined by equations (35) and (36).
Additionally, the relative share in production growth of those resources can be discovered by multiplying the above definitions by 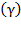 , denoting relative capital and labor incomes in terms of its productivity:
, denoting relative capital and labor incomes in terms of its productivity:
By multiplying both terms of the prior equations by 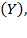 the average income in terms of productivity for capitalists and workers is obtained:
the average income in terms of productivity for capitalists and workers is obtained:
The average capital and labor share on production as income at each instant is:
Saving and Capital Accumulation
Equation (8) can be reformulated into 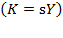 , where
, where 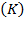 represents the stock of capital at each instant. The derivative of this definition can measure the rate of capital accumulation:
represents the stock of capital at each instant. The derivative of this definition can measure the rate of capital accumulation: 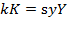 so
so 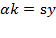 ; and the relative rate of saving is:
; and the relative rate of saving is:
Thus, 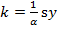 which substituted in equation (34) will yield an equivalent equation of equation (43). This would be capable of explaining why the relative rate of saving could vary and how capital accumulation could occur:
which substituted in equation (34) will yield an equivalent equation of equation (43). This would be capable of explaining why the relative rate of saving could vary and how capital accumulation could occur:
By multiplying both expressions of the previous equation by 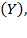 the amount of saving at each instant is deduced;
the amount of saving at each instant is deduced; 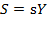 :
:
which is assumed to be equal to the quantity of capital accumulated at each instant. This capital accumulation includes consumption or depreciation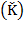 , that fraction of
, that fraction of 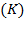 transferred to
transferred to 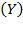 , and new investments of capital. Now it is feasible to determine how much savings at each instant could come from capital and labor, respectively:
, and new investments of capital. Now it is feasible to determine how much savings at each instant could come from capital and labor, respectively:
Swan’s formula defined by equation (9) is equivalent to equation (34). If instead inserting equation (8) in it, we replace 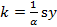 derived from equation (43), so that we obtain:
derived from equation (43), so that we obtain:
Thus, Swan’s equation (12) is ruled out because it does not provide a good measure of the influence of saving and capital accumulation on economic growth. Furthermore, if it were true that 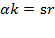 as Swan suggested, then
as Swan suggested, then 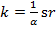 . After it is substituted into equation (9), it will yield equation (16), which is also equivalent to equation (48). This means that by equalizing equations (16) and (48),
. After it is substituted into equation (9), it will yield equation (16), which is also equivalent to equation (48). This means that by equalizing equations (16) and (48), 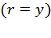 . Nevertheless, in the case that
. Nevertheless, in the case that 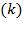 or
or 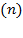 decline, it will be advantageous to use
decline, it will be advantageous to use 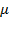 . Also, the residue
. Also, the residue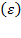 can be calculated by
can be calculated by 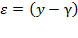 or
or 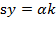 .
. 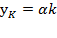 , so
, so 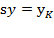 and thus,
and thus, 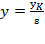 so that:
so that:
How can national savings be useful in financing the capital accumulation process? First, it must be clear that “(…) replacement falls far short of depreciation. Hence, investment net of depreciation cannot be identified with investment net of replacement” (Domar, 1953, p. 1-2). Let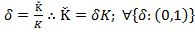 be the rate of depreciation so that
be the rate of depreciation so that 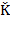 is the amount of capital effectively transferred to
is the amount of capital effectively transferred to 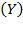 ,
, 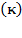 the remnant of capital, and
the remnant of capital, and 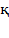 the new amount of capital investment. Ceteris paribus, the cost of production
the new amount of capital investment. Ceteris paribus, the cost of production 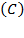 could vary pursuant to
could vary pursuant to 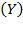 . Furthermore,
. Furthermore, 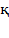 could appear as effective capital accumulation together with
could appear as effective capital accumulation together with 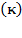 at each instant:
at each instant: 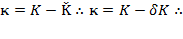
So, at each instant 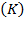 would reflect replacements into depreciation, and new investments which could imply technological progress.
would reflect replacements into depreciation, and new investments which could imply technological progress.
A function of 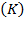 can be described as:
can be described as:
At each instant, 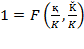 and due to
and due to 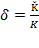 , we deduce that
, we deduce that 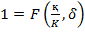 so that
so that 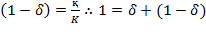 . By differentiating equation (51) and inserting those definitions, the following is obtained:
. By differentiating equation (51) and inserting those definitions, the following is obtained:
where 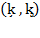 represent, respectively, the relative rates of depreciation and of the remnant of capital. Substituting equation (52) in equation (34) will reveal
represent, respectively, the relative rates of depreciation and of the remnant of capital. Substituting equation (52) in equation (34) will reveal 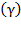 . If replaced in equation (43), it will explain the reasons for the changes on
. If replaced in equation (43), it will explain the reasons for the changes on 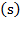 , and so on and so forth.
, and so on and so forth.
If 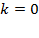 , then
, then 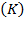 remains the same quantity and
remains the same quantity and 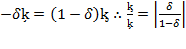 and if
and if 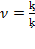 so:
so:
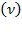 measures the elasticity of depreciation with which
measures the elasticity of depreciation with which  can be estimated:
can be estimated:
Given 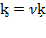 , after being substituted in equation (52), it will yield
, after being substituted in equation (52), it will yield 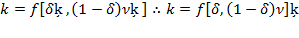 . Then, inserting equation (53), the result is the effective rate of capital accumulation governed by depreciation, which could include replacement and/or new capital of different technology at each instant (Villalobos, 2019a):
. Then, inserting equation (53), the result is the effective rate of capital accumulation governed by depreciation, which could include replacement and/or new capital of different technology at each instant (Villalobos, 2019a):
An Addendum: Swan-Solow Hybrid Equation
Swan (1956), Solow M. (1956), and Arrow, J. K et al. (1961)’s economic growth analysis comes from the same point, saving and capital accumulation. Also, their assumptions are the same. Surprisingly, Solow’s introduction of “A Contribution to the Theory of Economic Growth” starts by lessening Harrod and Domar’s assumptions as “dubious” and the result of “suspect.” Nevertheless, “the bulk of this paper is devoted to a model of long-run growth which accepts all the Harrod-Domar assumptions except that of fixed proportions,” and at the end, he suggested introducing “’Keynesian relations and rigidities” (Solow M., 1956, p. 66).6 Solow’s fundamental equation (Solow M., 1956, p. 69) is:
By applying the reverse to this equation, we can explain the precedent results. Following Solow’s definition, let 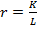 instead of
instead of 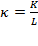 . When replaced inside
. When replaced inside 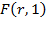 in the prior equation, it will yield
in the prior equation, it will yield 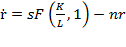 . The value (1) inside
. The value (1) inside 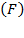 represents
represents 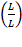 , which when inserted in the previous formula will result in
, which when inserted in the previous formula will result in 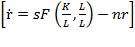 . Then, we can simplify so that
. Then, we can simplify so that 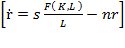 . We also know that
. We also know that 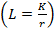 , so
, so 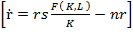 and
and 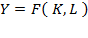 , then
, then 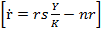 . Moreover,
. Moreover, 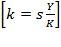 so
so 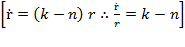 , and let
, and let 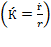 stand for the relative rate of growth of resource composition so that
stand for the relative rate of growth of resource composition so that 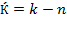 , as equation (30) states. Yet more simply: dividing
, as equation (30) states. Yet more simply: dividing 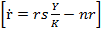 by
by 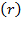 so that
so that 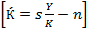 and from here we can get equation (9).
and from here we can get equation (9).
Solow’s fundamental equation expresses the path of resource composition: “Thus (6) states that the rate of change of the capital-labor ratio is the difference of two terms, one representing the increment of capital and one the increment of labor” (Solow M., 1956, p. 69). Swan’s basic formula of economic growth given in equation (12) is based on the relative rate of growth of output, which is explicitly defined by resource contributions: profit and wage rates. But if 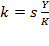 , we can return to Swan’s equation (12) and after inserting equation (30), which is Solow’s fundamental equation, we obtain equation (33); from this, a hybrid Swan-Solow equation of economic growth has been uncovered.
, we can return to Swan’s equation (12) and after inserting equation (30), which is Solow’s fundamental equation, we obtain equation (33); from this, a hybrid Swan-Solow equation of economic growth has been uncovered.
Evaluating the Developed Model: The Case of Costa Rica (2010 - 2017)
The purpose of this section is to provide an evaluation of the model we propose in this research by analyzing the case of Costa Rica. By examining the role of saving on capital accumulation and on economic growth during the period 2010 - 2017, we can reveal the robustness of the model. To achieve this result, it is necessary to measure resource contribution and share on production growth.7
Data and Methodology
Real values of annual Gross Domestic Product 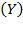 and of Gross Fixed Capital Formation
and of Gross Fixed Capital Formation 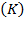 by the economy given at market prices and in millions of colons (1991=100) and computed until 2017 came from the Central Bank of Costa Rica (BCCR for its acronym in Spanish) (BCCR, 2019). The period of study begins in 2010 due to the changes in computing the number of workers - we call labor
by the economy given at market prices and in millions of colons (1991=100) and computed until 2017 came from the Central Bank of Costa Rica (BCCR for its acronym in Spanish) (BCCR, 2019). The period of study begins in 2010 due to the changes in computing the number of workers - we call labor 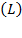 - in the economy according to the National Institute of Statistical and Census (INEC for its acronym in Spanish) (INEC, 2019). In this analysis, we work with data of
- in the economy according to the National Institute of Statistical and Census (INEC for its acronym in Spanish) (INEC, 2019). In this analysis, we work with data of 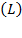 provided at the IV-trimester of each year. Additionally, we built indices for each of those variables by taking their first year 2010 real value as a basis to measure the relative variations at each year during 1910 - 1917; to make it clear by taking labor as an example:
provided at the IV-trimester of each year. Additionally, we built indices for each of those variables by taking their first year 2010 real value as a basis to measure the relative variations at each year during 1910 - 1917; to make it clear by taking labor as an example: 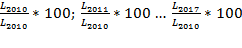 . These indicators are critical in the analysis of Costa Rica’s resource contribution and share on economic growth and the role of saving and capital accumulation during those years.
. These indicators are critical in the analysis of Costa Rica’s resource contribution and share on economic growth and the role of saving and capital accumulation during those years.
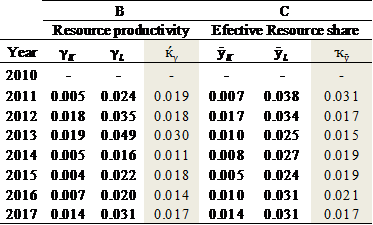
B. Analysis of Results
This section will describe and analyze the outcomes that the proposed model generates at each level when processing 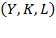 computed indices mentioned above. Table 1 registers the relative rates of variations of those effective indices
computed indices mentioned above. Table 1 registers the relative rates of variations of those effective indices 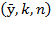 in that order and the resource composition
in that order and the resource composition 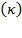 at each instant. According to the formulas revealing the fundamental model,
at each instant. According to the formulas revealing the fundamental model, 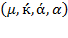 is computed with those rates, which measure
is computed with those rates, which measure 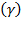 according to the fundamental equation (34) of economic growth and thus its potential level
according to the fundamental equation (34) of economic growth and thus its potential level  .
.
After the international economic crisis hit Costa Rica’s economy in 2008 - 2010 (BCCR, 2010; BCCR 2011), it grew from 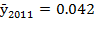 to
to 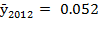 , which was possibly influenced by a moderate international economic growth (2% - 3%), especially in the United States of America (the main trading partner of the country) and increments in national consumption and
, which was possibly influenced by a moderate international economic growth (2% - 3%), especially in the United States of America (the main trading partner of the country) and increments in national consumption and  (BCCR, 2012). Labor employment grew 2.3 percent points between 2011 - 2012 as capital increased by almost 100%, and
(BCCR, 2012). Labor employment grew 2.3 percent points between 2011 - 2012 as capital increased by almost 100%, and 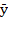 was slightly less than
was slightly less than 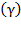 . Business expectations of Costa Rican entrepreneurs led to
. Business expectations of Costa Rican entrepreneurs led to 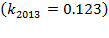 , a rate of 4.3 percent points compared to the prior year, led by industrial machinery and transport equipment especially in firms of the special regimen (BCCR, 2012), while
, a rate of 4.3 percent points compared to the prior year, led by industrial machinery and transport equipment especially in firms of the special regimen (BCCR, 2012), while 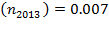 percent points. But
percent points. But 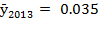 , approximately (-1.7) percent points over the previous year, influenced by a moderate increase in exportations and domestic consumption (BCCR, 2012).
, approximately (-1.7) percent points over the previous year, influenced by a moderate increase in exportations and domestic consumption (BCCR, 2012).
In short, while 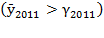 showing divergence between effective and potential production growth,
showing divergence between effective and potential production growth, 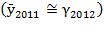 denoted convergence and
denoted convergence and 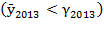 revealed divergence once again (Figures 1 and 2). In the subsequent years of the analyzed period, potential production growth diminished, possibly due to the strong decrement in employment. This implied a rise in effective production growth, which could be explained by greater labor exploitation rendered into greater labor productivity. This result could be caused by increments in the elasticity of resource composition
revealed divergence once again (Figures 1 and 2). In the subsequent years of the analyzed period, potential production growth diminished, possibly due to the strong decrement in employment. This implied a rise in effective production growth, which could be explained by greater labor exploitation rendered into greater labor productivity. This result could be caused by increments in the elasticity of resource composition 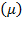 ; the greater
; the greater 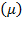 , the lesser
, the lesser 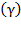 and the greater
and the greater 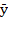 , as it appears have happened in 2011 and 2014 - 2016, when
, as it appears have happened in 2011 and 2014 - 2016, when 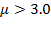 (Figures 3 and 4); this variable fluctuates over the composition of resources in those years (Figure 5). This result could provide an answer the next question: “Can we estimate, within limits, whether this increase in production was purely fortuitous, whether it was primarily caused by technique, and the degree, if any, to which it responded to changes in the quantity of labor or capital?” (Cobb & Douglas, 1928, p. 139).
(Figures 3 and 4); this variable fluctuates over the composition of resources in those years (Figure 5). This result could provide an answer the next question: “Can we estimate, within limits, whether this increase in production was purely fortuitous, whether it was primarily caused by technique, and the degree, if any, to which it responded to changes in the quantity of labor or capital?” (Cobb & Douglas, 1928, p. 139).
Table 1 Costa Rica: Effective and Potential Production Growth (2010 - 2017)

Source: Elaborated by the author. Based on Central Bank of Costa Rica (BCCR, 2019).
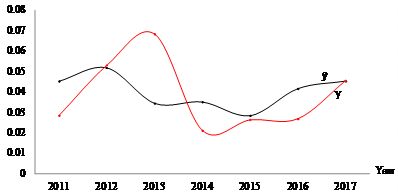
Figure 1 Costa Rica: Relative Rates of Effective and Potential Production Growth (2010 - 2017). Source: Based in Table 1.
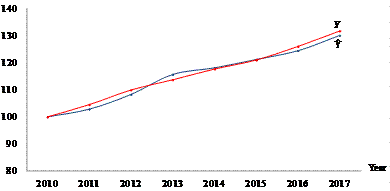
Figure 2 Costa Rica: Effective and Potential Production Growth Trends (2010 - 2017). Source: Based in Table 1.
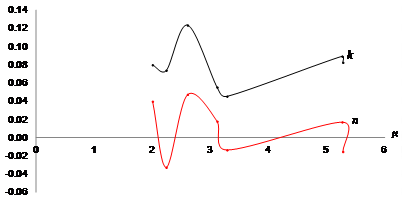
Figure 3 Costa Rica: Relative Rates of Capital and Labor at Resource Composition Level (2010 - 2017). Source: Based on Table 1.
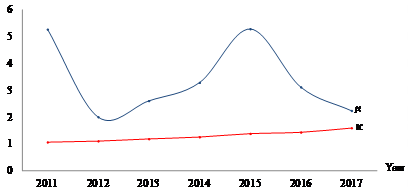
Figure 4 Costa Rica: Resource Composition and Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 1.
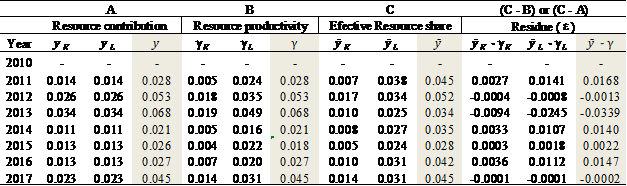
Divergences denoted by 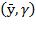 represent the residue
represent the residue as a result of the global production processes in the economy (Table 2, Figures 5 and 9). So, resource contribution to production growth converge
as a result of the global production processes in the economy (Table 2, Figures 5 and 9). So, resource contribution to production growth converge 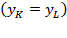 but potential resource productivity diverge
but potential resource productivity diverge 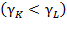 at any level of
at any level of 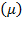 ; nevertheless,
; nevertheless, 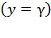 (Figure 6):
(Figure 6):
May it be possible to determine, again within limits, the relative influence upon production of labor as compared with capital? ... As the proportion of labor to capital changed from year to year, may be it possible to deduce the relative amount added to the total physical product by each unit of labor and capital and what is more important still by the final units of labor and capital in this respective year? (Cobb & Douglas, 1928, p. 139)
But, effective labor share on production growth 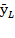 is increasingly greater than capital share
is increasingly greater than capital share 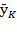 as
as 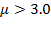 , in congruence with
, in congruence with 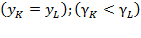 (Tables 2 and 3, Figures 7 and 8).
(Tables 2 and 3, Figures 7 and 8).
Regarding this issue, “…may we secure light upon the question as to whether or not the processes of distribution are modeled at all closely upon those of the production of value?” (Cobb & Douglas, 1928, p. 139-140). Average and total capital and labor share on effective production growth in Costa Rica during 2010 - 2017 could follow resource contribution and productivity (Table 4, Figures 10 and 11). Both average and gross capital income dropped during 2012 - 2015, when 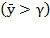 decreased as
decreased as 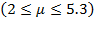 and
and 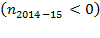 . Meanwhile, average labor fell less than the average capital income, but gross wage increased. Convergence appears once again showing an inverse relation between capital and labor gross income. Those results surged despite
. Meanwhile, average labor fell less than the average capital income, but gross wage increased. Convergence appears once again showing an inverse relation between capital and labor gross income. Those results surged despite 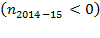 and perhaps due to an increment in real wage (BCCR, 2012; BCCR; 2015). As a general result, the greater
and perhaps due to an increment in real wage (BCCR, 2012; BCCR; 2015). As a general result, the greater 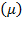 is, the lower average capital income is as compared to labor income (Figure 12). Additionally, the lower the gross capital income is, the greater gross labor income becomes (Figure 13).
is, the lower average capital income is as compared to labor income (Figure 12). Additionally, the lower the gross capital income is, the greater gross labor income becomes (Figure 13).
Table 2 Costa Rica: Relative Resource Contribution, Productivity, and Share on Production Growth and the Residue (2010 - 2017)
Source: Based on Table 1.
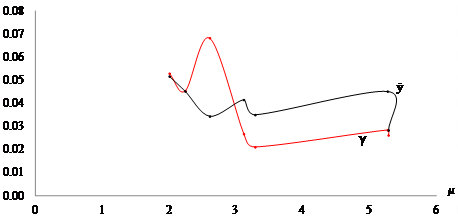
Figure 5 Costa Rica: Relative Rates of Effective and Potential Production Growth at Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 1.
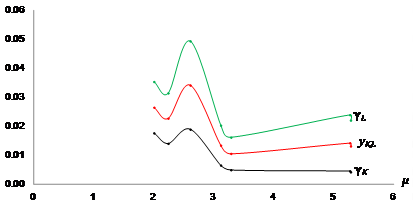
Figure 6. Costa Rica: Trends of Relative Rates of Capital and Labor Contribution to Production Growth and Productivity with respect to the Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 2.
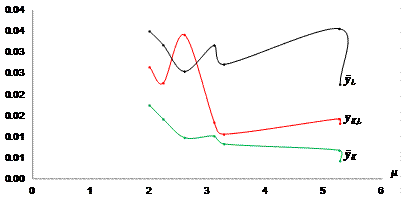
Figure 7 Costa Rica: Trends of Relative Rates of Capital and Labor Contribution to Production Growth and their Effective Shares with respect to the Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 2.
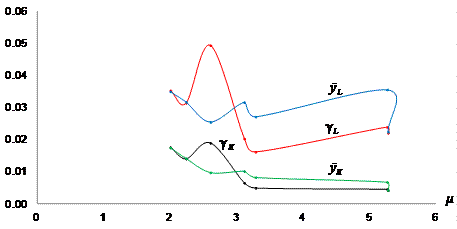
Figure 8 Costa Rica: Trends of Relative Rates of Capital and Labor Productivity and their Effective Shares on Production Growth with respect to the Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 2.
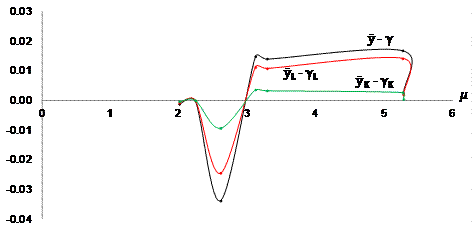
Figure 9. Costa Rica: Trends of Relative Resource Residue at Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 2.
Table 3 Costa Rica: Effective Relative Capital and Labor Productivity and Share on Production Growth (2010 - 2017)
Source: Based on Table 2.
Table 4 Costa Rica: Capital and Labor Share - or Income - on Production Growth (2010 - 2017)
Source: Based on Table 1.
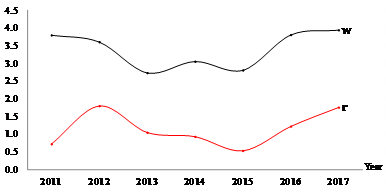
Figure 10 Costa Rica: Trends of Average Capital and Labor Income (2010 - 2017). Source: Based on Table 4.
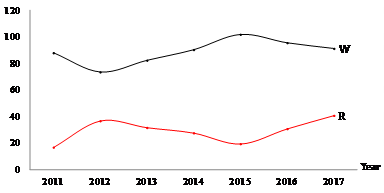
Figure 11 Costa Rica: Trends of Capital and Labor Gross Income (2010 - 2017). Source: Based on Table 4.
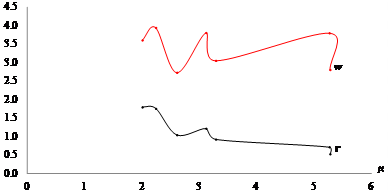
Figure 12 Tendency of Average Capital and Labor Share at the Elasticity of Resource Composition (2010 - 2017). Source: Based on Table 4.
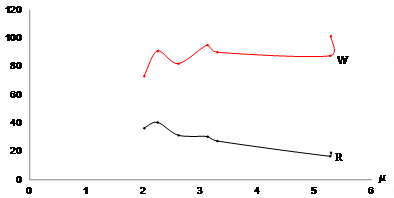
Figure 13 Costa Rica: Tendency of Total Capital and Labor Share at the Elasticity of Resource Composition (1910 - 1917). Source: Based on Table 4
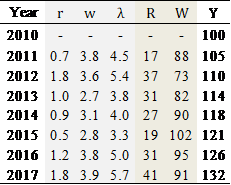
It is possible that the level of thrifts has been influencing the process of capital accumulation in Costa Rica during 2010 - 2017, but it is clear that it depends on foreign direct investment (BCCR, 2009, p. 10; BCCR, 2013, p. 13) and foreign savings (BCCR, 2010). As a result of the analysis of the effects of saving on capital accumulation and economic growth in Costa Rica, the model we propose determines that after a high rate of depreciation in 2011, it falls almost at the level of the rate of thrifts in the next year, dropping in 2012 (Table 5, Figures 15 and 16). In those years,  precipitates from
precipitates from 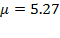 to
to 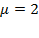 , and
, and 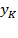 falls while labor contributes twice as much compared to capital to production growth.
falls while labor contributes twice as much compared to capital to production growth. 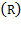 increases 2.7 times from 2011 to 2012 as long as average real labor incomes remained stagnant while its gross income
increases 2.7 times from 2011 to 2012 as long as average real labor incomes remained stagnant while its gross income 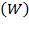 resulted in a 16% deterioration. In 2013, the rate of depreciation dropped 65% compared to the previous year, and it contrasted with the level of saving rate (92%) and capital accumulation (12.3%). In this year,
resulted in a 16% deterioration. In 2013, the rate of depreciation dropped 65% compared to the previous year, and it contrasted with the level of saving rate (92%) and capital accumulation (12.3%). In this year, 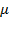 grew at
grew at 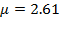 due to fixed capital formation coming from new buildings in the manufacturing sector, and residential and industrial machinery and transport equipment, and the high level of savings came especially from direct foreign investment (BCCR, 2012). Labor productivity increased from
due to fixed capital formation coming from new buildings in the manufacturing sector, and residential and industrial machinery and transport equipment, and the high level of savings came especially from direct foreign investment (BCCR, 2012). Labor productivity increased from 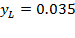 to
to 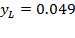 , but its share on production growth diminished from
, but its share on production growth diminished from 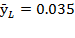 to
to 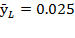 , denoting a higher level of labor exploitation.
, denoting a higher level of labor exploitation.
In the next years of the analyzed period, savings rates and capital accumulation returned to “normal” levels in the country (Table 5). In 2014, the rate of depreciation rose 3.18 times with respect to 2013, and 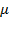 jumped to higher levels because
jumped to higher levels because 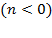 and capital accumulation rose (Figures 14 and 15).
and capital accumulation rose (Figures 14 and 15). 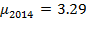 and
and 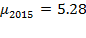 while
while 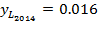 and
and 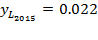 but the relative labor share was
but the relative labor share was 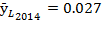 and
and 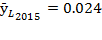 in a frank deterioration in comparison to 2013. In 2015, the rate of depreciation fell to -13%, while capital accumulation grew 8.2% in consonance with the increase in savings rate, which could have a great influence in “…the beginning of the first stage of construction of the Moin Container Terminal and the execution of electricity generation and road infrastructure projects” (BCCR, 2015, p. 13)8 which advanced the economy’s impact during 2016 (BCCR, 2017). As a general result, if savings must be provided by the economy through labor and capital income, it is shown in Table 5 that it could represent a great sacrifice of national consumption
in a frank deterioration in comparison to 2013. In 2015, the rate of depreciation fell to -13%, while capital accumulation grew 8.2% in consonance with the increase in savings rate, which could have a great influence in “…the beginning of the first stage of construction of the Moin Container Terminal and the execution of electricity generation and road infrastructure projects” (BCCR, 2015, p. 13)8 which advanced the economy’s impact during 2016 (BCCR, 2017). As a general result, if savings must be provided by the economy through labor and capital income, it is shown in Table 5 that it could represent a great sacrifice of national consumption 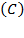 .
.
Table 5 Costa Rica: Capital and Labor Contribution to Savings and Capital Accumulation: Capital Depreciation, Remnant and New Investment (2010 - 2017)

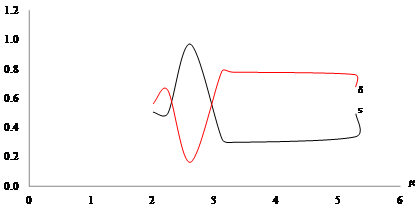
Figure 14 Costa Rica: Trend of the Rate of Depreciation and Savings (2010 - 2017). Source: Based on Table 5.
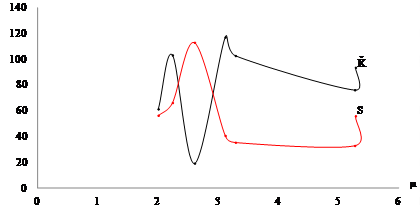
Figure 15 Costa Rica: Trend of the Levels of Depreciation and Savings (2010 - 2017). Source: Based on Table 5.
Conclusions
This research attempts to provide answers to Swan’s (1956) hypothesis that there is a linkage between savings, capital accumulation, and growth of the productive labor force on economic growth. For this, Swan’s (1956) crucial assumptions in his contemporary case were analyzed to pull out new formulas to measure the elasticity of resource composition or relative changes in the amount of labor in response to relative changes in the stock of capital and how this affects production growth. By expanding Swan’s (1956) unclassical case, we unveiled how to quantify the average resource productivity, whose ratio determines an equivalent measure of resource composition. The results suggest that the forces of market do “drive the rate of profit or interest r and the (real) wage rate w into” (inequality) “with the marginal productivities of capital and labour” (, p. 335).
But there are endogenous forces governing production processes, in particular resource composition and its elasticity, reinforced by technological changes. These are responsible for convergence at the level of resource contribution to production growth with divergence at the level of resource productivity. Complementary, exogenous forces, commonly forces of market, government policies, and natural phenomena, could distort the structural divergence, inducing inequities between resource productivity and resource share. The evaluation of the model we developed in this research by analyzing Costa Rica’s data reveals that the elasticity of resource composition is crucial in contrasting resource contribution to production growth and resource productivity with effective - real - resource share.
We found that resource productivity was greater than its contribution to production growth during 2010 - 2017, but it was greater for labor with respect to capital. Even though labor productivity was greater than its contribution to production growth at 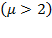 , labor’s share fluctuated closely around its contribution, and there are visible remains above labor productivity at
, labor’s share fluctuated closely around its contribution, and there are visible remains above labor productivity at 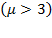 . Perhaps this is the reason why, between limits, in those years the average labor wage appeared to be somewhat higher than the average capital return, and why labor income increased sustainably while capital return declined. Among other results, Costa Rica appears to have had a clear relationship between savings and capital accumulation, including foreign savings as direct foreign investment, and the dynamic of economic growth. Of course, other forces exist like government policies and cycles of business in the country and in the world, especially linked to those main trading partners, which influenced those outcomes.
. Perhaps this is the reason why, between limits, in those years the average labor wage appeared to be somewhat higher than the average capital return, and why labor income increased sustainably while capital return declined. Among other results, Costa Rica appears to have had a clear relationship between savings and capital accumulation, including foreign savings as direct foreign investment, and the dynamic of economic growth. Of course, other forces exist like government policies and cycles of business in the country and in the world, especially linked to those main trading partners, which influenced those outcomes.
“Once the mind is accustomed to thinking in terms of trends of increase, the old static formulation of problems seems stale, flat and unprofitable” (Harrod, 1939, p. 15). We believe that we have contributed to finding answers to the theoretical problem of production growth contribution, productivity, and distribution. More interesting yet, this could provide answers to the problem of the residual factor (Solow, 1957) or to the suggestive phrase “beyond the contribution of capital and labour” (Swan, 1956). In our reasoning, it could indeed disclose the phenomenon of convergence and divergence and with it, the problem of inequality distribution of production growth between capitalists and workers and between workers (Stiglitz, 2015; Piketty, 2014; Krugman, 2015). Within limits, the main result of this research, never before done, is to have computed the relative, average, and gross capital and labor contribution to the economic growth and the rates of thrift, depreciation, and accumulation. Because of the limitations of data, we suggest that resources could not have been paid at their productivity, but in general “the processes of distribution are modeled at all closely upon those of the production of value” (Cobb & Douglas, 1928).
This endeavor could be useful on an academic scale, especially in economic science as well as in government policies and firms.