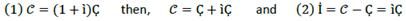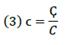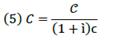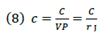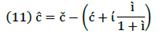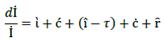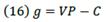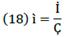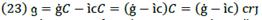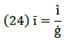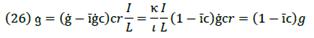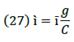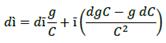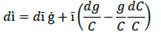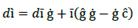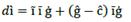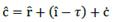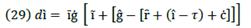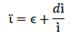Introduction
Production growth depends on various factors, many of which are challenging to explain. Economic theory uses facts that could be measured by different techniques, although this is not easy to conclude. What happens with financial capital and financial resources is where we must dig deeper into the concepts and facts. But to do so, we must make rational connections between concepts and between concepts and their fundaments. This is the purpose of this theoretical research, analyzing concepts and their relations as they seem to occur in a real economy. We examine financial resource contribution to production growth and financial capital participation on profit.
This research is an advance on “Production Cost, Prices and Income of Firms” (Villalobos, 2015). In the process of transforming inputs into outputs (Jehle & Reny, 2011, p. 126), input attributes are transferred into outputs. Money, as a coin or banknote, can be used to acquire resources, but itself alone is not a resource. Money as a concept can refer to anything, even those that can be a resource. As a means of transaction, money can facilitate the acquisition of goods and services of almost any kind. Some goods and services acquired by money are resources. Thus, money has the ability of acquire values as inputs, and by that it becomes capital.
What is called capital is anything (e.g. money) that can be used to generate any sort of benefit (e.g. economic profit 𝑔). By financial capital we understand certain amounts of assets, such as money, that could be reproduced by its profitable use no matter where it comes from (banks, stock market). This is possible if financial capital (credit, bonds, and shares) becomes a financial resource, because there is no way for financial capital to reproduce by itself. It is as a financial resource that financial capital (money or any other goods or services) given as loan Ҫ could make the global production process possible. Loans would not only facilitate the production process and production growth but also profit, and by this act, it would receive interest.
Interest is a ratio of profit, and because of this, financial resources would reflect the financial capital contribution to production growth. If an economy is a conjunction of resources, then money given-taken as a loan could be transmute into resources. A resource is anything useful for something else, especially to produce goods and services. However, it is not enough to produce it for sale; resources must be profitable. So, Ҫ becomes a financial resource, and as such, it seeks to participate in profit distribution. The rate of its participation is called the rate of interest ì, and so Ҫ and ì define debt 𝒞.
In a real economy, firms must deal with loans to acquire resources. In the production process, any resource assumes the form of production cost, so a loan becomes part of the cost as it is used to obtain resources. Credit is the way by which financial capital participates in the production process and also profit. The rate of interest is the means by which financial capital gets a fraction of profit as interest. Loans become financial resources in the hands of producers and through this, they contribute to production growth and generating profit.
Financial Resource on Production Cost
We call debt 𝒞 and it is formulated as 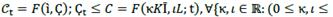
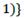 and C represents the total value of the cost of production including fixed resource K, intermediate resource
and C represents the total value of the cost of production including fixed resource K, intermediate resource  and labor L, and the rate of interest ì. So,
and labor L, and the rate of interest ì. So,
For producers, Ҫ is the amount of money that corresponds to a part or total value of resources on production cost. Thus,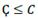 represents the magnitude of financial resources in the real value of production cost. So,
represents the magnitude of financial resources in the real value of production cost. So,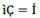 is not a cost but rather the quantity of interest (money) owed to financial resources for their contribution to production growth.
is not a cost but rather the quantity of interest (money) owed to financial resources for their contribution to production growth.
We will not complicate the computation of Ҫ, İ by using compound interest due to the economy periodically paying a quota composite of İ plus a portion of Ҫ. This quota may or may not imply proportional pays of İ and Ҫ. Experience shows that financial capital charges a large proportion of instead İ of Ҫ almost always from the beginning of 𝒞. This is to say that financial capital charges interest on producers and also on loans to consumers, even before they generate profit as value. It is a fact that producers periodically require Ҫ to finance the production process, so it is not easy to calculate how much producers pay on past-present debt. What we can suppose is that every so often (e.g. per month or year), the economy pays fractions of the value of production Ҫ, İ to the financial sector.
To simplify our discussion in this research, we suppose that Ҫ, İ correspond to the effective real value annually paid by the economy to the financial sector. So, Ҫ, İ could vary from time to time depending on changes on Ҫ, ì and the debt-term. Thus, to introduce Ҫ to the production process as part of the value of production cost, we proceed as follows:
could vary from time to time depending on changes on Ҫ, ì and the debt-term. Thus, to introduce Ҫ to the production process as part of the value of production cost, we proceed as follows:
Equation (3) denotes the ratio of loan and thus the magnitude of loan in relation to the whole cost of production. Hence, c denotes the composition of the cost of production as a loan plus the producer’s own capital (depreciation, profit). This means that c expresses the ability of the economy to sustain its production process. For this reason, it is necessary to analyze changes on 𝐶, Ҫ; thus, differentiating equation (3) obtains
Let 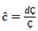 be the rate of change on the loan amount and
be the rate of change on the loan amount and  the rate of change on the cost of production, and by equation (3), we obtain
the rate of change on the cost of production, and by equation (3), we obtain
Let us call 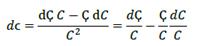 the rate of change in the ratio of loan. Therefore,
the rate of change in the ratio of loan. Therefore,
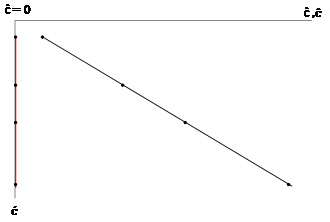
As result, ć will depend upon ĉ and on ĉ in opposite directions. So, the greater (lower) ĉ is than ĉ ceteris paribus (Figure 3), the greater (lower) the participation of financial resource on profit. If ĉ = 0, ć will be the opposite of ĉ, which is an indicator of the amount of profit that producers retain (Figure 1) or the contrary (Figure 2). In such a way, ĉ, ĉ, ceteris paribus, indicates the rate of participation of entrepreneurs on profit. For financial capital, we can say that its income is İ, while for producers it is just 𝑔.
But, we must keep in mind that participation on profit and contribution on profit have different connotations. For financial capital, its participation on profit is measured in terms of the rate of interest; meanwhile, for producers, it is computed in terms of the rate of profit. Contribution is measured here in relation to the value of production growth, which is possible only by producers. So, financial capital participates in profit because producers transform Ҫ into a financial resource (into C), and as such it contributes to production growth. Of course, financial capital indirectly participates in production growth due to producers transforming loans into capital resources. But, if we discuss capital resources, we also talk of capital resource contribution.
By operating on equation (1) and substituting the result in equation (3), we get
and by reorganizing it in function of 𝐶, we obtain
If C is the total value of the cost of production including fixed resource K, intermediate Ī and labor L, the result is
This equation illustrates the composition of the real value of the cost of production, in which Ҫ is included if it exists. This is very important for the economy due to its ability to obtain loans effectively, and producer’s own capital will rely on which kind of resources they invested. So,
By this equation, the resources that will require financing by financial capital are determined.
Defining the real value of production VP as
and the average cost of production c is
and operating on the above equation, C is obtained which is equivalent to equation (5):
In equation (10), it is perceived that 𝐶, Ҫ are given as part of VP denoted by crj. Additionally, ì plays a role on C through Ҫ, which will impact VP. By differentiating that equation, the result will be the change on C, taking into account all its components; that is to say,
Let  be the rate of change in the rate of interest and
be the rate of change in the rate of interest and 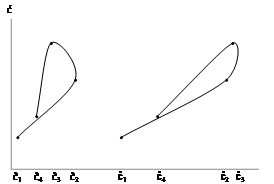 be the rate of change in debt, which will be influenced by changes in
be the rate of change in debt, which will be influenced by changes in 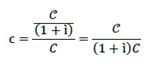 and the debt-term. By replacing it and equation (10) in the previous equation, the result is
and the debt-term. By replacing it and equation (10) in the previous equation, the result is
Let 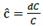 be the rate of cost. By reorganizing this result, we can rewrite that equation as
be the rate of cost. By reorganizing this result, we can rewrite that equation as
Equation (11) expresses 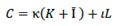 influenced by
influenced by  , which considers
, which considers 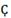 as part of C and the amount of interest İ that the economy must pay,
as part of C and the amount of interest İ that the economy must pay, 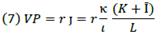 and the rate of change of the rate of interest
and the rate of change of the rate of interest 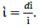
Through equation (4), we can rewrite equation (11) as follows:
So, after simplifying,
Equation (13) denotes that  depends on
depends on 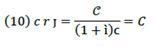 and on the change of the rate of interest. If
and on the change of the rate of interest. If  then
then  , but
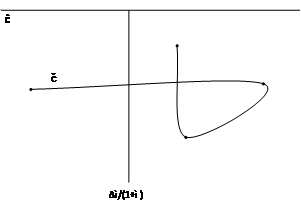
, but 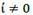 would occur, ceteris paribus, due to changes in the rate of profit in the economy and in the rate of financial capital participation on profit, which defines the path of debt. Figures 4 and 5 illustrate two possibilities.
would occur, ceteris paribus, due to changes in the rate of profit in the economy and in the rate of financial capital participation on profit, which defines the path of debt. Figures 4 and 5 illustrate two possibilities.

Figure 4 Path of debt due to ĉ and change in ì at different rates of profit ceteris paribus. Source: prepared by the author.
Reasons of change in interest
By equation (10), we obtain
The quantity of interest İ paid (e.g. per annum) by the economy (firms, industries) is
So,
From equation (14), it is clear that İ, when it exists, is a result of the global process of production, where resources are combined to get a value of production. It also means that İ is a value that comes from VP every time 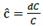 is part of C. By the derivate of equation (14), we obtain
is part of C. By the derivate of equation (14), we obtain
Where 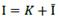 and after simplifying, the following is obtained:
and after simplifying, the following is obtained:
If 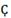 is the rate of change in the rate of interest and
is the rate of change in the rate of interest and 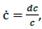 , then,
, then,
And
After simplifying,
Now, let  be the rate of change of İ, and substituting it in the above equation and by reorganizing it, we attain
be the rate of change of İ, and substituting it in the above equation and by reorganizing it, we attain
After reorganizing, the result is
This last equation expresses that the rate of change on İ will depend directly upon the rate of production growth 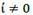 , the rate of change of production costs, the rate of change of loans, and the rate of change in interest rate. It refers to how the economy gets İ from profit to pay it to financial capital. By replacing
, the rate of change of production costs, the rate of change of loans, and the rate of change in interest rate. It refers to how the economy gets İ from profit to pay it to financial capital. By replacing  and equation (4), we get
and equation (4), we get
Equation (15) points out that the rate of change on İ is determined by the rate of change in loans and on the rate of change in interest rate. But this equation occults the fact that 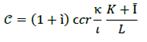 could influence the direction and magnitude of İ. So, expectation of financial capital on
could influence the direction and magnitude of İ. So, expectation of financial capital on 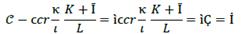 could establish a fundamental role in defining ì. If by equation (4)
could establish a fundamental role in defining ì. If by equation (4) 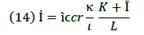 , then equation (15) will denote that producers will retain 𝔤.
, then equation (15) will denote that producers will retain 𝔤.
Interest and profit on resource contribution
Profit is the prime inducement for investors to go into global production and financial activities in an economy. Profit 𝔤 is measured by production value minus production cost value. So,
But gross profit is a result of every economic activity contribution to production growth by using productive resources. To get gross net producer’s profit, we deduce from 𝔤 the interest İ they will pay for financial resources. By equation (16) and 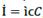 , we obtain
, we obtain
And
So, equation (17) denotes İ as featured in equation (14): the financial resource contribution to production growth. This fact is hidden by resource contribution to production growth expressed by 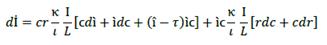 . But, as we said before, this financial resource contribution to production growth reflects the financial capital participation on profit.
. But, as we said before, this financial resource contribution to production growth reflects the financial capital participation on profit.
We can get the same result by a simpler proceeding, defining that
and by equation (14),
then, after some manipulations,
Where İ was deduced by equations (2) and (14). If ġ is the rate of profit calculated as
By equations (7) and (10), we get
and by substituting equation (9), we have
The rate of profit and the rate of interest could not exist if capital as money did not get to transform into productive resource (Robinson, 1953-1954). Capital is not as simple as any stock of things, like money, but rather those things that become production resources and by this on production cost. So, C is not a stock of resources but instead resource values used to be capitalized, and not just as simple capital. It is the nature of equation (20) to measure, relatively, profit resource contribution. But the motivation of equation (19) is to deduce how much profit corresponds to financial resources. Both rates result from the same process, but they have to be split up when profit is distributed between financial capital and producers.
By deducing equation (18) from equation (20), we get producer’s net profit 𝔤 in the economy:
By operating on equation (3) and replacing its result in equation (22), the result is
So, each portion of production cost value will get the same 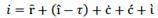 , and for this reason ì is just a fraction of
, and for this reason ì is just a fraction of  . So, let ì be the coefficient as follows:
. So, let ì be the coefficient as follows:
and
Substituting equation (25) in equation (23), we obtain
which is equivalent to equation (17).
Furthermore, by also substituting equation (20) in equation (25), the following is obtained:
By deriving equation (27), we find the change of ì due to changes in production cost and profit:
By simplifying,
Then,
If 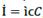 is the rate of change on profit, then,
is the rate of change on profit, then,
Finally, let 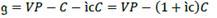 the rate of change on the coefficient ī, so,
the rate of change on the coefficient ī, so,
And
The result is that the rate of interest will change due to changes in the rates of changes 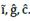 It is shown in equation (28) that, ceteris paribus,
It is shown in equation (28) that, ceteris paribus, 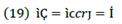 will introduce changes on
will introduce changes on 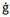 . It could motivate the financial sector to vary ī as a way of changing its participation on
. It could motivate the financial sector to vary ī as a way of changing its participation on 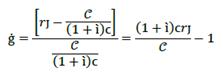 . In addition, it could happen as a result of changes in production growth. We already know that
. In addition, it could happen as a result of changes in production growth. We already know that
So, replacing it in equation (28), we obtain
And now we can define the rate of change on the rate of interest by using equation (25) to get
As  is the rate of change on the rate of interest, then,
is the rate of change on the rate of interest, then,
So, ί is also determined by production growth due to the financial capital expectation and the rate of cost. In the short-term, it is probably 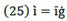 , which will be reflected in equation (30).
, which will be reflected in equation (30).
Return on producer’s capital
Additionally, if producers are paying ì to financial resource Ҫ, it is clear that ì represents the opportunity cost Ï for using its own capital as capital resource.2 This is to say that producers will attain a net rate of profit ġ. By deducing equation (18) or (19) from equation (21), we get
By multiplying both sides of equation (31) by C, we get the producer’s net profit ḡ as follows:
Then, by equation (8),
By replacing VP,C, we get
Now we found in equation (32) that the interest İ owed to financial resource and the interest as opportunity cost Ï appear as ì𝑐𝑟ƙ, so,
To prove the result given by equation (33), we deduce equation (32) from equation (18) as follows:
By simplifying,
and then,
Consequently,
and after rearranging that result,
Thus, the minimum return expected by producer’s own capital is what they could receive from financial capital at ì.3 Minimum return can be estimated by operating on equation (33) as follows:
So, by equation (3),  and replacing it in the previous equation we get
and replacing it in the previous equation we get
Now let 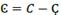 be the producer’s own capital, so,
be the producer’s own capital, so,
and ì is the minimum rate of return expected for producers and is equal to the rate of interest. By operationalizing, we find the minimum return expectation for producers as follows:
By deriving equation (34), we obtain the changes in return due to changes on ì, Ͼ. So,
Let 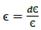 the rate of change on producer’s own capital, and at the rate of change on the rate of interest ί, we have
the rate of change on producer’s own capital, and at the rate of change on the rate of interest ί, we have
And by equation (34), we get
Then, let 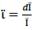 be the rate of change on the rate of return expected by producers, and thus,
be the rate of change on the rate of return expected by producers, and thus,
In equation (35), we show that the rate of change on the rate of return depends on the rate of change on the rate of producer’s own capital and the rate of change on the rate of interest. This equation is the counterpart of equation 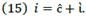 .
.
Let us see some extreme calculations as an academic matter; first, if, 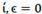 then of course
then of course 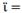 . Second, if
. Second, if 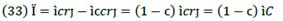 , then
, then  . Third, if
. Third, if 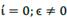 , then
, then 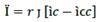 . Between these two last points, some combinations appear to show
. Between these two last points, some combinations appear to show 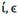 defining ϊ. These arrangements will not necessarily illustrate straight or curved lines but rather a cyclical situation, depending on economic dynamic. If ͼ rises at a different ί, the expectation of the rate of return could be lower than ί and producers could be motivated to invest their own capital. This means that producers could have a lower opportunity cost investing their own capital over a loan. In a case like this, producers would retain a great amount of profit by using their own capital rather than loans.
defining ϊ. These arrangements will not necessarily illustrate straight or curved lines but rather a cyclical situation, depending on economic dynamic. If ͼ rises at a different ί, the expectation of the rate of return could be lower than ί and producers could be motivated to invest their own capital. This means that producers could have a lower opportunity cost investing their own capital over a loan. In a case like this, producers would retain a great amount of profit by using their own capital rather than loans.
By equalizing equations (35) and (15), by replacing  in equation (35), we can illustrate different situations in an economy.
in equation (35), we can illustrate different situations in an economy.
And after operating on equation (15) and substituting the result in the previous equation, we get
Thus, the expectation of producers on its own capital will depend on changes to financial capital expectations on 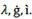
Supposing 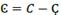 , ceteris paribus, during certain periods does mean that ì remains constant in that period. This also signifies in equation (25) that ī, ġ stay constant, which at the same time means that by equation (30), no changes occur in the economy. But ϲ could change at the constant ì and thus by equation (35),
, ceteris paribus, during certain periods does mean that ì remains constant in that period. This also signifies in equation (25) that ī, ġ stay constant, which at the same time means that by equation (30), no changes occur in the economy. But ϲ could change at the constant ì and thus by equation (35),  . So, it is possible, ceteris paribus, for producers to use loans to finance maintaining or replacing 𝐾, for instance, at the regular ì. If, ceteris paribus, it happens
. So, it is possible, ceteris paribus, for producers to use loans to finance maintaining or replacing 𝐾, for instance, at the regular ì. If, ceteris paribus, it happens  , then
, then 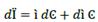 . If the economy is stable, financial capital could change their propensity ī on constant ġ and so ĩ will change, as suggested by equations (25) and (30).
. If the economy is stable, financial capital could change their propensity ī on constant ġ and so ĩ will change, as suggested by equations (25) and (30).
Conclusions
Financial capital is an amount of money that indirectly participates in production growth. As financial capital becomes a financial resource, it contributes to production growth and in the generation of profit. It is as a financial resource that financial capital participates in production cost. Interest rate is a ratio of the rate of profit and the means by which financial resource participates in profit. Financial resource contributes to production growth and thus in the generation of profit. Periodically, producers pay financial capital an amount of money as interest which is a part of profit. Interest is just a name that a portion of profit assumes when it must be paid to financial capital. Together, financial capital and interest becomes the producer’s debt.
So, changes in production cost must reflect changes in loans by means of the rate of change on a loan. This rate is an indicator of the participation of financial resources and producers in production growth and profit. These facts are revealed by the value of production and the rate of debt growth. In the long run, the rate of change on interest will depend on the rate of production growth and also on the technical feasibility, technological feasibility, and financial capital propensity on profit. For these reasons, the rate of profit could change, but it is less probable than the rate of interest. It would be due to the fact that the rate of profit is also influenced by market prices and rivalry intensity. So, the rate of interest as a ratio of the rate of profit could not vary by changes in the rate of profit. This explains why the rate of return of producer’s own capital could change from time to time.
We propose to have found different theoretical results with respect to those we know about harmonizing concepts and its fundamentals. Futures investigations must contribute to improving this analysis on production growth and financial capital participation. So, this study would be a useful contribution to enrich on the economic theory debate.
Notas
2 Keynes (1936, p.40) assumed a different criterion for defining user and supplementary cost, and normal profit in the long-period, introducing the interest cost and the third term he called risk-cost.
3 It is not an equalizing rate as Fischer (1930, p. 55) defined as rate of return over cost which it is but also an average rate of interest. However, we can state that 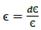 measures the minimum return of profit expected by producers on their own capital. That is to say:
measures the minimum return of profit expected by producers on their own capital. That is to say: 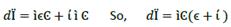 then
then 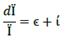 appropriate enough to their
appropriate enough to their 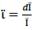 prospect, producers will probably wish to use loans. So, by comparing
prospect, producers will probably wish to use loans. So, by comparing 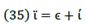 , producers could decide on using credit and own capital or only their own capital.
, producers could decide on using credit and own capital or only their own capital.