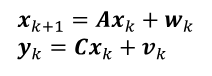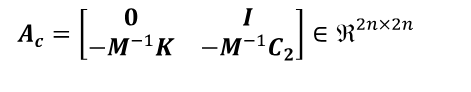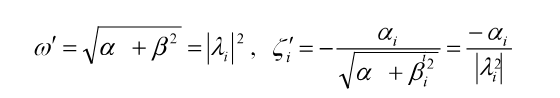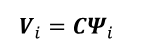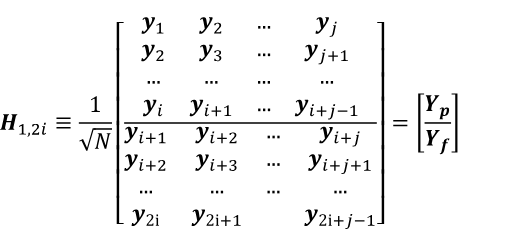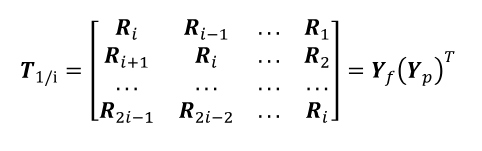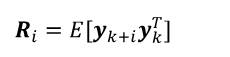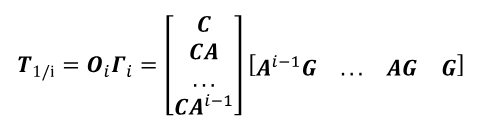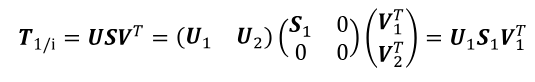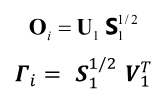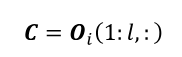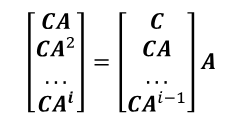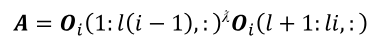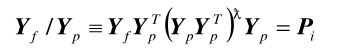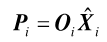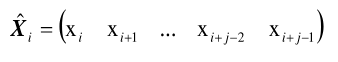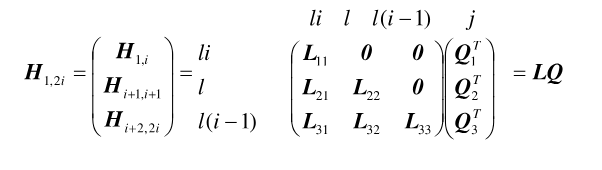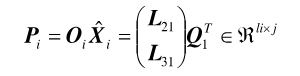Introducción
La identificación experimental de las propiedades modales de estructuras civiles, especialmente en edificios, a través de pruebas de vibraciones ambientales es una práctica cada día más popular. Esto porque su metodología experimental es relativamente sencilla, gracias a los avances tecnológicos en el campo de sensores y de transmisión de datos. En el marco de ensayos no destructivos y detección de daño, la extracción de las características modales a partir de las vibraciones es catalogado como un método global, ya que la vibración medida en cualquier punto de la estructura depende del sistema estructural global como un todo. Mientras tanto, los métodos ultrasónicos, termografía, entre otros, son denominados métodos locales (1). Los parámetros modales obtenidos de las vibraciones de una estructura pueden servir de insumo para conocer de cerca el comportamiento real de un edificio, lo cual permite validar hipótesis o criterios de diseño y generar retroalimentaciones a manuales o códigos de diseño. Además, sirven como base para la calibración de modelos estructurales analíticos, tarea que es indispensable para el diagnóstico estructural, la evaluación de la eficacia de una rehabilitación o el reforzamiento estructural y el monitoreo de salud estructural, entre otros (2).
Al ser las pruebas de vibración ambientales realizadas bajo condiciones operacionales de una estructura, también reciben el nombre de análisis modal operacional (3). En las últimas décadas, se han introducido diferentes métodos multivariables en el dominio de tiempo, combinados con la técnica de sensores ambulantes, dada la cantidad limitada de sensores disponibles, lo cual permite una identificación robusta de los parámetros modales y la recuperación de las formas modales operacionales. Dentro de los métodos antes aludidos, el de identificación subespacial estocástico ha ido ganando terreno en numerosas investigaciones a nivel internacional (4)-(10).
A nivel de Costa Rica, inicialmente, los métodos espectrales univariables eran los que más se habían utilizado en la identificación modal en edificios y puentes (11)-(13). No fue hasta los últimos años que se empezaron a implementar métodos multivariables en el dominio de tiempo, apoyados en la técnica de sensores ambulantes, primero, en materia de puentes (14), (15) y, últimamente, en los edificios (16)-(17).
Métodos de identificación de sistemas de solo salida
La extracción de los parámetros modales a partir de vibraciones ambientales con las siguientes dos características recibe el nombre de identificación de sistemas de solo salida. En primer lugar, la estructura es excitada por factores como el viento, micro-tremores del terreno y por los usuarios, entre otros. En segundo lugar, la entrada es desconocida y solo es posible contar con observaciones de la respuesta del edificio. El éxito de este tipo de identificación depende, por un lado, del hardware: un sensor de alta sensibilidad y sistema de adquisición de datos de alta resolución, donde los acelerógrafos o acelerómetros de alta sensibilidad lateral (3) son el tipo de sensor de vibración comúnmente utilizado para este propósito. Por otra parte, también influye el lado del software: contar con un método de identificación de sistemas robusto contra el ruido, capaz de identificar y discriminar los modos de vibración reales de los espurios.
Para la identificación de sistemas conociendo únicamente las salidas, existen métodos en el dominio de la frecuencia que generalmente son espectrales, no paramétricos, basados en la Transformada de Fourier, como las Funciones de Densidad Espectral de Potencia (18). La descomposición en el dominio de frecuencias (FDD por el acrónimo de su nombre en inglés: Frequency Domain Decomposition) se usa comúnmente cuando se cuenta con múltiples mediciones. Esta realiza la integración de información proveniente de múltiples canales a través de la técnica de descomposición de valores singulares (19) y las frecuencias modales se determinan mediante selección de picos. Por otro lado, existen métodos en el dominio del tiempo que son paramétricos, basados en un modelo matemático del sistema. Por ejemplo, el método de Identificación Subespacial Estocástico (SSI por sus siglas en inglés: Stochastic Subspace Identification) (20), el método de variable instrumental aplicado al modelo autorregresivo de media móvil (ARMA)(4), la Técnica de Excitación Natural junto con el algoritmo de Realización de valores propios (Eigensystem Realization Algorithm, con sus siglas: NExT-ERA)(21), entre otros.
Descomposición en el Dominio de Frecuencias (FDD)
La Descomposición en el Dominio de Frecuencia (FDD) (19) es un método no paramétrico de identificación de sistemas espectrales, que consiste en aplicar la Descomposición de Valores Singulares (SVD, por las siglas de Singular Value Decomposition en inglés) a la matriz de densidad espectral de potencia. En este, las entradas diagonales son los autoespectros y las que están fuera de la diagonal son espectros cruzados entre los diferentes canales de medición. Los autoespectros y los espectros cruzados se estiman mediante el periodograma modificado de Welch (22) y la FDD se realiza aplicando SVD a esta misma matriz de densidad espectral de potencia. La gráfica de los primeros valores singulares en el dominio de la frecuencia puede llamarse espectro FDD o de valores singulares, la cual resume la información de frecuencia de todos los canales en un mismo gráfico. Teóricamente, el número de valores singulares distintos de cero indica el rango de la matriz, por lo tanto, la existencia de más de un valor singular de magnitud importante en una determinada frecuencia indica la presencia de modos con frecuencias muy cercanas entre sí.
A pesar de que un método espectral como FDD es bastante directo y eficiente computacionalmente, la selección de picos para la identificación de frecuencias naturales puede ser bastante subjetiva, especialmente en el caso de que los picos no sean claros. En cambio, los métodos en el dominio del tiempo, como SSI, requieren más esfuerzo computacional y algunos parámetros del modelo deben establecerse previamente, pero se ajusta un modelo modal matemático a los datos y el diagrama de estabilización es una forma efectiva de discriminar los modos verdaderos de los espurios. En implementaciones prácticas, se podrían utilizar métodos espectrales y de selección de picos para realizar un control de calidad de los datos adquiridos y realizar una aproximación inicial de las características dinámicas de la estructura; por ejemplo, determinar el orden de sistema y, posteriormente, se podría aplicar el método SSI para detallar el análisis o asegurar los resultados (23).
Un estudio comparativo mediante simulación Monte Carlo de diferentes técnicas de identificación de sistemas de salida muestra que la técnica SSI proporciona la estimación más precisa de frecuencias naturales y formas modales (21). Por lo tanto, el objetivo del presente estudio consiste en la identificación de los parámetros modales operacionales de un edificio de concreto reforzado tipo marco, de seis niveles. Esto mediante una instrumentación con sensores ambulantes y utilizando las dos principales variaciones que existen de los métodos de identificación subespacial estocásticos: el basado en covarianzas (SSI-COV) y el basado en datos (SSI-DATA), ambos en el dominio del tiempo. Dicha experimentación se realiza con el fin de comparar la eficacia de estos últimos dos para el tratamiento de las señales de vibraciones ambientales recolectadas por acelerógrafos ambulantes.
Método de identificación subespecial estocástico
Los métodos de identificación subespaciales son un método en el dominio del tiempo que se clasifica en: identificación subespacial (SI, acrónimo de su nombre en inglés Subspace Identification), que utiliza datos de entrada y salida, e identificación subespacial estocástica (SSI, por Stochastic Subspace Identification), que es de solo salida, además, su objetivo consiste en identificar la matriz de sistema A y de observación C del modelo de espacio de estados estocásticos de tiempo discreto. Esto se ve en (1):
Aquí wk ϵ R2n×1 son las entradas desconocidas al sistema y wk ϵ Rl×1 representan el ruido en las mediciones, que son asumidos como ruido espacialmente blanco de media cero. En estas expresiones, n es igual a la cantidad de grados de libertad del sistema y l la cantidad de puntos de observación. Asimismo, xk = x (k∆t) = (qkT q̇kT)T es el vector del estado en tiempo discreto conteniendo a los vectores qk y q̇k de desplazamiento y velocidad discretos muestreados, respectivamente.
La matriz del sistema A en tiempo discreto se relaciona con la matriz de sistema Ac en tiempo continuo, mediante A=eAcΔt Por otro lado, la matriz Ac está relacionada con las matrices de masa M, de amortiguamiento C2 y rigidez K (de la ecuación de movimiento Mq¨(t) + C2q̇(t) + Kq(t) = f(t) con q(t) como el vector de desplazamiento de los grados de libertad del sistema) de la ecuación (2) de la siguiente forma:
Se puede calcular la frecuencia natural ωi y la razón de amortiguamiento efectivo ξi del modo i del sistema, a partir de los valores propios complejos λi = αi + jβi de la matriz de sistema Ac de tiempo continuo (que contiene información de masa, rigidez y amortiguamiento del sistema), mediante las siguientes expresiones de (3):
A pesar de que los vectores propios complejos de Ac corresponderían a las formas modales del sistema, estos deben ser mapeados a los puntos de observación o donde se ubican los sensores mediante la matriz de observación C, como en (4):
Aquí, Vi es la forma modal observada y ψi el vector propio de la matriz A para el modo i.
SSI-COV
El algoritmo SSI-COV aparece tempranamente como el método de variable instrumental modificada con aplicaciones en pruebas de laboratorio, tal como la identificación de una viga vertical de acero y el análisis modal de un carretón portador (24). Se pueden encontrar sus otras aplicaciones tempranas en la identificación de estructuras marinas y maquinaria giratoria (25), así como de la estructura de una aeronave (26). En los últimos años, también se puede encontrar numerosas referencias con su aplicación exitosa en puentes y edificios (14)-(16).
El primer paso de SSI-COV consiste en ordenar vectores de las mediciones en una matriz de datos de Hankel, como lo muestra (5):
Aquí, Yp representa las mediciones del pasado y Yf las del futuro. Luego, se calcula la matriz Toeplitz de bloques, vía multiplicación matricial entre las mediciones del futuro y la transpuesta de la matriz de las mediciones del pasado, como en (6):
En esta expresión, Ri son los bloques de covarianza de las mediciones, con un retraso i en el tiempo definido como en (7):
Esta ecuación con E (.) denotando el valor esperado.
Con base en la propiedad clave, derivada del modelo de espacio de estados estocásticos: Ri = CAi₋1G, con G = E(xk+1yTk), la matriz de Toeplitz puede ser factorizada en la matriz de observabilidad extendida Oi ϵ Rli×2n y la matriz de controlabilidad estocástica extendida invertida Γi ϵ R2n×li, como se muestra a continuación en (8):
Aquí, i es el orden de la matriz de Toeplitz, i.e., el número de filas y columnas de bloques.
La implementación numérica de la anterior factorización sería mediante la SVD, como muestra (9):
Expresión en la que U ϵ Rli×li y V ϵ Rli×li son matrices ortonormales, l es la cantidad de sensores, y S es una matriz diagonal que contiene valores singulares positivos en orden descendiente. El orden del sistema se determina separando el subespacio asociado al sistema U1 (correspondiente a valores singulares nulos o casi nulos S1) se compara (7) y (8), la matriz Oi, en la cual se hallan las matrices de sistema A y de observación C, puede ser calculada dividiendo la SVD en dos partes, como evidencia (10):
De la matriz Oi (que son los subespacios columna de la matriz Toeplitz), las matrices del Sistema A y de la observación C pueden ser obtenidas fácilmente. Mediante la notación que se utiliza en MATLAB, la matriz C sería el primer bloque de Oi, como en (11):
De la misma forma, la matriz del sistema A puede determinarse aprovechando la estructura desfasada de la matriz de observabilidad extendida Oi, como muestra (12):
En notación de MATLAB, A se puede extraer como lo expresado en (13):
Aquí, (.)λ denota la pseudoinversa.
Al final, mediante el análisis de valores y vectores propios de la matriz de sistema A y después de que los valores propios sean convertidos a polos en tiempo continuo, mediante (2), las frecuencias modales y la razón de amortiguamiento efectivo pueden calcularse con (3) y las formas modales observadas, con (4).
SSI-DATA
diferencia de SSI-COV, el SSI-DATA evita el cálculo de covarianzas y, por el contrario, realiza una
A diferencia de SSI-COV, el SSI-DATA evita el cálculo de covarianzas y, por el contrario, realiza una reducción de datos mediante la proyección ortogonal, aplicada directamente sobre una matriz Hankel de datos y que se lleva a cabo a través de la descomposición LQ (8), (20), seguida por la SVD para extraer el subespacio del sistema. Los algoritmos de SSI-DATA fueron mejorados por Van Overschee y De Moor (20), de modo que cuentan con diversas variantes que difieren en la elección de las matrices de ponderación antes de factorizar la matriz de proyección. Algunos de los algoritmos más conocidos incluyen CVA (27), N4SID (28), MOESP y IV-4SID (29). En este trabajo se utilizará la versión de SSI-DATA como la presentada en (4), sin entrar en detalles de ponderación y que solo difiere de SSI-COV al sustituir las covarianzas por la proyección ortogonal.
El primer paso de SSI-DATA consiste en la reducción de datos vía proyección del espacio de filas de las mediciones futuras en el espacio de filas del pasado, tal como se muestra en (14):
En la expresión, Yp y Yf ya fueron definidas en (5), (.)λ denota la pseudoinversa, y Pi ϵ Rli×j es la matriz de proyección ortogonal. El teorema principal de la identificación subespacial estocástica (20) demuestra que la matriz de observabilidad extendida Oi se puede encontrar a partir del resultado de la proyección ortogonal, como en (15):
Aquí X̂ ϵ R2n×j es la secuencia de estados estimados del sistema estocástico:
La implementación numérica de la proyección ortogonal de (14) puede ser llevada a cabo mediante una herramienta numéricamente robusta y estable, denominada descomposición LQ (la cual es la versión transpuesta de la conocida descomposición QR), la cual se aplica directamente a la matriz Hankel de datos, como en(17):
En la expresión, L es una matriz triangular inferior y Q es una matriz ortogonal. Lij son particiones de la matriz triangular inferior y Qison particiones de la matriz Q.
Se comprueba en (8) que el espacio de columna deseado de Oise puede obtener directamente del espacio de columna, como se ve en (18):
Esto es la clave de la razón por la que estos algoritmos reciben el nombre de identificación “subespacial”, puesto que se recupera información del sistema, como el subespacio de la matriz de proyección.
En el caso donde solo las matrices A y C son requeridas, estas pueden encontrarse aplicando directamente la SVD de (10) a
y las ecuaciones subsecuentes, así que se separa el subespacio del sistema del subespacio de ruido, a partir de los valores singulares no nulos, tal como fue expuesto en la sección anterior de SSI-COV.
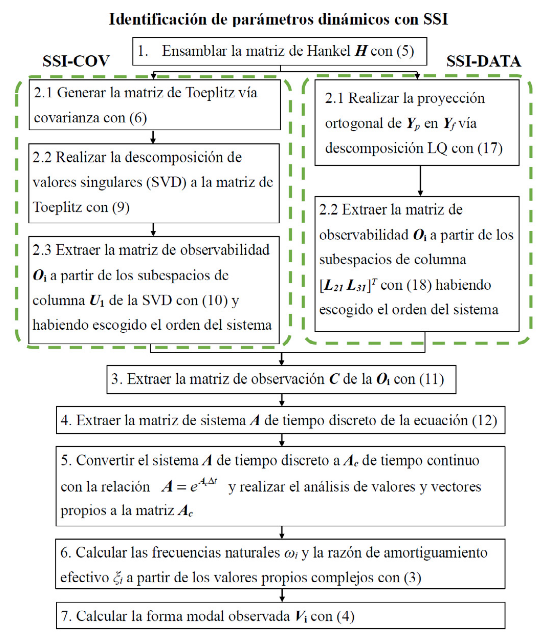
La implementación de ambas alternativas de SSI se ilustra a través del diagrama de flujo mostrado en la Fig. 1. Se observa que la principal diferencia entre ambos métodos radica en que SSI-COV utiliza covarianza y SVD para extraer los subespacios de columna que contienen la información deseada del sistema por identificar. En cambio, SSI-DATA los recupera vía proyección ortogonal de los datos del pasado en los del futuro.
Diagrama de Estabilización
En la implementación práctica de los métodos de identificación de sistemas en pruebas de vibración ambientales, siempre están presentes el ruido y señales correspondientes a modos transcientes no bien excitados o espurios en cualquier medición, además de las señales asociadas a modos físicos y estacionarios. Al no haber información previa sobre el número de modos que se pueden extraer de los datos, el diagrama de estabilización es utilizado para la discriminación entre los modos verdaderos del sistema y los modos de ruido o espurios.
Hay dos alternativas principales para construir el diagrama de estabilización. La primera consiste en fijar la dimensión de la matriz Hankel de la ecuación (5), representada por la variable i, y hacer que el orden del sistema, i.e., orden del subespacio U1 de la ecuación (9), aumente desde un valor más bajo hasta alcanzar un máximo definido por el usuario. Tiene la ventaja de que solo se tiene que hacer una vez SVD o descomposición LQ, según sea el algoritmo, y se consume menos tiempo en la construcción del diagrama de estabilización. Algo que podría ser una desventaja es que no existe un criterio claro para elegir el valor máximo del orden de sistema. Además, se podría estar incluyendo mucho más información de ruido en la matriz A del sistema y, en consecuencia, aparecerán más ruido o polos espurios en el diagrama que deben ser “limpiados” de alguna manera, por medio de otros posprocesamientos, para así aclarar el diagrama de estabilización (30).
La segunda alternativa, la cual es adoptada para este trabajo, consiste en fijar, primero, el orden de la matriz del sistema A contando la cantidad de picos presentes en un análisis espectral previo, por ejemplo, mediante FDD, y se aumenta el orden i de la matriz de Hankel o Toeplitz. El principal inconveniente de esta alternativa es que requiere mucho más esfuerzo computacional que la primera alternativa, junto con la incertidumbre en cuanto a la fijación sobre el orden de la matriz del sistema. La ventaja es que no es necesario determinar el tamaño máximo de la matriz de Hankel. Dicho aumento en su dimensión significa también un incremento en el orden de la matriz de observabilidad extendida, i.e., se estaría introduciendo más información para ajustar la matriz A del sistema a través de mínimos cuadrados, como se aprecia en (12) y (13).
Las mencionadas dos variantes del método subespacial estocástico SSI-COV y SSI-DATA, programadas en MATLAB y que también fueron utilizados en otras investigaciones (9), (14), (15), serán empleadas en la identificación de los parámetros modales operacionales de un edificio de concreto reforzado tipo marco, de seis niveles. Asimismo, serán implementadas con la segunda alternativa de diagrama de estabilización para la discriminación de modos, con el fin de comparar la eficacia de ambos para realizar el análisis modal operacional con las señales de vibraciones ambientales recolectadas por acelerógrafos.
Descripción del edificio e instrumentación
Descripción del edificio
El edificio bajo estudio es el módulo C del complejo de la Facultad de Ciencias Sociales de la Universidad de Costa Rica, que cuenta con cuatro edificios principales (módulos A, C, D y E) y un edificio de interconexión (módulo B), como se muestra en la Fig. 2(c). Está ubicado en la Ciudad de la Investigación de la sede Rodrigo Facio de la Universidad de Costa Rica, en Montes de Oca, San José. El edificio está destinado para el uso de oficinas, áreas de estudio, laboratorios y bibliotecas (las colecciones de libros se encuentran en el segundo y tercer piso). Se pueden apreciar las vistas frontal y trasera del edificio y los acabados de construcción utilizados en las Fig. 2(a) y 2(b).
El edificio bajo estudio (módulo C) puede ser analizado como un edificio independiente, puesto que estructuralmente está desligado del módulo de interconexión, así como de un bloque de escaleras que se aprecia hacia el extremo derecho de la Fig. 2(b), que en principio no interactúan entre sí. Es un edificio de seis niveles de altura con un sistema estructural conformado por marcos de concreto reforzado en ambas direcciones, con entrepisos de losas multitubulares de concreto pretensado y una estructura de cerchas metálicas para el techo; además, se utilizan placas aisladas sobre pilotes para la cimentación. Cada piso del edificio mide 3.5 m de altura, cuenta con cinco vanos de 8 m en el sentido longitudinal, junto con dos vanos de 8 m y uno de 5 m en el sentido transversal (Fig. 3). Lo anterior, así como otras características de interés, se resumen en el Cuadro I. Mientras tanto, las dimensiones geométricas del edificio, junto con las secciones utilizadas en las columnas y vigas se pueden encontrar en los cortes típicos mostrados en la Fig. 3.

Fig. 2. Diferentes vistas del edificio: a) Vista frontal, b) Vista trasera y c) Ubicación del módulo C dentro del complejo de la Facultad de Ciencias Sociales de la Universidad de Costa Rica. Fuente: modificado de (31).
Cuadro I Características del edificio C del complejo de la facultad de ciencias sociales
| Año de construcción | 2014 |
| Tipo de uso | Oficinas, biblioteca, laboratorios, etc. |
| Niveles | 6 |
| Altura total | 17.5 m |
| Periodo fundamental de osiclación para el diseño | 0.379 s (2.64 Hz) |
| Sistema sismorresistente | Marcos de concreto reforzado en ambos ejes |
| Sistema de cimentación | Placas aisladas sobre pilotes |
| Sistema de entrepiso | Losas multitubulares prefabricadas de concreto pretensado |
| Resistencia de concreto f’c | 28 MPa para columnas, vigas y entrepiso |
| Clasificación de regularidad según Código Sísmico de Costa Rica de 2012 | Irregular moderado en planta y en altura |
Otro aspecto a destacar son las áreas triangulares salientes que se observan en la planta de la Fig. 4(a) y en las Fig. 2(a) y 2(b), conformadas por marcos estructurales de concreto, que generan importante aporte a la irregularidad al edificio. En el caso del ducto del lado frontal, está rellenado con pared de mampostería en bloque de concreto anclado con pines, pero desligado de los marcos estructurales con varillas elastoméricas de 2 cm de espesor. En el caso del ducto del lado trasero, está cerrado con ventanería de vidrio. Mientras tanto, el cerramiento externo de los costados laterales del edificio (en el sentido transversal) también está hecho de paredes de mampostería desligados de los marcos estructurales, pero se observa que, a partir del segundo hasta el último nivel, estas cuentan con una sobrecapa de concreto. Por el otro lado, el cerramiento externo en el sentido longitudinal del edificio se realizó con paneles prefabricados del tipo PAMA de ESCOSA, exceptuando el primero y el último nivel, que es base de ventanería de vidrio.
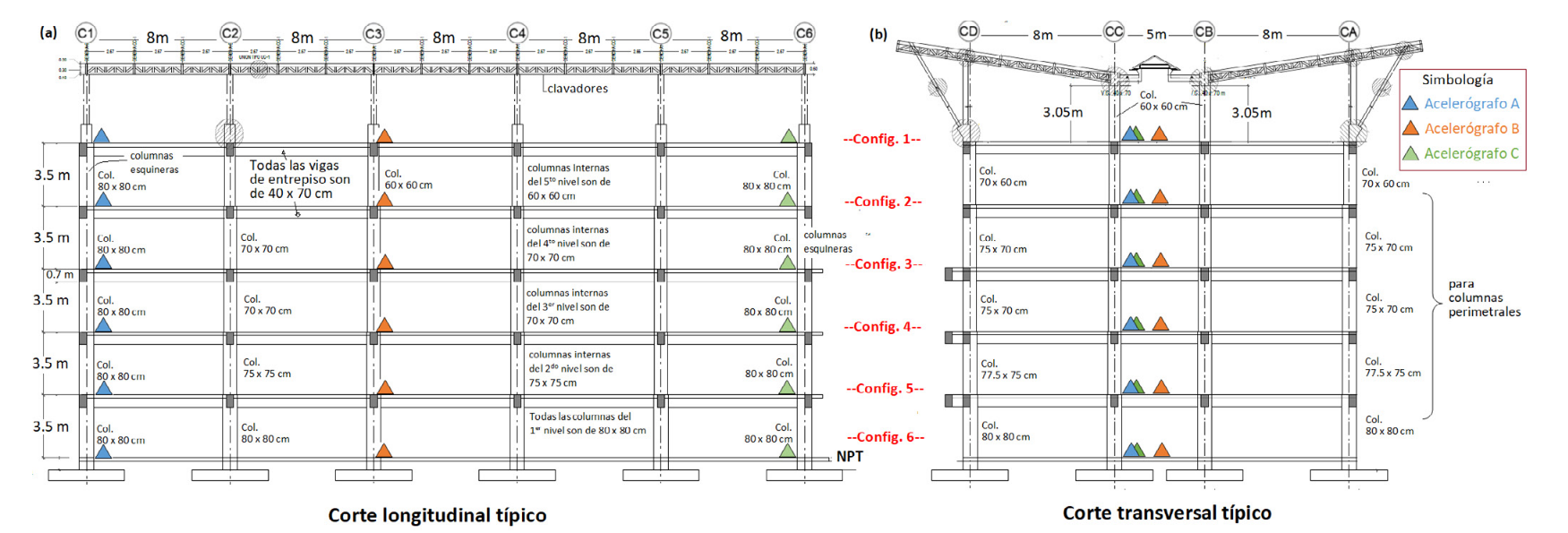
Fig. 3. Dimensiones del edificio y distribución en altura de acelerógrafos en las vistas de: a) Corte longitudinal típico y b) Corte transversal típico. Fuente: modificado de (31).
Instrumentación del edificio
La instrumentación del edificio fue llevada a cabo mediante cuatro acelerógrafos triaxiales Titan SMA de la marca Nanometrics, con algunas de sus características de interés mostradas en el Cuadro II. Con el propósito de tener suficientes puntos de observación, de modo que se puedan identificar experimentalmente las formas modales completas del edificio, se empleó la técnica de instrumentación mediante sensores ambulantes. Asimismo, se siguieron las recomendaciones (3) de colocar un sensor de referencia en el piso superior y en un lugar esquinero alejado del centro de rigidez del edificio, donde, en principio, se pueden captar las vibraciones procedentes de todos los modos del edificio, tanto traslacionales como torsionales. En nuestro caso, el acelerógrafo de referencia, representado por el círculo rojo indicado en la Fig. 4(a), permanece en el piso seis para todas las configuraciones de prueba. En cambio, los otros tres acelerógrafos ambulantes se van desplazando de piso en piso y se instalan en el pasillo central de cada nivel. La razón de la escogencia de este punto de referencia se debe a que el piso superior del edificio experimenta mayor amplitud de movimiento y tendrá una mayor relación señal/ruido; además, es poco probable encontrar en este lugar un nodo de amplitud cero en la forma modal.
Al ser este edificio de seis niveles, se cuenta con un total de seis configuraciones de prueba. La primera inicia desde el sexto piso y los tres acelerógrafos ambulantes se van desplazando hacia niveles inferiores sucesivamente de configuración en configuración, hasta el contrapiso que es la configuración seis, pero con el acelerógrafo de referencia siempre en el piso seis. La Fig. 4(b) muestra una imagen del acelerógrafo instalado sobre un entrepiso.
Cuadro II Características de los acelerógrafos TITAN SMA de la marca NANOMETRICS
| Tipo de acelerómetro utilizado | Balance de fuerzas con transductor capacitivo de desplazamiento |
| Rango de escala completa | Rango seleccionable de ± 4 g, ± 2 g, ± 1 g, ± 0.5 g, ± 0.25 g |
| Ancho de banda | DC hasta 430 Hz |
| Rango dinámico | 166 dB @ 1 Hz sobre un ancho de banda de 1 Hz155 dB. De 3 a 30 Hz |
| Sensibilidad (en modo de ± 4 g) | 0.5 μg por cuenta eléctrica del digitalizador interno de 24 bits |
En total, se cuenta con 19 nodos de medición triaxial para el edificio completo, incluyendo el nodo de referencia. Para cada configuración, se registró un bloque de datos de 20 min de duración y la sincronización entre los datos se basa en las estampas de tiempo que asignan el GPS de cada acelerógrafo. Se empleó una frecuencia de muestreo de 200 Hz, que es común en este tipo de pruebas de vibración ambiental.
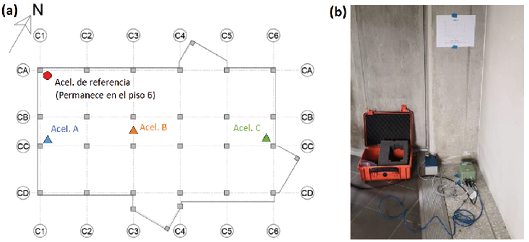
Fig. 4. a) Distribución en planta de los acelerógrafos y b) Ejemplo de instrumentación con acelerógrafo en un punto dado. Fuente: adaptado de (17).
Análisi modal operacional
Las historias de aceleración registradas por los acelerógrafos de la misma configuración son recortadas en su inicio y fin, para que comiencen y terminen en el mismo instante, según las estampas de tiempo de GPS. Asimismo, son agrupadas en bloques de datos de ocho canales, siendo dos canales por cada acelerógrafo en el plano horizontal, dado que es de interés la respuesta lateral del edificio. En el caso de análisis espectral mediante FDD, se obtiene un espectro de valores singulares por cada configuración con estos mismos bloques de datos, sin más pretratamiento. En el caso de análisis mediante métodos subespaciales estocásticos, estos datos son preprocesados, primero, con un filtro pasa-alto tipo Butterworth de orden ocho, con una frecuencia de corte de 0.1 Hz; luego, son decimados a una tasa de muestreo de 50 Hz, con los datos previamente pasados por un filtrado anti-alias, igualmente de Butterworth de orden ocho, con una frecuencia de corte de 20 Hz, un poco debajo de la frecuencia de Nyquist para evitar toda posibilidad de alias en la señal.
Resultado del método en dominio de frecuencias
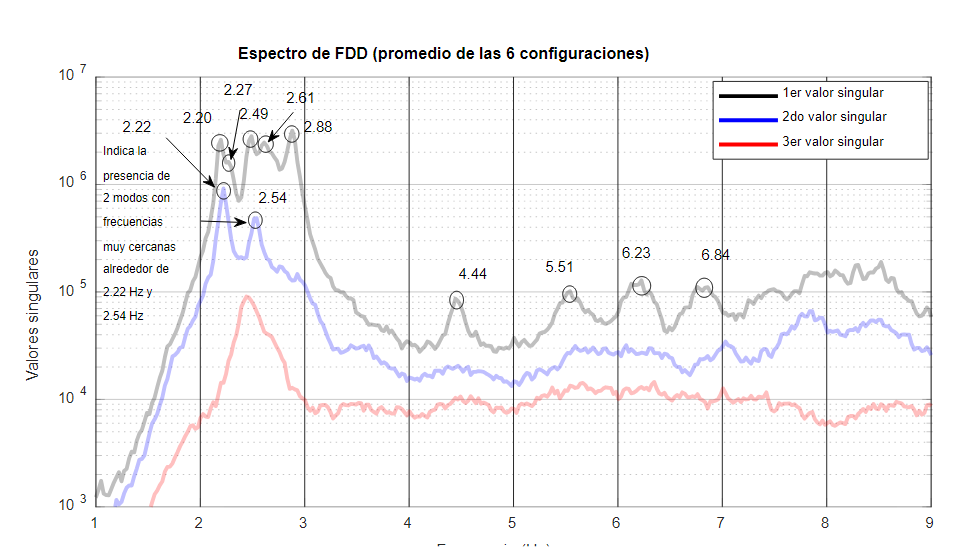
Se calculó un espectro de FDD por cada configuración, con una ventana de 40.96 s de longitud para el cálculo de periodograma de Welch, con lo cual se obtuvo una resolución de 0.024 Hz en los espectros de Fourier y se promediaron 60 de ellos a lo largo de los 20 min (1200 s) de datos, lo cual implica que solo existe un traslape de aproximadamente 50 % de datos en los periodogramas. Al final, los primeros tres valores singulares de los seis espectros de FDD, correspondientes a las seis configuraciones de prueba, son promediados para obtener la Fig. 5. Este sería el espectro de valores singulares para el edificio a nivel global, con acercamiento al rango de frecuencias de 1 a 9 Hz, que fue el rango de interés donde se identificaron modos, como se apreciará más adelante. Vale la pena mencionar que las curvas mostradas en este espectro no pasaron por ningún procesamiento posterior, como el de ajuste de curvas o el suavizado.
Del espectro mostrado en la Fig. 5, se observa una “meseta” de 2 a 3 Hz donde se encuentran múltiples picos, además de que la magnitud del segundo valor singular se acerca al primero en las frecuencias 2.22 Hz y 2.54 Hz. Estos son también los lugares donde se concentran cuatro picos pequeños: por un lado, dos de 2.20 Hz y 2.27 Hz (asociados a 2.22 Hz), por otro, dos de 2.49 Hz y 2.61 Hz (asociados a 2.54 Hz), lo cual es indicador de la presencia de modos con frecuencias muy cercanas entre sí. Sin embargo, de existir resultados provenientes de otra herramienta, como el método SSI, para una identificación más precisa, la selección de picos podría dejar la duda sobre si se tratan, en realidad, de un solo modo o de unos cuantos modos para toda la “meseta” y sobre si son efectivamente modos independientes con frecuencias muy cercanas entre sí. A pesar de ello, estos resultados permiten darse una idea inicial de las características modales de este edificio, además, contando la cantidad de todos los picos debajo de los 20 Hz y añadiendo algunos órdenes para la fijación de modos espurios, se estima un orden de sistema de 70 para los métodos en el dominio de tiempo.
Resultados de los métodos en el dominio del tiempo
La identificación modal con SSI-COV se realizó mediante diagramas de estabilización, los cuales se construyeron al incrementar el orden de la matriz Hankel, representado por el parámetro i, desde 10 hasta 70 filas de bloques de datos y con un orden de sistema definido como 70. Se considera que un modo está bien identificado si un diagrama muestra la apariencia de una línea o un bastión vertical y permanecen estables hasta el mayor orden especificado. Aquellos que no son estables, conforme se aumenta el orden de matriz Hankel, pueden tratarse de modos no bien excitados que no pueden identificarse en forma confiable, modos transitorios o simplemente producto del ruido. Se cuentan con los siguientes criterios de estabilización: las frecuencias son estables si existe menos de 1 % de diferencia entre las calculadas con el orden de matriz n-1 y el orden n, 3 % para formas modales y 5 % para el amortiguamiento. Un círculo azul en el diagrama de estabilización indica que la frecuencia es estable; el círculo azul con una equis (x) roja indica que, además, la forma modal también es estable; si se tuviera, sumada a las anteriores, una cruz verde (+), indica que también lo es el amortiguamiento.
Ejemplos de los diagramas de estabilización obtenidos tanto por el método SSI-COV como por SSI-DATA para cada configuración se muestran en la Fig. 6 para efectos comparativos, superpuestos con los espectros del primer valor singular obtenidos para cada configuración. Los ejemplos muestran un acercamiento al rango de frecuencias de 1 Hz hasta 6 Hz, que es donde se concentran los modos fundamentales de flexión en ambos ejes y de torsión; además, son los más importantes para estos edificios de baja altura.
Se observa que para las configuraciones uno y dos, ubicadas en los pisos seis y cinco, se obtuvieron resultados similares con los dos métodos. Se aprecian cinco líneas o bastiones estables de 2 Hz a 3 Hz, similar a lo que se había apreciado utilizando FDD, con dos modos alrededor de los 2.2 Hz, dos alrededor de los 2.5 Hz y uno cercano a los 2.9 Hz. No obstante, para las restantes configuraciones que corresponden a los pisos inferiores, SSI-DATA no pudo recuperar los mismos cinco modos con diagramas estables, puesto que, en las configuraciones tres y cuatro, solo se observan unos cuatro bastiones, mientras que en las configuraciones cinco y seis no se aprecian del todo bastiones estables. Una posible explicación de ello es que el método SSI-DATA es más exigente en cuanto a la amplitud necesaria de vibración que es registrada en las mediciones para realizar la identificación modal mediante diagramas de estabilización, dado que la amplitud de vibración es menor en niveles más bajos (i.e., una menor relación señal/ruido).
Por el contrario, el método SSI-COV sí pudo identificar estos cinco modos con bastiones estables en las restantes configuraciones. El único modo que no pudo ser identificado de ninguna manera es el asociado a una frecuencia de 4.5 Hz en la configuración cinco. Es posible que este no fue excitado durante el lapso de esta configuración, dado que ni siquiera se aprecia un mínimo pico en el espectro de FDD, razón por la que su forma modal asociada a esta configuración fue interpolada.
Esta comparación directa entre SSI-COV y SSI-DATA, con los mismos parámetros de modelo, demostró que SSI-COV tiene mayor versatilidad para trabajar con vibraciones ambientales en edificios, a pesar de que es posible mejorar los resultados de SSI-DATA reduciendo aún más la tasa de muestreo; por ejemplo, al decimar datos hasta una tasa de muestreo 25 Hz y aumentar el orden de sistema. Este último, además de aumentar el esfuerzo, también implica la aparición de más diagramas asociados a modos espurios o no bien excitados, que podrían complicar la lectura e interpretación de los resultados. La versatilidad de estos métodos tiene repercusiones en cuanto a la técnica de sensores ambulantes implementadas con configuraciones horizontales, i.e., que va desplazando de piso en piso, pues el hecho de que SSI-DATA no pudo recuperar todos los modos en todas las configuraciones hace imposible recuperar la forma modal completa del edificio.
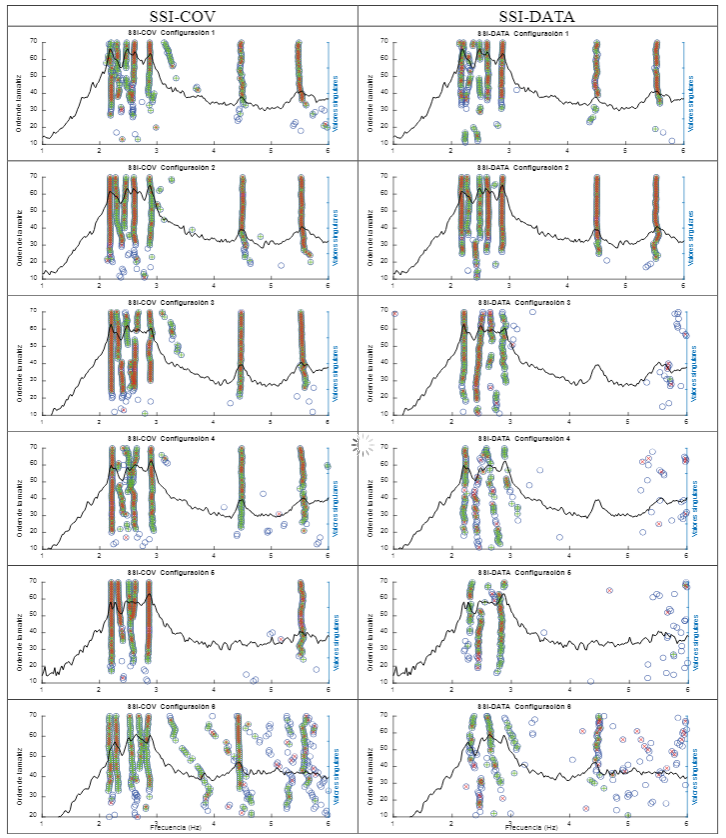
Fig. 6. Comparación de los diagramas de estabilización obtenidos con SSI-COV y SSI-DATA para las seis configuraciones.
Con base en el análisis anterior, se puede concluir hasta aquí que, aparentemente, el método SSI-COV trabaja mejor con los acelerógrafos en pruebas de vibración ambiental en edificios empleando la técnica de sensores ambulantes que SSI-DATA. Por esta razón, se tomarán de este método los resultados finales del análisis modal operacional del edificio. En el Cuadro III, se resumen las frecuencias y amortiguamientos asociados a los modos identificados, mientras sus formas modales operacionales se presentan en la Fig. 7, donde se muestran dos vistas: una frontal y otra lateral (algunos con cierta perspectiva en 3D para apreciar mejor su forma en dirección longitudinal y transversal). En total, se identificaron nueve modos por debajo de los 7 Hz, con cuatro modos traslacionales puros en ambos sentidos (denominados como 1-F para el primer modo de flexión y 2-F para el segundo) y cinco modos asociados a torsión, los cuales están acoplados de alguna forma con algún modo traslacional o de flexión. El modo 1-FT es más un modo de flexión que se da en sentido transversal, pero con algún grado de torsión; no obstante cuenta con una anomalía en la amplitud modal del nivel cuatro, que está totalmente desfasada de los demás niveles. No hay claridad sobre su razón, dado que es algo que ocurre únicamente en ese modo, lo cual también podría deberse a un eventual error surgido al tener que unir formas modales parciales de configuración en configuración para modos con frecuencias muy cercanas entre sí. Los modos 1-T(1) y 1-T(2) son modos torsionales en planta mezclados con la forma modal traslacional de primer modo de flexión en sentido transversal y longitudinal, respectivamente. Por otro lado, los modos 1-T(3) y 1-T(4) son también modos torsionales, pero combinados con la forma modal traslacional de segundo modo de flexión en sentido longitudinal y transversal, respectivamente. Dado que las frecuencias de estos cuatro modos de torsión están separadas, además de que poseen “crestas” independientes en el espectro de FDD y la evolución de las formas modales siguen cierta lógica, se considera que efectivamente deben ser modos de torsión acoplados con diferentes modos de flexión, debido a la irregularidad que posee el edificio.
Por otra parte, se presentan las frecuencias modales obtenidas por SSI-COV dentro un rango de máximo y mínimo en el Cuadro III, además del valor promedio. Esto se debe a que las frecuencias que se identifican en cada configuración varían entre ellas levemente, no obstante, no es estadísticamente significativo, pues, al contar únicamente con seis juegos de frecuencias, no es suficiente como para obtener parámetros estadísticos. Los resultados presentados del método SSI-DATA corresponden al promedio de las frecuencias identificadas en los niveles seis y cinco; son prácticamente iguales a los de SSI-COV. Lo mismo sucede con los valores obtenidos mediante la selección de picos en el espectro de FDD. Los amortiguamientos modales obtenidos por ambas variantes de SSI también se presentan en el mismo Cuadro III. Estos oscilan entre los 0.013 y los 0.052, sin embargo, referencias técnicas como (4) señalan que el método SSI tiende a subestimar el amortiguamiento del sistema.
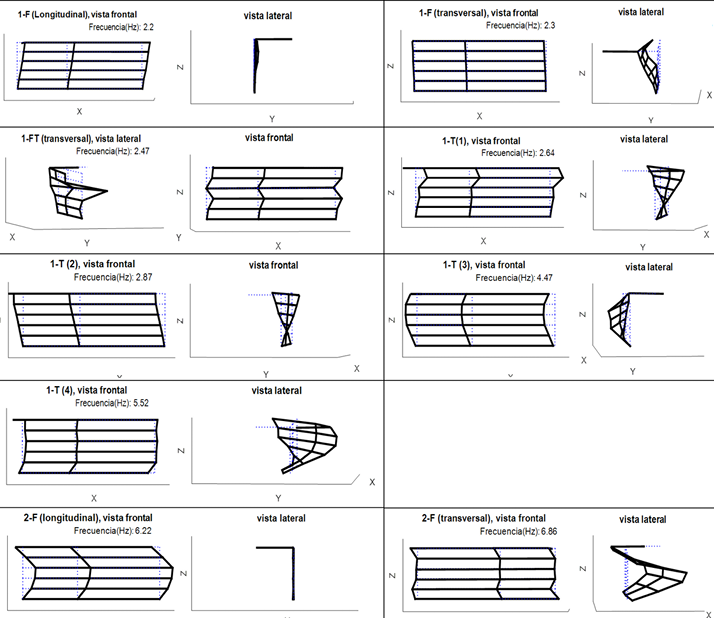
Fig. 7. Formas modales operacionales obtenidos con SSI-COV uniendo las seis configuraciones y su comparación con las formas modales analíticas del modelo de los elementos finitos.
Cuadro III Frecuencias naturales y amortiguamientos identificados
| Modo | Frecuencias (Hz) | Razón de amortiguamiento | |||||
| FDD | SSI-COV | SSI-DATA* | SSI-COV | SSI-DATA* | |||
| Mín. | Promedio | Máx. | |||||
| 1-F(longitudinal) | 2.20 | 2.176 | 2.197 | 2.218 | 2.190 | 0.023 | 0.024 |
| 1-F(transversal) | 2.27 | 2.277 | 2.295 | 2.324 | 2.322 | 0.032 | 0.027 |
| 1-FT(transversal) | 2.49 | 2.406 | 2.470 | 2.527 | 2.482 | 0.015 | 0.013 |
| 1-T(1) | 2.61 | 2.597 | 2.640 | 2.684 | 2.609 | 0.030 | 0.026 |
| 1-T(2) | 2.88 | 2.855 | 2.872 | 2.896 | 2.814 | 0.016 | 0.052 |
| 1-T(3) | 4.44 | 4.422 | 4.472 | 4.500 | 4.503 | 0.018 | 0.026 |
| 1-T(4) | 5.51 | 5.482 | 5.519 | 5.579 | 5.532 | 0.034 | 0.042 |
| 2-F(longitudinal) | 6.23 | 6.141 | 6.218 | 6.271 | 6.156 | 0.029 | 0.033 |
| 2-F(transversal) | 6.84 | 6.767 | 6.858 | 6.932 | 6.853 | 0.029 | 0.035 |
Corrpbpración de resultados con un modelo estructural de elemmentos finitos
Con la intención de corroborar e interpretar los resultados experimentales anteriores, se construyó un modelo estructural analítico de los elementos finitos para el edificio, siguiendo lo indicado en los planos constructivos (31). Vale la pena aclarar que estos no son los planos “as-built”, por lo que la realidad constructiva podría tener diferencias con lo indicado en los planos. Además, muchas zonas del edificio no son de libre acceso, por consiguiente, tampoco fue posible hacer una inspección visual detallada para la verificación. Asimismo, es importante aclarar que el comportamiento real de los edificios en condición operacional puede diferir significativamente del que se obtiene del modelo de los elementos finitos, debido a la participación de elementos o sistemas no estructurales del edificio que no se consideran generalmente en el modelado. Se puede calibrar el modelo introduciendo modificaciones o elementos estructurales, en busca de lograr la concordancia en el comportamiento, lo cual quedaría fuera del alcance de este trabajo. Un modelo estructural preliminar sería el que se utilizará para efectos de comparación.
La modelación se realizó en el programa de análisis estructural SAP2000. Tanto la geometría global del edificio como la de las secciones transversales de las columnas (con sus variaciones conforme se suben en los niveles), vigas y cercha metálica del techo fueron modeladas siguiendo lo especificado en los planos descritos en la sección III.A. El módulo de elasticidad de concreto se estimó con base en la ecuación de módulo de secante de ACI-318 (Ec = 4700√f’c MPa), con f’c= 28 MPa. El entrepiso se modeló con elementos tipo área (cascarón), que tienen un espesor equivalente de 18.5 cm en flexión, para generar el mismo momento de inercia de la sección multitubular de 20 cm, más 6 cm de sobrelosa indicados por el fabricante. Las uniones viga-columna fueron modeladas como totalmente rígidas. Las paredes de concreto de cerramiento externo, que se encuentran tanto en los costados laterales como en las zonas triangulares y que, en un principio, están desligados de los marcos estructurales, son igualmente modeladas con elementos tipo cascarón, pero con la asignación de un factor de reducción de rigidez en su plano (acción de membrana). De esta forma, quedan aportando de un 2 % a un 15 % de la rigidez original, factores que fueron obtenidos por iteraciones, hasta que las frecuencias naturales y el comportamiento del modelo se acercaran más a las experimentales. Se omitieron en el modelado de los buques de ventanas y puertas en las paredes.
En cuanto a las cargas permanentes aplicadas a los entrepisos, se tomaron en cuenta el peso propio de la losa multitubular (esta es modelada como elementos tipo área con una sección equivalente, pero sin masa), el peso de la sobrelosa, de la nivelación, mortero de pega y piso, además de los cielorrasos, instalaciones electromecánicas y paredes livianas de Gypsum. Estos se desglosan en el CUADRO IV. Los pesos de los paneles prefabricados son aplicados sobre las vigas perimetrales de la fachada frontal y trasera del edificio, como una carga uniforme lineal. Dado que se trata de un modelo estructural preliminar solo para efectos de comparación, no se añadieron cargas temporales al modelo.
Cuadro IV Cargas permanentes aplicadas en el modelo estructural
| Carga permanente aplicada sobre el entrepiso | Losa multitubular | 2.45 kN/m2 |
| Sobrelosa | 1.55 kN/m2 | |
| Cielos, instalaciones electromecánicas | 0.30 kN/m2 | |
| Paredes livianas de Gypsum | 0.50 kN/m2 | |
| Nivelación, mortero de pega y piso | 1.30 kN/m2 | |
| Total de carga permanente en entrepiso | 6.10 kN/m2 | |
| Carga lineal sobre vigas perimetrales de las fachada frontal y trasera | Paneles de 2.88 m de alto (pisos dos, tres y cuatro) | 7.10 kN/m |
| Paneles de 2.00 m de alto (piso cinco) | 5.10 kN/m | |
| Paneles de 0.80 m de alto + ventanería (piso seis) | 2.90 kN/m |
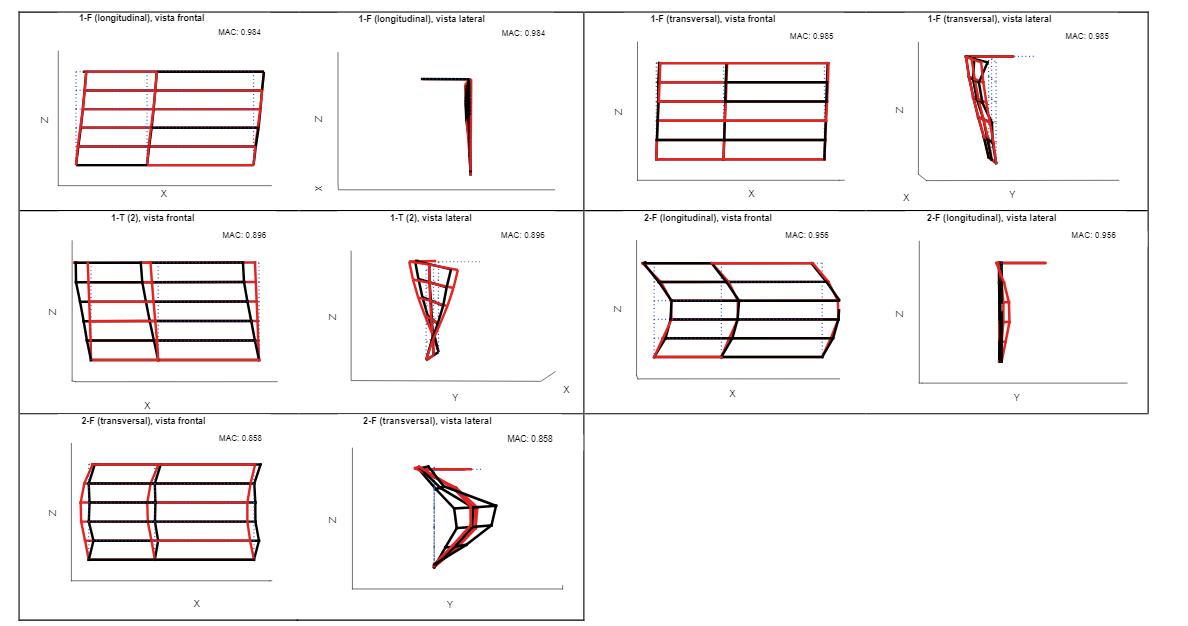
En la Fig. 8, se muestra el modelo estructural desarrollado y los primeros cinco modos que se obtuvieron en forma consecutiva, con la denominación de los modos experimentales a los que encajan. Se muestra en el Cuadro V la comparación de las frecuencias modales experimentales y las analíticas del modelo estructural, así como los valores de MAC (acrónimo de Modal Assurance Criterion en inglés) (32), el cual es simplemente el producto punto entre los vectores de forma modal experimental y analítica normalizada. Este expresa el nivel de colinealidad que existe entre dos vectores, de modo que, mientras más cercano a la unidad es su valor, se tiene mejor concordancia. En nuestro caso, estos son vectores de las formas modales operacionales observadas y las analíticas. La Fig. 9 muestra también una comparación cualitativa de estas formas modales en los puntos de observación experimental. Se aprecia que hay una muy buena concordancia en la dirección principal de la forma modal de los modos 1-F en sentido longitudinal y transversal, lo cual se ve reflejado en los valores de MAC (0.984 y 0.985, respectivamente). Lo mismo sucede con el modo 2-F en sentido longitudinal (MAC = 0.956) y, en un menor grado, con el modo 2-F en sentido transversal (MAC = 0.858).
Entre los múltiples modos de torsión experimental, el modo 1-T(2) es el que se ajusta mejor al único modo de torsión generado por el modelo analítico, con un MAC igual a 0.896 (el MAC con 1-FT es 0.094; con 1-T(1), es 0.855; con 1-T(3), es 0.497), Este también es el modo que más se acerca en términos de frecuencias. A pesar de algunos intentos por tratar de calibrar un poco el modelo, para generar múltiples modos de torsión que fueron identificados experimentalmente, estos no fueron fructuosos. Por ejemplo, se intentó variar más los factores de reducción de rigidez de diferentes paredes de relleno y afinar un poco más la distribución de cargas en vigas perimetrales, tratando de generar excentricidad.
A partir de experiencias obtenidas en otras estructuras, como la de Vásquez-González (16) en el edificio del módulo D de este mismo complejo de la Facultad de Ciencias Sociales y la de Liu-Kuan (14), (15) en materia de puentes, una posible explicación de este fenómeno es la interacción del sistema estructural principal. Esta se compone de los marcos de concreto reforzado con otros elementos estructurales, como la estructura metálica de techo o las escaleras, que también podrían tener influencias bajo la condición operacional, pero cuya modelación es una tarea difícil. Por otro lado, también se debe recordar que, en los niveles dos y tres, están las colecciones de libros de la biblioteca, pero se desconoce sobre su peso y ubicación, lo que podría generar mayor excentricidad de masa respecto al centro de rigidez.
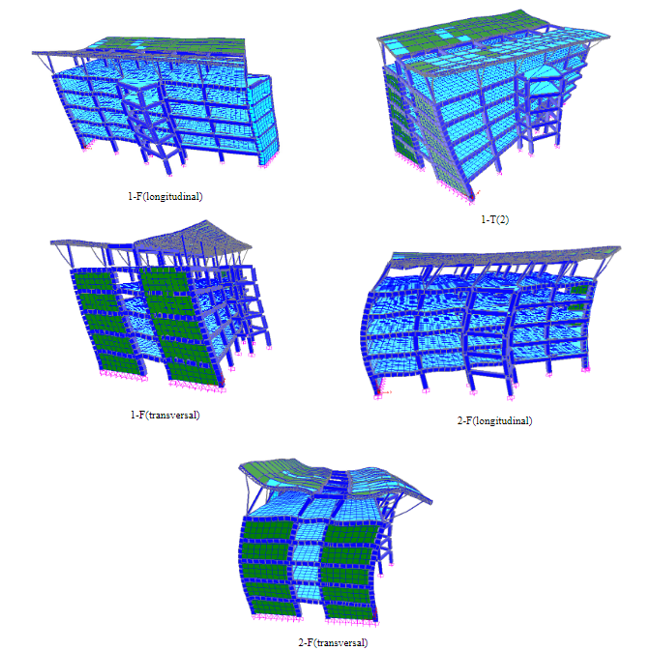
Fig. 8. Formas modales de los primeros cinco modos, obtenidas del análisis modal realizado en el modelo estructural del edificio
Cuadro V Comparación de las frecuencias modales experimentales y analíticas y el MAC
| Modo | Frecuencias | MAC | ||
| SSI-COV | Modelo | % Dif. | ||
| 1-F(longitudinal) | 2.197 | 2.265 | 3.10 | 0.984 |
| 1-F(transversal) | 2.295 | 2.534 | 10.41 | 0.985 |
| 1-T(2) | 2.872 | 2.905 | 1.15 | 0.896 |
| 2-F(longitudinal) | 6.218 | 6.074 | -2.32 | 0.956 |
| 2-F(transversal) | 6.858 | 6.511 | -5.06 | 0.858 |
Conclusiones
Se identificaron exitosamente nueve modos debajo de los 7 Hz para el edificio de concreto reforzado de seis niveles, con el método SSI-COV. Con ello, se pudo empatar y recuperar las formas modales completas a partir de los resultados parciales obtenidos del análisis de las diferentes configuraciones. Esto no se logró con el método SSI-DATA, pues no pudo identificar correctamente los modos para las configuraciones en pisos inferiores. Por lo tanto, al menos en este caso de edificio de concreto reforzado de baja altura, SSI-COV ha demostrado una mejor capacidad para la identificación modal a partir de vibraciones ambientales recolectadas vía acelerógrafos ambulantes en edificios.
De la comparación con un modelo estructural preliminar de elementos finitos, se observa una muy buena concordancia en la forma modal de los modos de flexión identificados en ambas direcciones del edificio. No obstante, solo un modo de torsión fue generado por el modelo analítico, en comparación con los cuatro que fueron identificados experimentalmente, cuya interpretación no se pudo concretar en este estudio y requiere de futuras investigaciones de mayor profundidad en cuanto a comportamientos de torsión bajo condiciones operacionales.
Esto porque no se pudo cuantificar y determinar la distribución de la carga de la biblioteca, la cual significaría un aporte considerable a la masa y podría influir en los modos torsionales. Además, el edificio podría contar con algún tipo de deficiencia estructural incipiente que altere su comportamiento, al tener más de diez años en operación. Sin embargo, a pesar de haber enfrentado sismos de magnitud considerable, tampoco se ha detectado algún tipo de agrietamiento aparente.
Asimismo, dada la dificultad que se ha tenido para identificar modos en pisos inferiores, debido a que la amplitud de vibración decrece conforme se desciende en altura, se recomienda que la técnica de sensores ambulantes sea implementada mediante configuraciones de prueba verticales, en lugar de horizontales que van de piso en piso.