Introdωucción

La Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (Unesco, 2012) señala que la educación matemática necesita generar cambios en su proceso de enseñanza y aprendizaje, y que el profesorado debe ser el promotor para que se realice con efectividad. Esto hace que el rol de quien es docente de matemática sea fundamental en el proceso educativo.

Los informes del Estado de la Educación en Costa Rica han presentado un panorama general de lo que está pasando en el ámbito educativo de nuestro país. A nivel del profesorado, el Programa Estado de la Nación (2017), en el sexto informe, señala que en la actualidad no se cuenta con un perfil docente en general. Así, menciona la urgencia de conocer ese perfil, ya que muchos docentes activos en el ámbito laboral o “aspirantes a ocupar puestos de trabajo carecen de la experiencia laboral requerida y, en general, tienen un bajo nivel académico, por lo que es una de las principales causas de que la educación no se desarrolle adecuadamente” (p. 274). Este perfil debe incluir tanto aspectos académicos como elementos del dominio afectivo del profesorado, específicamente, sus actitudes y creencias hacia la disciplina.

En este sentido, la investigación que presenta este artículo surgió a partir de la necesidad de identificar características de un perfil afectivo, entendido como las actitudes, creencias y emociones de docentes de matemáticas que laboran para el Ministerio de Educación Pública (MEP) y tienen experiencia en Olimpiadas Costarricenses de Matemática (Olcoma), en una región educativa específica, y docentes que también trabajan para el MEP, pero que no han participado en Olcoma. Al respecto, ^{Esnal, Pascual y Cuesta (2010}) expresan que el afecto de la persona docente de matemáticas influye significativamente en el aprendizaje de esta asignatura; lo cual posee implicaciones en la forma de enseñar la disciplina, la interacción con el estudiantado y el tipo de actividades de mediación pedagógica que se utilicen en el aula. Dado que la participación en Olcoma implica para la persona docente abordar otro tipo de contenido matemático al del MEP, podría pensarse que su perfil afectivo es diferente al de quien no participa.

El Ministerio de Educación Pública de Costa Rica (2012) potencializa las actitudes y creencias al considerarlas un eje disciplinario en la educación básica costarricense, menciona que “en el aprendizaje son decisivas la motivación y el interés y en general todas las dimensiones afectivas” (p. 37). En este sentido, el MEP (2012) señala que “el progreso de las actitudes y creencias positivas hacia las Matemáticas se debe promover en la acción de aula a través de la intervención docente, se deben tener en mente estos propósitos en las diversas tareas matemáticas” (p. 38).

En relación con esto, ^{Blanco, Guerrero, Caballero, Brígido y Mellado (2010}b), así como ^{Casis, Castro y Martínez (2017}) indican que la persona docente no debe generar temor hacia el aprendizaje de los contenidos, más bien debe implementar o mostrar afecto al momento de enseñar, ya que esto puede repercutir significativamente en el aprendizaje del estudiantado. Aunado a esto, Blanco et al. (2010b) consideran necesario analizar la influencia del dominio afectivo en el aprendizaje en las personas docentes de matemáticas, debido a que sus creencias y emociones hacia la asignatura tendrán un efecto tanto en el logro como en las creencias y actitudes hacia la asignatura por parte de la población estudiantil.

Al respecto, ^{Casis et al. (2017}) señalan que la actitud del docente dentro del aula está relacionada con la motivación, ansia y autoconfianza que tenga el estudiante hacia las matemáticas. Así, durante el proceso de aprendizaje, las actitudes de quien enseña matemáticas pueden influir de alguna manera en el estudiantado. En este sentido, ^{Mato y De la Torre (2010}), quienes referencian a Relich y Way (1994), mencionan que, si la persona docente de matemáticas posee malas actitudes, inseguridad y falta de conocimiento, puede propiciar estas en los estudiantes, es decir, generar en ellos significancia positiva o negativa.

En esta investigación se pretendió analizar cuáles son esos elementos descriptivos del dominio afectivo que posee la persona docente de matemáticas, con base en sus creencias y actitudes. Por ello, se trabajó tanto con personas docentes que han participado en Olcoma, como con aquellas que no, para establecer datos de posibles diferencias. Los resultados de esta investigación pretenden aportar insumos para que cualquier instancia o institución educativa logre conocer algunas características asociadas a un perfil afectivo de un profesor de matemáticas y, a partir de ello, se potencien y fomenten características afectivas de la misma forma que se desarrollan las habilidades matemáticas.

Dado que la cantidad de participantes en la investigación fue pequeña, intencional y no aleatoria, el estudio no pretendió realizar inferencias estadísticas, sino exploratorias y descriptivas para las personas colaboradoras. El fin es generar información para estudios posteriores, con una mayor cantidad de individuos, con el objetivo de verificar la existencia o no de diferencias significativas.

Marco Teórico

El dominio afectivo en la enseñanza de las matemáticas

Para ^{Blanco et al. (2010}a), las matemáticas son una asignatura temida por las personas, lo cual ha generado resistencia hacia ellas. Este afecto se ha transmitido a través de generaciones. Aunado a lo anterior, cuando se enseña o se aprenden las matemáticas, existen factores que determinan el afecto que se produce hacia esta área o a los procesos ligados a ella. Según ^{Gómez (2002}), algunas de las explicaciones de los bloqueos de aprendizaje vienen dados por sentimientos y actitudes que refuerzan las creencias. Además, el afecto hacia las matemáticas y la motivación de aprendizaje se deben contextualizar a partir de la realidad social de los sujetos, que provoca reacciones emocionales, y la pertinencia a un grupo social, así como de valoraciones y creencias asociadas con las diferentes formas de conocimiento matemático.

En este contexto, se señala la importancia del dominio afectivo en el aprendizaje y enseñanza de las matemáticas. Al respecto, ^{Gil, Blanco y Guerrero (2005}) destacan que, desde la década de los años setenta, diversos estudios relacionados con la educación matemática centraron su foco en la dimensión afectiva, y argumentaron a favor de la influencia de esta en el proceso de enseñanza y aprendizaje. Posteriormente, en los años noventa, las investigaciones concernientes a los dominios del conocimiento del profesorado de matemática tuvieron auge, e incluyeron el estudio de aspectos del dominio afectivo, como concepciones, creencias y actitudes hacia la enseñanza y aprendizaje de la disciplina (Blanco et al., 2010a).

^{Blanco et al. (2010}a) indican que gran parte de la investigación actual sobre la influencia de la dimensión afectiva en la enseñanza y el aprendizaje de las matemáticas surgió del trabajo de Douglas McLeod y sus estudios publicados en 1986, 1989 y 1992. En estos, se expuso que era importante considerar los descriptores básicos del dominio afectivo: creencias, actitudes y emociones. Sobre dicho dominio, ^{Gómez (2000}) señala que las cuestiones afectivas juegan un papel fundamental en el aprendizaje y enseñanza de la disciplina, además, apunta que algunas están arraigadas al sujeto y no son fácilmente desplazables por la instrucción. Al respecto, se indica que

Entre el aprendizaje y los afectos se establece una relación cíclica. Así cuando aprenden matemáticas, los alumnos desarrollan experiencias que les provocan distintas reacciones emocionales, que influyen en la formación de sus creencias que, a su vez, influyen en su comportamiento y rendimiento en otras situaciones parecidas, entonces la reacción emocional (satisfacción o frustración) se automatiza, generando actitudes. Algunas de estas creencias y actitudes se arraigan en el sujeto, estabilizándose conforme avanza el sistema educativo y siendo difícilmente desplazables por la institución y la práctica educativa. (^{Blanco, 2012}, p. 174).

Respecto al dominio afectivo, ^{Casis (2018}) y ^{McLeod (1992}) lo definen como una relación entre las actitudes, las creencias y las emociones de un individuo, donde los componentes del dominio afectivo son expresados de manera diferente a los pensamientos y lo cognitivo. Además, ^{Gómez (2000}) define la dimensión afectiva como “un extenso rango de sentimientos y humores (estados de ánimo) que son generalmente considerados como algo diferente de la pura cognición” (p. 22), acá también están incluidas las actitudes y creencias.

Es así como las creencias, actitudes y emociones tanto de estudiantes como de profesores pueden ser factores que influyen en el aprendizaje y enseñanza de las matemáticas. Según ^{Gómez (2003}), las dos primeras son parte del conocimiento; además, están compuestas por elementos afectivos, evaluativos y sociales, determinados por las intenciones personales e influyen en el comportamiento.

Elementos descriptivos del dominio afectivo en la enseñanza de las matemáticas

Creencias hacia las matemáticas

De manera más general, se puede decir que las creencias se señalan como un “conjunto de puntos de vista, de representaciones subjetivas, que la persona interioriza (individualizado) y refuerza o debilita por el transcurso de su vida. Este sistema establece el contexto dentro del cual los recursos, la heurística y el control funcionan” (^{Sánchez, 2008}, p. 3). En este sentido, ^{Padrón (2013}), citando a Moreno y Azcárate (2003), menciona que

Las creencias son conocimientos subjetivos que permiten explicar y justificar muchas de las decisiones y actuaciones personales y profesionales de los sujetos. No se fundamentan sobre la razón sino más bien sobre los sentimientos, las experiencias y la ausencia de conocimientos específicos sobre el tema con el que guardan relación. (p. 239)

^{Pajares (1992}), por su parte, expresa la diferencia existencial entre creencias y concepciones, ya que ambas suelen generar confusión. Las primeras son conceptualizadas como verdades personales que generaron algún impacto por circunstancias o presunciones obtenidas durante el proceso de vida de una persona, constituidas a partir de la reflexión y el afecto, son parte de lo metacognitivo. En cambio, las concepciones se caracterizan por tener una naturaleza cognitiva, ya que se basan plenamente en un esquema conceptual. Para complementar, ^{Gómez (2002}) expone que las creencias son estructuras metacognitivas, pues su función es interpretar información proveniente del medio en el cual una persona se desenvuelve y construye una noción tanto de la realidad como del mundo.

En el campo de la educación matemática, ^{Maroto (2015}) menciona que las creencias “forman parte del conocimiento perteneciente al dominio cognitivo, compuestas por elementos afectivos, evaluativos y sociales, con una fuerte estabilidad. Dicho conocimiento se refiere a las matemáticas y a su enseñanza y aprendizaje y está basado en la experiencia” (p. 89). Según ^{Ernest (1989}), para generar cambios importantes en la educación matemática, se debe estudiar las creencias de los individuos, dando énfasis al contexto, aprendizaje y percepción.

^{McLeod (1992}) indica que las creencias se componen de cuatro categorías, las cuales son:

a) Creencia sobre las matemáticas: para ^{Gil et al. (2005}), “son uno de los componentes del conocimiento subjetivo implícito del individuo (basado en la experiencia) sobre las matemáticas y su enseñanza y aprendizaje” (p. 18). Al respecto, ^{Donoso (2015}) indica que las creencias sobre las matemáticas corresponden a percepciones que los individuos se crean y se forman a lo largo de su vida. En particular, ^{Ernest (1989}) señala que las creencias sobre las matemáticas se pueden clasificar en tres visiones:

Instrumentalista: consiste en considerar las matemáticas una herramienta que puede ser manipulada y genera efectos deseados, con lo cual se producen más creencias; quien presenta esta tipología visualiza matemáticas como un proceso y reglas para el aprendizaje.

Platónica: los objetos matemáticos son entes abstractos, existentes y están presentes, solo hay que descubrirlos. Según ^{Campos (2008}), en esta visión la persona docente enseña los significados matemáticos de los conceptos y por medio de la lógica se analiza la resolución de los problemas.

Resolución de problemas: las matemáticas se crean por las personas a medida que surge la necesidad de resolver ciertos problemas. Es la percepción dinámica de las matemáticas.

b) Creencias sobre sí mismo como aprendiz de las matemáticas: en esta categoría, se incluyen las creencias de los individuos sobre las teorías, percepciones y valores que forman parte fundamental de la educación matemática. Además, ^{Gómez (1997}) valora las creencias acerca de uno mismo en cuanto a la educación matemática, con una fuerte carga afectiva, que incluyen creencias relativas al autoconcepto, a la atribución de causalidad y a la confianza. Por eso, Gómez (2000) menciona que existen elementos basados en el conocimiento subjetivo y las emociones que pueden influir en una persona cuando quiere ser partícipe de las matemáticas, y son los siguientes: el interés o motivación que se muestra hacia las matemáticas; las circunstancias que generan empatía con las matemáticas; la dedicación que se vaya a tener hacia los temas en matemáticas; la atribución afectiva que generan las matemáticas hacia el fracaso o no; y la influencia que tienen las matemáticas para una persona en un ámbito social.

Por lo tanto, ^{Gómez (2000}) recalca la importancia de que todas las personas estudiantes aprendan a tener confianza en sí mismos, independientemente de como se trabajen las matemáticas. En este caso, la persona docente se convierte en un factor que contribuye, o no, a que el alumno se valore a sí mismo de forma positiva como aprendiz de matemáticas.

c) Creencias sobre la enseñanza de las matemáticas: ^{Donoso (2015}) indica que el individuo adquiere y tiene sus propias creencias sobre cómo percibe la enseñanza de las matemáticas y cómo se desarrolla, no necesariamente durante su formación, con base en aquellas creencias surgidas a partir de sus experiencias. Esto es importante en cuanto a motivación se refiere.

Para ^{Gómez (2000}), las personas docentes son consideradas transmisoras de conocimiento y una fuente de ayuda. Con respecto a ellos, se indica que

Forman creencias sobre sus alumnos, sobre cómo deben enseñar, cómo deben evaluar, cuál debe ser su rol en el aula, etc., y estas creencias influyen en la manera en que actúan en clase. Al comprender la relevancia de las creencias del maestro en el proceso de enseñanza-aprendizaje, se entiende la necesidad de que ellos hagan cambios fundamentales sobre cómo conciben la enseñanza para que puedan insertar mejoras en su manera de enseñar. (^{Solís, 2015}, p. 237-238).

También, ^{Gómez (2000}) expresa que la persona estudiante siempre tiene una percepción acerca de cómo la persona docente debería de enseñar las matemáticas y, cuando esto no sucede según sus creencias, su motivación se ve afectada.

d) Creencias sobre la cultura matemática: ^{McLeod (1992}) indica que como se comporta o piensa una persona en su contexto social tiene influencia en la enseñanza y aprendizaje de las matemáticas, y en cómo valoran las concepciones matemáticas. Es decir, la valoración y vivencia del entorno pueden influir de forma positiva o negativa en el aprendizaje de esta materia. Al respecto, se considera que “los valores y las creencias a partir de su contexto social influyen en la selección de los conocimientos, y en las circunstancias y en las condiciones para que se dé el aprendizaje” (^{Gómez, 2000}, p. 83). ‘

^{Gómez (2000}) menciona que, para recolectar información acerca de la cultura matemática actual, desde la perspectiva de una persona, el fundamento del análisis debe presentarse en el conocimiento matemático; por ejemplo, dar énfasis a la importancia que otorgue a las matemáticas, cómo percibe el éxito o fracaso, el valor que tiene aprender y cómo concibe las definiciones matemáticas en su contexto.

Para este trabajo investigativo, se hizo la siguiente clasificación con base en los autores expuesto

Actitudes hacia las matemáticas 

El número de disertaciones y artículos publicados sobre la actitud hacia las matemáticas ha ido en aumento desde 1960. Esto muestra que el estudio sobre las actitudes tiene una larga tradición en la educación matemática y que se ha dado un interés creciente en este campo (^{Gómez, 2002}).

Las actitudes, para ^{Díaz y Hernández (2010}), “son experiencias subjetivas (cognitivo-afectivas) que implican juicios evaluativos, que se expresan en forma verbal o no verbal, que son relativamente estables y que se aprenden en el contexto social” (p. 45). Por su parte, ^{Martínez (2008}) las define como ideas, percepciones, gustos, preferencias, opiniones, creencias, emociones, sentimientos, comportamientos y tendencias a actuar. ^{Gómez (2002}) asume la definición de Hart (1989), en la cual se refiere a la actitud como una predisposición evaluativa (es decir, positiva o negativa) que se forma a partir de las intenciones personales e influye en el comportamiento. En este sentido, este mismo autor (2000, 2002) indica que, si el objeto es las matemáticas, se pueden distinguir dos grandes categorías: actitudes hacia las matemáticas y actitudes matemáticas. Las primeras se refieren a la valoración, el aprecio e interés por esta disciplina y por su aprendizaje. En este punto, destacan el componente afectivo en relación con el cognitivo; el cual se manifiesta en términos de interés, satisfacción, curiosidad, valoración, entre otros (Gómez, 2000, 2002).

Por su parte, ^{Martínez (2008}) señala que las actitudes hacia las matemáticas se dirigen a la disciplina en sí misma y a las personas matemáticas (aspecto social de la Matemática), la asignatura, determinadas partes de la matemática, los métodos de enseñanza de esta, y el interés por el trabajo matemático y científico.

Las actitudes matemáticas, por el contrario, tienen un carácter marcadamente cognitivo y se refieren al modo de utilizar capacidades generales como la flexibilidad de pensamiento, la apertura mental, el espíritu crítico y la objetividad; todas importantes en el trabajo en esta disciplina. Además, ^{Gómez (2009}) menciona que

Un profesor debe diferenciar entre actitudes hacia las matemáticas y actitudes matemáticas. Pensamos que es conveniente establecer esta diferencia, ya que el estímulo para la valoración de esta disciplina y el interés por el aprendizaje de la materia es muy diferente del cultivo del gusto y la preferencia en el modo de utilizar capacidades mentales importantes para el trabajo matemático. (p. 10)

Asimismo, ^{Gómez (2002}) señala que las actitudes constan de tres componentes: uno cognitivo, que se manifiesta en las creencias subyacentes a la actitud; uno afectivo, que se evidencia en los sentimientos de aceptación o de rechazo de la tarea o de la materia; y uno intencional o de tendencia, que se vincula a cierto tipo de comportamiento. ^{Martínez (2008}) describe los componentes de la siguiente manera:

Componente cognitivo (el conocer/el saber): se corresponde con la carga de información y la experiencia ad adquirida por el sujeto respecto al objeto de su actitud. Se manifiesta o expresa mediante percepciones, ideas, opiniones y concepciones a partir de las cuales la persona se coloca a favor o en contra de la conducta esperada. ^{Gamboa (2014}) señala que se puede identificar mediante la percepción que tiene el sujeto sobre sí mismo en relación con las matemáticas y hacia la materia en sí; se entiende como la facilidad del individuo para entender el papel de la disciplina (por ejemplo, autoconcepto, percepción a las matemáticas y aspectos didácticos).

Componente afectivo (la emoción/el sentir): se pone de manifiesto por medio de las emociones y los sentimientos de aceptación o de rechazo hacia la materia, los cuales el sujeto activa motivacionalmente ante la presencia del objeto, persona o situación que genera dicha actitud. Se refiere a la percepción del individuo hacia las matemáticas, expectativa con respecto a su relación con la materia, y se muestra a través de fobias o inseguridades que lo limitan en esta (^{Gamboa, 2014}). Según ^{Abraham et al. (2010}), para medir la actitud en la parte afectiva de las personas, se deben conocer sus sentimientos hacia las matemáticas (por ejemplo, aceptación, motivación, interés, bloqueo emocional, entre otros).

Componente comportamental (el comportamiento): se constituye en la conducta observable, esta será concebida como un conjunto de comportamientos, y razones de agrado y de desagrado hacia las matemáticas. ^{Gamboa (2014}) explica que el comportamiento se puede identificar por medio de la representación del individuo con respecto a las matemáticas, y se manifiesta en oposición al estar en la clase y en participar en actividades relacionadas con la materia; además, en la seguridad que tiene el sujeto sobre sus conocimientos con respecto a las matemáticas (por ejemplo, rechazo, confianza y curiosidad).

Según ^{Gómez (2002}), las creencias, actitudes y emociones están relacionadas entre sí. Por eso, el estudio de estos descriptores del dominio afectivo es de gran relevancia, pues permite conocer, a partir de los pensamientos y creencias, la influencia que puedan tener las personas docentes en la educación matemática. De forma consecuente, su actuar se evidencia a partir de su contexto en el aula.

Metodología

Tipo de investigación

Este estudio se enmarca en un enfoque mixto. Según Hernández et al. (2010), este tipo de investigación combina al menos un componente cuantitativo y uno cualitativo. Por consiguiente, en primera instancia, se trabajó con el enfoque cuantitativo, para el cual se aplicó un cuestionario de tipo escala Likert, con el fin de recolectar información y analizar los resultados obtenidos por parte de los sujetos de estudio. Este método es deductivo y no experimental, pues se analizan las actitudes y creencias docentes con experiencia en Olcoma y de docentes que no han participado en este proyecto.

En una segunda fase, se trabajó el enfoque cualitativo, mediante el estudio de casos y de un abordaje fenomenológico. Según ^{Villalobos (2017}), el estudio de casos ayuda a comprender el contexto social; por eso, a partir de lo obtenido en la primera fase, se formularon preguntas abiertas en una entrevista a profundidad, para abordar detalladamente los puntos vistas de las personas participantes acerca de sus actitudes y creencias. Así, se generaron conclusiones o hallazgos de mayor amplitud (^{Castro y Godino, 2011}).

Fuentes de información:

La muestra de estudio se compuso de docentes de III ciclo y educación diversificada de diez instituciones públicas diurnas de la Dirección Regional de Heredia. Se consideró esta zona por la participación de varios colegios públicos en el proyecto Olcoma. Por cada colegio público, se escogió a dos personas docentes de matemáticas, una con experiencia en Olcoma y otra sin esta. El total de docentes de matemáticas participantes fue de 20, quienes se dividieron en 10 docentes con experiencia en Olcoma y 10 sin experiencia en este proyecto.

Técnicas e instrumentos de recolección de información

Según Hernández et al. (2010), “en las modalidades del enfoque mixto, regularmente se aplican instrumentos que contengan elementos cuantitativos y cualitativos, o varios instrumentos tanto cuantitativos como cualitativos” (p. 272). Por lo tanto, se trabajó con una encuesta y una entrevista a profundidad.

Encuesta: para recolectar la información, en una primera etapa, se utilizó esta técnica por medio de un cuestionario. Este se estructuró con base en una escala tipo Likert, donde se emplearon las siguientes categorías: totalmente de acuerdo, de acuerdo, ni de acuerdo ni en desacuerdo, en desacuerdo y totalmente en desacuerdo; pues permiten tener variaciones exactas sobre las opiniones de los sujetos. De forma individual, las personas docentes de matemáticas de la muestra seleccionada respondieron este cuestionario, con la finalidad de identificar cuáles son sus actitudes y creencias con respecto a la asignatura.

Para construir los ítems, se revisó la fundamentación teórica y algunos cuestionarios ya validados (^{Acosta y Alsina, 2017}; ^{Gamboa, 2014}), otros fueron de creación propia o adaptados de otros instrumentos. Todos los ítems se redactaron según valoraciones positivas. Para medir el grado de acuerdo de las personas docentes sobre sus actitudes y creencias, se estableció una escala del 1 al 5 relacionada, para las opciones de respuesta desde “totalmente en desacuerdo” hasta “totalmente de acuerdo”.

Los ítems de relacionados con Actitudes hacia las matemáticas se agruparon con respecto a sus tres componentes: cognitivo, afectivo y conductual. Por su parte, las preguntas relacionadas con Creencias hacia las matemáticas se asociaron con las siguientes categorías: creencias sobre las matemáticas (visión instrumentalista, visión platónica, visión de resolución de problemas), creencias de los individuos respecto a sí mismos en matemáticas y creencias de los docentes hacia el talento matemático de los estudiantes.

Con respecto a la validez del instrumento, se realizó por medio del juicio de cuatro personas expertas y una prueba piloto. En el primer caso, se les entregó una lista con los ítems construidos y una guía para que calificaran cada uno de ellos. Se les solicitó evaluar los ítems según tres criterios: “incluir sin modificaciones”, “realizar modificaciones” y “no incluir en el instrumento”, y un apartado de observaciones.

Para el plan piloto, se seleccionó a 10 docentes de secundaria que laboraban para el MEP, totalmente externos a los de la muestra para evitar cualquier sesgo en la recolección de datos. Estos correspondían a cinco personas docentes con experiencia en Olcoma y otras cinco sin ella. Estos no pertenecían a la región central de Heredia, pero sí laboraban en la gran área metropolitana (GAM).

Entrevista a profundidad: se realizó después de la aplicación del cuestionario, debido a que primero se identificaron y describieron tanto las actitudes como las creencias de las personas docentes de matemáticas. Se llevó a cabo una entrevista estructurada, que para ^{Villalobos (2017}) es “cuando se tiene un conjunto de preguntas establecidas” (p. 289). En este caso, se empleó un banco de 19 preguntas abiertas con base en la información suministrada por las personas docentes en el cuestionario. La finalidad de la entrevista fue extraer, abordar o clarificar la información que se obtuvo después de aplicar el cuestionario.

Para la aplicación de la entrevista, se consideró a tres colegios de las 10 instituciones que se tuvo de muestra, fueron seleccionados de acuerdo con la disposición de las personas participantes. En cada centro educativo, se entrevistó a un docente que habían participado en Olcoma y a uno que no habían tenido esta experiencia. La entrevista se realizó virtualmente, por medio de la plataforma Zoom, en la fecha y la hora acordadas con cada docente. La recolección de los datos se dio durante la pandemia causada por la Covid-19. Debido a esto, se trabajó de manera virtual, con el uso de herramientas como los cuestionarios de Google y las reuniones virtuales a través de Zoom.

Estrategias para el análisis de datos

Con ayuda de un software, se llevó a cabo un análisis descriptivo de las respuestas dadas por las personas docentes. Se obtuvo porcentajes de respuestas, media aritmética y otros datos de interés para algunos de los ítems, con el fin de realizar comparaciones.

En el caso del promedio por ítem, se analizó de la siguiente forma, con base en lo expuesto por Cubillo et al. (2010), referenciado por ^{Gamboa (2014}):

a) Si la media toma el valor exacto de 3, se considera que la actitud o creencia en el aspecto indicado es neutral (ni negativa ni positiva).

b) Si la media es mayor que 3, la actitud o creencia es positiva o negativa (según el tipo de ítem). Para este caso se tomaron en cuenta dos rangos:

se interpreta como positiva moderada o negativa moderada, según corresponda.

se considera como muy positiva o muy negativa, según corresponda.

c) Si la media es menor que 3, la actitud o creencia es negativa o positiva (según el tipo de ítem). Para este caso se contemplaron dos rangos:

se interpreta como negativa moderada o positiva moderada, según corresponda.

se considera como muy negativa o muy positiva, según corresponda.

Para las creencias hacia las matemáticas, las dimensiones fueron: visión instrumentalista, visión platónica, visión de resolución de problemas. El valor numérico asignado a cada una fue el promedio obtenido a partir de los ítems relacionados. Con base en estas visiones, a la creencia sobre las matemáticas, se le asoció la visión de mayor promedio obtenida. Para la dimensión imagen, que posee relación directa con la creencia sobre los individuos respecto a sí mismos en matemáticas, el valor asignado a este fue el promedio obtenido a partir de los ítems relacionados.

Respecto a las dimensiones asociadas con las creencias, el valor asignado a cada una fue el promedio obtenido a partir de los ítems relacionados. Para el caso de las creencias de la persona docente de matemáticas hacia el talento matemático en las personas estudiantes, el valor numérico establecido a cada dimensión fue el promedio obtenido a partir de los ítems asociados con ellas.

Dada la cantidad de personas participantes, para analizar la normalidad de los datos, se utilizó la prueba de Shapiro-Wilk; mientras que para verificar si existían diferencias significativas, se aplicó la prueba de Wilcoxon, ambas con un nivel de significancia de 0,05.

El análisis de los datos de las entrevistas se hizo por medio del procedimiento de categorización de los datos recolectados a partir de una codificación abierta que, según ^{Flick (2007}), “trata de expresar los datos y los fenómenos en forma de conceptos” (p. 193).

Análisis De La Información

Para el reporte, con el fin de referenciar a las personas docentes que participan o no en Olcoma, se utiliza docentes- Olcoma y docentes-NoOlcoma. No se hace mención al nombre de ninguna persona participante; se utilizan las abreviaturas E#-Olcoma y E#-NoOlcoma para referirse a algunas de ellas cuando corresponda.

Primeramente, para verificar la fiabilidad de las respuestas obtenidas según las preguntas expuestas en el cuestionario, se realizó el Alfa de Cronbach para cada categoría. El valor obtenido según las categorías que se emplearon para la investigación fue: actitudes, cantidad de ítems 15, Alpha de Cronbach 0,960; creencias, cantidad de ítems 28, Alpha de Cronbach 0,932.

El mayor valor teórico que Alpha podría alcanzar es 1, en general todo valor mayor a 0,80 se considera aceptable (^{García, González y Jornet, 2010}). Por lo anterior, se podría decir que la fiabilidad del instrumento es aceptable.

Actitudes hacia las matemáticas

Componente cognitivo

Con base en los porcentajes de respuesta y el promedio obtenido para los ítems asociados al componente cognitivo, se pudo observar que en la mayoría de los ítems tanto docentes-Olcoma como docentes-NoOlcoma están totalmente de acuerdo.

Las personas docentes-Olcoma presentan un mayor consenso con respecto a que las clases de matemáticas estimulan el desarrollo académico de la mayoría de la población estudiantil. Además, consideran que no tienen problemas cuando se enfrentan a un tema en matemáticas y señalan que buscan actualizar sus conocimientos en la disciplina.

Al respecto, durante la entrevista, E2-Olcoma menciona que le encanta el aprendizaje de las matemáticas, y que siempre procura actualizarse mediante congresos y escuchando tanto diferentes posturas como metodologías para después ponerlas en práctica. No obstante, E2- NoOlcoma señala que siempre se encuentra en constante repaso, más cuando se enfrenta a matemáticas avanzadas, ya que siente seguridad con la mayoría de los temas en matemáticas de secundaria. Además, las personas docentes-NoOlcoma expresan dificulta para participar en actividades extra debido a su carga laboral.

Por otro lado, las personas docentes-NoOlcoma presentan valoración positiva a sentirse más cómodos al trabajar con algunos temas en matemáticas que con otros; consideran que las matemáticas presentan un alto grado de dificultad para la comunidad educativa, aun cuando muestran compromiso en el estudio. Al respecto, E1-NoOlcoma y E2-NoOlcoma mencionan que todos pueden aprender matemáticas, pero algunos presentarán mayor dificultad que otros. Al contrario, E1-Olcoma y E2-Olcoma consideran que cualquier persona puede aprender matemática, pero que se le debe enseñar según su contexto, y que no todas las personas aprenden de la misma manera ni al mismo tiempo. Con base en los promedios obtenidos en el componente cognitivo, las personas docentes-Olcoma poseen una valoración más positiva que los docentes-NoOlcoma, pues tienen la confianza de resolver cualquier problema matemático, se muestran más anuentes a actualizar sus conocimientos y no tienen preferencia en algún tema. Sin embargo, al aplicar las pruebas de Shapiro-Wilk (supuesto de normalidad) y Wilcoxon (para determinar si existen diferencias), se obtuvo que no hay diferencias significativas entre los docentes que han participado en Olcoma con quienes no lo han hecho.

No obstante, en la entrevista, se pudo observar una diferencia de opinión entre docentes-Olcoma y docentes- NoOlcoma respecto al grado de dificultad de las matemáticas para la comunidad educativa. Las personas docentes-Olcoma enfatizan que cualquiera puede aprender matemática, pero que se debe incluir un contexto para motivar y tener en cuenta los diferentes estilos de aprendizaje. Por su parte, las personas docentes-NoOlcoma consideran que a la mayoría de las personas se les dificulta aprender matemática aun cuando se muestran comprometidos.

Por tanto, con base en lo anterior, existe la posibilidad de que el desarrollo o manejo de la clase de ambas partes difiera en su metodología o en su forma de pensar acerca de la utilidad e importancia de la matemática como asignatura. Sin embargo, esto es solo una hipótesis que se debe profundizar con un estudio que incluya la observación de aula, como parte de las técnicas para recolectar la información.

Componente afectivo

Para los ítems asociados al componente afectivo, solo un docente-NoOlcoma marcó estar totalmente en desacuerdo con cada uno. En contra parte, la mayoría de las respuestas de los docentes de ambas poblaciones se distribuyeron entre totalmente de acuerdo y de acuerdo.

Ahora bien, si se engloban los porcentajes de respuesta obtenidos en cuanto estar totalmente de acuerdo y de acuerdo, se obtiene que las personas docentes-Olcoma presentan una actitud más positiva en todos los ítems, pues tuvieron el promedio más alto. Sin embargo, al aplicar las pruebas de Shapiro-Wilk y Wilcoxon no hubo diferencias significativas entre los docentes que han participado en Olcoma con aquellos que no lo han hecho.

En general, se puede mencionar que a la persona docente- Olcoma le gusta resolver ejercicios de matemáticas cuya complejidad sea alta, investiga sobre temas en matemática y tiene seguridad al resolver problemas que requieran un componente matemático.

Al respecto, en la entrevista, E2-NoOlcoma menciona que le cuesta interpretar los problemas en algunos temas en matemática y da como ejemplo la estadística. Destaca que, si bien aplicar fórmulas no se le dificulta, debe repasar la interpretación para poder llegar a conclusiones con las personas estudiantes durante el momento de aprendizaje. También, E2-NoOlcoma menciona que “la matemática sigue siendo un poco algo mecánico, tratar de buscar recetas para dar solución a un problema” (E1- NoOlcoma, comunicación personal, 24 de agosto de 2021). No obstante, E1-NoOlcoma expresa que siempre le han gustado los ejercicios que presentan un reto para las demás personas.

Por su parte, los tres docentes-OLCOMA están conscientes de que no todos los ejercicios o problemas en matemática pueden ser resueltos de forma inmediata, además, señalan les gusta investigar sobre matemática en los casos necesarios.

Los datos parecen destacar que las personas docentes- Olcoma poseen más seguridad al resolver ejercicios matemáticos, debido a que están acostumbrados a trabajar con ejercicios cuya complejidad es alta para otras personas y por su gusto por profundizar en temas de matemática. Según los datos recabados, las personas docentes- NoOlcoma recurren a un mayor uso de fórmulas para resolver un problema o concluir algún resultado.

Componente conductual

En los ítems asociados al componente conductual un docente-NoOlcoma marcó estar totalmente en desacuerdo en la mayoría de los ítems. Sin embargo, al englobar los porcentajes obtenidos en totalmente de acuerdo y en de acuerdo se observó que ambos grupos de docentes tenían actitudes positivas sobre el componente conductual, pero que hay una tendencia “más positiva” de los docentes-Olcoma, pues los promedios obtenidos para los ítems asociados fueron mayores. Sin embargo, al aplicar las pruebas de Shapiro-Wilk y Wilcoxon no se obtuvo diferencias significativas entre los docentes que han participado en Olcoma con quienes no lo han hecho.

Ahora bien, las personas docentes-Olcoma consideran que cuentan con la suficiente destreza, seguridad y motivación para aprender cualquier tema sin complicaciones o realizar alguna actividad relacionada con las matemáticas. Además, expresan tener seguridad para abordar cualquier tema con facilidad. Por ejemplo, E2-Olcoma asegura que los temas de enseñanza media no le representan mayor dificultad. Al contrario, E2-NoOlcoma menciona que debe repasar algunos temas en matemática para enseñarlos.

Una parte de las personas docentes-NoOlcoma expresa sentir inseguridad al trabajar en cualquier tema en matemáticas y poseer escasa motivación cuando asisten a alguna actividad matemática, por lo tanto, prefieren algunos temas. Por ejemplo, E3-NoOlcoma menciona que solo se siente cómodo al resolver problemas del plan de estudios de matemática para el área de secundaria. En general, las personas docentes-NoOlcoma indican que se les dificulta la participación de actividades, pues no están dentro del horario laboral.

Un pequeño porcentaje de las personas docente-NoOlcoma considera que ya han aprendido lo suficiente en matemática y que el interés por aprender temas nuevos se ha perdido. Por ejemplo, E2-NoOlcoma piensa que todos los temas en matemática ya están creados; esto podría generar falta de interés hacia el aprendizaje de nuevos tópicos.

Las personas docentes-Olcoma y NoOlcoma concuerdan en que cualquier persona puede aprender matemática. Por ejemplo, E1-Olcoma menciona que no todas las personas poseen la misma habilidad para aprender matemáticas, pero que, si se tiene una actitud adecuada y positiva hacia su aprendizaje, entonces cualquiera puede aprenderlas.

Los datos muestran que las personas docentes-Olcoma presentan una tendencia más positiva, pero no significativa, al enfrentarse a cualquier tema en matemática, aunque no lo hayan recibido durante su formación profesional.

Por tanto, se logra observar un mayor consenso en las personas docentes-Olcoma en cuanto a los ítems relacionados con el componente conductual de las actitudes. En general, les gusta aprender nuevos temas, sienten seguridad al trabajar con cualquier tema y se motivan al participar de actividades relacionadas con dicha asignatura. También, creen que cualquier persona puede aprender matemáticas y consideran que estas son importantes para las personas.

Clasificación según componente

Una vez analizadas las respuestas de docentes participantes por ítem, divididos entre quienes han participado en Olcoma y quienes no, se procedió a obtener el promedio de todos los ítems por componente, para realizar la clasificación correspondiente. Los datos se muestran en la Tabla 1.

Tabla 1 Promedio de respuesta de los docentes que han participado en Olcoma con los que no, sobre el componente cognitivo, afectivo y conductual 

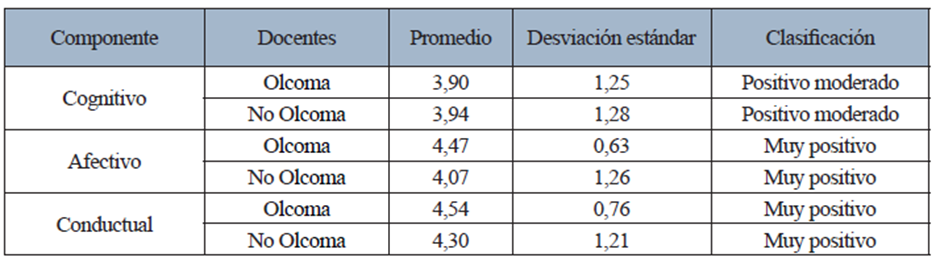
Fuente: elaboración propia

En general, para docentes-Olcoma y docentes-NoOlcoma se puede mencionar que las actitudes hacia las matemáticas, según los distintos componentes de estas, se pueden clasificar como positivas.

Ahora bien, en la Tabla 1 se puede visualizar que las personas docentes-NoOlcoma poseen un puntaje más alto en el componente cognitivo con respecto a los docentes- Olcoma. Esto en parte se da porque los docentes-NoOlcoma puntúan más alto en ítems relacionados con sentir afinidad o comodidad con ciertos temas en matemática, y consideran que las matemáticas pueden ser difíciles para las personas aun cuando muestran interés en la asignatura. Algo importante de observar es que la desviación estándar de los docentes-NoOlcoma es mayor comparada con la de los docentes-Olcoma; es decir, estos últimos poseen menor dispersión hacia las respuestas recabadas en el cuestionario.

Al analizar el componente afectivo, se percibe que las personas docentes-Olcoma poseen un mayor promedio, debido a que presentan características como investigar más sobre temas de matemáticas; esto podría generar confianza al resolver cualquier problema.

Por último, al analizar las respuestas de las personas docentes para la variable componente conductual, se puede decir que existe una tendencia más positiva por parte de las personas docentes-Olcoma, pues cuentan con más motivación al participar de alguna actividad relacionada con la matemática. También, sienten seguridad al resolver cualquier tema en matemática y les gusta aprender nuevos temas relacionados con la disciplina.

De lo anterior, se evidencia que las personas docentes- Olcoma destacan en las actitudes “más positivas”, debido a que desean fortalecer sus conocimientos, tienen seguridad hacia las matemáticas y están dispuestos a desarrollar más su perfil profesional. Aunado a lo anterior, al hacer las entrevistas, las personas docentes-Olcoma mencionan que si se quiere dar una enseñanza de calidad, se necesita un cambio constante de mentalidad, filosofía y analizar el contexto en el que se encuentran las personas estudiantes.

Como ya se indicó, para ambos grupos de docentes las actitudes son positivas; sin embargo, con base en los promedios, hay una tendencia más favorable en las personas docentes-Olcoma. Al aplicar la prueba de Shapiro-Wilk, se obtuvo que no se cumple el supuesto de normalidad; para verificar si existían diferencias significativas, se aplicó la prueba de Wilcoxon y se obtuvo que no hay evidencia de diferencias significativas en los docentes que han participado en Olcoma con quienes no lo han hecho. Las diferencias indicadas se presentaron, principalmente, en las opiniones expresadas en las entrevistas.

Creencias hacia las matemáticas

Visión instrumentalista

Al analizar el porcentaje de respuesta y promedio de cada grupo de docentes por ítem, se obtuvo que las personas docentes-Olcoma presentan un mayor promedio en ítems asociados a la importancia que tienen las matemáticas por su utilidad en la vida cotidiana y por permitir modelar situaciones reales. Sin embargo, al aplicar las pruebas de Shapiro-Wilk y Wilcoxon, se determinó que no hay evidencia para indicar diferencias significativas en los docentes que han participado en Olcoma con quienes no lo han hecho.

La mayoría de los docentes-Olcoma consideran que las matemáticas son útiles para resolver problemas. Al respecto, E2-Olcoma menciona, en la entrevista, la importancia de que una persona docente de matemática conozca el contexto donde labora, con la intención de poder realizar problemas que sean significativos para las personas estudiantes. También, las personas docentes-Olcoma entrevistadas comparten que la matemática debe aportar para la sociedad y verse como una herramienta útil para la vida cotidiana.

En cambio, en la entrevista E2-NoOlcoma y E3-NoOlcoma mencionan que tratan de incorporar el contexto o nombre de sus estudiantes en los problemas matemáticos, con la intención de entretener y llamar su atención, pero se percibe que no se enfocan en la aplicabilidad y el uso que puede tener la matemática en la vida cotidiana. También, E1-NoOlcoma expresa que las condiciones dentro de un aula son complicadas, como para creer que las personas estudiantes pueden resolver problemas con facilidad y creatividad.

Por otro lado, las personas docentes-NoOlcoma presentaron creencias como que la matemática es un campo de manipulación de símbolos y números; en la entrevista, E1-NoOlcoma reafirma esa creencia. Además, señalan que la mayoría del trabajo en matemática consiste en aplicar fórmulas.

Al contrario, las personas docentes-Olcoma afirman que la matemática es una herramienta o ciencia que aporta para los diferentes ámbitos de la vida cotidiana. En este sentido, E2-Olcoma menciona que es un proceso que puede ser intangible, pero que está presente.

NoOlcoma tienen una alta percepción de que la matemática es metódica. Por el contrario, a las personas docentes- Olcoma les apasiona más una matemática aplicada y de razonamiento. La información recabada sugiere que ellas tienen mayor tendencia a considerar que la matemática es útil para resolver problemas del día a día, por lo cual, buscan incorporar el contexto cotidiano en sus clases para una mayor comprensión de la materia.

Visión platónica

En la visión platónica, las personas docentes-NoOlcoma evidencian mayor promedio en la creencia de que todos los temas en matemáticas ya están creados y nada más se puede construir. Además, creen que las personas docentes de matemática se muestran atentos e interesados ante las preguntas que formulan los estudiantes.

En las entrevistas, se obtuvo que E1-Olcoma y E2-Olcoma concuerdan en que se vive en una sociedad donde puede existir una matemática sin descubrir, que los tiempos van cambiando y se puede investigar o redescubrir sobre nuevos temas. También, E1-Olcoma menciona: “Yo soy de los docentes que me gusta no tanto escucharlos, me gusta verlos también participar, que ellos se involucren en el trabajo, ya sea desde darme una solución a un problema como una idea para resolverlo” (E1-Olcoma, comunicación personal, 16 de septiembre de 2021).

Por otro lado, E1-NoOlcoma y E2-NoOlcoma mencionan que la matemática se basa en patrones, así como que los principios y principales axiomas en matemática ya están creados. Además, E3-NoOlcoma menciona que la matemática “es un campo de estudio que le permite al ser humano razonar sobre el porqué de las cosas” (E3- NoOlcoma, comunicación personal, 13 de septiembre de 2021).

Tanto las personas docentes-Olcoma como las personas docentes-NoOlcoma se muestran interesados por las preguntas que realizan las personas estudiantes, pero las primeras enfatizan que por medio de las interrogantes pueden determinar la comprensión de la materia. Sin embargo, E1-Olcoma menciona que los cuestionamientos realizados algunas veces por el estudiantado no necesariamente son de la asignatura o no tienen que ver con la materia, lo cual desmotiva al profesor.

Por último, con base en la información recabada, se logra percibir una diferencia, aunque no significativa, entre docentes-Olcoma y NoOlcoma sobre la visión platónica de las matemáticas, ya que difieren en la forma de pensar y de concebirlas, lo cual podría estarse dando por la forma en que desarrollan la clase y por las metodologías que aplican. Esto se puede profundizar en futuras investigaciones.

Visión resolución de problemas

Con respecto a la visión de resolución de problemas, los docentes-NoOlcoma presentan mayor promedio. Este no tuvo diferencia significativa con respecto al otro grupo de participantes en la creencia asociada a estimular distintos procesos de solución durante las actividades propuestas en el aula; sin embargo, en las entrevistas, esto no se vio reflejado. También, este grupo cree que hay una sola forma de pensar la solución correcta de un problema en matemática. Al respecto E1-NoOlcoma menciona:

Yo trato de que mis trabajos o mis exámenes tengan, digamos, tres niveles: un nivel que es superfácil donde cualquiera casi que lo podía contestar, un nivel intermedio que es en donde llega la mayoría y siempre habrá un problemita que va un poquito más allá. (E1-NoOlcoma, comunicación personal, 24 de agosto de 2021)

Por su parte, E2-NoOlcoma y E3-NoOlcoma buscan que sus problemas tengan diferentes tipos de niveles y que sean contextualizados, pero no enfatizan que estos admitan distintos procesos de resolución.

Por el contrario, según las entrevistas, tres docentes-Olcoma concuerdan en que les gusta estimular el razonamiento lógico en la resolución de problemas, y tienen como meta hacer que el estudiantado sea capaz de experimentar diferentes procesos de resolución y aumentar su participación en el aula. El docente E1-Olcoma señala:

Me encantan los problemas de razonamiento lógico, que tenga diferentes ejemplos, soluciones, que no solo sea una solución, que sean diferentes estrategias para llegarle la solución, (…) un problema no necesariamente tiene una única estrategia para llegarle a la solución, (…) independientemente del procedimiento del proceso que estén usando la cantidad de pasos o la forma como lo planteé en el problema, debería llegar a la misma solución. (E1- Olcoma, comunicación personal, 16 de septiembre de 2021)

Por otro lado, la mayoría de las personas docentes-Olcoma y NoOlcoma están de acuerdo con que “a menudo explico los contenidos de matemáticas por medio de preguntas que realizo a los y las estudiantes”. Si se engloban los porcentajes de respuesta de totalmente de acuerdo y de acuerdo de este ítem, se puede visualizar que los docentes-Olcoma tienen mayor promedio que los docentes-NoOlcoma, aunque esta diferencia no resultó significativa.

De las entrevistas, se obtuvo que las personas docentes- Olcoma concuerdan con que las preguntas son necesarias durante el proceso de aprendizaje, pues permiten profundizar más en un tema y les facilita inferir sobre el grado de entendimiento de la persona estudiante. En consecuencia, los datos parecen sugerir que los docentes-NoOlcoma proponen problemas o ejercicios que poseen diferentes niveles de dificultad y contextualizados, sin necesariamente tener distintas formas de abordarlos. En cambio, los docentes-Olcoma proponen diferentes tipos de problemas para estimular diferentes procesos de resolución. También, se percibe que las personas docentes-Olcoma utilizan, con mayor frecuencia, el método de preguntas durante el desarrollo de la clase.

Por tanto, la información analizada sugiere que las personas docentes-Olcoma y NoOlcoma tienen distintas creencias sobre la resolución de problemas. En este caso, si se contrastan los porcentajes de respuesta para los ítems con lo obtenido en las entrevistas, se logra percibir una creencia “más positiva” de las personas docentes- Olcoma. Sin embargo, estas diferencias no fueron significativas.

Creencia respecto a sí mismo

Las personas docentes-Olcoma poseen promedios más altos en los ítems asociados a las creencias sobre sí mismos si se comparan con las personas docentes-NoOlcoma. Sin embargo, estas diferencias no resultaron significativas.

En una tendencia más positiva, las personas docentes- Olcoma piensan que cometer errores en matemática es parte del proceso de aprendizaje de la asignatura. En este sentido, E1-Olcoma menciona que la persona estudiante al equivocarse y ser corregido genera un aprendizaje.

Por otra parte, un porcentaje de las personas docentes- NoOlcoma cree que cometer errores no es importante para el aprendizaje de las matemáticas. Por ejemplo, los entrevistados E2-NoOlcoma y E3-NoOlcoma consideran que un buen docente puede cometer errores, pero, por el contrario, E1-NoOlcoma enfatiza que los estudiantes tienen mayor seguridad en las clases de matemáticas cuando el profesor casi nunca se equivoca.

Además, los datos sugieren que las personas docentes- Olcoma y NoOlcoma se consideran buenos en matemática. Las personas docentes-NoOlcoma presentan un puntaje mayor cuando se trata de confianza y seguridad para temas propiamente de secundaria; en cambio los docentes-Olcoma muestran una creencia más positiva sobre su confianza para resolver cualquier problema matemático, y piensan que un excelente profesional es quien alienta, escucha y ayuda a las personas estudiantes a pensar por sí solos. Asimismo, consideran que un buen personal docente es aquel que sabe explicar. Al respecto, E1-Olcoma menciona que “un buen docente debe manejar bien la materia que está enseñando”. Además, señala varias cualidades de un buen docente: saber expresarse bien, ser bastante asertivo, y saber y buscar la mejor estrategia para mostrar las ideas o conocimientos.

Por otra parte, las personas docentes-NoOlcoma tienen una tendencia más positiva sobre el enunciado que expresa que un buen profesional es aquel que tiene un buen dominio técnico y aquel que resuelve la mayoría de los ejercicios en clase; consideran que entre más ejercicios se realicen mayor dominio del tema se va a tener.

Las personas docentes-Olcoma consideran de suma importancia el análisis y el razonamiento lógico durante el proceso del aprendizaje. Sin embargo, E1-Olcoma menciona que, en el sistema escolar, el currículo no lo deja plantear ejercicios para fortalecer dichas habilidades, que la persona estudiante debe tener su momento de práctica individual y que no ve necesaria la resolución de todos los ejercicios. En este sentido, E2-Olcoma señala que no basta con realizar todos los ejercicios, sino tener la habilidad y la disposición de transmitir el conocimiento o buscar diferentes formas de solución. También, expresa: “es bueno que un docente maneje los temas que va a dar, pero si tiene otros tipos de habilidades aportaría todavía más” (E2-Olcoma, comunicación personal, 12 de agosto de 2021).

Por tanto, los datos y las entrevistas sugieren que las personas docentes-Olcoma poseen un mayor consenso sobre la idea de que cometer errores es parte del aprendizaje. Además, destacan que un buen profesional docente es aquel que alienta y escucha a los estudiantes. También, consideran que tienen la suficiente confianza para poder resolver cualquier problema matemático que se les presente.

No obstante, un porcentaje de las personas docentes- NoOlcoma afirma que cuantos menos errores cometa un profesor, mayor seguridad brindará al estudiantado.

Aún más, considera que el dominio técnico y resolver todos los ejercicios en matemática son características de un buen profesional. Contrario a esto, la mayoría de docentes-Olcoma señala que es importante para la persona docente en matemática tener buen dominio técnico y resolver ejercicios, pero no más que saber desarrollar los conocimientos, así como emplear el razonamiento lógico y el análisis.

Promedio obtenido por las personas docentes hacia la creencia respecto a sí mismos

Según la Tabla 2, las personas docentes-Olcoma y NoOlcoma presentan una tendencia muy positiva hacia los ítems relacionados con la creencia sobre los individuos respecto a sí mismos en matemáticas.

Tabla 2 Promedio de respuesta de las personas docentes que han participado o no en Olcoma sobre la variable creencia de los individuos respecto a sí mismos en matemáticas 

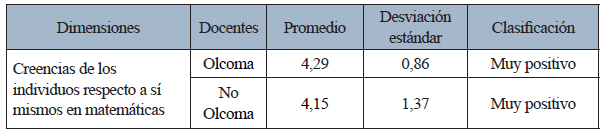
Fuente: elaboración propia

Los datos parecen sugerir que las personas docentes- Olcoma tienen la creencia sobre sí mismos más positiva con respecto a las personas docentes-NoOlcoma, ya que en varias características prevalece un mejor puntaje. Sin embargo, al aplicar las pruebas de Shapiro-Wilk y Wilcoxon, no se obtuvo evidencia para indicar diferencias significativas en los docentes que han participado en Olcoma con quienes no lo han hecho.

Con respecto a las personas docentes-Olcoma se puede señalar que guían a la persona estudiante a pensar por sí misma y a tener claro que el error incentiva su aprendizaje. En este sentido, E1-Olcoma menciona: “hay una máxima en educación que dice que del error se aprende” (E1-Olcoma, comunicación personal, 16 de septiembre de 2021). Aunado a lo anterior, expresan que si bien cualquier docente se puede equivocar, con la experiencia se adquiere seguridad.

Además, consideran que es necesario realizar varios ejercicios o problemas en matemática siempre y cuando tengan distintas formas de resolución. Enfatizan que un profesional de matemática debe ser especialista en su materia y tener la confianza para resolver cualquier problema. Al respecto, E1-Olcoma expresa: “un docente tiene que manejar la materia que está impartiendo” (E1- Olcoma, comunicación personal, 16 de septiembre de 2021).

Por otra parte, E1-NoOlcoma menciona que algunas veces prefiere ser buena conductista al enseñar matemática, por lo tanto, cree que no necesariamente guía al estudiante a pensar por sí mismo. También, considera que la persona docente puede equivocarse, pero entre menos errores tenga, más seguridad crea a las personas estudiantes. Igualmente, las personas docentes-NoOlcoma reconocen que utilizan ejercicios de diferentes niveles de dificultad en sus clases, pero no experimentan formas de resolución variadas y concuerdan en que la persona docente debe ser buena en su asignatura.

Creencias respecto al talento matemático

Con respecto al talento matemático, las personas docentes- NoOlcoma presentan un promedio mayor, aunque no resultó ser significativo, respecto a las personas docentes-Olcoma.

Por ejemplo, para la pregunta sobre si es fácil percibir cuando un estudiante tiene talento matemático, el porcentaje de respuesta positiva de docentes-NoOlcoma es mayor que docentes-Olcoma. También, para “Creo que la persona estudiante con talento matemático es el que tiene mejor rendimiento académico”, se obtuvo que el porcentaje de respuesta positiva de docentes- NoOlcoma está por encima de docentes-Olcoma. Sin embargo, al contrastar por medio de las entrevistas se puede considerar que los docentes, en general, poseen una creencia positiva.

Sobre esta última idea, en las entrevistas se obtuvo que E2-NoOlcoma, por ejemplo, considera que la persona estudiante con talento matemático es quien saca cien en las calificaciones. En general, los datos sugieren que las personas docentes-NoOlcoma perciben el talento matemático a partil del rendimiento académico del estudiantado. Esta podría ser una justificante del porqué visualizan el talento matemático de manera fácil (se basan en un número y no necesariamente en habilidades).

Se logra observar, por parte de las personas docentes- Olcoma, que la percepción del talento matemático consiste en analizar como el estudiantado se expresa, prestar atención a las actitudes que poseen durante el desarrollo de una clase, y estudiar las destrezas y habilidades que poseen hacia la matemática mediante la resolución de problemas. Esta forma de concebir el talento matemático podría explicar, en parte, las diferencias de opinión entre docentes Olcoma y NoOlcoma en los ítems del cuestionario. Sobre la percepción del talento matemático, se debe profundizar en futuras investigaciones.

Ahora bien, los docentes-Olcoma consideran que el alumnado con talento matemático progresa individualmente y puede lograr el éxito sin ninguna ayuda. En este sentido, en las entrevistas E1-Olcoma y E2-Olcoma expresaron que algunas personas estudiantes con talento matemático son autosuficientes y logran desarrollar sus habilidades por sí mismas.

Además, indican que, a través de preguntas, las personas docentes pueden identificar el talento matemático de las personas estudiantes, y percibir su pensamiento crítico y analítico, así como sus ideas creativas, avanzadas y abstractas. Por consiguiente, las personas docentes-Olcoma concuerdan en que las personas estudiantes con talento matemático suelen presentar diferentes actitudes dentro del aula, por lo general, buscan diferentes soluciones a cualquier problema, tienen capacidad de razonar de forma diferente al resto del estudiantado, realizan preguntas fuera de lo común, quieren saber más de la materia y se mantienen analizando o participando activamente durante una clase. Por su parte, las personas docentes- Olcoma tienen mayor afinidad por aquellos problemas que ponen a prueba a las personas estudiantes y esperan que estas se tomen el tiempo necesario para razonar y argumentar.

Por otro lado, las personas docentes-NoOlcoma poseen un porcentaje de respuesta más alto con respecto a las personas docentes-Olcoma sobre las afirmaciones de que el talento matemático puede ser desarrollado en el ámbito académico o que es innato. Esto se refuerza con la entrevista a E2-NoOlcoma y E3-NoOlcoma, quienes apoyan la idea de que todas las personas pueden aprender matemática, y que por medio de recursos y técnicas adecuadas se pueden fortalecer algunas habilidades matemáticas durante el desarrollo académico.

También, para la afirmación “La persona con talento matemático es aquella que termina más rápido todos los problemas matemáticos”, las personas docentes-NoOlcoma presentan una creencia más positiva, aunque no es significativa, con respecto a las personas docentes-Olcoma. Sin embargo, se obtiene, a través de las entrevistas, que las personas docentes-NoOlcoma realizan, en su mayoría, problemas en los cuales se requiere procedimientos rutinarios para la resolución, mientras que las personas docentes-Olcoma se enfocan más en problemas con distintos procesos de solución. Por último, sobre el ítem “La persona estudiante con talento matemático suele aburrirse en las clases de matemática”, el porcentaje de respuesta para ambos grupos de docentes es similar. Sin embargo, como ya se mencionó, en las entrevistas se logra percibir que las personas docentes-NoOlcoma realizan problemas más mecánicos, lo cual podría generar pérdida de interés en los estudiantes. Por ejemplo, E2-NoOlcoma indica que asigna problemas extra, de la misma materia, para la población estudiantil que termina rápido los ejercicios, lo cual podría generar saturación.

Se logra percibir que las personas docentes-Olcoma, algunas veces, realizan problemas con mayor dificultad, por lo tanto, el estudiantado que no posea talento matemático o que no se considere “bueno en matemática” podría perder interés al no poder resolverlos; contrario de quienes sí posean ciertas habilidades para el estudio de la materia.

Con base en lo anterior, la creencia hacia el talento matemático presenta algunas diferencias entre docentes Olcoma y NoOlcoma, pues poseen una distinción hacia el uso y la importancia de la resolución de problemas, así como que las características asociadas a una persona con talento matemático son distintas. No obstante, concuerdan en que la persona estudiante con talento matemático puede aburrirse en clases, aunque esto podría derivarse de aspectos metodológicos y no por disgusto hacia la materia. Para identificar al estudiantado con talento matemático, los docentes-Olcoma toman como referencia las habilidades, mientras que los docentes-NoOlcoma, las notas obtenidas en las evaluaciones.

Conclusiones

En general, se analizaron las características de las personas docentes de matemáticas que participaron en el estudio. La clasificación se hizo con base en las preguntas realizadas en el cuestionario, los promedios obtenidos en cada ítem y categorías, así como en las entrevistas. El asocie de una característica a un grupo específico se dio porque el promedio fue más alto (“más positiva”) con respecto al otro. Como se mencionó, ambos grupos de docentes presentan, en general, actitudes y creencias positivas, pero al obtener el promedio y los porcentajes de respuestas, en algunos ítems estas fueron mayores en un grupo que en el otro. Estas diferencias no resultaron significativas y los datos se complementaron con la opinión de las personas docentes durante las entrevistas.

A manera de resumen, las personas docentes-Olcoma destacan a nivel de actitudes en el componente cognitivo, afectivo y conductual, y en las creencias resaltan en aspectos relacionados con la resolución de problemas, sobre sí mismos y en talento matemático. Por su parte, las personas docentes-NoOlcoma sobresalen en la creencia instrumentalista y en la platónica relacionada con la matemática.

A nivel de actitudes, las personas docentes-Olcoma actualizan su conocimiento matemático constantemente y les gusta investigar para innovar en sus clases. Además, expresan que cualquier persona puede aprender matemáticas si se lo propone y consideran que las matemáticas son un estímulo para el desarrollo académico del estudiantado. Tienen seguridad y confianza para resolver problemas de cualquier tema en esta asignatura, pero son conscientes de que los problemas no necesariamente se resuelven rápido. Por último, disfrutan y muestran interés por participar en actividades relacionadas con las matemáticas.

Ahora bien, con respecto a las creencias, las personas docentes-Olcoma consideran que las matemáticas son útiles para la vida cotidiana y que, a partir de ellas, se pueden modelar situaciones reales. Además, creen que hay matemáticas por descubrir y que no es solamente un campo de manipulación de símbolos. También, consideran importante utilizar problemas contextualizados para motivar e incrementar el interés hacia la asignatura, de manera que proporcionan problemas con distintos procesos de solución para fomentar el razonamiento lógico dentro de sus clases.

Asimismo, las personas docentes-Olcoma creen que las matemáticas se pueden explicar mediante preguntas generadoras. Si bien conciben que una buena persona profesional en matemáticas debe ser excelente en dicha asignatura, puede cometer errores. Además, saben escuchar e interpretar las dudas de las personas estudiantes.

Aunado a lo anterior, las personas docentes-Olcoma perciben que las personas con talento matemático son quienes piensan de forma crítica y analítica; generan ideas creativas, avanzadas y abstractas; y se ven seducidas por los problemas matemáticos fuera de lo común, de lo contrario pueden aburrirse. Consideran que el talento matemático se puede fortalecer en el ámbito académico, aunque cada persona ya lo tiene, y determinar mediante las preguntas que se realizan a las personas estudiantes y las actitudes que poseen en el aula.

Por otro lado, a nivel de actitudes, se describe a la persona docente-NoOlcoma como un profesional que considera las matemáticas difíciles para las personas estudiantes, aún cuando muestran un compromiso hacia la asignatura; no obstante, piensan que las matemáticas pueden estimular el desarrollo académico del estudiantado. Además, sienten más comodidad al trabajar con algunos temas en matemáticas que con otros, y consideran que tienen dominio y seguridad al abordar el contenido matemático necesario para impartir clases en secundaria.

En cuanto a las creencias, las personas docentes- NoOlcoma consideran que las matemáticas son importantes para la vida cotidiana. Sin embargo, creen que la mayoría de los temas en matemáticas ya están creados. También, las consideran un campo de manipulación de fórmulas y símbolos, por tanto, que los problemas tienen solo una forma de resolverse. Asimismo, estos docentes realizan problemas con diferentes niveles de dificultad, utilizan problemas contextualizados, consideran que cualquier persona puede aprender matemáticas y que un buen profesional docente es aquel que resuelve todos los ejercicios en matemáticas, siente empatía por las personas estudiantes y se considera hábil en la asignatura.

Con respecto al talento matemático, las personas docentes- NoOlcoma piensan que se puede percibir fácilmente, pues consideran que la persona estudiante con esta habilidad posee buenas calificaciones, es decir, relacionan el talento matemático con el rendimiento académico. Además, consideran que la persona estudiante con talento matemático, por lo general, termina rápido los ejercicios, posee pensamiento creativo, avanzado y suele aburrirse en clase. Por último, mencionan que el talento matemático es innato, pero que también se puede desarrollar durante el ámbito académico.

Los resultados obtenidos permiten observar algunas diferencias en el dominio afectivo de docentes-Olcoma y NoOlcoma, que podrían asociarse con la participación en el proyecto de Olimpiadas Costarricenses de Matemática. Esto porque participar en Olcoma implica, para la persona docente, el estudio de temas matemáticos que no son propios de secundaria, con un nivel de complejidad y exigencia más alto.

La participación en Olcoma es decisión de la persona docente. Por ello, las actitudes y creencias hacia las matemáticas, así como el talento matemático del profesorado podrían estar relacionados con su interés de involucrarse en este proyecto y capacitar al estudiantado. Sobre estos temas se debe realizar más investigación. El propósito de estos resultados es dar insumos para profundizar en el dominio afectivo de la persona docente de matemáticas y su concepción sobre el talento matemático