INTRODUCCIÓN

El yacón, Smallanthus sonchifolius (Poepp. & Endl.) H. Rob., es una planta andina, importante por su valor nutracéutico. Las raíces tienen alto contenido de fructooligosacáridos e inulina, y las hojas alto contenido de compuestos fenólicos ( ^{Choque-Delgado et al., 2013} ). Hasta finales de la década de 1990 el yacón era un cultivo marginal, de huerto familiar; luego, se promovió su producción, debido a los resultados de investigaciones realizadas, principalmente en Japón ( ^{Hermann et al., 1999} ).

En el año 2003, se estimaba en 600 ha la superficie sembrada de yacón en Perú, cuya producción sobrepasaba la demanda ( ^{Seminario et al., 2003} ). Estimaciones posteriores indicaron que las siembras fueron de 250 a 300 ha por año, en concordancia con la oferta y la demanda. La raíz se vende fresca y procesada; se exportaron más de 40 t como productos procesados y se prevé un incremento de la demanda en los próximos años ( ^{Comisión del Codex Alimentarius, 2012} ).

Los estudios sobre yacón se han orientado, principalmente, a conocer la diversidad morfológica y genética ( ^{Mansilla et al., 2006} ; ^{Vegas et al., 2015} ), y el potencial como alimento funcional y medicinal ( ^{Valentová y Ulrichová, 2003} ; ^{Arnao et al., 2011} ; ^{Choque-Delgado, 2013} ; ^{Satoh et al., 2013} ). Otra línea de estudio es la producción de semilla ( ^{Manrique et al., 2014} ); sin embargo, existen vacíos de información sobre la agronomía, productividad, poscosecha y la fisiología de la planta, bajo diversos tratamientos culturales ( ^{Seminario et al., 2003} ; ^{Manrique et al., 2005} ).

En el análisis de productividad de una especie en particular, se correlacionan las características morfo-fisiológicas de la planta (variables respuesta) y los factores del manejo y del clima (variables causa). Para este propósito, el área foliar (AF) y el peso seco (PS) de la planta son dos variables indispensables; estas se evalúan por etapas fenológicas o en intervalos temporales definidos. Con estas dos variables básicas, se pueden calcular índices como tasa absoluta de crecimiento, tasa relativa de crecimiento, índice de área foliar, tasa de asimilación neta e índice de cosecha. Estos índices permiten explicar el comportamiento de la planta en estudio ( ^{Gardner et al., 1985} ).

La evaluación del PS es relativamente fácil, es suficiente tomar la planta o sus partes y secarlas en estufa, siguiendo un protocolo establecido. No sucede lo mismo con el AF. La evaluación directa y destructiva del AF, por cualquiera de sus formas (siluetas en papel, peso fresco y seco, planímetro, integrador de área), requiere alta inversión de tiempo y de dinero en equipos costosos; además del efecto negativo en la planta por la remoción de las hojas.

Se han desarrollado métodos no destructivos para la estimación del AF de especies agrícolas, dentro de los cuales destaca el uso de ecuaciones alométricas. Estas se obtienen al correlacionar las medidas lineales de las láminas (o los foliolos, según el tipo de hoja) con su área. Menos usada es la correlación entre PS y AF.

La alometría establece que existe relación entre los cambios en las dimensiones relativas de las partes de un organismo y el tamaño total del mismo; lo que indica que existe relación entre los cambios en la forma y el tamaño del organismo ( ^{Gayon, 2000} ; ^{Shingleton, 2010} ). Esta relación también es aplicable a las dimensiones de las partes de un organismo ( ^{Pérez et al., 2009} ). Bajo este mismo concepto, ^{Gardner et al. (1985)} y ^{Rodríguez y Leihner (2006)} , plantearon que existe relación isométrica (la forma no cambia, pero sí el tamaño) entre las medidas lineales de las hojas (largo y ancho máximo) y el AF, de modo que, esta relación se puede probar mediante análisis de regresión entre las variables indicadas.

La derivación de ecuaciones de regresión, entre las medidas lineales y el AF, para estimar el AF de las especies agrícolas como maíz – Zea mays – ( ^{Montgomery, 1911} ), papa – Solanum tuberosum – ( ^{Jerez et al., 2014} ), caña de azúcar – Saccharum officinarum – ( ^{Brito et al., 2007} ), tomate – Lycoperscum esculentum – ( ^{Carmassi et al., 2007} ), frijol – Phaseous vulgaris – ( ^{Bhatt y Chanda, 2003} ), te – Tea sinensis – ( ^{Zenginbal et al., 2006} ), arveja – Pisum sativum – ( ^{Galindo y Clavijo, 2007} ), yuca – Manihot esculenta – ( ^{Burgos et al., 2010} ) y repollo – Brassica oleracea – ( ^{Olfati et al., 2010} ), se encuentra ampliamente citada en la literatura. También se han obtenido ecuaciones similares para especies forestales ( ^{Cabezas-Gutiérrez et al., 2009} ), frutales pequeños ( ^{Fallovo et al., 2008} ) y ornamentales ( ^{Giuffrida et al., 2011} ).

Esta búsqueda debe hacerse para cada especie; además, en algunos casos, se requiere encontrar la ecuación para cada cultivar o genotipo, por las diferencias intraespecíficas que pueden presentarse en el comportamiento de la forma y las dimensiones de las hojas; por ejemplo, café ( ^{Zambom da Silva et al., 2011} ; ^{Espindula et al., 2013} ), caña de azúcar ( ^{Brito et al., 2007} ), vid ( ^{Legorburo et al., 2007} ), papa ( ^{Jerez et al., 2014} ), yuca ( ^{Burgos et al., 2010} ) y repollo ( ^{Olfati et al., 2010} ).

El objetivo de este trabajo fue estimar el área foliar de ocho morfotipos de yacón mediante análisis de regresión lineal simple.

MATERIALES Y MÉTODOS

La investigación se realizó entre junio 2014 y julio 2015, en el Programa de Raíces y Tubérculos Andinos de la Facultad de Ciencias Agrarias, Universidad Nacional de Cajamarca (distrito, provincia y departamento de Cajamarca), Perú. Localizado a 3,5 km de la ciudad de Cajamarca, 7° 10’ 00’’ S, 78° 30’00’’ W, 2650 msnm, 14 °C de temperatura media diaria, 65% de humedad relativa y 650 mm de precipitación pluvial anual.

Se trabajó con hojas maduras de ocho morfotipos de yacón del norte peruano (Ancash-Piura), los cuales están caracterizados morfológicamente mediante descriptores estandarizados ( ^{Seminario et al., 2004} ). Este germoplasma se mantienen ex situ desde 1993. Los morfotipos en estudio tienen hojas triangulares, con base truncada (I, VII ), hastada (III, IV), ligeramente cuneada (II) y cordada (V, VI, VIII); sus bordes pueden ser aserrados (I, II), doblemente aserrados (III, IV, V, VII) y crenados (VI, VIII ) ( Figura 1 ).

Figura 1  Imágenes de las hojas de ocho morfotipos de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) (I-VIII) del norte peruano. En I se indica la forma como se tomaron las dimensiones de largo (L) y ancho mayor (W) de la lámina. Cajamarca, Perú. 2014-2015. Figure 1. Leaves images of eight yacon morphotypes ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) (I-VIII) of the north of Peru. In image I, the way the blade dimensions length (L) and greater width (W) were taken is indicated. Cajamarca, Peru. 2014-2015. 

Cada morfotipo estuvo representado por diez plantas, sembradas a 0,90 m entre surcos y 0,60 m entre plantas. Se colectaron cien hojas de cada morfotipo, incluyendo hojas de los estratos basal, medio y terminal de plantas, al inicio de la floración; estas hojas fueron inmediatamente dibujadas en papel. Las dimensiones de largo (L) y ancho mayor (W) de las láminas se tomaron como se indica en la Figura 1-I .

El área de las láminas de las siluetas (área real de las láminas –AR–), se midió mediante planímetro digital, siguiendo las instrucciones del manual del usuario. El valor obtenido fue la variable dependiente, que se usó para el análisis de regresión con las dimensiones lineales de las láminas. Los valores del AR y de las dimensiones de cada lámina fueron introducidos en una hoja de cálculo de Microsoft Excel 10. Se determinaron los valores de L², W², L x W y L/W, de modo que la base de datos quedó conformada como la describen ^{Rojas y Seminario (2014)} .

La estimación del área de las láminas mediante el análisis de regresión siguió el procedimiento usado por otros autores en otras especies ( ^{Cabezas-Gutiérrez et al., 2009} ; ^{Giuffrida et al., 2011} ; ^{Jerez et al., 2014} ; ^{Rojas y Seminario, 2014} ). El procedimiento consiste en realizar regresiones entre L, W, L², W², L x W, L/W y el AR (medida con planímetro) de las láminas de las hojas muestra de cada morfotipo. En la ecuación de regresión AR = a + bx, tenemos que: AR = área de la lámina, “a” y “b” constantes, “x” = dimensión lineal de la lámina foliar o su combinación.

La selección de las mejores ecuaciones se hizo tomando en cuenta el coeficiente de determinación r² y la significación del análisis de varianza (ANOVA). Si r² es cercano a 1, indica muy alta o perfecta relación entre variables ( ^{Burgos et al., 2010} ; ^{Vásquez, 2013} ). Por otro lado, si en la prueba de F, se encuentra significación estadística a nivel de 5% (p≤0,05) o a 1% (p≤0,01) de probabilidades, indica que la ecuación es predictiva o altamente predictiva, respectivamente, del área real ( ^{Cardona et al., 2009} ; ^{Burgos et al., 2010} ). Seleccionada la ecuación que mostró la más alta correlación entre el AR y las dimensiones lineales, en cada morfotipo, se reemplazaron los valores y se obtuvo la estimación del área laminar en porcentaje, con relación al AR (100%).

La forma general de las hojas de los ocho morfotipos fue similar, con diferencias en la base y el borde. Además, en campo, no siempre es posible conocer con certeza el morfotipo en cuestión; por este motivo, se realizó una prueba para estimar el área laminar de las hojas de todos los morfotipos, como si fueran uno solo; de este modo, se obtuvo una ecuación para estimar el AF del yacón en general, cuando no se conoce el morfotipo específico.

La hoja de yacón tiene peciolo con nervadura central gruesa y alas foliares fotosintéticas a ambos lados ( Figura 1 ), con un área que podría ser significativa, respecto del área total de la hoja. Esta área peciolar fue evaluada por separado, con el propósito de conocer su incidencia en el área foliar total. Se tomó una muestra de treinta hojas por morfotipo; se dibujaron las siluetas en papel y se midió el área del peciolo y de la lámina, con planímetro. El área del peciolo se expresó en porcentaje, con respecto al área total de la hoja.

RESULTADOS Y DISCUSIÓN

Valores de largo, ancho y área medida (real) de las láminas

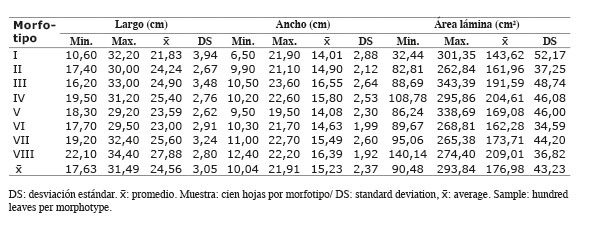
Los valores más altos del largo de lámina, correspondieron al morfotipo VIII (27,88 cm); y, los valores más altos del ancho laminar, correspondieron al morfotipo III (16,55 cm). El AR (área real, medida con planímetro) varió de 143,62 cm² (morfotipo I) a 209,01 cm² (morfotipo VIII). La alta variación del largo y ancho dentro de los morfotipos se evidencia por el valor de la desviación estándar (DS) ( Cuadro 1 ). Las hojas más grandes se observaron en los morfotipos VIII, IV y III, los cuales deberían ser objeto de otros estudios para probar esta diferencia y potencial de selección para la producción de hoja.

Cuadro 1 Valores de largo (L), ancho mayor (W) y área real de las láminas foliares de ocho morfotipos de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Table 1. Leaf blades length (L), greater width (W) and real area values of eight yacon morphotypes ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015. 

Estimación del área laminar mediante análisis de regresión

Según el valor r² y la pendiente de las líneas de regresión, las ecuaciones más eficientes para estimar el área foliar en los morfotipos en estudio, fueron las que se presentan en las Figuras 2 y 3 . Estas ecuaciones mostraron, además, alta significación estadística al 1% de probabilidades (p≤0,01) en el ANOVA ( Cuadro 2 ), lo que confirma el alto poder predictivo de las variables regresoras y la funcionalidad de las ecuaciones ( ^{Cardona et al., 2009} ; ^{Burgos et al., 2010} ).

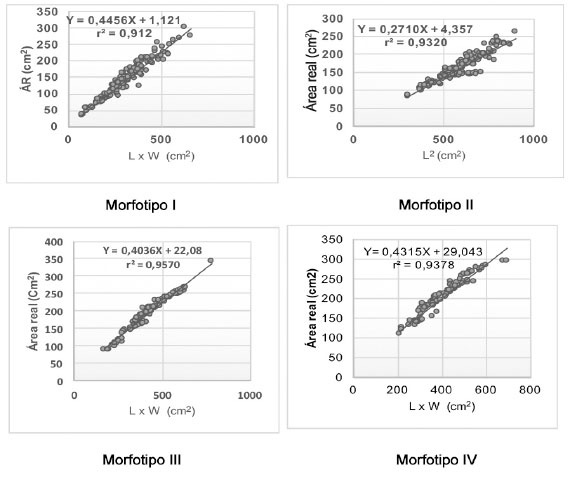
Figura  Diagrama de dispersión, línea de regresión y ecuación de regresión de la mejor relación entre el área real (AR) y el largo (L) y ancho mayor (W) de las láminas foliares de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Muestra:cien hojas por morfotipo. Figure 2. Scatterplot, regression line and regression equation of the best relation between the real area (AR) and length (L) and greater width (W) of the leaf blades of yacon ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015. Sample: hundred leaves per morphotype. 

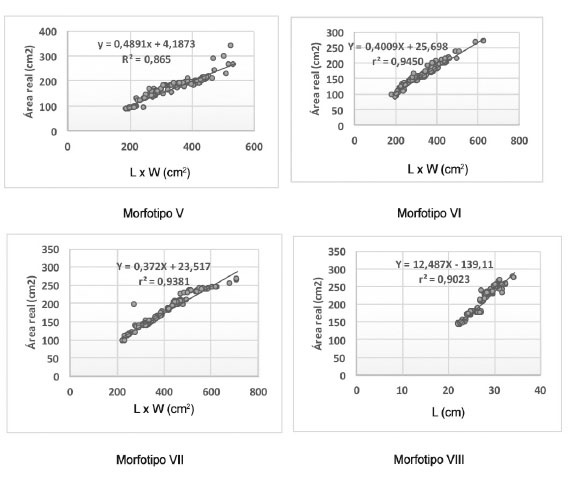
Figura 3 Diagrama de dispersión, línea de regresión y ecuación de regresión de la mejor relación entre el área real (AR) y el largo (L) y ancho mayor (W) de las láminas foliares de yacón ( Smallanthus sonchifolius (poep. & endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Muestra:cien hojas por morfotipo. Figure 3. Scatterplot, regression line and regression equation of the best relation between the real area (AR) and length (L) and greater width (W) of the leaf blades of yacon ( Smallanthus sonchifolius (poep. & endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015. Sample: hundred leaves per morphotype. 

Cuadro 2  Cuadrados medios (CM) y significación para las regresiones seleccionadas entre el área y la dimensión de las hojas de ocho morfotipos de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Table 2. Square means (CM) and significance for selected regressions between the area and leaves dimensions of eight yacon morphotypes ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015. 

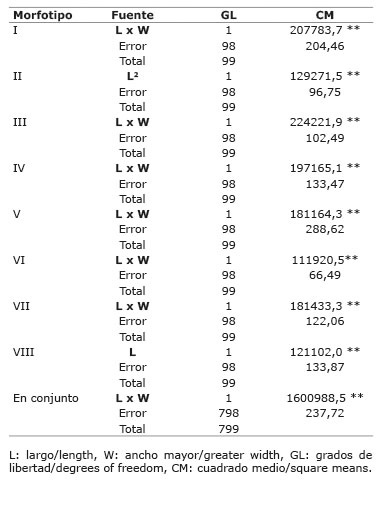
^**Altamente significativo a 1% de probabilidades / Highly significant at 1% probability.

Con base en las ecuaciones seleccionadas, se diferenciaron dos grupos: el primero, formado por los morfotipos I, III, IV, V, VI y VII, en el cual, la ecuación que mejor estimó el área de las láminas fue aquella en la que intervino el producto L x W. El grupo incluyó morfotipos con hojas de base truncada (I, VII), hastada (III) y cordada (V, VI). El segundo grupo fue aquel, en donde, la mejor ecuación para estimar el área, requirió la intervención de L² (morfotipop II, de base ligeramente cuneada) y L (morfotipo VIII, de base cordada).

En todos los casos, el área estimada con las ecuaciones seleccionadas por su mayor exactitud y precisión, se ubicó alrededor del 100%, con respecto al área real o medida ( Cuadro 3 ), lo cual confirma la hipótesis y confiere confiabilidad para el uso de las ecuaciones. Las DS (± 5,54% a ± 10,05%) se ubicaron dentro de los rangos registrados en la literatura: ± 11,50% a ± 21,27% ( ^{Blanco y Folegatti, 2005} ), ± 4,5 a ±10,5 ( ^{Williams y Martinson, 2003} ).

Cuadro 3 Área laminar estimada en relación al área real, según la ecuación seleccionada para cada morfotipo de yacón ( Smallathus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Table 3. Estimated leaf area in relation to the real area, according to the selected equation for each yacon morphotype ( Smallathus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015.  

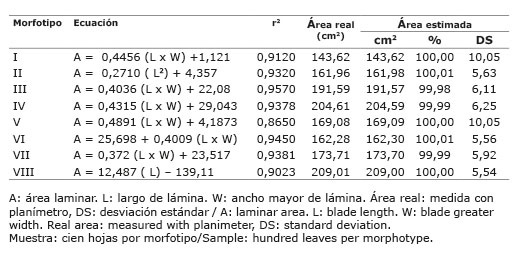
Los estudios en otras especies agrícolas ( ^{Fallovo et al., 2008} ; ^{Giuffrida et al., 2011} ; ^{Jerez et al., 2014} ), muestran la existencia de relaciones similares entre el AR y las dimensiones lineales de las hojas. En consecuencia, para estimar el AF de los morfotipos de yacón en estudio, es necesario tomar las medidas de las hojas, reemplazar los datos en la ecuación respectiva y hacer el cálculo pertinente.

La aplicación de las ecuaciones así obtenidas, resulta funcional por las características de la planta de yacón: produce entre seis a trece tallos por planta y cada tallo produce de trece a dieciséis pares de hojas, según el morfotipo y la densidad de plantación ( ^{Seminario et al., 2001} ; ^{Seminario et al., 2003} ).

Análisis de regresión para las láminas de los ocho morfotipos, en conjunto

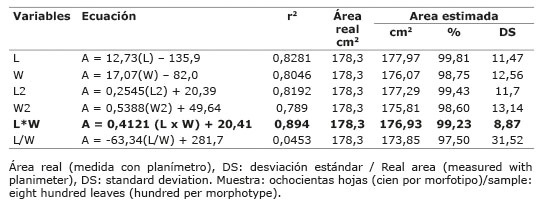
Las regresiones para las medidas lineales de las láminas y el AR de los ocho morfotipos de yacón, como si fueran uno solo ( Cuadro 4 ), mostraron alta relación entre variables, excepto con el cociente L/W. La ecuación que permitió la mejor estimación del área de las láminas fue aquella en donde intervino el producto L x W. A saber, A = 0,4121 (L x W) + 20,41, con r² = 0,894). El valor del estadístico r² indicó que el 89,4% del área de la hoja se explica por el producto de L x W. Por otro lado, la ecuación estimó el valor del área foliar en 99,23% ± 8,87%, en relación al área real o medida.

Cuadro 4 Ecuaciones de regresión con el largo (L) y ancho mayor (W) de las láminas foliares y, área real y área estimada de ocho morfotipos de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano, considerados en conjunto. Cajamarca, Perú. 2014-2015. Table 4. Regression equations with the length (L) and greater width (W) of the leaf blades and real area and estimated area of eight yacon morphotypes ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru, taken together. Cajamarca, Peru. 2014-2015. 

El diagrama de dispersión y la línea de regresión ( Figura 4) , permitieron una mejor visualización de la estrecha relación entre variables. El ANOVA para la ecuación seleccionada indicó alta significación estadística ( Cuadro 2 ), lo cual confirmó su eficiencia para estimar el área; de modo que, esta ecuación se puede usar para estimar el área foliar laminar del yacón en forma general, sin considerar el morfotipo.

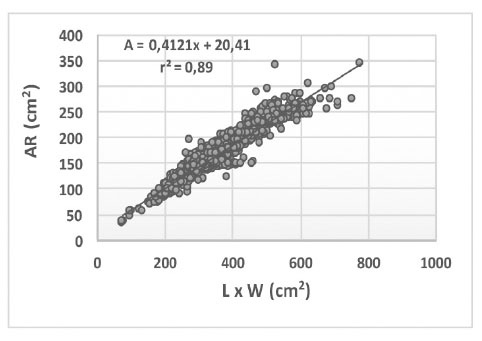
Figura 4 Diagrama de dispersión, línea de regresión y ecuación de regresión para la relación entre el área real (AR) y el producto de largo (L) x ancho mayor (W) de las láminas, de ocho morfotipos considerados en conjunto de yacón ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano, en conjunto. Cajamarca, Perú. 2014-2015. Muestra: ochocientas hojas. Figure 4. Scatterplot, regression line and regression equation for the relation between the real area (AR) and the product of length (L) x greater width (W) of the leaf blades of eight yacon morphotypes ( Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru, taken together. Cajamarca, Peru. 2014-2015. Sample: eight hundred leaves. 

Área del peciolo de las hojas de yacón y su incidencia en el área fotosintética total

El área del peciolo varió de 29,20 cm² (morfotipo I) a 54,60 cm² (morfotipo V). Esta fue equivalente a 11% y 17% del área total de la hoja, respectivamente ( Cuadro 5 ), con un promedio de 15%. Por lo tanto, se recomienda que para estudios, en donde se necesita mayor precisión respecto del área fotosintética de cada morfotipo, se adicionen estos porcentajes al área medida o estimada de la lámina.

Cuadro 5  Área del peciolo (%) con respecto al área total de la hoja de ocho morfotipos de yacón Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) del norte peruano. Cajamarca, Perú. 2014-2015. Table 5. Petiole area (%) relative to the total leaf area of eight yacón morphotypes Smallanthus sonchifolius (Poep. & Endl.) H. Rob.) of the north of Peru. Cajamarca, Peru. 2014-2015. 

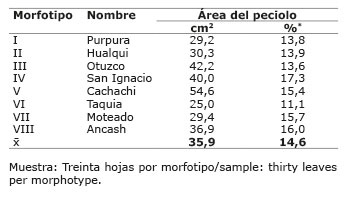
^*Con relación al área total de la hoja / In relation to the total area of the leaf.