Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Agronomía Mesoamericana
On-line version ISSN 2215-3608Print version ISSN 1659-1321
Agron. Mesoam vol.22 n.1 San Pedro Jun. 2011
Índices de selección para producción de maíz forrajero
Carlos Alejandro Tucuch-Cauich2, Sergio Alfredo Rodríguez-Herrera3, Manuel Humberto Reyes-Valdés3, Juan Manuel Pat-Fernández2, Fulgencio Martín Tucuch-Cauich4, Hugo Salvador Córdova-Orellana+
1 Tesis de Doctorado.
2 Colegio de la Frontera Sur, Unidad-Campeche. Calle 10 x 61 núm. 264, Col. Centro, CP 24000 San Francisco de Campeche México. ctucuch@ecosur.mx, jpat@camp.ecosur.mx
3 Instituto Mexicano del Maíz, Universidad Autónoma Agraria Antonio Narro, Buenavista Saltillo Coahuila México. srodriguez@uaaan.mx, mhreyes@uaaan.mx
4 Campo Experimental Edzná. Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias km 15.5, Carretera Campeche-Pocyaxum Mpio. Campeche Campeche C.P. 24250, A.P. 341. tucuch.martin@inifap.gob.mx
+ Centro Internacional de Mejoramiento de Maíz y Trigo. Km 45 carretera México-Veracruz.El Batán Texcoco, Edo. De México.
Dirección para correspondencia
Resumen
Índices de selección para producción de maíz forrajero. El objetivo del presente trabajo fue estimar índices de selección de caracteres agronómicos que ayuden a seleccionar los materia les genéticos que se utilizan en la producción de forraje y evaluar la eficiencia relativa de los índices estimados. Se evaluaron 28 cruzas directas (método IV de Griffing), producto de un diseño de cruzas dialélicas, con ocho líneas de maíz de alta calidad proteínica (QPM), en el Rancho Ampuero en Torreón, Coahuila, México, en el año 2003 y 2004. El diseño experimental utilizado fue bloques completos al azar con dos repeticiones, las variables evaluadas fueron: altura de planta (AP), altura de mazorca (AM), rendimiento de forraje verde (RFV) y rendimiento de forraje seco (RFS). Se encontró que: a) se obtuvo mayor eficiencia al combinar caracteres correlacionados con el carácter de interés, b) la correlación entre caracteres per se, causó decrementos en la eficiencia del índice, c) la respuesta teórica a la selección, al usar índices, fue mayor que la basada solamente en rendimiento de forraje verde, d) los índices de selección más eficientes fueron los que tomaron en cuenta el rendimiento de forraje verde y aquellas variables con más alta correlación genética (AP y AM), e) el índice seleccionado fue el que incluyó las variables altura de planta, altura de mazorca y rendimiento de forraje verde (I=-20,88 X1 +49,26 X2 -0,11 X3) con una eficiencia relativa de 1,5 7%.
Palabras claves: Correlación genética, correlación fenotípica, producción forrajera, varianza genética y eficiencia relativa.
Abstract
Selection indexes for yield forage maize. The objective of this research was to estimate selection indexes of agronomic traits that help in selecting the genetic material used in the production of forage, and evaluate the relative efficiency of the indexes estimated. We evaluated 28 direct crosses (Griffing’s method IV), the product of diallel crosses design with eight lines of high quality protein maize (QPM). The study was done in the Rancho Ampuero in Torreon, Coahuila, Mexico, in 2003 and 2004. The experimental design was a randomized complete block with two repetitions, the variables evaluated were: plant height (PH), ear height (AM), green forage yield (RFV) and dry forage yield (RFS). It was found: a) greater efficiency by combining characters correlated with the trait of interest, b) the correlation between characters per se, causes decreases in the efficiency of the index, c) the theoretical response to the selection was greater when using selection indices than when done solely on forage yield, d) the most efficient selection indices took into account the yield of green fodder and those variables with the highest genetic correlation (AP and AM ), e) the index selected included the variables plant height, ear height and forage yield (I=-20,88 X1 +49,26 X2 -0,11 X3) with a relative efficiency of 1,5 7%.
Keywords: Genetic correlation, phenotypic correlation, forage production, genetic variance and relative efficiency.
Introducción
El maíz (Zea mays L.), es por tradición un cultivo de suma importancia en México, tanto para la alimentación humana como para la animal, aunque en este caso, se utiliza tanto como forraje verde ensilado o como rastrojo (el cual tiene un bajo valor nutritivo). La producción de forraje es una actividad agropecuaria esencial para el desarrollo de la ganadería, y en particular el que se obtiene del cultivo del maíz, ya que este cultivo por su diversidad genética se adapta a diferentes regiones del país.
La respuesta a la selección podría ser más eficiente si se consideran simultáneamente otros caracteres con alta heredabilidad y positivamente correlacionados con el rendimiento de forraje verde (Bujak et al. 2007). Al respecto se ha realizado investigación para la selección simultánea de caracteres en especies animales y vegetales, con éxito. Actualmente se requiere estudiar en el maíz forrajero una metodología para determinar que caracteres deben incluirse en la selección simultánea, a fin de mejorar la producción y calidad del forraje al mismo tiempo (Milligan et al. 2003).
A la fecha, ninguno de los híbridos de maíz usados para forraje en México ha sido desarrollado en programas de mejoramiento genético para mayor producción y calidad forrajera, siendo seleccionados para rendimiento de grano (Peña et al. 2004).
Así, Smith (1936), fue quien sugirió el empleo del concepto de una función discriminante como una forma lógica y sistemática en la selección de líneas para mejorar simultáneamente varia s características cuantitativas, y el objetivo principal del índice de selección maximizar el promedio del valor genético de una población; de esta manera se desarrolló el presente trabajo de investigación con ocho líneas de maíz blanco de alta calidad de proteína (QPM) y sus cruzas dialélicas, evaluándose cuatro caracteres agronómicos con los siguientes objetivos: a) Estimar índices de selección de caracteres agronómicos y de calidad nutritiva, con mayor eficiencia relativa, que ayuden a seleccionar los mejores materia les genéticos utilizados en la producción de forraje y, b) comparar los diferentes tipos de índices, estableciéndose para comprobar la hipótesis que los índices de selección que se formen con mayor número de caracteres correlacionados con rendimiento de forraje verde serán los más eficientes.
Materiales y métodos
El presente trabajo se realizó durante los años 2003 y 2004, en terrenos del Rancho "Ampuero" en Torreón Coahuila, situado dentro de la Comarca Lagunera; localizado a 25º 33´ N y 103º 26’ O y 1200 mssn de altitud. En el año 2003 las temperaturas máximas y mínimas fueron 36,13 y 16,8ºC y precipitación media de 154 mm y en el 2004 las temperaturas máximas y mínimas fueron 37,1 y 16,3ºC y precipitación media de 217 mm. Se evaluaron durante dos años 28 cruzas simples producto de un dialélico entre ocho líneas de maíz blanco normal, de alta calidad de proteína (QPM) (Cuadro 1), proporcionados por el programa de mejoramiento genético de maíz del Centro Internacional de Mejoramiento de Maíz y Trigo (CIMYT).
En la evaluación de los materiales se utilizó un diseño experimental de bloques completos al azar, con dos repeticiones, las parcelas constaron de dos surcos de 21 plantas cada uno, la separación entre planta y planta fue de 16,5 cm, y 80 cm entre surco y surco. La densidad de población fue de 80 000 plantas/ha.
La siembra se realizó manualmente el 15 de julio de 2003 y el 25 de abril de 2004. En ambos años, se fertilizó con la fórmula 120-60-00, se aplicaron 60 unidades de nitrógeno y todo el fósforo en la siembra, y el resto del nitrógeno en la escarda o sea al quitar o arrancar la maleza del maíz, antes del primer riego de auxilio. El manejo del cultivo en los dos años del estudio fue el óptimo, aplicándose tres riegos de auxilio y uno de pre siembra. El aporque se llevó acabo a los 26 días después de la siembra con una escarda mecánica y el control de plagas se realizó durante todo el ciclo de desarrollo del cultivo mediante la aplicación de insecticidas.
Los datos de las variables evaluadas se tomaron en diez plantas individuales de cada parcela útil, las variables evaluadas fueron: altura de Planta (AP), medida como la distancia en metros de la superficie del suelo hasta la base de la espiga, y se tomó en la etapa de floración; altura de mazorca (AM), medida como la distancia en metros de la superficie del suelo hasta el nudo de la mazorca principal; rendimiento de forraje verde (RFV), se estimó también con base en una muestra de diez plantas tomadas de la parcela útil o de las 21 plantas por parcela sin seleccionar y transformado posteriormente a toneladas por hectárea; la muestra se tomó en la etapa en que el grano alcanzó un tercio de la línea de leche. De esta muestra se tomó una sub muestra de un kilogramo, la cual se puso en una estufa de aire forzado a la temperatura de 60°C, y se secó hasta que llegó a peso constante, con esta se determinó el rendimiento de forraje seco (RFS) haciendo la conversión a toneladas por hectárea.
Para cada una de las variables evaluadas se realizó un análisis de varianza combinado a través de ambientes con dos repeticiones y uno de covarianza para cada una de las combinaciones posibles lo cual servirá para la construcción de los índices de selección.
El comportamiento de los híbridos y progenitores se basó en el análisis dialélico (Griffing 1956), bajo el supuesto del modelo II, método IV (cruzas directas F1), este método evalúa únicamente el comportamiento de las cruzas F1 directas, y se consideró que las líneas en cuestión son representativas de la población, ya que se puede asumir que las líneas forman una sola población desde el punto de vista que todas son de grano QPM, y las conclusiones que se deriven serán válidas para ese conjunto de líneas, asumiendo que todas ella provienen de una población virtual, de la cual son representativas (Steel y Torrie 1992).
Los componentes de varianza estimados a través del dialélico, son predictivos de una población sintética formada con dichas líneas. De tal manera, el índice podría utilizarse para seleccionar las primeras generaciones de dicha población (o variedad) sintética. (Griffing 1956).
Con las estimaciones de varianzas y covarianzas genotípicas y fenotípicas se obtuvieron los coeficientes de correlación fenotípica y genotípica, con la finalidad de determinar los caracteres correlacionados significativamente con el rendimiento de forraje verde, lo cual coincide con el trabajo reportado por Cerón y Sahagún (2005), donde usaron las covarianzas genotípicas y fenotípicas para la construcción del índice. Los índices de selección se construyeron con base en las varianzas genotípicas y fenotípicas derivadas del análisis de varianza y covarianza (Singh y Chaudary 1979), de acuerdo con los principios establecidos por Smith (1936) y Hazel (1943), donde se establece que cada unidad de selección presenta un valor genético agregado (H), definido por la expresión:
H= a1G1 + a2G2 + ........... + anGn
Donde Gn es el valor genotípico o el valor reproductivo para cada caracter y an la ponderación económica correspondiente a cada variable.
En caso de que un caracter no tenga un valor económico, su coeficiente an será igual a cero. Para el uso de esta ecuación tendrían que conocerse directamente los valores Gn lo cual es imposible, por lo que dicha expresión se estima por el valor fenotípico agregado del individuo, que es propiamente el índice de selección (I) el cual es una función de los valores fenotípicos para un cierto número de caracteres.
Al usar el concepto de funciones discriminantes Smith (1936), estableció que el valor genético de una planta puede expresarse como una función lineal de los valores genotípicos de varios caracteres. La suma de dichos valores genotípicos ponderados por (ai), la relación del avance unitario de un caracter expresado en términos del avance de los otros, produce el valor genético o valor genotípico agregado de una planta. Como los valores genotípicos (gi) no pueden evaluarse directamente, se usan los valores fenotípicos de cada caracter ponderados por sus coeficientes de regresión parcial (bi) bajo la siguiente expresión:
I=b1X1 + b2X2 + .........+bnXn
Donde Xn es el valor fenotípico para cada carácter y bn los coeficientes que maximizan el avance esperado del valor genético agregado (H), por medio de selección. De esta manera, la selección de los valores de H se realiza en forma indirecta por medios de los valores de I.
Una relación que maximiza la ganancia genética, reportada por Harris (1964); es la siguiente
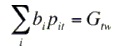
T= 1,2,. .. . .,n
En el presente trabajo sólo se consideró al rendimiento de forraje verde como parte del valor genético agregado, con una ponderación económica de uno y a las demás variables se les asignó un valor económico de cero (X1=0, X2 = 0, X3 = 1, X4 = 0). De esta manera, el valor genético agregado quedó reducido a:
H= Gr
Donde Gr es el valor genotípico promedio para el rendimiento de la cruza. Así la expresión que maximiza la ganancia genética esperada se puede expresar como:
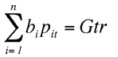
Las ecuaciones simultáneas para obtener los coeficientes bi, quedan expresadas de la siguiente forma:
b1 P11 + b2P21 + . . . + bnPn1 = G1r
b1P12 + b2P22 + . . . + bnPn2 = G2r
. . . .
. . . .
b1 P1n + b2 P2n + . . . + bn Pnn = Gnr
Donde Pij es la covarianza fenotípica entre los caracteres i y j, y Gij la covarianza genotípica entre el carácter i y el rendimiento, en el caso de que ambos subíndices correspondan al mismo carácter, Pij representa la varianza fenotípica y Gir la varianza genética.
En el lado izquierdo se tienen varianzas y covarianzas fenotípicas y en el derecho varianzas y covarianzas genotípicas. Las relaciones anteriores se pueden representar en forma de matriz de la siguiente forma:
Pb=G
Donde:
P = matriz de varianza y covarianza fenotípica.
b = vector de coeficientes de ponderación.
G = vector de varia nzas y covaria nzas genotípicas.
La solución para despejar los coeficientes bn es la siguiente:
b = P-1 G
donde:
P-1 = es la matriz inversa de P.
Ya calculados los coeficientes bn se construye el índice de selección para cada individuo.
Por definición, la respuesta a la selección de un determinado grupo de índices escogidos es la diferencia entre su media y la de todos los índices y se expresa por la siguiente ecuación, de acuerdo con Robinson et al. (1951):
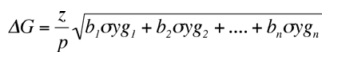
ΔG = Ganancia genιtica.
z/p = Diferencial de selección estandarizado. (Con valor de 1.4)
b1,2,n = coeficiente de ponderación.
σygn = covarianza genιtica del rendimiento (y) con el carácter n.
La relación que permite conocer la eficiencia relativa de un índice dado, se expresa por:
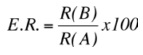
R(A) = respuesta a la selección al considerar únicamente al rendimiento como criterio de selección.
R(B) = respuesta a la selección con el uso del índice de selección para los caracteres considerados como componentes del carácter primario.
Para facilitar los cálculos de los coeficientes de los índices de selección, la ganancia genética por ciclo, y la eficiencia relativa del índice se utilizó el programa estadístico de Reyes (2003).
Montes et al. (2008), y Vergara e Iriarte (2002), mencionan que el índice de selección se puede estimar de acuerdo con los objetivos de cada sistema de producción. Para ello se debe considerar que cada índice es particular para cada sistema, ya que este va a depender de los parámetros genéticos (heredabilidad y correlaciones), sistema de producción, comercialización y la importancia económica relativa que se le de a cada carácter.
Resultados y discusión
Los coeficientes involucrados en la construcción de los índices para todas las combinaciones posibles de caracteres se presentan en el Cuadro 2, así como los factores por los cuales es necesario multiplicar el diferencial de selección estandarizado k para obtene el avance genético, y las eficiencias relativas de cada índice, en éste se muestra que los valores económicos del índice fueron de: 0, 0, 1, 0.
En cuanto a la asignación de los valores económicos (0, 0, 1,0) Robinson (1951), al trabajar con maíz, definieron el rendimiento como el valor genotípico agregado; al puntualizar que un carácter con un (ai) igual a cero, puede ser una parte muy valiosa del índice, si presenta variabilidad genética y correlaciones genéticas altas con el valor genotípico agregado. Se utilizó una presión de selección de 20%, que dio un diferencial de selección estandarizado de 1,4. Las varianzas y covarianzas genotípicas y fenotípicas usadas en la construcción del índice se presentan en los Cuadros 3 y 4.
En la columna de la izquierda, cada símbolo I se define como un subíndice, cuyos valores corresponden con los subíndices de las variables involucradas en cada caso. Los valores anotados en cada columna Xi, son los coeficientes de dicha variable para cada índice de selección. Se observa que se obtuvieron coeficientes que fluctuaron entre -21,94 a -7,75 para altura de planta; 34,33 a 49,31 para altura de mazorca; -0,27 a 0,15 para rendimiento de forraje verde y para rendimiento de forraje seco -0,22 a 0,29. En cuanto a los resultados obtenidos en la construcción de índices de selección se encontró que, en general, la eficiencia de los mismos se ve incrementada con la adición de caracteres.
Los índices con mayor eficiencia relativa fueron: I(2) con un valor de 5,86%; I(1, 2, 3) con un valor de 1,57% y el I(1, 2, 3, 4) con un valor de 1,53%. La eficiencia relativa de los índices, puede ser incrementada con el uso de componentes de rendimiento, cuya relación casual con el mismo tenga sólidas bases fisiológicas (Reyes 1985). Lo anterior concuerda con lo reportado por Tenkovano et al. (2002), quien menciona que los componentes de rendimiento pueden servir como criterios de selección indirecta del rendimiento.
En este trabajo se demostró que la eficiencia relativa de los índices simples fue similar a la eficiencia de la selección directa para rendimiento I (3). La combinación de los caracteres tendió a mejorar la eficiencia de los índices, al respecto, se recomienda usar todas las combinaciones posible de todas las variables estudiadas (Milligan et al. 2003).
Se encontró que la selección basada solo en rendimiento de forraje verde I(3) presentó una eficiencia relativa de 0,34% y que los índices que involucran a dos caracteres dieron eficiencias similares a este índice (I(1, 2)=1,52%), I(1, 3)=0,47%, I(1, 4)=0,43% ).
Los resultados indican que por lo general los índices que involucran a tres caracteres dieron las eficiencias relativas más altas I(1, 2, 3)=1,57%, I(1, 2, 4)=1,53% , I(2, 3, 4)=1,34%.
En cuanto al I(1, 2, 3, 4) basado en la combinación de los cuatro índices tuvo una eficiencia relativa de 1,53%.
Los índices recomendados, en ciertos casos, no son los más eficientes, esto se debe a que es necesario aplicar la lógica y el sentido común; ya que por ejemplo en el I(2) con eficiencia de 5,86%, es muy improbable que se alcanzara este valor en la realidad, lo que indica este valor es que la variable AM es importante en la población seleccionada, ya que estuvo correlacionada fuertemente con el rendimiento (Mihaljevic et al. 2005). En general, la eficiencia se incrementó a medida que aumentó el número de caracteres en el índice, habiéndose obtenido la máxima eficiencia con los I (1, 2, 3) con un valor de 1,57% y el I (1, 2, 3, 4) con un valor de 1,53% de eficiencia relativa.
Existe una estrecha correspondencia entre la eficiencia relativa del índice y el valor de la correlación genotípica del caracter respectivo, con el rendimiento (Cuadro 3). Así, los caracteres correlacionados con el rendimiento fueron más eficientes (I (2)=5,86% y I (4)= 0,49%), que los no correlacionados (I (1)= 0,22), lo cual indica que la selección basada en caracteres no correlacionados con rendimiento es ineficaz. La eficiencia relativa (5,86%) del índice I (2) mayor que la selección basada solo en rendimiento de forraje verde (I (3)=0,34%), hace suponer que existe una alta proporción de genes comunes a los caracteres altura de mazorca y rendimiento, por lo que altura de mazorca(X2) puede ser un buen indicador de la variabilidad genética potencial del rendimiento de forraje verde(X3).
El hecho de que los índices basados en la combinación de dos caracteres dieron eficiencias similares a la selección directa (0,34%) esta situación puede explicarse bajo el supuesto de que ciertos caracteres no involucrados en el índice, estuvieron positivamente correlacionados con uno o con los dos caracteres del índice y negativamente correlacionados con el rendimiento de forraje verde, cuyo efecto detrimental podría ser compensado incluyéndose en el índice otros caracteres positivamente correlacionados con el rendimiento de forraje verde (Tenkovano et al. (2002).
Los índices basados en la combinación de tres caracteres, en general fueron más eficientes que los índices de dos caracteres. Este resultado podría tener su explicación, en el sentido de que al aumentar en el índice, el número de caracteres correlacionados con el carácter por mejorar, se obtendría mayor avance genético; al respecto, se menciona que el índice de selección fue eficiente para obtener ganancia genética para rendimiento de grano y que la correlación es una medida de la comunidad de genes que gobiernan en común el carácter objeto de la selección y los caracteres del índice (Daros et al. 2004).
Si algunos genes del carácter de interés son comunes a dos o más del índice, pueden originarse correlaciones entre éstos, pudiéndose reflejar en la obtención de valores bajos de avance genético. Sobre este en particular, se ha señalado que la intercorrelación de caracteres influye en los valores de los coeficientes de ponderación de los caracteres del índice (Hazel 1943). De aquí se desprende que los índices más eficientes son aquellos que incluyen los no correlacionados, pero correlacionados con el carácter por mejorar.
Los índices (2, 3, 4), (1, 2, 3) y (1, 2, 4) dentro del grupo de índices de tres caracteres, fueron los más eficientes debido a que altura de mazorca (X1) y altura de planta (X2) tuvieron una correlación genética positiva altamente significativa con el rendimiento de forraje verde (X3); adicionalmente, el RFS (X4), presentó la mayor covarianza genética con rendimiento de forraje verde (Cuadro 4); sin embargo, sus eficiencias no fueron de las más altas.
En cuanto al I (1, 2, 3, 4) basado en la combinación de los cuatro caracteres, se esperaba obtener la máxima eficiencia relativa, puesto que se involucraron todos los evaluados; sin embargo, fue superado por el I (1, 2, 3), lo cual indica que existió un número óptimo de caracteres a combinar, independientemente de los seleccionados o correlacionados, este concepto puede tener implicaciones lógicas en el futuro de la formación de los índices de selección.
El índice recomendado es I (1, 2, 3) con una eficiencia de 1,57%, por lo cual se infiere que con esta combinación de caracteres se espera obtener el más alto valor genético del carácter rendimiento de forraje verde.
Los índices más eficientes en el presente trabajo fueron aquellos que consideraron el rendimiento, lo cual concuerda con Robinson (1951); por otra parte, se menciona que una característica que siempre debe estar incluida en la construcción de índices de selección es el rendimiento (Mihaljevic et al. 2005); sin embargo, en otros estudios se ha observado que los índices más eficientes en ocasiones no incluyen al rendimiento (Oyervides 1979).
Los resultados indicaron que cuando la selección se realiza en base a un criterio multivariado, se obtiene una ganancia predicha mayor cuando se incluye el rendimiento, como parte de ese criterio de selección; sin embargo, no ocurre así cuando en el índice se considera otro carácter distinto al rendimiento. Esto concuerda con Robinson et al. (1951), quienes observaron una ganancia predicha mayor para los índices de selección multivaria da que para la de los caracteres per se. Por otra parte la ganancia predicha tiene un incremento al incluir en la construcción del índice otros caracteres considerados componentes de rendimiento.
Al respecto, los índices de selección ayudan a seleccionar los mejores individuos para el próximo ciclo de selección en base a los valores fenotípicos observados (Ceron et al. 2006). Rabiei et al. (2004), y Gethi y Smith (2004), siendo además, un criterio de selección eficaz para el mejoramiento de plantas. Se ha reportado que los índices de selección asistida por marcadores, en generaciones sucesivas de cruzamientos permitirían lograr la obtención de un genotipo ideal (Peleman y Van der Voort 2003).
Las correlaciones genotípicas entre los caracteres bajo estudio, presentan una correlación positiva altamente significativa entre altura de mazorca y rendimiento de forraje verde (r= 0,87) (Cuadro 3), así como con rendimiento de forraje seco (r= 0,58), para el caso de altura de planta con rendimiento de forraje verde (r= 0,58) y altura de planta y rendimiento de forraje seco (r= 0,75) como era de esperarse mostraron una correlación altamente significativa en sentido positivo; se observó que entre rendimiento de forraje verde y rendimiento de forraje seco existe una correlación altamente significativa en sentido positivo (r= 0,99).
El rendimiento estuvo correlacionado significativamente con todas las variables estudia das (Cuadro 3), lo cual es deseable ya que AM y AP caracteres de fácil determinación y al resultar altamente correlacionado con RFV, podría usarse con gran ventaja en la selección de este carácter, con este resultado cabe la posibilidad de aumentar el RFV mediante la selección de plantas con mayor altura de planta y mazorca y más si se tiene en cuenta que estos caracteres presentan alta heredabilidad, el progreso que se puede esperar por el uso de este carácter en generaciones tempranas es importante.
La correlación genética entre dos caracteres juega un papel importante en la respuesta correlacionada de la selección y asegura un máximo mejoramiento de los índices de selección al combinar diferentes caracteres (Mohammadi et al. 2003, Badu 2007).
En el caso específico de la selección por índice, a pesar de que este método de selección demuestra propiciar un mayor progreso genético esperado por generación, su aplicación debe ser cautelosa cuando incluya dentro de su construcción una baja correlación genética con un alto estimativo de error estándar, lo cual impide configurar de manera clara la relación existente entre los rasgos en estudio (Restrepo et al 2008).
En cuanto a los genotipos seleccionados en base al índice de selección con la mayor eficiencia relativa, se encontró que los mejores genotipos fueron las cruzas CML159 X CM144, CML147 X CML159, CML147 x CML150, CLQ6203 X CML173, CML148 X CML150 y CML144 X CML150, con un rendimiento promedio por hectárea de 13,86, 4,93, 4,80, 4,80, 4,51, 4,50 y 4,34 toneladas respectivamente, los cuales resultaron de sustituir el valor de Xn por los valores fenotípicos de cada carácter ponderados por sus coeficientes de regresión parcial (bi):
I=b1X1 + b2X2 + .........+bnXn
I=-20,8813 X1 +49,2625X2 -0,1173X3
Donde Xn es el valor fenotípico para cada carácter y bn los coeficientes que maximizan el avance esperado del valor genético agregado por medio de selección.
En conclusión, puede afirmarse que cuando se selecciona un carácter como medio para mejorar otro, deberá considerarse, el grado de asociación del carácter por mejorar.
En el Cuadro 4 y 5 se muestran las matrices de varianzas y covarianza tanto genotípicas como fenotípicas utilizadas para la construcción de los índices de selección.
En el Cuadro 6 se encuentran los genotipos seleccionados en base al índice de selección recomendado con la mayor eficiencia relativa, el cual involucra las variables altura de planta, altura de mazorca y rendimiento de forraje verde.
La alta correlación genotípica positiva entre RFV, AP y AM indica que AP y AM pueden servir como indicadores de la potencialidad genética del rendimiento de forraje verde, es decir que fueron las variables más importantes en la construcción de los índices de selección.
La eficiencia de los índices de selección para rendimiento de forraje verde se incrementó, a medida que aumentó en el índice, el número de caracteres correlacionados con él por lo tanto se acepta la hipótesis planteada.
La correlación entre caracteres per se, causa decrementos en la eficiencia del índice, y la inclusión de caracteres no correlacionados con el carácter objeto de la selección, abate los coeficientes de ponderación del índice de selección. La respuesta teórica a la selección, usando índices, fue mayor que la basada solamente en rendimiento de forraje verde.
Los índices de selección más eficientes, fueron aquellos que tomaron en cuenta el rendimiento de forraje verde y las variables con las que tuvo la más alta correlación genética. El índice seleccionado fue el que incluyó las variables altura de planta, altura de mazorca y rendimiento de forraje verde (I=-20,88 X1+49,26X2-0,11X3) con una eficiencia relativa de 1,57% por ciclo y se obtuvo por ciclo una ganancia genética por hectárea de 5,54 t.
Literatura citada
Bujak, H; Kaczmarek, J; Jedynski, S; Dmochowska-Huba K; Adamczyk J; Kurczych, Z. 2007. Index Selection in Maize Breeding. Plant Genetic and Breeding 24 (94):58-65. [ Links ]
Badu, AB. 2007. Genetic variances and correlations in an early tropical white maize population after three cycles of recurrent selection for striga resistance. Maydica 52(2):205-217. [ Links ]
Cerón, RJJ; Crossa J; Sahagún-Castellanos. 2005. Un índice de selección basado en componentes principales. Agrociencia 39(6):667-677. [ Links ]
Cerón, RJJ; Crossa J; Sahagún-Castellanos J; Castillo- González F; Santacruz- Varela, A. 2006. A Selection index method based on Eigennalysis. Crop Sci. 46:1711-1721. [ Links ]
Daros, M; Fei-Xeira do Amaral A; Gonzaga-Pereira M; Santona-Santos F. 2004. Recurrente selection in inbred popcorn families. Sci. Agric. 61(6):609-614. [ Links ]
Gethi, JG; Smith, ME. 2004. Genetic responses of single crosse of maize to striga hermonthica (Del.), and striga asiatica (L.). Crop Sci. 44:2068-2077. [ Links ]
Griffing, B. 1956. Concept of general and specific combining ability in relation to diallel crossing systems. Australian J. Biol. Sci. 9:463-493. [ Links ]
Hazel, LN. 1943. The genetic basis for constructing selection indexes. Genetics 28(3): 476-490. [ Links ]
Harris, DL. 1964. Expected and predicted progress from index selection involving estimates of population parameters. Biometrics 29:46-72. [ Links ]
Mihaljevic, R; Schon, CC; Melchinger AE. 2005. Correlations and QTL correspondence between line per se and testcross performance for agronomics traits in four populations of European maize. Crop science 45(1):114-122. [ Links ]
Milligan, SB; Balzarini, M; White, WH. 2003. Broad-sense heritabilities, genetic correlations, and selection indices for sugarcane borer resistance and their relation to yield loss. Crop sci 43:1729-1735. [ Links ]
Mohammandi, SA; Prasanna, BM; Singh, NN. 2003. Sequential path model for determining interrelationships among grain yield and related characters in maize. Crop science 43:1690-1697. [ Links ]
Montes, VD; Vergara, GO; Prieto, ME. 2008. Determinación de un índice de selección para el peso al nacer y a destete en ganado bovino de la raza brahman. Revista MVZ Córdoba 13(2):1365-1368. [ Links ]
Peleman, JP; Van der Voort, JR. 2003. Breeding by design. Trends in Plant Sci. 7:330-334. [ Links ]
Peña, RA; González, CF; Núñez, HG; Jiménez, GC. 2004. Aptitud combinatoria de líneas de maíz para Alta producción y calidad forrajera. Rev. Fitotec. Mex. 27(Núm. Especial 1):1-6. [ Links ]
Oyervides, GM . 1979. Estimación de los parámetros genéticos, heterosis e índices de selección en variedades tropicales de maíz adaptadas a Nayarit. Tesis Maestría. Colegio de Postgraduados. Chapingo, México. 118 p. [ Links ]
Rabiei, R; Valizadeh, M; Ghareyazie, B; Moghaddam, H. 2004. Evaluation of selection indices for improving rice grain shape. Field Crops Research 89(2-3):359- 367. [ Links ]
Reyes,VMH. 1985. Índices de selección para rendimiento en girasol (Heliantus annus) L. Tesis de Maestría. UAAN. Saltillo, Coahuila, México. 47 p. [ Links ]
Reyes, VMH. 2003. MathGenome: a Mathematica application for basic genetics. Disponible en http://www.uaaan.mx/~mhreyes/mtgnm.htm. (software). [ Links ]
Robinson, H F; Comstock, R E; Harvery, PH. 1951. Genotypic and phenotypic correlation in corn and their implication in selection. Agron. J. 43:282-287. [ Links ]
Smith, HF. 1936. A discriminant function for plant selection. Biometrics. Ann. Eugen. 7(2):240-250. [ Links ]
Steel, RGD; Torrie, JH. 1992. Bioestadística. Principios y Procedimientos. Editoria l. Graf América. México. 622 p. [ Links ]
Tenkovano, A; Ortiz, R; Baiyer, KP. 2002. Phenotypic and genetic correlations in Musa populations in Nigeria. African Crop Sci. 10(2):121-132. [ Links ]
Vergara, O; Iriarte, C. 2002. Determinación de un índice de selección para el peso al nacer y al destete en ganado cebú. Rev. MVZ Córdoba 7(1):148-151. [ Links ]
Correspondencia a: Carlos Alejandro Tucuch-Cauich & Juan Manuel Pat-Fernández. Colegio de la Frontera Sur, Unidad-Campeche. Calle 10 x 61 núm. 264, Col. Centro, CP 24000 San Francisco de Campeche México. ctucuch@ecosur.mx, jpat@camp.ecosur.mx
Sergio Alfredo Rodríguez-Herrera & Manuel Humberto Reyes-Valdés. Instituto Mexicano del Maíz, Universidad Autónoma Agraria Antonio Narro, Buenavista Saltillo Coahuila México. srodriguez@uaaan.mx, mhreyes@uaaan.mx
Fulgencio Martín Tucuch-Cauich. Campo Experimental Edzná. Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias km 15.5, Carretera Campeche-Pocyaxum Mpio. Campeche Campeche C.P. 24250, A.P. 341. tucuch.martin@inifap.gob.mx
Hugo Salvador Córdova-Orellana. Centro Internacional de Mejoramiento de Maíz y Trigo. Km 45 carretera México-Veracruz.El Batán Texcoco, Edo. De México
Recibido: 8 setiembre, 2010. Aceptado: 23 de mayo, 2011.














