Introduction
The monitoring of training load has become essential for coaches and team staff due to it has shown strong relationships with changes in physical fitness performance (Jaspers et al., 2017), injury risk (Malone et al., 2018) as well as neuromuscular fatigue (Garrett et al., 2019). In addition, the quantification of training load is useful to monitor rehabilitation programs (Greig et al., 2019).
In addition, the distribution of training load is important to ensure sufficient after-game recovery, prevent pre-match fatigue (Akenhead et al., 2016; Akenhead y Nassis, 2016; Coutinho et al., 2015; Fessi et al., 2016; Jeong et al., 2011; Malone et al., 2015) and allow training prescription and planification. Training load could be classified into kinematic, neuromuscular, and physiological variables (Gómez-Carmona et al., 2020). Players' kinematic profile has been assessed several times (Jaspers et al., 2017) by evaluating distance covered, which has often been described based on different speed zones in different team sports such as futsal (De Oliveira Bueno et al., 2014), soccer (Malone et al., 2018), or basketball (Sampaio et al., 2014).
Due to each team dynamic and game characteristics are associated to their internal logic (Parlebas, 2002), each team sport differ in the thresholds for classifying the speed zones. However, into each team sports there is no agreement too. Different zones have been proposed in soccer such as: (A) male professional players of Portuguese First Division: zone 1 (0-6.9 km/h), zone 2 (7.0-9.9 km/h), zone 3 (10.0-12.9 km/h), zone 4 (13.0-15.9 km/h), zone 5 (16.0-17.9 km/h), and zone 6 (>18.0 km/h) (Aguiar et al., 2013); (B) collegiate male players: walking (0-6.9 km/h), jogging (7-13.9 km/h), running (14-19.9 km/h), and sprint (>20 km/h) (Clemente et al., 2017); or (C) recreational male players: seven groups where zone 1 (0-2 km/h), zone 2 (2-5 km/h), zone 3 (5-9 km/h), zone 4 (9-13 km/h), 13-16, 16-20, and > 20 km/h), and the bands were summarized in three groups as low-intensity movement (< 9 km/h), moderate-intensity running (9-13 km/h), and high-intensity running (> 13 km/h) (Randers et al., 2014).
Regarding indoor sports, specific speed zones were found in futsal following Naser, Ali & Macadam (2017) that divided high-speed intensities in high-intensity (>15 km/h) and sprinting (>25 km/h) in semiprofessional male players or following Makaje et al. (2012) that determined intervals in standing (0-0.9 km/h), walking (1.0-4.9 km/h), jogging (5-7.9 km/h), low-speed running (8-11.9 km/h), moderate-speed running (12-17.9 km/h), high-speed running (18-23.9 km/h), and sprinting (>24 km/h) in elite-level male players. In basketball, the most used speed zones distribution were stationary/walking (<6.0 km/h), jogging (6.0-12.0 km/h), running (12.1-18.0 km/h), high-intensity running (18.1-24.0 km/h), and sprinting (>24.1 km/h) (Pino-Ortega et al., 2019; Vázquez-Guerrero et al., 2019) during the evaluation of elite-level youth players. However, there are other classifications based on individual player capacities (maximum reached speed), such as those proposed by Reina-Román et al.(2019), divided into six zones: zone 1 (50-60%), zone 2 (60-70%), zone 3 (70-80%), zone 4 (80-90%), zone 5 (90-95%), and zone 6 (>95%) in amateur female basketball players.
The fact that each author differs in the classification of speed zones makes the comparison and general conclusions about distance covered at different speed zones in each team sports difficult. The design of a method for obtaining speed zones applicable in all sports modalities and adapted to the specific characteristics of each player/team will make it possible to compare the demands between studies (Rojas-Valverde et al., 2019; Rojas-Valverde et al., 2020). Therefore, the purposes of the present study were to propose a criterion for speed zone intervals in team sports in order to allow comparison and further general conclusions based on a consensus in speed zone definition and to analyze its practical application in basketball.
Methods
Participants
A total of 94 basketball players (age: 17.6±0.8 years; height: 1.91±0.08 m; body mass: 82.5±8.8 kg; BMI: 22.7±1.8 kg/m2) participated in the present study. They were active members of 8 clubs, participants in the U18 Basketball EuroLeague Tournament, Istanbul, Turkey 2016-17. The data were collected from 13 official matches for seven days, for a total of 925 data cases. All players met the following inclusion criteria: >8min of participation in each match period and played in all matches. In addition, the participants did not present any physical limitations or musculoskeletal injuries that could affect testing (Bastida-Castillo et al., 2019). The study was conducted according to the Declaration of Helsinki and was approved by the Bioethics Commission of the University of Murcia (ID: 2061/2018). Participants and teams were informed of the risk and provided informed written consent.
Instruments and Procedures
The data were recorded with an inertial measurement unit (IMU) called WIMU PRO™ (RealTrack Systems, Almeria, Spain). This equipment and its measurements are valid and reliable for high-intensity performance (Bastida Castillo et al., 2017). This IMU contains four 3D accelerometers, as well as other sensors (three 3D gyroscopes with 8000 degrees/second full-scale output range, a 3D magnetometer, a 10 Hz GPS, an 18 Hz UWB, etc.); this portable instrument detects and measures movement using a micro-electromechanical system (sampling frequency 10 to 1000 Hz). The full-scale output ranges of the four 3D accelerometers are ±16 g, ±16 g, ±32 g, and ±400 g. In order to obtain a clean signal, the accelerometer company introduced an optimum filter process related to the different sample frequencies (Gómez-Carmona et al., 2019).
Each device has eight gigabytes of internal memory, a USB port, and its own GHz microprocessor. The device has 4h battery life, weighs 70 g, and its dimension is 81x45x16 mm. The ultra-wideband system occupies a very large frequency band (>0.5 GHz) that is only allowed to transmit at very low power; besides, the signal emits little noise that can coexist with other technologies without influencing them (Bastida-Castillo et al., 2019).
System installation
The UWB reference system was composed of six antennae placed around the field. The inertial device was attached to each player before the game in the medial line between scapulae at T2-T4 level using an adjusted neoprene vest, following previous study protocols (Reche-Soto et al., 2019). The antennae were set up around the court, following Luteberget, Spencer, & Gilgien (2018), in optimal conditions. The antennae with UWB technology were fixed 5 m from the perimeter line in the corners (n = 4) and 7 m from the middle line of the field (n = 2) and from behind the goals (n = 2) (Figure 1), forming an octagon for better signal emission and reception. All of the antennae were positioned at the height of 3 m and held by a tripod (Bastida-Castillo et al., 2019). Once installed, they were switched on one by one, with the master antenna turned on last. From that moment, it was necessary to respect a 5-minute protocol in which the antennae calculate their positioning and the distance between them. Finally, unlike GPS sensors, UWB manufacturers provide a method that allows data time synchronization. In this case, the master antenna manages the time using a common clock that allows data recording simultaneously. Time position coordinates were calculated with an 18 Hz sampling rate (Bastida-Castillo et al., 2019). The accuracy and the reliability of UWB technology obtained satisfactory results for speed (bias= 0.09 km/h; ICC=0.979) and distance (bias= 0.57-5.89%; %TEM= 1.19; bias= 0.18 m) (Bastida Castillo et al., 2018).
Data processing
Many positioning algorithms can be classified into five main categories based on estimated measurements (Alarifi et al., 2016). Typically, with a time difference of arrival (TDOA), only one transmitter is necessary (i.e., antenna master); it requires multiple receivers to share the data and cooperate to determine the location of the transmitters. This cooperation needs significant bandwidth in comparison with other algorithms. TDOA, together with a time of arrival (TOA), offers higher accuracy than other algorithms because of the increased time resolution of the UWB signals. So, in this study, the TDOA algorithm was used to estimate positioning. S PROTM software (RealTrack Systems, Almeria, Spain) exports the data on the x and y position coordinates (Bastida-Castillo et al., 2019). The data were downloaded after the session.
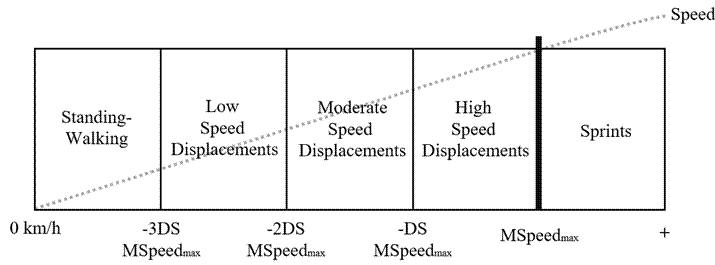
Speed zones classification
The distance covered at high intensity and sprint describes the player's performance in steam sports. So, this new proposal is based on maximal velocity and divides intensities into different basic locomotor values such as walking, jogging, and running at low, moderate, high, and sprint intensities. In order to perform the intensity intervals, the mean maximum speed (MSpeedmax) and standard deviation (DSSpeedmax) were achieved by each player during the competition. Intervals were defined from the following data (see Figure 1) as: (1) Speedstanding-walking-jogging = 0 km/h to mSpeedmax - 3xDS Speedmax; (2) Speedlow- displacement = MSpeedmax - 3xDS Speedmax to MSpeedmax - 2xDS Speedmax; (3) Speedmoderate-displacement = MSpeedmax - 2xDS Speedmax to MSpeedmax - DS Speedmax; (4) Speedhigh-displacement = MSpeedmax - DS Speedmax to MSpeedmax; and (5) Sprints = MSpeedmax or more.
Statistical Analysis
The normality of the data was verified with the Kolgomorov-Smirnov Exploratory Test. A one-way analysis of variance performed a quantitative inferential analysis of the data to verify the possible differences by periods in each variable, followed by Bonferroni post-hoc analysis if necessary. The effect size was calculated through omega partial squared and interpreted as <.01 insignificant, .01<.06 low, .06<0.14 moderate, >0.14 high (Cohen, 1988). Alpha was prior set at p <.05, and the Excel program was used for initial tabulation of data and SPSS (v22, IBM, Chicago, IL) for inferential and descriptive analyzes.
Results
After the analysis and consequently with previously cited authors, five speed categories were established for basketball following the methodology described above, as shown in Figure 2.
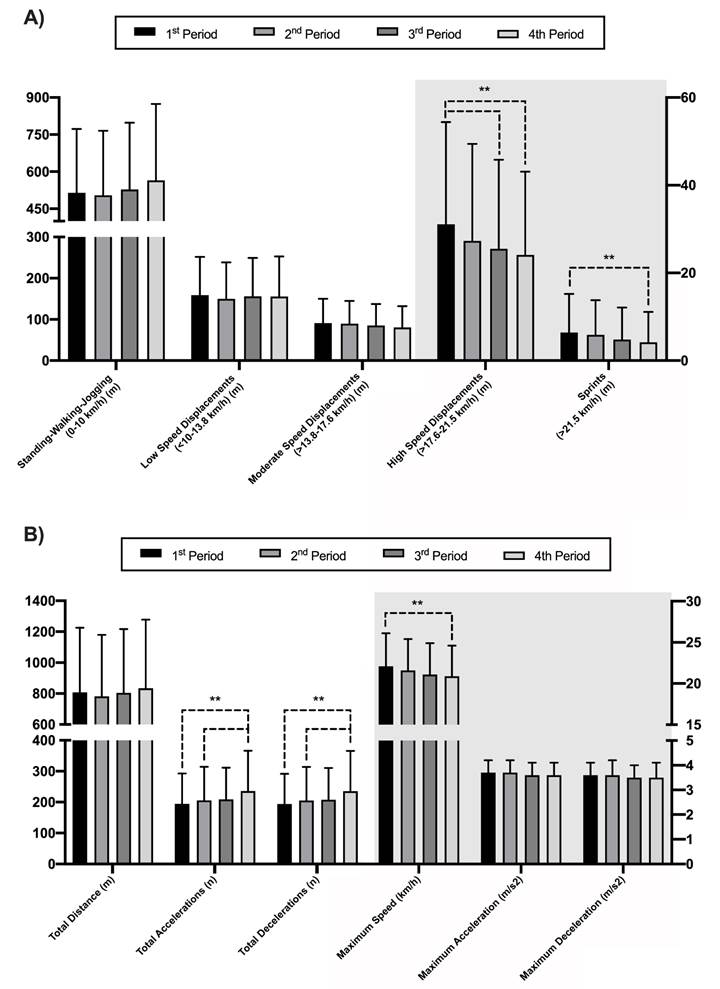
Figure 3A shows the comparative analysis of workload demands by periods in the proposed speed zones. Statistical differences were found in High-Speed Displacements (F= 4.67; p= .003; ω p 2 = .10 moderate) and Sprints (F= 3.81; p= .01; ω p 2 = .18 moderate). Specifically, the differences in High Speed displacements were found between periods 1st and 4th (p=.003) and 1st vs 3rd (p=.031), but not between 1st vs 2nd (p= .308), 2nd vs 3rd (p= 1.00), 2nd vs 4th (p= .593) or 3rd vs 4th (p= 1.00); and in Sprints between 1st and 4th (p= .015), but not between periods 1st vs 2nd (p= 1.00), 2nd vs 3rd (p= .857), 1st vs 3rd (p= .199), 2nd vs 4th (p= .103) or 3rd vs 4th (p= 1.00). Conversely, there were no significant differences between periods in Standing-Walking-Jogging (F= 2.10; p= .10), Low Speed Displacements (F= .38; p= .77) and Moderate Speed Displacements (F= 1.80; p= .15).
In addition, Figure 3B shows the comparative analysis of workload demands by periods in total distance, maximum speed, and changes of speed. Significant differences were found in maximum speed (F= 3.05; p= .03; ω p 2 = .05 low), total accelerations (F= 5.72; p< .001; ω p 2 = 0.12 moderate), and total decelerations (F=5.85; p< .001; ω p 2 = .13 moderate). Specifically, differences were found in maximum speed between the 1st and the 4th (p= 0.043); in total acceleration between 1st vs 4th (p< .01) and 2nd vs 4th (p= .02); and in total deceleration between 1st vs 4th (p< .01) and 2nd vs 4th (p= .018). There were no differences in maximum accelerations (F= 1.24; p= .29), maximum deceleration (F= .28; p= .84), and Total Distance (F= .61; p= .61).
Discussion
Currently, the velocity thresholds of sport displacements have been defined by the companies that develop sport technology in their own software (Cunniffe et al., 2009), adapted from previous studies (Jennings et al., 2012) or determined by authors’ criteria (Mohr et al., 2003). The main problems are no consensus on how to determine a velocity threshold, the comparison of activity profiles across and within sports, and the lack of speed zones individualization considering the sports modality and the players’ level or sex (Sweeting et al., 2017). Given the challenges of assigning a specific velocity zone criterion for different populations, the purpose of the present study is to propose a speed zone interval criterion to use in team sports in order to allow a comparison and further general conclusions based on a consensus in speed zone definition, as well as to apply this method in basketball.
The two aspects that researchers have to consider in classifying the time-motion analysis related to speed are the number of speed zones and the speed threshold of each of them. The most extended time-motion analysis classification is composed of five groups (standing, walking, jogging, running, and sprinting) and was defined by movement characteristics evaluated by single observers (Bangsbo et al., 1991). From this classification, different studies proposed (a) speed two-speed zones with different thresholds in Australian football (Aughey, 2010), hockey (Jennings et al., 2012) and rugby league (Johnston et al., 2013); (b) three-speed zones (Clarke et al., 2015); (c) five-speed zones (Carling et al., 2012) or (d) six-speed zones in rugby (Suarez-Arrones et al., 2012), hockey (Macutkiewicz & Sunderland, 2011) or soccer (Gómez-Carmona et al., 2018). The difference between five- and six-speed zones is due to low-intensity displacements (standing and walking) being merged in one zone following two-speed zones classifications. Therefore, the proposed classification used five zones because the displacements in standing and walking zone are not important to sports performance in different team and individual sports like soccer (Oliva-Lozano et al., 2020), badminton (Rojas-Valverde, Gómez-Carmona, et al., 2020), or basketball (Pino-Ortega et al., 2020; Svilar et al., 2018).
In this sense, differences were only found in high-speed displacements, sprinting displacements, and maximum speed reached during the tournament. Physical performance related to the capacity to accelerate and sprint is important in sports performance. Numerous studies conducted on team sports have found a relationship between higher covered distance and higher time spent at high-intensity displacements and success in team sports such as soccer (Bradley et al., 2013; Miñano-Espin et al., 2017; Oliva-Lozano et al., 2021; Reche-Soto et al., 2019) or basketball.
Concerning the speed thresholds, no consensus in sports science literature was achieved. Generic velocity thresholds are universally administered in external load monitoring in sport contexts. But, the application of absolute versus individualized thresholds has been discussed in the literature (Hunter et al., 2015). In this sense, the current tendency is to individualize speed thresholds related to players’ and competition level and the sex of participants.
For this purpose, different methods have been proposed. Bradley & Vescovi (2015) recommended a speed threshold based upon fitness data reported in the literature with data collected in competition and training. Another alternative is the exploration of velocity zones through data-mining techniques. The first approach was achieved by Dwyer and Gabbett (2012) using GMMs. This method assumes that the data points are generated from a user-defined number of Gaussian distributions with unknown parameters. The problem is that no consider the sequential pattern of consecutive velocity data points and a limited number of observations typically associated with sprinting incorrectly assumes a Gaussian distribution, limiting their applications (Park et al., 2019).
Following data-mining techniques, Sweeting et al. (2017) applicated the k-means clustering for categorizing velocity. This technique operates iteratively to assign each observation to one of the k-specified clusters. Although, this method is also limited by the discreet way each velocity observation is treated. With this method, the velocity zones at high intensity are underestimated due to the low number of actions and displacements at high-velocities in competitive sports (Bradley et al., 2010; Carling et al., 2012; Meylan et al., 2017). Finally, the last proposal of data-mining techniques was the Spectral clustering algorithm, which generalizes to provide any number of partitions and is designed for discrete or categorical data. In this sense, Park et al. (2019) said: ''Spectral clustering was considered more appropriate for velocity data considering that the structure of the individual clusters (zones) is not suitably described by the center and dispersion of the complete data-set'' (p.6).
Finally, the disadvantages of all methods described are the difficult application to the sport context reality, the high level of statistical packages software management, and the large amount of data to determine these thresholds. Therefore, to solve the different drawbacks mentioned, a new method to calculate the speed threshold has been proposed, considering the underestimation of speed thresholds in the high-intensity actions (running and sprinting) and facilitating the team staff's calculation. For this reason, the maximum speed reached in the competition was utilized to calculate. This process makes the actualization of these values along the season and the calculation of the speed thresholds easier than other methods proposed in scientific literature.
However, team staff must treat speed zones with extreme caution since many contextual variables could influence these zones, such as the age, the category, the level of the competition, the experience or level of expertise, the playing style of your team and the opposing team, the playing position, sex, and even the performance of the players (individual and/or collective). (Mujika et al., 2018). Future research not only needs to consider contextual variables in speed zone threshold; other variables that influence the workload of the training sessions and official matches should be integrated, such as the degree of opposition, the density of the task, the number of players, the competitive load, the space, the tactical load, since we should not fall into a one-dimensional analysis, a bias that does not allow us to have a holistic view of the subject-object of study (Halouani et al., 2014; Impellizzeri et al., 2019).
Limitations
While the results of this study have provided a new proposal of speed zone interval criterion to use in team sports in order to allow comparison and further general conclusions based on a consensus in a speed zone, some limitations to the study must be acknowledged. One of the limitations in this research concerns the sample studied (94 youth basketball players in a 3-days congested fixture tournament), although it has been shown to be effective in detecting low and high intensity speed thresholds. In this sense, the application of this method to fix speed thresholds should be addressed in the future with other sports and competition levels to determine its accuracy. Despite this fact, the method proposed has considered the analysis of the previous values obtained in team sports (Barros et al., 2007; Datson et al., 2017; Di Salvo et al., 2007; Hunter et al., 2015; Park et al., 2019; Rampinini et al., 2007), with particular emphasis in maximum speed as a base value so as not to underestimate the load at a high intensity (Casamichana et al., 2018).
Conclusion/practical applications
Firstly, the present study adds a new method to analyze the distance covered in different speed zones through inertial devices in basketball. A categorization based on the maximum speed and their respective standard deviations is a useful method in order to have a more individualized criterion to be applied to a specific player, team, or sport. The present method avoids the bias of comparing players or teams in different conditions and different game dynamics and could be used in different sports such as basketball. For this reason, this method could be considered an alternative to individualize zones not only related to speed in the distance covered, other variables such as accelerations, decelerations, or impacts, among others, could be classified following it.
The use of distance covered at different intensities classified as speed zones is very relevant in sports performance. This variable indicates how the player displacements are performed during the game, at volume (total meters) and intensity (meters per zone). The distribution of meters in each speed zone should be considered to design training sessions, plan workload during microcycles and macrocycles, and control the acute and chronic fatigue of the players throughout the season to improve sports performance and reduce the injury risk. Therefore, individualizing these speed zones per player and team is necessary to achieve the desired effect with the planned stimuli.
Funding: The authors Carlos D. Gómez Carmona was supported by a grant from the Spanish Ministry of Education, Culture, and Sport (FPU17/00407). This research has not received specific financial support.
Conflict of Interest Disclosure: The authors declare that the research was conducted without any commercial or financial relationships that could be construed as a potential conflict of interest. This manuscript is original and not previously published, nor is it being considered elsewhere until a decision is made as to its acceptability by the journal.