1. Introducción
Los términos modelización matemática, modelo matemático, modelación matemática son utilizados en la literatura y en investigaciones en educación matemática, y su significado varía de acuerdo con el contexto, su relación con el sentido de realidad o bien, con la forma en la cual se utiliza. Diferentes investigaciones a nivel internacional se han enfocado particularmente en las concepciones sobre modelización matemática y su relación con sus prácticas de enseñanza. En este sentido, se plantea la diferencia entre modelización y modelación matemática (Villa-Ochoa, 2007), así como las diferencias entre la modelización matemática y la resolución de problemas, a partir de las características que cada concepto incluye o enfatiza.
Gould (2013), a partir de la implementación de los Estándares Estatales Básicos para Matemáticas, en el 2010 en los Estados Unidos de Norteamérica, estableció un estudio para determinar las concepciones y los conceptos erróneos del profesorado de secundaria sobre los modelos matemáticos y el modelado que permitiera el desarrollo de programas de formación y desarrollo profesional docente. El estudio se llevó a cabo bajo un enfoque mixto y se analizaron, particularmente, conceptos básicos de modelos matemáticos, modelado matemático y modelado matemático en educación. Los resultados del estudio arrojaron que el profesorado de matemática de secundaria en los Estados Unidos tenía varios conceptos erróneos sobre modelos y modelización, específicamente, respecto a aspectos del proceso de modelización matemática, sobre todo al requisito indispensable de efectuar elecciones y suposiciones para su resolución, así como el origen o proveniencia de los problemas a abordar, los cuales deben ser de escenarios del mundo real.
Similarmente, Correa et al. (2015) establecieron un estudio que indaga las concepciones sobre la modelación matemática de dos formadores de docentes y su relación con los objetivos, los tipos de problemas y las dinámicas de clase que ellos llevan a cabo. Dentro de los principales hallazgos dan cuenta de la modelación matemática como un proceso de construcción de un modelo a partir de un enunciado que la mayoría de las veces requiere un cambio de representación matemática atendiendo principalmente al propósito de reforzar los conceptos propios de la disciplina.
Frejd y Bergsten (2018), en su investigación, presentan un análisis temático de las concepciones de nueve profesionales en modelización, particularmente sobre la noción de modelado matemático que representa el conocimiento académico. Los resultados fueron organizados a partir de cuatro aspectos: descripción, comprensión, abstracción y negociación como características clave de los modelos matemáticos. La investigación finaliza con una discusión sobre los posibles beneficios para la educación matemática, desde la perspectiva de los diseños curriculares o las prácticas docentes.
Por su parte, Guerrero-Ortiz y Reyes-Rodríguez (2021) reportan los resultados obtenidos de una investigación cualitativa, cuyo propósito central fue caracterizar las concepciones de docentes en formación respecto a la modelación en la enseñanza de las matemáticas. Lo anterior, a partir del significado que le otorgan al término modelación, las concepciones sobre el papel de la modelación en el aula y las características de las tareas de modelación. Al respecto, evidenciaron diferentes concepciones dependientes de su etapa de formación profesional, lo cual propone aportes interesantes al grupo de formadores de formadores, de manera que se potencien actividades para el desarrollo de habilidades de modelación.
Alineado a los estudios descritos anteriormente, el propósito de esta investigación radica en determinar las concepciones, el significado en su uso y las perspectivas de la modelización matemática como estrategia u objeto de enseñanza a partir de una entrevista aplicada a personas docentes formadoras en Educación Matemática. Esto por cuanto se considera importante caracterizar esas concepciones para emprender acciones en términos curriculares o de capacitación y formación que potencien un mejor abordaje de la modelización matemática en el plan de formación del futuro profesorado en matemática.
Al respecto, Frejd y Bergsten (2018) indican que si se tiene conocimiento de la concepción del personal docente sobre la modelización matemática se pueden generar acciones en relación con el diseño de planes de estudio que incorporen de forma explícita el modelado, así como orientar procesos de capacitación o formación que conlleven implicaciones directas sobre las prácticas docente.
2. Referente Teórico
La modelización matemática se relaciona con una realidad física o conceptual compleja para la cual se plantea un modelo que la representa y que describe aquellos aspectos sustanciales y relaciones funcionales. Para Ríos (1995), la modelización matemática es un proceso que contribuye a realizar una aproximación a problemas del mundo real mediante las matemáticas. En ese sentido, sostiene que la modelización matemática “debe ser una fase obligada de la enseñanza de las matemáticas” (p. 18).
Para Bassanezi y Biembengut (1997) la mayoría de los autores y las autoras, cuando se refieren a la modelización matemática, lo hacen como el proceso que utiliza conceptos y técnicas, esencialmente matemáticas, para el análisis de situaciones reales. Por su parte, Castro y Castro (1997) afirman que "la modelización matemática es, fundamentalmente, una forma de resolución de problemas de la vida real, pero no es una forma de resolución cualquiera, sino que conlleva la consideración del problema como un todo" (p. 110). En ese sentido, Castro y Castro (1997) refieren cinco pasos, que comparten otras personas investigadoras, para el proceso de modelización matemática: identificar un problema real, brindarle distintas representaciones matemáticas, uso de teorías o herramientas matemáticas para resolver la situación dada, interpretación de la solución y refinamiento de esta.
A partir de estas concepciones se pueden visibilizar rasgos invariantes que, fundamentalmente, asocian la modelización con la interacción entre el mundo real y el mundo matemático.
Según Blomhøj y Højgaard (2003), todo proceso de modelización conlleva un modelo matemático. Es decir, la modelización matemática conlleva un proceso de manera implícita o explícita para establecer una relación entre alguna idea matemática y una situación real. En otras palabras, con el fin de crear y usar un modelo matemático, es necesario, en principio, recorrer todo el camino de un proceso de modelización.
De acuerdo con Rico (2007), el proceso de hacer matemáticas, que conocemos como modelización, implica, en primer lugar, traducir los problemas desde el mundo real al matemático. Este primer proceso se conoce como modelización horizontal, el cual se sustenta en actividades como identificar las matemáticas atinentes al problema; utilizar diversos modos de representación para el problema; comprender la relación entre los lenguajes natural, simbólico y formal; la búsqueda de patrones o relaciones; el reconocimiento de similitudes con problemas análogos; la traducción de la situación dada a un modelo matemático y el uso de herramientas y recursos pertinentes.
Una vez traducido el problema a una expresión matemática, el proceso puede continuar. La persona que modela puede plantear, a continuación, cuestiones en las que utilice conceptos y destrezas matemáticas. Esta parte del proceso se denomina modelización vertical, la cual incluye el uso de diferentes representaciones, de lenguaje simbólico, formal y técnico, el ajuste al modelo o modelos matemáticos, la integración de modelos y la argumentación y la generalización.
Al respecto, Freudenthal (1991) resume estos dos procesos de matematización indicando que la horizontal implica una traducción del mundo o realidad cotidiana al mundo de los símbolos, por cuanto la vertical es un movimiento interno dentro del mundo de los símbolos.
Finalmente, Ramos-Rodríguez et al. (2014) definen el proceso de modelización como un proceso que conlleva cuatro fases principales, a saber: 1. La identificación del modelo real, a partir de situaciones extraídas de la realidad y susceptibles de ser analizadas a partir de modelos matemáticos. En esta fase es sustancial el proceso de abstracción y simplificación, así como la comprensión de la situación problema planteada. 2. La construcción del modelo matemático. En esta fase se establecen los datos, conceptos, relaciones, condiciones y premisas relevantes para ser traducidas al lenguaje matemático. 3. Elección de los contenidos y métodos matemáticos apropiados para modelar la situación en análisis. 4. Interpretación y validación de los resultados obtenidos, esto en comparación o contraste con la situación real planteada.
Con lo planteado anteriormente, se puede establecer con claridad la diferencia entre modelización matemática y resolución de problemas, esto, por cuanto la resolución de problemas se enfoca en resolver preguntas matemáticas específicas, mientras que la modelización matemática implica la creación de modelos matemáticos para entender y resolver problemas del mundo real. La resolución de problemas, además, se enfoca en la solución de situaciones específicas de contextos matemáticos o extra-matemáticos que pueden ser abordados con métodos, técnicas y algoritmos matemáticos. Estos problemas suelen ser bien definidos y tienen una solución única o un conjunto finito de soluciones.
Los problemas, a menudo, se presentan en un contexto cerrado y se espera que el estudiantado aplique fórmulas y procedimientos matemáticos conocidos para llegar a una solución (Rodríguez y Bareiro, 2018).
Tal y como fue establecido con anterioridad, además del término modelización matemática, en la literatura internacional se ha utilizado modelación matemática. Este concepto, según lo establecen Bassanezi y Biembengut (1997), se constituye en el método de enseñanza-aprendizaje que utiliza el proceso de modelización.
Según Blomhøj (2004), la modelación matemática “puede ser vista como una práctica de enseñanza que coloca la relación entre el mundo real y la matemática en el centro de la enseñanza y el aprendizaje, y esto es relevante para cualquier nivel de enseñanza” (p. 1). Esta comprensión guarda coherencia con la idea de modelo que posibilita la relación señalada, pero, además, deja ver que lo que llama el “mundo real” es lo que nombra como “situación extramatemática”.
Porras et al (2023), a partir de distintos autores (Huincahue, 2017; Blum y Borromeo-Ferri, 2009; Biembengut y Hein, 2004; Mora, 2015; Bossio et al 2015; Bossio et al, 2018; Villa-Ochoa, 2013), han determinado que la modelación matemática puede ser considerada como herramienta didáctica, proceso de aprendizaje, método de enseñanza e investigación, y estrategia de enseñanza o vehículo mediante el cual vincula los contextos socioculturales con las matemáticas en la escuela.
Por su parte, Villa-Ochoa (2007) define la modelación matemática como "la actividad que se lleva a cabo en el contexto de las clases de matemáticas y cuya naturaleza se inspira en la actividad científica de la modelización (p. 70). Según investigaciones de este autor, la modelación matemática, como enfoque pedagógico, centra su atención en el desarrollo de conceptos y definiciones matemáticas que facultan una mayor compresión de la disciplina, así como en la reflexión respecto a la creación de modelos..
A partir de la caracterización de la modelización y la modelación matemática, Villa-Ochoa (2007) establece una distinción entre ambos términos basado en los siguientes criterios: el propósito del modelo, los conceptos matemáticos, el contexto y otros factores. En cuanto al modelo, en el caso de la modelización, la construcción del modelo obedece a brindar solución a un problema o fenómenos de otras disciplinas; o bien, para la generación de conocimientos científicos. Por su parte, el modelo matemático en el caso de la modelación, es un vehículo para la construcción del conocimiento matemático con significado para el estudiantado.
En cuanto al criterio sobre conceptos matemáticos, en la modelización, los conceptos surgen del proceso de matematización mientras que, en la modelación, son considerados a priori según los propósitos de la clase y las consideraciones del profesorado. Respecto al contexto, en la modelización matemática, está dado por el fenómeno o situación que se desea atender; en la modelación, el contexto es seleccionado por el profesorado pensando en los propósitos de la clase y en la cercanía respecto al estudiantado.
En ambos casos, tanto en la modelización como en la modelación uno de los procesos esenciales lo constituye la construcción del modelo matemático. En cuanto a la concepción de este término, se asume, a partir de la definición de modelo, para puntualizar en el concepto propiamente matemático. Al realizar un análisis de las definiciones de modelo, se constata lo polisémico del término. Desde la perspectiva de las ciencias y bajo una visión epistemológica, según Adúriz-Bravo y Morales (2002), un modelo se entiende como “una entidad no lingüística que sirve al individuo a modo de representación simbólica interna y operativa, el mapa, de algunos aspectos del mundo” (p. 79).
Para Islas y Pesa (2004), un modelo científico es una representación idealizada de un sistema real, de forma que el modelo contempla ciertos aspectos de la realidad que son usados para la generación de teorías o ideas respecto al mundo. Por su parte, Castro y Castro (1997) apuntan que un modelo es una esquematización abstracta de la realidad.
Las definiciones dadas para modelo coinciden en establecer una relación entre la realidad y un esquema abstracto, matemático y lingüístico que representa de manera idealizada o simplificada de dicha realidad.
A partir de la relación entre la realidad y su representación descrita en un modelo, así como las características que lo dotan de utilidad, se puede revisar las definiciones establecidas para modelo matemático.
Castro y Castro (1997) consideran que, propiamente en el ámbito de las matemáticas, cuando se utiliza la frase “matematizar la realidad a través de un modelo” (p. 106) es porque “determinados hechos y sus relaciones se expresan mediante términos y relaciones matemáticas abstractas” (p. 107).
Al respecto, Blomhøj (2004) establece que
Un modelo matemático es una relación entre ciertos objetos matemáticos y sus conexiones por un lado, y por el otro, una situación o fenómeno de naturaleza no matemática. Este aspecto fundamental del concepto de modelo desde ya tiene significativas implicaciones didácticas. En primer lugar, esto implica que, cuando la matemática es aplicada a una situación extra-matemática, algún tipo de modelo matemático está involucrado explícita o implícitamente en ella. Segundo, para que un alumno experimente con un modelo matemático y sea capaz de reflexionar sobre las relaciones existentes en él, es una precondición epistemológica que este alumno sea capaz de percibir la situación o fenómeno modelado y la matemática en juego, como dos objetos separados pero al mismo tiempo interrelacionados. (p. 21)
A su vez, Biembengut y Hein (2004) establecen, como modelo matemático, un conjunto de relaciones y símbolos vinculados a cualquier rama de las matemáticas, en donde el tipo de conocimiento que se desarrolla en determinada rama genera instrumentos sustanciales para las aplicaciones matemáticas.
De esta manera, se establecerá como modelo matemático un conjunto de símbolos, tal y como lo establecen Biembengut y Hein (2004), pero también relaciones matemáticas mencionadas por Blomhøj (2004) que permitan explicar, predecir y solucionar una situación o fenómeno dado.
El proceso mediante el cual se construyen los distintos modelos matemáticos se ha denominado ciclos o fases de la modelización matemática. En cuanto a ello, varios investigadores lo han descrito a partir de diversos esquemas (Blum y Niss, 1991; Castro y Castro, 1997). Estos esquemas dependen del objetivo, sentido de realidad y necesidades que se planteen respecto a la modelización matemática. Borromeo (2018) plantea las siguientes clasificaciones a partir de los ciclos de modelización
Esta clasificación se basa en el proceso que se lleva a cabo al momento de analizar un proceso de modelización matemática. Según Borromeo y Meister (2021), los ciclos de modelización precisan y examinan cómo se organiza y funciona el proceso de modelización; implica comprender cómo se traducen datos, las nociones involucradas, los supuestos, relaciones y condiciones del problema al lenguaje y la teoría matemática.
Además, sobre el proceso en general de modelización matemática se señala que:
se seguirá, seguramente un ciclo de aproximaciones sucesivas a la solución, hasta alcanzar un grado de satisfacción suficiente. Seguramente, ello puede llevar a preguntas muy generales y de carácter tal vez epistemológico (qué es aquella realidad, cómo influye el que los modeladores pertenezcan a ella, por qué razón la representación matemática resulta adecuada para encontrar soluciones…); ello no obstante, y tras un tiempo considerable de uso de esta manera de trabajar, se la considera un instrumento confiable para comprender situaciones, resolver problemas de muy variada naturaleza. (Borromeo et al., 2021, p. 19)
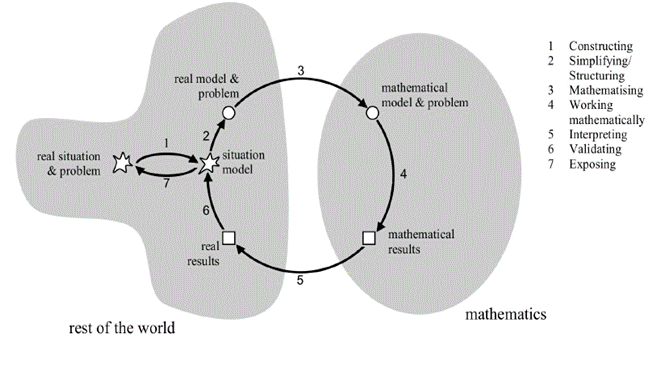
En la Figura 1 se muestra uno de los esquemas más conocidos respecto al proceso de modelización, que constituye el proceso dado por Blum y Leiß (2007), que se describe a continuación.
Como se puede notar, dicho modelo enfatiza la relación entre las situaciones problema de la vida real o “resto del mundo” y la matemática. Se utilizan las numeraciones para describir los pasos a seguir en la evolución de una situación problema hasta su resolución mediante un modelo matemático.
Sobre este modelo, Borromeo et al. (2021) indican que este parte de una situación o problema en el mundo real, sobre el cual se da el proceso de construcción de un primer modelo a partir del entendimiento parcial del problema. La persona que está creando el modelo identifica la información del problema, define cómo abordarlo según su pensamiento matemático, lo idealiza y simplifica. Lo anterior implica recurrir a recursos como un modelo real hecho de dibujos o fórmulas matemáticas y uso de conocimiento extramatemático.
La fase de matematización es similar a la anterior, pero incluye un mayor uso de herramientas o conocimientos de naturaleza matemática para el planteamiento del modelo, así como el uso de ciertas competencias matemáticas de la persona modeladora.
Una vez obtenidos los resultados matemáticos, estos son interpretados y validados según el contexto real, de acuerdo con la representación mental de la situación; o bien, con base en el análisis y reflexión entre la correspondencia del problema y su representación. Posteriormente, se realiza, de acuerdo con el modelo de la situación, una contrastación del modelo obtenido con la situación real.
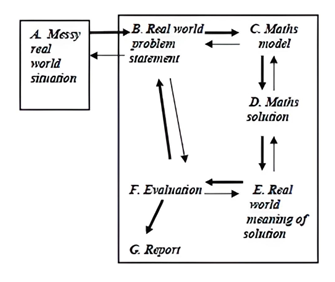
Una simplificación de dicho esquema es la que se presenta en la Figura 2, donde las entradas A-G representan las distintas fases del proceso de modelización y las flechas, la transición entre dichas fases. Como se puede notar, constituye un ciclo que no finaliza en la construcción del modelo, sino que incluye la evaluación del modelo y el inicio de un nuevo ciclo en caso de que los resultados del modelo sean insatisfactorios.
Así como existen diversas perspectivas de investigación sobre modelización matemática, se pueden referenciar diversos ciclos de modelización que están relacionados con situaciones problema que son utilizadas en los procesos de modelización.
Por su parte, en el ciclo de la Figura 3, también denominado ciclo didáctico o pedagógico, se puede observar una dicotomía entre el mundo real y la matemática; sin embargo, difiere del modelo anterior en que se muestra una transición de la situación problema, proveniente del mundo real, al modelo matemático, la evaluación del modelo en contexto y su interpretación, o resultados en el contexto real.
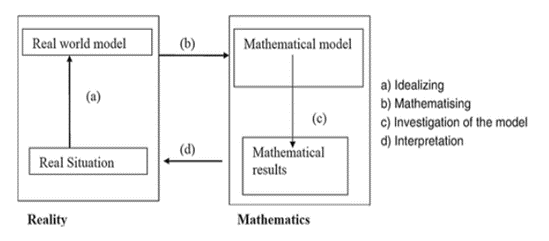
Fuente: Blum (1996) y Kaiser (1995).
Figura 3 Ciclo de modelización didáctico o pedagógico según Blum y Kaiser
El ciclo de la Figura 4, denominado ciclo de modelización psicológico, se origina en estudios psicológicos en matemática aplicada o de educación matemática. Sus promotores son los psicólogos Verschaffel, Greer y De Corte (Verschaffel et al., 2000).
Tal y como se puede observar en la Figura 4, dicho modelo incorpora la situación del modelo, que puede ser descrita como una representación mental de la situación que está dada en el problema. Las situaciones problema analizadas en este tipo de ciclo tienen un fuerte componente de texto lingüístico, también llamados Word Problem (Nesher et al., 2003).
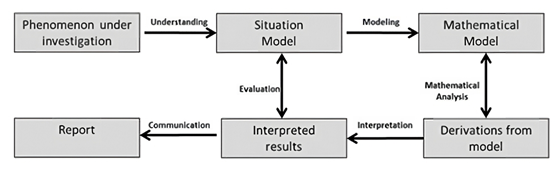
Fuente: Verschaffel et al. (2003).
Figura 4 Ciclo de modelización psicológico según Verschaffel et al.
Teniendo en cuenta las distintas diferencias entre los ciclos, Kaiser y Sriramam (2006) las engloban en 5 perspectivas distintas de investigación al abordar la modelización: realista, contextual, educacional, socio-crítica y epistemológica. Estas diferentes posturas se distinguen por sus objetivos centrales, sus antecedentes y por la forma de asumir la enseñanza y aprendizaje de las matemáticas. Así, la realista se centra en la solución de problemas del mundo real; la contextual, sobre objetivos psicológicos; la educativa remite a objetivos pedagógicos (didácticos y conceptuales); la sociocrítica contiene una visión emancipadora y crítica del mundo, y la epistemológica no solo contempla situaciones del mundo real, sino cualquier actividad susceptible de ser modelada.
Algunas personas autoras incluyen la perspectiva cognitiva, que centra su análisis en los procesos cognitivos que se dan en la modelización. Esto en busca de transparentar los procesos a nivel cognitivo que activan los sujetos en cada etapa del ciclo de modelización o al pasar de una etapa a otra (Bosch, et al. 2006). Una evidencia de este interés lo constituye el ciclo de modelización según Blum (Blum y Leiß, 2007), en el cual se expresa no solo las fases del ciclo de modelización, sino los procesos de transición entre las distintas etapas.
Es importante acotar que la construcción de modelos implica el desarrollo de una serie de habilidades y competencias. En este sentido, de acuerdo con la Organización para la Cooperación y el Desarrollo Económicos (OCDE), la construcción de modelos matemáticos requiere de competencias tales como reflexionar, analizar, estructurar, criticar y comunicar, tanto el modelo matemático como los resultados en la aplicación del modelo (OCDE, 2006).
3. Metodología
3.1 Enfoque
El estudio se ha enfocado en el significado, concepción y perspectivas que tiene el profesorado de docentes en formación respecto a la modelización matemática como proceso matemático, estrategia didáctica u objeto de enseñanza, por lo que interesa sus comentarios y discursos en relación con los objetos y procesos implicados en dicho proceso. Lo anterior nos ha conducido a seleccionar un tipo de investigación descriptiva, con enfoque cualitativo, esto por cuanto interesa describir y analizar “la realidad tal como otros la experimentan, a partir de la interpretación de sus propios significados” (Martínez, 2011, p. 7).
3.2 Participantes en el Estudio
La población de interés para este estudio estuvo conformada por el profesorado de docentes en formación de Enseñanza de la Matemática de una universidad pública en Costa Rica. Fueron consultados 28 docentes, que impartieron cursos del área de matemática en el periodo comprendido entre el 2017 al primer semestre 2021. De dicha población se obtuvieron 20 respuestas que constituyen a las personas participantes. De las cuales, 12 eran hombres y 8 mujeres; 14 contaban con el grado de maestría, 4 con doctorado y 2 con licenciatura. Sus especialidades o formación eran en las áreas de matemática aplicada (2), matemática pura (1), estadística (2), educación matemática (13) o informática educativa (2).
El instrumento aplicado contó con la anuencia del personal docente participante de la investigación, a través de una descripción en el instrumento donde se explicaba el propósito y se solicitaba su anuencia a participar mediante un consentimiento informado que garantizaba, además, la confidencialidad de la información.
3.3 Técnicas de Recolección
El instrumento para la recopilación de los datos consistió en una entrevista, la cual se aplicó de manera virtual, e incluyó preguntas abiertas cuyo propósito fue profundizar la forma en la cual se ha desarrollado la modelización matemática en el plan de estudios, desde si ha sido posible su implementación, estrategias para su abordaje y concepciones sobre la modelización, sobre las cuales se llevó a cabo el análisis. Dichas preguntas fueron validadas por criterio de expertos, con especialistas del área de matemática pura o educación matemática, con experiencia en planes de estudio de formación de personas educadoras en enseñanza de la matemática. El instrumento se aplicó en el segundo semestre del 2021, distribuido en tres apartados, donde se indagó sobre las siguientes categorías: la modelización como estrategia de enseñanza (incluye aspectos relacionados sobre modelación matemática), la modelización en planes de estudio de enseñanza de la matemática y la modelización como proceso matemático (aspectos relacionados con la modelización matemática): Las preguntas fueron las siguientes
¿Qué dificultades ha presentado el estudiantado ante tareas o problemas de modelización o de resolución de problemas?
¿Considera usted que la modelización matemática ha sido desarrollada en los cursos que usted ha impartido por medio de problemas matemáticos o de problemas extramatemáticos de la realidad, o artificialmente construidos?
¿Ha utilizado tecnología para favorecer el uso de habilidades en modelización matemática en sus cursos? En caso afirmativo, por favor, indique el tipo de tecnología y la manera en la cual la ha utilizado para el desarrollo de la modelización matemática.
¿Qué condiciones se requieren para la integración de la modelización matemática en el desarrollo de los cursos que ha impartido y del plan de estudios de la carrera en general?
¿Qué restricciones dificultan o impiden la integración de la modelización matemática en el desarrollo de los cursos que ha impartido y del plan de estudios de la carrera en general?
¿Cómo considera usted que se ha concebido la modelización matemática en los distintos cursos del plan de estudios?
¿Qué estrategias sugiere incorporar en el plan de estudios para el desarrollo de competencias o habilidades en el área de modelización matemática?
Las respuestas a las preguntas fueron agrupadas de la siguiente manera: la modelización como estrategia de enseñanza (incluye aspectos relacionados con modelación matemática), la modelización en planes de estudio de enseñanza de la matemática y la modelización como proceso matemático y sus diferencias con la resolución de problemas (aspectos relacionados con la modelización matemática). Por su parte, las categorías de análisis, surgieron al aplicar el MAXQDA 2022 y Atlas.ti versión 23 en el análisis de las respuestas.
3.4 Análisis de la información
Para el análisis de las respuestas obtenidas, se utilizó el análisis de contenido a partir de las herramientas MAXQDA 2022 y Atlas.ti versión 23. Esta técnica permite preguntar a los datos qué es esencial en esta respuesta y qué significa, a través del objeto de referencia y su relación (Bardin, 1991; Frejd, 2012).
Para el análisis de la información se establecieron los siguientes núcleos de referencia y categorías de análisis en la Tabla 1.
Tabla 1 Núcleos, categorías de análisis y sus respectivas preguntas asociadas en la entrevista realizada a docentes1
| Núcleo | Categorías de Análisis | Preguntas Asociadas |
| NR01 La modelización como estrategia de enseñanza. En el sentido de la modelación matemática, coloca la relación entre el mundo real y la matemática en el centro de la enseñanza y el aprendizaje (Blomhøj, 2004) De esta manera, interesa analizar, por un lado, las estrategias de enseñanza y condiciones para el desarrollo de la modelización en el aula y; por otro lado, desde la perspectiva del aprendizaje, las dificultades presentadas por el estudiantado. | 1. NR011: Dificultades presentadas por el estudiantado 2. NR012: Estrategias de enseñanza utilizadas y competencias desarrolladas 3. NR013: Condiciones para el desarrollo de la modelización en el aula | ¿Qué dificultades ha presentado el estudiantado ante tareas o problemas de modelización o de resolución de problemas? ¿Qué estrategias sugiere incorporar en el plan de estudios para el desarrollo de competencias o habilidades en el área de modelización matemática? ¿Qué condiciones se requieren para la integración de la modelización matemática en el desarrollo de los cursos que ha impartido y del plan de estudios de la carrera en general? |
| NR02 La modelización en planes de estudio de enseñanza de la matemática.Este núcleo refiere al análisis del nivel de abordaje y competencias desarrollas en el plan de estudios. | 1. NR021: Nivel de abordaje en el plan de estudio. 2. NR022: Competencias implicadas. | ¿Ha utilizado tecnología para favorecer el uso de habilidades en modelización matemática en sus cursos? En caso afirmativo, por favor, indique el tipo de tecnología y la manera en la cual la ha utilizado para el desarrollo de la modelización matemática. ¿Qué restricciones dificultan o impiden la integración de la modelización matemática en el desarrollo de los cursos que ha impartido y del plan de estudios de la carrera en general? |
| NR03 La modelización como proceso matemático y sus diferencias con la resolución de problemas. En este sentido, interesa conocer si la percepción de las personas docentes tiende a considerar la modelización equivalente a la resolución de problemas o si se visualiza como una representación matemática de la realidad o como proceso de matematización. | 1. NR031: Resolución de Problemas. 2. NR032: Representación Matemática. 3. NR033: Matematización de la vida real. | ¿Considera usted que la modelización matemática ha sido desarrollada en los cursos que usted ha impartido por medio de problemas matemáticos o de problemas extramatemáticos de la realidad, o artificialmente construidos? ¿Cómo considera usted que se ha concebido la modelización matemática en los distintos cursos del plan de estudios? |
Fuente: Elaboración propia
Nota: 1 Docentes en formación de Enseñanza de la Matemática de una universidad pública en Costa Rica
Con estos elementos se procedió a realizar la Guía de Análisis, la cual se compone de los núcleos, subcategorías y los predicados. A partir de dicha guía se procedió a interpretar el contenido de las respuestas obtenidas en el instrumento aplicado partiendo de lo estipulado en el marco teórico.
4. Resultados y Discusión
A partir de la guía de análisis, los núcleos y categorías determinadas, se interpretaron las respuestas obtenidas. A continuación, se expondrán los resultados obtenidos en relación con los núcleos y categorías definidas.
4.1 La modelización como estrategia de enseñanza
En cuanto a la categoría NR011 Dificultades presentadas por los estudiantes, de las personas docentes consultadas, 8 docentes consideran que una de las dificultades corresponde a la construcción o determinación del modelo matemático, 4 docentes comentan que la dificultad radica en aspectos de comprensión de la tarea o situación problema, y 3 docentes manifiestan que las dificultades pueden deberse a los conocimientos base del estudiantado; particularmente estas tres personas docentes mencionan deficiencias en el área de álgebra.
En cuanto a la determinación del modelo matemático, se obtuvieron comentarios que refieren a la dificultad para el estudiantado de la aplicación de la modelización matemática:
D1:“Plantear problemas y modelos, tanto a nivel práctico como teórico. Particularmente en entender el problema a resolver.”
Este comentario refleja también la opinión de las 4 personas docentes que consideran que una de las dificultades radica en la comprensión que puede llegar a poseer el estudiantado sobre el problema, esto en ocasiones ligado a que:
D16: “no logran abordar la traducción de la situación a lenguaje algebraico”.
Esta opinión se enlaza con la de tres docentes en cuanto a que la dificultad tiene que ver con la apropiación de conocimientos previos, en particular algebraicos o analíticos, tal y como se evidencia también en el siguiente comentario:
D24: “Tienen deficiencias sobre la comprensión de funciones como la cuadrática, la logarítmica y la exponencial”.
Estos resultados evidencian dificultades en la modelización horizontal establecida por Rico (2007) y las actividades matemáticas relacionadas con este proceso no solo en la identificación de las matemáticas atinentes al problema, sino a la comprensión de la relación entre los lenguajes natural, simbólico y formal, así como la traducción del problema a un modelo matemático.
Respecto a la categoría NR012 Estrategias de enseñanza utilizadas y competencias desarrolladas, particularmente sobre las competencias que se fomentan, en su mayoría, según las personas docentes consultadas, son el análisis (8 docentes), el uso y tratamiento de datos (6 docentes) y la resolución de situaciones problema enfocadas en el abordaje de un conocimiento matemático específico (8 docentes).
Las tres competencias citadas coinciden con lo establecido por García y Benítez (2011), y por Beltrón et al. (2019), al considerar como componentes fundamentales de la modelización matemática el razonar o pensar, la argumentación, el uso del lenguaje simbólico, formal y técnico, así como el plantear y resolver problemas en una variedad de situaciones. En específico, lo referente a la resolución de problemas enfocados en el abordaje de un conocimiento matemático refleja una característica de la modelación, dado que, a priori, se definen los conocimientos matemáticos que se pretende abordar (Villa-Ochoa, 2007).
Dentro de las estrategias de enseñanza utilizadas se hace referencia a proyectos y al uso de herramientas computacionales. Las personas docentes mencionan las siguientes:
D7: “Se plantean problemas que responden a una situación de un contexto en el que intervienen variables que pueden tener cierta familiaridad con el contexto del estudiantado”.
D3: “Trabajo con bases de datos reales o bien mediante la recolección de información con un objetivo en mente, es decir, plantear qué se va a hacer con los datos (modelo de análisis de la información), antes de recolectar la información”.
Esta última estrategia tiene relación con la opinión de 6 docentes en cuanto al uso y tratamiento de datos como base en el desarrollo de la modelización matemática en el aula.
Hubo docentes que plantearon actividades con un contexto cercano a los estudiantes, tal y como lo establece Villa-Ochoa (2007) como característica de la modelación. Se plantean dos ejemplos dados por el cuerpo docente sobre problemas de modelación trabajados en sus cursos:
D18: “Construcción de una función que calculara el impuesto de renta según el salario recibido y según lo aprobado en la nueva Ley de Impuesto sobre la renta (Ley 7092).”.
D15: “En Geometría Analítica se trabajó con un ejemplo de determinar el epicentro de un terremoto a partir de cierta información detectada en ciertos puntos, asumiendo que la dispersión de las ondas sísmicas es circular”.
Finalmente, en cuanto a la categoría NR013 Condiciones para el desarrollo de la modelización matemática en el aula; en primer lugar, se establece la necesidad de un marco conceptual común sobre modelización. En la Figura 5, se reporta la ocurrencia que los docentes mencionan en los conceptos como condiciones para el desarrollo de la modelización, y de manera imperante, la mayoría coincide en el manejo uniforme del concepto de modelización. una persona docente establece lo siguiente:
D6: “Tener claro qué se entenderá por modelización matemática en el desarrollo del plan de estudios. Tener clara la diferencia o relación entre modelización matemática y resolución de problemas, (…) en (…) los docentes a cargo de los cursos”.
Otro de los aspectos que las personas docentes consultadas manifiestan respecto a las condiciones idóneas para la implementación de la modelización matemática es que se requiere de una disposición activa por parte del profesorado que, en la Figura 5, aparece como disposición profesorado, docente o profesor. En este sentido, dos de las personas participantes establecen lo siguiente:
D10: “Anuencia del profesorado en realizar actividades que promuevan esa competencia”.
D11: “Buena disposición por parte del docente y del estudiantado. Considero que existen cursos que por su naturaleza más teórica no permiten tanto implementar actividades de modelización, pero en la medida que el curso lo permita es importante hacerlo”.
4.2 La modelización en planes de estudio de enseñanza de la matemática
n cuanto al núcleo NR02 La modelización en planes de estudio de enseñanza de la matemática, se obtuvieron los siguientes resultados respecto a las categorías definidas. La categoría NR021 Nivel de abordaje en el plan de estudio, muestra una clara tendencia del profesorado
En cuanto al núcleo NR02 La modelización en planes de estudio de enseñanza de la matemática, se obtuvieron los siguientes resultados respecto a las categorías definidas. La categoría NR021 Nivel de abordaje en el plan de estudio, muestra una clara tendencia del profesorado a considerar que la modelización en el plan de estudios ,en efecto, es abordada o trabajada con el estudiantado. No obstante, por los resultados obtenidos en el núcleo anterior (NR01), este abordaje se da desde la perspectiva de la modelación matemática.
En un modelo de co-ocurrencia de códigos, sin embargo, se puede evidenciar que NR02 La modelización en planes de estudio de enseñanza de la matemática tiene una fuerte proximidad con NR03 La modelización como proceso matemático. Esto a pesar de que el profesorado tiende a utilizar, en mayor medida, la modelación matemática. Posiblemente, la percepción del profesorado respecto al plan de estudios tiende a visibilizar mayormente la modelización matemática por la naturaleza y áreas de los cursos dentro del plan de estudios.
Esta percepción de cercanía entre el plan de estudios y la modelización matemática, sin embargo, es contraria a las respuestas dadas por el profesorado en cuanto al abordaje de la modelización matemática en el plan de estudios, respuestas que tienden a considerar, en mayor medida, la modelación y la resolución de problemas.
Desde esta visión, el ciclo de modelización presente a partir de la co-ocurrencia de códigos es el ciclo didáctico o pedagógico desde una perspectiva educativa más orientada a la introducción o desarrollo de conceptos (Kaiser y Sriramam, 2006; Borromeo, 2017), lo cual coincide con Villa-Ochoa (2007) en cuanto a las características de la modelación matemática, y reafirma lo planteado con anterioridad.
Respecto a la categoría NR022 Competencias implicadas, los resultados son similares a los obtenidos en la categoría NR012 Estrategias de enseñanza utilizadas, en donde las competencias de análisis, uso y recopilación de datos, así como la resolución de problemas son las que sobresalen en el uso de la modelización matemática en el plan de estudios.
Al analizar los resultados obtenidos, respecto al uso de tecnología para el abordaje de la modelización matemática, 12 docentes afirman haber utilizado algún tipo de tecnología, entre los programas o software que se mencionan están R (para análisis de datos), Python, Geogebra, Wolfram yTracker.
4.3 La modelización como proceso matemático y sus diferencias con la resolución de problemas
En cuanto al núcleo NR03 La modelización como proceso matemático, existe una clara tendencia a considerar la modelización matemática equivalente a la resolución de problemas (NR031: Resolución de Problemas), tal y como se muestra en la Figura 6.

Fuente: Elaboración propia
Figura 6 Conceptos de ocurrencia: modelización como proceso matemático y sus diferencias con la resolución de problemas
En particular, se asocia la modelización matemática con problemas tanto de origen o contexto matemático como extramatemático, al respecto un docente afirma:
D12: “Problemas matemáticos o extra-matemáticos. Además también con problemas construidos los cuales llamaría idealizados para poder resolverlos”.
Otro docente, por ejemplo, concibe la modelización matemática como la resolución de problemas:
D5: “Resolución de problemas matemáticos”
En este sentido, no visualiza la modelización matemática a partir de lo establecido por Blomhøj y Højgaard (2003), en donde conlleva un proceso o ciclo para la determinación de una relación matemática que contribuya en la solución de una situación problema de la realidad.
En cuanto a la categoría NR031 Resolución de Problemas, se evidencia aún más la relación establecida entre la modelización matemática con la resolución de problemas sin distinción en cuanto a su contexto o vinculación con la realidad. Por ejemplo, una persona docente considera que:
D4: “La modelización se concibe estrechamente ligada a la resolución de problemas extramatemáticos artificialmente construidos”.
En cuanto a la categoría NR032 Representación Matemática, 3 personas docentes conciben la modelización matemática como una representación matemática de la realidad, tal y como se evidencia en el siguiente comentario, el cual se refiere a la definición de modelización matemática:
D1: “proceso de extraer de un contexto los principales elementos que permitan representar el fenómeno en lenguaje matemático y en donde se concreten los elementos fundamentales”.
Esto coincide con lo planteado por Bassanezi y Biembengut (1997), en donde indican que la mayoría de los autores y autoras se referían a la modelización matemática como proceso matemático para el análisis de situaciones reales.
Sin embargo, solo 3 de las 20 personas docentes consideran la modelización matemática como una representación de la realidad.
Finalmente, la categoría NR033 Matematización de la vida real, está en estrecha relación con la representación matemática; no obstante, hace alusión al vínculo existente entre el modelo matemático y una situación problema con un contexto real. En este sentido, algunas personas docentes manifestaron lo siguiente:
D7: “En un primer momento, se concibe como la presentación de problemas contextualizados, donde se deban interpretar conceptos matemáticos a partir de situaciones reales para reconocer la importancia de la matemática en la vida cotidiana. En etapas más avanzadas, se concibe como la presentación de situaciones reales de la vida cotidiana a las cuales se les debe dar solución y sean los propios estudiantes los que busquen las herramientas matemáticas necesarias para hacerlo”.
Tal y como se desprende del comentario de esta persona docente, al inicio de los cursos utiliza la modelación, sin embargo, conforme avanza en el curso o en el plan de estudios, se tiende a procesos de modelización en los cuales los conceptos matemáticos surgen durante el proceso y no son establecidos de forma intencional por el profesorado. (Villa-Ochoa, 2007).
En cuanto a las interacciones entre los códigos, existe una fuerte interacción entre NR02 La modelización en planes de estudio de enseñanza de la matemática con la NR031 Resolución de problemas, incluso mayor que la interacción entre esta y la modelización como proceso matemático, lo que evidencia la perspectiva que se tiene de la modelización matemática en el proceso de formación de docentes.
5. Conclusiones
A partir de la consulta realizada al profesorado que se desempeña como formador de docentes de un plan de estudios en Enseñanza de la Matemática sobre modelización matemática como proceso matemático y como estrategia metodológica, se destacan las siguientes conclusiones, en términos de la caracterización que se pretendía del significado y perspectivas en modelización matemática de un grupo de personas docentes formadoras de la carrera Enseñanza de la Matemática:
1. Existe una relación vinculante en el desarrollo de la modelización matemática, en el plan de estudios, con la concepción de resolución de problemas, incluso, sin distingo del tipo de contexto, real o artificial. Desde esta visión algunos de los docentes se pueden ubicar en una perspectiva educativa conceptual según Kaiser y Sriramam (2006).
2. Se concibe, dentro de la modelización matemática como estrategia de enseñanza, dificultades por parte del estudiantado en cuanto a las concepciones propias de modelización matemática, ciclos y fases, así como la relacionada con conocimientos matemáticos previos, los cuales tal vez no poseen, o bien, no recuerdan. Algunas de las personas docentes concuerdan en considerar que la fase de comprensión de la situación problema al modelo real, según Blum y Leiß (2007), es la que provoca mayores dificultades en el estudiantado.
3. Dentro de las estrategias de enseñanza más utilizadas está el planteamiento de problemas para el abordaje de un conocimiento matemático específico, así como el tratamiento y uso de datos; con lo cual se vuelve a reafirmar la perspectiva educativa conceptual establecida por Kaiser y Sriramam (2006).
4. En cuanto a las condiciones que deben presentarse para el desarrollo de la modelización en el aula, se coincide con la necesidad de que la persona docente posea conocimiento sobre los procesos de modelización matemática, así como una buena disposición para el planeamiento e incorporación de actividades que promuevan el abordaje de problemas de modelización matemática en los procesos de enseñanza-aprendizaje.
5. La modelización en el plan de estudio de enseñanza de la matemática, en el cual laboran las personas docentes consultadas, en palabras de estas, fomenta competencias como el análisis de situaciones problemas, observación y uso de datos relevantes, así como la resolución de problemas mediante diferentes técnicas. Se considera que los procesos de modelización matemática están presentes en el plan de estudios; no obstante, el nivel de incorporación está relacionado estrechamente con la resolución de problemas, y no con un proceso específico.
6. La concepción de las personas docentes respecto a la modelización como proceso matemático evidenció una posición más marcada hacia la modelización como un proceso de resolución de problemas.
De la información recabada del personal docente, resulta relevante destacar que, aunque la modelización matemática es una actividad propia del aprendizaje de la disciplina, su uso, en el caso del proceso de formación profesional docente, se ha centrado en resolver problemas y no en el uso de esta como estrategia didáctica.
Se evidencia una ausencia conceptual de este proceso en el personal docente en función de la formación de docentes, causada, tal vez, por una carencia en el plan de estudios, que lo asume como una actividad propia del desarrollo de los cursos, pero no desde una perspectiva educativa. Es decir, no se desarrolla qué es la modelización matemática, sino que se asume su uso como parte del aprendizaje matemático.
Por ello, se enfatiza en la necesidad de que todo plan de estudios enfocado a la formación de docentes de matemática incorpore, como parte de su currículum, el abordaje de la modelización matemática no solo como proceso para resolver problemas, sino desde un punto de vista teórico y conceptual que le permita al profesorado en formación conocer sobre diferentes concepciones de esta, dificultades, competencias, procesos y ciclos asociados a ella, y concientizarse sobre su uso como un recurso para la contextualización de la matemática a la vida real. Esto, además, aportará a la persona docente en formación herramientas para su desarrollo profesional.
Esta investigación se desarrolló durante la pandemia por COVID-19, por lo que una de las limitaciones fue la aplicación de los instrumentos. Se esperaba poder aplicar el instrumento de forma presencial, no obstante, Asimismo, se esperaba poder realizar observaciones de aula que permitieran contrastar la información recopilada, no obstante, las clases se brindaban en presencialidad remota con poco espacio.