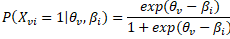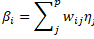Introduction
Cattell’s investment theory (1963, 1971, 1987) distinguishes between fluid intelligence and crystallized intelligence. The former has been related to the capacity of solving novel and complex problems using cognitive processes such as inductive and deductive reasoning, concept formation, and classification (Kvist and Gustafsson, 2008). Crystallized intelligence has been linked with specific knowledge gained from culture, and it is acquired through education and experience (Kvist and Gustafsson, 2008).
In recent years, researchers have tried to take advantage of developments in cognitive psychology within the context of psychometric tests to understand fluid intelligence (Arendasy and Sommer, 2005, 2013; Carpenter, Just, and Shell, 1990; Embretson, 1995; Primi, 2001; Rupp and Mislevy, 2006; Schweizer, Troche, and Rammsayer, 2011). This psychometric-cognitive approach has been considered significant in the efforts to bring evidence of construct validity of the studied variables (Embretson, 2002; Yang and Embretson, 2007).
In tests’ development, the construction of items has traditionally relied on the expertise and creativity of the builders. This domain then appears within a “black box”, so that the microstructure of the items in terms of its constituent parts is opaque (Yang and Embretson, 2007). While some computerized algorithms permit the automated generation of items (e.g., Arendasy and Sommer, 2005), the vast majority of educators, psychologists or people concerned of building new tests and/or in studying the processes underlying their resolution can’t always rely on this sophisticated technique that is also limited to very few constructs. Still the possible consequences linked to the use of the tests require that researchers, educators or decision-makers rely on methods that help them evaluate the reliability of the items of the tests they built as a function of the construct they are interested in.
This is the case of the figural reasoning test (FRT), a prototype fluid intelligence test, developed at the University of Costa Rica (UCR) and built by a team of psychologists and psychometricians. In addition, because of its possible use in the selection process of students, it is crucial to examine the cognitive operations involved in the process of solving items and their impact in explaining the level of difficulty of the items. Thanks to the development of recent mathematical models we can collect information that help evaluating the validity of items and tests constructed by experts.
A model that naturally links the cognitive psychology arena and the psychometric view is the linear logistic test model (LLTM; Fischer, 2005). This model allows estimating person’s ability and item difficulty taking into account a set of weights reflecting the hypothesized cognitive processes or operations to solve each item. The LLTM is often understood to be an extension of the Rasch model (Fisher and Molenaar, 1995); but as a formal model, the latter is a special case of the LLTM. It means that, with a particular weight matrix, the LLTM can be transformed as a Rasch model. In order to provide an understandable definition of the LLTM, we first specify the Rasch model and then we show the linear constraint that LLTM imposes on the difficulty parameters.
The Rasch model can be represented as:
where P(X vi = 1| θ v , β i ) is the probability that person v gives a correct response to item i, given her ability θ v and the difficulty of the i as β i .
In the LLTM, the item difficulty parameters, β i , are decomposed into a linear combination of elementary parameters that can be expressed as follow:
The number of elementary parameters p is restricted to p <= k-1, where k is the number of items. In the equation, w ij is the given weight of the basic parameter j on item i and η j is the estimated difficulty of the basic parameter j. Traditionally, this constraint on β i has been used to examine the validity of a set of hypothesized cognitive operations involved in the solving process of a given set of items (Scheiblechner, 1972). In this application of the LLTM, the set of elementary parameters j = 1…, p, and the complete set of all items forms the W matrix, where the rows represent items and the columns represent cognitive operations. In the columns, a zero value indicates that a particular cognitive operation is not involved in the solution process of an item and larger values denote the number of times that a hypothesized cognitive operation is required to solve an item. Other applications of the LLTM allow evaluating position effect of item presentation, content-specific learning effect, effect of item response format, etc. (for details see Kubinger, 2009).
The aim of this research is to evaluate -via LLTM- the underlying cognitive operations (rules, from hereinafter) to solve the items of the FRT as suitable predictors of their level of difficulty. In a first study, we randomly assigned a sample of high school students into ‘study sample’ (i.e., 60%) and ‘validation sample’ (i.e., 40%). The study sample served to evaluate the proposed set of rules and the validation sample aimed to replicate the findings of the study sample. The participants belong to the target population of students who can apply for admission to the University of Costa Rica (i.e., last year high school students). Study 2 examined whether or not the evaluated set of rules of Study 1 could be generalized to a sample of students from the University of Costa Rica. Given that the selection process of these students involved scores on general abilities of reasoning in verbal and in math contexts and the average grade of the students throughout the last two years of high school, we expected that university students could exhibit larger scores on the FRT than high school students.
To fulfill the objectives of this quantitative research, we relied on R, a language and environment for statistical computing (R Core Team, 2017). For data processing and plotting we used the R packages reshape (Wickham, 2007), Hmisc (Harrell Jr, 2018), plyr (Wickham, 2011), and ggplot2 (Wickham, 2016) and the LLTM was estimated and tested with the eRM package (Mair, Hatzinger, and Maier, 2018).
Study 1
2.1 Method
2.1.1 Participants
Participants consisted of 1751 Costa Rican students (Study sample n = 1050, Validation Sample n = 701; using the R function called “sample” without replacement) who were in their final year of high school and who wish to enroll in academic programs offered by the University of Costa Rica. The sample consisted of 44% females. A 62.2% of the students came from public high schools, 23.9% from private high schools, 0.2% from schools abroad, and the remaining 13.7% with an undefined state of provenance because they did not register the requested information.
To participate all the students registered through an official website that was enabled to those who were interested in some of the academic programs that were collaborating to the project in 2008, namely: Law, Computing, Mechanical Engineering, Pharmacy, Chemistry, Mathematics, Statistics, and Actuarial Sciences. The volunteers were then informed of the place and date and they were informed that it had no consequence for their admission at the UCR, since the research had merely diagnostic purposes. One limitation of our sample is that not all academic programs were represented. Nevertheless, the high number of participants may compensate the lack of representativeness.
Instrument
The figural reasoning test (FRT) is an unidimensional test proposed as an indicator of fluid intelligence by measuring inductive reasoning skills in figural matrices and series. The FRT measures general reasoning skills involving cognitive processes such as identification of rules, and comparison or classification of perceptual similarities between geometric shapes with the aim of completing series (i.e., Test 1) and matrices (i.e., Test 2). Items within each test are ordered by ascending level of difficulty and the given time to solve Test 1 and Test 2 was respectively three and five minutes.
Procedure
Based on the work developed by Jacobs and Vandeventer (1972), Carpenter et al. (1990), and Primi (2001), the FRT items were dissected into a set of rules involved in their resolution to explain their level of difficulty (see Figure 1). The procedure consisted in two of the authors (T.C. and M.P.V.G.) individually resolving and describing each item, with discrepancies resolved through discussion with a third author (M.M.D.). From this procedure the extracted rules were used for specifying the W matrix of weights required by the LLTM:
Increase or decrease of the size (R1): Progressive variation of the size of the figure in two ways (i.e., increasing or decreasing).
Addition or subtraction (R2): An element of a figure or figure is added or removed.
Simple Motion (R3): Motion that can be given according to various configurations: from left to right, right to left, bottom to top, top to bottom, diagonally, clockwise direction, counterclockwise.
Change of shape or texture (R4): Replacing a figure, or its filling texture, for another figure, or texture filling.
Stylization (R5): Incomplete or irregular figure that progressively acquires a known figure.
Reflection (R6): Transformation of a figure as if it were placing the resulting image in a mirror. In the example, there is a reflection of the geometric shape but not for its filling texture.
Irregular Movement (R7): Movement of figures that do not follow a simple defined pattern.

Note: The description of each rule is given in the text below. Source: Own elaboration based on the items constructed for the FRT in 2011.
Figure 1: Illustration of rule 1 (i.e., R1) to rule 7 (i.e., R7).
Furthermore, there is an additional set of characteristics of the items that could increase the items difficulty such as:
Use of the distractors (R8): This variable indicates whether distractors (response options) facilitate the process of solving an item properly.
Number of elements (R9): Refers to the number of figures in a series or in a matrix. The mean of figures by item is approximately 26 and has an associated standard deviation of 16.56. This indicator has been related to the amount of information that must be processed in working memory (Primi, 2001).
Level of the rules (R10): Rules were classified according to their ease to be inferred: simple or complex.
Number of rules (R11): This variable corresponds to counting the rules needed for solving an item. The assumption behind this variable is that the greater number of rules required for solving the item, the greater working memory load (Primi, 2001).
Data analysis
As mentioned previously, the rules described above were employed to construct the W matrix for the LLTM. In Table 1, a zero value indicates that a particular rule was not necessary to solve a given item and values larger than zero indicate either the number of times a rule was employed (e.g., from rule 1 to rule 7), the use of distractors (e.g., R8; 1 = use of distractors), the number of elements (e.g., R9), the level of rule (e.g., R10; 1 = complex), or the number of rules (i.e., R11).
Table 1: Cognitive operations specified as the W matrix.
| Item | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 |
| Test1-Item1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 23 | 0 | 1 |
| Test1-Item2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 1 |
| Test1-Item3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 0 | 3 |
| Test1-Item4 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 45 | 0 | 2 |
| Test1-Item5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 1 |
| Test1-Item6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 2 |
| Test1-Item7 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 1 |
| Test1-Item8 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 14 | 0 | 2 |
| Test1-Item9 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 2 |
| Test1-Item10 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 9 | 1 | 2 |
| Test1-Item11 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 27 | 1 | 2 |
| Test1-Item12 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 36 | 0 | 1 |
| Test2-Item1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 81 | 0 | 2 |
| Test2-Item2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 24 | 0 | 2 |
| Test2-Item3 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 48 | 0 | 3 |
| Test2-Item4 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 14 | 0 | 2 |
| Test2-Item5 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 12 | 0 | 3 |
| Test2-Item6 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 36 | 0 | 2 |
| Test2-Item7 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 26 | 0 | 4 |
| Test2-Item8 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 18 | 0 | 2 |
| Test2-Item9 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 12 | 0 | 3 |
| Test2-Item10 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 36 | 1 | 3 |
| Test2-Item11 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 36 | 1 | 3 |
| Test2-Item12 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 18 | 1 | 1 |
Note: R1 = Increase or decrease of the size; R2 = Addition or subtraction; R3 = Simple Motion; R4 = Change of shape or texture; R5 = Stylization; R6 = Reflection; R7 = Irregular Movement; R8 = Use of the distractors; R9 = Number of elements; R10 = Level of the rules; R11 = Number of rules. Source: Own elaboration based on the calculation of the W matrix for the LLTM in 2017.
The LLTM allowed estimating the trait levels of the subjects, the difficulty of the items, and the effect of the rules (i.e., the W matrix) on the items difficulty. To evaluate the adequateness of the LLTM to data we considered four criteria. First, we tested the fit of the Rasch model to the data by means of Likelihood Ratio Test (Andersen, 1973); therein, item parameters of different subsamples were compared. For valid models, item parameters should not vary across subsamples in respect to an arbitrary split criterion (e.g., median). Second, to evaluate the unidimensionality axiom we used the Martin-Löf Test (Glas and Verhelst, 1995), which checks if two sets of items form a Rasch scale. Third, we examined the correlation between the difficulty parameters estimated by the Rasch model (i.e., the β Rasch ) and the LLTM (i.e., the β LLTM ). A strong correlation (i.e., r >= 0.80) between the LLTM and Rasch model estimates provides evidence of the W matrix as a good approximation of the item parameters (Gorin, 2005). Finally, we tested the W matrix in a new sample of participants in order to find further evidences of validity for the rules proposed in Study 1. Study 2 deals with this regard.
Results
Rasch Model
Study Sample. The fit of the Rasch model according to Andersen’s likelihood-ratio test -median as split criterion- χ(23) = 79.39, p < 0.01, was unsatisfactory. This is not surprising because it is known that this statistic is sensitive to large samples (Bond and Fox, 2001). Figure 2 (i.e., the scatterplot titled study sample) shows a graphical model test based on β Rasch parameters with confidence ellipses for each item. As Figure 2 shows items are not fairly away from the diagonal, which suggests that item parameters do not vary across high and low test performance. Therefore, we considered that the graphical model test supported the fit of the Rasch model to data.
The Martin-Löf Test -median as split criterion- indicated that the unidimensionality assumption is achieved χ(143) = 82.36, p = 1. In addition, data analysis showed that the Rasch model did not fit 10 participants (0.95%); that is, Infits Mean Square Statistics (InfitMSQ) outside the range of 0.5 and 1.5 (Linacre, 2012). The InfitMSQ for items was in a desirable range of 0.85 and 1.03. Item difficulty was in the range of -2.76 and 3.07 (M difficulty = 0.10), and person ability was in the range of -4.00 and 2.77 (M ability = 0.330). The person-item map of the study sample (see Figure 3) shows the distribution of the person’s abilities (Top panel) on the same metric as the item difficulties (Bottom panel). The Rasch person-item map shown in Figure 3 orders the level of reasoning ability of participants and item difficulty from left to right. Persons with ‘low reasoning score’ (i.e., at the left of the scale) have difficulty even with easiest items; persons with ‘high reasoning score’ are plotted at the right of the scale. Items at the left of the scale are easier to perform. Items become more difficult to perform further right the scale. Moreover, the figure shows that items are located at each point on the scale and they cover all their areas. This pattern indicates that items cover most participants on the scale.
Validation sample. Andersen’s likelihood-ratio test indicated an unsatisfactory fit of the Rasch model to data, χ(23) = 84. 61, p < 0.001; nevertheless, visual inspection suggests an adequate pattern (see Figure 2 the scatter plot titled Validation sample). Similar to the findings of Study sample, the Martin-Löf Test, χ(143) = 78.74, p = 1, shows that the unidimensionality assumption in the FRT is accomplished. The InfitMSQ criterion revealed that Rasch model did not fit 3 participants, while items were in the satisfactory range of 0.849 and 1.10. Person ability (M ability = 0.33) and item difficulty (M difficulty = 0.09) were in the range of -3.20 and 2.78 and in the range of -3.07 and 3.32, respectively. The person-item map followed a similar pattern of study sample, that is, a close correspondence between items difficulty and person’s ability (see Figure 3).
Data analysis of study sample and validation sample supported the fit of the Rasch model to data; thus, we can go further inspecting the FRT via LLTM.

Note: Graphical model test based on linear relation between the β Rasch estimates of the high performance group (raw scores > median; y axis) and the low performance group (raw scores <= median; x axis). Source: Own elaboration based on the calculation of the Rasch Model in 2017.
Figure 2: Scatter plot for Study sample (left side) and Validation sample (right side).

Note: The top panel shows persons’ distribution according their ability level (x axis). The bottom panel shows each item (y axis) according the level of difficulty (x axis). Note: T1.1 = Test 1 item 1; T2.1 = Test 2 item 1. Source: Own elaboration based on the calculation of the Rasch Model in 2017.
Figure 3: The Rasch person-item map for Study sample and Validation sample.
Linear logistic test model (LLTM)
The estimated difficulty parameters of the Rasch model and the LLTM were highly related for the study sample, r(22) = 0.93, p < 0.001, and for the validation sample, r(22) = 0.92, p < 0.001. Table 2 shows the η parameters and their respective 95% confidence interval for the two samples. The 95% confidence intervals reported in Table 2 did not include zero, suggesting that, every rule reliably contributed to predict the difficulty of the items. Item parameters in eRm package are estimated as easiness parameters and, by implication, negatives η values denote that a specific rule makes an item more difficult (Mair, Hatzinger, and Maeir, 2007). The pattern of results for both samples was as follow. The η values belonging to R8 and R9 were positives, which suggests that using distractors and a larger number of figures aid to solve the items properly. The remaining parameters contributed to increase the items difficulty. As observed, R5, which has been called stylization, shows the largest contribution to the level of difficulty, while R7 (i.e., irregular movement) is the following most important rule explaining level of difficulty. Finally, R11, number of rules, contributes to the level of difficulty of the items.
Table 2: Estimates of η parameter for Study sample and Validation sample.
| - | Study sample | Validation sample | |||
| Rule | η parameter | Approximate 95% confidence intervals | η parameter | Approximate 95% confidence intervals | |
| R1 | -.40 | [-.46, -.34] | -.45 | [-.52, -.38] | |
| R2 | -.36 | [-.43, -.29] | -.31 | [-.40, -.22] | |
| R3 | -1.47 | [-1.54, -1.40] | -1.40 | [-1.48, -1.31] | |
| R4 | -.74 | [-.81, -.66] | -.81 | [-.90, -.72] | |
| R5 | -6.00 | [-6.31, -5.69] | -6.62 | [-6.69, -5.58] | |
| R6 | -.54 | [-.66, -.43] | -.58 | [-.72, -.44] | |
| R7 | -1.87 | [-2.09, -1.66] | -2.09 | [-2.35,-1.84] | |
| R8 | .36 | [.24, .48] | .40 | [.25, 0.55] | |
| R9 | .01 | [.01, .02] | .02 | [.01, .02] | |
| R10 | -1.16 | [-1.27, -1.06] | -.99 | [-1.11, -.87] | |
| R11 | -.24 | [-.28, -.19] | -.19 | [-.25, -.14] | |
Note: R1 = Increase or decrease of the size; R2 = Addition or subtraction; R3 = Simple motion; R4 = Change of shape or texture; R5 = Stylization; R6 = Reflection; R7 = Irregular movement; R8 = Use of the distractors; R9 = Number of elements; R10 = Level of the rules; R11 = Number of rules. Source: Own elaboration based on the calculation of the LLTM in 2017.
Study 2
Method
Participants
Study 2 sought to test the rules of the TRF that were characterized in Study 1 thanks to a new sample of 162 students who were in their first year at the University of Costa Rica. We regarded this group as the UNI group. As we mentioned above, students of the UNI group were part of a selection process that involved indicators of reasoning abilities and academic achievement during the last two years of high school.
The sample was composed of 34% of females with 42% of the participants who had studied in public high school. All of them were recruited in 2010 and were currently taking classes of “Humanidades” that group students from a wide variety of careers offered by the UCR.
Data analysis
As a consequence of this admission process is suitable to predict higher levels of reasoning abilities for the UNI group -as compared with high school students of Study 1. In this respect some studies suggest that persons achieving higher scores on general mental ability and working memory capacity usually attempt to construct a potential solution that can be compared to response alternatives (i.e., constructive matching; Arendasy and Sommer, 2013; Primi, 2002; Putz-Osterloh, 1981). In contrast, respondents showing lower scores on measures of these cognitive processes tend to spend more time inspecting response alternatives to eliminate incorrect response alternatives (i.e., response elimination; Arendasy and Sommer, 2013; Primi, 2002; Putz-Osterloh, 1981). Accordingly, we foresee that R8, use of distractors, could be estimated either as a smaller or an insignificant parameter in the UNI group.
In the next section, we presented results of data analysis of the UNI group so as to examine the adequateness of the LLTM to this data set. Later, the LLTM parameters for all groups are presented.
Results
Andersen’s likelihood-ratio test indicated a good fit of the Rasch model to data of the UNI group, χ(21) = 27.616, p = 0.15. Figure 4 corroborates this result by showing that the confidence ellipses and the diagonal overlap each other. The Martin-Löf Test, χ(119) = 47.559, p = 1, brought support to the unidimensionality axiom. The InfitMSQ criterion (see Bond and Fox, 2001) indicated that six participants were outside of the suitable range (i.e., InfitMSQ between 0.5 and 1.5) and that all items fall in the appropriate range of 0.79 and 1.10. Person’s abilities and item difficulties were in the range of -1.60 and 3.80 (M ability = 0.67), and in the range of -4.25 and 2.39 (M difficulty = 0.00), respectively.

Note: Graphical model test based on linear relation between the β Rasch estimates of the high performance group (raw scores > median; y axis) and the low performance group (raw scores <= median; x axis). Source: Own elaboration based on the calculation of the Rasch Model in 2017.
Figure 4: Scatter plot for university students group.
Additionally, the person-item map suggests (see Figure 5), in general, an adequate distribution between item difficulties and person abilities. Nonetheless, the four items located at the left of the scale do not show correspondence between their difficulty level and the ability of participants. This finding can be interpreted as a higher level of reasoning abilities for university students compared to high school students. The correlation between difficulty parameters of the Rasch model and the LLTM, r(20) = .97, p > 0.001, suggested that the latter model captured the data structure as well as the Rasch model.

Note: The top panel shows persons’ distribution according their ability level (x axis). The bottom panel shows each item (y axis) according the level of difficulty (x axis). Note: T1.1 = Test 1 item 1; T2.1 = Test 2 item 1. Source: Own elaboration based on the calculation of the Rasch Model in 2017.
Figure 5: The Rasch person-item map for university students of Study 2.
Figure 6 shows η parameters (i.e., the estimated parameter for each rule) for study sample, validation sample, and UNI group. Parameters including zero in their respective 95% CI indicate a no reliable effect on item difficulty. Figure 6 shows that in the case of the UNI group, rules R1, R2, R6, and R8 do not play a major role in influencing the difficulty of the items. These results suggest that the hypothesized set of cognitive operations, related to the ability of high school students solving the FRT, cannot be completely generalized to UNI group.

Note: Dots represent the LLTM η parameters and lines represent 95% CIs. Note: Study = High school students from the study sample; Validation = High school students from the validation sample; UNI = University students. Source: Own elaboration based on the calculation of the LLTM in 2018.
Figure 6: Cleveland dot plot for η parameter for each rule according groups.
Discussion
One of the main contributions of this study relies on the identification and validation of the most important sources of items difficulty that, at same time, contribute to bring evidence of construct validity of the figural reasoning test (FRT). This work also suggests that high school and university students use different strategies when solving figural matrices.
In Study 1 we randomly assigned high school students to different groups: study sample and validation sample. Data from study sample were used to test the proposed set of rules (i.e., the W matrix) and data from validation sample were employed to bring further support to the rules. Study 2 tested again the W matrix in the UNI group and we argued that this group should exhibit higher levels of reasoning abilities due to the admission process at the University of Costa Rica.
Data analysis of validation sample suggests that the proposed set rules are a suitable set of cognitive operations underlying the solution process of FRT. In general, our set of rules was in accord with studies suggesting that types of rules and number of rules influence the item difficulty of figural matrices (Arendasy and Sommer, 2005; Carpenter et al., 1990; Embretson, 2002; Primi, 2001). In the FRT participants had to maintain a set of rules in memory while they conjecture relationships between rules with the aim of choosing the option they expected was accurate. Thus, the significant effect of number of rules on the difficulty of items could reflect working memory capacity, which has been regarded as an important predictor of fluid intelligence tests (Colom, Rebollo, Palacios, Juan-Espinosa, and Kyllonen, 2004; Kyllonen and Christal, 1990; Süß, Oberauer, Wittmann, Wilhelm, and Schulze, 2002). Surprisingly, R9 -number of elements, seems to facilitate the process of solving the items, finding that is in disagreement with other studies (Arendasy and Sommer, 2005; Carpenter et al., 1990; Embretson, 2002; Primi, 2001). We suspect that the number of elements in an item helps to discriminate between good and bad distractors. This hypothesis is based on relationships among R8 -use of distractors, R9 -numbers of elements, and group dynamics. Specifically, the study sample and the validation sample groups in which R8 helps to solve the items also show a different and a larger facilitation of R9 as compared to the UNI students group (first year at the University).
Study 2 revealed how the effect of some rules changes as function of persons’ ability level. A re-analysis of Study 1 data brings evidence of group differences on the relevance of R8 -use of distractors. Particularly, it suggests that high school students (i.e., the study and validation samples), when confronted to the FRT, tend to deal with items by constructive matching as compared with UNI students. Naturally, this finding has to be addressed in detail by verbal reports and other methodologies such as eye-movements analyses. Future studies should put more emphasis in solution strategies since a recent study demonstrated that response elimination can detrimentally affects the construct validity of figural matrices (Arendasy and Sommer, 2013). Furthermore, the remaining discrepancies between η parameters of the UNI versus study and validation samples indicate that it is not opportune to reduce groups’ differences to high or low in performance in the FRT. Our data insinuate more meaningful variations in the so-called fluid intelligence. The present findings are also highly relevant in the domain of education. First, it is well known that fluid intelligence predicts many forms of academic and school achievements and that it correlates with a good management in daily life (Deary, 2012; Smolen and Chuderski, 2015). Therefore, a better understanding of the specific mechanisms involved in fluid intelligence will inform educators about the sources of variation for people in academic contexts, thereby providing a broad view for developing more opportune strategies for teaching and evaluation. Second, although fluid intelligence has been conceived as a stable trait that is relatively unaffected by interventions (Carroll, 1993). However a lot of time and money is invested in training programs with the aim of enhancing their intelligence. In this respect it is imperative that professionals on education inform people about the controversy and the lack of evidence for improving intelligence through these training programs. We suggest that one alternative to clarify this controversy is through the understanding of the mechanisms underlying the individual and group differences in fluid intelligence.
To conclude, this study represents a successful application of LLTM to a fluid intelligence test. Beyond this specific example, the same strategy of analysis could be applied to the construction of other tests-particularly in those for which the automatized generation of items is not possible-and other constructs; it also may help educators, researchers and decision-makers to improve their pursue of relying on the most refined instruments.