Introduction
Whenever a curriculum reform arises there are expectations, however in making a curricular assessment evidence can show reality differs from originally thought. Precisely, Burkhart (2014) describes different ideas on curricular reality, according with this author there are at least four stages:
Proposed Curriculum: corresponding to official documents.
Assessed Currículum: containing all results obtained in official tests (both national and international), usually standardized.
Implemented Currículum: formed by what is really taught in most school rooms.
Achieved Currículum: comprised of what the student body learns.
In this research an analysis is made on the first three stages concerning a private primary education curriculum in Costa Rica located in one province of Heredia urban area. This establishment has preschool, primary and secondary education levels.
Particularly, in the case of primary since 2014 a transformation was started in Mathematics, including a new curriculum and teachers' training aimed at focusing on method strategy and new curricular design.
This implementation was completed by assigning an academic Mathematics coordinator for primary, performed by a specialist in Mathematics teaching high school teacher, whom supported the primary teachers on discipline and curriculum matters.
Nonetheless, an intrinsec curriculum evaluation was necessary (Brovelli, 2001; Molina Bogantes, 2017) allowing to identify the weaknesses and strengths of the institutional mathematics curriculum (CMI) by using instruments from different actors that comprise the education system (Molina Bogantes, 2017).
Background
García-Martínez et al. (2018) did a research using a mixed designed, with recurring approach to integrate empirical and theoretical information, through a deductive process, thus in a transectional way with a group of 4465 individuals from ten Big Mteropolitan Area (GAM) schools in Costa Rica with diverse modes and school environments, from which a sample of 246 teachers and 5 principals (3 from primary and 2 from secondary) was extracted, the first participated in filling Likert scale questonaires with 89 items and the latter, in focused interviews.
Within the highlighted results and directly connected with this research we find it is not posible to cut off the implementation of a cuurriculum from the way as perceived by the teachers, and how they perform their activities inside the schoolroom, the foregoing due to the close relationship with planning and linking necessity from the management to execute a curricular design (García-Martínez et al., 2018).
Loría, & Lupiáñez (2019) did a qualitative research with a phenomenological design. The goal was to identify and describe the changes in didactic knowledge of a group of teachers as structural part of their profesional expertise. There were 9 teachers, 8 actives, most working at prívate schools and with few years of experience. The research was focused in a 100 hour course in bimodal type.
They employed instruments such as: an initial questionnaire, non participant school room observation which implied review of planning and exams, registration of participants' presentations, registration of their contributions and personal interventions in connection with the presented themes and concepts, participants' written thoughts, audio recordings, final works presented by participants and final evaluation questionnaire of the course. The data analysis used emerging methods and reiterated interpretations of the contributions by the informers and diverse sources, using codes, categories and content analysis in the observation transcriptions and the other documents. Finally, they triangulated the different inputs: written course productions, registrations of schoolroom observations, plannings and evaluations designed by teachers.
From the findings it was highlighted that regarding the planning of the student work, the authors indicate there are institutional directives and internal guidelines compelling the teachers to make adjustments which in some opportunities hinder the curriculum fulfillment. Although the monthly plannings and lesson plans must be parallel textbooks, in the latter registration of detailed ideas, examples, tasks and activities which not necessarily correspond directly to the first ones due to institutional directives; nevertheless, in some instances teachers register those adjustments on their own logs.
According to Gamboa Graus and Boirrero Springer (2017), who made a meta-analysis, where they synthesize research results on curriculum coherence, situated in the educational context, emphasizing the individual student and the teacher in the Mathematics teaching-learning process, indicating about teachers that their efforts in planning remain even in the dosage of contents to be offered, class scheduling and systems, which in said process lose the integral vision of the curricular design.
The authors point out the lack of didactic contextualization as a frequent problem, corresponding to coherence among objectives and contents with methodology and evaluation, for constant changes in the last two, as they are dynamic processes. Regarding the negative results generated when analyzing the student performance, they indicate the cause is the low curriculum correspondence being taught to what pupils learn and live.
Curricular design
Fort he effects of this article consideration is given to the curricular design used by the educational center is a linear model, because it is based on the description of a series of learning and teaching activities, where activities are planned for the teacher to achieve specific skills related to the subjects content, with an identifiable methodology and which concludes with an evaluation within a established timetable (Molina Bogantes, 2017; Quesada Solano et al., 2007).
Additionally, any curricular design is implicit within a three phase process: building, execution and evaluation. In phase two, it is a dynamic process developed in the schoolrooms, through planning, lessons development, which involve school administrators and learning evaluations. The third phase must be a constant process directly concerning phase two, with the purpose of identifying difficulties, improvement opportunities and elements for decision-making, the foregoing through a comparative process between the curricular design first phase (expectation) and execution (reality) (Molina Bogantes, 2017; Quesada Solano et al., 2007; Rojas Vargas, 2017).
Also it is considered that a curricular design must be open and reflectible, but must be in a systematic way to contribute to the building of knowledge and to orient educative actions, in a coherent and articulated way, the latter is denominated a level of micro curriculum concretion because it implies the plannings of the educational process (Molina Bogantes, 2017; Quesada Solano et al., 2007).
Didactic Planning and Learning Evaluation
According to Cao (2018), any amendment to the curriculum in the XXI century, implies changes not only in curricular networks, but in the teaching methods, the didactic materials and the manner to perform the evaluation.
Regarding the teaching methods, these are placed in the lesson plan; for Molina Bogantes (2017), the didactic planning is the document evidencing the teacher's making of concrete decisions to organize, execute and evaluate the aspired learnings, corresponding to an actions script developed inside the classrooms, which must consider the context and interests of the population in close relation with the national official programs, in this specific case with the institution curricular design or for what for the autor corresponds to Curriulum Center Project (PCC) which in referring to the educational institution in this article will be denominated Institutional Mathematics Curriculum (CMI).
Additionally, it is essential for a successful curriculum implementation the teaching body to master the curriculum they must deliver, including the institution mathematical and pedagogical knowledge curriculum expectations (Mena González et al., 2019).
The following features are deemed indispensable in a didactic planning: flexible, permanent, precise, relevant, coherent, pertinent, prospective, participative and functional, therefore, in their design most of them must be considered. Among them they have defined functions: avoiding improvisation, guaranteeing full development of the curricular design and optimizing time, among others (Molina Bogantes, 2017).
According to Artigue (2018) there are unpredictable scenarios in a curriculum implementation and this is associated with problems impacting the didactic planning among them:
Directives from administration related with specific criteria of shape, content and mediation, which in some occasions interfere with the embodied expectations in the curriculm designs and which are binding for the teacher.
New organizational concepts that have been correctly described and lack examples, both of the curricular design and the pedagogic mediation.
The students' needs implying an alternate lesson plan requiring new ideas, sequence or examples (Lupiáñez Gómez, & Ruiz-Hidalgo, 2018).
In this close relationship with the didactic planning an evaluation of the learnings is set, the second must keep direct relationship with the specific skills set up in the lesson plan.
Evaluation purpose is to offer information on the teaching-learning process and determine the difficulties, aspects to improve and supply inputs for decision-making on learning activities or promotion. The formative or summative evaluation types provide information of different nature: The first allows to observe in unsanctioned detail the student work, this through observation, worksheets or notebooks; and the second, offers evidences of the link between the didactic planning at administrative level and the students' acquired skills, but this time in function of a pointage sanction in the written test, quizz or assignments (Rojas Vargas, 2017).
Curriculum Evaluation
Curriculum evaluation, according to (2017) corresponds to a global action including the actors in an institutional project. Therefore, it involves the expected aspirations, the way planned to reach such goals and the judgment of the product generated in the classrooms through some type of measurement, the foregoing with the intention to accomplish a joint assessment.
Curriculum evaluation aims to verify its validty, in terms of how much is achieved with its planning and implementation, reach satisfying results to claims made by society to educational institutions (Molina Bogantes, 2017), this implies a cycle among design, execution and evaluation.
Accordingly, Artigue (2018) points out regulation mechanisms are a necessity and in them, those involved must participate because even though when the design and implementation are careful, there are always scenarios that can not be foreseen. Generally, the design is cared, intermediate implementation efforts are made and they decrease in monitoring or evaluation.
Furthermore, Arnaz (1981) establsihes that it is through curriculum evaluation that the curriculum worth can be established when put into practice in a teaching-learning process.
Institutional Mathematics Curriculum (CMI)
This section contains the description of the institutional project for primary, in which the Mathematics expectations are presented. The primary education is divided in three terms.
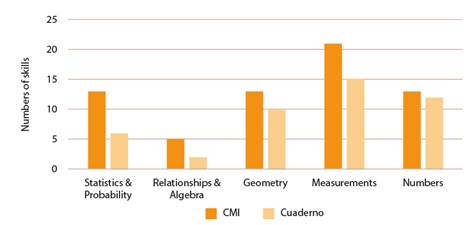
The CMI is divided in these areas: Numbers, Relationships and Algebra, Statistics and Probability, Geometry and Measurements. For each one there is a set of mathematical skills that must be developed in the classroom.
In the CMI it is deemed to work the five mathematical areas all school years. Additionally, the annual lesson percentage time that must be dedicated to the Number area rounds about 40%, while in the other areas said percentage varies between 10% and 20% approximately. Also it can be observed that time percentage to be assigned to the Relationships and Algebra area increases in each school level as advancing. Additionally, it is important to indicate the CMI is based on Costa Rica official Mathematics Programs (Ministerio de Educació Pública (MEP), 2012).
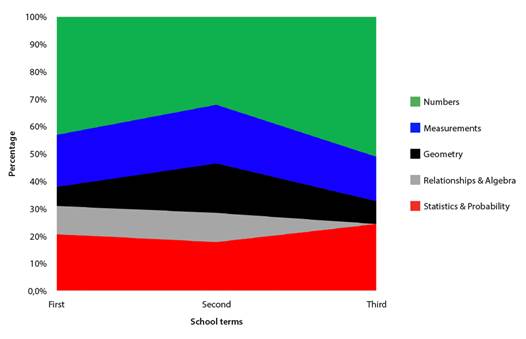
Also, the institution has a dosage allowing it to organize specific skills on time and same should be the foundation of the teachers' plannings. In this document it is discussed to work out skills of almost every area en each of the three school levels. To exemplify said disposition, in Figure 1 distribution of the second year mathematics areas distribution is shown.
Note: Own elaboration based on MEP (2012).
Figure 1: Time percentage to be dedicated to each mathematics area on second year level
In Figure 1 time dedicated to Numbers shown varies according to school year: first it is 43%, second it is 31% and third climbs to 50% approximately.
Percentages of the Measurements and Statistics and Probability areas oscillate between 16% and 24% in the three levels, while the Geometry area in the second level more time is devoted regarding the other two. The Ralationships and Algebra area must be worked out only during the first two levels and lastly, for the Statistics and Probability area has a 10% and 15% respectively.
Methodology
It was worked under the post positivism paradigm, with a mixed design and as the quantitative and qualitative technics data are integrated for the interpretation, it is denominated integral complemented triangular; additionally, a longitudinal mode was employed between the years 2017-2018 (Elías Hernández, 2019; Villalobos Zamora, 2017).
For effects of this research the population of primary is provided with approximately 120 students and 8 mathematics teachers.
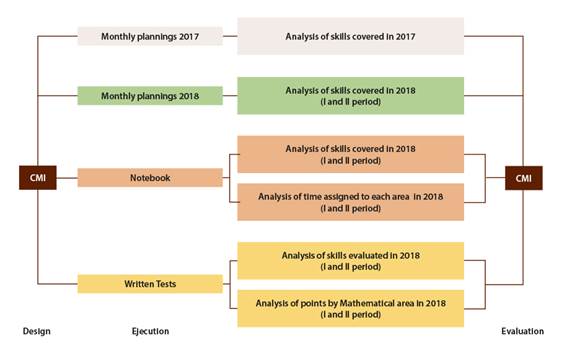
Such as pointed out by Molina Bogantes (2017) in order to perform a circular evaluation, it is necesssary to analyze the different actors, that is, the CMI, the teachers (with their plannings and evaluations) and students (with their notebooks) are the subjects of interest in this section.
Two techniques were used, the first the descriptive-interpretative analysis (Cohen et al., 2011), which compared CMI with:
Monthly Plannings of 2017.
Monthly Plannings of first and second 2018 periods.
A school year notebook from a randomly selected student.
Written tests applied during the first and second period of 2018 (such documentation included mathematics skills to evaluate each test).
The foregoing in recursive manner, to complete a cycle starting and finishing in the CMI, the handling of the information implied a didactic-pedagogical analysis of each of the specific mathematical skills, from a perspective that should visualize if a set of them, selected by the teacher for the didactic planning achieved to encourage the CMI expectations. Additionally, this content analysis procedure was applied to the students' notebooks, however this process was more complex as it included interpretation whether the proposed activities encourage the specific skills from the didactic perspective, a process that should be done by a specialist at the CMI and Mathematics teaching.
The second technique is associated with the statistical analysis, the generated information was codified with the analysis of the documents in the following way: (0) was assigned to non matching aspects and (1) to those matching; when making a comparison between the CMI and each element: didactic planning, notebooks and exams. Therefore, the information was transformed into numeric data and an integreal information analysis was performed.
For the effects of the research presented herewith and because of the information quantity obtained, only the second year documents were used, which was obtained from the recursive comparison between the CMI and the other documents.
Regarding the analysis, it was performed in the following way:
The information was clustered according to the documentation type and school year.
One or two content analysis was performed of each document compared to CMI.
Information was computerized in terms of 0 and 1 for a descriptive statistical analysis.
In the case of pointage of written tests, all ítems were analyzed and categorized according to the matheatical area.
Figure 2 shows a diagram of the performed process.
Results, Analysis and Discussion
Skills: Monthly Plannings 2017
CMI and 2017 monthly plannings were compared, in order to establish and verify the coincidence percentage between both documents, as an example the analysis made between Statistics and Probability and Geometry areas is presented.
After making the one on one comparison of the specific skills of Statistics and Probability in the first period, it is determined the plannings and CMI coincide completely. However, the Geometry panorama is different as is shown following.
Table 1: Skills comparison of the Geometry area and the CMI and the second years planning, in the second period of 2017
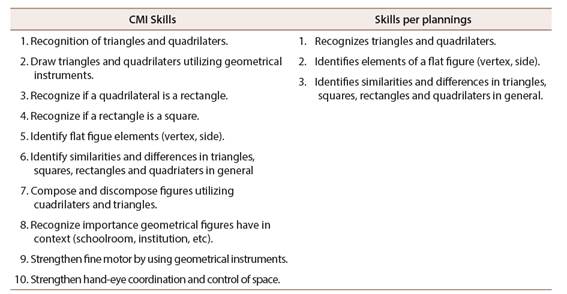
Note: Own elaboration based on CMI and 2017 second grade monthly plannings.
In Table 1 it is seen in the plannings only three specific skills are considered in the Geometry area, associated with recognition of triangles and quadrilaters, as well as their elements, differences and similarities, while in accordance with CMI those mathematical skills must be considered together with others which implied a more articulated work with these figures, including CMI skills 3 and 4 look for a deeper analysis of these geometrical figures and 7 favors their usage, however, these expectations are not indicated in the plannings. Following, a general area analysis during 2017 is shown.
Table 2: Comparison of number of mathematical skills from CMI and those worked out per second grade teaching plannings for 2017
| - | CMI | Plannings 2017 |
|---|---|---|
| Statistical and Probability | 16 | 10 |
| Relationshipss and Algebra | 05 | 02 |
| Geometry | 16 | 07 |
| Measurements | 25 | 19 |
| Numbers | 19 | 11 |
| Total | 81 | 49 |
Note: Own elaboration based on CMI and 2017 second grade monthly plannings.
As can be seen in Table 2, in neither of the mathematical areas totality was accomplished with current CMI skills in 2017, the more affected being Numbers and Geometry areas.
Only 49 skills out of 81 which should be tackled were used, the second grade teacher covered a 60,4% of the CMI for that year, although during the first period all Statistics and Probability skills were posed.
It is important to emphasize this level teacher worked out other mathematical skills, but not the ones indicated by the CMI. Therefore, at the beginning of 2018, this information was disclosed with the institution teacher body, in order to avoid similar situation in the 2018 plannings.
Skills: Plannings for 2018
For 2018, this analysis was only made for the first two periods of the school year, since the goal was to follow up and make adjustments at the last period of said year.
For this analysis the same previous strategy was followed, one on one the current mathematical skills were analyzed in the plannings and they were compared to CMI and the summary is presented following.
Table 3: Comparison of number of mathematical skills per CMI area and those worked out according to second grade teaching plannings in the first two periods of 2018
| - | CMI | Plannings 2018 |
| Statistics and Probability | 13 | 07 |
| Relationships and Algebra | 05 | 04 |
| Geometry | 13 | 06 |
| Measurements | 21 | 11 |
| Numbers | 13 | 12 |
| Total | 65 | 40 |
Note: Own elaboration based on CMI and 2018 second grade monthly plannings.
As shown in Table 3, in spite the teachers were instructed of the importance of the update of the plannings according to the CMI, in this education level some of the mathematics skills are being ignored. An improvement is detected regarding to what happened in 2017, with regard of the number of skills in the Numbers and Relationships and Algebra areas, however, the Geometry, Measurements and Statistics and Probability were neglected (compare to data on Chart 2).
Generally, according to plannings, a 61,5% of the CMI mathematical skills was covered. This panorama is very similar to what happened in 2017.
Skills: Notebook 2018
To continue evaluating the CMI implpementation, the notebook notes were checked from a second grade student (randomly chosen) thus in order to be able to evidence the proposed mathematical skills in the plannings were really developed in class (and not only in the plannings). As per the mediation activities planned by the teacher.
Note: Own elaboration.
Figure 3: CMI mathematical skills developed according to the mediation activities visible in a second grade student's notebook in the first two periods of 2018
According to Figure 3, in the student's notebook it can be seen activities to develop some skills mainly in the Geometry and Measurements areas which were not considered in the plannings (see Table 3), such as:
Establishing relationships between meter and centimeter. (Measurements)
Identify in the student's context situations where it is necessary to make length measures. (Measurements)
Compare lengths without a ruler. (Measurements)
Estimate currency quantities. (Measurements)
Compare monetary quantities. (Measurements)
Draw triangles and quadrilaters using geometrical instruments. (Geometry)
Compose and discompose figures by using quadrilaters and triangles. (Geometry)
In Figure 4 evidence shows the accomplished work by the student where the first two skills are taken previously described.

Note: Images of the investigation.
Figure 4: Second grade student's notebook. Activities performed Thursday Jul-26 and Tues Jul-31, 2018
Considering the above, according to the notebook, a 69,2% of the CMI mathematical skills was covered.
A posible explanation explaining the reason of the incorporation of mediation activities which were not planned in the teacher's planning, is that there is a continuous review of these plannings by the administrative authorities and the mathematics academic coordinator, a suposition arises the incorporation of these themes without evidence in the delivered plannings for the performance of this research, this situation is considered frequent because within the schoolroom dynamics it is usual to make adjustments according to the the population's needs and therefore differences are to be found between the monthly plannings and lesson plannings (Gamboa Graus, & Borrero Springer, 2017; Loría, & Lupiañez, 2019).
It is important to highlight a student's notebook gives lots of information that may subject to analysis, disclosing related data with time dedicated to each of the mathematical areas, the used didactic resources, the types of activities to aboard previous knowledge, put skills in practice and encouraging them. Should be pointed out the institution has as a rule to date on the notebook any student absence.
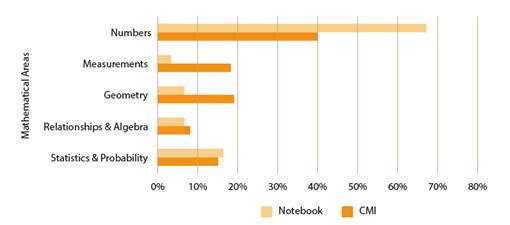
Time Assigned to Each Area: Notebook 2018
For this stage all the written dates in the student's notebook were considered, the activities performed in each term and the lessons accounted for, as can be seen in Figure 4. These activities were categorized according to the corresponding mathematical area, time percentages assigned to each area, in the first and second school period. The results show Numbers reached 67,1%, Measurements 3,3%, Geometry 6,6%, Relationships and Algebra 6,6% a lastly, Statistics and Probability 16,4%.
To the Numbers area more than two thirds of the time are given, while the other areas are hurt by less time assignment, including almost voiding them, as in the case of Measurements.
Note: Own elaboration.
Figure 5: Comparison of time percentages assigned to each mathematical area according to CMI and according to a student's notebook in periods I and II of second grade in 2018
Should time be compared which according to CMI must be dedicated to each mathematical area in the second year, with the above described percentages the following representations is obtained.
In Figure 5 difference is shown of more than 20% of time dedicated to Numbers area, in comparison to what really should be dedicated to that area, this makes the Measurements, Geometry and Statistics and Probability areas to have dedicated less time. Additionally, if consideration is given that according to as analyzed previously (see Table 3 and Figure 3), where 100% of the mathematical skills are being considered in the different mathematical areas, then in this learning level there is an important gap between what is planned in the forseen curriculum and the implemented one (Burkhardt, 2014).
Skills Evaluated: Written Tests
In order to analyze part of the assessed curriculum (Burkhardt, 2014), written tests applied during the first and second period were requested. Additionally, from the tests the cluster of mathematical skills were assigned which would be graded in each test, therefore, this allowed to analyze the CMI skills considered to be subject of summative evaluation were chosen and what percentage of same were evaluated in each area.
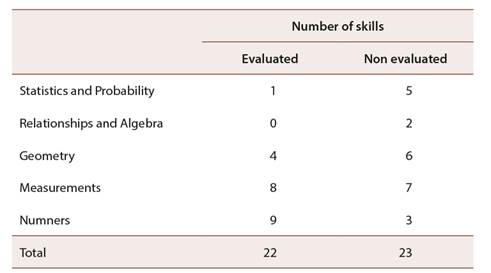
Table 4: Number of evaluated skills and non evaluated by mathematical area, in the first and second period of 2018 school year in second grade
Note: Own elaboration based on second grade written tests first and second period.
In Table 4 it is observed in the written tests only skills from Numbers, Measurements, Geometry and Statistics and Probability were evaluated, the latter in minor measure. In the case of Numbers almost all the skills worked out at classroom level were and those from Relationships and Algebra were not.
This reinforces as pointed out in previous analysis, where not only in the pedagogic mediation certain mathematical skills and even entire areas are neglected, but also in evaluation the Realationships and Algebra as well as Statistics and Probability areas are the most affected, in this case.
Area Score: Written Tests
Upon reviewing each of the written tests applied to the students during the first and second period of 2018, each of the ítems was analyzed and categorized according to the mathematical area. Later, the assigned itemized points were added and the result was that Numbers is much more evaluated than the other mathematical areas (a 65%), the Statistics and Probability area few were the ítems evidenced in written tests (a 6%). 18% of the score are questions about Measurements and only an 11% for Geometry. No items were assigned to Relationships and Algebra area.
It can be affirmed there is a preference for Numbers area by the teachers to work out at classroom level and in evaluation. Precisely, this affirmation is reinforced upon analyzing the score destined to each mathematical area in written tests.
Conclusions
Even when institutional efforts are aimed at offering a better educational offer in Mathematics and this is laudable, because it interrupts the generality indicated by Artigue (2018) on the lack of interest in monitoring and evaluation of curricular designs, even this institution has pending actions in the implementation of the CMI.
Data have evidenced there are differences between what is pointed out in the CMI and the time to be assigned to each of the mathematical areas in the didactic plannings, as written on the student's notebook and the percentage of the itemized points according to the mathematical area, therefore the differences are evident among the stages of foreseen curriculum, implemented curriculum and evaluated curriculum (Burkhardt, 2014). In Figure 6 the relationship of these three stages is shown in second grade CMI.
Notes: Own elaboration with information from Burkhardt (2014).
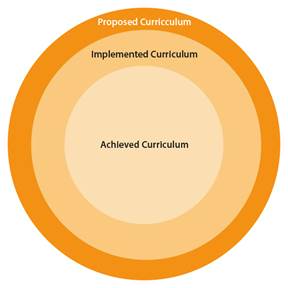
Figure 6: CMI and the relationship among the curriculum stages, as per first and second period data of 2018
Particularly, the difference evidenced in this research between the CMI and the plannings indicates there is not a complete bind between the curriculum implementation and the activities made in the mediation such as described by García-Martínez et al. (2018).
The Numbers area has more time dedicated during lessons (67,2%) and the highest score is given in written tests (65%). A posible explanation of this situation es the initial weak formation in mathematics of the primary teachers in Costa Rica (Alpízar-Vargas, & Alfaro-Arce, 2019; Morales-López, 2017; Ruiz, 2013), for which it is supposed in the education practice work is given to those themes better known by them. Alpízar-Vargas, & Alfaro-Arce (2019) point out in their research that, in the initial formation of primary teachers, an average of only 8% of the courses have a mathematical component.
Additionally, in spite there are curriculum changes (as is the case of this institution) it is hard the teachers assume a modification of their professional practice in spite of the institutional efforts (Mena González et al., 2019; Osta, 2018).
This reserach socialized with administrative authorities and teachers body in two instances: February 2018 and August 2018. The first session was purpotedly to communicate the 2017 results. In socializing the analysis data present in this research with the institution teachers, they indicated that in that year it was not clear to them the institutional directives over the new Mathematics approach, this agrees with Artigue (2018) whom indicates the administrative dispositions could influence the implementation of a curriculum.
In the second instance, the goal was to communicate the results of the first and second period of 2018, in this occasion to take immediate measures regarding the third period of said year.
Within the most important decisions taken at the end of 2018, was the prioritization of those neglected areas both in pedagogic mediation as in written tests. Also, it was decided the researchers to make observations in some mathematics lessons. To finalize, it is recognizable the process made by this institution in creating, executing and evaluating its mathematics curriculum, train its teaching staff, create the mathematic academic coordinator position for primary, among other decisions always with the goal of improving the teaching-learning process of Mathematics.
Declaración de contribuciones
Las personas autoras declaran que han contribuido en los siguientes roles: R. P. V. contribuyó con la escritura del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación. M. Z. C. contribuyó con la escritura del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación.