Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revistas de Ciencias Administrativas y Financieras de la Seguridad Social
Print version ISSN 1409-1259
Rev. cienc. adm. financ. segur. soc vol.5 n.2 San José Jan. 1997
Daniel Muñoz Corea
Economista, Departamento de Estudios Económicos
Dirección Actuarial y de Planificación Económica.
Resumen
En el presente artículo se dedica a analizar los principios en los que se basa la "Teoría de Selección de Cartera" formulada por H. Markowitz, para la configuración de carteras óptimas de bajo riesgo, es decir, carteras que incluyen un conjunto de activos que reconocen el máximo rendimiento combinado con el mínimo riesgo.
Sin duda alguna, la metodología que se postula en esta teoría resulta interesante para los técnicos de la CCSS vinculados con la administración y evaluación de las inversiones de los fondos de reserva del Seguro de Invalidez, Vejez y Muerte, por cuanto posibilita el diseño de una estrategia de inversiones capaz de superar las limitaciones que presenta el mercado financiero nacional, particularmente en lo que concierne a la poca diversidad de instrumentos financieros y a la baja calidad y disponibilidad de información.
Introducción
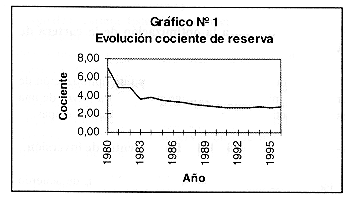
En los últimos años el Seguro de Invalidez, Vejez y Muerte, ha experimentado una caída sostenida en su coeficiente de reserva, es decir en la razón reserva actuarial acumulada/egresos totales del período. Como puede observarse en el gráfico Nº 1, este indicador pasa de 6,99 en 1980 a 2,85 en 1996. Entre los factores que explican este comportamiento destacan tanto el proceso de envejecimiento de la población como el proceso de maduración del sistema.
Conviene señalar, que si bien el método actual de financiamiento de este Seguro (método de prima escalonada) plantea la posibilidad de incrementar la prima en el momento en que los ingresos por contribuciones y rendimientos de la reserva ya no resulten suficientes para cubrir los egresos de las prestaciones en ejercicio, desafortunadamente aún no se conoce a ciencia cierta el grado en que esta medida incrementaría los ingresos totales de IVM, toda vez que un ajuste de este tipo incide económicamente sobre la remuneración de los factores productivos, la distribución funcional del ingreso y la competitividad del país con sus socios comerciales.
Otro conjunto de medidas para revertir esta tendencia del coeficiente de reserva y garantizar el equilibrio financiero del Régimen para un determinado período, se relaciona con el incremento de la edad de retiro, la disminución de la morosidad y de la evasión y/o la disminución de la tasa de reemplazo; sin embargo, de todos es conocida la dificultad que entraña este proceso de reformas.
En este contexto, una medida que ha venido ganando importancia en los últimos tiempos para disminuir, al menos parcialmente, la presión que tiene el Régimen de generar mayores ingresos, es la diseñar una estrategia de inversiones para incrementar el rendimiento de la reserva, sin que ello implique descuidar el principio de seguridad que debe prevalecer en las inversiones que realiza.
Con el propósito de contribuir al diseño de una estrategia de inversiones, que logre superar las limitaciones que presenta el mercado financiero costarricense, el presente artículo analiza los principios en los que se basa la Teoría de Selección de Cartera, para la configuración de carteras óptimas de bajo riesgo.
La Teoría de Selección de Cartera
En 1990 le fue otorgado a Harry Markowitz el Premio Nobel de Economía por el desarrollo de esta Teoría. Podríamos decir que son seis los aportes fundamentales de Markowitz al campo de las finanzas. En primer lugar, postula que no sólo los retornos son importantes a la hora en que los inversionistas deciden sobre la composición de una cartera de inversión, sino también el riesgo al que se exponen para generar los mismos. En segundo lugar, reconoce que en términos generales los inversionistas son adversos al riesgo y que demandan cierto premio por participar en inversiones que consideren riesgosas.
El tercer aporte consiste en la introducción de una función de utilidad a través de la cual cada inversionista puede cuantificar su trade off entre el riesgo de la cartera y el retorno esperado. En cuarto lugar, establece que la manera apropiada para medir el riesgo de un activo individual es sopesando su impacto sobre la variabilidad del retorno (volatilidad) de la cartera completa de inversiones, es decir, no se debe evaluar el riesgo de un activo separado de la cartera de la cual es parte. El quinto aporte, el cual se encuentra muy relacionado con el punto anterior, establece que a través de una adecuada diversificación de activos es posible disminuir el riesgo que enfrenta el inversionista, hasta converger al riesgo de mercado1. Finalmente, y como resultado de los aportes anteriores, Markowitz llega a identificar carteras óptimas (eficientes) que incluyen un determinado conjunto de activos, que generan el máximo retorno combinado con el mínimo riesgo.
La aplicabilidad del Modelo de Selección de Cartera a las inversiones de IVM.
La metodología del Modelo de Selección de Cartera es actualmente utilizada por muchos fondos de pensiones de los Estados Unidos, Europa y Sudamérica. Una de las ventajas del modelo es que permite adaptar su metodología no sólo a las restricciones legales y a las necesidades de liquidez del inversionista, sino también a su grado de aversión al riesgo y a sus necesidades de retorno.
Entre las diversas estrategias que podrían aplicarse al Seguro de IVM, una de las más interesantes a considerar es la configuración de una cartera mixta de bajo riesgo. Esto implicaría maximizar el rendimiento, dado un nivel mínimo de riesgo, a través de una cartera donde, en mayor proporción, los recursos estén invertidos en activos considerados libres de riesgo pero de bajo retorno (tales como los títulos de renta fija del gobierno) y, en menor proporción, en activos de riesgo pero de mayor retorno (tales como los títulos de renta variable).
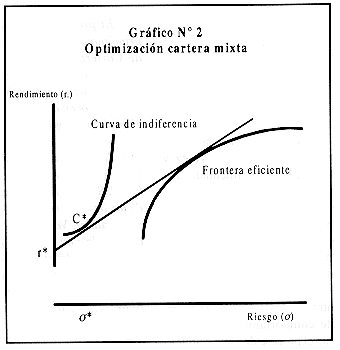
Gráficamente, el proceso de optimización conllevaría a obtener una cartera C* donde el retorno es maximizado en el nivel r*, dado el nivel de riesgo o*.
Requerimientos para la optimización de la cartera de IVM
En términos generales, el proceso de optimización de una cartera mixta de bajo riesgo para IVM a través de una estrategia activa de inversiones, requeriría de tres etapas:
a-Selección y análisis de los instrumentos de inversión
En esta primera etapa, se debe establecer, de acuerdo con las preferencias del Seguro de IVM como inversionista institucional y a la información disponible en el mercado, el conjunto de activos financieros que formarían la cartera de inversiones, así como del set de carteras factibles de ser conformadas por los activos disponibles. Algunas de las principales decisiones en esta etapa se centran en el tipo de títulos del sector público que conviene tener en la cartera, el tipo de inversiones, que se realizarían en el sector privado, y si se debe invertir o no en títulos valores de otros países.
Esta etapa es sin duda alguna la más importante del proceso de inversión, pues la elección de tales instrumentos debe estar en función de las necesidades de liquidez, de las restricciones legales, del grado de aversión al resto y de las necesidades de retorno del Régimen. Dado que ello requiere de un amplio conocimiento del mercado financiero nacional e internacional, se considera indispensable la asesoría de instituciones financieras especializadas en esta materia.
En lo que concierne a la selección y análisis de los activos libres de riesgo, los cuales representarían la mayor proporción de los activos totales de la cartera, la teoría establece que lo ideal es poseer títulos indexados perfectamente a los precios y que la madurez de los mismos sea idéntica al periodo de duración. Esta es la única forma de mantener garantizado a través del tiempo el retorno de tales activos.
En este sentido, conviene señalar que si bien en la actualidad la reserva de IVM posee una importante proporción de su cartera en títulos indexados (títulos TUDES y Tasa real), estos están sujetos al riesgo de tasa de interés, porque los intereses reales pueden cambiar impredeciblemente a través del tiempo, afectando con ello el flujo de reinversión de intereses. Para inmunizar estos títulos contra este riesgo debe analizarse la viabilidad de mantenerlos hasta el tiempo que indique su duración.
Por su parte, en lo que respecta de los activos considerados riesgosos, que ocuparían la menor proporción de la cartera, se debe tener presente que su selección y análisis debe basarse son sólo en su retorno sino también en la variabilidad de ese retorno (volatilidad) y en las coincidencias de las alzas y bajas de los precios de cada activo con los demás (correlación).
Acá conviene tener clara la diferencia que existe entre el riesgo particular de un activo y la contribución del mismo al riesgo de la cartera. Este último concepto es el que resulta relevante a la hora de la toma de decisiones de inversión, dado que un activo muy riesgoso puede reducir el riesgo de la cartera de encontrarse su retorno, por ejemplo, negativamente correlacionado con el retorno de la cartera. En este sentido, sería muy conveniente poder simular la incorporación de diferentes activos al portafolio de inversiones de IVM para observar en que medida ellos contribuyen a mejorar el perfil de retorno-riesgo.
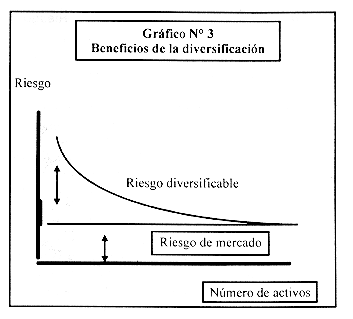
También debe tenerse presente en este campo, el papel fundamental que juega la diversificación para la disminución del riesgo. El gráfico N° 3 ilustra cómo una adecuada diversificación permitiría reducir el riesgo que enfrentaría el Seguro de IVM, pues al incrementarse el número de activos componentes de la cartera, se disminuye la exposición al riesgo propio de cada uno de ellos, hasta converger al riesgo de mercado.
b-Determinación de la frontera eficiente e identificación del portafolio óptimo de activos riesgosos.
Esta etapa involucra la determinación de las mejores oportunidades riesgo-retorno disponibles de las posibles carteras de inversión, las cuales pueden representarse gráficamente a través de la frontera eficiente que ilustra en el Gráfico N° 2. Para la construcción de esta frontera, se requiere analizar tanto los retornos, como la matriz de convariancias y varianzas que resulta de los activos riesgosos previamente seleccionados.
Cada punto sobre esta curva implica una cartera eficiente, es decir, la mezcla de activos que más retorno logra para un riesgo determinado, y que menos riesgo padece para un retorno determinado.
La escogencia del mejor portafolio riesgoso del set disponible, resultará de combinar la información de la frontera eficiente con la del set de activos libres de riesgo.
3-Determinación de la mezcla óptima entre activos libres de riesgo y activos riesgosos.
Finalmente, corresponde determinar la mezcla óptima entre el portafolio óptimo de activos riesgosos y el set de activos libres de riesgo. Lo anterior, mediante la maximización de la función de utilidad que se diseñe para IVM, como inversionista institucional. Lo importante acá, es que el diseño de esta función de utilidad debe permitir asignar un puntaje por bienestar o utilidad a cualquier cartera de inversión, dependiendo de su retorno y riesgo, posibilitando a su vez, la penalización del riego conforme con el grado de adversión del Seguro de IVM.
Criterios de evaluación
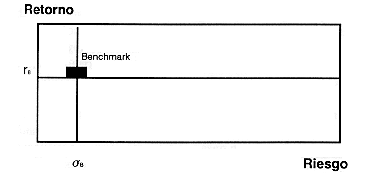
Un aspecto fundamental de este modelo es que permite evaluar el retorno y el riesgo obtenido mediante una estrategia activa de inversiones, comparándolo con el retorno y el riesgo que se obtendría de la aplicación de una estrategia de inversiones pasiva. Como se ilustra en el siguiente diagrama, los resultados de una estrategia activa se considerarían satisfactorio en el tanto se ubiquen a la izquierda y hacia arriba de un índice (Benchmark) seleccionado para representar el resultado retorno-riesgo de la estrategia pasiva.
Conclusión
La necesidad del Seguro de Invalidez, Vejez y Muerte de incrementar sus ingresos en un contexto de mercado financiero poco desarrollado, indiscutiblemente impone la exigencia de avanzar hacia nuevas y más eficientes formas de administración de carteras de inversión. Dado que la teoría de Selección de Cartera establece principios apropiados para llevar adelante un proceso eficiente de inversiones, no cabe duda de que la conceptualización de estos principios constituye el primer paso para avanzar en esa dirección.
Bibliografía
D. Fisher y R. Jordan, "Security Analysis and Portfolio Management", Prentice Hall, sixth edition, 1995.
J. Fabozzi, F. Modigliani, M. Ferri, "Mercados e Instituciones Financieras", Prentence Hall Hispanoamerica, primera edición, 1996. [ Links ]
Ley Constitutiva Caja Costarricense de Seguro Social. [ Links ]
Reglamento Seguro Invalidez, Vejez y Muerte, 1995. [ Links ]
Reglamento para la Inversión de las Reservas del Régimen de Pensiones de Invalidez, Vejez y Muerte, CCSS. [ Links ]
1. El riesgo de mercado o riesgo sistemático es aquel riesgo del cual no es posible aislarse a través de la diversificación, pues
afecta al mercado en su conjunto.