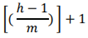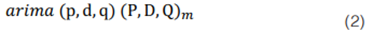Introducción
El tráfico vehicular es un problema complejo de resolver a nivel mundial, no sólo por el crecimiento de vehículos, sino que también por la dinámica entre las variables que lo componen, como las limitaciones de la red vial, densidad poblacional, el cambio en el comportamiento y hábitos de las personas, accidentes de tránsito, eventos climáticos, obras viales, períodos de vacaciones o estacionales. Costa Rica no está exenta a estos problemas, en los últimos 10 años el crecimiento de la cantidad de autos es de un 60% (1); durante cada año de la última década, la cantidad de vehículos que son inscritos ante el Registro Nacional superó los nacimientos reportados en el territorio (2); el 50% de personas que laboran lo hace en un cantón distinto al de su residencia, las personas se movilizan para trabajar, estudiar o realizar trámites o actividades de comercio. Todo esto implica un mayor flujo de vehículos de transporte público, privado y comercial que se concentra en el Gran Área Metropolitana (GAM) quien aglutina el 60% de los atascos vehiculares (1).
Ante la necesidad de gestionar el transporte vehicular terrestre, los sistemas de transporte inteligente (STI) ofrecen una alternativa de apoyo a la solución de estos problemas. A pesar de que en Costa Rica no posee una tecnología muy avanzada es necesario aprovechar y hacer uso de lo disponible y combinar este recurso con otras herramientas para apoyar el planeamiento, gestión y diseño de políticas de transporte y movilidad. Actualmente Costa Rica posee tecnologías de transporte que funcionen 24/7 en la ruta 27 y logra capturar el flujo vehicular en un intervalo de una hora.
Diversos autores han evaluado el rendimiento de modelos de predicción de flujo de tráfico, (3) resume recientes avances y retos para el pronóstico del tráfico considerando aspectos como métodos de predicción, horizonte de predicción, escala, contexto de predicción, fuente de datos, factores exógenos, variable a predecir, tipo de optimización, entre otros. El horizonte de predicción observado es variado, 2, 15, 30 minutos o una hora, hasta 2 días. Entre las tecnologías utilizadas para recabar datos en carretera se encuentran sensores piezoeléctricos, magnéticos, inductivos, de infrarrojos, de microondas o videocámaras, utilizados en autopistas con y sin intersecciones, así como en zonas urbanas o rurales. Existe relativamente poca evidencia de análisis de flujo de tráfico en países subdesarrollados cuya tecnología es limitada tanto en adquisición, uso, implementación y mantenimiento. El término ''corto plazo''en las predicciones de flujo de tráfico se relaciona con un horizonte de predicción de hasta una hora (4). Entre las propuestas de corto plazo (5) utilizan un modelo híbrido de estadística neuronal para el pronóstico de flujo de tráfico urbano con muestras de 1 hora, para 3 meses; (6) proponen un modelo de corrección de errores vectoriales de umbral de tiempo-espacio (TS-TVEC) para la predicción del estado del tráfico a intervalos de una hora, demostrado además que es un buen intervalo de tiempo para realizar distintos análisis con los datos recolectados. Otros autores utilizan intervalos más cortos, (7) analiza intervalos de 15 minutos, (8) intervalos de 5 minutos, mientras que (9) explican que pueden bastar 5 minutos para que la congestión vehicular se genere.
Usualmente en series de tiempo horarios pueden presentarse características que deben ser analizadas con detenimiento; como lo es la estacionalidad compleja (10). Los métodos de pronóstico estacionales básicos y muy utilizados son los métodos Ingenuo Estacional (SNAIVE), Holt-Winters y ARIMA Estacional (SARIMA); este último implementado con errores de entre 4 y 10% (MAPE) (11). Modelos más sofisticados utilizan Máquina de Soporte Vectorial (12), predicciones Espacio-Temporales (13), Espacio-Temporal de flujo de tráfico con K vecinos más cercanos (KNN) (14) y Redes Neuronales (15) o con propagación hacia atrás (BP) (16). A pesar de que se ha desarrollado una gran cantidad de modelos aplicados al tráfico vehicular, el reto persiste, no solo por las características del fenómeno, sino que además porque las tecnologías y tipos de datos cambian (17); aun así, los modelos básicos como SNAIVE y ARIMA son referencia para pronosticar antes de aplicar cualquier modelo sofisticado y complejo (18).
Para el desarrollo de esta investigación los modelos que se utilizan son el SNAIVE, el SARIMA y el de Autoregresión con Redes Neuronales (NNAR), que permiten el modelado complejo de relaciones no lineales entre las variables de entrada y de salida para datos horarios y con alta estacionalidad. El estudiar y aplicar diferentes métodos de predicción permite contribuir con las investigaciones y hallazgos en tema del transporte en Costa Rica, diseño de políticas públicas y la formación de una opinión crítica de la ciudadanía sobre temas estratégicos. En (19) explica que el fin es utilizar la tecnología digital y datos para mejorar el control en las calles, la experiencia y calidad del pasajero y/o conductor en Costa Rica, puesto que el país presenta uno de los mayores índices de insatisfacción vial a nivel mundial.
El método ingenuo es uno de los métodos básicos de predicción, simple de aplicar y efectivo, (20) es ruidoso, no filtra ningún tipo de ruido, lo que hace que el modelo sea muy volátil a las predicciones, determina los pronósticos como iguales al último valor de la misma temporada anterior. Esta estacionalidad se considera en el término agregado y permite detectar y manejar una serie de tiempo que tenga variaciones o patrones sistemáticos cada cierto periodo (T). Formalmente, se representa el pronóstico para el tiempo T+h como en la ecuación 1:
Donde,
h= horizonte de predicción
m= periodo estacional
SARIMA es una extensión del modelo ARIMA desarrollado para tratar la estacionalidad compleja en dos partes: el proceso autorregresivo (AR) se basa en la idea de que el valor actual de la serie Xt puede explicarse en función de valores pasados (p), los cuales determinan el número de rezagos (k). Para calibrar esta componente, se busca cuántos términos AR se necesitan para explicar el patrón de autocorrelación en una serie de tiempo. El orden de media móvil MA, se basa en un modelo lineal ''determinado por fuente externa'', es decir, modela aquello que los retardos no capturaron en el modelo de AR. Un modelo de promedio móvil usa errores de pronóstico basados en un modelo de regresión, donde cada resultado del MA puede considerarse como un promedio móvil ponderado de los últimos errores de pronóstico: La (I) de ''Integrado''indica que los valores de los datos han sido reemplazados por la diferencia entre sus valores y los valores anteriores. Este proceso puede realizarse más de una vez con el fin de que el modelo sea estable en media y varianza. En la ecuación 2 se muestra SARIMA con componente que modela la dependencia regular asociada a observaciones consecutiva (p, d, q) y la estacional que está asociada a observaciones separadas por periodos (P, D, Q).
Donde,
p : orden de tendencia de autoregresión
d : orden de diferencia de tendencia
q : orden de tendencia de promedio móvil
P : orden autorregresivo estacional
D : orden de diferencia estacional
Q : orden de media móvil estacional
𝑚: periodo estacional
Una Red Neuronal consiste en un conjunto de neuronas artificiales o nodos conectados entre sí mediante enlaces que son los trasmisores de señales. Estas neuronas están dispuestas en capas, la primera capa de neuronas se encarga de recibir la información que es sometida a diversas operaciones y producir información de salida para continuar su camino por la red. En cada enlace se incrementa o inhibe el estado de activación de las neuronas adyacentes de acuerdo con ciertas ponderaciones o pesos y el valor del resultado es regulado por una función de activación que controla el límite que no se debe sobrepasar antes de que la información se propague a otra neurona. En la Autoregresión con Redes Neuronales los valores rezagados de la serie de tiempo se utilizan como entrada al modelo y la salida son los valores predichos de la serie de tiempo (21), el modelo Autoregresivo NNAR (Neural Networks AR) es un modelo unidireccional con una capa intermedia (10), implementada por el paquete ''forecast''. La ecuación 4 hace referencia a una serie estacional 𝑝 inputs o un modelo de red con 𝑃 últimos observaciones de la serie, P observaciones de la serie estacional y 𝑘 nudos en la capa interna.
Donde:
𝑝: retardos
P: cantidad de veces que vuelve atrás en busca de ciclicidad
𝑘: nodos en capa oculta
𝑚: estacionalidad
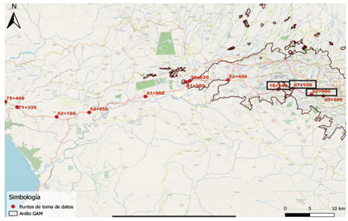
Evaluaremos los tres modelos en los datos horarios de flujo de tráfico vehicular registrados por un punto de conteo sobre la ruta 27 en Costa Rica. En esta ruta se registra datos en 12 puntos de conteo ubicados a lo largo de la carretera, figura 2, mediante sensores piezoeléctricos, los cuales capturan la cantidad de vehículos por hora para cada tipo de vehículo.
La base de datos analizada contiene un histórico desde enero 2015 a enero 2020 y fue obtenida del Ministerio Publico de Obras y Transporte, contienen un total de 1 031 398 observaciones y 8 variables: Punto de conteo, Sentido, Fecha y Hora, cantidad de vehículo por tipo (Liviano, Autobús, Camión) y cantidad de ejes de los camiones (2, 3 y 4, 5).
Metodología
Los pasos seguidos y objetivos para el desarrollo del análisis fueron desarrollados con el software R y son los siguientes:
Limpieza de datos. Detectar, corregir o eliminar registros corruptos y atípicos.
Exploración de datos. Analizar los datos mediante estadística descriptiva y técnicas de visualización. Análisis de puntos de conteo y tipos de vehículos. Analizar puntos con mayor flujo de tráfico vehicular anual, mensual, diario, horario y su distribución. Análisis de Normalidad, prueba de Lillie.test, Autocorrelación, box.test, Estacionariedad, adf.test.
Partición de la serie en datos de entrenamiento y datos de prueba. Selección datos de entrenamiento, flujo de tráfico vehicular recolectados cada hora del año 2019 desde el 1° de enero al 30 diciembre y datos de prueba, día 31 de diciembre del 2019.
Aplicación métodos de predicción. Implementar los tres modelos de predicción: SNAIVE, SARIMA Y NNETAR.
Comparación del rendimiento de los modelos de predicción. Se pronóstica el flujo de tráfico horario para el 31 de diciembre siendo el horizonte de predicción de 24 horas. Se corren los tres modelos con los datos de entrenamientos y se comparan mediante las métricas de error: RMSE (Error Cuadrático Medio), MAE (Error Absoluto Medio), MAPE (Error Absoluto Medio Porcentual). Estos miden su rendimiento tanto para los datos de entrenamiento y de prueba. Se analizan los residuos, se calibran los modelos para comparar el rendimiento.
Validación modelos. Validar modelo mediante validación cruzada utilizando 4 días de enero 2020 (7, 14, 21 y 28). Se toman esos días para mantener la consistencia del comportamiento del martes como lo fue para el 31 de diciembre
Análisis y resultados
El análisis descarta puntos de conteo debido a mediciones faltantes como consecuencia de fallos en los sensores o funcionamiento no correcto. Los puntos de conteo 2+900, 7+100 y 10+540 tienen un comportamiento visual similar a lo largo del tiempo y se encuentran ubicados en área de mayor afluencia de tráfico, ubicado desde el puente sobre el rio Tiribi hasta el puente sobre el rio Corrogres. Un 94% del tránsito en la ruta corresponde a los vehículos livianos. El tramo con mayor concentración vial es de aproximadamente 10 km entre los puntos de conteo 2+900 y 10+540. El punto 2+900 se encuentra a dos kilómetros más novecientos metros a partir del Gimnasio Nacional en la Sabana (antes del peaje de Escazú) y es el punto de mayor concentración de flujo con 2.269 vehículos por hora en promedio. Esta serie predictiva se utilizará para evaluar los modelos de predicción; de acuerdo a prueba ACF el pasado permite predecir el futuro de la serie y sigue un patrón cada 24 retardos con valores altos positivos y negativos, esto indica una alta estacionalidad en los datos. La prueba Dickey Fuller aumentada arroja un , concluyendo que la serie de tiempo es estacionaria.
Particionamos la serie en dos submuestras, la muestra de entrenamiento corresponde a todos los días del año 2019 menos un día, con la cual generaremos los modelos, y la muestra de prueba con el último día del año con la cual se realiza la prueba de los modelos. Para el modelo SNAIVE se utiliza la función snaive(); que toma dos parámetros: la serie de entrenamiento y un periodo estacional de 24. Para apoyar la parametrización del modelo SARIMA, se utiliza la función auto.arima(). El mejor modelo SARIMA obtenido es (5,0,1) (2,10) (24) que indica un orden de tendencia de autoregresión no estacional de 5, una diferencia no estacional de cero (que se corrobora con la prueba Dickey Fuller aumentada de estacionariedad) y que al menos uno de los errores anteriores del AR tenía validez. Es decir, no es necesario un orden de media móvil estacional; requiere una diferencia estacional y toma un periodo estacional de 24. Para el modelo NNAR se utiliza la función nnetar(), la cual toma como parámetros la serie de entrenamiento y el periodo estacional de 24. Se ajusta un modelo NNAR (33,1,17) (24), el modelo utiliza las últimas 33 observaciones como entradas para pronosticar la salida. Para series de tiempo estacionales el valor por defecto es 1, para indicar las veces que vuelve atrás en busca de ciclicidad y utiliza 17 neuronas en la capa oculta. Para todos los modelos se utiliza un horizonte de predicción de 24.
Tomando como día de prueba el 31 diciembre del 2019, en la figura 2 se muestran las predicciones de los métodos aplicados. Visualmente el modelo de NNAR tiene el ajuste más cercano a los valores reales de flujo de tráfico vehicular, al contrario de SNAIVE y SARIMA que se encuentran más lejanos a los valores reales. Sin embargo, el modelo SARIMA aparenta tener una línea menos ajustada que el de Ingenuo Estacional. Un aspecto que tienen en común es que en los extremos de las horas predichas (los extremos del inicio como del final) los modelos parecen ajustar adecuadamente. Sin embargo, existe una parte en que la diferencia entre las predicciones y los valores originales se hace más grande. Esto se da en horas de las tarde - que corresponden a las horas ''pico''- y los cambios de flujo de tráfico entre estas horas afectan el rendimiento de los modelos.
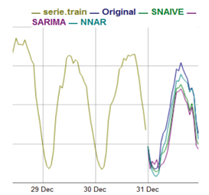
Figura 3 Ajuste de las predicciones horaria, SNAIVE, SARIMA y NNAR con los valores reales del 31 diciembre.
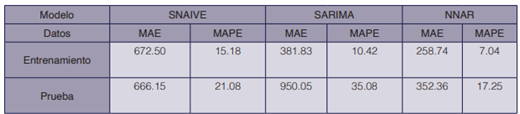
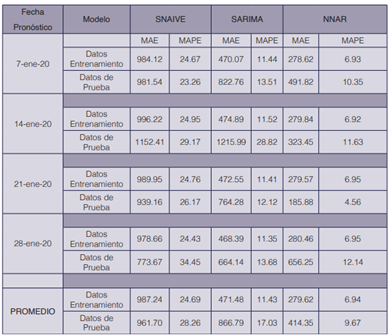
En el cuadro 1 se muestran los errores de predicción para los modelos generados con la muestra de entrenamiento y prueba. El MAE de 352.36 y MAPE de 17.25 del modelo NNAR presentan valores menores que los obtenidos con SNAIVE y SARIMA. Si tomamos como referencia el MAPE para comparar los modelos, para los datos de entrenamiento curiosamente el modelo SARIMA tiene un error menor que SNAIVE. Con un MAPE de 10.42 SARIMA indica que aprende bien el comportamiento, pero no mantiene este comportamiento tan bien con los datos de prueba, es decir, no posee una buena generalización de los datos. En cambio, SNAIVE tiene un error menor de 21.08. Esto, además se refleja con las pruebas de correlación para los residuos.
El análisis de los residuos de los modelos hace notar la no normalidad para las tres propuestas y la independencia solo para NNAR con un valor p=0.37. No existe un modelo perfecto, pero sí, el modelo con el mejor ajuste para evaluación. Se deben de analizar los valores de los errores, tomando en cuenta que si el modelo no predice bien esto no quiere decir que se deba de hacer un modelo más complicado, si no, que puede mejorarse y asumir que cuando los residuos son pequeños entonces la predicción será buena.
SARIMA y SNAIVE mantienen errores más altos que NNAR, a pesar de que el MAPE de SARIMA y NNAR son similares. Esto quiere decir que ambos modelos pueden mejorarse para lograr capturar los tiempos en que son difíciles de capturar. Por ejemplo, se encontró que el modelo SARIMA no logra capturar correctamente las horas pico (entre las 7:00am-8:00am y entre las 4:00pm-5:00pm) para el día de diciembre. Por otro lado, el modelo NNAR es más robusto a los cambios de horario que pueden suceder en las horas pico; existe una variación en los resultados obtenidos, parece que el algoritmo, puede aprender bien pero no predecir ajustadamente como se esperaría.
Los modelos se validan para cuatro fechas del mes de enero del año 2020, manteniendo el día martes, con fechas 7, 14, 21 y 28 de enero del 2020. Se obtienen los errores de cada uno de los modelos para estas fechas de predicción, seguidamente se obtienen el promedio de cada uno de ellos para proceder a realizar la comparación de los resultados de pronóstico. En el Cuadro 2 se muestran los resultados de los errores de cada modelo para datos de entrenamiento y de prueba y el promedio de estos errores para cada modelo. Se observa que el modelo SNAIVE es el que tienen los errores promedio más altos con un MAPE de 24.60 para los datos de entrenamiento y de 28.20 para los de prueba. Seguido del modelo SARIMA que tienen un MAPE de 11.40 para los datos de entrenamiento y 17.00 para los datos prueba; indicando que el modelo SARIMA tiene un mejor rendimiento, logrando aprender y prediciendo el flujo de tráfico horario de la ruta mejor que el SNAIVE. Sin embargo, NNAR arroja una mayor reducción en los errores; para los datos de entrenamiento el modelo tiene un MAPE de 6.90 y de 9.60 para los datos de prueba. El buen resultado de NNAR y SARIMA puede deberse a que se basan en rezagos. Esto indica que el modelo con mejor ajuste para la evaluación es el NNAR y además porque el valor del MAPE en los datos de prueba y de entrenamiento está dentro del rango aceptable de 4-10 para la mayoría de los casos en predicciones para las aplicaciones sobre sistemas de transporte inteligente.
La prueba Ljung-Box de los residuos para el modelo NNAR muestra independencia para todas las fechas de predicción, 7 de enero con valor p=0.64, 14 de enero con p= 0.70, 21 de enero con p=0.62 y 28 de enero con un valor p=0.1. Este valor depende del número de rezago que se defina, para este caso se utiliza el valor recomendado de multiplicar el período estacional de 24 por 2 dando como resultado 48 rezagos. Si se utilizara un rezago menor los valores p son levemente mayores a 0.05 cumpliéndose el supuesto de que los residuos son independientes. Vale la pena recordar las palabras de Box: ''Todos los modelos están equivocados de alguna forma, pero algunos son útiles''. Por lo tanto, se esperaba que los residuos fallaran esta prueba cuando se tiene suficientes datos, esto solo muestra que el modelo no ha capturado perfectamente la información en los datos. La motivación es mejorar el modelo mediante calibraciones y/o ajustes de los parámetros. Por lo que se concluye, que los tres modelos son adecuados para predecir, siendo el modelo NNAR el de menor error.
Conclusiones y recomendaciones
Los modelos de predicción SNAIVE, SARIMA y NNAR son caracterizados por su capacidad de capturar la estacionalidad compleja en las series de tiempo y han resultado ser útiles para predecir el flujo vehicular de vehículos livianos a corto plazo de la ruta 27. Para la predicción del día 31 de diciembre del 2019 se concluye que el modelo NNAR tiene un mejor rendimiento de predicción con un MAPE de 17.25 en los datos de prueba. Además, tiene un mejor aprendizaje de los datos de entrenamiento para el 31 de diciembre con un MAPE de 7.04 y cumple con el supuesto de independencia de los residuos con un valor p=0.37. Los modelos SARIMA y NNAR en general tienen un buen error de entrenamiento, por lo que los modelos han sido capaces de aprender la relación entre los datos de entrada y los resultados.
A partir de los resultados de la validación cruzada, se confirma que el modelo con mejor rendimiento es el NNAR con un MAPE de 6.94 para entrenamiento y 9.67 de prueba. Las predicciones para las aplicaciones sobre sistemas de transporte inteligente el rango aceptable es de 4 a 10 y el MAPE del NNAR está dentro de ese rango. Así mismo, conforme se alimenta con más datos el modelo NNAR, el MAPE tiende a decrecer, mejorando así el aprendizaje de los datos y la predicción. Además, el supuesto de independencia de residuos se cumple en todos los casos en la validación.
Es importante realizar más pruebas de validaciones conforme avanzan los días para continuar con el mejoramiento y observar el rendimiento del modelo a lo largo del tiempo. El hecho que funcione una primera vez no asegura que funcione siempre, dado que los datos cambian, las características, patrones y reacciones dentro de los modelos también. Se recomienda actualizar los modelos con frecuencia para asegurar pruebas que sean objetivas y confiables. Dado que existe un impacto en los residuos en los modelos debido a las horas pico, fechas festivas, fines de semana o bien porque quizás haya sucedido un evento atípico en la ruta, entre otros, es en lo posible recomendable realizar análisis específicos de estos fenómenos