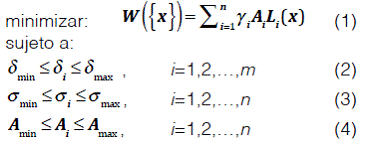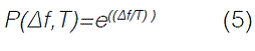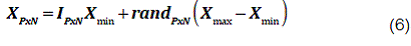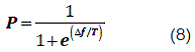Introducción
Durante la última década, el diseño óptimo de estructuras se realiza empleando diferentes algoritmos de optimización, usados por los ingenieros con el objeto de encontrar estructuras más livianas. Estos métodos se dividen en dos categorías generales: (i) Métodos basados en gradientes. (ii) Algoritmo de optimización estocástica.
Las técnicas de optimización comúnmente utilizadas son los algoritmos basados en gradientes, los cuales utilizan la información del gradiente para buscar la solución en el espacio cerca al punto inicial de partida. En general, los métodos basados en gradientes convergen más rápido y pueden obtener soluciones con mayor exactitud. Sin embargo, la adquisición de la información del gradiente puede ser costosa o incluso imposible de obtener, además un buen punto de partida es vital para la ejecución exitosa de estos métodos. En la mayoría de problemas de optimización se pueden encontrar zonas prohibidas (restricciones), espacios convexos o no convexos, funciones multimodales y multidimensionales, lo que hace que no puedan ser resueltos fácilmente por estos métodos. Por tal razón, se han desarrollado diversos algoritmos de optimización estocásticos inspirados en imitar procesos naturales, biológicos o sociales a nivel computacional que han permitido a los investigadores optimizar complicados problemas de ingeniería. En el contexto de la optimización de armaduras, existen numerosos enfoques como: Algoritmos Genéticos (AG) [1][2][3][4][5][6], Optimización con Colonias de Hormiga (Ant Colony Optimization - ACO) [7][8][9][10][11], Optimización con Enjambre de Partículas (Particle Swarm Optimization - PSO) [12][13][14][15], Búsqueda Armónica (Harmony Search - HS) [16][17][18][19], entre otros.
Recientemente, Millán, Begambre y Millán [20] desarrollaron un algoritmo estable y eficiente llamado Algoritmo Simulated Annealing Modificado (ASAM) para resolver problemas de optimización con o sin restricciones. El algoritmo se basa en el proceso de enfriamiento de metales empleado en el Simulated Annealing (SA) clásico [21] pero posee tres características fundamentales (exploración preliminar, paso de búsqueda y probabilidad de aceptación) que lo diferencian de este. Para mayores detalles se recomienda consultar [20].
La optimización estructural es un problema con múltiples mínimos locales, susceptibles de solución a través de métodos estocásticos diseñado para identificar mínimos globales Por lo tanto, este artículo propone el uso de ASAM para el diseño óptimo (minimización de peso) de armaduras con variables continuas. En su primera parte este trabajo presenta la descripción del problema de optimización estructural. Seguidamente se describe brevemente el algoritmo ASAM, sus fundamentos y los parámetros que lo controlan. Finalmente, para demostrar la eficacia del algoritmo, varios problemas de referencias relacionados con el diseño de armaduras sujetas a restricciones de esfuerzos y desplazamientos son analizados y los resultados obtenidos son comparados con los reportados por otros autores.
Descripción del Problema
El principal objetivo en este tipo de problemas de optimización es minimizar las secciones transversales de los miembros de la estructura A i con el fin de encontrar el peso mínimo de la estructura satisfaciendo simultáneamente las limitaciones que el problema de optimización impone. Por consiguiente la formulación matemática de este problema de optimización se describe de la siguiente manera:
donde W ({ x }) es el peso de la estructura; n es el número de miembros que compones la estructura; m es el número de nodos; γ i es la densidad del material del miembro i; L i es la longitud del miembro i; A i es la sección transversal del miembro i elegida entre A min y A max ; σ i y δ i son los esfuerzos en los miembros y deflexiones en los nodos, respectivamente.
Algoritmo Simulated Annealing Modificado (ASAM)
Antes de sintetizar las características de ASAM, vale la pena describir brevemente el funcionamiento del Simulated Annealing básico. SA comienza con un cierto estado S. A través de un proceso único crea un estado vecino S’ al estado inicial. Si la energía o la evaluación del estado S’ son menores que el estado S cambia el estado S por S’. Si la evaluación de S’ es mayor que la de S puede estar empeorando, por lo que elige S’ en vez de S con una cierta probabilidad que depende de las diferencias en las evaluaciones y la temperatura del sistema T. La probabilidad de aceptar un peor estado se calcula por la siguiente ecuación:
donde,
P; probabilidad de aceptar el nuevo estado.
∆f; diferencia de las evaluaciones de la función para cada estado.
T; temperatura del sistema. e; número de Euler.
Inicialmente, con valores grandes para T, frecuentemente se aceptan soluciones con un mayor valor de función objetivo; a medida que el valor de T disminuye, tal tipo de soluciones raramente se aceptan, y cuando T se acerca a cero, solo se aceptan aquellas soluciones que mejoran la anterior. Varios estudios teóricos demuestran que sí T decrece con la suficiente lentitud, el proceso converge a la solución óptima. La función para reducción de temperatura más utilizada es: Tk+1=Tk∙α, donde Tk+1 es el nuevo valor ajustado de T, Tk corresponde al previo valor de T y α es una constante que está comprendida en el intervalo [0.8-0.99].
SA comienza con una solución inicial escogida aleatoriamente en el espacio de búsqueda y la compara con otra que también se selecciona estocásticamente en el espacio de búsqueda, lo que afecta al algoritmo cuando se tienen funciones altamente dimensionales y modales generando mayores tiempos de búsqueda y soluciones subóptimas. Además, la probabilidad de aceptación de una solución peor se encuentra en un intervalo de entre 0 y 1, lo cual causa que a temperaturas iniciales el algoritmo acepte un gran número de soluciones de peor calidad ( aumentando el riesgo de quedar atrapado en un óptimo local ).
En este contexto el algoritmo ASAM, tiene 3 características fundamentales que lo hacen diferente respecto al Simulated Annealing básico. Dichas características son las siguientes:
Exploración preliminar
En esta etapa el algoritmo realiza una exploración en todo el espacio de búsqueda que viene dado por la siguiente matriz:
donde,
Pnúmero de puntos (estados) que se desean en el espacio de búsqueda.
Nnúmero de dimensiones del problema.
IPxNmatriz identidad de tamaño PxN.
X min límite inferior del problema. X max límite superior del problema.
rand PxN matriz PxN de números aleatorios (aleatoriedad pura) entre 0 y 1.
Para comenzar el proceso de optimización con ASAM se evalúan todos los puntos generados con la ecuación (6) mediante la función objetivo del problema y se escoge el que tenga menor valor (en el caso de estar buscando el valor mínimo de la función) como punto inicial de la búsqueda.
Paso de búsqueda
A partir del punto inicial determinado en la etapa anterior, se genera un paso de búsqueda para determinar el estado vecino. Este paso depende de un radio de acción que se reduce gradualmente a medida que desciende la temperatura del sistema. Es decir, cuando el algoritmo está en determinada temperatura, con radio de acción definido por la ecuación (7), la transición del punto inicial al nuevo punto (paso de búsqueda) se realiza mediante la adición de números aleatorios que están comprendidos entre cero y el valor del radio. Esto permite que el algoritmo realice una exploración global a temperaturas altas y una exploración local a temperaturas bajas, dando un equilibrio entre la exploración y la explotación del algoritmo.
donde,
Ri: radio inicial ciclo. α: coeficiente de reducción del radio.
Probabilidad de aceptación
En esta propuesta la probabilidad de aceptación de una solución (estado) peor viene dada por:
P; probabilidad de aceptar el nuevo estado.
∆f; diferencia de las evaluaciones de la función para cada estado.
T; temperatura del sistema. e; número de Euler.
Esta probabilidad se encuentra en un intervalo entre 0 y ½, lo que permite al algoritmo tener un rango menor de aceptación de peores soluciones.
En resumen, las 3 modificaciones propuestas en ASAM [20] tienen la finalidad de mejorar la exploración inicial, permitir un balance entre exploración inicial y final y controlar la convergencia en la etapa final de búsqueda.
Problemas Numéricos
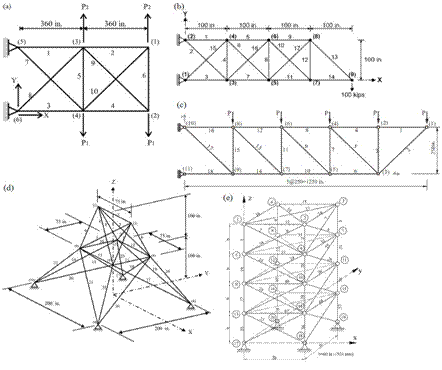
Los siguientes 5 problemas clásicos (ver Figura 1) fueron utilizados para investigar la exactitud numérica, eficiencia y validación del algoritmo ASAM:
Armadura plana de 10 barras.
Armadura plana de 17 barras.
Armadura plana de 18 barras.
Armadura en el espacio de 25 barras.
Armadura en el espacio de 72 barras.
Se realizaron 100 corridas independientes del algoritmo para cada problema. Los mejores y peores diseños, peso de la estructura, peso promedio y desviación estándar logrados con ASAM son comparados con otras técnicas de optimización y son reportados en las tablas. La implementación del algoritmo fue realizada en Matlab®, bajo el sistema operativo Windows 7 y el equipo utilizado fue un Intel Core i7-2.4 GHz, 8GB (RAM).
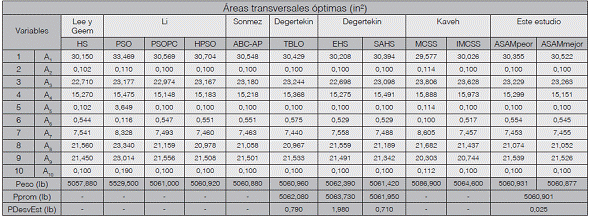
Cuadro 1 Comparación de diseños óptimos armadura plana de 10 barras (Caso I)
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Cuadro 2 Comparación de diseños óptimos armadura plana de 10 barras (Caso II)
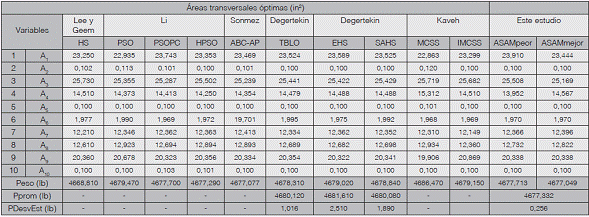
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Cercha plana de 10 barras
La Figura 1a muestra la geometría y las condiciones de carga de la armadura que consta de 10 barras. Esta estructura es un ejemplo estándar y ha sido utilizada por muchos investigadores, incluyendo Lee y Geem [16], Li [13], Sonmez [22], Degertekin [23][19], y Kaveh [24]. En este problema, dos condiciones de cargas fueron consideradas: Caso I: P1=100 kips y P2=0; Caso II: P1=150 kips y P2=50 kips. Los miembros están fabricados de un material con módulo de elasticidad E=10000 ksi y densidad por unidad de volumen de ρ=0,10 lb/in3. El área mínima y máxima para la sección transversal de los miembros es 0,1 ≤ Ai(in2) ≤ 35. Los desplazamientos de los nodos libres no deben exceder ±2 in en dirección vertical y horizontal, además los esfuerzos admisibles tanto a tensión y compresión no deben superar 20 ksi. El problema tiene 32 restricciones no lineales (10 restricciones de tensión, 10 restricciones de compresión y 12 restricciones de desplazamiento).
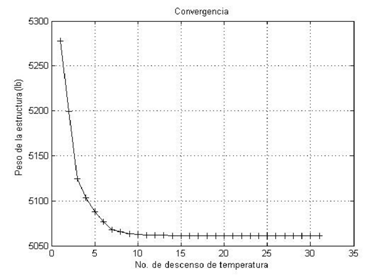
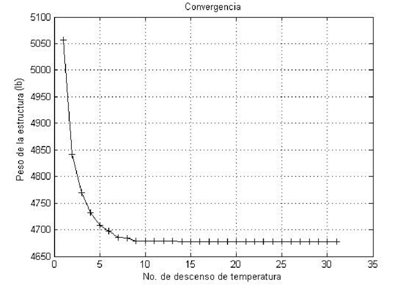
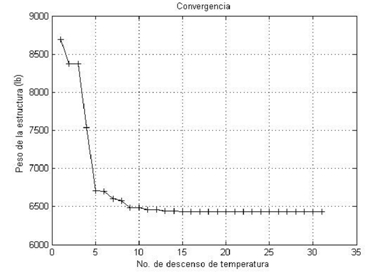
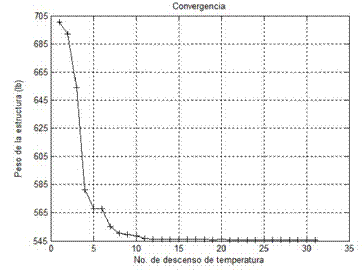
En los cuadros 1 y 2 se muestran los mejores y peores diseños encontrados por ASAM para la cercha de 10 barras sujeta a las condiciones de carga del Caso I y II, respectivamente. Otros resultados publicados por diferentes autores para el mismo problema utilizando distintos enfoques de optimización incluyendo búsqueda armónica (HS) [16][19], optimización con enjambre de partículas (PSO,PSOPC, HPSO) [13], colonia de hormigas (ABC-AP) [22], optimización basada en enseñanza aprendizaje (TLBO) [23] y sistema de búsqueda magnética (MCSS y IMCSS) [24] son también listados en los cuadros 1 y 2. Los pesos mínimos obtenidos con ASAM son 5060,877 lbs y 4677,049 lbs para el Caso I y II, respectivamente, solo siendo superados por los reportados en Lee y Geem [16], diseño que viola algunas restricciones. Es interesante observar que para el Caso I el peor peso (5060,931 lbs) y el promedio (5060,901 lbs) encontrados por ASAM superan a los mejores valores reportados por Li [13], Degertekin [23][19] y Kaveh [24]. Para el Caso II el peor (4677,71 lbs) y promedio (4677,332 lbs) obtenidos con ASAM también son ligeramente mejores que los reportados por otros autores. Finalmente las desviaciones estándar de los pesos para el Caso I (0,025 lb) y II (0,256 lb), muestran la estabilidad y precisión de ASAM para la resolución de este problema. En la Figura 2 y Figura 3 se puede observar la gráfica de convergencia de este problema para el Caso I y II, respectivamente.
Armadura plana de 17 barras
Este problema tiene 17 variables independientes y 52 restricciones no lineales (17 restricciones de tensión, 17 restricciones de compresión y 18 restricciones de desplazamiento). En la figura 1b se muestra la geometría y solicitaciones de carga a la que está sometida la estructura. La densidad del material para todos los miembros es de 0,268 lb/in3 y el módulo de elasticidad de 30000 ksi. El máximo esfuerzo permitido en las barras fue de ±50 ksi con una restricción de desplazamiento en los nodos libres de ±2 in en ambas direcciones. La única carga se encuentra en el nodo 9 y es de 100 kips. El área mínima y máxima para la sección transversal de los miembros es 0,1 ≤ Ai(in2) ≤ 35.
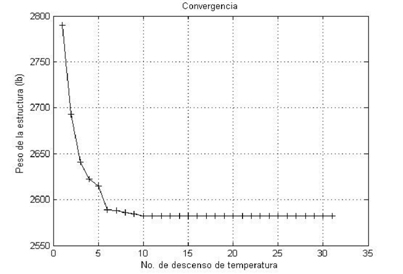
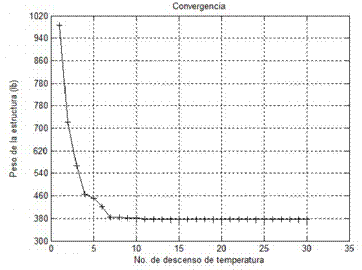
Esta armadura ha sido analizada por Lee y Geem [16] empleando HS, Li [13] con tres técnicas de enjambre de partículas (PSO, PSOPC, HPSO) y Baghlani [25] por medio de FA (Firefly Algorithm) y un hibrido (FBSFA). El mejor y peor peso encontrados por ASAM fueron de 2581,923 lbs y 2581,947 lbs, respectivamente. Es importante mencionar que los pesos reportados con HS (2580,810 lbs), PSO (2724,370 lbs), HPSO (2581,940 lbs) y FA (2577,570 lbs) son menores que los de ASAM, esto debido a que estos diseños violan algunas restricciones. En el Cuadro 3 se comparan los resultados encontrados en este estudio con los autores mencionados anteriormente y en la Figura 4 se encuentra la gráfica de convergencia.
Armadura plana de 18 barras
La figura 1c muestra la geometría y condiciones de carga de la armadura de 18 elementos y 11 nodos. El valor de la carga es P=20 kips que actúa en dirección gravitacional en los nodos 1, 2, 4, 6 y 8. Todos los miembros son de un material con modulo elasticidad E=10000 ksi y densidad de 0,10 lb/in3. El esfuerzo máximo permitido a tensión y compresión es 20 ksi. Adicionalmente, la restricción de esfuerzo al pandeo de Euler debe ser tenida en cuenta para los elementos que se encuentran a compresión. El esfuerzo al pandeo de Euler para el miembro i se calcula como:
donde Li y Ai son la longitud y área de la sección transversal del elemento. K es una constante determinada por la geometría y se le asignó un valor de 4 [22]. El número de variables se redujo a cuatro grupos de la siguiente manera: (G1) elementos 1, 4, 8, 12, 16; (G2) elementos 2, 6, 10, 14, 18; (G3) elementos 3,7, 11, 15; (G4) elementos 5,9, 13, 17. El área mínima fue 0.10 in2 y la máxima 50 in2. El problema tiene 36 restricciones no lineales y sin restricciones de desplazamiento.
El mejor y peor resultado de obtenido con ASAM son presentados en el Cuadro 4. Además esta tabla contiene los resultados reportados por otros autores incluidos Imai y Schmit [26] quien utilizó el Método Multiplicador (MM), Lee y Geem [16] que emplea HS y Sonmez [22] lo resuelve por ABC-AP. Los resultados de ASAM (6430,531 lbs) son casi iguales a los encontrados por Imai y Schmit (6430 lbs) y Sonmez (6430,529 lbs). Aunque, el algoritmo HS [16] produce un diseño más ligero (6421,880 lbs) que el algoritmo presentado en este estudio (6340.531 lbs), el algoritmo HS viola algunas limitaciones de esfuerzos, mientras que la solución óptima encontrado por ASAM cumple con todos los requisitos de restricción. Por último, la Figura 5 muestra la gráfica de convergencia de ASAM para este problema.
Cuadro 3 Comparación de diseños óptimos armadura plana de 17 barras
| Áreas transversales óptimas (in²) [129] [130] [131] [132] | [133] [134]|||||||||
|---|---|---|---|---|---|---|---|---|---|
| [135] Variables | [136]Lee y [137] Geem | [138]Li [139] [140] | [141]Baghlani [142] | [143]Este estudio [144] | [145] [146] [147]|||||
| HS | [148]PSO | [149]PSOPC | [150]HPSO | [151]FBSFA | [152]FA | [153]ASAMpeor | [154]ASAMmejor | [155] [156]||
| 1 | [157]A1 | [158]15,821 | [159]15,766 | [160]15,981 | [161]15,896 | [162]15,896 | [163]15,942 | [164]15,850 | [165]15,994 | [166] [167]
| 2 | [168]A2 | [169]0,108 | [170]2,263 | [171]0,100 | [172]0,103 | [173]0,100 | [174]0,100 | [175]0,101 | [176]0,100 | [177] [178]
| 3 | [179]A3 | [180]11,996 | [181]13,854 | [182]12,142 | [183]12,092 | [184]12,099 | [185]12,023 | [186]12,138 | [187]12,124 | [188] [189]
| 4 | [190]A4 | [191]0,100 | [192]0,106 | [193]0,100 | [194]0,100 | [195]0,100 | [196]0,100 | [197]0,100 | [198]0,100 | [199] [200]
| 5 | [201]A5 | [202]8,150 | [203]11,356 | [204]8,098 | [205]8,063 | [206]8,066 | [207]8,035 | [208]8,052 | [209]8,024 | [210] [211]
| 6 | [212]A6 | [213]5,507 | [214]3,915 | [215]5,566 | [216]5,591 | [217]5,579 | [218]5,519 | [219]5,544 | [220]5,557 | [221] [222]
| 7 | [223]A7 | [224]11,829 | [225]8,071 | [226]11,732 | [227]11,915 | [228]11,935 | [229]11,777 | [230]11,933 | [231]11,876 | [232] [233]
| 8 | [234]A8 | [235]0,100 | [236]0,100 | [237]0,100 | [238]0,100 | [239]0,100 | [240]0,100 | [241]0,100 | [242]0,100 | [243] [244]
| 9 | [245]A9 | [246]7,934 | [247]5,850 | [248]7,982 | [249]7,965 | [250]7,939 | [251]7,924 | [252]7,954 | [253]7,932 | [254] [255]
| 10 | [256]A10 | [257]0,100 | [258]2,294 | [259]0,113 | [260]0,100 | [261]0,100 | [262]0,100 | [263]0,100 | [264]0,100 | [265] [266]
| 11 | [267]A11 | [268]4,093 | [269]6,313 | [270]4,074 | [271]4,076 | [272]4,044 | [273]4,077 | [274]4,039 | [275]4,072 | [276] [277]
| 12 | [278]A12 | [279]0,100 | [280]3,375 | [281]0,132 | [282]0,100 | [283]0,100 | [284]0,100 | [285]0,100 | [286]0,100 | [287] [288]
| 13 | [289]A13 | [290]5,660 | [291]5,434 | [292]5,667 | [293]5,670 | [294]5,668 | [295]5,632 | [296]5,700 | [297]5,644 | [298] [299]
| 14 | [300]A14 | [301]4,061 | [302]3,918 | [303]3,991 | [304]3,998 | [305]4,021 | [306]4,029 | [307]4,037 | [308]4,006 | [309] [310]
| 15 | [311]A15 | [312]5,656 | [313]3,534 | [314]5,555 | [315]5,548 | [316]5,536 | [317]5,603 | [318]5,550 | [319]5,565 | [320] [321]
| 16 | [322]A16 | [323]0,100 | [324]2,314 | [325]0,101 | [326]0,103 | [327]0,100 | [328]0,100 | [329]0,100 | [330]0,100 | [331] [332]
| 17 | [333]A17 | [334]5,582 | [335]3,542 | [336]5,555 | [337]5,537 | [338]5,572 | [339]5,620 | [340]5,558 | [341]5,570 | [342] [343]
| Peso (lb) [344] | [345]2580,810 | [346]2724,370 | [347]2582,850 | [348]2581,940 | [349]2581,900 | [350]2577,570 | [351]2581,947 | [352]2581,923 | [353] [354]|
| Pprom (lb) [355] | [356]- | [357]- | [358]- | [359]- | [360]- | [361]- | [362]2581,936 [363] | [364] [365]||
| PDesvEst (lb) [366] | [367]- | [368]- | [369]- | [370]- | [371]- | [372]- | [373]0,010 | [374]||
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Cuadro 4 Comparación de diseños óptimos cercha plana de 18 barras
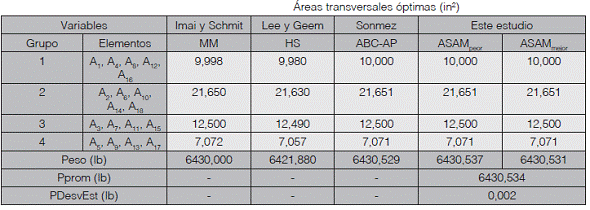
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Armadura en el espacio de 25 barras
La torre de transmisión de 25 barras se utiliza ampliamente en la optimización estructural para verificar diversas metodologías de diseño y para comparar las diferentes técnicas numéricas. Varios investigadores han resuelto este problema implementando distintas técnicas de optimización, como: Li y colaboradores [13] utilizando la heurística de optimización con enjambre de partículas (HPSO), Sonmez [22] diseñó con algoritmo de colonia de hormigas con penalidad adaptativa (ABC-AP), Camp usando un algoritmo de colonias de hormiga (ACO) [7] , algoritmo big-bang-big-crunch (BB-BC) [27] y una técnica heurística llamada TLBO [28],Lamberti [29] analizó este problema con una variación de simulated annealing denominada CMLPSA, y por ultimo Kaveh [30] aplicó un hibrido de bang-big-crunch (HBB-BC). En la figura 1 d se muestra la topología y numeración de nodos para el problema en mención.
La densidad del material para todos los miembros es de 0,01 lb/in3 y el módulo de elasticidad de 10000 ksi. El máximo esfuerzo permitido en las barras fue de ±40 ksi con una restricción de desplazamiento en los nodos libres (dirección x,y,z) de ±0,35 in. El área mínima y máxima para la sección transversal de los miembros es 0,01 in2 y 3,40 in2 respectivamente. El número de variables se redujo a 8 grupos de la siguiente manera: (G1) elemento 1; (G2) elementos 2, 3, 4, 5; (G3) elementos 6, 7, 8, 9; (G4) elementos 10, 11; (G5) elementos 12, 13; (G6) elementos 14, 15, 16, 17; (G7) elementos 18, 19, 20, 21; (G8) elementos 22, 23, 24, 25. La estructura está cargada de acuerdo a Camp [28].
El Cuadro 5 lista una comparación de los diseños desarrollados por ASAM con otras técnicas de optimización. La armadura más liviana diseñada por ASAM es de 545,171 lbs. Si bien, el diseño desarrollado por Kaveh [30] tiene un peso más bajo, de acuerdo con Degertekin [19], este diseño viola algunas restricciones. En comparación con las mejores soluciones propuestas por Li [13], Sonmez [22], Camp [7][27][28] y Lamberti [29], ASAM muestra una ligera mejoría en el peso mínimo de la estructura. Finalmente, la media de los pesos (545,261 lbs) y la desviación estándar (0,123 lbs) logrados con ASAM, muestran la estabilidad que tiene el algoritmo aquí propuesto. La Figura 6 muestra la gráfica de convergencia de ASAM para este problema.
Cuadro 5 Comparación de diseños óptimos armadura en el espacio de 25 barras
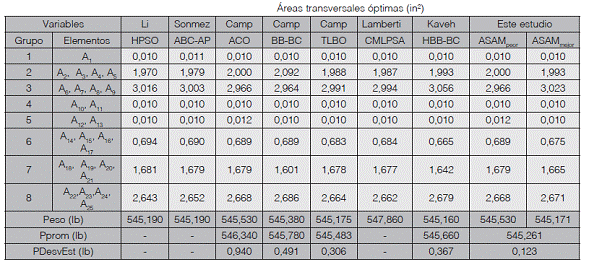
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Cuadro 6 Comparación de diseños óptimos armadura en el espacio de 72 barras
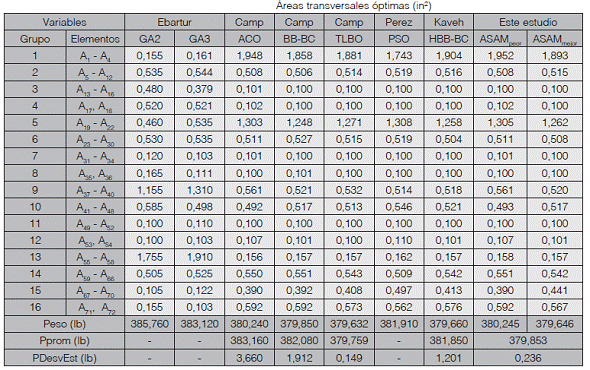
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N.
Armadura en el espacio de 72 barras
La armadura de 72 barras ha sido diseñada por distintos investigadores usando una variedad de enfoques y técnicas: Erbartur [31] usando GA; Camp [7][27][28] por medio de ACO, BB-BC, y TLBO; Perez [12] usó PSO, y Kaveh [30] diseñó con HBB-BC. La figura 1e muestra la numeración de nodos y elementos de la armadura. Para su análisis es categorizada en 16 grupos de variables de diseño.
El material tiene un peso por unidad de volumen de 0,10 lb/in3; y módulo de elasticidad de 10000 ksi. Las limitaciones impuestas a la estructura incluyen: un desplazamiento máximo de ± 0,25 in en los nodos superiores en las direcciones x, y o z; y un esfuerzo máximo admisible de ± 25 ksi en cualquier elemento. El rango de áreas de sección transversal aceptables varía de 0,1 in2 a 3,0 in2. La armadura está cargada según Camp [28].
El Cuadro 6 el diseño de ASAM con otras técnicas de optimización. El mejor diseño de ASAM es 379,646 lbs el cual es más ligero que otros diseños publicados. El peso promedio alcanzado fue de 379,853 lbs con una desviación estándar de 0,236 lb. La comparación de los resultados de ASAM con los de otros métodos heurísticos muestra que ASAM proporciona una mejora en la calidad y consistencia de los diseños de armaduras. La Figura 7 muestra la gráfica de convergencia de ASAM para este problema.
Conclusiones
Se ha conseguido evaluar el desempeño del Algoritmo Simulated Annealing Modificado (ASAM) en el problema de diseño óptimo de armaduras con variables continuas. Los valores de secciones transversales de los elementos y pesos obtenidos por ASAM, fueron comparados con los resultados reportados por otros autores empleando diferente enfoques estocásticos, mostrando que son coherentes y satisfactorios (ver cuadros 1, 2, 3, 4, 5 y 6), dando así validez al trabajo aquí realizado.
En cuanto a la técnica empleada, se puede observar que ASAM tiene precisión, robustez, y versatilidad para enfrentar diversos tipos de problemas, con diferentes números de elementos y con restricciones de esfuerzos y desplazamientos. Esto se ve reflejado en los pesos, pesos promedios, desviación estándar y áreas de los elementos conseguidos.