Antecedentes
Los balísticos, contrariamente a la ceniza transportada por el viento, aunque tienen un radio de acción reducido de unos pocos kilómetros, no dejan por ello de ser peligrosos pues pueden herir e incluso matar a animales y personas que estén a su alcance. Tres ejemplos de este tipo de incidentes puede encontrarse en Oikawa et al. (2016) y Kaneko, Maeno y Nakada (2016) para el caso de Mount Ontake, en el que murieron 63 escaladores fueron impactadas letalmente al no poder guareserse de balísticos que fueron eyectados a 1 kilómetro de distancia, en Kilgour, Manville, Della Pasqua, Graettinger, Hodgson y Jolly (2010) para Mount Ruapehu, en que se afectaron a 2 escaladores y en Breard et al. (2014) para el caso de eyecciones laterales en la erupción de Te Maari. Durante la erupción del volcán Turrialba, acaecida el 29 de octubre del 2014, sucedió un caso que perfectamente pudo haber cobrado una vida. Un bloque balístico recorrió los 745 m que separan la fuente en el cráter del puesto de guardaparques, impactando las instalaciones con tal fuerza que no solo hizo un agujero en el techo, sino que continuó moviéndose destrozando el inodoro, deteniéndose después de haber destrozado también el piso de madera, dichosamente sin herir ni matar a ninguna persona. La posibilidad de que hubiese afectado a alguien se ha considerado razón suficiente para analizar la posible trayectoria de los balísticos, entendiéndose por ello fragmentos de lava (bombas) o de roca (bloques) que son expulsados en una erupción explosiva. Son clastos de unos centímetros hasta varios metros que se separan de la columna eruptiva para seguir trajectrias aproximadamente parabólicas.
La dinámica del transporte balística ha sido analizando usando observaciones de campo de los depósitos (Biass et al., 2016; Fitzgerald et al., 2014; Kilgour et al., 2010), por medio de video (Chouet, Hamisevicz y McGetchin, 1974; Taddeucci et al., 2012; Taddeucci, Alatorre-Ibarguengoitia, Palladino, Scarlato y Camaldo, 2015), por experimentos de laboratorio (Alatorre-Ibargüengotia, Morales-Iglesias, Ramos-Hernandez, Jon-Selvas y Jimenez-Aguilar, 2016; Graettinger, Valentine; Sonder, Ross y White, 2015), por simulación numérica (De’ Michieli Vitturi, Neri, Ongaro, Savio y Boschi, 2010; Biass et al., 2016).
Wilson (1972) desarrolló el primer algoritmo matemático que incluyó la variación del coeficiente de arrastre con el número de Reynolds, para calcular las trayectorias balísticas en la literatura vulcanológica Steinberg y Lorenz (1983) llamaron la atención a que la máxima distancia que alcanza un fragmento depende no solo del ángulo inicial sino también de la distribución de las velocidades y del coeficiente balístico de los fragmentos. Fagents y Wilson (1993) mejoraron el método propuesto en Wilson (1972) al incluir la reducción del coeficiente de arrastre cerca del cráter. Bower y Woods (1996) se concentraron en los balísticos producidos por erupciones de baja explosividad.
En el actual trabajo se han incluido 4 conclusiones generales que esperamos ayuden a aumentar la seguridad tanto de los visitantes como del personal administrativo. El lector interesado para mayor detalle puede consultar Biass et al. (2016), D’Elia et al. (2020) y Giordano y De Astis (2021).
El trabajo está divido en 6 partes,: a) una descripción de la trayectoria del fragmento de interés; b) breve descripción del software BALÍSTICA, diseñado por el autor para poder analizar la posible trayectoria de un balístico bajo diferentes condiciones; c) los parámetros requeridos para llevar a cabo ese análisis, tales como velocidad y ángulo iniciales, geometría del cráter, valores razonables del coeficiente de arrastre, así como los semi-ejes del elipsoide a que se aproxima el clasto, y su densidad; d) seguidos del análisis de la posible trayectoria en que el concepto de Ro (la distancia que el clasto recorre totalmente acoplado a los gases de su entorno volcánico propuesto por Fagents y Wilson (1993), es modificado para incluir la asimetría del cráter; e) un breve análisis de riesgo; finalizando con f) unas conclusiones en las que se incluyen 4 recomendaciones generales que se espera reduzcan el peligro asociado a este tipo de situaciones.
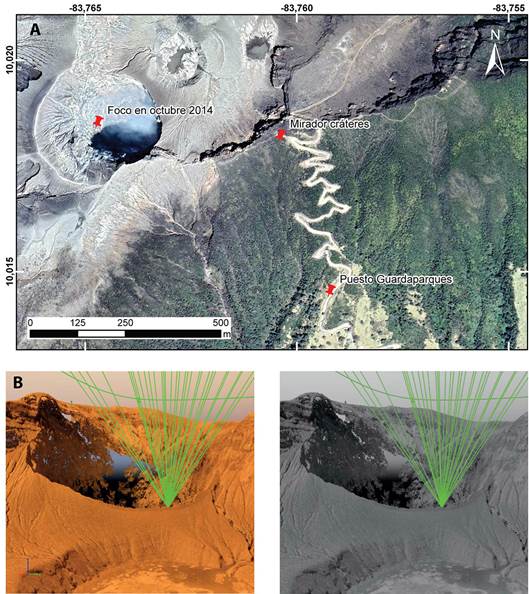
Otro aspecto que se analizará, una vez realizado en cálculo anterior, será no solo saber con qué velocidad y tiempo tardó en llegar al puesto de guardaparques, sino con que tiempo y velocidad puede llegar al Mirador de los cráteres Central y Activo, ubicado a unos 400 m del centro del cráter Activo (Fig. 1).
Software BALÍSTICA
Un balístico es, en esencia, una masa que es lanzada con una cierta velocidad, cuya trayectoria podría predecirse si se conociera con bastante precisión las posibles fuerzas (arrastre, Magnus, gravedad, entre otras) que la afectan durante su recorrido. En la realidad, sin embargo, no se ha logrado elaborar una formulación teórica de muchos de los efectos de esas fuerzas, fuera que en la mayoría de los casos no es posible desplegar el equipo de medición necesario en el área en que se esperaría el evento. Además, en el campo lo único que se puede medir es la geometría, forma y peso del proyectil (siempre y cuando no se fragmente), a veces el ángulo de incidencia, además de estimar la distancia entre el punto de salida del cráter (que si posee un diámetro importante, también hay que hacer un estimado) y de su impacto.
BALISTICA es una suite de software científico diseñada para simular trayectorias de clastos mediante distintos modelos balísticos. Actualmente, la suite se compone de 8 modelos distintos, desde modelos analíticos Newtonianos hasta modelos que toman en cuenta la geometría de los clastos para calcular el efecto de su forma en el coeficiente de arrastre. BALISTICA ataca dos objetivos complementarios: (a) disminuir la barrera de entrada de aprendizaje de fenómenos balísticos mediante un gradiente suave de dificultad de modelos, y (b) proveer un conjunto de herramientas de distinta sofisticación durante el proceso de investigación científica que se ajuste a la cantidad y calidad de información disponible para desarrollar hipótesis geofísicas.
La suite BALISTICA está implementada en Python (v3.6) con el fin de maximizar su accesibilidad para la comunidad científica debido a su amplio uso en códigos científicos (Oliphant, 2007).. Estructuralmente, el código extiende clases base que definen un modelo balístico y su interfaz de usuario correspondiente. Con el fin de maximizar el número de configuraciones de sistemas en donde puede instalarse sin cambios mayores, BALISTICA hace uso solamente de algunas bibliotecas de dominio público para manipulación de datos y cómputo numérico con el fin de ser autocontenida. El código es abierto, y se encuentra disponible en un repositorio de GitHub (Núñez-Corrales y Brenes-André, 2021), bajo la licencia Apache 2.0. Para inicios de 2022, será posible instalarlo directamente mediante ‘pip install’ gracias a su inclusión al Python Package Index.
BALISTICA es un análisis retrospectivo en que algunas de esas fuerzas son totalmente eliminadas y, en aquellas fuerzas que sí se tomen en cuenta, se hace utilizando parámetros cuyo valor deben ser estimados razonablemente. El caso del proyectil ideal, aquel en que solo es afectado por la gravedad, es el único para el que se ha podido obtener una solución matemática cerrada que, por su simplicidad, suele formar parte del primer curso de física universitaria. El siguiente caso en complejidad es el del fragmento sometido a una fuerza de arrastre Fa, proporcional a la velocidad instantánea Vi, o sea Fa = kVi. Aunque también puede ser resuelto matemáticamente si se tiene conocimiento de cálculo diferencial, presenta el inconveniente de que el valor de Vi depende de la textura y forma de la masa. El cálculo de la trayectoria y de otros parámetros como el tiempo de vuelo, cuando se incluyen otro tipo de fuerzas, solo es posible con ayuda de programas de cómputo. El análisis se complica aún más con aquellos balísticos volcánicos donde, en una parte de su trayectoria están afectados por una fuerza (la de arrastre, por ejemplo) y, en otra parte, por una fuerza adicional, como puede ser el caso del viento.
Aunque el software libre EJECT, diseñado para ambiente WINDOWS. desarrollado por Mastin (2001) ha sido utilizado en varias ocasiones para analizar los balísticos, hemos evitado usarlo por forzar al investigador a asimilar cada uno de los clastos a una de solo 2 posibles geometrías: una esfera o bien un cubo, y en este último caso debe escogerse entre 2 alternativas: una en que una de las caras del cubo es impactada perpendicularmente durante todo su trayectoria,(cubo alto) o aquella en que el fluido impacta simétricamente en uno de sus vértices,(cubo bajo).
La aplicación de EJECT a balísticos del Popocatepetl dio como resultado alcances máximos de 4750 m si se consideraba el clasto como una esfera, y de solo 3430 m si se consideraba como un cubo bajo , siendo el valor medido en campo de 3700 m (Alatorre-Ibargüengotia y Delgado-Granados, 2006) Esta gran diferencia se debe, en buena parte a que la variación del coeficiente de arrastre con el número de Reynolds, aunque determinada experimentalmente via tunel de viento, fue obtenida en condiciones muy diferentes a las que se dan en realidad. Elobjeto en el túnel de viento no puede rotar, y el flujo utilizado no es turbulento.
Para facilitar esta clase de análisis, el autor diseñó un conjunto de programas que analiza la trayectoria de balísticos en situaciones crecientemente complejas. Inicia con el caso ideal, en que no solo se computan los parámetros standards (alcance, máxima altitud, tiempo de vuelo, velocidad y ángulo de llegada), sino que también permite representar gráficamente las situaciones más comunes: variación de la altura “z” conforme aumenta la distancia “x” del punto de lanzamiento (o sea, la trayectoria), así como la variación tanto de x como de z con el tiempo; y la variación de la velocidad respecto a x, z y el tiempo t. Este tipo de gráficos, que generalmente no se analizan en el curso de introductorio de física, se han incluido para dar más libertad al vulcanólogo al analizar un caso real. Por esa misma razón, el punto de salida y el de llegada se especifican con coordenadas geográficas, como suele hacerse en el campo.
A partir de aquí y manteniendo en lo posible la misma forma de introducir los datos, así como de generar los gráficos, se procede a agregar al caso ideal una fuerza proporcional a la velocidad o bien una fuerza proporcional a la velocidad al cuadrado, que es el caso más común, con un coeficiente de arrastre constante durante toda la trayectoria. Este caso puede ampliarse al incluir el efecto del viento, cuya dirección se define por medio del azimut. La complejidad aumenta al incluirse la densidad y el efecto de la forma del fragmento (asimilando a un elipsoide) vía la esfericidad, terminándose con un programa que incorpora la posible variación con la velocidad del coeficiente de arrastre con esfericidades variables.
Sobre el fragmento
El proyectil del Turrialba que cayó en el baño de mujeres (Fig. 2) se generó durante el evento del 29 octubre del 2014.
Datos al momento de finales de octubre 2014
Centro del cráter: 10°1’6.66’’N - 83°45’52.94’’W.
Mirador de los cráteres: 10°1’5.52’’N - 83°45’37.41’’W.
Puesto Guardaparques: 10°0’52.33’’N - 83°45’33.21’’W.
Distancia foco al Mirador: 475 m.
Distancia foco al puesto Guardaparques: 745 m.
Altitud del fondo del cráter: 3080 m s.n.m.
Altitud borde inferior del cráter: 3150 m s.n.m.
Altitud del borde superior del cráter: 3310 m s.n.m.
La figura 1A (tomada de Google Earth) permite visualizar la ubicación de los sitios en interés, y la figura 1b (tomada por un dron) muestra la geometría del cráter.
Al haberse extraviado el fragmento, desde el inicio deben hacerse algunas suposiciones razonables con base en el material fotográfico disponible. Se le considera un paralelepípedo regular de dimensiones 13 cm x 7 cm x 5 cm, usando de escala el pulgar de la persona que lo sostiene, medido en 5 cm. La densidad se ha tomado en 2500 kg/m3. Suponiendo que el fragmento tiene una densidad de 2500 kg m-3 significa una masa de 1,137 kg.
Análisis
La erupción que dio origen al fragmento se prolongó por varios días (del 29 de octubre al 1 de noviembre de 2014), lo que condujo a causando que el cráter creciera en diámetro (de unos 100 a 185 m de diámetro) y en profundidad. Por otro lado, ese crecimiento fue asimétrico, por lo que el centro del cráter Activo actual no coincide con el centro del cráter Activo posterior a octubre del 2014 (Alvarado et al., 2016). Por ello el análisis de la posible trayectoria se hará considerando, como una primera aproximación, que el piso del cráter en el momento de la eyección estaba a una altitud de 3080 m s.n.m, que el borde inferior (limitando con el cráter Central) estaba una altitud de 3150 m s.n.m. y el más alto (sector SW del cráter Activo) a una altitud de 3310 m s.n.m. (G. E. Alvarado, com. escrita, 2020).
Incorporación del concepto de R o
Fagents y Wilson (1993) proponen que en los primeros centenares de metros (Ro) el fragmento no presenta un arrastre apreciable pues, debido a la onda expansiva, el gas y el fragmento se mueven a la misma velocidad. Así, mientras está dentro del cráter y encerrado entre sus paredes, el fragmento está completamente acoplado a una fase gaseosa y de cenizas, cuya velocidad respecto al suelo va disminuyendo al tiempo que el fragmento, por inercia, se mantiene moviendo, causando que la velocidad relativa entre ellos vaya aumentando hasta que se dé un desacople total entre el fragmento y la onda expansiva a una distancia denominada Ro, a partir de la cual establece una trayectoria relativamente parabólica (Fitzgerald et al., 2014; Lorenz, 1970; Mastin, 2001).
Según se destaca en Clarke (2012, p. 141), “nearly all vulcanian eruptions are well within the turbulent regime”, o sea, número de Reynolds entre 105 y 107 con viscosidades del flujo variando en un amplio rango de 10-4 a 10-1 Pa s. Por lo tanto, para ser conceptualmente coherentes, la trayectoria en esta segunda etapa se calculará suponiendo un régimen Newtoniano con un coeficiente Cd constante.
En términos generales, hay dos maneras de modelar la velocidad de eyección de los fragmentos: uno que considera los piroclastos atrapados dentro de un jet confinado (Steinberg y Babenko, 1978), aplicable al rompimiento (burst) del bloqueo (slug); y otro que considera la expansión dentro de una atmósfera estacionaria, que es relevante para cuando la burbuja explota en la superficie (Wilson, 1980).
Si bien en el trabajo de Fagents y Wilson (1993) se incluye la formulación matemática, los resultados numéricos que ahí se citan son solo para casos muy específicos, lo que impide comparar con los datos obtenidos para el fragmento. Lo más cercano que se puede llegar, para una densidad de 2500 kg/m3, como se ha supuesto en el presente análisis, corresponden a un clasto con velocidad inicial de 100 m/s que, una vez recorrida la distancia Ro, se eyecta con ángulo inicial de 45° y o bien de 66°. De acuerdo a los resultados numéricos citados esos ángulos están asociados a un Ro = 503 m y 365 m, respectivamente.
Como una primera aproximación, en este trabajo el fragmento se considerará eyectado desde la parte superior de la columna de magma, o sea, desde una altura de 3080 m s.n.m. Su posible trayectoria se dividirá en una primera etapa con un proyectil ideal lanzado con una velocidad y ángulo inicial α, que recorre una distancia Ro, para luego continuar, en una segunda etapa como un proyectil lanzado con una velocidad de 100 m/s y uno de los dos ángulos (45° o bien 66°) mencionados en Fagents y Wilson (1993), sometido a un régimen Newtoniano con un coeficiente de arrastre Cd constante. Las coordenadas del nuevo punto de lanzamiento serían Xi = 745 - Ro cos α, y una altura de Zi = 3080 + Ro sen α sobre el nivel del mar.
El ángulo inicial α de la segunda etapa depende del arrastre causado por el gas y residuos que encontró en la primera etapa. Por lo que se analizarán diversos ángulos posibles. El coeficiente Cd asociado a la segunda etapa se determina ajustando el parámetro K=b/m para queel clasto impacte el puesto de guardaparques El parámetro K = b/m es calculado utilizando b = ½ Cd S ρ donde Cd el coeficiente de arrastre (drag coefficient) dependiente de la forma, S el área transversal (supuesta 0,075 * 0,03 m2) y ρ la densidad del fluido, que se supondrá la del aire en esa parte del trayecto (humedad relativa 70 %, temperatura 10 °C) e igual a 1,243 kg m-3, y m es la masa del fragmento. Los resultados para 45° y Ro = 503 se resumen en el cuadro 1 y para 66° y Ro = 365 se resumen en el cuadro 2.
Cuadro 1 Caso de un proyectil lanzado a un ángulo de 45° con una velocidad de 100 m/s, dentro de una nube de Ro = 503 m.
| α (°) | Xi (m) | Yi (m) | Θfinal | Vfinal (m/s) | K= b/m | Cd |
| 60 | 493 | 3515 | 83 | 60,8 | 0.00245 | 1,28 |
| 65 | 532 | 3536 | 82,9 | 64,1 | 0.0022 | 1,14 |
| 70 | 573 | 3553 | 82,1 | 67,8 | 0.00193 | 1,01 |
| 75 | 614 | 3566 | 80,6 | 71,4 | 0.00168 | 0,88 |
Cuadro 2 Caso de un proyectil lanzado a un ángulo de 66° con una velocidad de 100 m/s, dentro de una nube de Ro = 365 m.
| α (°) | Xo (m) | Yo (m) | Θfinal | Vfinal (m/s) | K= b/m | Cd |
| 60 | 563 | 3396 | 78,8 | 90,8 | 0.000727 | 0,38 |
| 65 | 591 | 3411 | 78,3 | 94,6 | 0.000627 | 0,33 |
| 70 | 620 | 3423 | 77,9 | 98,1 | 0.00055 | 0,28 |
| 75 | 651 | 3432 | 77,2 | 102 | 0.000455 | 0,23 |
Para ambos casos, el ángulo de impacto al techo de la caseta es mucho más alto (82° y 78°) que los 65° estimados en campo considerando la altura del techo respecto al piso y el desplazamiento horizontal del agujero en el techo respecto al posible punto de impacto en el suelo. Ya que la velocidad de salida es la misma (100 ms-1) se observa que al aumentar el ángulo de salida de 45° a 66° tanto el valor de Ro como de los valores de Cd varían apreciablemente se corre el riesgo de que para las ecuaciones citadas en Fagents y Wilson (1993), haya más de una combinación de velocidad y ángulo que den resultados que se comparen con las condiciones reales de nuestro caso de estudio.
Aproximación a R o
Para evitar, al menos en parte, esa situación, sin renunciar a lo esencial de la propuesta de Fagents y Wilson (1993) se propone una manera alternativa de calcular la posible trayectoria del bloque balístico que, como se verá más adelante, produce resultados razonables.
La forma del cráter al momento de la erupción se asemeja más a un embudo, con simetría axial, cuyo borde, a una altitud de 3310 m s.n.m., debe saltarse el clasto para impactar el puesto de guardaparques a una altitud de 3310 m s.n.m.. Al lado opuesto, en dirección al mirador, se encuentra el borde más bajo con una altura de 3150 m s.n.m. y con el piso de lava a 3080 m s.n.m. En la parte superior el cráter tiene un diámetro de 180 m. La distancia del centro del cráter al puesto de guardaparques es de 710 m y a hasta la fuente es de 745 m.
El ángulo inicial de salida respecto al piso, para que el clasto salga del cráter apenas rozando el borde a 3310 s.n.m., se puede considerar igual al ángulo que subtiende la hipotenusa de un triángulo recto cuyo cateto opuesto es la vertical desde el borde del cráter hasta la horizontal del piso (longitud de H = 3310 - 3080 = 230 m) y un cateto cuya longitud es la suma de los 35 m de la fuente hasta el centro y los 90 m de la proyección del radio del cráter. Ese ángulo se calculó en β = 61,47°.
La trayectoria del clasto se dividirá en dos partes. En la primera el clasto se moverá desde la fuente como un proyectil ideal completamente acoplado con la fase gaseosa. La incorporación del concepto de Ro se hace suponiendo que el gas prácticamente estará confinado mientras esté a una altura menor o igual a 3310 m s.n.m., que corresponde con la altura del borde más alto. El modelo elaborado por Fagents y Wilson (1993) supone que el gas está confinado en un cráter en forma de embudo con simetría axial, pero con todo el borde a una misma altura, por lo que su presión se reduce circularmente una vez que sobrepase la altura del borde. Varios modelos multifase para la mezcla gas-partículas muestran que esa reducción de presión dentro del conducto se equilibra con la presión atmosférica en un radio no mayor a 50 m alrededor del conducto (Morrissey y Chouet, 1997; Formenti, Druitt y Kelfoun, 2003). En este trabajo se analizarán 2 posibles ángulos α = 65°, 70°.
Por coherencia, la velocidad y ángulo de llegada de la primera etapa, en la que el proyectil recorre una distancia X (= H/tanα) hasta alcanzar una altura de 230 m sobre el piso, deben ser los correspondientes valores iniciales de la segunda etapa. Asi el balístico será una masa lanzada desde una altura de 230 m respecto al piso de lava que recorrerá horizontalmente los últimos A = 745 -X metros en un régimen Newtoniano con coeficiente de arrastre constante. La velocidad inicial en esta segunda etapa será aquella que le permita recorrer esa distancia A, con un parámetro K fijo previamente calculado.
En el cuadro 3, las 2 primeras filas corresponden al análisis efectuado con K= 0,00157 (corresponde a Cd = 0,82, propio de un cilindro más largo que ancho), que generan velocidades iniciales excesivamente grandes. Las siguientes dos filas corresponden al análisis con K= 0,0008 (calculado con un Cd = 0,42, propio de una semiesfera), cuyas velocidades iniciales se acercan más a lo esperado. Los cuatro casos generan ángulos de llegada que se desvían de los 65° estimados en campo.
Cuadro 3 Análisis de posibles trayectorias del clasto según ciertas suposiciones, indicadas en el texto.
| Fila | α (°) | X (m) | A (m) | Vo (ms-1) | Θf | Vf (ms-1) |
| 1 | 65 | 107 | 638 | 190 | 83,9 | 74,9 |
| 2 | 70 | 83,7 | 661 | 290 | 86,6 | 77,1 |
| 3 | 65 | 107 | 638 | 116 | 78 | 88 |
| 4 | 70 | 83,7 | 661 | 144 | 81 | 93,7 |
| 5 | 65 | 98 | - | 125 | 61 | 109 |
| 6 | 61 | - | 647 | 109 | 74,6 | 83,3 |
| 7 | 63 | 133 | - | 150 | 59 | 133 |
| 8 | 59 | - | 612 | 97 | 74,8 | 84 |
El modelo se puede hacer más realista si se incluye que no todo el borde del cráter está totalmente a la misma altura, por lo que una vez que el frente del gas que arrastra el clasto llegue al punto del borde a la menor altura (3150 m s.n.m.), el gas dejará de estar completamente confinado y se irá escapando hasta alcanzar el borde más alto (3310 m s.n.m.), momento a partir del cual el gas se expande totalmente alrededor, como se propone en Fagents y Wilson (1993), aunque la presión no presentaría simetría axial. Para un ángulo de salida de 66° con simetría axial, Fagents and Wilson (1993) calcularon un Ro = 365 m para un clasto de 2500 kgm3 de densidad.
En las filas 5 y 6 del cuadro 3, se presentan los resultados más coherentes, obtenidos por prueba y error. La fila 5 muestra que en la primera etapa el clasto se eyectó a 125 ms-1 con un ángulo de 65° alcanzando sin ningún arrastre la altura de 192 m recorriendo 97 m horizontalmente (215 m en línea recta desde la fuente), punto al que llega con una velocidad final de 109 ms-1 formando un ángulo de 61°. Fagents y Wilson (1993) calcularon un valor de Ro = 365 m para una velocidad y ángulo inicial de 100 ms-1 y 66°.
En la segunda etapa (fila 6) asociada a medio con un valor de K= b/m constante igual a 0,0008, el clasto sale eyectado en con una velocidad inicial de 109 ms-1 y un ángulo de 61° (por coherencia iguales a la velocidad y ángulos finales de la primera etapa) llegando a impactar la caseta, con una velocidad de 83,3 ms-1 y un ángulo de 74,6° (algo alejado de los 65° que se midieron en el campo). El valor de K = b/m se calculó con la masa estimada a partir de las posibles dimensiones del clasto y un valor de Cd = 0,42. La razonabilidad de los parámetros calculados a partir del modelo, a falta de mediciones directas, solo puede establecerse examinando su coherencia interna. A partir de los valores calculados por Fagents y Wilson (1993), para un ángulo de salida de 66° con una velocidad inicial de 100 ms-1 lo más cercano a nuestros valores, se calculó una velocidad y ángulo de llegada de 94,6 ms-1 y 78,3°, un Cd = 0,33 y un Ro = 365 m (Cuadro 2), que debe ser mayor al de nuestro modelo dado que se consideraron que el gas está totalmente confinado hasta alcanzar el punto más alto del borde.
Como argumento adicional, la velocidad inicial concuerda con Shapiro (1953) y Wilson, Sparks, y Walker (1980), quienes proponen que en una erupción la velocidad del sonido será también la velocidad de la onda expansiva, que para erupciones como la que se dio en el evento del 2014 estaría en el rango de 100 a 150 m/s (Woods,1988).
Un último control sobre la razonabilidad de los resultados obtenidos, puede efectuarse usando de guía el trabajo de Bower y Woods (1996). Según la figura 5a de ese trabajo, un clasto eyectado con una velocidad de 100 ms-1 tiene asociado una onda de choque a una altura de 300 m del cráter, comparable con los 192 m que se usaron en este trabajo. De acuerdo a la figura 5b la presión a la salida del cráter está en el rango 104 a 105 Pascales, en tanto que una velocidad de salida de 120 ms-1 se ha asociado a un magma con 3 % de volátiles, de acuerdo a lo encontrado en campo para varios volcanes Costa Rica (G. E. Alvarado, com. escrita, 2020), eyectado con una presión en el rango de 105 a 106 Pascales.
En resumen, se propone que el clasto fue eyectado con una velocidad inicial de 125 ms-1 y un ángulo inicial de 65° llegando a impactar el techo de la caseta con una velocidad y ángulo de llegada de 83,3 ms-1 y de 75°.
Por completitud, se examinará el caso en que el clasto se desacopla de un gas que deja de estar confinado respecto a cualquier punto del borde, utilizando una altura de 20 m sobre el borde más alto del cráter. Así, según la fila 7, en la primera etapa para que un clasto lanzado con un ángulo de 63° alcance sin arrastre un punto situado a una distancia horizontal de 133 m y una altura de 250 m de la fuente, entonces debe eyectarse con una velocidad inicial de 150 ms-1. La velocidad final con que lo alcanza es de 133 ms-1 formando un ángulo de 59° con la horizontal. En la segunda etapa (fila 8) los cálculos con un ángulo de 59° (igual a los 59° al finalizar la primera etapa) y K= 0,0008 muestran que solo se requiere una velocidad inicial de 97 ms-1 (lejos de los esperados 133 ms-1) para que impacte el techo de la caseta, haciéndolo con un ángulo de 75° (algo alejado de los 65° que se midió en el campo) y una velocidad de 84 ms-1.
Este análisis deja claro, en el caso del cráter asimétrico del Turrialba, que el campo de velocidades de los balísticos no es esférico, o sea la velocidad inicial depende de la dirección en que el clasto es lanzado.
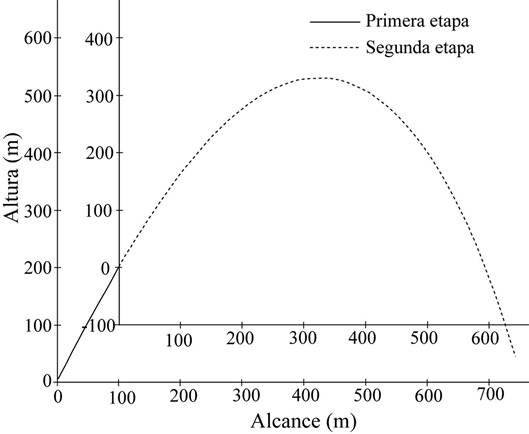
En la figura 3 se muestran la trayectorias para la primera etapa (sin arrastre), y la segunda etapa, con el clasto moviéndose en un régimen Newtoniano con Cd constante.
El cálculo efectuado no toma en cuenta la velocidad terminal Vter en la dirección z, calculada como Vter = √g/K = 110,7 ms-1) por ser esta mayor a la velocidad en la dirección z con que impacta (82,48 ms-1).
Nuestro modelo mejora el propuesto por Fudali y Melson (1972) porque ellos suponen que el proyectil se desplaza sin ningún arrastre en toda su trayectoria, subestimando así la velocidad inicial del clasto y sobrestimando el ángulo inicial de la trayectoria con el máximo alcance. Según se muestra en el cuadro 4, para una velocidad inicial de 109 ms-1 el máximo alcance (distancia de la fuente a punto de impacto, a la misma altura) se logra con un ángulo menor a los 45°. Este rango de ángulos depende de los valores de Cd utilizados, lo que evidencia la necesidad de programas de cómputo como el BALÍSTICA que se ha utilizado en este trabajo.
Cuadro 4 Variación del alcance respecto al ángulo inicial.
| Θ (°) | 30 | 35 | 40 | 42 | 44 | 45 |
| Alcance (m) | 683,7 | 715,3 | 728,6 | 728,9 | 726 | 723,8 |
En este trabajo el movimiento sin arrastre se incluye en la primera etapa pero a la luz de la propuesta de Fagents y Wilson (1993), incluyéndose después el arrastre del aire en la segunda parte de su trayectoria, además de considerar la asimetría del cráter asimétrico vía el ángulo de salida, lo que lo hace mucho más realista.
Llama la atención que, para número de Reynolds alrededor de los 105 esperables para este tipo de erupciones (Clarke, 2012), un valor de Cd = 0,42 (asociado a una semi-esfera) de mejores resultados que uno de Cd = 0,82 (asociado a un cilindro largo) o bien de Cd = 1,15 (asociado a un cilindro corto con las 3 dimensiones similares) como se esperaría dada la forma del clasto. El lector que desee profundizar en este aspecto es referido a Nardone y Koll (2018)
Los resultados de este trabajo sugieren que el clasto siempre expuso al aire la cara más alejada de la mano, la que básicamente es un rectángulo de área 35 cm2 (equivalente a un círculo de 3,3 cm de radio). Esa área transversal va disminuyendo conforme se acerca al otro extremo, por lo que se movió de manera similar a como lo hace una cápsula espacial al regresar al suelo. Las estrías que, se observan en el clasto posiblemente redujeron el arrastre de manera similar a cómo funcionan las depresiones que se le hacen a las bolas de golf para aumentar su alcance. No es posible sugerir algún mecanismo que diera origen a estas estrías por cuanto para este trabajo no se tuvo acceso al fragmento en sí, solo a la foto que incluimos líneas arriba. El lector que desee ampliar sobre este punto es referido a Alam et al. (2011), quienes analizan la forma y profundidad de las depresiones con que se fabrican las bolas de golf y sus efectos. Aunque el valor de Cd varía con la velocidad, en la zona de turbulencia (número de Reynolds Re alrededor de 105) oscila entre 0,28 y 0,42. Igualmente se refiere a Choi, Jeon y Choi (2006), quienes analizan el caso de una esfera en que el hemisferio impactado por el aire es liso, en tanto que al hemisferio opuesto se le efectuaron depresiones.
Caso del Mirador
El Mirador para visitantes (Fig. 1), a una altitud de 3240 m s.n.m, es un punto importante a analizar por cuanto es un punto de reunión de personas, lo que aumenta su vulnerabilidad. Al estar más cerca del cráter puede ser impactado por fragmento de una menor energía, pero aun así peligrosos. El análisis se llevará a cabo suponiendo que el borde del cráter está a la más baja altura: 3150 m s.n.m., o sea solo 70 m sobre el piso de lava por lo que el ángulo mínimo de salida será de 51,8° dado que la fuente está a solo 55 m de la pared del cráter. Para poder comparar los resultados se supondrá que el clasto así como la mezcla de gas y ceniza (K = 0,0008) son las mismas que en el caso de la caseta de guardaparques. Como en el caso anterior, solo se considerarán cálculos en los que la velocidad y ángulo inicial de la segunda etapa sean iguales a los correspondientes valores finales de la primera etapa.
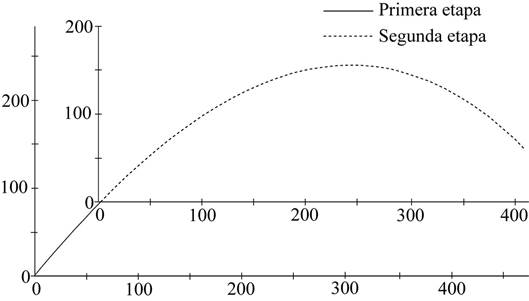
El resultado más aceptable que se obtuvo es que el clasto, luego de ser eyectado con una velocidad inicial de 89 ms-1 a un ángulo de 55°, llega a un punto situado horizontalmente a 65 m de la fuente, y una altitud de 86 m sobre el piso de lava (108 m en línea recta, y 1,3 s después) con una velocidad de 79 ms-1 y un ángulo de 50°. A partir de este punto recorre el resto del trayecto en 9,9 s llegando con un ángulo de 50° y una velocidad de 53,2 ms-1 (Fig. 4) equivalente a una energía cinética asociada de 1,6 kJ, que aunque menor a la calculada para el puesto de guardaparques, es todavía suficiente para perforar una lámina de techo de zinc normal. Esta menor velocidad inicial pudiera ser el resultado de la reducción en presión del gas, inicialmente confinado en el cráter, conforme se fue escapando al romperse el bloqueo. También es congruente con las velocidades de 80 a 90 ms-1, reportadas en Self, Kienle y Huot (1980), para erupciones freatomagmáticas en transición a estromboliana de los cráteres de 1977 del volcán Ukinrek.
Análisis del peligro
Después del incidente de Mount Otake se han publicado varios trabajos referidos al posible daño estructural que pueden causar los balísticos (Alatorre-Ibarguengoitia, Morales-Iglesias, Ramos-Hernandez, Jon-Selvas y Jimenez-Aguilar, 2016; Biass et al., 2016; Fitzgerald et al., 2014; Tsunematsu, Chopard, Falcone y Bonadonna, 2014; Williams et al., 2017) Una primera visión de los posibles daños asociados a los valores de velocidad de llegada, o equivalentemente, la energía cinética con que impacta el fragmento puede lograrse usando de guía la figura 5. Así una masa de 2 kg, como la del clasto, con una energía cinética de alrededor 3 kJ es capaz de penetrar una lámina de metal, justo lo que se obtuvo con una velocidad de impacto de V = 83,3 ms-1 (equivalentes a una energía ½ m V2 = 4,107 kJ) en nuestro caso.
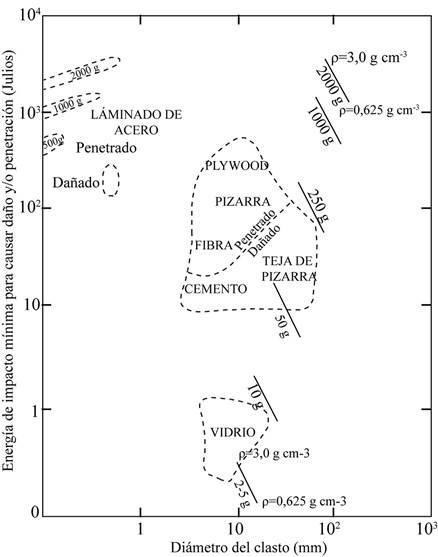
Fig. 5 Relación del daño que causa el impacto del clasto en función de la energía y el diámetro del mismo. Adaptado de la figura 1 de Blong (1981).
Mayor precisión se obtiene usando el trabajo de Williams et al. (2017) que incluye resultados para masa de 3 a 10 kg, densidades en el rango 1775 a 3030 kgm-3, velocidades de impacto de hasta 79 ms-1 y ángulo de impacto de 50° y 90° respecto a la superficie, que son muy cercanos a los que se tiene en este trabajo. En nuestro caso, la lámina del techo del puesto de guardaparques está inclinada un ángulo de 20° respecto a la horizontal, y el ángulo de impacto se estimó en 65°, respecto a la horizontal, o bien 25° respecto a la vertical, por lo que el clasto impactó la lámina con un ángulo de (20° + 25°).
Según la figura 5 de ese trabajo, el clasto analizado muy probablemente hubiera atravesado una pared de concreto (dado la energía asociada de 4,1 kJ), una energía básicamente 4 veces la requerida para atravesar una lámina de metal. Por ello atravesó el techo, destrozó el sanitario y llegó a romper el suelo que, al ser de madera, requiere de menos energía para dañarlo.
Conclusiones
El software BALÍSTICA mostró ser una herramienta útil en el análisis de fragmentos balísticos volcánicos. En este trabajo en particular permitió incluir el arrastre del aire, el concepto de Ro propuesto por Fagents y Wilson (1993) y modificarlo para considerar la asimetría del cráter, pudiéndose establecer una solución de continuidad entre la primera y segunda etapas de la trayectoria, al poder usarse los valores finales de velocidad y ángulo de la primera como valores iniciales de la segunda, reduciéndose el número de factores ajustables. Por esa misma razón, el valor del coeficiente de arrastre Cd se fijó desde el inicio y su correspondiente valor de K = b/m fue establecido con un valor de masa m determinado independientemente, haciendo más realista al modelo. Los resultados obtenidos para el puesto de guardaparques (1 fila), y para el Mirador se resumen el cuadro 5.
Cuadro 5 Resumen de los valores que definen la trayectoria calculada del clasto para los dos casos examinados.
| Lugar | Vel. Ini. (ms-1) | Ang. Ini. (°) | Vel. Fin. (ms-1) | Ang. Fin. (°) | Tiem. Vuel. (s) | Cd |
| Puesto | 125 | 65 | 83,3 | 74,6 | 20,3 | 0,42 |
| Mirador | 89 | 55 | 53,2 | 50 | 11,2 | 0,42 |
En el cuadro 6, para la segunda etapa, se comparan el ángulo y velocidad final de un clasto bajo dos condiciones diferentes: la obtenida al incluir el arrastre como se ha descrito aquí, y aquella en que el clasto se considera eyectado con el mismo ángulo inicial pero con una velocidad inicial ajustada para que logre dar en el blanco suponiendo una trayectoria con arrastre nulo.
Cuadro 6 Comparación de los resultados, para la segunda etapa, obtenidos incluyendo el arrastre (la primera fila) y considerando el caso ideal (la segunda fila) para un clasto que impacta el puesto de guardaparques, o bien el Mirador.
| Lugar | Vel. Ini. (ms-1) | Ang. Ini. (°) | Vel. Fin. (ms-1) | Ang. Fin. (°) | Tiem. Vuel. (s) |
| Puesto | 109 | 61 | 83,3 | 74,6 | 18,5 |
| 80 | 61 | 100,2 | 67,2 | 16,6 | |
| Mirador | 79 | 50 | 53,2 | 50 | 9,9 |
| 69 | 50 | 58,1 | 40,2 | 9,2 |
El tiempo de vuelo es mayor pues el arrastre enlentece la caída. El ángulo de llegada es mayor porque la componente vertical se acerca asintóticamente a la velocidad terminal al mismo tiempo que la componente horizontal siempre se va reduciendo dando como resultado que la trayectoria se vaya acercando a la vertical. La velocidad final con arrastre es menor que la ideal debido a que la componente horizontal se va reduciendo por efecto de arrastre, mientras que en el caso ideal esa componente se mantiene constante.
Utilizando balísticos con densidades, masa de clasto y velocidades de impacto en rangos cercanos a los encontramos en este estudio, Williams et al. (2017) encontró experimentalmente que, para la misma energía cinética, un clasto que impacta una superficie oblicuamente (50° respecto a la normal a la superficie) tiene menor probabilidad de penetrarla que cuando la impacta perpendicularmente. Por ejemplo, con una energía cinética de 3 kJ, es un 64% más probable que un impacto perpendicular dé como resultado un daño DS2 (desprendimientos en el lado opuesto del impacto, sin llegar a atravesarlo) que un impacto similar a un ángulo de 50°. Dada la resistencia a impacto del concreto reforzado, esta situación se cumple aun para impactos oblicuos con el doble de energía que el caso perpendicular. Igualmente, esos autores reportaron daños congruentes a los observados en el puesto de guardaparques para energías similares a la energía de 4 kJ calculada en este trabajo. Dadas las variaciones en los procesos de fabricación, para los casos de una penetración completa solo es posible establecer un rango de energía de 4 a 12 kJ (Jenkins, Spence, Fonseca, Solidum, y Wilson, 2014). Estructuras de madera (como cedro) pueden soportar impactos de hasta 13 kJ, como las producidas por un fragmento de 128 mm, equivalente a 2,66 Kg, que impacta con una velocidad de 83 m s-1 (Yamada et al., 2018).
Por lo anterior, se considera efectuar las siguientes recomendaciones:
Recomendación 1: Incorporar, como parte regular en el análisis de peligro por balísticos volcánicos, los resultados expuestos en Williams et al. (2017) al diseñar estructuras tendientes a reducir el riesgo.
Las conclusiones del Cuadro 6 muestran que la inclusión del arrastre en el cálculo de la trayectoria da como resultado una favorable menor velocidad de llegada, o equivalentemente, una menor energía de impacto. Por su parte, el ángulo de llegada se aproxima más a la vertical cuando se incluye el arrastre. Por ende, en una edificación con un diseño en que las paredes sean verticales la inclusión del arrastre lleva a que la colisión del clasto con la pared sea más oblicuo por lo que es menos probable que la perfore, siendo más probable que rebote y que el clasto y las esquirlas producto del impacto lleguen más lejos, quizá hasta 15 m (Williams et al., 2017). Respecto al techo, sin embargo, esa misma aproximación a una vertical conllevaría a que, si el techo es horizontal, el clasto colisione casi perpendicularmente, aumentando la posibilidad de que lo perfore. Para disminuir esa posibilidad se da la,
Recomendación 2: en el caso de que se prevean una sola fuente de balísticos, las estructuras deben diseñarse con techos de dos aguas, orientadas de manera que los posibles balísticos que lleguen a impactar el techo lo hagan lo más oblicuamente posible. Caso de que se prevean dos o más fuentes, sobre todo si no son colineales, debe analizarse la posibilidad de que los techos sean a 4 aguas.
No debe dejarse por fuera que un clasto que llegue a rebotar puede, sobre todo en el caso de clastos con altas energías cinéticas, quizá debido a su pequeño tamaño, puede la pared de causar que, la parte opuesta al impacto se desprenda material que puede salir lanzado como pequeños proyectiles que impacten a las personas que se hayan protegido adentro, quizá recostándose instintivamente a la pared.
Así, por ejemplo, clastos de baja densidad, altamente vesiculados (densidades en el rango de 1775 a 2213 kg m-3) llegan solo a causar daños tipo DS2 (en el caso del concreto implica desprendimientos en el lado opuesto del impacto, sin llegar a atravesarlo), aún con energías tan altas como 3689 J. Por ello se efectúa la,
Recomendación 3: se incorpore en los estudios de peligro la posibilidad de que el material utilizado en la construcción del refugio pueda descascararse por el impacto, utilizando de guía a Li, Reid y Ahmad-Zaidi (2006) o un trabajo similar. Posibles soluciones pueden pasar por un cambio en los métodos constructivos, en los materiales utilizados, o bien en revestir con una lámina lisa delgada la parte interna de la pared que pueda ser impactada