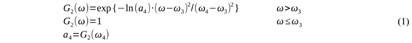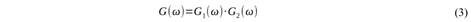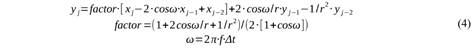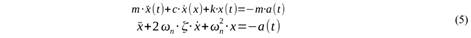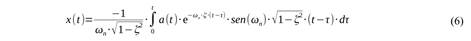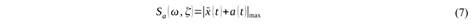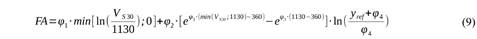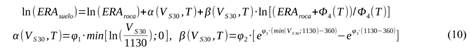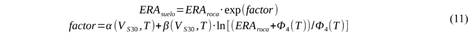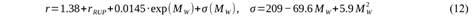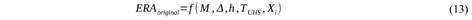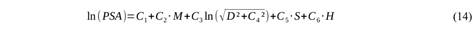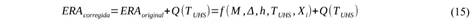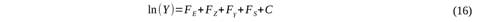Introducción
En todo trabajo de estimación de la amenaza sísmica un factor fundamental lo constituye la selección adecuada de las relaciones de atenuación que se van a utilizar, para las que a veces se usa la abreviatura de su nombre en inglés GMPE (Ground Motion Prediction Equations). Desde los trabajos iniciales en términos de intensidad macrosísmica a los actuales en términos de los espectros de respuesta de aceleración siempre este ha sido un problema difícil de resolver. La solución ideal es la obtención de relaciones de atenuación locales, para lo cual es necesario tener datos suficientes para poder calcular los parámetros de la relación por inversión. Esto era más sencillo en los tiempos en que se usaba la intensidad macrosísmica, ya que se preparaban con más facilidad modelos de isosistas aplicables a la región de estudio (Álvarez y Chuy, 1985; Chen, Chen, Güendel y Kulhánek, 2002). El paso a parámetros del movimiento del terreno, originalmente PGA y PGV, redujo la posibilidad de obtener formulas locales, pues no era muy extensivo el uso de acelerómetros y solo los países más ricos tenían la posibilidad de instalar redes de acelerógrafos que permitieran hacer dichos estudios de atenuación. La mayor parte de los países, o no disponían de ningún acelerógrafo, en cuyo caso tenían que basarse en la experiencia de los autores para seleccionar relaciones que se adecuaran a las características geólogo-tectónicas de la región (Álvarez, Lindholm y Villalón, 2017), o disponían de pocos datos que se usaban para discriminar entre relaciones obtenidas por otros autores (Molina et al., 2008). Estos métodos aproximados introducen un error en los estimados finales de amenaza sísmica. En el caso de Nicaragua, los estimados de amenaza sísmica hasta 2007 aproximadamente, se hicieron siempre en términos de PGA, usando relaciones de atenuación obtenidas para otras regiones con características geodinámicas semejantes. Incluso los relaciones obtenidas para Centroamérica usaban muy pocos datos de Nicaragua en sus base de datos (Climent et al., 1994). . En ese caso es imposible estimar ese error. En 2008 concluye un proyecto regional de estimación de la amenaza sísmica (RESIS-II) para los países de América Central (Molina et al., 2008), donde ya se trabaja con los espectros de amenaza uniforme. La selección de relaciones de atenuación para toda la región se apoyó en los datos de aceleración disponibles, los que se usaron para discriminar entre diferentes posibilidades de relaciones de PGA y espectro de respuesta.
En este último caso se pueden obtener criterios sobre su influencia en los resultados. Por ejemplo, en el proyecto RESIS-II mencionado se analizaron varias relaciones de atenuación comparándolas con los datos disponibles a nivel regional y al final seleccionaron algunas, pero los propios autores apuntan que: “...para PGA, presentan un sesgo negativo después de los límites de -σ, por lo que su uso supone una sobrestimación de la amenaza a distancias menores a los 200 km…” (Molina et al. 2008, p. 122). Este problema influyó en que para Nicaragua se obtuviesen valores muy altos de PGA en comparación con los estudios anteriores (las fuentes sísmicas que más influyen en la amenaza sísmica de sus ciudades principales están a distancias cortas de las mismas), tanto, que hacían dudar de su aplicabilidad.
Otra variante alternativa a la solución del problema es el uso de relaciones de atenuación de intensidades combinadas con relaciones de conversión intensidad-movimiento del terreno. Sin embargo, la misma no tuvo mucha difusión, pues resultaba que había dos fuentes de incertidumbre en lugar de una sola. Un ejemplo del uso de tal procedimiento fue el mapa preparado por Álvarez y Chuy (1995) para las normas de construcciones sismorresistentes de 1999 en Cuba (Norma Cubana, 1999).
En los momentos actuales todos los trabajos se orientan al uso de relaciones de atenuación publicadas y un compendio de las relaciones existentes es presentado por Douglas (2021). En el caso de Nicaragua se dispone actualmente de una cantidad apreciable de registros acelerográficos y surge la pregunta: ¿Qué hacer cuando se observa un sesgo de los valores experimentales con respecto a los predichos en una relación? En este trabajo se discute un procedimiento para modificar las relaciones de atenuación publicadas en base a datos locales para eliminar dicho sesgo y poder realizar estimaciones de amenaza sísmica más acordes con la realidad. Como se discutirá más adelante, no se pueden estimar nuevas relaciones de atenuación, pero si se podrá evitar que las que se usen introduzcan un sesgo en los cálculos de la amenaza sísmica, como ocurrió en el caso del proyecto RESIS-II.
Materiales y métodos
En Nicaragua se han realizado registros acelerográficos en 3 períodos. El primero corresponde a registros analógicos del período 1968-1983. Dichos registros han sido procesados en mayor o menor grado por diferentes autores. Una nueva red, esta vez de acelerógrafos digitales se comenzó a instalar en 1996 y se fueron deteriorando los equipos hasta que en 2009 se retiró el último. Finalmente, en 2014 se inició un proceso de instalación de acelerógrafos triaxiales de banda ancha en diferentes lugares del del área del Pacífico de Nicaragua hasta un total de 24. En este trabajo pudieron procesarse los acelerogramas del primer y tercer períodos (hasta 2018). Los registros de las estaciones en el período 2014-2018, obtenidos con estaciones acelerográficas de 24-bits 130-SMHR de REF-TEK, mayoritariamente se incorporan al sistema de adquisición de datos y aparecen mezclados con los de otras estaciones, no acelerográficas, en los archivos “WAV” que crea el SEISAN (Ottemöller, Voss y Havskov, 2018). Los mismos tienen un muestreo de 200 Hz. Las características de frecuencia de los equipos son prácticamente planas en el rango de frecuencias de 0,0001 a 200 Hz, dadas por una función de dos polos reales. La amplitud de los registros acelerográficos se mide en unidades convencionales, dadas por el fabricante, que denomina “counts” (en español sería “cuentas”). Estos registros deben ser convertidos a unidades de aceleración, que en este trabajo se seleccionaron como (m/seg2) y (g), a la vez que debe eliminarse la influencia del equipamiento sobre ellas, lo que se realizó usando los archivos de calibración que da el fabricante, uno por cada estación y componente, a través de una división espectral, usando para ello el programa SAC2000 (Goldstein, Dodge, Firpo y Minne, 2003).
Los registros del primer período fueron obtenidos de una colección de acelerogramas para América Central (Douglas et al., 2004), en un devedé que contiene los acelerogramas (escalados a m/seg²). El trabajo consistió en la selección de los datos, un cambio de formato para que pudiesen ser procesados de la misma forma que los de la red actual, pero en el caso de la deconvolución del equipamiento no se usaron las características de frecuencia de los equipos, sino que se aplicó un filtro Butterworth con 4 polos y límites de frecuencia 0,25-25 Hz, similar a la que se usa por una herramienta de selección y procesamiento incluida en el devedé. Ese procesamiento también se hizo con el SAC2000 (Goldstein et al., 2003)
Con estas premisas se recopilaron todos los acelerogramas disponibles, se deconvolucionaron para eliminar la influencia del equipamiento y se realizó su conversión a formatos preseleccionados, en este caso “sac” y “xy”. Una vez realizada la conversión de formatos se preparó un archivo de acelerogramas donde se catalogan los mismos por fecha, estación y componente. Estos acelerogramas no tienen aún un procesamiento específico. Por lo general son ruidosos, siendo lo más común la presencia de ruido de alta frecuencia.
Para calcular los espectros de respuesta correspondientes se realiza un procedimiento estándar.
1) Se realiza un corte de la señal analizada en un intervalo (t1,t2), y a continuación se realiza el ajuste del 0 y la eliminación de la tendencia.
2) Se calcula el espectro de Fourier, que permite determinar si se puede extraer una señal útil, ya sea directamente o aplicando filtros.
3) Se usan filtros gaussianos pasa alta y pasa baja en el dominio de las frecuencias y “Notch” en el dominio del tiempo para eliminar el ruido presente en los acelerogramas. Esto implica una selección entre registros útiles y registros no utilizables
4) Se calcula el espectro de respuesta de aceleración de los registros útiles
El acelerograma se pasa por un filtro pasa alta, pasa baja o pasa banda controlado por 4 frecuencias f1<f2<f3<f4. La señal es igual a 0 para f<f1 y f>f4, e igual a 1 para f2<f<f3. Para evitar “aliasing” f3<f4<100 Hz. Para ello se emplean filtros gaussianos en el dominio de la frecuencia. El filtrado “Notch” se usa para eliminar una sola frecuencia, o mas bien una banda muy estrecha de frecuencia. Es un caso muy común cuando aparece una frecuencia de 60 Hz que cubre toda la señal útil, lo que está asociado generalmente a la influencia de motores eléctricos.
El filtro pasa baja deja pasar solo las señales de una frecuencia superior a un umbral y el pasa alta las de una frecuencia inferior a un umbral. El filtro gaussiano pasa baja usado, tipo “roll-off” se define como (por facilidad en la representación de las fórmulas se expresan en término de ω=2πf):
Este filtro tendrá un valor unitario para ω≤ω3, y una caída hasta el valor a4(ω4) cuya inclinación dependerá de la diferencia entre “ω4” y “ω3”. Las características del filtro se regulan por ambos parámetros, y los valores recomendados son ω3=0,9ω4 y α4=1x10-4 (DST, 2002). El filtro pasa alta se define como:
Este filtro tendrá un valor unitario para ω≥ω2, y una caída hasta el valor “a1(ω1)” cuya inclinación dependerá de la diferencia entre “ω1” y “ω2”. Las características del filtro se regulan por ambos parámetros, y los valores recomendados son ω1=0,5ω2 y a1=1x10-4 (DST, 2002). Un filtro pasa banda entre los valores (ω1, ω4) con respuesta unitaria en la banda (ω2, ω3) se obtiene multiplicando ambos filtros
Un caso de filtro pasa-banda a la inversa (es decir, que elimina las frecuencias en un pequeño intervalo) es el llamado “Notch”. Este es un tipo de filtro de rechazo (“rejection filter”) que trabaja en el dominio del tiempo.
Las “yj” corresponden a la salida y las “xj” a la entrada, “Δt” es el intervalo de muestreo de la señal de entrada, “f” es la frecuencia a eliminar. El ancho de banda que se elimina en la práctica se controla por el parámetro r=1+d, donde “d” corresponde a dicho ancho (en Hertz). La teoría de este tipo de filtro se puede encontrar en (Kanasewitch, 1981). En el trabajo se usó una subrutina desarrollada por Boore (2008).
El estudio de los acelerogramas ha estado fuertemente motivado por las necesidades de la ingeniería civil de obtener información útil para el diseño de estructuras sismorresistentes. El más conocido de estos parámetros es el espectro de respuesta (Hudson, 1979). Se parte de un esquema consistente en un edificio situado sobre una base que está sometida a una aceleración temporal debida a un terremoto que corresponde a un sistema lineal amortiguado con un grado de libertad que responde a:
donde “a(t)” es la aceleración del terreno debida al terremoto, “k” es la rigidez de la estructura, “c” es la amortiguación, “m” es la masa del edificio y “x(t)” es el movimiento del edificio respecto al terreno. Además ωn = (k/m)½ es la frecuencia natural de oscilación (solución para el caso c=a(t)=0) y ζ = c/ (2m·ωn) es una fracción de amortiguamiento crítico. Esta ecuación tiene la solución general:
Esta fórmula contiene la llamada integral de Duhamel, que debe ser resuelta por métodos numéricos. A partir de ella se calculan mediante derivación los valores relativos de velocidad y aceleración. El espectro de respuesta de aceleración (ERA) se define como:
Para el cálculo del mismo se usa el programa “fft”, obtenido por cortesía del Departamento de Ciencias de La Tierra de la Universidad de Trieste (DST, 2002), que fue modificado para incluirle diversas opciones. Este programa realiza también el análisis de Fourier y los ajustes del cero y la tendencia. El algoritmo para el cálculo del espectro de respuesta que tiene incluido fue desarrollado en el proyecto (ENEA-ENEL, 1981)
Debe señalarse que es práctica habitual calcular una versión aproximada del espectro de respuesta denominada “espectro de pseudo aceleración (PSA)”, con PSA = ω²Sd, donde Sd = |x(t)|max. Las diferencias entre ambos pueden ser significativas, pero para los efectos de amenaza sísmica, donde los espectros de respuesta se calculan para un coeficiente de amortiguamiento crítico del 5%, ambos pueden considerarse equivalentes (Papagiannopoulos, Hatzigeorgiou y Beskos, 2013). Por tanto en este trabajo, que va orientado exclusivamente a amenaza sísmica se usan indistintamente las relaciones de atenuación para ERA y pseudo aceleración.
Un problema que se presenta en el uso de datos experimentales para ajustar relaciones de atenuación es que los acelerogramas se registran por lo general en suelos de diversos tipos, mientras que las relaciones se calculan para un tipo específico de suelo. A veces se calculan para “roca” donde no siempre se define roca de la misma forma. En algunas relaciones que se definen para “suelo”, entra una amplia variedad de ellos, que se procesan de forma conjunta (Douglas, 2021). En los últimos tiempos se tiende a considerar esa problemática caracterizando los suelos y la roca por un valor de VS30 (promedio pesado por espesor de estratos de las velocidades de la onda S en los primeros 30 m del suelo), y se han obtenido relaciones de atenuación que permiten ajustar el tipo de suelo por el valor de ese parámetro. Chiou y Youngs (2008, 2014) encontraron una dependencia entre los espectros de respuesta en suelo y en una roca de referencia en función de “VS30”:
donde ERA - espectro de respuesta de aceleración y “FA” es un factor de amplificación que se calcula como:
“FA” se estima en términos de (g) y (φ1,..φ4) se suministran tabulados por los autores para un rango amplio de valores del período del ERA. De la relación (9) se ve que el valor de VS30 de referencia yref es 1130 m/seg, cuestión muy importante para tener en cuenta cada vez que se use esta conversión. Otra cosa por considerar es el valor de 360 m/s que aparece en dos términos de la relación. Lo mismo que el 1130 m/seg puede ser un umbral superior, el 360 m/seg puede ser uno inferior. Si bien en la literatura se habla de que por encima de VS30=1130 m/seg no hay diferencias apreciables en los valores de la aceleración, del VS30=360 m/seg no se dice nada, y el segundo factor de la relación toma el mismo valor para cualquier VS30<360 m/seg por lo que quizás la misma pierda precisión en ese rango.
Los autores señalan que esta formulación puede ser usada para pseudo aceleración con 5% de amortiguamiento crítico de terremotos en zonas activas bajo las condiciones: 3.5 ≤ M ≤ 8.5 para terremotos de corrimiento por el rumbo, 3.5 ≤ M ≤ 8.0 para terremotos con fallamiento normal e inverso, profundidad al techo de la ruptura ≤ 20km, 0 ≤ RRUP ≤ 300 km y 180 m/sec ≤ VS30 ≤ 1500 m/sec. Estas condiciones son satisfechas por la inmensa mayoría de los datos disponibles para este estudio.
Esta relación podría usarse para obtener el valor de ERAroca que equivaldría al valor de ERAsuelo medido de los acelerogramas. La relación anterior toma la forma (agrupando los términos no dependientes de ERAroca y ERAsuelo):
Se puede reescribir (9) entonces como:
El proceso consiste en solucionar la ecuación trascendente (11), hallando ERAroca para un valor dado de ERAsuelo. En el trabajo esto se hace con el algoritmo de Brent (1973), de acuerdo con su realización en la subrutina “zeroin” de Netlib (2020).
Debe señalarse que en el estudio de la influencia del suelo, no pocos autores consideran que el valor de VS30 por si solo no es suficiente para reflejar el problema completamente. En su lugar se plantea una combinación de VS30 y κ0 (Bard, Bora, Hollender, Laurendeau y Traversa, 2020) donde κ0 es un parámetro de atenuación específico del suelo a altas frecuencias. Sin embargo, dichos autores dan un posibilidad de usar solamente el valor de VS30, donde cualquier dependencia con respecto a κ0 está “escondida” detrás de la dependencia de VS30., que es expresada por un término en “ln(VS30/1000)”, algo del tipo de que aparece en la fórmula (9).
Los mayores valores de aceleración se registran en las componentes horizontales. Pero al registrar las aceleraciones en dos componentes, generalmente perpendiculares entre sí, en la inmensa mayoría de los casos en una se registran mayores amplitudes que en otra. La solución más simple es calcular la media geométrica entre las componentes. Boore, Watson-Lamprey y Abrahamson (2006) comparan distintos métodos de enfrentar ese problema, y al final concluyen que la media geométrica simple es solo alrededor de un 3 % menor que cuando se usan métodos más sofisticados. Extrapolando estos resultados a los ERA, en este trabajo se usa la media geométrica de las dos componentes horizontales. Para comparar con relaciones de atenuación publicadas se usan indistintamente las expresadas en ERA y PSA. El uso de esta fórmula ya es habitual en tareas de amenaza sísmica y ya ha sido incluida como opción en el programa R-CRISIS (Ordaz y Salgado-Gálvez, 2019).
Un factor muy importante es la forma de medir las distancias en las relaciones de atenuación: hipocentral (rhipo), de Joyner y Boore (r JB ) y de ruptura (r RUP ). La distancia hipocentral se calcula directamente. La forma de medir las últimas dos requiere conocimientos sobre el foco del terremoto, información de la que no siempre se dispone, por lo que no se usa la r JB y para r RUP se usa una aproximación que aparece en Cauzzi et al. (2014), basada en una estadística global. El valor de r RUP se estima, a partir de la distancia hipocentral rhipo y la magnitud MW, por la relación:
para 5,5 ≤ M W ≤ 7,6 y r RUP ≤ 150 km. Para M W < 5,5, r RUP r hipo .
El ajuste de datos experimentales a relaciones de atenuación publicadas se realiza como:
- Se considera una relación de atenuación genérica expresada de forma general como:
donde “Xi” es un vector que incluye una multiplicidad de factores que entran en las relaciones de atenuación más sofisticadas, M la magnitud, Δ la distancia epicentral, h la profundidad y TUHS es el período del espectro de amenaza uniforme a usar. El caso más simple es el que depende solo de la magnitud y la distancia hipocentral, por ejemplo, según Schmidt (2014):
donde “D” =distancia hipocentral, “S” es un coeficiente relacionado al tipo de suelo, y H representa la incertidumbre en la predicción. Según el autor, para “roca” ambos son iguales a “0”. Muchas relaciones publicadas tienen pocas variables Xi a evaluar, pero otras relaciones tienen una expresión mucho más compleja, con decenas de variables en ocasiones, por lo que resulta complejo utilizarlas, como es el caso de algunas de las incluidas en el proyecto NGA-West2 (PEER, 2013).
- Se ajustan las relaciones de atenuación a los datos experimentales a través del análisis de los residuos {lnERA observado (T) - lnERA predicción (T)} para los que se calcula una estadística normal (μ,σ) para cada valor del período.
El ajuste de relaciones publicadas a datos locales ya fue planteado por Yenier y Atkinson (2015), que presentan una expresión obtenida por datos simulados:
en la que Y es la variable del movimiento del terreno a evaluar, y los FX representan funciones de la fuente, de la dispersión geométrica, de la atenuación inelástica y de las características del suelo, mientras que el término C es un factor de calibración empírico que considera los residuos entre las simulaciones y los datos reales, el cual se indica que debe ajustarse según el caso.
- Se añade a la relación original una corrección Q(TUHS): El sesgo “Q” contiene los valores (μi, σi) - media y dispersión estándar correspondientes al ajuste de los datos experimentales: Q(TUHS) = {μi(TUHS), σi(TUHS)}, donde “i” se mueve por los distintos valores de TUHS utilizados.
Resultados
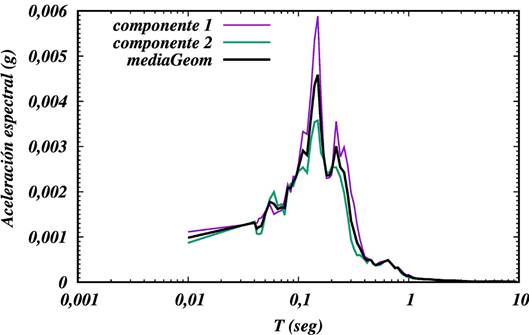
Para los fines de amenaza sísmica lo más común es trabajar con las componentes horizontales de la aceleración, aunque para algunos casos, como los de las represas de cortinas altas también se use la componente vertical. La diferencia entre los registros de aceleración entre ambas componentes horizontales puede ser bastante grandes y es tendencia trabajar con algún tipo de media entre ellos. Aunque existen procedimientos sofisticados para hacer este proceso, una buena aproximación consiste en calcular su media geométrica (Boore et al., 2006). En este trabajo, en lugar de calcular la media geométrica de las aceleraciones y luego calcular el ERA de esa media, se calcularon los ERA de cada componente y luego se calculó la media geométrica de ambos (Fig. 1). Primeramente, entre los acelerogramas sin procesar, se realizó una selección de los acelerogramas que permitían obtener un espectro de respuesta confiable en ambas componentes, ya que muchos de los aceleregramas estaban inutilizados por el alto nivel de ruido en una o las dos componentes y no eran aprovechables, y en otros casos solo existían los de una sola componete horizontal. Para poder combinar ambas componentes se garantizó un procesamiento idéntico de las mismas (ventana temporal, ajuste del cero y la tendencia, filtrado). El filtrado resultó un factor determinante en el proceso. La mayoría de los datos se encuentran en el intervalo de magnitud (Mw) (4, 5), donde la relación señal/ruido no es muy buena y el ruido inutiliza gran parte de los acelerogramas. Al final fueron obtenidos 739 espectros de respuesta de aceleración horizontal (media geométrica de las dos componentes). Su distribución por magnitud y distancia se muestra en la figura 2. Estos datos se encuentran dentro del rango de validez de las relaciones de atenuación con que se van a comparar y de la relación de conversión suelo-roca de Chiou y Youngs (2014). Resulta evidente de la figura que no existe una cobertura uniforme en magnitud y distancia para obtener una relación confiable de atenuación mediante inversión de los datos disponibles. Es por ello que se tomó la decisión de modificar o “corregir” relaciones publicadas para su uso en estimados de amenaza sísmica para Nicaragua. Incluso, al no estudiar la dependencia en magnitud y distancia de forma independiente, se deja intacta la variabilidad del tratamiento de estos parámetros de las fórmulas originales. Esto hace que se pase dicha variabilidad a los estimados de amenaza sísmica (Álvarez, 2021).
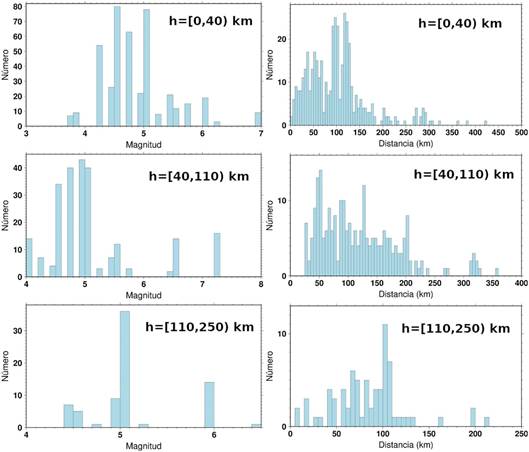
Fig. 2 Distribución por magnitud y distancia de los espectros de respuesta obtenidos. h representa el intervalo de profundidad.
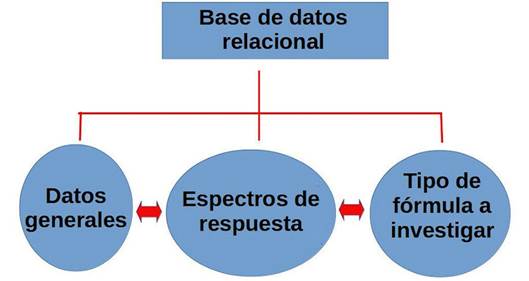
Se colocaron los datos en una base de datos, lo permite fácilmente su actualización progresiva y una amplia versatilidad. Se diseñó una base de datos relacional de 3 tablas usando “postgresql”, una con datos del terremoto, otra con los valores del ERA para diferentes períodos del UHS y la última con tipo de relación a investigar, distancias y otros parámetros. En la figura 3 se presenta la estructura de la base de datos, cuyas tablas contienen: (erdat) - datos primarios: fecha-hora, coordenadas, estación, distancia epicentral y filtrado realizado; (erval) - valores del espectro de respuesta en los períodos (0,01, 0,02, 0,05, 0,1, 0,2, 0,5, 1, 1,5, 2, 5, 9,5) seg; (erzon) - tipo de relación de atenuación a buscar (cortical, interfase e intraplaca), distancias. Igualmente se preparó un conjunto de “scripts” en SQL para realizar las selecciones de los datos a utilizar. Debe señalarse que como el objetivo del trabajo es de aplicación en estudios de amenaza sísmica, donde se trabaja con un número reducido de períodos del espectro UHS, aquí se seleccionaron para la base de datos solo 11, aunque los resultados del cálculo de los espectros de respuesta se obtuvieron para muchos más (86 períodos entre 0,01 y 9,5 seg).
En el llenado de la base de datos se utilizaron el ERA original calculado en la estación y uno convertido a roca rígida (VS30=1130 m/seg) calculado como solución de la ecuación (10). Esta es la parte más débil del procedimiento, pues se debe conocer el valor de VS30 para cada estación. No existen estimaciones directas de este parámetro, por lo que se usa un valor aproximado determinado globalmente por el USGS (2020) usando un método basado en el gradiente del relieve. No fue posible realizar validaciones in-situ de los valores de bajo las estaciones acelerográficas y considerando precisamente los errores implícitos en el método usado por el USGS en la estimación global del VS30, es que se decidió añadir otro valor de ERA calculado como la media geométrica de los dos anteriores. Esto se hizo porque en los estimados de amenaza sísmica hay que evitar los errores de sobreestimación de la amenaza, y el uso alternativo de este “espectro corregido” puede contribuir a eliminar ese tipo de error. La decisión de usarlo o no corresponde al momento en que se realicen los estimados de amenaza sísmica. Se calcularon dos tipos de distancia, la hipocentral y la de ruptura, esta última por la relación (12). La clasificación del tipo de zona sísmica se apoyó en resultados previos de análisis de la sismicidad (Álvarez, 2021). Se delimitaron 5 zonas corticales (0, 40) km, 1 de interfase (40, 110) km y 1 de subducción profunda (110, 250) km (Cuadro1). Esta división es basada en un análisis de la sismicidad junto con las características sismotectónicas de la región (Álvarez, 2021). En específico se basa fuertemente en el catálogo confeccionado para la región (Álvarez, 2021). Se diferencia de la usada por Molina et al. (2018) en que se extiende la zona de interfase en detrimento de la de intraplaca, por el interés de colocar de forma diferenciada los terremotos que en la etapa previa al inicio de la localización automatizada de los hipocentros se determinaban con profundidades predefinidas de 33, 50 y 100 km.. Aparte de ello, la subdivisión de la zona cortical responde a que muchas relaciones de atenuación globales tienen parámetros diferentes en diferentes entornos tectónicos, fundamentalmente asociados a un tipo de mecanismo focal.
Cuadro 1 Zonas analizadas y cantidad de ERA en cada una.
| Zona | Cantidad de ERA |
| Interfase | 239 |
| Intraplaca | 74 |
| Cortical, centro de la cadena volcánica | 147 |
| Cortical, región este de Nicaragua y sur de la cadena volcánica | 34 |
| Cortical, borde oeste de la cadena volcánica | 64 |
| Corticales, borde este de la cadena volcánica | 86 |
| Cortical, subducción somera | 95 |
El siguiente paso fue seleccionar, entre relaciones de atenuación publicadas, aquellas que más se adaptaran a los datos disponibles para “ajustarlas” a ellos. Debe tenerse en cuenta, que como se convirtieron los acelerogramas registrados en suelo al equivalente en una roca rígida (VS30 = 1130 m/seg), valor que raras veces se usa en las relaciones publicadas, existe siempre un sesgo con respecto a la relación a comparar, que raras veces considera ese valor de VS30, a lo que se suma la variación asociada a los datos experimentales, algo que algunos autores llaman variación regional (Montalva, Bastías y Rodríguez-Marek, 2017). Las relaciones de atenuación seleccionadas (Cuadro 2) incluyen algunas usadas anteriormente en trabajos de amenaza sísmica en Centroamérica (Molina et al., 2018; Reinoso et al., 2005) y otras de zonas tectónicas parecidas que cumplieran la condición de que el vector “Xi” de (13) fuera simple y se pudiese completar satisfactoriamente sin tener que documentar en detalle cada uno de los acelerogramas usados. Por tal motivo se excluyeron los casos de medición de distancias “rJyB”. Cada una de ellas fue determinada para un valor diferente de VS30, tal como se muestra en el cuadro 2. Algunas de ellas permitían fijar su valor y en el cuadro se muestra el utilizado en este trabajo. Esta característica de la variabilidad de la VS30 que caracteriza las relaciones de atenuación, hace que los residuos que se calculen incluyan tanto el efecto local como la diferencia con el VS30 de referencia.
Cuadro 2 Relaciones de atenuación seleccionadas. Los coeficientes de las relaciones habitualmente se publican junto con el trabajo principal, pero los de Akkar, Sandikkaya y Bommer (2014) se tomaron de (Sandikkaya, 2014), y los de Cauzzi et al. (2015) se obtuvieron por cortesía de Dr. Ezio Faccioli.
| No. | Referencia | VS30 | Corticales | Subducción |
| 1 | Schmidt (2014) | > 600 m/seg | X | X |
| 2 | Akkar et al. (2014) | 750 m/seg | X | - |
| 3 | Cauzzi et al. (2015) | 1130 m/seg | X | - |
| 4 | Idriss (2014) | > 450 m/seg | X | - |
| 5 | Montalva et al. (2017) | 1130 m/seg | X | X |
| 6 | Yenier y Atkinson (2017) | 1130 m/seg | X | X |
| 7 | Youngs et al. (1997) | “roca”, no especifica VS30 | - | X |
| 8 | Zhao et al. (2006) | > 1100 m/seg | X | X |
Los datos para realizar el ajuste de los residuos ln{ERAobservado(T)} - ln{ERApredicción(T)} (y también ln{ERAobservado(T)} - ln{PSApredicción(T) por la equivalencia que se asumió}se seleccionaron a partir de la base de datos. Se tuvo especial cuidado que para cada período TUHS bajo análisis no se seleccionaran acelerogramas que producto del filtrado no hubiesen incorporado esos períodos en el cálculo del ERA. Se realizó un análisis estadístico simple - media (μ) y dispersión estándar (σ) - como corresponde al caso univariado, lo que se complementó con histogramas ajustados a la distribución normal. Este análisis se hace para cada uno de lo períodos del UHS seleccionados, por lo que se habla, para cada relación estudiada de (μi, σi).
Se realizaron diferentes pruebas de subdivisión de eventos corticales en tipos de estilo tectónico así como para tratar de forma independiente los terremotos de la interfase y de la subducción profunda, pero la cantidad de datos disponibles no permitía obtener resultados estadísticamente significativos, por lo finalmente se decidió realizar los ajustes de las relaciones para terremotos corticales como un todo e interfase - subducción profunda (llamado en las figuras subducción), este último incluyendo todos los terremotos con h ≥ 40 km. Cuando esto se hacía no se obtenían variaciones significativas en μij (respecto al μi total), y lo que se hacía era aumentar el σij respecto a σi de la muestra como un todo, siendo “i” el período del TUHS y “j” la zona de características sismotectónicas. Esto no demuestra que no existan diferencias entre los distintos casos, sino que la muestra de datos utilizadas no permite diferenciarlas. En la figura 4 se presenta un ejemplo de ajuste de residuos para el caso de las relaciones de atenuación de Schmidt (2014), y en el cuadro 3se presentan los valores de (μi,σi) correspondientes. Una mejor visualización de la estadística de los residuos en este caso se muestra en la figura 5para 3 de los períodos analizados.
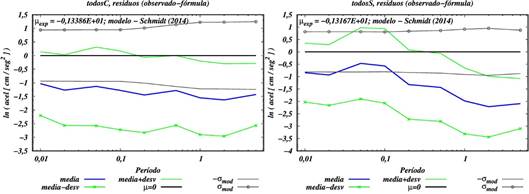
Fig. 4 Ajuste de datos observados a la relación de Schmidt (2014). En negro y gris se presentan los datos de la relación (μmod, σmod) original, y en azul y verde los residuos (μobs, σobs). (a) corticales, (b) interfase y subducción.
Cuadro 3 Valores de la corrección (μ(TUHS), σ(TUHS)) para las relaciones de Schmidt (2014). Los valores para TUHS=0,01 seg en realidad corresponden a los calculados por el modelo para el caso de PGA.
| T | 0,01 | 0,02 | 0,05 | 0,1 | 0,2 | 0,5 | 1. | 2. | 5. |
| μcortical | -1,0317 | -1,2675 | -1,1319 | -1,2778 | -1,4473 | -1,2817 | -1,5509 | -1,6288 | -1,4296 |
| μsubducción | -0,8403 | -0,9351 | -0,4654 | -0,5887 | -1,3204 | -1,4359 | -1,9813 | -2,2136 | 2,0895 |
| σcortical | 1,1697 | 1,2978 | 1,4427 | 1,4468 | 1,3806 | 1,2810 | 1,33490 | 1,3317 | 1,1139 |
| σsubducción | 1,1893 | 1,2258 | 1,4385 | 1,5047 | 1,3983 | 1,3716 | 1,3317 | 1,2250 | 1,0102 |
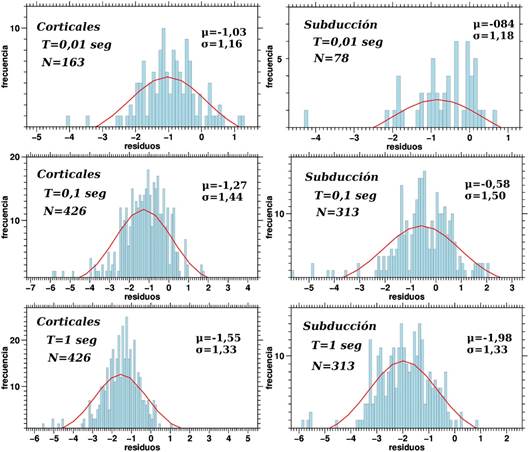
Fig. 5 Comportamiento de los residuos en el ajuste de las relaciones de Schmidt (2014) para 3 de los períodos analizados. TUHS=0,01 seg se usa para simbo lizar el PGA.
Para todas las relaciones presentadas en el cuadro 2 se realizó el análisis del tipo representado en el cuadro 3y las figuras 4 y 5. La amplitud de la dispersión estándar de los residuos es muy parecida en todos los casos, diferenciándose mucho más en el sesgo. En la figura 6se muestran los valores del sesgo “μ” obtenido en el análisis de residuos de las relaciones estudiadas, divididas en corticales y de interfase-intraplaca, que son nombradas como “subducción”.
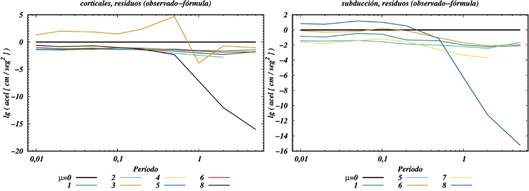
Fig. 6 Comparación de los valores de μi (media del sesgo para los períodos analizados) para todas las relaciones de atenuación seleccionadas. Los números corresponden a 1) Schmidt (2014), 2) Akkar et al. (2014), 3) Cauzzi et al.(2015), 4) Idriss (2014), 5) Montalva et al. (2017), 6) Yenier y Atkinson (2017), 7) Youngs et al. (1997) y 8) Zhao et al. (2016).
De esta figura se ve que en la mayoría de las relaciones estudiadas el sesgo presenta un comportamiento bastante regular comprendido en un diapasón estrecho de valores. Hay dos excepciones. En primer lugar, las relaciones de Zhao et al. (2006) con valores muy elevados para los períodos mayores a 0,5 seg, y en segundo lugar las de Montalva et al. (2017) con gran variabilidad en el caso de eventos corticales, y algo apartada de las restantes en el caso de eventos de subducción. Esto puede ser un criterio de exclusión para su aplicación en estudios de amenaza sísmica. En la confección de los gráficos de resultados se usaron el gnuplot (Williams y Kelley, 2017) y el GMT (Wessel y Smith, 1998).
Usando los valores de Q(μi,σi) para cada una de las relaciones de atenuación se obtienen nuevas relaciones (fórmula 15) que tienen una validez local para un valor de VS30=1130 m/seg. Este valor de referencia es determinado por la relación de conversión de Chiou y Youngs (2014).
Discusión
El objetivo final del proceso señalado de modificación o “corrección” de relaciones de atenuación publicadas es su uso en estimados de amenaza sísmica. Las relaciones modificadas contienen dos elementos:
- conversión al caso de roca rígida (VS30 = 1130 m/seg)
- ajuste a características locales
El primero de los factores hace que los estimados de amenaza sísmica que se obtengan por el método probabilista estándar de Esteva-Cornell (Cornell, 1968; Esteva, 1967) estén referidos a ese valor de VS30. Esto evita el uso de relaciones de atenuación publicadas referidas a valores diferentes de VS30, que deje en la indeterminación para que valor en realidad se está calculando la amenaza sísmica. Por otra parte, los requerimientos constructivos habituales hacen necesario que los estimados de amenaza sísmica se realicen para roca simple, con un valor de VS30 mucho más bajo (generalmente 750-850 m/seg), por lo que se requiere que los resultados finales sean convertidos al valor necesario de VS30. En los códigos sísmicos este valor se asocia a una clasificación de suelos, donde se adjuntan mapas de zonación o tablas donde se refiere que el valor de PGA que se da corresponde a roca. Dichas clasificaciones varían de un caso a otro. Por ejemplo el código europeo (EUROCODE, 2009) define roca para un valor de VS30>800 m/seg, mientras que el ASCE (2017) define el valor para suelo tipo “BC” en 762 m/seg.
El problema de las características locales es muy importante. La estructura de la corteza y el tipo de proceso que ocurre en los terremotos es diferente de una región a otra, y esto hace que sus efectos varíen grandemente, incluso dentro de una misma región. Esto es muy evidente cuando se trata de intensidades sísmicas (Álvarez y Chuy, 1985), disponibles prácticamente en cualquier lugar del mundo, pero cuando se trata de parámetros del movimiento del terreno no siempre hay datos suficientes para estimar esa variabilidad. Por ello el uso de registros locales de aceleración es muy importante a la hora de definir una relación de atenuación que caracterice a una región en particular. El cálculo de una modificación o corrección por datos experimentales a relaciones publicadas, en gran medida resuelve este problema. Debe señalarse que el estudio no incluyó las variaciones por distancia y magnitud en los datos experimentales, por lo que aún se manifiesta cierta incertidumbre que en los cálculos de amenaza sísmica se puede tratar mediante el uso de la técnica de árbol lógico.
Los estimados de amenaza sísmica de una forma u otra conducen a la obtención de los llamados espectros de amenaza uniforme (UHS de sus siglas en inglés) para diferentes períodos de retorno, y el valor de VS30 para el que se prepararon las relaciones de atenuación. Por tanto, a partir de los estimados para VS30=1130 cm/seg, se deben obtener los correspondientes a la VS30 deseada, lo que, para ser consecuente con el procesamiento de los datos iniciales, se hace aplicando directamente la fórmula (10) a los espectros de amenaza uniforme obtenidos. Se considera que este uso de una relación de escalado de los espectros en función de VS30 en los dos sentidos, minimiza el error que se cometa (se compensa) y debe ser menor que al aplicar una relación obtenida para otra región con condiciones sismotectónicas semejantes. En la figura 7 se presenta un esquema del proceso. El mismo fue recientemente aplicado en un estudio de amenaza sísmica de Nicaragua (Álvarez, 2021). En la figura 8 se muestra el mapa de amenaza sísmica propuesto en dicho trabajo para usar en la nueva norma sísmica de Nicaragua. En su confección se usaron algunas de las relaciones de atenuación corregidas del cuadro 2, con las que se prepararon los ficheros de atenuación externos que lee el programa R-CRISIS (Ordaz y Salgado-Gálvez, 2019), responsable de los cálculos fundamentales.
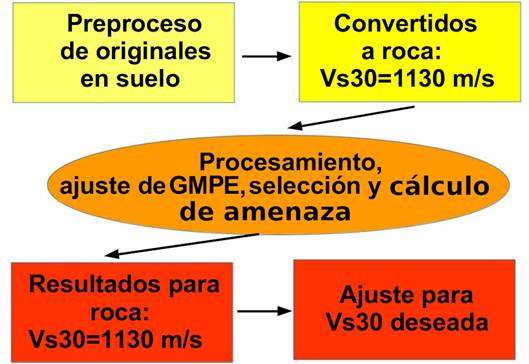
Fig. 7 Esquema del procedimiento para usar las relaciones de atenuación corregidas en una estimación de la amenaza sísmica.
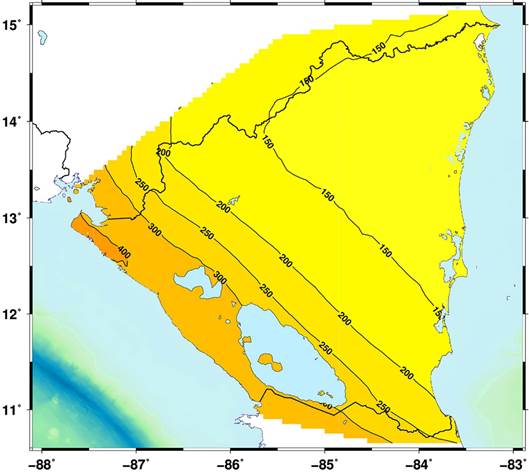
Fig. 8 Mapa de amenaza sísmica - aceleración en (g) - con un percentil 84 para período de retorno de 475 años, y un valor de VS30 = 760 m/seg. Tomado de (Álvarez, 2021)
Debe señalarse que el valor de referencia de VS30 (1130 m/seg) depende de la relación de conversión roca-suelo usada (Chiou y Youngs, 2008, 2014). En caso de usarse otra relación con diferente valor de referencia el método es igualmente válido.
Se ha analizado un caso en que se dispone de una información relativamente amplia de datos de aceleraciones registradas, pero que resulta insuficiente para obtener relaciones de atenuación (GMPE en inglés) específicas. En presencia de estas condiciones, en lugar de buscar relaciones de atenuación publicadas para entornos semejantes y tratar de seleccionar las que más se parezcan a los valores observados, se considera más lógico modificar aquellas que más se acerquen a dichos valores observados, mediante la adición de un factor de corrección Q(μ,σ). Esto es de gran importancia si el objetivo final es realizar una estimación de la amenaza sísmica. Se considera que este procedimiento permite obtener estimados de dicha amenaza más precisos que cuando se usan directamente las relaciones de atenuación publicadas, pues en este último caso se hacen inferencias de que el comportamiento de la atenuación es tal como reflejan las relaciones, cuando en la práctica no es realmente así, lo que puede conducir a errores apreciables.
Conclusiones
• Se propuso un procedimiento para ajustar relaciones de atenuación publicadas (GMPE) a los datos locales de espectros de respuesta obtenidos de registros locales de aceleración.
• Se preparó una base de datos con los datos de los espectros de respuesta de las componentes horizontales de acelerogramas registrados en Nicaragua (739 espectros). Se convirtieron los espectros de los acelerogramas registrados en diversos tipos de suelo al caso de roca rígida (VS30=1130 m/seg)
• Con esa base de datos se estudiaron los residuos de su ajuste a 13 relaciones de atenuación publicadas y se obtuvieron los valores de (μi,σi) (sesgo y dispersión estándar) para un máximo de 9 períodos en el rango (0,01-5 seg).
• Las relaciones de atenuación modificadas se obtuvieron añadiéndole el sesgo “μi” y sustituyendo su dispersión estándar original por la encontrada en el ajuste de los residuos.
• Se recomendó un procedimiento para usar estas relaciones de atenuación corregidas en un trabajo de estimación de la amenaza sísmica. Este procedimiento disminuye el error que se comete al utilizar relaciones de atenuación seleccionadas por semejanza en las condiciones sismotectónicas. El mismo fue utilizado en un trabajo reciente de estimación de la amenaza sísmica para Nicaragua (Álvarez, 2021).