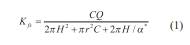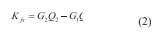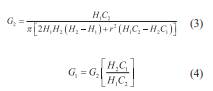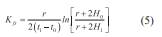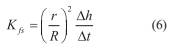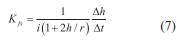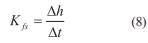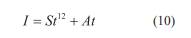Introducción
La denominada Gran Área Metropolitana (GAM), localizada en el Valle Central de Costa Rica, concentra el 57% de la población del país en una zona de 1780 km2, la cual representa apenas el 3,5% del área total del territorio nacional. El 70% de la población dentro del GAM es servida por sistemas de tanque séptico, y la gran mayoría del agua empleada en usos domésticos, comerciales e industriales es de origen subterránea. Ocho áreas han sido reconocidas dentro de la GAM como acuíferos o zonas de interés hidrogeológico (Plan GAM, 2013), siendo el sistema acuífero Barva-Colima el más importante, pues abastece aproximadamente al 50% de la población.
A pesar de que en el país se cuenta con abundante legislación y normativa para evitar el impacto de posibles efluentes sépticos sobre la calidad de las aguas subterráneas, el 95% de los episodios de contaminación de acueductos en Costa Rica para el período 2001 a 2012 se originaron por fuente fecal (Mora et al., 2013). Más recientemente, en enero de 2016 un episodio de contaminación de la captación de agua de dos comunidades del sur del GAM, resultó en 61 casos de infección por Hepatitis A (periódico La Nación 22 enero 2016). Para el caso de los acuíferos Barva y Colima, se ha observado también una clara tendencia en el aumento de la concentración de nitratos con los años. Las mayores concentraciones se han registrado en las zonas de acuíferos superficiales cercanos a centros urbanos, sugiriendo el impacto de las actividades humanas en la calidad del agua (Rodríguez & Loaiciga, 1995). Estudios isotópicos han demostrado que los nitratos en estos acuíferos son derivados de dos fuentes: aguas residuales en las zonas urbanas y semiurbanas y, fertilizantes nitrogenados en las zonas cultivadas con café (Reynolds, et al., 2006).
Este panorama indica claramente la necesidad de establecer distancias de separación adecuadas entre los sitios de disposición de los efluentes residuales y las captaciones y/o acueductos.
Para el caso específico de tanques sépticos, es importante verificar la distancia mínima requerida entre los campos de infiltración y las captaciones y/o cabezas de pozos para evitar la contaminación por agentes patógenos, especialmente virus por su mayor persistencia y potencial de contaminación en relación a bacterias y parásitos. El uso extendido de tanques sépticos, así como la tradición de cultivo de café en el Valle Central, representan una presión constante para la preservación de la calidad de las aguas subterráneas.
Para la determinación de esta distancia de separación que permite prevenir contaminación potencial en captaciones de agua potable, en Costa Rica se emplea el criterio del tiempo de tránsito. Según la norma costarricense, se establece un tiempo de tránsito de 70 días en materiales porosos y de 100 días en materiales fracturados (Rodríguez, 1994). De acuerdo con dicha norma, se considera que el tiempo de tránsito establecido representa un lapso adecuado para permitir la remoción de los patógenos, y por tanto cualquier sistema de captación deberá estar separado a una distancia tal que el transporte por advección (empleando la velocidad de poros) no sea menor a ese lapso de tiempo. El tiempo total de tránsito incluye, el tiempo necesario para alcanzar el nivel de aguas en zonas no saturadas, así como el tiempo de transporte dentro del agua subterránea necesario para completar los 70 o 100 días de recorrido. Para modelar el transporte advectivo, los materiales se idealizan como medios continuos o continuos equivalentes, y en la zona no saturada se emplea un gradiente hidráulico vertical unitario y la conductividad hidráulica vertical saturada.
De acuerdo con esta metodología, la conductividad hidráulica en la zona no saturada es el parámetro más importante para la estimación de una distancia de separación adecuada, sin embargo, este parámetro es el que presenta mayores dificultades en términos de la obtención de un valor representativo para condiciones saturadas de campo (Comegna, et al., (1996); Sobieraj et al, 2004). Estas dificultades se deben a diversos motivos.
Quizás el más importante es debido al hecho de que es virtualmente imposible alcanzar condiciones de saturación en campo con los métodos comúnmente empleados para la obtención de este parámetro, es por esto que el valor obtenido a partir de ensayos de campo es normalmente referido como conductividad hidráulica saturada de campo y representado con el símbolo K fs (ASTM, 1990). En este documento se adopta la misma simbología y también se emplea el término permeabilidad como equivalente. Por otro lado, en condiciones controladas de laboratorio o en ensayos de campo realizados bajo el nivel freático, es posible alcanzar la saturación total de la muestra. Otros motivos que dificultan la definición de un valor representativo de K fs son: la variabilidad espacial y temporal (Boivin y Touma, 1988); el método de ensayo utilizado y las condiciones topográficas (Roose et al., 1993); las diversas metodologías de análisis existentes y el cumplimiento o no de las condiciones de contorno consideradas para cada una de ellas (Elrick y Reynolds,2002); pericia y procedimientos de ejecución de ensayos, volumen de suelo ensayado (Oosterbaan y Nijland,1994); y variabilidad natural de los diferentes tipos de suelos y rocas (granulometría, estructura porosa del depósito, composición mineralógica, grado de saturación, presencia de macroporos (Rico y Del Castillo, 1998; Bear,1988). En el Cuadro 1 se presenta un resumen de valores de conductividad hidráulica saturada para diferentes tipos de suelos y rocas.
Cuadro 1 Rangos de valores de conductividad hidráulica saturada (Ks) para suelos y rocas (adaptado de Bear,1988 y Hoek & Bray, 1981).
| Suelos | K s (cm/s) | Rocas | Localidad |
|---|---|---|---|
| Arcillas no alteradas | 10-11 - 10-7 | Granitos no fracturados | Materiales impermeables |
| Limos, arenas finas, suelos francos, arcillas estratificadas | 10-7 - 10-3 | Rocas con juntas rellenas, areniscas y calizas no fracturadas | Materiales semipermeables |
| Arena limpia, Arenas con grava | 10-3 - 100 | Rocas fracturadas | Materiales muy permeables |
| Gravas | 100 - 102 | Altamente fracturadas o con juntas abiertas | Materiales muy permeables |
Son escasas las referencias sobre los valores de conductividad hidráulica saturada de campo para los materiales que constituyen la zona no saturada de los principales acuíferos del Valle Central. Foster et al. (1985) estimaron valores de permeabilidad a partir de ensayos de infiltración en agujeros cilíndricos practicados en tobas y lavas de la zona norte de Heredia, a profundidades de 0,5 y 1,5 m respectivamente. Dichos autores asumieron el valor de la tasa de infiltración terminal como el valor de K fs . Estos valores (en cm/s) se encuentran en el rango 2,31E-4 a 5,78E-3 para las lavas, y 2,3E-5 a 1,16E-3 para las tobas. Para estos últimos el valor más frecuente de K fs es aproximadamente 1,3E-4. Por su parte, Mora (1998) determinó una serie de propiedades físicas, hidráulicas y mecánicas para depósitos de origen volcánico en cuatro sitios del Valle Central. Dichos depósitos corresponden con materiales producto de la meteorización de cenizas, tobas, lahares y lavas; y fueron clasificados en su mayoría como limos de alta plasticidad. La conductividad hidráulica saturada de campo fue obtenida a través de ensayos con el permeámetro Guelph. Los valores de K fs (en cm/s) se encuentran en el rango de 1,0E-2 a 1,5E-4 para las tobas, y 1,3E-5 a 4,3E-5 para los productos de la meteorización de lahares, cenizas y lavas. Los valores citados en Foster et al. (1985) y Mora (1998), se encuentran en el rango de materiales semipermeables a muy permeables del Cuadro1, resaltando la importancia de caracterizar de manera adecuada su comportamiento hidráulico para evaluar su potencial como barrera natural de protección de los acuíferos de la zona.
Debido a la creciente contaminación de los recursos hídricos tanto superficiales como subterráneos por fuentes antropogénicas, el Servicio Nacional de Riego y Avenamiento (SENARA) ha definido y promovido varias metodologías hidrogeológicas que se deben aplicar para determinar parámetros hidráulicos de acuíferos y de la zona no saturada. Estas metodologías fueron inicialmente publicadas en la Gaceta No.243 del miércoles 15 de diciembre del 2010 (pág. 37) donde se indica que los métodos que serán aceptados para la determinación de la infiltración de los suelos serán los siguientes:
Método de anillos (Método de Kostiakov): está diseñado para medir velocidad de infiltración, sin embargo cuando la velocidad está estabilizada se asume como la conductividad hidráulica del medio. Este método se utilizará básicamente en estudios de balance hídrico (recarga acuífera) y además para el cálculo de tiempos de tránsito se deben realizar a una profundidad representativa del estrato geológico.
Método de Porchet, Lefranc y Guelph: están diseñados para medir conductividad hidráulica y se emplea básicamente para estudios de cálculo de tiempos de tránsito.
Además se indica que para todos los métodos anteriores (Doble Anillo, Porchet y Le Franc deberá considerarse el estado de saturación del suelo).
Este acto administrativo fue reemplazado por la resolución R-D-046-2012-MINAET del 01 de febrero del 2012, publicado el 31 de julio del año 2012 en la Gaceta No. 147. En el artículo 8 del capítulo 7, referido al tema de zonas de recarga se señala nuevamente que los métodos para la determinación de la infiltración son el método de anillos y los métodos de Porchet, Le franc y Guelph.
En mayo del año 2017el SENARA a través de la Dirección de Investigación y Gestión Hídrica (DIGH) publicó los términos de referencia para presentar estudios hidrogeológicos que requieran trámites ante el SENARA (SENARA, 2018). Según dichos términos para estudios en la zona no saturada se pueden emplear los métodos Doble Anillo, Porchet, Guelph, LeFranc y Hvorslev.
Algunas de las especificaciones técnicas sugeridas por el SENARA para las diferentes metodologías a utilizar en las pruebas de infiltración son las siguientes:
Pruebas de Porchet: dimensiones del agujero de 40 cm de profundidad por 20 cm de diámetro y la duración mínima de la prueba de 60 minutos. Se deben realizar con saturación de suelo de al menos 2 horas previas a los ensayos.
Pruebas de anillos: Ensayos a nivel del terreno, con una duración mínima de la prueba de 120 minutos. Se deben realizar con la saturación del suelo de al menos 2 horas previas a los ensayos.
Prueba de Guelph: ensayos a nivel de terreno, duración mínima de 60 minutos.
De esta manera, el profesional encargado de realizar estudios para la evaluación del impacto de efluentes de tanques sépticos sobre las captaciones de aguas subterráneas, cuenta con varias metodologías de campo aprobadas por la normativa costarricense para la estimación del valor de K fs .
Tres de esas metodologías son de interés para este estudio: método Doble Anillo (DA), método de Porchet (MP) y permeámetro de Guelph (PG). Las siglas anteriores se emplean a partir de aquí en el resto del documento para facilitar su referencia. Los autores de este trabajo no tienen conocimiento de publicaciones científicas para suelos de Costa Rica, que presenten análisis comparativos de los valores de permeabilidad obtenidos con dichas metodologías. Alvarado & Barahona (2017), presentan una comparación entre estos tres métodos para suelos de la Cuenca del río Suquiapa en El Salvador. Esta comparación sin embargo es en términos de las tasas de infiltración y no de los valores de K fs , pues dicho análisis está enfocado hacia la estimación de recarga de acuíferos por precipitación. Los resultados obtenidos por los autores citados muestran una mejor correlación entre los resultados de los métodos PG y DA (correlación lineal de r2 =0,74); y una correlación muy pobre al comparar ambos métodos con los resultados de la prueba MP.
A nivel internacional, varias comparaciones han sido realizadas entre los diversos métodos de ensayo de uso rutinario para la obtención de K fs . Mohanty et al. (1994) al comparar varios métodos, incluyendo PG, DA, Anillo Simple (AS), Permeámetro de Disco (PD) y ensayos de laboratorio (EL), obtuvieron valores menores con el método PG, atribuyendo esto al menor volumen muestreado en este ensayo, la alteración de paredes del agujero y al aire atrapado en los poros que disminuye el área de flujo. Prieto et al. (2006) compararon el infiltrómetro de tensión con el DA, obteniéndose valores de K fs mayores para este último. Los autores atribuyen esta diferencia a la mayor área de infiltración. Archer et al. (2014) citando a varios autores, indica que los valores obtenidos con PG son siempre menores a los obtenidos con los métodos PD, EL, permeámetro de velocidad (PV) y métodos de ensayo en pozos bajo el nivel freático (condición saturada). Estas diferencias se atribuyen a diversos factores: menor volumen ensayado, sello de poros durante la excavación del agujero, atrapamiento de aire en la zona vadosa, colmatación del pozo y discontinuidad de la red de poros.
El cálculo de los valores de K fs a partir de los datos obtenidos con métodos de ensayo en la zona vadosa, es en general realizado a partir de una ecuación que relaciona la tasa de infiltración con parámetros geométricos que dependen de la configuración del ensayo y las condiciones de contorno asumidas o impuestas durante la prueba. Es decir, para un mismo conjunto de datos es posible aplicar diferentes ecuaciones de acuerdo con las condiciones de contorno actuantes. Elrick y Reynolds (1992) demuestran con datos numéricos que la diferencia en estimación de K fs puede ser muy alta especialmente para suelos muy finos. Realizan una comparación numérica entre dos soluciones analíticas para permeámetro de carga constante, una solución que considera los efectos gravitacionales, depresión y capilares en el flujo y otra, propuesta por Glover (1953, en Zangar 1953) que solamente considera el gradiente de presión. La diferencia entre los valores de K fs puede ser mayor al 90% para suelos finos y de 30% para suelos gruesos. Aún más, comparando resultados obtenidos con una misma ecuación pero realizando un mala escogencia de los parámetros representativos del suelo, el error puede estar en el orden de hasta 240%, especialmente al analizar suelos menos permeables (Bosch, 1997).
Los objetivos planteados para esta investigación son: a) la realización de quince ensayos de permeabilidad in-situ en dos localidades del Valle Central empleando los métodos PG, DA y MP; b) comparar los resultados obtenidos entre los tres diferentes métodos de ensayo y, c) comparar los valores de K fs obtenidos para un mismo método de ensayo a partir de uso de diferentes ecuaciones o aproximaciones numéricas considerando diferentes condiciones de contorno.
En la Figura 1 se muestra la ubicación de los dos sitios de ensayo. El primero corresponde a la finca propiedad de Acueductos y Alcantarillados (AyA) en San Rafael de Alajuela, donde se realizaron pruebas en dos puntos para una total de seis pruebas; y el segundo sitio corresponde con las instalaciones deportivas de la Universidad de Costa Rica (UCR) en Sabanilla de Montes de Oca, donde se seleccionaron tres puntos de ensayo, para un total de nueve ensayos. Todas las pruebas de campo se ejecutaron en agosto de 2004.
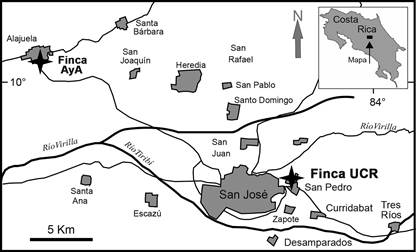
Fig. 1: Ubicación de las pruebas de infiltración (estrellas). Se indican algunas poblaciones, ríos y carreteras principales
Los autores de este trabajo consideran que los resultados de esta investigación contribuyen al entendimiento de las diferencias numéricas de estimación de K fs en suelos limosos y, en mostrar los factores con mayor influencia en los resultados. Por otro lado los valores obtenidos para cada ensayo con los tres métodos se comparan con valores mencionados en publicaciones a nivel internacional permitiendo interpretar el grado de homologación de los métodos usados.
Ensayos de campo para obtener conductividad hidráulica saturada en zona no saturada
Actualmente existen diferentes procedimientos para la determinación de la conductividad hidráulica saturada tanto para suelos como para rocas. Para el caso de procedimientos en roca el lector puede referirse a Hoek & Bray (1981). En este trabajo se analizan procedimientos relacionados con suelos o materiales no consolidados.
Estos procedimientos pueden ser clasificados de manera general en dos tipos: aproximaciones basadas en correlaciones y, aproximaciones basadas en mediciones hidráulicas.
Los primeros se basan en relaciones de correlación empíricas obtenidas entre alguna propiedad medible del suelo (porosidad, tamaño de grano, tipo de suelo, etc.) y la conductividad obtenida previamente por procedimientos de medición. Para su utilización basta obtener valores de la propiedad correlacionada y a partir de esta calcular la conductividad hidráulica. Este procedimiento es de rápida implementación, sin embargo la validez de su aplicación en muchos casos se restringe a zonas muy localizadas.
Los segundos están basados en la medición del efecto de la aplicación de caudales o cargas hidráulicas sobre el material bajo estudio. Estos procedimientos se han transformado en ensayos estandarizados que pueden ser realizados tanto en laboratorio como en campo; para este fin se han desarrollado diferentes metodologías según las condiciones de saturación del terreno, escala del ensayo y tipo de carga o caudal aplicado. En el cuadro 2 se presenta una clasificación de estos métodos.
Los ensayos de laboratorio se realizan sobre muestras extraídas del estrato de interés, las cuales son llevadas al laboratorio, donde es posible controlar la condición de saturación del material, esto es posible a través de la aplicación de procedimientos definidos hasta alcanzar la saturación completa del material. Una vez el material se encuentra saturado, se procede a la realización del ensayo, el cual puede realizarse bajo la aplicación de carga hidráulica constante o variable. Claramente, la extrapolación para las condiciones de campo del valor de conductividad saturada (Ks) así obtenido, dependerá de la homogeneidad y anisotropía del depósito de suelo. Un descripción detallada de estos métodos puede ser consultada en Lambe y Whitman (1995).
Los ensayos de laboratorio se realizan sobre muestras extraídas del estrato de interés, las cuales son llevadas al laboratorio, donde es posible controlar la condición de saturación del material, esto es posible a través de la aplicación de procedimientos definidos hasta alcanzar la saturación completa del material. Una vez el material se encuentra saturado, se procede a la realización del ensayo, el cual puede realizarse bajo la aplicación de carga hidráulica constante o variable. Claramente, la extrapolación para las condiciones de campo del valor de conductividad saturada (K s ) así obtenido, dependerá de la homogeneidad y anisotropía del depósito de suelo. Un descripción detallada de estos métodos puede ser consultada en Lambe y Whitman (1995).
Los ensayos de campo por otro lado, son realizados directamente sobe el material bajo condiciones de depósito. En este sentido, estos métodos pueden llevar en cuenta las variaciones de homogeneidad y anisotropía. Estos métodos, al igual que los ensayos de laboratorio, pueden ser realizados bajo la aplicación de cargas constantes o cargas variables. Como se muestra en el Cuadro 2, dependiendo de la escala y condición de saturación, existen diferentes metodologías para la determinación del valor de conductividad hidráulica. Algunos ensayos de gran escalada por medio de trazadores han sido realizados en Costa Rica para estudios geotérmicos e hidrogeológicos (Parini et al., 1996; Torres y Axelsson, 2015; Macías et al., 2016; Macías y Vargas., 2017).
Cuadro 2 Métodos de Campo y Laboratorio para la obtención de conductividad hidráulica (basado en Oosterbaan y Nijland (1994).
| Ensayo | Condición | Observaciones y Métodos | |
|---|---|---|---|
| Laboratorio | Carga Constante Carga Variable | Muestras extraídas del terreno y ensayadas bajo condiciones controladas de carga y saturación | |
| Campo | Gran Escala | Bajo Nivel Freático | Pruebas Bombeo Trazadores |
| Pequeña Escala | Sobre Nivel Freático Bajo Nivel Freático | Infiltrómetros Ensayos en pozos Ensayos en perforaciones Ensayos tipo “Slug” Ensayo Le Franc Ensayo Hvorslev Ensayo Lugeon | |
Para efectos de este estudio, son de interés los métodos de pequeña escala aplicados a suelos localizados sobre el nivel freático. Para la obtención de la conductividad hidráulica saturada, estos procedimientos requieren de la “saturación” previa del material, a través de la infiltración de agua; es por esto que son conocidos como métodos de infiltración, y los ensayos pueden ser realizados a través del uso de infiltrómetros, permeámetros colocados en perforaciones, o a partir de la aplicación de cargas hidráulicas directamente en perforaciones y/o pozos no revestidos. Dependiendo de la geometría del ensayo, cada uno de estos procedimientos adopta una serie de simplificaciones para así obtener una solución analítica o ecuación que permita modelar el flujo de agua en el terreno.
Es importante resaltar como se indicó en la introducción, que los métodos de infiltración difícilmente alcanzan la condición de saturación, debido principalmente a la dificultad de desplazar completamente el aire atrapado en los poros. Por este motivo, la conductividad hidráulica en este caso es referida como conductividad hidráulica saturada de campo K fs .
A continuación se presenta una breve descripción de los métodos de infiltración empleados en este estudio:
-Permeámetro Guelph (PG): permeámetro de carga constante en agujero de perforación.
-Método de Porchet (MP): método de carga variable, el cual puede ser analizado como método en agujero de perforación o en pozo, dependiendo de las dimensiones del agujero, no revestido.
-Doble Anillo (DA): método de carga variable con infiltrómetro.
Método de Permeámetro Guelph (PG)
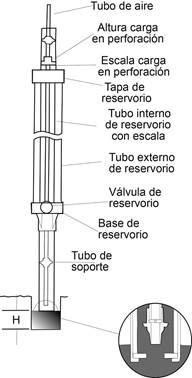
Este permeámetro fue desarrollado en la Universidad de Guelph, con el objetivo de determinar, entre otros parámetros, la conductividad hidráulica saturada de campo para depósitos en la zona no saturada, a través de un ensayo realizado en agujeros cilíndricos. Funciona mediante el Principio de Mariotte, por medio del cual se mantiene una carga H constante en el agujero (Fig. 2). El ensayo consiste en medir el caudal de infiltración necesario para mantener dicho nivel constante, hasta alcanzar una condición de flujo cuasi-permanente.
El mecanismo del permeámetro incluye un reservorio que se utiliza para llenar de agua el agujero que se ha perforado previamente en el terreno con el taladro. Al descender el líquido por efecto de la infiltración, se crea un vacío dentro del reservorio que permite mantener una carga constante de agua en el agujero. La carga constante dentro del agujero permite que en poco tiempo se establezca una situación de equilibrio, formando una “burbuja” de suelo saturado con dimensiones específicas. Esta “burbuja” es muy estable y su forma depende del tipo de suelo, el radio del agujero y la carga de agua.
Una vez que se ha formado esta 'burbuja’, se establece un flujo constante del reservorio hacia el terreno que puede ser medido y que, junto con el diámetro del agujero y la carga de agua se utilizan para determinar el valor de la conductividad hidráulica del suelo (K fs ).
El procedimiento de ejecución de los ensayos utilizando el Permeámetro Guelph requiere ciertos cuidados. El hundimiento del permeámetro en la base del agujero puede producir un valor menor de la conductividad hidráulica, ya que el nivel actual es más bajo que el nivel asumido y porque la descarga desde el permeámetro puede ser reducida por un área de infiltración menor (Bagarello, 1997).
El análisis de los datos obtenidos durante el ensayo para una carga H puede ser realizado a través del empleo de la ecuación 1, la cual considera los efectos del empuje hidráulico de la columna de agua en el agujero, la fuerza gravitacional y las fuerzas capilares (Elrick y Reynolds, 1992):
Donde
Q = caudal infiltrado cuasi-estabilizado
(L3/T) r = radio de agujero de perforación (L)
C = factor de forma adimensional (depende de H/ r). Reynolds et al. (1983) y Bosch (1997) recomiendan el empleo de relaciones H/r entre 5 y 10.
α*= parámetro que correlaciona K fs y el potencial mátrico φm (α* = K fs / φm) con dimensión (1/L).
La ecuación 1 puede ser empleada para conocer K fs para cada par de valores de Q y H medidos; sin embargo es necesario conocer a priori el valor de α*. Para evitar esto, el procedimiento de ensayo se realiza para dos cargas hidráulicas diferentes H1 y H2, obteniéndose para cada una de ellas pares de valores Q1 , C 1 y Q 2 , C 2 respectivamente. Al ser sustituidos dichos valores en la ecuación 1, se obtiene un sistema de ecuaciones con dos incógnitas K fs y α*. La ecuación resultante para obtener K fs es (Soilmoisture, 2012):
En este trabajo se empleó para el cálculo de K fs solamente la secuencia de ecuaciones 2 a 4. En caso de obtenerse valores negativos de K fs , la ecuación 1 puede ser empleada. Otros procedimientos de cálculo para condiciones de contorno diferentes pueden ser revisados en Torfs (2008).
donde:
Método de Porchet (MP)
Este procedimiento es también reconocido en la literatura inglesa como “inverse auger method”. En Costa Rica sin embrago se ha adoptado la terminología francesa para referirse al mismo. El método consiste en la excavación o perforación de un agujero cilíndrico, al cual se le inyecta agua en uno o varios ciclos para saturar el terreno circundante. Posterior a la saturación, se inyecta un volumen predefinido de agua (para alcanzar una altura de agua inicial en el agujero Ho (Fig.3). Seguidamente se procede a medir la disminución del nivel del agua hasta alcanzar una tasa de decaimiento estable.
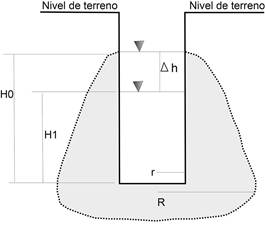
Fig. 3: Ensayo de Porchet. Ho, H1=alturas de lámina de agua para tiempos t0= 0 y t1; r = radio agujero de perforación; R= radio estimado de bulbo de saturación.
Se han propuesto diferentes formulaciones para analizar los datos de este ensayo. Básicamente dichas formulaciones pueden clasificarse en: métodos que consideran solamente el potencial gravitacional, y métodos que consideran los potenciales gravitacional, de presión y capilar. Dichas formulaciones se presentan a continuación.
Formulaciones basadas en el potencial gravitacional
En este caso se considera que el flujo es definido por el potencial gravitacional, y se emplea un valor unitario del gradiente hidráulico. Dependiendo del área en la que se considera que ocurre la infiltración, se han propuesto varios modelos:
Flujo en pared y base del agujero:
Esta formulación es de uso común en Costa Rica por la comunidad hidrogeológica, debido principalmente al uso del libro de texto de Custodio y Llamas (1983) para la enseñanza de esta materia. Una deducción de esta ecuación se presenta en el apéndice 1.
Flujo en la base del agujero con área corregida: Estas formulaciones se basan en la corrección (disminución) de la tasa de infiltración estabilizada al considerar que el área de infiltración es mayor al área de la base del agujero. Esta corrección se realiza a partir de una relación volumétrica entre el volumen de suelo saturado y el volumen del agujero (Tricker, 1978; Roose et al., 1993). Para este estudio se empleó la formulación sugerida por la Asociación Brasileña de Ingeniería Geológica ABGE (Dos Santos y Corrêa, 1996), originalmente presentada por Rodio (1960).
la tasa de infiltración global como la tangencial, desde que el valor actualizado de h sea considerado. Esta formulación es sugerida por la ABGE (originalmente presentada por Rodio, 1960) para ensayos en agujeros excavados, con columnas de agua de 20 a 30 cm y valores de gradiente de 3 y 5 respectivamente. Es decir, esta relación corresponde con la ecuación i = 0, 2h-1, donde h es la altura de columna de agua expresada en metros.
Donde R, representa el radio del área de infiltración real (Fig. 3), cuyo valor puede ser obtenido a partir de la ecuación parabólica R2+R-H=0 donde H representa una variable genérica para indicar la altura de la columna de agua en el agujero para la cual se hace el análisis. Es decir, en este método se considera que la parte superior del bulbo de saturación puede ser representada por una parábola.
Formulaciones basadas en gradiente hidráulico no unitario
Estas formulaciones se basan en la consideración explicita de los potenciales gravitacionales, de presión y capilaridad, para representar el flujo de infiltración, o alternativamente en el empleo explícito de un valor de gradiente hidráulico no unitario para considerar los efectos del potencial de presión y capilaridad. Las formulaciones empleadas en este estudio se presentan a continuación:
Gradiente hidráulico no unitario:
Esta es la misma ecuación A3 mostrada en el apéndice 1. En este caso se observa que el área de infiltración considerada incluye la base y pared del agujero. Esta ecuación se evalúa de forma incremental a diferencia de la ecuación resultante de la integral de A3 (ecuaciones 5 y A4 del apéndice)). Es decir, este método puede considerar tanto Aunque esta expresión no se presenta de manera explícita en el manual de la ABGE, se empleó en este estudio para interpolar los gradientes hidráulicos para cargas menores a 30 cm como las empleadas en esta investigación. Para efectos de este estudio, cuando se emplearon columnas de agua superiores a 30 cm se restringió el valor de gradiente hidráulico a un valor máximo de 5.
Solución analítica de Philip (1957) para el problema de infiltración: Este procedimiento se detalla en la descripción del método DA.
Método de doble anillo (DA)
Este método consiste en el hincado parcial de dos cilindros abiertos colocados concéntricamente a la profundidad de interés (Fig. 4), posterior a un período previo de saturación. Se coloca una altura de agua predefinida en los dos anillos, y posteriormente se procede a medir la tasa de infiltración del agua en el anillo interior. Es importante mantener la misma altura en ambos anillos para evitar flujo cruzado entre ellos. Esta medición se puede realizar de dos maneras: con nivel variable, el cual consiste en medir el descenso del nivel de agua a lo largo del tiempo; o alternativamente como nivel constante, donde se procede a reponer el volumen de agua infiltrado de manera tal a mantener el nivel inicial constante. En ambos casos, se monitorea el ensayo hasta alcanzar una tasa de infiltración constante. El procedimiento estándar adoptado por la American Society for Testing and Materials (ASTM), puede ser revisado en la norma D 3385 - 9403 para el caso del ensayo con carga constante. En este trabajo se empleó el método de carga variable.
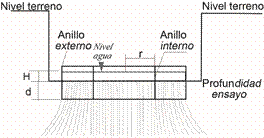
Fig. 4: Esquema de ensayo del doble anillo, donde H = altura de lámina de agua, d = profundidad de hincado de anillos y r = radio anillo interno (líneas punteadas indican direcciones asumidas para las líneas de flujo).
Existen diferentes métodos de cálculo para la obtención de K fs a partir de los datos de este ensayo. Tres procedimientos son descritos a continuación.
El primero considera que la conductividad hidráulica K fs es numéricamente igual a la tasa de infiltración estabilizada (ecuación 8) de acuerdo a las deducciones descritas en el apéndice 2. Esta es la misma consideración realizada por el SENARA, como se mencionó en la introducción.
Donde Δh y Δt representan la variación de altura de la columna de agua en el anillo interno en un periodo de tiempo definido La tasa de infiltración puede evaluarse de manera instantánea (entre dos medidas consecutivas) o de manera global (en relación a la altura inicial de columna de agua). En el largo plazo ambas tasas deberían converger. Sin embrago para tiempos menores, diferencias importantes pueden observarse entre ambas, lo cual influye directamente sobre la estimación de K fs .
El segundo procedimiento considera los efectos gravitacionales, de presión por la altura de la lámina de agua y capilaridad sobre la tasa de flujo infiltrada. El valor de K fs se obtiene con la ecuación 9 (Reynolds y Elrick, 1990):
Donde
C1 = 0,316π y C2 = 0,186π, son constantes adimensionales.
α*= parámetro que correlaciona Kfs y el potencial mátrico φm (α* = K fs / φ m) con dimensión (1/L). Este parámetro debe ser obtenido a través de otro método (PG) o estimado por tablas (Soilmoisture, 2012).
Los resultados del ensayo DA también pueden ser evaluados con la solución analítica presentada por Phillip (1957) para el problema de infiltración vertical para suelo homogéneo con lámina de agua en la superficie. Esta solución es:
Donde I representa la infiltración acumulada (L); S la sortividad (capacidad del suelo para tomar o ceder agua por efectos capilares, L/T1/2) y, A es la tasa de infiltración a largo plazo (L/T) y representa los efectos gravitacionales en el flujo. Es decir, esta ecuación al igual que la ecuación 9, considera la carga por columna de agua, los efectos capilares y gravitacionales y su variación en el tiempo. El parámetro A ha sido relacionado con la conductividad hidráulica encontrándose que K fs varía entre 1,5 a 3 veces el valor de A (Angulo et al, 2016). Algunos autores han empleado un factor de 2A/3 para estimar K fs (Gupta el al., 2006; Torfs, 2008). De esta forma, los datos de campo en forma de infiltración acumulada y tiempo total son ajustados por mínimos cuadrados para obtener los parámetros S y A.
Materiales y métodos
Se escogieron dos zonas para llevar a cabo los ensayos de conductividad hidráulica. Una de ellas corresponde con la Finca del Instituto Costarricense de Acueductos y Alcantarillados (AyA), ubicada en San Rafael de Alajuela, cuya superficie está constituida por materiales limosos. El otro sitio corresponde con una finca propiedad de la Universidad de Costa Rica (UCR), donde se ubican las instalaciones deportivas, en Sabanilla de Montes de Oca cuya superficie está caracterizada por suelos limos arenosos. En la finca del AyA se escogieron dos sitios y en la finca de la UCR tres sitios para la realización de los ensayos. En cada sitio se realizaron tres pruebas según las metodologías PG, MP y DA. En total se realizaron 15 ensayos.
Clasificación de suelos
La clasificación de los materiales ensayados en ambas fincas se realizó por medio de ensayos geotécnicos ejecutados en muestras con peso de 1000 gramos en el laboratorio de geotecnia del Instituto Costarricense de Electricidad. Se determinaron los límites líquido, plástico, índice de plasticidad y el porcentaje de humedad natural. Los materiales de la finca de AyA son clasificados como limos, mientras que los materiales de la Finca de la UCR se clasifican como limos arenosos (Cuadro 3). Vale destacar entre ellos que la humedad natural varía del 40% al 49%.
Cuadro 3 Rangos de valores de conductividad hidráulica saturada (Ks) para suelos y rocas (adaptado de Bear,1988 y Hoek & Bray, 1981).
| Ensayo | LL | LP | ÍP | Wn (%) | Clasificación S.U.C.S. | Ubicación |
|---|---|---|---|---|---|---|
| 1 | 62,0 | 35,0 | 27,0 | 40,0 | MH-Limo | Finca AyA San Rafael, Alajuela |
| 2 | 51 | 33 | 18 | 32,0 | MH-Limo | Finca AyA San Rafael, Alajuela |
| 3 | 51,0 | 39,0 | 12,0 | 46,0 | MH-Limo arenoso | Finca UCR, Sabanilla, Mtes. Oca |
| 4 | 48,0 | 39,0 | 9,0 | 49,0 | ML-Limo arenoso | Finca UCR, Sabanilla, Mtes. Oca |
| 5 | 47,0 | 32,0 | 15,0 | 41,0 | ML-Limo arenoso | Finca UCR, Sabanilla, Mtes. Oca |
Pruebas de conductividad hidráulica
Entre los días 26 y 30 de agosto del año 2004, se procedió a realizar los ensayos de conductividad hidráulica. En cada uno de los sitios, el procedimiento seguido consistió en realizar una limpieza del lugar y la remoción de la capa vegetal de suelo. Seguidamente se procedió a realizar una perforación cilíndrica con el equipo de barreno provisto en el set de herramientas del PG. Luego de la adecuación del agujero se realizó la prueba. El permeámetro empleado es del modelo 2800KI, tomado en alquiler de la Escuela de Geología de la Universidad de Costa Rica. Una vez finalizado el ensayo PG, se procedió a realizar la prueba MP en el mismo agujero (Fig. 5A). Una vez finalizadas dichas pruebas, se realizó una excavación rectangular hasta la base de la perforación, con un ancho aproximado de 60 cm para la realización del ensayo DA (Fig.5B). Se emplearon dos cilindros abiertos con diámetros de 30 y 45 cm. Ambos fueron hincados 10 cm en el terreno siguiendo la recomendación de Valverde (1998).
En el Cuadro 4 se presenta el resumen de las condiciones de carga utilizadas, tiempo de duración y tasas de infiltración obtenidas para los ensayos PG. Las mediciones durante estos ensayos se realizaron en intervalos de 1 y 2 minutos dependiendo de la respuesta observada.
Cuadro 4 Condiciones para las pruebas de conductividad hidráulica realizadas con el Permeámetro Guelph
| Ensayo/Sitio | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Finca A y A | Finca A y A | Finca U.C.R. | Finca U.C.R. | Finca U.C.R. | |
| Suelo | Limo | Limo | Limo arenoso | Limo arenoso | Limo arenoso |
| Carga 1 (cm) | 15,0 | 20,0 | 5,0 | 10,0 | 20,0 |
| Carga 2 (cm) | 24,0 | 24,0 | 10,0 | 10,0 | 20,0 |
| Radio (cm) | 3,5 | 3,2 | 3,5 | 3,2 | 3,5 |
| Profundidad agujero (cm) | 63,0 | 57,5 | 60,0 | 60,0 | 55,0 |
| Tasas infiltración R1-R2 (cm/min) | 0,10-0,16* | 0,20-0,30 | 0,40-0,60 | 0,30-0,57 | 0,50-0,20 |
| Tiempo duración de ensayo (min) | 80 | 67 | 32 | 48 | 96 |
*Para este ensayo se emplearon los valores de tasa de infiltración global, debido a que la tasa instantánea mostraba un comportamiento muy variable.
En el Cuadro 5 se presenta el resumen de las condiciones de carga, tiempo de duración y tasas de infiltración obtenidas para los ensayos MP. Las tasas reportadas corresponden con los valores interpretados de la condición estable o cuasiestable. Las mediciones durante estos ensayos se realizaron en intervalos de 2 a 5 min dependiendo de la respuesta observada. Para el ensayo 1 las dos últimas lecturas se realizaron en un intervalo de 18 y 22 minutos respectivamente.
Cuadro 5 Condiciones para las pruebas de conductividad hidráulica realizadas con el método de Porchet
| Ensayo | Lugar | Suelo | Duración (mín) | Carga Inicial(cm) | Carga final (cm) | Tasa infiltración global (cm/mín) | Tasa infiltración instantánea(cm/mín) |
|---|---|---|---|---|---|---|---|
| 1 | Finca A y A | Limo | 70,0 | 44,8 | 43,6 | 0,017 | 0,018 |
| 2 | Finca A y A | Limo | 20,0 | 50,5 | 48,5 | 0,1 | 0,005 |
| 3 | Finca U.C.R. | Limo arenoso | 20,0 | 45,0 | 14,6 | 1,52 | 1,05 |
| 4 | Finca U.C.R. | Limo arenoso | 18,0 | 44,8 | 12,2 | 1,81 | 0,90 |
| 5 | Finca U.C.R. | Limo arenoso | 45,0 | 43,5 | 26,5 | 0,38 | 0,28 |
En el Cuadro 6 se presenta el resumen de las condiciones de carga, tiempo de duración y tasas de infiltración obtenidas para los ensayos DA. Las tasas reportadas corresponden con los valores interpretados de la condición estable o cuasiestable. Las mediciones durante estos ensayos se realizaron en intervalos de 2 minutos. Para el ensayo 1 las dos últimas lecturas se realizaron en un intervalo de 14 y 28 minutos respectivamente.
Cuadro 6 Condiciones para las pruebas de conductividad hidráulica realizadas con el método de Doble Anillo (DA).
| Ensayo | Lugar | Suelo | Duración (mín) | Carga Inicial(cm) | Carga final (cm) | Tasa infiltración global | Tasa infiltración instantánea(cm/mín) |
|---|---|---|---|---|---|---|---|
| 1 | Finca A y A | Limo | 56,0 | 11,2 | 11,0 | 0,00357 | 0,00357 |
| 2 | Finca A y A | Limo | 14,0 | 9,5 | 8,5 | 0,0075 | 0,005 |
| 3 | Finca U.C.R. | Limo arenoso | 20,0 | 13,4 | 10,1 | 0,165 | 0,20 |
| 4 | Finca U.C.R. | Limo arenoso | 12,0 | 8,3 | 7,2 | 0,110 | 0,050 |
| 5 | Finca U.C.R. | Limo arenoso | 16,0 | 9,0 | 7,8 | 0,075 | 0,10 |
Análisis de resultados
En este apartado se presentan los procedimientos de cálculo empleados para cada método de ensayo, y los valores de K fs obtenidos. En el cuadro 7 se resumen dichos métodos.
En relación a los ensayos PG, se calculó tanto la tasa de infiltración instantánea como la global para cada carga aplicada. Los cálculos de K fs fueron realizados empleando la tasa instantánea, de acuerdo con el ejercicio explicativo presentado en el manual del PG. Solamente para las estimaciones en el ensayo 1 se empleó la tasa global, debido al comportamiento variable de la tasa instantánea (oscilante alrededor de la tasa global). La tasa global representaría el comportamiento medio de infiltración y además mostró un comportamiento más asintótico y estable.
Para el análisis de los datos obtenidos con MP se emplearon dos aproximaciones. La primera considera la tasa instantánea de infiltración, es decir, la tasa se calcula como la razón de cambio de nivel entre dos lecturas consecutivas (aproximaciones 2, 3 y 4 del Cuadro 7). Para el uso de las ecuaciones mostradas en el Cuadro 7, se requiere con esta aproximación, la actualización del valor de la variable h (altura de columna de agua en agujero) para cada tiempo en que se realiza el cálculo de la permeabilidad. Es decir, para las aproximaciones 3 y 4 del mismo cuadro, es necesario obtener los valores de h y R para el tiempo en que se desee calcular la permeabilidad. En relación con la aproximación 3, se calculó el gradiente hidráulico para cada paso de tiempo considerando la relación i = 0,2h-1, arriba referida. La segunda aproximación considera el empleo de la tasa de infiltración global, eso es, la razón de cambio en el nivel de agua en relación a la altura original (aproximaciones 5, 6, 7 y 8 del cuadro 7). Para las aproximaciones 6 y 8, los valores de i y R son calculados a partir de H0, por lo cual permanecen constantes para cualquier valor de tiempo al cual desee calcularse Kfs. En este caso para el empleo de la aproximación 7, se utilizó el valor de A, el cual representa la condición de infiltración a largo plazo, el valor de K fs es aproximado con la ecuación 7 pero empleando el valor de gradiente resultante de la columna inicial de agua.
Para el análisis de los datos obtenidos con DA, cuatro metodologías de cálculo fueron empleadas como se muestra en el cuadro 7. Las dos primeras utilizan la ecuación 8, la cual es evaluada para las condiciones de tasa instantánea y tasa global. El tercer método emplea el valor del parámetro A resultante del ajuste por mínimos cuadrados de la ecuación 10 con los datos de campo. En este caso Kfs es aproximada por la constante de proporcionalidad 3/2 la cual representa el límite inferior del rango reportado en la literatura. El cuarto método corresponde con la aproximación 12 mostrada en el cuadro 7, la cual emplea la ecuación 9. En este caso se utilizó la estimación del parámetro α* previamente obtenida en el análisis PG. Para esta aproximación se utilizó la tasa de infiltración global y la altura inicial de la columna de agua.
En el Cuadro 8 se presentan los valores de K fs obtenidos para cada procedimiento de cálculo. En el mismo cuadro se indican los parámetros α*(ecuación 1), A (ecuación 10) y los coeficientes de correlación (r2) obtenidos del ajuste con la ecuación de Phillip para los ensayos MP y DA. Estos mismos valores se presentan en forma gráfica en la Figura 5.
Cuadro 8 Valores de conductividad hidráulica K fs (cm/s), parámetro α* (cm-1), parámetro A (cm/s) y coeficientes de correlación para el ajuste con la Ecuación 10.
| Método de Análisis | Ensayo 1 (A y A) | Ensayo 2 (A y A) | Ensayo 3 (U.C.R.) | Ensayo 3 (U.C.R.) | Ensayo 3 (U.C.R.) |
|---|---|---|---|---|---|
| Parámetro α* (cm-1) Porchet actualizando H (tasa inst.) Aproximación logarítmica Gradiente hidráulico no unitario Corrección por área de infiltración Porchet con Ho constante (tasa global) Aproximación logarítmica Gradiente hidráulico no unitario Según tasa de infiltración teórica Corrección por área de infiltración Doble anillo | 4,35E-3 1,16E-5 1,49E-6 9,81E-5 1,09E-5 1,35E-6 5,82E-6 9,07E-5 | 8,85E-3 2,62E-6 3,02E-7 1,97E-5 5,14E-5 5,55E-6 6,12E-5 3,77E-4 | 7,92E-3 1,65E-3 6,63E-4 1,41E-2 1,43E-3 1,10E-4 5,69E-4 6,90E-3 | 3,15E-2 1,61E-3 8,43E-4 1,39E-2 1,77E-3 1,29E-4 3,61E-4 7,76E-3 | 2,31E-2 2,63E-4 5,61E-5 2,13E-3 2,85E-4 2,94E-5c 1,84E-4 1,78E-3 |
| 9. Doble anillo (tasa instantánea) | 5,95E-5 | 7,67E-3 | 3,33E-3 | 8,33E-4 | 1,67E-3 |
| 10. Doble anillo (tasa global) | 5,95E-5 | 1,20E-3 | 2,75E-3 | 1,53E-3 | 1,25E-3 |
| 11. Según tasa de infiltración teórica | 1,47E-4 | 2,73E-3 | 2,85E-3 | 3,21E-3 | 1,27E-3 |
| 12. Considerando multipotenciales | 4,26E-6 | 1,65E-5 | 3,23E-4 | 4,85E-4 | 3,28E-4 |
| r2 Porchet | 0,907 | 0,875 | 0,978 | 0,962 | 0,983 |
| A Porchet (cm/s) | 1,55E-4 | 2,02E-3 | 1,63E-2 | 1,06E-2 | 5,12E-3 |
| r2 Doble Anillo | 0,974 | 0,553 | 0,988 | 0,928 | 0,986 |
| A Doble Anillo (cm/s) | 9,78E-5 | 1,82E-3 | 1,90E-3 | 2,14E-3 | 8,49E-4 |
Los valores del Cuadro 8 presentan gran variabilidad y diferencias de hasta 3 órdenes logarítmicas para un mismo ensayo. Estas variaciones pueden responder a las diferencias en la metodología de los ensayos, las metodologías de análisis para un mismo ensayo, diferencias en las metodologías de cálculo adoptadas, y por manio- sitios 1 y 2 donde se empleó el depósito interno bras propiamente dichas en cuanto a la duración del permeámetro. Es importante resaltar que para y ejecución de los ensayos. el ensayo en el sitio 1 se observaron variaciones
Los tres métodos de ensayo, consiguen cap- bruscas (incrementos y disminuciones) en la tasa tar una mayor permeabilidad en los suelos de la de infiltración instantánea, interpretándose que UCR, coincidente con una textura más arenosa. responde al avance de un frente de saturación no Esto se ve reflejado claramente en las mayores estabilizado y posiblemente relacionado con la tasas de infiltración tanto en los ensayos MP naturaleza fina del material y el menor contenido como DA, aun cuando se emplearon en la ma- de humedad natural.
Comparando los resultados del método MP los sitios de la UCR. En el ensayo PG, también se con el método PG, las siguientes observaciones observa un menor caudal de infiltración para los son hechas. Para las aproximaciones 2 y 5 (basadas en el ajuste analítico de la curva de infiltración y considerando solamente el efecto gravitacional), los valores de permeabilidad MP son en general iguales o superiores en orden logarítmica (excepto para el ensayo 2 donde se obtuvo un valor menor), y las diferencias porcentuales oscilan entre 163 y 1022 %, manteniendo los valores PG como referencia. Estos procedimientos al considerar solo la acción gravitacional, parten del supuesto que el suelo está saturado y que el ensayo se ha extendido lo suficiente para permitir el establecimiento del flujo permanente o cuasi-permanente. Para las aproximaciones 2 y 5, los resultados más similares entre MP y PG fueron obtenidos para el ensayo 5, donde los valores de permeabilidad se encuentran dentro del mismo rango logarítmico aunque con diferencias porcentuales de 163 a 184%. Para este mismo ensayo 5 se obtuvo el mayor coeficiente de correlación para el ajuste de Phillip. En este caso el coeficiente de infiltración A es 0,307 cm/min, valor bastante similar al 0,38 cm/min obtenido al finalizar los 45 minutos de duración de este ensayo. Según este dato, si este ensayo se hubiera extendido hasta 70 min habría permitido obtener una tasa de infiltración en el rango de un 10% del valor teórico. Para los ensayos restantes los coeficientes de correlación son menores, y las tasas de infiltración al finalizar los ensayos son bastante mayores a los valores teóricos (a excepción del ensayo 2, cuyo bajo valor r2 no permite concluir al respecto). Es muy posible que el procedimiento de ejecución de estos ensayos sea un factor importante que explique la diferencia encontrada entres estas metodologías. Esto debido a los cortos periodos de saturación previa y de monitoreo. Adicionalmente, como indican Reynolds et al., (1983) este procedimiento sobrestima el valor de K fs al despreciar el flujo radial.
Los procedimientos de cálculo 3, 4, 6 y 8 con los cuales se analizaron los datos del ensayo de MP, arrojan valores ligeramente menores o muy superiores a los del análisis PG. Estas diferencias oscilan entre -95 y 9521 %. Como se comentó, estos procedimientos emplean como estrategia la utilización de gradientes hidráulicos no unitarios y/o correcciones de área para considerar efectos adicionales al gravitacional. Es por este motivo que dichos métodos son muy sensibles a la tasa de infiltración utilizada así como el valor de gradiente empleado.
Para los aproximaciones 3 y 6 se definió como 5 el valor máximo de gradiente hidráulico; esto genera valores de permeabilidad dentro del mismo orden o hasta 2 órdenes logarítmicos menores que el PG, en dependencia con la tasa de infiltración empleada. En este caso para el ensayo 5 se obtiene incluso valores menores a los obtenidos con las metodologías 2 y 5, a pesar de que para este ensayo la tasa de infiltración estaba cercana al valor teórico, y se esperaría que fuera menor al último valor medido. Es decir este procedimiento podría estar sobredimensionando el valor del gradiente hidráulico. En este caso se requeriría un gradiente hidráulico de 2 para obtener valores en el rango del PG. Al final de este ensayo, la columna de agua era de 26,5 cm, mayor a los 20 cm que de acuerdo a las recomendaciones de la ABGE resultaría en un valor de i = 3. Es decir, los efectos no gravitacionales en este ensayo deberían influir en menor grado a los previstos por la metodología recomendada por la ABGE. Para los ensayos restantes, la duración corta de estos en relación al valor teórico para la estabilización influye en la obtención de valores de permeabilidad mayores al PG. El hecho de que algunos se encuentren en el mismo orden logarítmico puede ser el resultado de una combinación numérica inesperada. Para los procedimientos de cálculo 4 y 8, los valores de permeabilidad son muy superiores a los del análisis PG, esto se debe a un alto valor de la tasa de infiltración (aun no estabilizada) y posiblemente a que la aproximación del cilindro de saturación por medio de una parábola no represente las condiciones encontradas en estos suelos. El área de infiltración obtenida con el parámetro R (ecuación 6), es menor al área húmeda del cilindro, lo que implica que este método restringe todo el flujo gravitacional a un área pequeña y por lo tanto sobreestima el valor de K fs . Es importante mencionar que los ensayos MP fueron realizados para relaciones H/r variables entre 13 y 16. Reynolds et al.,(1983) demuestran que para relaciones H/r igual a 10, el flujo gravitacional representa apenas el 1,5% del total. La no consideración del flujo radial o la atribución total del flujo a efectos gravitacionales (procedimientos 4 y 8) produce una sobrestimación de K fs . Para corroborar y mejorar la interpretación de estos procedimientos 4 y 8, así como las observaciones realizadas para los procedimientos 3 y 6, es recomendable la medición directa en campo de las dimensiones del bulbo de saturación.
En relación a la aproximación 7, los valores obtenidos de permeabilidad presentan las menores diferencias porcentuales en relación a los valores de PG (-83 a 22%). En general los valores se encuentran en el mismo rango o un rango logarítmico menor. Este procedimiento de cálculo es sensible al valor de gradiente hidráulico empleado, y al ajuste teórico del valor A, el cual a su vez es afectado por las condiciones de ejecución del ensayo. Para el ensayo 5 se obtuvo un valor K fs menor en un rango logarítmico al obtenido con PG. Para este caso se requeriría de un gradiente de 1,8 para obtener valores en el mismo rango, esto es ligeramente menor al valor teórico de 2 estimado para los procedimientos 3 y 6. Reynolds et al., (1983) demuestran que el gradiente de presión (debido a la columna de agua en el agujero) es un valor que varía tanto con la profundidad del pozo (aumenta con la profundidad) así como a través de la base del agujero (mayor hacia la pared del pozo), no existiendo por tanto un valor único. Los procedimientos 3, 6 y 7 intentan reducir esta variación del gradiente por medio del uso de un único valor representativo. Determinar sin embargo cuál es ese valor representativo resulta más en un procedimiento de ajuste que en un método de cálculo, a falta de un criterio numérico más robusto para su determinación. Es interesante observar que para los ensayos 1,3 y 4 los valores de K fs obtenidos se encuentran dentro del mismo rango que los PG, a pesar de menores valores de coeficiente de correlación en relación al ensayo 5, pero aun así considerados como altos (0,91 a 0,98, Cuadro 8). Esto es indicativo de que un valor de correlación alto, no necesariamente implica una estabilización de la tasa de infiltración, sino se refiere a la calidad del ajuste teórico de los datos de campo hasta el momento en que se tomaron las lecturas. Un buen ajuste no implica necesariamente que de continuar el ensayo el valor de A no vaya ser modificado, es decir para estos ensayos, es probable que el valor de A sea menor al calculado debido principalmente a la corta duración de los mismos. Es importante que el analista considere este tipo de limitaciones al momento de interpretar y evaluar los datos de este tipo de ensayos. Para estos ensayos entonces, la combinación de un alto valor de A con una sobreestimación del gradiente hidráulico produjo valores cercanos a los obtenidos con PG. Probablemente los valores más correctos estén representados por una combinación de valores menores de A con menores valores de gradiente hidráulico como lo sugiere el análisis del ensayo 5. La corta duración de la etapa de monitoreo de estos ensayos restringe su análisis.
En relación al método DA, todos los valores de permeabilidad son superiores a los obtenidos con el procedimiento PG. Solamente para el método de cálculo 12 se obtuvo valores dentro del mismo rango logarítmico. Para los procedimientos 9, 10 y 11 estos se encuentran uno a dos rangos logarítmicos por encima, traduciéndose en diferencias porcentuales de 98 a 27155%. Para el método 12 estas diferencias oscilan entre 15 y 227%. Los métodos 9, 10 y 11 se basan en la consideración solamente de los efectos gravitacionales, por lo tanto consideran que el suelo está en condiciones de saturación total para su validez. Los valores mayores de permeabilidad parecen estar relacionados con las mayores tasas de infiltración obtenidas al finalizar dichos ensayos, las cuales según los valores teóricos de A aún no se habían estabilizado. Es decir estos ensayos se terminaron en condiciones aun no estabilizadas de saturación. Es por este motivo que los valores obtenidos con la metodología de cálculo 12 se encuentran dentro del rango de los valores PG, al considerar los efectos de capilaridad y presión de columna de agua.
Diferencias como las descritas en los párrafos anteriores han sido reportadas en la literatura. van Hoorn (1978), comparando los resultados del infiltrómetro de un anillo y empleando el mismo procedimiento 10 del cuadro 7, con resultados de MP empleando el mismo procedimiento 5 del Cuadro 7, obtuvo valores de K fs un 28% mayores para el infiltrómetro en el caso suelos franco arcillo limosos. Esta diferencia disminuye a medida que el contenido de arena aumenta. En este estudio también se obtuvo valores mayores con el método DA en relación al método MP para los suelos más finos de la finca del AyA. Gupta et al. (2006) comparan resultados de los ensayos PG y DA para suelos franco arenosos encontrando valores superiores de K fs para DA en un 44%.
En este caso emplearon el procedimiento11 del Cuadro 7, pero aplicando un factor de 2A/3 para estimar la permeabilidad. Aún con este factor menor los valores fueron superiores. Dichos autores atribuyeron este comportamiento a macroporos y fisuras muestreadas con la mayor área del procedimiento DA. Para los datos de este estudio, aun aplicando el factor 2/3, los valores DA se mantienen superiores a los obtenidos con el procedimiento PG, y esta diferencia es mayor para los suelos más finos del AyA. Torfs (2008) comparó diferentes métodos de ensayos y diferentes metodologías de cálculo para suelos francos y francos arenosos. Para efectos de este estudio es de interés la comparación hecha entre los métodos DA empleando las aproximaciones 9 y 11 con un factor 2A/3 (Cuadro 7), método MP empleando el procedimiento 5, y el método PG con la aproximación 1 del Cuadro 7. Los resultados indican que los valores DA son superiores a los MP, y estos a su vez son iguales o superiores a los obtenidos con el método PG. Los valores PG están en general entre una y dos órdenes logarítmicas menores a los otros procedimientos, los cuales a su vez se encuentran dentro del mismo orden logarítmico. Atribuyen los menores valores de PG al menor volumen ensayado, posible colmatación de poros durante el ensayo y a que la formulación emplea además de los efectos gravitacionales, los efectos de presión y capilar. En este estudio se observa el mismo comportamiento de forma clara en los suelos de la finca del AyA, mientras que en los suelos más arenosos de la UCR los valores MP están dentro del mismo rango o menores, excepto para los procedimientos 5 y 8, los cuales arrojan valores de permeabilidad en el rango de 1,0E-2 (cm/s), valores que no parecen representativos de este tipo de suelos (Cuadro 1). Noshadi et al. (2012) realizaron una serie de ensayos en suelos franco limoso, incluyendo los métodos PG, MP y análisis en pozo bajo nivel freático (AH, Auger Hole). El método MG fue evaluado con la misma aproximación 5 y el PG con la aproximación 1 de doble carga. Obtuvieron valores MP mayores por un factor de 2 en comparación con los otros métodos. Esta diferencia la explican por la no consideración de efectos de capilaridad y presión de columna de agua, y adicionalmente por el aire atrapado en los poros. Archer et al. (2014) presentan una comparación de diferentes metodologías de cálculo para analizar los datos del ensayo de carga constante. Indican que para suelos gruesos las diferencias entre los métodos de cálculo sin considerar capilaridad y considerando capilaridad no son significativamente diferentes, sin embargo cuando se considera suelos finos, esta diferencia se aprecia de manera clara, siendo evidente que los valores de K fs son menores al considerar los efectos de capilaridad.
Al comparar los valores obtenidos con los métodos PG y AH (Auger Hole, para análisis en pozo bajo nivel freático) en suelos finos limosos, este último arrojó valores mayores, siendo necesario multiplicar el primero por un factor de 2. Atribuyen esta diminución a dos aspectos: alteración de la cara del agujero por la excavación y a la no consideración de capilaridad. Consideran que para las condiciones del sitio en estudio la solución propuesta por Reynolds et al. (1983), que incluye los efectos de gravedad y presión, genera un valor más representativo de la permeabilidad aunque menor al obtenido con el método AH. Ebrahimi & Moradi (2015) realizaron una comparación para suelos arenosos entre los métodos PG y DA, empleando una aproximación de carga única para el primero (ecuación 1 de este documento), y una relación potencial para el segundo. Obtienen valores PG superiores en un 12% y dentro del mismo rango logarítmico. Atribuyen esta diferencia a la incertidumbre en el valor de α* y al posible flujo horizontal durante el ensayo PG.
Como se indicó en la introducción, el procedimiento adoptado en Costa Rica para la definición de distancias de separación entre captaciones de agua y sistemas de tanques sépticos, es muy sensible al valor de conductividad hidráulica empleado. Variaciones en un orden de magnitud de K fs se transformarían en variaciones de la misma magnitud en términos de velocidad de desplazamiento de los patógenos. Cuando se emplean criterios de separación basados en concentraciones máximas aceptables de patógenos, los cambios de permeabilidad pasan a ser menos relevantes (aunque siempre importantes) en comparación con los valores de concentración inyectados al terreno, siendo más sensibles estas variaciones cuando se inyectan bajas concentraciones (Macías y Vargas, 2016; Macías et al., 2017).
Conclusiones
Los valores de K fs obtenidos en este estudio, se encuentran dentro del rango de valores para suelos limosos - limo arenosos (Cuadro 1). Algunos valores de orden superior fueron observados para los métodos MP con corrección de área. Sin embargo este procedimiento de cálculo se mostró bastante liberal en relación a la estimación del valor de permeabilidad.
Los resultados obtenidos muestran una clara tendencia de menor permeabilidad en los suelos limosos encontrados en la fina del AyA, en comparación con los suelos limo-arenosos observados en los sitios muestreados en las instalaciones de la UCR. Esto es, los procedimientos de ensayo son consistentes y reflejan las variaciones de permeabilidad encontradas en las dos propiedades ensayadas. En términos comparativos, las estimaciones de K fs son mayores para el procedimiento de Doble Anillo, seguidas por las estimaciones hechas con el Método de Porchet, finalmente valores menores fueron obtenidos para el Permeámetro Guelph. Esta misma tendencia ha sido reportada en la literatura internacional, atribuyendo el menor valor del Permeámetro Guelph a diversos factores: menor volumen ensayado en el método PG, colmatación de poros durante el ensayo, diferencias en la formulación al considerar los efectos de capilaridad y presión de columna de agua, aire atrapado en los poros, alteración de la pared del agujero por efecto de la excavación, incertidumbre en la selección del parámetro α*, posible flujo horizontal y presencia de macroporos.
Los autores de este trabajo consiguieron corroborar que la no inclusión de efectos capilares en las ecuaciones de cálculo de K fs es un aspecto que puede contribuir a la obtención de menores valores con el método PG, sin embargo también consideran que para las condiciones de los ensayos realizados en este estudio, el procedimiento de ejecución de los mismos, en relación a la etapa de saturación previa y tiempo de monitoreo jugo un papel más importante. Es muy probable que los mayores valores obtenidos con los métodos DA y MP estén influenciado por las mayores tasas de infiltración, aún no estabilizadas.
En relación a los procedimientos de cálculo, las estimaciones más similares se obtuvieron entre el PG, el ajuste teórico de Philip y, las consideraciones multipotenciales. Esto es indicativo de que el empleo de tasas de infiltración menores (esperadas a un tiempo prolongado) así como la incorporación de los efectos de capilaridad y presión de columna de agua permitirían obtener valores comparables. Los procedimientos basados en gradiente hidráulico no unitario y corrección por área, se mostraron muy sensibles tanto al valor escogido de gradiente como a la tasa de infiltración. Sería interesante para próximos estudios incorporar la medición de las dimensiones del bulbo de saturación en campo como parte de la rutina del procedimiento. Esto con el objetivo de validar si para este tipo de suelos se mantiene la consideración de un frente de saturación con perfil parabólico y, para estimar valores de gradiente hidráulico representativos para cargas mayores a los 30 cm. También es muy recomendable homogenizar cargas hidráulicas para los procedimientos PG y MP (mantener cargas alturas de columna de agua similares) sí estos se van a realizar en el mismo agujero, y en lo posible mantener relaciones H/r entre 5 y 10.
Los resultados y observaciones mostradas en este estudio son válidos para los suelos analizados. Es recomendable realizar estas mismas comparaciones para otros sitios del país, y verificar si estas mismas observaciones son válidas para suelos con diferente granulometría. Esto es de gran importancia teniendo en vista el impacto que la incertidumbre en la determinación de K fs genera sobre la viabilidad o no de proyectos donde se evalúa la distancia de separación entre sistemas de tanques sépticos y captaciones de agua. Especialmente por la relevancia del parámetro K fs en la metodología adoptada en Costa Rica.