Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Geológica de América Central
On-line version ISSN 0256-7024Print version ISSN 0256-7024
Rev. Geol. Amér. Central n.49 San Pedro de Montes de Oca Jul./Dec. 2013
Soil-water retention curve and beginning of monitoring in Tierra Blanca Joven (TBJ)
Curva de retención suelo-agua e inicio de monitoreo en Tierra Blanca Joven (TBJ)
*Dirección para correspondencia:
Abstract
In El Salvador during the rainy season or when major earthquakes occur, the areas covered by the volcanic tephras Tierra Blanca Joven (TBJ) suffer mass movements, liquefaction and erosion; causing important environmental, social and economic losses. To start the characterization of these unsaturated soils, suction values of a fall unit of TBJ were obtained using pressure plate, centrifuge and filter paper to build a Soil-Water Retention Curve. The use of this curve into finite elements software can help to acquire shear strength and permeability properties. The filter paper showed to be a practical method but close to saturation the pressure plate is needed. With the centrifuge, scatter results were observed. Also field test using Quickdraw tensiometer (suction) and TMS3 (soil moisture content) are being conducted to propose a field methodology for an early warning system for the slopes, that could help in urban planning and risk assessment.
Keywords: Tierra Blanca Joven, suction, filter paper, pressure plate, centrifuge, tensiometer, soil moisture sensor.
Resumen
En El Salvador durante la época de lluvias o cuando ocurren terremotos, las áreas cubiertas por las tefras volcánicas Tierra Blanca Joven (TBJ) sufren movimientos de ladera, licuefacción y erosión provocando pérdidas ambientales, sociales y económicas importantes. Para iniciar la caracterización de estos suelos parcialmente saturados, valores de succión de una unidad de caída de TBJ fueron obtenidos con la olla de presión, centrífuga y papel filtro para construir la Curva de Retención Suelo-Agua. El uso de esta curva en programas de elementos finitos ayuda a conocer los esfuerzos cortantes y la permeabilidad. El papel filtro probó ser un método práctico pero es necesario usar la olla de presión al ir saturándose. Pruebas de campo con tensiómetro (succión) y TMS3 (humedad) se llevan a cabo para proponer metodología de campo para un sistema de alerta temprana para las laderas, que puede ayudar a la planificación urbana y estudios de riesgo.
Palabras clave: Tierra Blanca Joven, succión, papel filtro, placa de presión, centrífufa, tensiómetro, sensor de humedad de suelo.
Introduction
Tierra Blanca Joven (TBJ) is a volcanic tephra that covers most of the Metropolitan Area of San Salvador (MASS), being sensitive to moisture changes and vibrations leading to intensive mass wasting processes. Recently Hernandez (2004), Lexa et al. (2011), Chavez et al. (2012a) and Chavez et al. (2012b) have presented some of the properties of this material, being the most important its unsaturated state meaning that in the soil there’s presence of air, water, solids and the air-water interface or the contractile skin (Fredlund et al., 2012).
The grain size curve range of the studied TBJ fall deposit (unit G) is displayed in figure 1. The unnormalized major elements weight obtained with X-ray fluorescence spectrometer (Communication of Spera, 2012) of a G unit fall deposit of TBJ shows that is composed mainly by SiO2 (68.4%), Al2O3 (14.4%), Na2O (3.32%), FeO (2.7%), CaO (2.45% ) and K2O (2%). TBJ is composed mainly by quartz (32.9%), plagioclase (39.9%), orthoclase (13.7%), corundum (2.1%), hypersthene (4.2%) and magnetite (1.3%).
Studies made by Chavez et al. (2012a) of the units D, F and G of TBJ into the environmental scanning electron microscope (ESEM) show that there are voids (where water can enter and capillary forces can develop); and big size grains are covered by smaller ones. Furthermore, using the results of the quantitative data of the ESEM is concluded that TBJ is composed of silica rich volcanic glass, feldspar and small amounts of clay (Communication of Lexa, 2012).
According to Houston & Houston (1997), man induced changes in the surface and the groundwater regime can affect the behavior of unsaturated deposits that normally are in a metastable condition, but when saturated a decrease in the strength and stiffness (loss of suction and/or cementation) produce a collapse or volume change that triggers erosion, slab failure and mass movements (Fig. 2). In the slopes of TBJ, shallow slips take place during periods of heavy rainstorm, these processes occur similarly during earthquakes (Chavez et al., 2012a; Chavez et al., 2012b; Baum et al., 2001).
Suction, is defined as the free energy state of the soil water (Murray & Sivakumar, 2010) and is responsible of the increase of shear strength (besides cementation) in natural moisture samples of TBJ reported by other authors (Chavez et al., 2012b), but using equipment for saturated soils. The total suction is the sum of matric and osmotic suctions (Murray & Sivakumar, 2010; Fredlund et al., 2012). The matric suction is related primarily to capillarity, but is influenced by surface adsorption effects also. The osmotic suction is the difference in salt concentrations in the pore water in the system being analyzed, and the surrounding water. For geotechnical applications is more important the matric suction (Hoyos et al., 2008; Ng et al., 2008; Sivakumar, 2010; Fredlund et al., 2012), but for soils with excessive evaporation or excessive infiltration the osmotic suction (and total suction) can be important (Fredlund et al., 2012). Matric suction (Blatz et al., 2008) is generally considered the most important component of total suction in non-plastic cohesionless soils with a relatively pure pore fluid; the osmotic suction can be important in high plastic clays with elevated activity connected with its mineralogy or where the pore fluid activity is high because the presence of dissolved salts. The term matric suction (Fredlund et al., 2012) is used to indicate the negative pressure of water relative to atmospheric air pressure (uw - ua); where uw is water pore pressure and ua air pore pressure. This paper presents some methods and models to measure and represent the matric suction and water content.
Authors like Guzman & Melara (1996); Hernandez (2004); Rolo et al. (2004) mention the incidence of suction and cementation into the strength and stiffness behavior of TBJ. During the tests made for measuring the suction in TBJ for this paper it was observed that, when saturated and then dried in the oven with a temperature of 110° for 24 hours, the strength of TBJ is increased significantly making difficult even to break it, but if soaked the apparent cohesion was lost crumbling apart. The cementation of the collapsible soils (Houston & Houston, 1997; Ng & Menzies, 2007 and Chavez et al., 2012a) could consists of dried clay, salts, oxides, interparticle forces in clayey soils and chemical precipitates, which may have been added after deposition. In the surface of TBJ slopes, a crust layer is formed (Hernandez, 2004) and is composed of sulfates and minerals coming out by evaporation; this crust protects in some way and for a short time, against erosion and prevents the scape of moisture from the slope. The increased salts at the surface of the slopes (Fredlund et al., 2012) can increase the total suction (osmostic suction) and reduce the evaporation of water from the ground surface.
According to Rahardjo & Leong (1997) and Fredlund et al. (2012), the soil-water retention curve (SWRC), also known as soil-water characteristic curve, is an important constitutive relationship for unsaturated soil mechanics. The SWRC relates changes of gravimetric water content, volumetric water content or saturation of a soil to matric suction. It has a similar role as the consolidation curve in saturated soil mechanics. Engineering properties like shear strength, volume change and coefficient of permeability for unsaturated soils (Fredlund, 1997; Rahardjo & Leong, 1997; Fredlund et al., 2012) are predicted with the SWRC and with the properties of the saturated soil. Is important to mention that unlike the saturated soils the coefficient of permeability for unsaturated soils is not a constant (Fredlund et al., 2012) and varies considerable with respect to matric suction or stress state. With less water content the permeability is smaller by many orders of magnitude, if compared when saturated.
In the figure 3a is presented some typical SWRC curves, according to the soil type. There are three stages (Sillers et al., 2001) in the SWRC (Fig. 3b): 1) the capillary saturation zone, where the pore water is in tension but the soil remains saturated due to capillary forces; 2) desaturation zone, where the water within the pores is replaced by air, this area ends at the residual water content, θr, where pore water becomes immobile within the soil matrix and the increase of suction does not change the water content; 3) zone of residual saturation, where the water is strongly held to the soil and only there´s moisture movement as a vapor flow.
The SWRC of unsaturated soils (Fredlund et al., 2012) differ if its initial state (Fig. 3b) goes from dry to saturation (adsorption curve) or from saturation to dry state (desorption curve) because hysteresis. Both curves have a similar form, but the values at the starting point of the desorption curve may be different than the end point of the adsorption curve, because of air entrapment in the soil.
In figure 4 the different approaches to obtain the unsaturated soil property functions are illustrated. For final design Fredlund et al. (2012) recommend the use of the direct measurement experiments (triaxial, shear box, oedometer and ring shear for unsaturated soils) and the indirect measurement experiments (SWRC measurement); being the last alternative proposed by the authors of this paper, because it can be introduced in El Salvador more quickly and simply. For preliminary designs the classification tests (grain-size distribution) and data base mining can be used.
In the table 1 presents some methods to measure matric, osmotic and total suction, along with the suction range and time of each test. Most of the methods for measuring soil suction were developed by soil science, hydrogeology, petroleum, agricultural, ceramics, geotechnical and geo-environmental engineering (Vanapalli et al., 2008; Fredlund et al., 2012). For the present research, the filter paper and pressure plate were chosen, but also the centrifuge was used to build the SWRC to prove a faster method.
According to Liu et al. (2011) and Seki (2007) different models to describe the soil water retention characteristics are available and have been evaluated (e. g. Van Genuchten, 1980; Brooks & Corey, 1964; Kosugi 1996; Durner, 1994; Seki, 2007). However, it is important to obtain parameters on the base of experimental data (6-9 points of suction vs. water content can be enough to obtain the complete SWRC). Some of the methods have equations that use two or three parameters (variables used to define a model) that are obtained after an iterative process; the model parameters (Sillers et al., 2001) affect the shape of the SWRC.
Methodology
Suction vs. moisture content values of a fall deposit of TBJ “G” unit (Figs. 5 and 6) of the proximal zone (13°43’5.83”N, 89° 9’33.24”W) were obtained by the authors in the laboratory, using pressure plate, centrifuge and filter paper (Fredlund & Rahardjo, 1993; Fredlund, 1997; Rahardjo & Leong, 1997; Bulut & Leong, 2008; Murray & Sivakumar, 2010, Fredlund et al., 2012) to build the Soil Water Retention Curve (SWRC) (Fig. 6).
Filter Paper
The filter paper method is an affordable and relatively simple laboratory test method; in addition total (non-contact method) and matric suction (contact method) can be measured using this technique. The samples were sieved using the 2 mm mesh size.
The methodology suggested by ASTM D 5298 and resumed by Fredlund et al. (2012) was followed. A filter paper is sandwiched between two bigger size protective filter papers. Then this arrangement is inserted into the soil sample (Fig. 7) in a glass jar container, which is sealed. For matric suction, good contact between the filter paper and the soil has to be established. The prepared containers (three samples were tested, for each moisture content) were put into a cooler in a controlled temperature room for equilibrium. After equilibrium (10 days at least) is established between the filter paper and the soil, the gravimetric water content of the filter paper disc is measured. Moisture and dry weight of the filter paper are needed. All the process for water content measurements are weighed with 0.0001 g accuracy; also it´s necessary to use latex gloves and tweezers to handle the filter paper and recipients. Two people are needed to follow the process after reaching the equilibrium time (10 days at least), while one person is opening the sealed glass jar, the other person is putting the filter paper into the recipient very quickly (less than 5 seconds) using the tweezer and obtaining the weights rapidly (ASTM D 5298, 1996; Fredlund et al., 2012 ).
The gravimetric water content of the filter paper is converted to suction using a calibration curve according to the filter paper used. Three calibration curves (Table 2) were used (Bicalho et al., 2007,) for the Whatman No. 42 filter paper, to interpret the measured filter paper gravimetric water contents (Fig. 6). According to different authors (Fredlund et al., 2012) the calibration curves and data for different batches of Whatman No. 42 filter paper do not show changes and this filter paper appears to be more consistent than the Scheleicher & Schuell No. 589-WH (989-WH in the USA) filter paper.
With the paper filter method is possible to reach elevated suction values (for TBJ, 20 000 kPa was reached) and for almost the whole range, however according to Bicalho et al. (2007) the suction data below 10 kPa is best if obtained with the pressure plate. When the water content of the samples of TBJ were close to be saturated it was difficult to obtain good results, since the paper filter was soaked, so the results were discarded. According to Fredlund et al. (2012) the contact filter paper method becomes inaccurate in high matric suction range since water transport is dominated by vapor transport.
Pressure Plate
The pressure plate uses the principle of axis translation which is a way to measure negative pore water pressures (suction) above 100 kPa, avoiding the problem of cavitation (Marinho et al., 2008 and Vanapalli et al., 2008).
The principle of axis translation is a laboratory technique that (Marinho et al., 2008) raise artificially the atmospheric pressure experimented by a soil sample in a sealed chamber (Fig. 8); increasing the air pressure moves the water pressure in the soil to an easily measurable positive pressure.
In the figure 9 is presented a scheme of the equipment and used methodology. There are different pressure plates capable of supporting different pressures. The disturbed soil was sieved using the 2 mm mesh size.
According to Vanapalli et al. (2008) the applied pore air pressure, ua is the matric suction when the pore water pressure, uw is set to zero (open to atmospheric pressure condition).
Because it takes less time to reach equilibrium the soil samples are laid into a 5 cm diameter and 1 cm height retention rings. For each suction data obtained, ten samples were tested. Two ceramic plates were used; the 100 kPa (more porous) for low suctions and the 300 kPa ceramic plate for more elevated suction values. It was not possible to get higher suction values (1500 kPa) since a proper air compressor was not available at the time.
The ceramic plate was saturated introducing water into the neoprene diaphragm and then the samples were accommodated into the retaining rings. Similar to the paper filter method, a good contact between the ceramic plate and the soil is needed. Afterwards, water was placed into the surface of the ceramic plate and the pressure plate was closed and left overnight for saturation.
Once saturation is complete (ceramic plate and soil samples), the remaining water on the surface of the ceramic plate was extracted; sealing the chamber by fastening the cover bolts afterwards.
A single pressure step was applied and the equilibrium time varied between 2 days to hours, depending of the imposed suction. Equilibrium was reached when there was no more water was dripping from the outflow tube of the pressure plate . In this moment the retention force or suction from the soil particles is the same as the pressure exerted by the system (Vanapalli et al., 2008). Afterwards, the water content of the samplesit was obtained.
Good correlation was observed between the results of the filter paper and this method. For lower suction values (close to saturation) the pressure plate data has to be used since filter paper results were discarded.
Centrifuge
In an effort to find a faster method, a centrifuge was used to obtain the average distribution of matric suction in order to build the SWRC (Khanzode et al., 2002; Reatto et al., 2008; Cropper et al., 2011). The results presented some scatter, probably linked to the consolidation during centrifugation (Fig. 6).
The equation used to get the suction values, using an International Equipment Company (USA) centrifuge (Fig. 10) with a diameter of 11.5 cm, is:
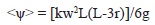
Where <ψ> is the average distribution of matric soil-water potential; L the sample length; w the angular velocity (rad s-1); r the radial distance to the effluent outlet (m) and k is a conversion factor equal to 9807 Pa m−1.
Samples were sieved using the 2 mm mesh size and placed into sample holders (2 cm of diameter; 4.5 and 6.5 cm of height) with small perforations on the bottom to allow the drainage of water; filter paper was placed between the sample and the bottom disk to prevent migration of the fine particles during centrifugation; each sample was saturated overnight.
Some samples were placed at a different height (distance of the soil from the center of rotation of the centrifuge) to obtain different points of suction for each angular velocity. Centrifugation was performed for periods of 90 minutes, two and three hours, seeking for equilibrium, and then the water content of each sample was obtained.
Mathematical models for the soil-water retention curve (SWRC)
According to Seki (2007) the models of Brooks & Corey (1964), Van Genuchten (1980) and Kosugi (1996) (which are unimodal pore size distribution models) can represent many SWRC of soils with a homogeneous pore structure; but in soils with a heterogeneous distribution of pore size, these models do not represent the measured soil water retention curve accurately, in such case models like Durner (1964) and Seki (2007) can be used.
To obtain the SWRC of the different models the software SWRC Fit (Seki, 2007) was used. It can be executed directly from the web page (http://seki.webmasters.gr.jp/swrc/). This program was developed to perform the nonlinear fitting of the SWRC, where no explicit input of the initial estimate is required.
In figures 11, 12 and 13, some results of the SWRC using the models that define the soil water retention characteristics are presented.
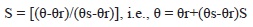
Where S is saturation; θ is the volumetric water content, representing the fraction of the total volume of soil that is occupied by the water contained in the soil; θs is the saturated water content, and θr is the residual water content (Fig. 3).
The Brooks and Corey (1964) model is expressed as:
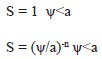
The parameter a is related to the air entry value of the soil and the n parameter is related to the pore size distribution of the soil. The model is not continuous for the entire SWRC range (Sillers et al., 2001); the equation becomes a constant for suction values less than the air entry value (a), and the SWRC is a decreasing function when soil suction values are larger than the air entry value (a). Because of this abrupt change in (a), numerical instability can be expected when modeling unsaturated soil behavior.
The Van Genuchten (1980) model is described as:
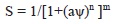
The parameter a is related to the inverse of the air entry value; the n parameter is related to the pore size distribution of the soil and the m parameter to the asymmetry of the model (Sillers et al., 2001).
According to Seki (2007), Kosugi developed a model deriving the soil water retention curve from the log-normal pore size distribution.
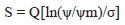
Ψm denotes the median matric suction, S(ψm) = 0.5 corresponding to the median pore radius; σ defines the standard deviation of the log-transformed soil pore radius (σ>0), characterizing the width of the pore size distribution.
Where Q(x) is the complementary cumulative normal distribution function, defined by Q(x) = 1-Ф(x), in which Ф(x)is a normalized form of the cumulative normal distribution function.
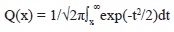
The Durner (1994) multimodal retention function is made for soils with a heterogeneous pore structure.
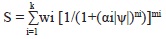
Where k is the number of subsystems (Durner, 1994) that form the total pore-size distribution, and wi represents weighting factors for the sub-curves, subject to (0<wi<1, Σwi = 1). As for the unimodal curve, the parameters of the sub-curves (αi, ni, mi) are subjected to the conditions, αi >0, mi>0, ni>1. αi is a scaling factor that determines the position of the pore size maximum, and mi and ni are dimensionless curve shape parameters.
Seki (2007) proposed a multimodal pore-size distribution model, combining the ideas of Durner and Kosugi.
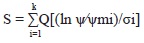
Where (0<wi<1, Σwi = 1). The special case of k = 2 can be termed as a bimodal log-normal pore-size distribution.
Discussion and Conclusions
For problematic soils, (Houston et al., (2001) recommend the identification and description earlier in the project of these deposits; also the estimation of the extent and degree of wetting; possible collapse strains/settlements; and to identify potential mitigation alternatives. In order to do that there is a need to use unsaturated soil mechanics to have a better design and understanding of the behavior of the soil. Common methods are described in figure 4 and Table 1. The results presented in this paper use some of them to measure and represent matric suction; a Soil Water Retention Curve (SWRC) of “G” fall unit of TBJ was obtained. Nowadays different geotechnical software like Geoslope, Soilvision and Plaxis are able to run simulations using this kind of information for slope stability and infiltration-evaporation simulations. Research on osmotic and total suction is important in TBJ (Fredlund et al., 2012) because of the presence of a salts crust on the surface of the slopes (salts precipitate as white deposits after evaporation), which prevents moisture loss from the slope.
Comparison (Fig. 6) between the lab and field results of different methods and authors (filter paper, pressure plate, tensiometer and suction probe) revealed a good correspondence. The consolidated state and the grain size distribution of TBJ might influence the observed differences in the SWRC results.
With the results obtained during the current assessment is possible to conclude that from all the methods used for obtaining the SWRC, the filter paper technique prove to be the most practical. Is able to measure matric and total suction, time needed is shorter and is possible to measure suction for almost the whole range. But for suction values < 10 kPa the pressure plate results are required. To obtain the matric suction through the filter paper, several equations (Bicalho et al., 2007) were used but, when compared to the pressure plate results, the Oliviera and Marinho equations (Table 2) show a better fit; the results of other equations begin to detach after 100 kPa. The results of the mathematical models used to describe the SWRC (Fig. 11, 12 and 13), indicated that the filter paper data also has a better coefficient of determination (R2) than the values obtained with the pressure plate. Historically, the Van Genuchten model (1980) has been widely adopted because it has a higher degree of fitting to data from a variety of soil types and the model parameters have a physical meaning (Sillers et al., 2001).
Because of the limited range measured with the pressure plate during the curse of the current research (<145 kPa), the results of the mathematical models diverge in the segment of the SWRC with absence of lab data (Fig. 11). For this reason, it is recommended to obtain data with the pressure plate up to the possible limit of 1500 kPa .
The time period for measuring the SWRC (Khanzode et al., 2002) is reduced considerably using the centrifuge method in comparison to the pressure plate or filter paper. Reatto et al., (2008) reported a good correlation between the SWRC obtained with the centrifuge and the pressure plate, however, other authors (Cropper et al., 2011) concluded that centrifugation changes the total porosity and pore size distribution decreasing the permeability; therefore, the centrifuge method requires more research before it can be recommended for routine measurement of SWRC. Also, when using the centrifuge test drying of the sample occurs (desorption curve), which differs from the filter paper where saturation (adsorption curve) takes place (Fig. 3b and 6). After centrifugation, the height difference between the TBJ samples was measured, showing a consolidation of at least 1 mm and the data showed scattered results. These results suggest that the permeability change during the test and is linked with the time of the samples inside the centrifuge. Accessories for the cups or buckets of the centrifuge (Nimmo & Mello, 1991; Nimmo et al., 1992; Nimmo et al., 1994; Caputo& Nimmo, 2005) like ceramic plates and water, reservoirs may be required to have better results.
With the results obtained through the ESEM, it is possible to infer a bi-modal pore size distribution (Murray & Sivakumar, 2010), meaning that within the aggregates there are fine intra-aggregate pores, while between them there are larger inter-aggregates pores. To confirm this situation is necessary to use the mercury intrusion porosimetry (MIP) technique (Romero & Simms, 2008; Murray & Sivakumar, 2010). According to Durner (1994) the difference in the pore size distribution can be the reason why the curves in figure 13 don´t fit with a simple sigmoidal curve close to the saturation point. When combining the data from the pressure plate and filter paper tests, the model of Durner (1994) obtains the best results (R2=0.99517). The difference in the pore systems can be related to the grain size distribution, weathering, and biological soil-forming processes (Durner, 1994) that lead to secondary pore systems in the large pore range in soils of any texture.
The comparison with the gravimetric water content (32 %) of two small mudflows in TBJ (13° 43´15.7”N, 89° 12´03.18”W) indicated the possibility to use the SWRC for an early warning system, using field equipment. The aim of field monitoring is to start identifying different factors that could affect the stability of TBJ slopes over time (changes in moisture content, suction, temperature, surface runoff or others) and connect them to the different mass movements observed in TBJ slopes (collapse-overturn, detachment and flows). Processes like evapotranspiration, tree roots action, saturation and temperature cycles can also aid in the deterioration of the slopes producing weathering in the surface.
According to Rahardjo & Leong (1997) it is more appropriate to use the wetting curve (adsorption) for analyzing infiltration problems and the drying curve for evaporation situations. But cracks or fissures in the field can increase the permeability estimated with the SWRC.
Field monitoring is used in slopes of weathered soils (Ng et al., 2008) to verify the design assumptions or to check the validity of analytical and numerical models. Currently, field monitoring is starting in Tierra Blanca Joven (TBJ). The use of Quickdraw tensiometers (direct measure of matric suction, Fig. 6) and TMS3 by TOMST (new version, to obtain soil moisture content and temperature) could be a good way to build a methodology for an early warning system for the slopes (Fig. 5, 14 and 15). The evolution and changes of suction and water content, experimented in different places of the MASS will help in the understanding of the relation between rain and critical soil moisture content of TBJ over time.
The practical reading range for the Quickdraw tensiometer starts from 0 kPa (saturated) to 77.5 kPa and 74 kPa for elevations (above sea level) of 600 m and 900m, respectively (Communication with Soilmoisture, 2012). Also some of the key issues to use a tensiometer (Marinho et al., 2008; Tarantino et al., 2008) include having a good contact between the soil pore water and the porous filter, avoiding the cavitation and the discrimination of a good measurement.
For the TMS device, a calibration curve is needed. Laboratory and field calibration curves are planned for the chosen monitoring places in different units of TBJ. In the preliminary results using TMS1 (January to August of 2013) (Fig. 5, 15 and 16) is possible to observe some tendency in the results in spite of different conditions in each monitored places. Soil moisture is determined by the time domain transmission (TDT) principle for the full range of soil moisture (50-200 MHz operation range in water to air, respectively) by the TMS (TOMST Measuring System) device.
TMS measures temperature at levels -10, 0 and +12 cm relative to soil surface when installed vertically; in the preliminary results for TBJ the average temperature difference between surface and inside the slope is 2.5°. Gravimetric water content of monitored TBJ units during the beginning of the dry season revealed elevated capability of retention of water and weathering processes (oxidation) that can contribute in the problematic of mass movements during the rainy season.
Both probe readings (TMS and tensiometer) are unaffected by different soil types, soil temperatures or salinity conditions.
Acknowledgments
The work has been funded in the framework of cooperation between the Oficina de Planificación del Área Metropolitana de San Salvador (OPAMSS), Czech Technical University in Prague (ČVUT), Universidad de El Salvador (UES) and Ministerio de Medio Ambiente y Recursos Naturales de El Salvador (MARN). Authors acknowledge support of Oficina de Planificación del Área Metropolitana de San Salvador (OPAMSS), TOMST, Agronomy Faculty and Civil Engineer School of Universidad de El Salvador. Special thanks go to Jaroslav Lexa, Walter Hernandez, Jan Schrofel, Jan Valenta, Martin Šanda, Tomaš Haase, Martin Šimral, Cesar Elias, Edgard Peña, Lesly Mendoza, Cecy, Andres and Daniel Chávez for assistance during this project. We are grateful to the reviewers and editors whose remarks improved the quality of the paper.
References
AGUS, S., LEONG, E. & RAHARDJO, H., 2001: Soil-water characteristic curves of Singapore residual soils.- In: Toll, D., (ed.): Unsaturated soil concepts and their application in geotechnical practice.- Kluwer Academic Publishers, Netherlands: 285-309. [ Links ]
American Section of the International Association for Testing Materials (ASTM), 1996: Standard test method for measurement of soil potential (suction) using filter paper. (D. 5298-92).- 998 pp. Annual Book of ASTM Standards Vol. 04.08, Philadelphia. [ Links ]
BAUM, R., CRONE, A., ESCOBAR, D., HARP, E., MAJOR, J., MARTINEZ, M., PULLINGER, C. & SMITH, M., 2001: Assessment of landslide hazards resulting from the February 13, 2001, El Salvador earthquake.- 22 pp. USGS, Open-File Report 01-119. [ Links ]
BICALHO, K., CORREIA, A., FERREIRA, S., FLEUREAU, J-M. & MARINHO, F., 2007: Filter paper method of soil suction measurement.- Proceedings of 13th Panamerican conference on soil mechanics and geotechnical engineering, Isla Margarita, Venezuela: 215-219. [ Links ]
BULUT, R. & LEONG, E.C., 2008: Indirect measurement of suction.- Geotechnical and Geol. Eng. 26(6): 633-644. [ Links ]
CAPUTO, M. & NIMMO, J., 2005: Quasi-steady centrifuge method for unsaturated hydraulic properties.- Water Resou. Res. 40: W11504, 1-5. [ Links ]
CHAVEZ, J., VALENTA, J., SCHRÖFEL, J., HERNANDEZ, W. & ŠEBESTA, J., 2012a: Engineering geology mapping in the southern part of the Metropolitan Area of San Salvador.- Rev. Geol. Amer. Central, 46: 161-178. [ Links ]
CHÁVEZ, J., HERNANDEZ, W. & KOPECKY, L., 2012b: Problemática y conocimiento actual de las tefras Tierra Blanca Joven en el Área Metropolitana de San Salvador, El Salvador.- Rev. Geol. Amer. Central, 47: 117-132. [ Links ]
CROPPER, S., PERFECT, E., VAN DEN BERG, E. & MAYES, M., 2011: Comparison of average and point capillary pressure–saturation functions determined by steady-state centrifugation.- Soil Sci. Soc. Am. J., 75(1): 17-25. [ Links ]
DURNER, W., 1994: Hydraulic conductivity estimation for soils with heterogeneous pore structure.- Water Resou. Res. 30: 211-223. [ Links ]
FREDLUND, D. G. & RAHARDJO, H., 1993: Soil mechanics for unsaturated soils.- 510 pp. Ed. Wiley-Intescience Publications, New York. [ Links ]
FREDLUND, D. G. & XING, A., 1994: Equations for the soil-water characteristic curve.- Can. Geotech. J. 31: 521-532. [ Links ]
FREDLUND, D. G., 1997: An introduction to unsaturated soil mechanics.- In: HOUSTON, S. & FREDLUND, D. (ed.): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng. Geotechnical Spec. Pub. 68: 1-37. [ Links ]
FREDLUND, D.G., RAHARDJO, H. & FREDLUND, M,D., 2012: Unsaturated soil mechanics in engineering practice.- 926 pp. Ed. John Wiley & Sons, New Jersey. [ Links ]
GUZMÁN, M.A., & MELARA, E., 1996: Propiedades ingenieriles del suelo del Área Metropolitana de San Salvador, El Salvador.- Rev. ASIA, 122: 14–22. [ Links ]
HERNÁNDEZ, E.W., 2004: Características geotécnicas y vulcanológicas de las tefras de Tierra Blanca Joven de Ilopango, El Salvador.- 115 pp. Universidad. Politécnica de El Salvador, San Salvador, El Salvador [M.Sc. Thesis]. [ Links ]
HOUSTON, S.L. & HOUSTON W.L., 1997: Collapsible soil engineering.- In: HOUSTON, S. & FREDLUND, D. (eds): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng. Geotechnical Spec. Pub. 68: 170-199. [ Links ]
HOUSTON, S., HOUSTON, W., ZAPATA, C. & LAWRENCE, C., 2001: Geotechnical engineering practice for collapsible soils.- In: TOLL, D . (ed.): Unsaturated soil concepts and their application in geotechnical practice.- Kluwer Academic, The Netherlands: 333-355. [ Links ]
HOYOS, L.R, LALOUI, L. & VASALLO, R., 2008: Mechanical testing in unsaturated soils.- Geotechnical and Geol. Eng. 26(6): 675-689. [ Links ]
KHANZODE, R., VANAPALLI, S. & FREDLUND, D., 2002: Measurement of soil-water characteristic curves for fine-grained soils using a small-scale centrifuge.- Can. Geotech. J. 39: 1209–1217. [ Links ]
LEXA, J., ŠEBESTA, J., CHÁVEZ, J.A., HERNANDEZ, W. & PÉCSKAY, Z., 2011: Geology and volcanic evolution in the southern part of the San Salvador Metropolitan Area.- J. Geosci. 56: 105–140. [ Links ]
LIU, X., YO, X., & XU, S., 2011: A new method to estimate the parameters of van Genuchten retention model using degree of phosphorus saturation (DPS).- African Journal ofJ. Agricultural Research,. 6(20): 4800-4806. [ Links ]
MARINHO F., TAKE, W. & TARANTINO, A., 2008: Measurement of matric suction using tensiometric and axis translation techniques.- Geotechnical and Geol. Eng. 26(6): 615-631. [ Links ]
MURRAY, E. & SIVAKUMAR, V., 2010: Unsaturated soils: a fundamental interpretation of soil behavior.- 284 pp. Ed. Wiley-Blackwell, United Kingdom. [ Links ]
NG. C., & MENZIES, B., 2007: Advanced unsaturated soil mechanic and engineering.- 654 pp. Ed. Taylor and Francis, United Kingdom. [ Links ]
NG, C., SPRINGMAN, S. & ALONSO, E., 2008: Monitoring the performance of unsaturated soil slopes.- Geotechnical and Geol. Eng. 26(6): 799-816. [ Links ]
NIMMO, J. & MELLO, K., 1991: Centrifugal techniques for measuring saturated hydraulic conductivity.- Water Resou. Res. 27(6): 1263-1269. [ Links ]
NIMMO, J., AKSTIN, K., MELLO, K., 1992: Improved apparatus for measuring hydraulic conductivity at low water content.- Soil Sci. Soc. Am. J. 56: 1758-1761. [ Links ]
NIMMO, J., STONESTROM, D., AKSTIN, K., 1994: The feasibility of recharge rate determinations using the steady-state centrifuge method.- Soil Sci. Soc. Am. J. 58: 49-56. [ Links ]
RAHARDJO, H. & LEONG, E.C., 1997: Soil water characteristic curves and flux boundary problems.- In: HOUSTON, S. & FREDLUND, D. (eds): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng., Utah: 88-112. [ Links ]
REATTO, A., MEDRADO, E., BRUAND, A., SOUZA, E. & WERNECK, J., 2008: Validity of the centrifuge method for determining the water retention properties of tropical soils.- Soil Sci. Soc. Am. J. 72: 1547-1553. [ Links ]
ROLO R., BOMER, J., HOUGHTON, B., VALLANCE, J., W., BERDOUSIS, MAVROMMATI, P., C. & MURPHY, W., 2004: Geologic and engineering characterization of Tierra Blanca pyroclastic ash deposits.- Geological. Society of. America,., Special. Paper, 375: 55-67. [ Links ]
ROMERO, E. & SIMMS, P., 2008: Microstructure investigation in unsaturated soils: s review with special attention to contribution of mercury intrusion porosimetry and environmental scanning electron microscopy, indirect measurement of suction.- Geotechnical and Geol. Eng. 26(6): 705-727. [ Links ]
SEKI, K., 2007: SWRC fit - a nonlinear fitting program with a water retention curve for soils having unimodal and bimodal pore structure.- Hydrol. Earth Syst. Sci. Discuss. 4: 407-437. [ Links ]
SILLERS, W., S., FREDLUND, D., G. & ZAKERZADEH, N., 2001: Mathematical attributes of some soil-water characteristic curve models.- In: TOLL, D . (ed.): Unsaturated soil concepts and their application in geotechnical practice.- Kluwer Academic, The Netherlands: 243-283. [ Links ]
TARANTINO, A., RIDLEY, A. & TOLL, D., 2008: Field measurement of suction, water content, and water permeability.- Geotechnical and Geol. Eng. 26(6): 751-782. [ Links ]
VANAPALLI, S., NICOTERA, M. & SHARMA, S., 2008: Axis translation and negative water column techniques for suction control.- Geotechnical and Geol. Eng. 26(6): 645-660. [ Links ]
American Section of the International Association for Testing Materials (ASTM), 1996: Standard test method for measurement of soil potential (suction) using filter paper. (D. 5298-92).- 998 pp. Annual Book of ASTM Standards Vol. 04.08, Philadelphia. [ Links ]
BAUM, R., CRONE, A., ESCOBAR, D., HARP, E., MAJOR, J., MARTINEZ, M., PULLINGER, C. & SMITH, M., 2001: Assessment of landslide hazards resulting from the February 13, 2001, El Salvador earthquake.- 22 pp. USGS, Open-File Report 01-119. [ Links ]
BICALHO, K., CORREIA, A., FERREIRA, S., FLEUREAU, J-M. & MARINHO, F., 2007: Filter paper method of soil suction measurement.- Proceedings of 13th Panamerican conference on soil mechanics and geotechnical engineering, Isla Margarita, Venezuela: 215-219. [ Links ]
BULUT, R. & LEONG, E.C., 2008: Indirect measurement of suction.- Geotechnical and Geol. Eng. 26(6): 633-644. [ Links ]
CAPUTO, M. & NIMMO, J., 2005: Quasi-steady centrifuge method for unsaturated hydraulic properties.- Water Resou. Res. 40: W11504, 1-5. [ Links ]
CHAVEZ, J., VALENTA, J., SCHRÖFEL, J., HERNANDEZ, W. & ŠEBESTA, J., 2012a: Engineering geology mapping in the southern part of the Metropolitan Area of San Salvador.- Rev. Geol. Amer. Central, 46: 161-178. [ Links ]
CHÁVEZ, J., HERNANDEZ, W. & KOPECKY, L., 2012b: Problemática y conocimiento actual de las tefras Tierra Blanca Joven en el Área Metropolitana de San Salvador, El Salvador.- Rev. Geol. Amer. Central, 47: 117-132. [ Links ]
CROPPER, S., PERFECT, E., VAN DEN BERG, E. & MAYES, M., 2011: Comparison of average and point capillary pressure–saturation functions determined by steady-state centrifugation.- Soil Sci. Soc. Am. J., 75(1): 17-25. [ Links ]
DURNER, W., 1994: Hydraulic conductivity estimation for soils with heterogeneous pore structure.- Water Resou. Res. 30: 211-223. [ Links ]
FREDLUND, D. G. & RAHARDJO, H., 1993: Soil mechanics for unsaturated soils.- 510 pp. Ed. Wiley-Intescience Publications, New York. [ Links ]
FREDLUND, D. G. & XING, A., 1994: Equations for the soil-water characteristic curve.- Can. Geotech. J. 31: 521-532. [ Links ]
FREDLUND, D. G., 1997: An introduction to unsaturated soil mechanics.- In: HOUSTON, S. & FREDLUND, D. (ed.): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng. Geotechnical Spec. Pub. 68: 1-37. [ Links ]
FREDLUND, D.G., RAHARDJO, H. & FREDLUND, M,D., 2012: Unsaturated soil mechanics in engineering practice.- 926 pp. Ed. John Wiley & Sons, New Jersey. [ Links ]
GUZMÁN, M.A., & MELARA, E., 1996: Propiedades ingenieriles del suelo del Área Metropolitana de San Salvador, El Salvador.- Rev. ASIA, 122: 14–22. [ Links ]
HERNÁNDEZ, E.W., 2004: Características geotécnicas y vulcanológicas de las tefras de Tierra Blanca Joven de Ilopango, El Salvador.- 115 pp. Universidad. Politécnica de El Salvador, San Salvador, El Salvador [M.Sc. Thesis]. [ Links ]
HOUSTON, S.L. & HOUSTON W.L., 1997: Collapsible soil engineering.- In: HOUSTON, S. & FREDLUND, D. (eds): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng. Geotechnical Spec. Pub. 68: 170-199. [ Links ]
HOUSTON, S., HOUSTON, W., ZAPATA, C. & LAWRENCE, C., 2001: Geotechnical engineering practice for collapsible soils.- In: TOLL, D . (ed.): Unsaturated soil concepts and their application in geotechnical practice.- Kluwer Academic, The Netherlands: 333-355. [ Links ]
HOYOS, L.R, LALOUI, L. & VASALLO, R., 2008: Mechanical testing in unsaturated soils.- Geotechnical and Geol. Eng. 26(6): 675-689. [ Links ]
KHANZODE, R., VANAPALLI, S. & FREDLUND, D., 2002: Measurement of soil-water characteristic curves for fine-grained soils using a small-scale centrifuge.- Can. Geotech. J. 39: 1209–1217. [ Links ]
LEXA, J., ŠEBESTA, J., CHÁVEZ, J.A., HERNANDEZ, W. & PÉCSKAY, Z., 2011: Geology and volcanic evolution in the southern part of the San Salvador Metropolitan Area.- J. Geosci. 56: 105–140. [ Links ]
LIU, X., YO, X., & XU, S., 2011: A new method to estimate the parameters of van Genuchten retention model using degree of phosphorus saturation (DPS).- African Journal ofJ. Agricultural Research,. 6(20): 4800-4806. [ Links ]
MARINHO F., TAKE, W. & TARANTINO, A., 2008: Measurement of matric suction using tensiometric and axis translation techniques.- Geotechnical and Geol. Eng. 26(6): 615-631. [ Links ]
MURRAY, E. & SIVAKUMAR, V., 2010: Unsaturated soils: a fundamental interpretation of soil behavior.- 284 pp. Ed. Wiley-Blackwell, United Kingdom. [ Links ]
NG. C., & MENZIES, B., 2007: Advanced unsaturated soil mechanic and engineering.- 654 pp. Ed. Taylor and Francis, United Kingdom. [ Links ]
NG, C., SPRINGMAN, S. & ALONSO, E., 2008: Monitoring the performance of unsaturated soil slopes.- Geotechnical and Geol. Eng. 26(6): 799-816. [ Links ]
NIMMO, J. & MELLO, K., 1991: Centrifugal techniques for measuring saturated hydraulic conductivity.- Water Resou. Res. 27(6): 1263-1269. [ Links ]
NIMMO, J., AKSTIN, K., MELLO, K., 1992: Improved apparatus for measuring hydraulic conductivity at low water content.- Soil Sci. Soc. Am. J. 56: 1758-1761. [ Links ]
NIMMO, J., STONESTROM, D., AKSTIN, K., 1994: The feasibility of recharge rate determinations using the steady-state centrifuge method.- Soil Sci. Soc. Am. J. 58: 49-56. [ Links ]
RAHARDJO, H. & LEONG, E.C., 1997: Soil water characteristic curves and flux boundary problems.- In: HOUSTON, S. & FREDLUND, D. (eds): Unsaturated soil engineering practice.- Amer. Soc. Civil Eng., Utah: 88-112. [ Links ]
REATTO, A., MEDRADO, E., BRUAND, A., SOUZA, E. & WERNECK, J., 2008: Validity of the centrifuge method for determining the water retention properties of tropical soils.- Soil Sci. Soc. Am. J. 72: 1547-1553. [ Links ]
ROLO R., BOMER, J., HOUGHTON, B., VALLANCE, J., W., BERDOUSIS, MAVROMMATI, P., C. & MURPHY, W., 2004: Geologic and engineering characterization of Tierra Blanca pyroclastic ash deposits.- Geological. Society of. America,., Special. Paper, 375: 55-67. [ Links ]
ROMERO, E. & SIMMS, P., 2008: Microstructure investigation in unsaturated soils: s review with special attention to contribution of mercury intrusion porosimetry and environmental scanning electron microscopy, indirect measurement of suction.- Geotechnical and Geol. Eng. 26(6): 705-727. [ Links ]
SEKI, K., 2007: SWRC fit - a nonlinear fitting program with a water retention curve for soils having unimodal and bimodal pore structure.- Hydrol. Earth Syst. Sci. Discuss. 4: 407-437. [ Links ]
SILLERS, W., S., FREDLUND, D., G. & ZAKERZADEH, N., 2001: Mathematical attributes of some soil-water characteristic curve models.- In: TOLL, D . (ed.): Unsaturated soil concepts and their application in geotechnical practice.- Kluwer Academic, The Netherlands: 243-283. [ Links ]
TARANTINO, A., RIDLEY, A. & TOLL, D., 2008: Field measurement of suction, water content, and water permeability.- Geotechnical and Geol. Eng. 26(6): 751-782. [ Links ]
VANAPALLI, S., NICOTERA, M. & SHARMA, S., 2008: Axis translation and negative water column techniques for suction control.- Geotechnical and Geol. Eng. 26(6): 645-660. [ Links ]
*Correspondencia a:
José A. Chávez. Oficina de Planificación del Área Metropolitana de San Salvador (OPAMSS), San Salvador, El Salvador. Czech Technical University in Prague, Faculty of Civil Engineering, Department of Geotechnics, Czech Republic. Correo electrónico jose.alexander.chavez.hernandez@fsv.cvut.cz
Reynaldo López. Universidad de El Salvador, Facultad de Ciencias Agronómicas, San Salvador, El Salvador.
Lubomir Kopecky. Czech Technical University in Prague, Faculty of Civil Engineering, Department of Mechanics, Czech Republic.
José Landaverde. Universidad de El Salvador, Escuela de Civil, San Salvador, El Salvador.
1. Oficina de Planificación del Área Metropolitana de San Salvador (OPAMSS), San Salvador, El Salvador
2. Czech Technical University in Prague, Faculty of Civil Engineering, Department of Geotechnics, Czech Republic
3. Universidad de El Salvador, Facultad de Ciencias Agronómicas, San Salvador, El Salvador
4. Czech Technical University in Prague, Faculty of Civil Engineering, Department of Mechanics, Czech Republic
5. Universidad de El Salvador, Escuela de Civil, San Salvador, El Salvador
*Corresponding author: jose.alexander.chavez.hernandez@fsv.cvut.cz
Recibido: 02/04/2013 ; aceptado: 26/11/2013















