Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Geológica de América Central
On-line version ISSN 0256-7024Print version ISSN 0256-7024
Rev. Geol. Amér. Central n.47 San Pedro de Montes de Oca Dec. 2012
Análisis de estabilidad de taludes considerando La incertidumbre de los datos: caso comunidad de Mansiones de Montes de Oca, San José, Costa Rica
Slope stability considering uncertanty of data: study case of Mansiones, Montes de Oca, san jose, Costa Rica
Slope stability considering uncertanty of data: study case of Mansiones, Montes de Oca, san jose, Costa Rica
*Dirección para correspondencia:
Abstract
A deterministic model of slope stability has been evaluated with fuzzy input parameters by the method of vertices, dividing the fuzzy numbers into groups of intervals (cuts or α levels). Later on, in the model, the fuzzy numbers have been replaced by the intervals, reducing it to a number of analyses of intervals using only conventional mathematics. The stability of the slope is measured by comparing the fuzzy set, representing the state of stability, with four predefined stability states, using a technique of grouping. The result of this process indicates that under static conditions, the slope of the community of Mansiones is certainly stable and under pseudo-static conditions (horizontal acceleration of 20% g), the slope could have an imminent failure.
Keywords: slope stability, uncertainty, geotechnics, landslide, hazard.
Resumen
Se ha evaluado un modelo determinístico de estabilidad de taludes con parámetros de entrada difusos, mediante el método de los vértices, dividiendo los números difusos en grupos de intervalos (cortes o niveles α), posteriormente, en el modelo se han remplazado los números difusos por los intervalos, reduciendo el método a una serie de análisis de intervalos que usan solamente matemática convencional. La estabilidad del talud se ha medido comparando el conjunto difuso que representa el estado de estabilidad, con cuatro estados de estabilidad predefinidos, mediante una técnica de agrupamiento. El resultado de este proceso indica que en condiciones estáticas, el talud de la comunidad de Mansiones es indudablemente estable y que en condiciones pseudoestaticas (aceleración horizontal de 20%g), el talud presentaría una falla inminente.
Palabras clave: estabilidad de taludes, incertidumbre, geotecnia, deslizamiento, amenaza.
Introducción
Los proyectos geotécnicos siempre tienen que lidiar con la incertidumbre de los datos, la cual es considerada como inherente al geotecnista en el proceso de diseño y es compensada con la aceptación de un cierto riesgo, es decir, utilizando un factor de seguridad. Según Casti (1990) existen dos tipos de incertidumbre: (1) la ignorancia, que incluye los errores de medición, la indecisión sobre la forma matemática del modelo y la confusión sobre el nivel de abstracción apropiado; y (2) la variabilidad, que incluye la estocasticidad, la variación espacial y la heterogeneidad individual.
La Teoría de Probabilidades ha sido utilizada como una excelente herramienta para manejar la incertidumbre, pero los requerimientos de abordar los dos tipos de incertidumbre de una manera rigurosa, la tornan poco práctica para ser utilizada en los análisis geotécnicos rutinarios (Juang et al., 1998). En el caso de los estudios de estabilidad de laderas y taludes lo recomendable sería incorporar técnicas que consideren la incertidumbre, que tengan un enfoque determinístico más que probabilístico y que sean de fácil uso.
Juang et al., (1998) echan mano del argumento de Vick (1992) que establece que las incertidumbres deben describirse lo mejor posible a partir de opiniones, experiencias e información disponible; y expresan la incertidumbre de los parámetros como un intervalo, estimando los límites inferior y superior del mismo. Estos autores expresan la incertidumbre como un conjunto difuso (fuzzy set), pues tienen razón para creer que no todos los valores en el intervalo cuentan con el mismo grado de respaldo. Un conjunto difuso es definido por Zadeh (1965) como un conjunto de valores pares [x, μ(x)], donde el número x pertenece a un conjunto con un grado de asociación de μ(x), que varía de 0 a 1.
La Teoría de Probabilidades ha sido utilizada como una excelente herramienta para manejar la incertidumbre, pero los requerimientos de abordar los dos tipos de incertidumbre de una manera rigurosa, la tornan poco práctica para ser utilizada en los análisis geotécnicos rutinarios (Juang et al., 1998). En el caso de los estudios de estabilidad de laderas y taludes lo recomendable sería incorporar técnicas que consideren la incertidumbre, que tengan un enfoque determinístico más que probabilístico y que sean de fácil uso.
Juang et al., (1998) echan mano del argumento de Vick (1992) que establece que las incertidumbres deben describirse lo mejor posible a partir de opiniones, experiencias e información disponible; y expresan la incertidumbre de los parámetros como un intervalo, estimando los límites inferior y superior del mismo. Estos autores expresan la incertidumbre como un conjunto difuso (fuzzy set), pues tienen razón para creer que no todos los valores en el intervalo cuentan con el mismo grado de respaldo. Un conjunto difuso es definido por Zadeh (1965) como un conjunto de valores pares [x, μ(x)], donde el número x pertenece a un conjunto con un grado de asociación de μ(x), que varía de 0 a 1.
En los modelos geotécnicos rutinarios es suficiente usar un subconjunto de un conjunto difuso, lo que se conoce como un número difuso (fuzzy number) (Juang & Elton, 1996), el cual presenta una distribución convexa y tiene al menos un valor con un grado de asociación de 1 (Juang et al., 1998). La forma de la distribución, por su simplicidad de formulación y facilidad de cálculo, es triangular, la cual está definida por tres valores: un mínimo, un máximo y la moda (Juang et al., (1998). La moda tiene el grado más alto de asociación (100%) a la hora de representar la incertidumbre de un parámetro, conforme el valor del parámetro se aparta de la moda, el grado de asociación (confiabilidad) decrece y cuando su valor alcanza el mínimo (o el máximo) el grado de asociación se reduce a cero (Juang et al., 1998).
En la práctica rutinaria de la Geotecnia, contar con una base de datos estadísticamente significativa es muy difícil (muy costosa de obtener), por lo que es suficiente el uso de números difusos para representar la incertidumbre, es decir, la evaluación de la incertidumbre por medio del juicio profesional basado en la información disponible (Juang et al., 1998).
La mayoría de los análisis geotécnicos se realiza con modelos determinísticos, si los parámetros de entrada de estos modelos son inciertos y se adoptan números difusos para sus valores, la salida será un número difuso (o números difusos), es decir, la incertidumbre es propagada a través del proceso de solución (Juang et al., 1998).
Uno de los enfoques disponibles más recomendados para evaluar un modelo determinístico con parámetros de entrada difusos, es el método de los vértices, el cual se basa en el concepto de los cortes α de números difusos e involucra un análisis de intervalos (Juang et al., 1998). La idea básica de este método es dividir un número difuso en un grupo de intervalos (cortes o niveles α) (Fig. 1), donde α es cualquier valor en el rango de 0 a 1, escogido en función del grado de confiabilidad μ(X), posteriormente, en el modelo se remplazan los números difusos por los intervalos, reduciendo el método a una serie de análisis de intervalos que usan solamente matemática convencional (Juang et al., 1998).
En la práctica rutinaria de la Geotecnia, contar con una base de datos estadísticamente significativa es muy difícil (muy costosa de obtener), por lo que es suficiente el uso de números difusos para representar la incertidumbre, es decir, la evaluación de la incertidumbre por medio del juicio profesional basado en la información disponible (Juang et al., 1998).
La mayoría de los análisis geotécnicos se realiza con modelos determinísticos, si los parámetros de entrada de estos modelos son inciertos y se adoptan números difusos para sus valores, la salida será un número difuso (o números difusos), es decir, la incertidumbre es propagada a través del proceso de solución (Juang et al., 1998).
Uno de los enfoques disponibles más recomendados para evaluar un modelo determinístico con parámetros de entrada difusos, es el método de los vértices, el cual se basa en el concepto de los cortes α de números difusos e involucra un análisis de intervalos (Juang et al., 1998). La idea básica de este método es dividir un número difuso en un grupo de intervalos (cortes o niveles α) (Fig. 1), donde α es cualquier valor en el rango de 0 a 1, escogido en función del grado de confiabilidad μ(X), posteriormente, en el modelo se remplazan los números difusos por los intervalos, reduciendo el método a una serie de análisis de intervalos que usan solamente matemática convencional (Juang et al., 1998).
En un análisis de estabilidad de laderas se pueden considerar como parámetro inciertos a la profundidad del nivel freático, los parámetros de resistencia al corte (c y Φ) y el peso unitario del material, los cuales pueden representarse como conjuntos difusos y procesarse con el método descrito anteriormente. En el caso del estudio que se aborda más adelante, se han considerado como parámetros inciertos a los parámetros de resistencia al corte y el peso unitario del suelo, la profundidad del nivel freático no ha sido considerada, pues no se ha identificado un nivel freático en el espesor de suelos estudiado.
La metodología seguida se ilustra a continuación, de acuerdo con lo propuesto por Juang et al. (1998):
En cada nivel α seleccionado se obtiene un intervalo para cada parámetro incierto (c, Φ y γ).
Como cada intervalo tiene dos puntos finales, se obtiene un total de 6 vértices. Para cada vértice los parámetros (c, Φ y γ) son valores fijos, al igual que otros parámetros usados en el análisis de estabilidad, es decir se debe realizar un total de 8 análisis para cada nivel α, obteniéndose de cada uno un factor de seguridad (FS). El mínimo y el máximo de los 8 valores de FS definen el intervalo resultante de FS.
Este proceso se repite para los niveles α seleccionados, obteniéndose un conjunto de intervalos de FS. Estos intervalos de FS y los correspondientes niveles α definen un conjunto difuso de FS, el cual proporciona más información que un solo valor de FS. El conjunto difuso resultante es esencialmente una “quasi” distribución del FS y no necesariamente una distribución triangular.
De acuerdo con Juang et al. (1998) la estabilidad de un talud se puede clasificar en cuatro estados: (1) la falla es inminente (f); (2) la falla es probable (fp); (3) el talud es probablemente seguro (ps) y (4) el talud es indudablemente seguro (s). Se han adoptado conjuntos difusos para representar los cuatro estados de estabilidad en condiciones estáticas y pseudoestáticas, según la experiencia profesional de los autores de este trabajo (Fig. 2).
La metodología seguida se ilustra a continuación, de acuerdo con lo propuesto por Juang et al. (1998):
En cada nivel α seleccionado se obtiene un intervalo para cada parámetro incierto (c, Φ y γ).
Como cada intervalo tiene dos puntos finales, se obtiene un total de 6 vértices. Para cada vértice los parámetros (c, Φ y γ) son valores fijos, al igual que otros parámetros usados en el análisis de estabilidad, es decir se debe realizar un total de 8 análisis para cada nivel α, obteniéndose de cada uno un factor de seguridad (FS). El mínimo y el máximo de los 8 valores de FS definen el intervalo resultante de FS.
Este proceso se repite para los niveles α seleccionados, obteniéndose un conjunto de intervalos de FS. Estos intervalos de FS y los correspondientes niveles α definen un conjunto difuso de FS, el cual proporciona más información que un solo valor de FS. El conjunto difuso resultante es esencialmente una “quasi” distribución del FS y no necesariamente una distribución triangular.
De acuerdo con Juang et al. (1998) la estabilidad de un talud se puede clasificar en cuatro estados: (1) la falla es inminente (f); (2) la falla es probable (fp); (3) el talud es probablemente seguro (ps) y (4) el talud es indudablemente seguro (s). Se han adoptado conjuntos difusos para representar los cuatro estados de estabilidad en condiciones estáticas y pseudoestáticas, según la experiencia profesional de los autores de este trabajo (Fig. 2).
La estabilidad de un talud existente se puede medir comparando el conjunto difuso que representa el estado actual de estabilidad (obtenido a través de análisis presentado arriba), con los cuatro estados de estabilidad definidos en la figura 2 (estados de estabilidad pre-definidos), mediante la técnica de agrupamiento descrita a continuación (Juang et al. 1998):
1- Dividir el rango entre el límite inferior y la moda del conjunto difuso de FS resultante en N intervalos, esto da como resultado N+1 valores de FS. Se debe repetir este procedimiento para el rango entre la moda y el límite superior, obteniéndose entonces un total de 2N+1 valores de FS.
2- La “credibilidad” de representar el conjunto difuso de FS resultante con cada uno de los cuatro estados de estabilidad pre-definidos, se determina con una puntuación definida por:
1- Dividir el rango entre el límite inferior y la moda del conjunto difuso de FS resultante en N intervalos, esto da como resultado N+1 valores de FS. Se debe repetir este procedimiento para el rango entre la moda y el límite superior, obteniéndose entonces un total de 2N+1 valores de FS.
2- La “credibilidad” de representar el conjunto difuso de FS resultante con cada uno de los cuatro estados de estabilidad pre-definidos, se determina con una puntuación definida por:
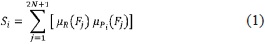
donde:
Si: es la puntuación de credibilidad del estado de estabilidad i (i = 1, 4),
Fj: es uno de los valores de FS (j = (1, 2N+1) definidos en el paso (1),
μR (Fj): es el grado de asociación del valor de Fj en el conjunto difuso FS resultante,
μPi(Fj): es el grado de asociación del valor de Fj en el conjunto difuso que representa el estado de estabilidad predefinido.
3- El paso (2) se repite para los cuatro estados de estabilidad, para luego determinar la credibilidad relativa de cada estado como sigue:
Fj: es uno de los valores de FS (j = (1, 2N+1) definidos en el paso (1),
μR (Fj): es el grado de asociación del valor de Fj en el conjunto difuso FS resultante,
μPi(Fj): es el grado de asociación del valor de Fj en el conjunto difuso que representa el estado de estabilidad predefinido.
3- El paso (2) se repite para los cuatro estados de estabilidad, para luego determinar la credibilidad relativa de cada estado como sigue:

donde:
m: es el número del estado de estabilidad (m=4 en este caso)
Wi : es la credibilidad relativa de representar el conjunto difuso FS resultante por medio del estado de estabilidad i.
4- Los valores de Wi obtenidos se deben comparar, el estado de estabilidad con el mayor valor de Wi es el que mejor representa el estado de estabilidad actual del talud bajo consideración.
Wi : es la credibilidad relativa de representar el conjunto difuso FS resultante por medio del estado de estabilidad i.
4- Los valores de Wi obtenidos se deben comparar, el estado de estabilidad con el mayor valor de Wi es el que mejor representa el estado de estabilidad actual del talud bajo consideración.
Caso de estudio: análisis de estabilidad del talud de la comunidad de mansiones de Montes de Oca
El caso de estudio pertenece al distrito de San Rafael, cantón de Montes de Oca, provincia de San José y se localiza en la hoja topográfica Moravia (escala 1:10 000 del IGN), dentro de la cuenca hidrográfica del río Torres. La comunidad de Mansiones de San Rafael de Montes de Oca (Fig. 3) se ubica entre las coordenadas Lambert Costa Rica Norte 214 250 – 214500 N y 536 250 – 536 500 E.
Marco geológico
En el área de estudio se encuentran diversos afloramientos de una unidad de cenizas correlacionable con la unidad de Cenizas Mansiones de Camacho et al. (2004), la cual se presenta en cortes cortes de carretera, así como en el escarpes que se ubica detrás de las casas que forman parte de la comunidad de Mansiones. De forma concordante con las descripciones de Camacho et al. (2004), se observaron 2 capas de ceniza dentro de la unidad de Cenizas Mansiones:
Capa superior: ceniza no consolidada de color gris, de apenas 10 cm de espesor, que no presenta evidencias de meteorización, la cual parece corresponder con depósitos de la erupción del Volcán Irazú de 1963-1965 (Figura 4).
Capa inferior: de color café amarillento a rojiza, presenta un grado de meteorización y consolidación notablemente mayor al de la capa superior (Figura 5).
La comunidad de Mansiones se ha desarrollado sobre un deslizamiento que en algún momento tuvo actividad, el cual actualmente no presenta evidencias de actividad reciente. Este deslizamiento muestra pendientes fuertes en la parte del escarpe o corona y topografía “hummocky” (ondulada) en la parte del depósito, con un lóbulo frontal que ha provocado un leve desvío del curso del río Torres.
Capa superior: ceniza no consolidada de color gris, de apenas 10 cm de espesor, que no presenta evidencias de meteorización, la cual parece corresponder con depósitos de la erupción del Volcán Irazú de 1963-1965 (Figura 4).
Capa inferior: de color café amarillento a rojiza, presenta un grado de meteorización y consolidación notablemente mayor al de la capa superior (Figura 5).
La comunidad de Mansiones se ha desarrollado sobre un deslizamiento que en algún momento tuvo actividad, el cual actualmente no presenta evidencias de actividad reciente. Este deslizamiento muestra pendientes fuertes en la parte del escarpe o corona y topografía “hummocky” (ondulada) en la parte del depósito, con un lóbulo frontal que ha provocado un leve desvío del curso del río Torres.
Propiedades físicas y mecánicas de los suelos volcánicos
El sitio de estudio está comprendido dentro de una única Unidad Geotécnica, la cual está compuesta por los depósitos volcánicos (cenizas), provenientes del Volcán Irazú y que, en términos generales, se describen como limos con plasticidad variable y arenas limosas de plasticidad alta.
A partir de ocho muestreos y nueve ensayos de campo, con sus respectivos ensayos de laboratorio, se determinó que los suelos volcánicos de Mansiones corresponden con limos elásticos arenosos de plasticidad alta (MH), arenas limosas de plasticidad alta (SM), limos arenosos de plasticidad intermedia (MI), limos elásticos arenosos de plasticidad muy alta (MV), limos elásticos de plasticidad muy alta (MV) y limos elásticos arenosos de plasticidad extremadamente alta (ME). Un resumen de los resultados de los ensayos se presenta en el cuadro 1.
Para el análisis de estabilidad de laderas se han considerado como parámetros inciertos los parámetros de resistencia al corte (c y Φ) y el peso unitario del material, los cuales se ha representado como números difusos en la figura 6.
A partir de ocho muestreos y nueve ensayos de campo, con sus respectivos ensayos de laboratorio, se determinó que los suelos volcánicos de Mansiones corresponden con limos elásticos arenosos de plasticidad alta (MH), arenas limosas de plasticidad alta (SM), limos arenosos de plasticidad intermedia (MI), limos elásticos arenosos de plasticidad muy alta (MV), limos elásticos de plasticidad muy alta (MV) y limos elásticos arenosos de plasticidad extremadamente alta (ME). Un resumen de los resultados de los ensayos se presenta en el cuadro 1.
Para el análisis de estabilidad de laderas se han considerado como parámetros inciertos los parámetros de resistencia al corte (c y Φ) y el peso unitario del material, los cuales se ha representado como números difusos en la figura 6.
Los niveles α seleccionados son 0,25; 0,5; 0,75 y 1,0. Los intervalos de cada parámetro incierto para los niveles α seleccionados se presentan en el cuadro 2.
Análisis de la estabilidad del talud de la comunidad de Mansiones
Para cada nivel α se realizaron los 8 análisis de estabilidad requeridos (Fig. 7), con sus correspondientes resultados en términos del factor de seguridad, el cual se ha calculado utilizando el método de Jambu y el programa PC-SLOPE. En cada nivel α se ha establecido el intervalo resultante considerando el factor de seguridad mínimo y máximo de los 8 resultados. Este proceso se ha aplicado bajo condiciones estáticas y pseudoestáticas, para así definir los conjuntos difusos o “quasi” distribuciones del FS (Fig. 8 y cuadro 3).
La estabilidad del talud se ha medido comparando el conjunto difuso que representa el estado actual de estabilidad, con los cuatro estados de estabilidad definidos en la figura 2 (estados de estabilidad pre-definidos), mediante la técnica de agrupamiento de Juang et al. (1998).
El rango entre el límite inferior y el FS de nivel α=1.0, de los dos conjuntos difusos resultantes, se ha dividido en 5 intervalos, lo cual arroja 6 valores de FS. El procedimiento se ha repetido entre el FS de nivel α=1.0 y el límite superior, con lo que se ha obtenido un total de 11 valores de FS y para cada uno de estos valores se ha establecido su grado de asociación en el conjunto difuso resultante y en los conjuntos difusos para representar los cuatro estados de estabilidad (Cuadros 4 y 5). En los mismos cuadros se presentan los resultados de los cálculos para definir la credibilidad de cada estado de estabilidad, así como la credibilidad relativa de los mismos estados.
ConclusionesEl rango entre el límite inferior y el FS de nivel α=1.0, de los dos conjuntos difusos resultantes, se ha dividido en 5 intervalos, lo cual arroja 6 valores de FS. El procedimiento se ha repetido entre el FS de nivel α=1.0 y el límite superior, con lo que se ha obtenido un total de 11 valores de FS y para cada uno de estos valores se ha establecido su grado de asociación en el conjunto difuso resultante y en los conjuntos difusos para representar los cuatro estados de estabilidad (Cuadros 4 y 5). En los mismos cuadros se presentan los resultados de los cálculos para definir la credibilidad de cada estado de estabilidad, así como la credibilidad relativa de los mismos estados.
De acuerdo con la composición de los depósitos volcánicos, que se localizan en la comunidad de Mansiones y sus alrededores, estos se pueden describir como limos con plasticidad variable y arenas limosas de plasticidad alta.
La representación con números difusos de los parámetros inciertos (c, Φ y γ) ha permitido la definición de conjuntos difusos o “quasi” distribuciones del factor de seguridad de la ladera, en condiciones estáticas y pseudoestáticas.
La comparación de los conjuntos difusos que representan el estado de estabilidad con cuatro estados de estabilidad pre-definidos, mediante la técnica de agrupamiento de Juang et al. (1998), arroja los siguientes resultados:
En condiciones estáticas, el talud de la comunidad de Mansiones es indudablemente estable.
En condiciones pseudoestáticas (aceleración horizontal de 20%g), el talud de la comunidad de Mansiones presentaría una falla inminente.
La conclusión anterior conduce a establecer que se requiere el refuerzo del talud, dado el alto riesgo que representa el impacto de un deslizamiento sobre la comunidad de Mansiones.
La comparación de los conjuntos difusos que representan el estado de estabilidad con cuatro estados de estabilidad pre-definidos, mediante la técnica de agrupamiento de Juang et al. (1998), arroja los siguientes resultados:
En condiciones estáticas, el talud de la comunidad de Mansiones es indudablemente estable.
En condiciones pseudoestáticas (aceleración horizontal de 20%g), el talud de la comunidad de Mansiones presentaría una falla inminente.
La conclusión anterior conduce a establecer que se requiere el refuerzo del talud, dado el alto riesgo que representa el impacto de un deslizamiento sobre la comunidad de Mansiones.
Referencias
CAMACHO, D., CHAVES, J. & MURILLO, D., 2004: Diagnóstico de la susceptibilidad al deslizamiento e inundación, análisis del contexto sísmico y reconocimiento de peligros volcánicos para el cantón de Montes de Oca.- 106 págs. Univ. Costa Rica, San José (Sem. Grad). [ Links ]
CASTI, J.L., 1990: Searching for Certainty.- 407 págs. William Morrow, New York. [ Links ]
JUANG, C.H., ELTON, D.J., 1996: A practical approach to uncertainty modeling in geotechnical engineering.- 14 págs. Uncertainty in The Geologic Environment: From Theory to Practice, ASCE Geotech. Spec. Pub. New York. [ Links ]
JUANG, C.H., YUIN-YAO JHI & DER-HER LEE, 1998: Stability analysis of existing slopes considering uncertainty.- Engineering Geol. 49: 111-122. [ Links ]
VICK, S.G., 1992: Risk in geotechnical practice.- Geotech. News, 10(1): 55-57. [ Links ]
ZADEH, L.A., 1965: Fuzzy sets.- Information and Control, 8: 338-353. [ Links ]
*Correspondencia:
Rolando Mora: Escuela Centroamericana de Geología, Apartado: 2-14-2060UCR Universidad de Costa Rica, San José, Costa Rica. Autor para contacto: rmorach@gmail.com
Raquel Granados: Escuela Centroamericana de Geología, Apartado: 2-14-2060UCR Universidad de Costa Rica, San José, Costa Rica
1 Escuela Centroamericana de Geología, Apartado: 2-14-2060UCR Universidad de Costa Rica, San José, Costa Rica
2 Autor para contacto: rmorach@gmail.com
(Recibido: 19/10/2012 ; aceptado: 17/12/2012)














