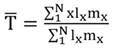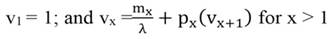Introduction
Vaquita, Phocoena sinus (Norris & McFarland, 1958), endemic to the Northern Gulf of California (henceforth, UG) is the most endangered marine mammal in the world (Rojas-Bracho, Reeves, & Jaramillo-Legorreta, 2006; Jaramillo-Legorreta et al., 2019). It is listed as Critically Endangered by the International Union for Conservation of Nature, included in the US Endangered Species Act and in Mexico´s list of endangered species (Rojas-Bracho & Reeves, 2013).
Major efforts have been made to assess abundance and status of vaquita (Thomas et al., 2017). The population has decreased from ~1 000 individuals 40 years ago (Taylor & Gerrodette, 1993) to only 400-500 in the 1990s (Gerrodette, Barlow, Taylor, & Silber, 1994). Conservation policies and the expenditure of considerable economic resources (US $ 60 million up to 2017) (Montalvo & Ortuño, 2017) have not reversed the vaquita decline. Efforts to deter bycatch mortality include buy-out of permits and boats, alternative economic activities, compensations to reduce fishing, and innovations in fishing gear (Avila-Forcada, Martínez-Cruz, & Muñoz-Piña, 2012; García-Gómez & Chávez-Nungaray, 2017). Despite efforts, by 2018 the population dropped to < 20 (Jaramillo-Legorreta et al., 2019) raising the question of whether vaquita can recover. Encouraging results have been reported recently: mothers have been sighted with calves (Taylor et al., 2019). For descriptions of the historical impact of bycatch from gillnet fishing, particularly poaching of totoaba, the readers are referred to D’Agrosa, Lennert-Cody and Vidal (2000) and the many references in Cisneros-Mata (2020).
To investigate the viability of vaquita we used stochastic Leslie matrix models (SLMMs), conducted a population viability analysis (PVA) (Boyce, 1992; Lamberson, Noon, Voss, & McKelvey, 1994) and computed probabilities of its persistence through time. SLMMs simulate effects of random survival and birth per age class (Caswell, 1989). Important considerations for PVAs are availability of data and model solutions; analytical solutions and simulations can be combined in some instances (Moloney, Cooper, Ryan, & Siegfried, 1994; Cisneros-Mata, Botsford, & Quinn, 1997). Often there is scarce life-cycle information to construct numerical models. Here we use knowledge on vaquita and related species to address relative effects of demographic and anthropogenic factors under several scenarios.
Materials and methods
Study area: Vaquita inhabits a small portion of the UG off San Felipe, Baja California, around Rocas Consag and of El Golfo de Santa Clara, Sonora at depths of 30 to > 100 meters (Jaramillo-Legorreta et al., 2019) (Fig. 1; after Rojas-Bracho et al., 2006). Salinity in the Colorado River (CR) delta varies from 38 to 35.4 PSU with prevailing anti-estuary conditions (Lavín & Sánchez, 1999).
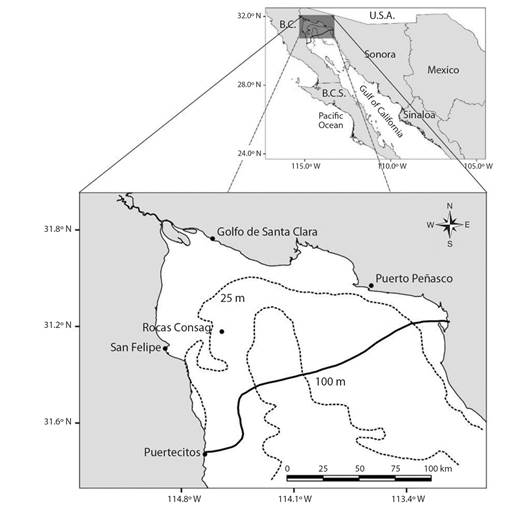
Fig. 1 Distribution range of Phocoena sinus. The continuous line is the Southern limit of sightings, acoustic recordings, and recovery of carcasses and the broken lines depict bathymetric contours.
We compiled information from scientific literature and reports on vaquita life history, threats, and abundance. The only proven source of vaquita mortality is incidental take in gillnets and a small proportion in trawl nets (D’Agrosa et al., 2000; Rojas-Bracho et al., 2006; Urrutia-Osorio, Jaramillo-Legorreta, Rojas-Bracho, & Sosa-Nishizaki, 2015; Flessa et al., 2019). Gillnet mortality from poaching of the endemic sciaenid fish totoaba (Totoaba macdonaldi) has been a major threat to vaquita (Vidal, 1993). The totoaba fishery was banned in 1975, yet constant poaching persisted (Cisneros-Mata, Montemayor-López, & Román-Rodríguez, 1995), and has recently (for the past ~10 years) severely aggravated (Thomas et al., 2017; Cisneros-Mata, 2020).
Decimated populations are subject to low fitness further compromising their existence. For vaquita, inbreeding depression was discarded when its abundance was in the low to mid 100s (Rojas-Bracho & Taylor, 1999; Rosel & Rojas-Bracho, 1999; Taylor & Rojas-Bracho, 1999). Population dynamics at low numbers are governed by demographic stochasticity because survival and fecundity operate at the individual level increasing the risk of extinction by chance survival only (Lee, Seather, & Engen, 2011). Given its current low population size we consider demographic stochasticity (or chance events) to be critical for the recovery of vaquita.
We further hypothesize the existence of an Allee effect (Dennis, 1989) related to maternal care, characteristic of several mammal species. Mothers nurse and protect their newborns (Hill, Greer, Solangi, & Kuczaj, 2007) as in P. phocoena in the North Sea (Camphuysen & Krop, 2011). For this species on the Atlantic coast of the USA, maternal care lasts between 9 and 10 months (Koopman & Zahorodny, 2008). In our models we assumed that if there is no altruistic conspecific care, a newborn will die if its mother dies, generating a “double death” effect. We caution that this double death may not adjust to the traditional definition of Allee effects, although we considered as such for reasons discussed below.
We began the analyses by constructing an age-structured life table (Begon, Mortimer, & Thompson, 1996). In life tables, lx are age-specific survival probabilities from birth to age class x (lx = p0 pl p2 ... px-1). We used survival rates of P. sinus and P. phocoena, a related porpoise from the North American coasts (Gaskin, Smith, Watson, Yasui, & Yurick, 1984; Fenton et al., 2017). The probability of surviving from age class 1 to 2, p0, was 0.71; this is the square of p3 = 0.84, as suggested by Barlow (1986). p1 and p2 were linearly interpolated from those two values (p0 and p3); survival rates for age classes 4 to 20 were considered constant (0.84).
Annual parturition rates at-age x, mx, were 0.9 for age classes ≥ 6, while m4 was considered as 1/2 of m6, and m5 was linearly interpolated. In P. phocoena annual pregnancy rates vary between 0.91 and 0.24 (Gaskin et al., 1984). The parturition rate for vaquita is 1-2 years (Hohn, Read, Fernández, Vidal, & Findley, 1996; Taylor et al., 2019).
Sex ratio was arbitrarily considered 1:1 in all cases. For P. phocoena a slight bias towards males has been observed (Lockyer, 2013; Kesselring, Viquerat, Brehm, & Siebert, 2017). Vaquita longevity is 21 years, and first reproduction occurs in the fourth year of age (Barlow, 1986; Hohn, et al., 1996).
With this baseline life table, using the Euler-Lotka equation (Birch, 1948):
(1)
and the Solver tool in Excel, we derived a vector of “natural” survival rates constrained to yield 643 vaquitas for 1993. This number, considered an initial condition for our models, was back-estimated by eye based on the abundance trend in Jaramillo-Legorreta et al. (2019) who give a mean of 550 vaquitas for 1997, 225 for 2008 and 100 for year 2015. The net population growth rate λ for this baseline table was also estimated from the Euler-Lotka equation.
Reproductive value, vx, the weighted contribution to population growth by individuals of different ages was computed as (Caswell, 1989):
(2)
Note that reproductive value for the first age class will always be 1. To summarize results, we estimated the average reproductive value for three age groups which we call here juveniles (0.5 to 2.5 years), adults (3.5 to 12.5 years) and older adults (13.5 to 21.5 years).
Generation time, the mean age (years) of mothers of a cohort of newborn daughters, was obtained as (Pielou, 1977):
(3)
where N is the total number of age classes. is used by the International Union for the Conservation of Nature to assess extinction risk of wild populations (Bird et al., 2020).
We used the baseline life table and performed 2 000 Monte Carlo trials using a SLMM (Caswell, 1989) to project random annual vaquita abundance trajectories over 38 years starting with a total population of 643 in year 1993. Demographic stochasticity was included considering individual birth and survival rates as Bernoulli trials (Kokko & Ebenhard, 1996). Population trajectories were generated drawing independent, uncorrelated random numbers to avoid effects in variance (McNamara & Harding, 2004). This produced a graphical view of how a vaquita population would have grown had by-catch mortality not been present; it also allowed to estimate the net population growth rate without consideration of Allee effects and bycatch mortality.
We then added Allee effects to the same Leslie matrix to ascertain how this natural process would affect random population trajectories and λ. We considered that if a female that gave birth died for any reason, her newborn also died that same year. For each trajectory we estimated the net annual rate of increase as λt = Nt+1/Nt (Nur, 1987) where Nt is the total number of vaquitas in a given year t; the mean annual growth rate was then computed as the geometric mean over the 38 years, and of the 2 000 random trajectories.
To simulate the effect of bycatch mortality, we multiplied age-specific survival rates by a constant factor (< 1) for an initial population size of 643 in 1993 constrained to end with 550 vaquitas in 1997. Parturition rates remained constant. This allowed us to determine changes in survival rates and reproductive values, which we attributed to bycatch mortality in fishing nets. This procedure was repeated to fit the mean abundance estimates given also by Jaramillo-Legorreta et al. (2019) for years 2008, 2015, 2016, 2017 and 2018. We note that the latest estimate of abundance is for year 2018 (Dr. Lorenzo Rojas, pers. comm., March 17, 2021).
Monte Carlo simulations were used to determine quasiextinction risk (QR). We recorded the first passage time, i.e., the year when a population trajectory first fell below critical thresholds (Nc); when a trajectory fell below Nc it was discarded from the original 2 000 trajectories. We initiated with a population having 13 individuals, approximately corresponding to year 2018 (Jaramillo-Legorreta et al., 2019). For a given year, QR was estimated as the ratio of first passage time and the number of trajectories remaining that year (Ginzburg, Slobodkin, Johnson, & Bindman, 1982).
QRs were computed discarding bycatch mortality under three Nc scenarios: 5, 10 and 20 vaquitas in years 2023, 2028, 2033, and 2038. In other words, we computed the probability that the vaquita population will fall below 5, 10 and 20 individuals in those four years given that bycatch mortality is 100 % eliminated starting in 2019. Simulations were done in Matlab® version R2018b, a platform that can handle matrix algebra appropriately (Miller, Morgan, Ridout, Carey, & Rothery, 2011).
Results
When Allee effects are considered, survival rates decrease for the younger age classes, and the highest impact is attributed to bycatch mortality (Fig. 2). It is worth noting the resilience of the vaquita population. In the hypothetical case that bycatch is 100 % eliminated in year 2019 even with a mean number of 13 the model population steadily recovered. This can be more readily appreciated in the inset of Fig. 2.
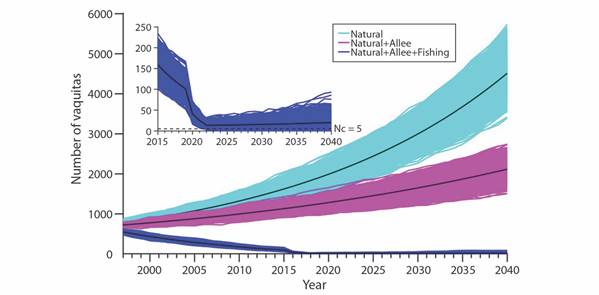
Fig. 2 2 000 random trajectories of the vaquita population considering natural mortality, natural mortality and Allee effects, and natural mortality, Allee effects in addition to bycatch mortality in gillnets. Inset shows a detailed view of the trajectories considering bycatch mortality as well as the Nc = 5 critical threshold population size.
A steady decrease in age-specific survival was observed in the subsequent periods of 1993-1997 through 2009-2015, followed by a sharp decrease in 2016, increase in 2017 and a final decrease in 2018. Our analysis indicates that the age groups with the lowest survival rates are juveniles (0.5 to 3 years), and the oldest (> 16.5 years) (Fig. 3).
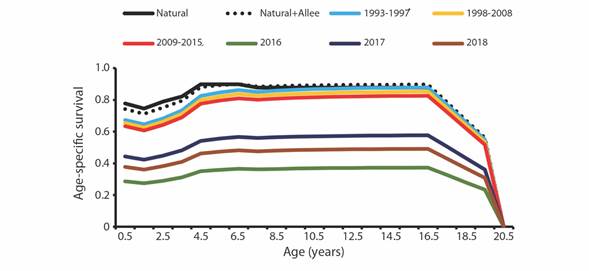
Fig. 3 Annual age-specific survival rates of vaquita under various scenarios. Nat + Allee represents schedules including natural mortality and an Allee effect related to maternal care. The remaining lines represent the survival schedules assuming added bycatch mortality to fit estimated annual abundances in Jaramillo-Legorreta et al. (2019).
Our analyses indicated that the net population growth rate sharply decreased due to bycatch (Table 1). If no Allee effect is considered, the population would grow 4.4 % per year; when the Allee effect is present the mean net growth rate is 2.6 % per year. When bycatch mortality is considered, the growth rate λ reduces to < 1 meaning that the population is declining. The estimated effect of bycatch plummeted the population for 100 (on average) or less individuals, as indicated by λ < 1. Generation time decreased concomitantly with population size, reproductive value of juveniles and adults, and λ.
Table 1 The effect of Allee effect and bycatch on population size (N), net population growth rate (l) and mean reproductive value (RV), and generation time (T) for three age groups of vaquitas: juveniles (j), adults (a) and older adults (oa)
| Scenario/Parameter | N (vaquitas) | Year | l | RVj | RVa | RVoa | |
| Natural | 643 | 1993 | 1.044 | 1.74 | 3.09 | 1.51 | 9.2 |
| Natural + Allee | 643 | 1993 | 1.026 | 1.66 | 3.31 | 1.60 | 9.4 |
| Natural + Allee + Bycatch | 550 | 1197 | 0.965 | 1.28 | 3.05 | 1.63 | 8.7 |
| Natural + Allee + Bycatch | 225 | 2015 | 0.938 | 1.14 | 2.79 | 1.59 | 8.2 |
| Natural + Allee + Bycatch | 100 | 2015 | 0.910 | 1.02 | 2.57 | 1.56 | 7.7 |
| Natural + Allee + Bycatch | 40 | 2016 | 0.429 | 0.46 | 1.70 | 1.65 | 4.2 |
| Natural + Allee + Bycatch | 25 | 2017 | 0.648 | 0.57 | 1.66 | 1.43 | 5.1 |
| Natural + Allee + Bycatch | 13 | 2018 | 0.557 | 0.51 | 1.61 | 1.48 | 4.7 |
The reproductive value RV also decreased with increasing mortality. Table 1 provides the average reproductive value for three age groups (juveniles, adults, and older adults). When bycatch mortality is considered, as the number of vaquitas decreased through time the mean RV also decreased almost 75 % for juveniles (1.66 to 0.51); for adults, RV decreased almost by half (3.31 to 1.61), and for the older adults, RV reduced only slightly (1.60 to 1.48).
A graphic depiction of reproductive value is given in Fig. 4, which shows how Allee effect and bycatch affects these demographic parameters.
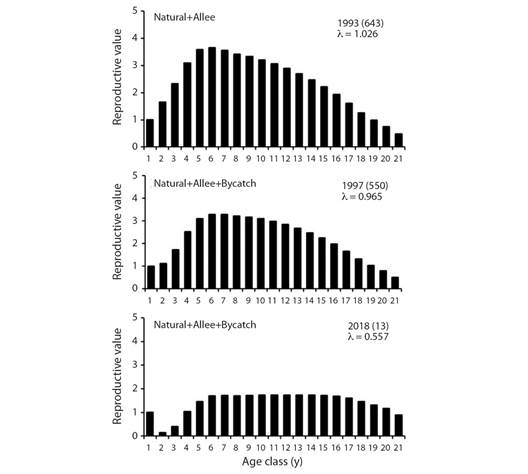
Fig. 4 Age-specific reproductive values for three models of P. sinus. Years and abundance (in parentheses) are shown as well as net growth rate l. The 643 vaquitas for year 1993 were estimated from data in Jaramillo-Legorreta et al., (2019) and represent the initial condition for our models.
For the three thresholds of vaquitas considered (5, 10, 20) the probability of quasiextinction (QR) decreases through time because of an upward mean population trend starting in 2022 (Table 2, cf. inset Fig. 2).
Table 2 Quasiextinction risk of a model vaquita population starting with a size of 13 in 2018 and assuming that bycatch mortality is eliminated starting in 2019. Allee effect and demographic stochasticity are considered in 2 000 simulations
| Threshold (# vaquitas) | Year | |||
| 2023 | 2028 | 2033 | 2038 | |
| 5 | 0.0094 | 0.0103 | 0.0056 | 0.0034 |
| 10 | 0.0340 | 0.0132 | 0.0061 | 0.0045 |
| 20 | 0.0500 | 0.0254 | 0.0094 | 0.0099 |
Discussion
In this work we assumed that the relative number of bycaught vaquitas reflect the age structure, decreasing in numbers with age. In a sample of 56 collected carcasses -the majority bycaught in gillnets most (33) were juveniles followed by older adults (16) and adults (7) (Hohn et al., 1996); no vaquitas were found of ages 3 to 6 or 17 to 20 years. This could be the result of a relatively small sample size or other, unknown factors. Our assumption is based on the facts that 1) fishing effort in the vaquita habitat including poaching of totoaba increased as compared to the 1990s (Rodríguez-Quiroz, Aragón-Noriega, Valenzuela-Quiñonez, & Esparza-Leal, 2010), and 2) bycatch of vaquita increased accordingly (Urrutia-Osorio et al., 2015).
Demographic stochasticity acts on individual rates at small population sizes (Lande, 1993; Legendre, Clobert, Moller, & Sorci, 1999). With few conspecifics, Allee effects and demographic stochasticity might further depress growth rate (Courchamp, Clutton-Brock, & Grenfell, 1999; Berec, Angulo, & Courchamp, 2007), not evident at high population numbers (Akçakaya, 2000). Allee effects emerge due to decreased cooperation by conspecifics in decimated populations (Lande, 1998); for vaquita we use the term facilitation instead of cooperation (Courchamp et al., 1999) because survival of a female vaquita that just gave birth will increase the likelihood of her calf to survive. We did not find evidence for Phocoeanidae of alloparental altruistic care of newborns by conspecifics (Mann & Smuts, 1998; Gero, Engelhaupt, Rendell, & Whitehead, 2009). Therefore, survival of a mother and her newborn represents an important proportional gain in the decimated vaquita population.
An Allee effect is defined as “a positive relationship between any component of individual fitness and either numbers or density of conspecifics” (Stephens, Sutherland, & Freckleton, 1999). Here we find that this double death effect results in a decline in per capita growth rate as compared to the absence of double death. Per capita growth is defined as r = ln (λ) (Caswell, 1989) and, as shown in Table 1, with a double death effect λ (and thus r) decreases. Consequently, this double death effect correlates with fitness, hence our definition as an Allee effect. This is the first work considering the double death effect in vaquita, which has the potential to reduce population growth. Rojas-Bracho et al. (2006) estimated that the maximum vaquita population net growth rate λ was lower than 1.04 (or 4 % per year). Our baseline analytical estimate of λ for a population without Allee effect is 4.4 % per year, and when an Allee effect is included λ decreases to 2.6 % per year. Hohn et al., (1996) found pregnant and lactating juveniles in their sample of gillnetted vaquitas, providing evidence in favor of this demographic process.
When bycatch mortality was included, λ decreased to -3.5 % per year in year 1997 and to -44.3 % per year in 2018. Previous works show that fishing decreases the reproductive value (RV) and λ in shark populations (Gallucci, Taylor, & Erzini, 2006). For vaquita bycatch mortality is the “harvested” portion of the population which according to our calculations reduces RV. Further, our results (cf. Table 1) corroborate that in age-structured populations there is a direct relationship between λ , / and RV (Schaffer, 1981; Caswell, 1982; O’Grady, Reed, Brook, & Frankham, 2008).
Despite demographic stochasticity and an Allee effect acting as assumed in the present work, vaquita has the potential to recover from exceedingly small numbers. If bycatch mortality is eliminated in 2019, the model population recover from only 13 individuals in 2018. This seems to be related to the high sensitivity of to survival of the youngest age-classes and of adults and thus to the effect of bycatch mortality in RV. For other cetaceans it was found that λ is more sensitive to survival of adults than calves (Young & Keith, 2011). Due to a lagged response because of the age structure, the recovery is not immediate; it takes three years (2019 to 2022) for the population to change from strong negative to a slight positive trend. It is unfortunate that there are no abundance estimates of vaquita for the years 2019 to 2021 to include in the present work. Because of the continued totoaba poaching at least during 2019 (Aceves-Bueno, Read, & Cisneros-Mata, 2020), it is likely that the population is smaller now.
Historically, gillnets have produced constant vaquita mortality (Vidal, 1995) which urged the elimination of totoaba poaching. From the late 1980s through the 1990s, 30-40 vaquitas died annually in totoaba gillnets (Silber, 1990; Vidal, 1993), a high rate relative to the population size (Taylor & Gerrodette, 1993). For a population having between 300 and 500 vaquitas, incidental deaths in totoaba nets were 5-10 % per year (Villa, 1993). From 1992-2009 bycatch represented 10.78 % of the population and rose to 21.11 % from 2010-2013 based on numbers in Urrutia-Osorio et al. (2015). This increased bycatch mortality coincides with intensified totoaba poaching over the past decade (Cisneros-Mata, 2020).
There have been unsubstantiated arguments for a negative effect on the vaquita population of less Colorado river water into the upper gulf of California (see Flessa et al., 2019). What has not been discarded is the obvious: vaquitas perish in gillnets. Hence, we conclude the same as the vast majority of previous studies: more fishing nets in upper Gulf of California resulted in higher incidental mortality of vaquitas. Moreover, bycatch in totoaba gillnets has an overwhelming negative effect (Morzaria-Luna, Ainsworth, Kaplan, Levin, & Fulton, 2013).
Variability in mitochondrial DNA is related to effective genetic population size Ne and vaquita lacks such variability. Ne is the minimum size below which the genetic makeup is randomly affected in the population (Wright, 1931) and is generally lower than total population size (Cypriano-Souza, da Silva, Engel, & Bonatto, 2018). Previous work (Taylor & Rojas-Bracho, 1999) discarded inbreeding depression but concern was raised if the population remained small. Ne for vaquita could be 1/10 (Frankham, 1995), 1/3 (Nunney, 1993) or 1/2 (Nunney, 1995) of total population. Thus, an investigation of the genetic pool and Ne at the current population size of vaquita is urgently needed.
Extraordinary efforts to assess and save the vaquita have included aerial and boat surveys, passive acoustic techniques, and captive care (Barlow, Fleischer, Forney, & Maravilla-Chávez, 1993; Taylor & Gerrodette, 1993; Barlow, Gerrodette, & Silber, 1997; Jaramillo-Legorreta, Rojas-Bracho, & Gerrodette, 1999; Jaramillo-Legorreta et al., 2007; Jaramillo-Legorreta et al., 2019; Rojas-Bracho et al., 2019). Despite such efforts, results have been deceptive because no effective actions have been implemented to eliminate bycatch mortality (Bobadilla, Álvarez-Borrego, Avila-Foucat, Lara-Valencia, & Espejel, 2011; Morzaria-Luna et al., 2013). Moreover, unless poaching of totoaba is completely eliminated it will be futile to implement any form of use for this species, including a catch and release program (see discussion in Cisneros-Mata, 2020). As many studies have previously recommended, serious efforts are needed to eliminate bycatch mortality of vaquita completely and promptly, else it will be impossible to recover this species. Demographically, vaquita seems viable even at extremely low numbers; its genetic makeup will be the factor governing its long-run viability. A recent study (Morin et al., 2020) is encouraging in this respect since it concludes that even with current low numbers the vaquita maintains the genetic diversity of a healthy population.
Ethical statement: authors declare that they all agree with this publication and made significant contributions; that there is no conflict of interest of any kind; and that we followed all pertinent ethical and legal procedures and requirements. All financial sources are fully and clearly stated in the acknowledgements section. A signed document has been filed in the journal archives.












 uBio
uBio