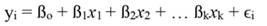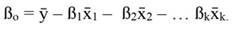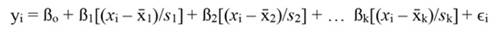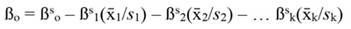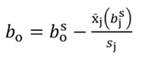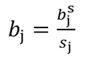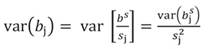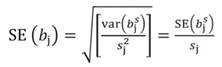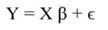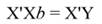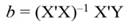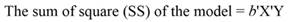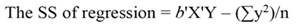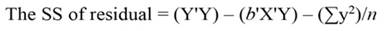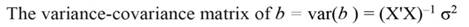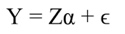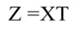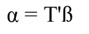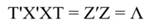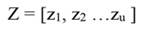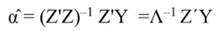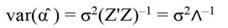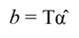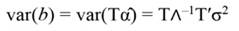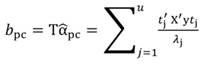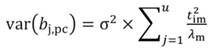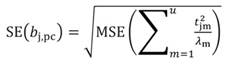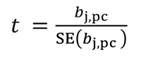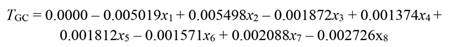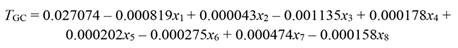Introduction
The Amazon rainforest has a significant impact on both water and carbon cycles, due to its enormous extension (~ 5.1 × 106 km2) and the high amount of carbon stored in its vegetation, about 86 Pg (Saatchi, Houghton, Alvalá, Soares, & Yu, 2007). Tree growth can be defined as the increase of biomass through time and it is often estimated by measuring the increment of stem diameter over time - a proxy of biomass gains at the ecosystem level (Wagner, Rossi, Stahl, Bonal, & Herault, 2012; Wagner et al., 2014; Dias & Marenco, 2016; Antezana-Vera & Marenco, 2020). As tree growth is greatly affected by factors that affect photosynthesis, sun-induced fluorescence - a proxy of ecosystem photosynthesis has been used to estimate the effect of environmental factors on total carbon gain of the ecosystem (Lee et al., 2013; Yang et al., 2018; Green et al., 2020).
Tree growth can be affected by intrinsic factors (e.g., genetic make-up) and environmental factors, such as nutrient availability, irradiance, temperature, rainfall, and soil water content (SWC). The influence of environmental factors on tropical tree growth has been widely studied (Wagner et al., 2012; Mendes, Marenco, & Magalhães, 2013; Wagner et al., 2014; Dias & Marenco, 2016; Méndez, 2018). However, the drivers of tree growth are rather difficult to elucidate because they are often correlated (Bowman, Brienen, Gloor, Phillips, & Prior, 2013; Wagner et al., 2014). Therefore, the effects of climatic parameters, such as temperature, rainfall or SWC on tree growth, are still under investigation in the Amazon (Laurance et al., 2009; Wagner et al., 2014; Dias & Marenco, 2016). Rainfall and SWC seem to be the major factors that affect tree growth in the Amazon region, but there is still under debate whether Amazonian trees grow faster in the wet season than in the dry season. Although in most studies tree growth or ecosystem photosynthesis seems to decrease in the dry season (Méndez, 2018; Wagner et al., 2014; Yang et al., 2018; Antezana-Vera & Marenco, 2020), the opposite effect has also been reported (Laurance et al., 2009; Green, et al., 2020). Whereas Laurance et al. (2009) reported that tree growth was fastest during the dry period and positively correlated with maximum temperatures (T max), Wagner et al. (2014) found no significant effect of T max on tree growth.
Climatic parameters are often correlated, and hence collinearity can lead to imprecise results by increasing the Variance Inflation Factor (VIF), as an increase in VIF can lead to false non-significant effects. Moreover, because of collinearity, the sign of a regression coefficient may change (from positive to negative or vice versa, Montgomery, Peck, & Vining, 2012). This is important because the significance and sign of regression coefficients are crucial to understand the effect of climatic variables on tree growth. Principal Component Analysis (PCA) is commonly used to deal with the collinearity problem, whereby a new set of independent variables (orthogonal components) is computed from the original regressors. However, PCA’s disadvantage is the lack of a direct association between a response variable and the extracted components. To overcome this difficulty, PCA’s orthogonal components can be used to perform Principal Component Regression (PCR). An accurate estimate of the effect of climatic variability on tree growth is essential due to the influence of the Amazon forest on the global carbon balance and regional climate. Thus, this study aimed to determine the collinearity-free effect of climatic variability on tree growth in the central Amazon. We hypothesize that the influence of highly correlated climatic variables such as relative humidity and VPD on tree growth can only be detected after removing the effect of collinearity.
(Equation 2) Materials and methods
Study site and plant material: The study was conducted from January 2013 to December 2017 (the experimental period) at the Tropical Forest Experiment Station (ZF2 Reserve), in central Amazonia, located 60 km North of Manaus (02°36’21” S & 60°08’11” W). The area is a terra-firme rainforest plateau at about 120 m above sea level. Annual rainfall is 2 420 mm, with a mild dry season, with the driest months from July through September (≤ 100 mm per month. The soil is an Oxisol with low fertility, clay texture and pH of 4.2 to 4.5 In this site, tree density is high, about 600 tree ha-1 (> 10 cm diameter at breast height-DBH), canopy height can reach 35-40 m, and most of trees have less than 30 cm in diameter, while leaf area index varies from 4.7 in dry season to 5.0 in the wet season. Mean wood density is about 0.75 g cm-3, and species diversity is high (Dias & Marenco, 2016). At a site 30 km of Manaus, Prance, Rodrigues, and Silva (1976) recorded 179 species of trees in one hectare (≥ 15 cm DBH).
During the experimental period, air temperature (T), photosynthetically active radiation (PAR), RH, and rainfall data were daily recorded above the forest canopy, at the top of a 40-m-tall observation tower (02°35’20” S & 06°06’55” W). Temperature, RH and PAR data were logged at 15 min (PAR) or 30 min intervals (T and RH) with specific sensors (Humitter 50y, Vaisala, Ov, Finland; LI-190SA, Li-Cor, Lincoln, NE, USA) connected to a data logger (Li-1400, Li-Cor), while daily rainfall data were collected with a tipping bucket gauge (ECR-100, Em5b, Decagon Devices, Pullman, WA, USA). The PAR data were integrated over a 24-h period to obtain a daily value (mol m-2 day-1). We also computed VPD and potential evapotranspiration (EVT) and measured soil water content (SWC, %, v/v). VPD was obtained as VPsat - RH × VPsat, where VPsat is the saturation vapor pressure; VPsat (kPa) = 0.61365exp[17.502T /(240.97 + T )], being T (ºC) the air temperature (Buck, 1981). EVT was obtained as: EVT = 0.0023R a × (T mean + 17.8) (T max - T min)0.5, where R a denotes the extraterrestrial radiation (Hargreaves & Samani, 1985). Undisturbed soil samples were collected at a depth of 100 to 200 mm every two weeks to determine SWC after drying the samples at 105 °C, and then a mean monthly value was obtained.
In this study we collected data from 325 trees from more than 48 species (Digital Appendix), which had a mean diameter at breast height (DBH, diameter at 1.3 m from the ground) of 23.1 ± 11.8 cm. From tree diameter, tree height was estimated to be 22.5 ± 5.2 m (Nogueira, Nelson, Fearnside, França, & Oliveira, 2008). In these trees we measured radial growth at breast height at monthly intervals over 60 months (2013-2017) using stainless steel dendrometer bands, which had been installed three years before the beginning of the study.
Statistical analyses: To assess the effects of the monthly microclimatic variability on tree growth Principal Component Regression (PCR) was used. We used this approach to remove the effect of collinearity among climatic variables. In this analysis, we used detrended tree growth (T GC, hereafter referred to as simply tree growth) instead of undetrended tree growth (T GR, i.e., raw data), because a time-related trend in growth data can affect PCR results (Monserud & Marshall, 2001). This step was accomplished by using a first-order autoregression (Montgomery et al., 2012). Then the tree growth of the whole data set (N = 325) was randomly split into two subsets, one with 75 % of the trees (244 trees) was used to estimate the regression coefficients, and the remaining (25 %, i.e., 81 trees) was used for validation. Prior to PCR analysis the climatic data were standardized. In the PCR model, instead of including all the examined factors, we only used those that combined explained most of the variance (i.e., eigenvalues equal or greater than one). Also, for comparison the significance of the regression coefficients based on standard Multiple Linear Regression (MLR) were also computed. A MLR model can be represented by (Montgomery et al., 2012):
(Equation 1)
In Equation 1, yi denotes the dependent variable, x i the regressor, ßo the intercept, ßj the slope of the regression, and ϵ the error term, being ßo given by:
For standardized regressors, with mean x̄j and standard deviation s j, yi and ßo become:
The coefficients obtained from standardized regressors (hereafter denoted by the superscript s) can be transformed back to the original regressor units, as follows:
Likewise, the variance of b s j and standard error (SE) of b s j can be transformed back to the original coefficients:
In matrix notation Equation 1 can be represented by:
In Equation 9, Y represents the vector of observations (dependent variable); X, the matrix of the corresponding regressors, β the vector of coefficients, and ϵ the vector of random error terms. The normal equations of the linear regression are given in Equation 10, while the estimates of β (often termed ß̂, and hereafter denoted by b) are given by Equation 11.
The sum of square (SS) of the model (Equation 12), SS of regression (Equation 13), SS of residual (Equation 14), and the covariance-matrix of b (Equation 15) are given by:
Being the mean square error (MSE = s 2) an estimator of σ2, and s = √(MSE). When the regressors are highly correlated principal components can be used for transforming those regressors into a new set of uncorrelated variables (orthogonal variables with each other). In terms of standardized regressors, the PCR can be computed, as follows (Montgomery et al., 2012):
In Equation 17, T is a matrix whose columns represent eigenvectors (derived from X data), while in Equation 20, the columns of Z represent a new set of orthogonal scores (i.e., the z-scores), which are termed principal components (Montgomery et al., 2012). The α̂ coefficients (Equation 21) and the covariance of α̂ (Equation22) are given by:
The standardized regressors, b pc are given by Equation 25, while the variance and standard error (SE) of b pc are given by Equation 26 and Equation 27, respectively. In Equation 25, the “pc” indicates that the principal components corresponding to near-zero eigenvalues have been removed from the analysis.
The step described in Equation 25 is important to obtain a new set of coefficients, after removing the smallest λi. This is a crucial step in principal component regression. The second part of Equation 25 shows the computation. Note that Z = XT, then Z´=T´X´, and ∧-1 Z´Y = α̂ (Equation 21).
In Equation 27, the MSE is obtained as the regression of Y on the u- principal components retained in the reduced model, while t jm denotes the jth element of the eigenvector t m (m = 1 …u). The significance of the principal component estimator (b pc) can be tested on individual coefficients by using the statistic t n-k-1, where k represents the number of principal components in the reduced model, as described in Equation 28.
Statistical analyses were carried out using Statistica 7.0 (Stat Soft Inc., 2004).
(Equation 29) Results
Monthly means of the climatic variables were 26.4 °C (temperature), 78.9 % (RH), and 28.9 mol m-2 day-1 (PAR). Mean rainfall was 213.7 mm month-1, SWC 44.3 % (v,v), VPDmean 7.41 hPa, and EVT 120.7 mm month-1. On the other hand, the mean values between seasons were (dry vs wet season): T mean (27.0 vs 26.0 °C, P = 0.001), RHmean (74.5 vs 82.1 %, P < 0.001), VPDmean (9.2 vs 6.1 hPa, p < 0.001), and evapotranspiration (126.2 vs 117.7 mm month-1, P = 0.034). Rainfall, PAR, and the other climatic variables varied within the wet and dry season as described in (Fig. 1).

Fig. 1 Undetrended tree growth (T GR) and climatic variables recorded in the wet season (November to May) and dry season (June to October) during the years of 2013 to 2017. A. Undetrended tree growth, B. RHmin and RHmax, C. PAR, D. T min and T max, E. Rainfall, and F. VPDmin and VPDmax. Abbreviations are shown in Table 1.
The undetrended radial tree growth was 0.105 ± 0.11 mm per month (N = 325 trees), with a lower radial increment across the driest season (Fig. 1A). A preliminary analysis showed that by including all the 13 factors in the PCR model (full model), no effect on tree growth was observed, even when the regression explained 23.7 % of the total variance (F (13,46) = 1.10, P = 0.382, R2= 0.237). In fact, the full PCR model corresponds to the MLR model of tree growth on all the climatic variables (full model MLR). The principal component analysis (PCA) showed that the first four factors out of the 13 factors extracted by PCA (in bold face in Fig. 2) together accounted for 92.9 % of the total variance and had eigenvalues higher than one (λ j = 8.16, 1.86, 1.05, and 1.01). Whereas the values of λ 5 to λ 13 were lower than 1.0 (Fig. 2). Therefore, we retained the first four factors (Kaiser criterion) and used their corresponding eigenvectors to obtain the z j scores, hereafter referred to as principal components (z j ). In comparison with the full PCR model, the significance of the four-principal component model was improved (F (4,55) = 2.45, P = 0.056, R2 = 0.151). By reducing the complexity of the model, the amount of variance on tree growth explained by the regression model was also reduced (23.7 against 15.1 %). Moreover, the four-factor model showed that only the principal components z 1 and z 3 had a significant effect on tree growth, whereas z 2 and z 4 did not (i.e., z 1: P = 0.03, z 2: P = 0.46, z 3: P = 0.04, and z 4: P = 0.86). Therefore, only z 1 and z 3 were retained for further analysis and hereafter referred to as the reduced model. As expected, significance of the reduced model was further improved by retaining only the two significant components, i.e., z 1 and z3 (F (2,57) = 4.73, P = 0.012, R2 = 0.142), with both regression coefficients being significant (α1 = -0.003927, P = 0.03) and α3 = -0.010267, P = 0.04). As z 1 and z 3 were retained in the reduced PCR model, only Factor 1 and Factor 3 are shown (Fig. 2), and for further information tree growth (T GC) is included in Fig. 2 as a supplementary variable. In Fig. 2, by taking T GC as a reference point, climatic variables were separated into three groups. The first group comprised RHmin, RHmean, rainfall, and SWC; which together with T GC are in quadrant (III) on the factor plane. These results suggest a positive correlation between each of them and T GC . The second group (PAR, EVT, T max and VPDmax) is located in quadrant I (i.e., diagonally opposite to T GC), and thereby indicating a negative correlation between the variables of this group and T GC. The third group included variables located in adjacent quadrants, i.e., quadrant II (RHmax) and quadrant IV (T min, T mean, VPDmin and VPDmean), and then indicating a low correlation between each of these variables and T GC. We further investigated the relationship between the climatic variables and T GC after removing the effect of collinearity (i.e., by PCR).

Fig. 2 Principal Component Analysis of climatic variables. The eigenvalues of the first four factors account for 92.9 % of total variance. In the factor plane, tree growth (T GC) was included as a supplementary variable. Abbreviations are shown in Table 1.
The PCR regression coefficients (α1 and α3) were used to compute the beta coefficients, b pc (in b pc, the subscript pc stands for principal components) and their SE (Equation 25 and Equation 27). The coefficients b pc based on standardized regressors are shown in Table 1, while those coefficients ( b j) obtained by MLR are shown and Table 2.
After removing the effect of collinearity, we found that tree growth was significantly responsive to variation in PAR (x 1), rainfall (x 2), T max (x 3), RHmean (x 4), RHmin (x 5), VPDmax (x 6), SWC(x 7), and EVT (x 8). Whereas T min, T mean, RHmax, VPDmin, and VPDmean had no significant effect on tree growth (Table 1). Tree growth increased with a rise in rainfall, SWC, RHmean, and RHmin, whereas it decreased with increasing PAR, T max, EVT, and VPDmax, as shown in Equation 29 (based on standardized regressors, Table 1) and Equation 30, for regressors in the original scale. To validate the PCR model (Equation 30) we used growth data of 81 trees, which showed that the R2 derived from the validation data set was even slightly higher than the R2 of data used to build the model (R2 = 0.12 vs. 0.17, Fig. 3).

Fig. 3 A. Tree growth (T GC, square, N = 244) and the regression line (solid line, T GC-PCR) as a function time. B. The validation of the PCR model on growth data (N = 81 trees) is also shown. The solid blue line corresponds to the regression line, while the diamond represents the T GC of validation trees. PCR: principal component regression, T GC-PCR: PCR line fitted to data.
By applying the standard MLR approach, we found that none of the climatic parameters modified tree growth (F (13,46) = 1.10, P = 0.382, R2= 0.237, Table 2). Furthermore, in comparison with the results obtained with the PCR reduced model (only factor 1 and factor 3), the MLR coefficients (b j) had much larger SE (Table 2). For instance, the SE of RHmean and VPDmean were more than two orders of magnitude higher than those obtained by PCR, due to the effect of collinearity. Besides having larger SE, some coefficients (T max, RHmin and EVT) had opposite sign. In retrospect, using the result from PCR and hence discarding from the MLR model those climatic variables with no significant effect on tree growth (Table 1) did not yield any significant regression coefficient (F (8,51) = 1.55, P = 0.16, R2 = 0.19).
Table 1 Regression coefficients of standardized climatic variables (b S pc), standard error (SE) of b S pc, variance inflation factor (VIF), and t (57df) and P values obtained by principal component regression (PCR) of tree growth (T GC) on principal component z 1 and z 3 (F (2.57) = 4.73, MSE = 0.001473, P = 0.0125, R2 = 0.142)
| Variable | Beta (b s pc) | SE (b s pc) | VIF | t (57) | P value |
| PAR | -0.005019 | 0.002164 | 1.0 | -2.348939 | 0.022 |
| Rainfall | 0.005498 | 0.002188 | 1.0 | 2.545052 | 0.014 |
| T mean | 0.001380 | 0.001250 | 1.0 | 1.118301 | 0.268 |
| T min | 0.006063 | 0.003198 | 1.0 | 1.919855 | 0.060 |
| T max | -0.001872 | 0.000628 | 1.0 | -3.019680 | 0.004 |
| RHmean | 0.001374 | 0.000583 | 1.0 | 2.387525 | 0.020 |
| RHmin | 0.001812 | 0.000632 | 1.0 | 2.905751 | 0.005 |
| RHmax | -0.001084 | 0.001128 | 1.0 | -0.972707 | 0.335 |
| VPDmean | -0.000745 | 0.000667 | 1.0 | -1.131649 | 0.262 |
| VPDmin | 0.001446 | 0.001312 | 1.0 | 1.116269 | 0.269 |
| VPDmax | -0.001571 | 0.000616 | 1.0 | -2.582338 | 0.012 |
| SWC | 0.002088 | 0.000691 | 1.0 | 3.059548 | 0.003 |
| EVT | -0.002726 | 0.000939 | 1.0 | -2.938550 | 0.005 |
EVT: potential evapotranspiration, PAR: photosynthetically active radiation, T: temperature, T max: mean maximum T, T mean: mean T, T min: mean minimum T, RH: relative humidity, RHmax: mean maximum RH, RHmean: mean RH, RHmin: mean minimum RH, VPD: air vapor pressure deficit, VPDmax: mean maximum VPD, VPDmin: mean minimum VPD, VPDmean: VPD mean, and MSE: mean square error. Climatic data were standardized prior to statistical analysis. For T GC, N = 244. Significant P values are in bold face.
Discussion
Most of the climatic variables assessed had a significant effect on tree growth. The exceptions were T min, T mean, RHmax, VPDmin and VPDmean which did not modify tree growth. Thus, these results partially support our hypothesis, as highly correlated variables such RHmax, VPDmin and VPDmean influenced tree growth. We found that PCR explained 12 % of the total variance (R2 = 0.12), which is not unexpected, as many factors can affect tree growth (Bowman et al., 2013). For instance, Wagner et al. (2012) found that only about 9 % of the variation in tree growth can be attributed to seasonal climate variability, which is slightly lower than the proportion of total variance explained by climatic variability in our study.
The standard MLR explained 23.7 % of total variance in tree growth. Nevertheless, due to the large standard error (SE) associated with each coefficient (Table 2), none of the regression coefficients significantly affected tree growth. On the other hand, even small-magnitude coefficients obtained by PCR, such as RHmean and RHmin, showed a significant effect on tree growth. This finding supports our hypothesis, as the detrimental effect of collinearity becomes evident when the correlation between climatic variables was disregarded and the data subjected to MLR. The large SE of MLR coefficients undermined the predictive power of the MLR model, and therefore, the influence of the climatic variables on tree growth was underestimated. For instance, the VIF of RHmean, RHmax, and VPD computed by MLR (Table 2) were over three orders of magnitude greater than that of genuinely independent orthogonal regressors (Table 1), which magnified the SE up to 200-300 times (e.g., RHmax, VPDmean and VPDmax) as compared with the SE obtained by PCR. We found that some MLR coefficients (e.g., T max and RHmin) had opposite sign.
Table 2 Regression coefficients ( b j), standard error (SE), VIF, and t (46 df) and P values obtained by standard multiple linear regression (MLR) of tree growth (T GC) on climatic variables (F (13,46) = 1.10, MSE = 0.001624, P = 0.382, R2 = 0.237)
| Variable | b j | SE( b j) | VIF | t value | P value |
|---|---|---|---|---|---|
| PAR | -0.000863 | 0.008981 | 2.9 | -0.09609 | 0.923870 |
| Rainfall | 0.005264 | 0.011935 | 5.2 | 0.44107 | 0.661226 |
| T mean | -0.043624 | 0.038490 | 53.8 | -1.13341 | 0.262915 |
| T min | 0.020023 | 0.016432 | 9.8 | 1.21854 | 0.229230 |
| T max | 0.060980 | 0.058528 | 124.5 | 1.04189 | 0.302907 |
| RHmean | 0.229039 | 0.200442 | 1459.8 | 1.14267 | 0.259088 |
| RHmin | -0.093012 | 0.117944 | 505.4 | -0.78861 | 0.434383 |
| RHmax | -0.295352 | 0.225920 | 1854.5 | -1.30733 | 0.197599 |
| VPDmean | 0.309690 | 0.237523 | 2049.8 | 1.30383 | 0.198778 |
| VPDmin | -0.292876 | 0.228333 | 1894.3 | -1.28267 | 0.206034 |
| VPDmax | -0.201591 | 0.175032 | 1113.1 | -1.15174 | 0.255380 |
| SWC | 0.007049 | 0.009000 | 2.9 | 0.78321 | 0.437519 |
| EVT | 0.001124 | 0.019793 | 14.2 | 0.05679 | 0.954959 |
Climatic data were standardized prior to statistical analysis. Note that in comparison with PCR coefficients (Table 1) T max, RHmin and EVT had opposite sign. Abbreviations as described in Table 1.
The misleading effect of collinearity can occur because the variance of a regression coefficient (say b 1 ) is inversely proportional to the amplitude of the regressor [i.e., var(b 1) = σ2/∑(x i - x̄)2]. Hence, when the variance is so large, and the actual value of a coefficient is close to zero, a regression coefficient with opposite sign can result (Montgomery et al., 2012). This is remarkable because it can be concluded that a variable x j has a positive (or negative) effect on Y, when in fact the opposite is true. Tree growth increased with rising mean and minimum RH, whereas it decreased with increasing VPDmax and EVT. Thus, by observing the VIF factor presented in Table 2, it is tempting to discard from the regression model not only RH but also VPD. Firstly, because a VIF value above 10 is an indicative of strong collinearity among regressors (Montgomery et al., 2012). Secondly, because it may be expected that the effects of these variables are already included within the effect of temperature. However, discarding these variables from the model may weaken its predictive strength as EVT, RHmean, RHmin and VPDmax had a truly independent effect on tree growth. Collinearity dramatically increases the VIF, making it difficult to quantify the individual contribution of a regressor with little but real independent effect on a dependent variable, such as tree growth (Montgomery et al., 2012; Bowman et al., 2013).
Tree growth was positively responsive to an increase in rainfall intensity, whereas T max and PAR had a negative effect on growth rates. The effect of T max on tree growth found in this study agrees with the results of Way and Oren (2010), who reported that tree growth of tropical species can be negatively affected by warming. On the other hand, our results disagree with those of Wagner et al. (2014) and Laurance et al. (2009). Wagner et al. (2014) reported no effect of T max, whereas Laurance et al. (2009) found a positive effect of maximum temperature on tree growth. This discrepancy can be ascribed to difference in environmental conditions during data collection. For instance, Green et al. (2020) reported that ecosystem photosynthesis increases in the central Amazon when VPD increased from 0.1 to 10 hPa. In tropical rainforests, the optimum temperature for photosynthesis is about 29 °C (Liu, 2020), with decreasing photosynthetic rates at higher temperatures. This can help explain the decline in tree growth with rising T max. Beside the effect of temperature on photosynthesis, a raise in temperature has also an effect on transpiration via the effect of temperature on water viscosity (Darcy´s Law). In fact, in this experimental site, EVT can increase in the dry season when temperatures are higher (Antezana-Vera & Marenco, 2020).
There are reports associating tree growth or ecosystem photosynthesis to variations in temporal rainfall variability in the Amazon region (Lee et al., 2013; Méndez, 2018; Yang et al., 2018) or VPD (Lee et al. 2013; Green et al., 2020). Some studies that aim to assess the effect of rainfall seasonality on tree growth in the Amazon have led to different results. Dias and Marenco (2016) and Silva et al., (2003) found no increase in tree growth during the wet season, whereas Wagner et al. (2014), Méndez (2018), and Antezana-Vera and Marenco (2020) reported that tree growth increased with an increase in rainfall intensity. Likewise, Lee et al. (2013) and Yang et al. (2018) reported a decline in photosynthesis-related activity during the dry season. Altogether these results indicate that the magnitude of the effect of drought on tree growth is related to the length of the dry season. In this study, we demonstrated that PCR could be a handy tool. We provide evidence that an increase in VPDmax (from 17 hPa - wet season to 23 hPa in the dry season) leads to a reduction in tree growth. Interestingly, such effect was only observed after removing the effect of collinearity. Marenco et al. (2014) showed that photosynthesis of canopy leaves (22-27 m tall trees) is closely related to stomatal conductance (g s). They reported that g s increased and reached its maximum value at a VPD of 16 hPa, and then it declined and became almost null at a VPD of 28 hPa. Likewise, Mendes and Marenco (2017) observed that g s increased with increasing VPD in the range of 5 to 10 hPa. These results show that the effect of VPD on photosynthesis depended on the level of atmospheric moisture. Green et al. (2020) reported that ecosystem photosynthesis can increase at VPD values lower than 10 hPa, Lee et al. (2013), on the other hand, estimated that ecosystem photosynthesis declined as VPD progressively increased from 3.5 hPa (wet season) to 32 hPa in the dry season, which is in agreement with the results found in our study.
Solar radiation is intrinsically associated with tree growth via its effect on photosynthesis, and it has been reported that in tropical rainforests an increase in solar radiation can lead to an increase in tree growth (Wagner et al., 2014). On the contrary, we found that an increase in PAR leads to a decline in tree growth, which agrees with the results of Yang et al. (2018) and Méndez (2018). Yang et al. (2018) observed a decrease in solar-induced fluorescence during the drought of 2015-2016 in the Amazon region. Likewise, in a study carried out at the same experimental site, Antezana-Vera and Marenco (2020) found that transpiration significantly increased with an increase in PAR and VPD. An increase in transpiration rates does not mean an increase in g s and photosynthesis. In fact, most of the time, g s decreases as transpiration increases in response to an increase in VPD (Dai, Edwards, & Ku, 1992), which can explain the negative effect of PAR and VPD on tree growth reported in this study.
Our results are relevant because of the global importance of the Amazon forest and because of the effects of the ongoing climate changes, which have increased the temperature (about 0.16 °C per decade) and altered rainfall distribution, ranging from lower rainfall intensity (longer dry seasons) in Eastern and Southern Amazonia to higher rainfall intensity in the Northern Amazon (Marengo et al., 2018). The dry season is associated with a rise in solar radiation, temperature, and VPD (Lee et al., 2013; Green et al., 2020), which ultimately can lead to a decline in photosynthesis (Lee et al., 2013; Marenco et al., 2014; Yang et al., 2018). Because most of the climatic variables are correlated, assessing the collinearity-free effect is important to accurately quantify the climatic drivers of tree growth. Increased dry season length has been forecasted for some parts of the Amazon (Marengo et al., 2018), which ultimately may reduce tree growth, not only reducing soil water availability, but also by increasing VPD and reducing RH. Our results demonstrate that trees of the central Amazon grow more slowly during the dry season, not only due the effect of a drop in rainfall intensity, but also in response to the effect of an increase in maximum temperature, evapotranspiration, and maximum vapor pressure deficit, and a decline in mean and minimum relative humidity. To our knowledge this is the first time the collinearity-free effect of RHmin, RHmean, EVT and VPDmax on tree growth in the Amazon region has been evaluated. The novelty of this study is to demonstrate the orthogonal effect of VPDmax and RHmin on tree growth in the central Amazon, which contributes to enhance the current knowledge of the ecophysiology of Amazonian trees.
Ethical statement: authors declare that they all agree with this publication and made significant contributions; that there is no conflict of interest of any kind; and that we followed all pertinent ethical and legal procedures and requirements. All financial sources are fully and clearly stated in the acknowledgements section. A signed document has been filed in the journal archives.












 uBio
uBio