Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.59 n.3 San José Sep. 2011
Recuperación de la biomasa mediante la sucesión secundaria, Cordillera Central de los Andes, Colombia
Jorge Ignacio del Valle1, Héctor Iván Restrepo2 & Mónica María Londoño3
1. Universidad Nacional de Colombia sede Medellín, Apartado Aéreo 568, Medellín, Colombia. Telefax 57 (4) 4309343-ext 49178; jidvalle@unal.edu.co
2. Grupo de investigación en Bosques y Cambio Climático, Universidad Nacional de Colombia sede Medellín;hirestrepoo@unal.edu.co
3. Universidad Nacional de Colombia sede Medellín; monica82villegas@yahoo.es
Dirección para correspondencia
1. Universidad Nacional de Colombia sede Medellín, Apartado Aéreo 568, Medellín, Colombia. Telefax 57 (4) 4309343-ext 49178; jidvalle@unal.edu.co
2. Grupo de investigación en Bosques y Cambio Climático, Universidad Nacional de Colombia sede Medellín;hirestrepoo@unal.edu.co
3. Universidad Nacional de Colombia sede Medellín; monica82villegas@yahoo.es
Dirección para correspondencia
Abstract
Biomass recovery through secondary succession in the Cordillera Central de los Andes, Colombia. Estimations on biomass recovery rates by secondary tropical forests are needed to understand the complex tropical succession, and their importance on CO2 capture, to offset the warming of the planet. We conducted the study in the Porce River Canyon between 550 and 1 700m.a.s.l. covering tropical and premontane moist belts. We established 33 temporary plots of 50mx20m in secondary forests, including fallows to succesional forests, and ranging between 3 and 36 years old; we measured the diameter at breast height (D) of all woody plants with D≥5cm. In each one of these plots we established five 10mx10m subplots, in which we measured the diameter betweem 1cm≤D<5cm of all woody plants. We estimated the biomass of pastures by harvesting 54 plots of 2mx2m, and of shrubs in the fallows by harvesting the biomass in 18 plots of 5mx2m. We modeled Bav (above ground live biomass of woody plants) and Brg (coarse root biomass) as a function of succesional age (t) with the growth model of von Bertalanffy, using 247t/ha and 66t/ha as asymptote, respectively. Besides, we modeled the ratios brg/bav=f(D) and Brg/Bav=f(t). The model estimated that 87 years are required to recover the existing Bav of primary forests through secondary succession, and 217 years for the Brg of the primary forest. The maximum instantaneous growth rate of the Bav was 6.95 t/ha/yr at age 10. The maximum average growth rate of the Bav was 6.26 t/ha/yr at age 17. The weighted average of the absolute growth rate of the Bav reached 4.57t/ha/yr and the relative growth rate 10% annually. The ratio brg/bav decreases with increasing D. The ratio Brg/Bav initially increases very rapidly until age 5 (25%), then decreases to reach 25 years (18%) and increases afterwards until the ratio reaches the asymptote (26.7%). Rev. Biol. Trop. 59 (3):1337-1358. Epub 2011 September 01.
Key words: above-ground live biomass recovery, annual tree-rings in tropical trees, coarse roots biomass, root/shoot ratio, chronosequences, secondary succession, tropical Andean forests.
Resumen
En bosques secundarios premontanos tropicales es escasa la información sobre el tiempo requerido para recuperar la biomasa aérea y subterránea de los primarios. Por lo tanto, establecimos 33 parcelas de 0.1ha entre 550 y 1 700m en bosques secundarios que cubrían estadios serales de 3 a 36 años y estimamos la biomasa de las plantas y de las raíces gruesas con ecuaciones locales. Así como la biomasa de las pasturas y barbechos por cosecha de 54 y 18 parcelas, respectivamente. También se calculó la edad de las parcelas con informantes locales, sensores remotos, C14 y anillos de crecimiento. En cada parcela medimos la biomasa aérea viva por hectárea (Bav) y la de las raíces gruesas por hectárea (Brg). Modelamos la Bav y Brg en función de la edad mediante la ecuación de von Bertalanfy con asíntotas de 247t/ha (Bav) y 66t/ha (Brg) resultantes de la medición de 33 parcelas de 0.1ha en los bosques primarios. Con la razón Brg/Bav=f(t) estimamos 87 años para que los bosques secundarios recuperen la Bav existente en los primarios y 217 años para recuperar la Brg. La tasa máxima de crecimiento instantáneo de la Bav fue 6.95t/ha/año a los 10 años y la tasa media máxima de crecimiento 6.26t/ha/año a los 17 años. La media ponderada de la tasa de crecimiento absoluto de la Bav alcanzó 4.57t/ha/año y la relativa 10% anual. La razón Brg/Bav inicialmente aumenta muy aceleradamente hasta 4-5 años (25%), luego disminuye hasta 25 años (18%) para luego incrementar hasta 26.7%.
Palabras clave: anillos anuales en árboles tropicales, biomasa raíces gruesas, bosques andinos tropicales, razón biomasa aérea biomasa radical, recuperación biomasa aérea viva, sucecesión secundaria tropical.
El área de bosques tropicales se está reduciendo significativamente como consecuencia de la deforestación (Wibowo & Byron 1999, Achard et al. 2002) pero gran parte de éstas pueden luego formar bosques secundarios. Para centro y sur América se citan cifras desde 65 hasta 165 millones de hectáreas de bosques secundarios y tasas de deforestación desde 0.4 hasta 6.4% anual (Smith et al. 1997, Dupuy et al. 1999, Pereira & Viera 2001, FAO 2007) y se prevee que la deforestación y degradación de los bosques continuarán en la mayoría de los países en desarrollo debido principalmente a la expansión de la frontera agrícola (FAO 2007).
A medida que los bosques primarios tropicales desaparecen arrasados por las actividades antrópicas, los bosques secundarios los han remplazado en muchas de sus funciones ambientales y económicas. Los bosques secundarios son importantes porque recuperan la fertilidad de los suelos perdida durante las fases de cultivo en los sistemas de agricultura rotativa y migratoria (Sánchez 1975, Jordan 1989, Denich 1991, Pereira & Vieira 2001, Vaccaro et al. 2003, Fukushima et al. 2008), albergan la biodiversidad vegetal y animal superviviente a medida que los bosques primarios desaparecen (Chokkalingam et al. 2001, Toledo et al. 2005, Núñez 1988, Vilches et al. 2008, Chazdon et al. 2009), contribuyen con la restauración de las características estructurales y funcionales de los bosques primarios (Saldarriaga et al. 1988, Saldarriaga 1994, George et al. 1991, Steininger 2000, Guariguata & Ostertag 2001, De Jung et al. 2001, Toledo et al. 2005, Fukushima et al. 2008), controlan la erosión y poseen características hidrológicas deseables como menor escorrentía superficial, alta evapotranspiración, regulación hídrica, aumento de la precipitación mediante la condensación oculta (Smith et al. 1997, Wadsworth 1997, Chokkalingam et al. 2001), son una importante fuente de maderas de alta calidad y leña (National Academy of Sciences 1980, George et al. 1991, Toledo 1997, Müller & Solís 1997, Smith et al. 1997, Wasdsworth 1997, de las Salas 2002, Vilches et al. 2008) y presentan tasas positivas de acumulación de carbono atmosférico (Chacón et al. 2007, Yepes et al. 2010), y constituye así un sumidero activo de este elemento en tanto que los bosques primarios no crecen (Bormann & Likens 1979a, 1979b, Fearnside & Guimarães 1996, Brown 2000) o lo hacen a tasas muy bajas (Clark et al. 2001). Pueden por ello ser una alternativa costo-efectiva y rápida para reducir las concentraciones atmosféricas de CO2 contribuyendo con la mitigación de los efectos del calentamiento global (Brown & Lugo 1982, 1990, Salimon & Brown 2000, Pereira & Vieira 2001, Orrego & del Valle 2003, Vaccaro et al. 2003, del Valle 2003, Sierra et al. 2007).
Nuestra hipótesis establece que los bosques secundarios del área de estudio pueden recuperar la biomasa aérea y subterránea de los primarios, aunque es escasa la información sobre el tiempo requerido para que ello suceda en los bosques secundarios premontanos tropicales. Más limitada aún es la información relacionada con las tasas medias e instantáneas absolutas y relativas de acumulación de Bav en estos bosques. La información es aun más precaria cuando se trata de la biomasa subterránea. Esta información es muy útil para formular proyectos con la vegetación natural en el marco del Mecanismo de Desarrollo Limpio del protocolo de Kioto así como proyectos de deforestación evitada o REED (Reducing Emissions from Deforestation and Degradation). Este estudio se propone: i) determinar el tiempo requerido para que los bosques secundarios de la cordillera Central de los Andes colombianos recuperen la biomasa viva aérea y radical de los bosques primarios; ii) determinar las tasas máximas y medias de acumulación de la biomasa aérea viva y radical, iii) proponer una forma sintética de expresar la acumulación de la biomasa en las secuencias cronológicas sucesionales que permitan expresar en una sola cifra el desempeño de la totalidad de la secuencia cronológica y iv) evaluar la asignación de energía a la biomasa radical y aérea en función del tamaño de los árboles y de la edad de la secuencia cronológica sucesional estudiada.
Materiales y métodos
Sitio del estudio: Llevamos a cabo el estudio en el cañón del río Porce, cordillera Central de los Andes de Colombia en áreas pertenecientes a los municipios de Amalfi y Anorí, entre 120 y 147km por carretera hacia el noroeste desde la ciudad de Medellín. El área se encuentra entre las coordenadas geográficas 6º46’27”-7º2’13” N y 75º13’2”-75º1 4’0” W.
Tanto en las partes bajas del cañón como en las altas la precipitación anual es de unos 2 400mm (Universidad Nacional de Colombia 2006b). La precipitación es levemente bimodal con un “veranillo” hacia mediados del año; no obstante las precipitaciones promedio durante este período superan los 100mm mensuales. Sólo enero y febrero son ecológicamente secos (precipitaciones mensuales inferiores a 60mm). Con base en el gradiente local se estima que la temperatura media varía desde cerca de 24°C a 550m de altitud hasta unos 18°C a 1 700m. El relieve montañoso fluvio-erosional se desarrolla sobre esquistos y neises. Los suelos son residuales, superficiales, bien drenados, de reacción fuertemente ácida y muy baja fertilidad. Han sido clasificados como Typic Troporthents, familia esquelético-arenosa (Universidad Nacional de Colombia 2006b).
Aunque se registra actividad humana en el área de estudio desde hace 9 000 años, el hombre afectó los bosques del cañón de río Porce desde hace unos 3 000 años cuando desarrolló la agricultura de tumba y quema (Espitia 1998). La baja población indígena de la etnia Tahamí declinó hasta extinguirse después de la conquista hispánica y, por tanto, los posibles efectos de la intervención antrópica amerindia parece que habían desaparecido, pues hacia mediados del siglo XIX el cañón del río Porce aún permanecía en gran medida cubierto de impenetrables “selvas vírgenes” según relatara Codazzi en 1852 (Codazzi 2005). Esto debió ser cierto en la margen derecha del río Porce, donde se ubica la mayoría de las parcelas, debido tanto a las pronunciadas pendientes que se desprenden entre 300 y 1 800m y de altitud, como al clima malsano y baja fertilidad de los suelos. No obstante, había una importante minería de oro. La mayor transformación de las coberturas boscosas originales debió haber ocurrido a mediados del siglo XX con la construcción de la carretera Porcecito (Estación del Ferrocarril)-Cancán-Amalfi iniciada en 1935 (El Heraldo de Antioquia 1935) y que unió el Ferrocarril de Antioquia con las ricas regiones auríferas de los municipios Amalfi, Anorí, Zaragoza y Remedios y sólo alcanzó la cabecera municipal de Amalfi en 1960 (Álvarez 1987). Las tierras desmontadas se dedicaron básicamente a la ganadería extensiva y, en mucha menor proporción, a la agricultura. La transformación de los bosques en pasturas se llevó a cabo mediante la tala y quema del bosque y siembra de pastos. Las malezas se controlan, por lo regular, mediante quemas periódicas.
Toma de datos en las parcelas: Por cuanto las pasturas ganaderas han sido el principal uso económico de la tierra (Universidad Nacional de Colombia 2006a), establecimos las parcelas en áreas previamente ocupadas por este uso, según la información obtenida tanto de sensores remotos (fotografías aéreas e imágenes Ikonos) como de los habitantes locales, entre mayo 2005 y octubre 2006. En los bosques secundarios identificados establecimos 33 parcelas temporales de 50mx20m. A todas las plantas leñosas (generalmente árboles) con D≥5cm, les medimos el diámetro normal (D) con calibrador a 1.3m sobre el suelo. En cinco subparcelas de 10mx10m medimos todas las plantas leñosas con 5cm>D≥1cm. Tratamos que las parcelas representaran la sucesión desde estados tempranos hasta los más avanzados identificados en la región con el fin de disponer de la secuencia cronológica más extensa posible. El rango altitudinal de las parcelas varió desde 550m hasta 1 700m. Asimismo, se estimó la biomasa de los bosques primarios en 33 parcelas permanentes de 0.1ha cada una (50mx20m), previamente establecidas aleatoriamente en un bosques de 700ha cuyo rango altitudinal se encuentra entre 950 y 1 300m (Orrego & del Valle 2003). En Sierra et al.(2007) se justifica estadísticamente el número y tamaño de las parcelas.
Estimación de la biomasa viva en las plantas de los bosques secundarios: Ajustamosrelaciones alométricas locales mediante las cuales la biomasa aérea de los árboles (bav) y la biomasa de las raíces gruesas (brg), con diámetro mayor de 5mm, se expresaron en función del diámetro de los árboles. En estas funciones y= aDk donde y está representada por la bav o la brg, según el caso, a y k son parámetros del modelo y D el diámetro a la altura del pecho de los árboles. Las funciones se transformaron en lineales mediante logaritmos: ln(y)=ln(a)±(k)ln(D) donde ln significa logaritmo natural. Estimamos los parámetros intercepto (ln(a)) y pendiente (k) con mínimos cuadrados ordinarios. Empleamos las ecuaciones de biomasa resultantes para transformar las mediciones de los diámetros de los árboles de todas las parcelas en biomasa aérea viva anhidra (bav en kg) y de raíces gruesas (brg en kg). Para ello medimos el diámetro D de 30 árboles que cubrieron todo el rango de tamaños existentes en las parcelas. Luego de derribados pesamos el tronco fresco, ramas, ramitas y follaje. Mediante 3-4 alícuotas de 500-1 000g del follaje, y las ramas y las ramitas y secciones transversales de los troncos secadas en el laboratorio (a 80°C hasta peso constante) transformamos el peso fresco en seco. La suma de los pesos secos de los distintos componentes del árbol constituye la bav total o la brg total del árbol. Estimamos la biomasa de las palmas altas (Oenocarpus batua y Dictyocarpumlamarkianum) y pequeñas, y la de los bejucos con ecuaciones alométricas ajustadas para la misma zona (Orrego & del Valle 2003, Sierra et al. 2007). También estimamos la biomasa de la vegetación herbácea y leñosa pequeña con una función exponencial negativa en función del área basal obtenida en los bosques de esta región (Herrera et al. 2003). Cosechamos y pesamos en el campo en las pasturas actuales la Bav en 54 parcelas de 2mx2m. Determinamos el peso anhidro de la biomasa de tres alícuotas de 500-1 000g de peso fresco por parcela secadas en el laboratorio a 80°C hasta peso constante con el fin de estimar el peso seco de la biomasa fresca pesada en el campo. Este peso sirvió para estimar el punto de partida de la acumulación de la Bav en la secuencia cronológica o tiempo sucesional. En barbechos, producto de pasturas recién abandonadas, cosechamos la biomasa viva en 18 parcelas de 5mx2m. Como en el caso anterior transformamos la biomasa fresca en anhidra con tres alícuotas por parcela. Para pesar la biomasa fresca de los árboles empleamos una balanza electrónica de baterías de 150kg de capacidad y 10g de precisión. Pesamos las alícuotas en el campo con una balanza de baterías y precisión de 0.1g. Dentro de cada parcela tomamos tres muestras de suelo hasta 30cm de profundidad para determinar la masa de las raíces finas (raíces con diámetro ≤0.5cm) constituida tanto por raíces vivas como muertas por la dificultad para separarlas. Para ello empleamos el barreno bipartite root auger, Eijkelkamp, que extrae una muestra de 8cm de diámetro y 15cm de profundidad. En laboratorio lavamos todo el suelo y extrajimos las raíces finas utilizando tamices de diferentes diámetros de ojo de malla y secamos a 80ºC para obtener su peso seco final. Calculamos la media de la masa de raíces finas por parcela, y con el área del cilíndro correspondiente del barreno encontramos el factor de expansión por hectárea para esta variable.
Estimación de la edad de la secuencia cronológica: Estimamos la edad de las parcelas sucesionales cruzando información de estas líneas de información: a) Consultamos con habitantes de la región con tradición en el manejo de fincas ganaderas y de pasturas. Promediamos sus opiniones independientemente consultadas cuando no diferían sustancialmente; b) Anillos de crecimiento en especies en las que se ha encontrado que éstos son anuales, o a las que mediante radiocarbono les demostramos su anualidad (véase el literal d). Uno o dos árboles de cada parcela seleccionados entre los de mayor tamaño fueron derribados para su análisis. De la parte inferior del fuste extrajimos una rodaja o sección transversal de unos 15-20cm de espesor. Una vez que la muestra se secó al aire, la pulimos progresivamente con papel de lija desde grado 80 hasta grado 600. Luego demarcamos y contamos los anillos de crecimiento a simple vista o empleando lupas. Partimos de la hipótesis de que, en esencia, los árboles de los bosques secundarios son coetáneos (Finegan 1997, del Valle 2003, Yepes et al. 2010). Por tanto, la edad de los árboles equivale a la edad sucesional del rodal al que pertenece la parcela; c) Sensores remotos. El análisis de los cambios de las coberturas vegetales con base en los sensores remotos disponibles que cubrían el área del proyecto: fotografías aéreas (Escalas 1:20 000 a 1:25 000) de 979 y de 1993-1994 e imágenes Ikonos-2 de 2003; d) C14% moderno. En cada uno de los árboles derribados (literal b) extrajimos muestras de madera de la base del centro anatómico de árboles procedentes de 24 parcelas. Contratamos análisis de C14% moderno a la celulosa pura al The Marzeev Institute of Hygiene and Medical Ecology de Ucrania (IHME) con el fin de datar la fecha de formación del carbono más antiguo de cada árbol. Luego, utilizando el efecto de las bombas nucleares en la concentración del C14 en el CO2 atmosférico datamos los árboles mediante el software Calibomb (Hua & Barbetti 2004, Reimer et al. 2004). Para estimar la edad restamos 2005, o 2006, años en que cortamos los árboles, del año en que probablemente se inició la sucesión secundaria de cada parcela según los diferentes métodos de datación empleados.
Modelos de crecimiento: Con base en los pares de datos de las 33 parcelas: biomasa aérea viva por hectárea (Bav) y edad (t), biomasa de las raíces gruesas (Brg), edad (t), el promedio de la Bav de los barbechos y la edad (t) estimada para esta cobertura, estimamos por máxima verosimilitud los parámetros del modelo von Bertalanffy (Kiviste et al. 2002).
Y = A(1 – b exp(– kt))1/(1–m), (1)
donde Y es la Bav o la Brg en t/ha, A es la asíntota en t/ha, t es la edad en años, b es el parámetro de localización que corresponde al valor que toma Y cuanto t=0 (es decir, Y0), k es la tasa intrínseca de crecimiento orgánico y m es la constante alométrica que gobierna la forma de la curva y asegura la flexibilidad del modelo. En lugar del parámetro de constante alométrico m empleamos el parámetro de forma n=1/ (1-m). No estimamos el parámetro b dentro del modelo sino que usamos la biomasa de pastos (Y0), la asíntota y el parámetro n para calcular el valor que hace pasar la curva de Bav por el punto (0,Y0), así: b=1-(Y0/A)1/n. Para la Brg Y0=0; b=1. Empleamos como asíntota la Bav y la Brg de las parcelas de los bosques primarios (Orrego & del Valle 2003, Sierra et al. 2007). Estas biomasas fueron 247t/ha (Coeficiente de variación, CV=63%) y 66t/ha (CV=87%) para la Bav y la Brg, respectivamente. Para ambas asíntotas el error fue inferior a ±10% on α=0.05 (Sierra et al. 2007). Para corregir la heterocedasticidad, común en este tipo de modelos, empleamos una estructura de varianza potencial que consiste en elevar a una potencia el inverso del i-ésimo residual. Verificamos la homocedasticidad mediante gráficos de residuales.
Resultados
Ecuaciones de biomasa: Obtuvimos las siguientes ecuaciones alométricas de biomasa:
ln(bav) = -2.447 + 2.493 x ln(D) (2)
(n= 30; r2= 91.4%; CME=0.214; Durbin & Watson (D-W)=2.13)
ln(brg) = -3.324 + 2.257 x ln(D) (3)
(n= 30; r2= 84.5%; CME=0.341; D-W=2.16)
En las ecuaciones (2) y (3) bav es la biomasa aérea viva de las plantas leñosas (kg), brg es la biomasa de las raíces gruesas (kg), D el diámetro a la altura del pecho de las plantas leñosas (cm), n es el tamaño de la muestra, CME el cuadrado medio del error. Estas ecuaciones son estadísticamente satisfactorias de acuerdo con el coeficiente de determinación y resultaron homocedásticas con la transformación logarítmica (residuales no mostrados). De acuerdo con el estadístico D-W no presentan problemas de autocorrelación.
Biomasa aérea viva y radical: Las 54 parcelas de pasturas cosechadas tuvieron media 8.4±4.3t/ha (±desv. estándar, DE) de Bav (12.2% de error con p<0.05); las 18 de barbechos bajos 15.3±7.5t/ha DE (19.3% de error con p<0.05). En la fase de pasturas se puede considerar inexistente la biomasa de raíces gruesas por la naturaleza fibrosa de las raíces de las gramíneas. Pero la masa de raíces finas compuesta tanto de raíces vivas como muertas fue 7.9±6.6t/ha DE en las pasturas (20.1% de error para p<0.05) y 7.0±3.1t/ha DE en los barbechos (12.5% de error para p<0.05), en los cuales tampoco estimamos el contenido de raíces gruesas.
En el Cuadro 1 presentamos las características más relevantes de las 33 parcelas medidas en los bosques secundarios. El rango de edades de estas parcelas varió desde 3 hasta 36 años, el de Bav desde 17 hasta 400t/ha. La Brg varió desde 5 hasta 58t/ha. Como cabría esperarlo, se percibe cierta tendencia en cuanto al aumento de las variables estructurales
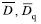 , G, Bav y Brg en función de la edad, al tiempo que N tiende a disminuir. Las palmas sólo representaron 0.12% de la biomasa aérea. La biomasa herbácea y leñosa representaron 0.8% y los bejucos 0.1%. Debido a la baja proporción de estos tres compartimientos respecto de la biomasa total no presentamos sus contenidos en el Cuadro 1.
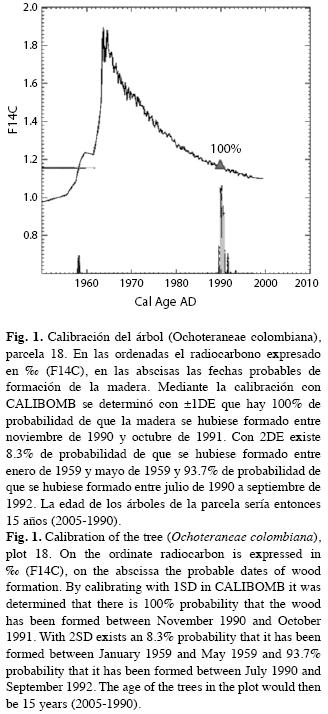
, G, Bav y Brg en función de la edad, al tiempo que N tiende a disminuir. Las palmas sólo representaron 0.12% de la biomasa aérea. La biomasa herbácea y leñosa representaron 0.8% y los bejucos 0.1%. Debido a la baja proporción de estos tres compartimientos respecto de la biomasa total no presentamos sus contenidos en el Cuadro 1.Edad de las parcelas: Con los pastos como punto de partida de la secuencia cronológica sucesional, asignamos a la biomasa allí almacenada cero años de edad (t=0). Los habitantes locales con experiencia en el manejo de pasturas ganaderas les asignaron a los barbechos dos años de edad. Esta información se pudo verificar. Hubo concordancia en las edades de las parcelas de los bosques secundarios menores de 10 años entre la opinión experta de los habitantes locales, los sensores remotos y los anillos de crecimiento. La edad asignada por los informantes fue el criterio más determinante en la datación de los barbechos en los que no se hicieron análisis de radiocarbono. En sucesiones más viejas la opinión experta no resultó confiable. Las dataciones con radiocarbono (Cuadro 1) arrojaron entre 71-100% de probabilidad (dentro de ±1DE, incertidumbre asociada al análisis de radiocarbono, véase Cuadro 1) de que la madera más antigua se había formado en uno a máximo tres años consecutivos de acuerdo con el software Calibomb (Hua & Barbetti 2004, Reimer et al. 2004). Ello significa que dentro de una desviación estándar (Cuadro 1) la calibración del análisis de radiocarbono, eje y de la Fig. 1, intercepta la fase descendente de la curva del radiocarbono atmosférico en un solo año o hasta en tres años consecutivos. Por ejemplo, en la Fig. 1 hubo 100% de probabilidad de que el contenido de radiocarbono de la madera de Ochoteraneae colombiana (150.7±0.87% DE moderno) de la parcela 18 (Cuadro 1) intercepta la curva de radiocarbono atmosférico para el trópico en dos años consecutivos: noviembre de 1990 y octubre de 1991. Por tanto, para estimar la edad en que se inició la sucesión de la parcela 18 restamos 2005, año en que cortamos el árbol, de 1990. Datamos con radiocarbono, con anillos de crecimiento y con las fotografías aéreas de 1993-1994 las parcelas con edades entre 12 y 15 años. Las áreas abandonadas después de tomadas estas fotos tendrían máximo 12 años en 2005 y las que se encontraban en barbechos unos 14-15 años. En estos casos los anillos de crecimiento coincidieron muy cercanamente con estas dataciones. Las parcelas con 18-30 años de edad aparecían como pastos en las fotos de 1979, en barbecho incipiente (Parcela 30) o en bosques secundarios jóvenes (Parcelas 31-32). Las parcelas con más de 18 años aparecían en las fotografías de 1993-1994 como bosques secundarios avanzados. En estas parcelas las dataciones con radiocarbono y el conteo de anillos fueron muy útiles para asignar la edad. La parcela 34 aparecía en las fotografías de 1979 como bosque secundario al que le estimamos unos 10 años por comparación con bosques secundarios de aproximadamente esa edad. Nuestro estimado de 36 años de edad coincidió con la datación con radiocarbono.
Modelos de crecimiento: En los cuadros 2 y 3 presentamos los principales resultados de la modelación de la Bav por hectárea y de la Brg por hectárea. La estimación del modelo von Bertalanffy arrojó resultados estadísticos aceptables de acuerdo con los valores de t de Student para los estimadores paramétricos que fueron altamente significativos (Cuadros 2 y 3). Las ecuaciones (4) y (5) representan los modelos de crecimiento de la Bav y de la Brg, respetivamente:
Bav = 247(1 – 0.7545 x e-0.0599(t))2.4072 (4)
Brg = 66(1 – e-0.0206(t))0.8882 (5)
Brg = 66(1 – e-0.0206(t))0.8882 (5)
En la ecuación 4, calculamos el parámetro b=1-(8.4/247)1/2.4072 con el propósito de que en t=0, la biomasa aérea de los pastos (Y0) fuese 8.4t/ha, punto inicial de la biomasa aérea. La Bav de los bosques secundarios alcanza 99% de la correspondiente a los primarios (247t/ha) en 87 años. Para obtener esta edad se reemplaza en la ecuación 4 la Bav por 0.99*247 y se despeja t. La Brg tarda 217 años en llegar al 99% de la encontrada en los bosques primarios (66t/ha).
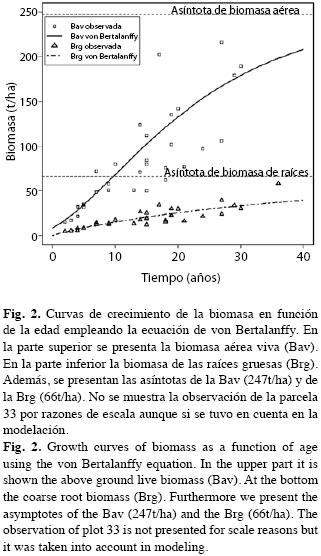
En la Fig. 2 mostramos el comportamiento del modelo von Bertalanffy para la biomasa aérea viva y para la biomasa de raíces gruesas. No aparece el dato de Bav correspondiente a la parcela 33 por superar la escala de la asíntota, aunque sí la incluimos en la modelación. A medida que la edad aumenta, la biomasa, tanto aérea como radical, tienen mayor dispersión entorno de la línea del modelo. En efecto, los puntos que representan las parcelas se dispersan reflejando alta heterocedasticidad. Sin embargo, en la estimación de los modelos corregimos este defecto y obtuvimos residuales homocedásticos que cumplen con los supuestos teóricos de la regresión.
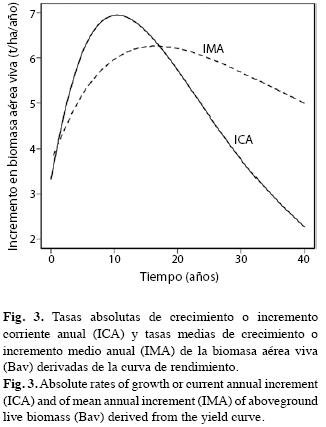
En la Fig. 3 presentamos la tasa de crecimiento absoluto de la Bav (d(Bav)/dt≈ICA, Incremento Corriente Anual de los forestales) y la tasa de crecimiento medio
 , o IMA, Incremento Medio Anual de los forestales) correspondiente a las ecuaciones 6 y 7.
, o IMA, Incremento Medio Anual de los forestales) correspondiente a las ecuaciones 6 y 7. 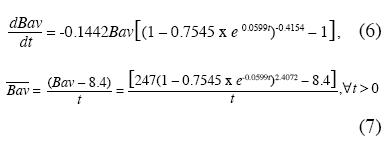
La tasa máxima de crecimiento absoluto se presenta en t≈10 años donde d(Bav)/dt= 6.95t/ha/año. La tasa máxima de crecimiento medio ocurre en t≈17 años con ≈6.26t/ha/año.
Obtuvimos la media ponderada de la tasa de crecimiento absoluto de la biomasa aérea (MPTCA) empleando el procedimiento del cálculo integral llamado valor medio de una función:
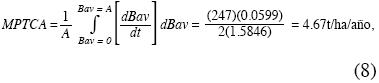
De igual manera, la media ponderada de la tasa del crecimiento relativo (MPTCR) es:
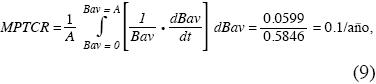
O sea, la MPTCR es 10% anual.
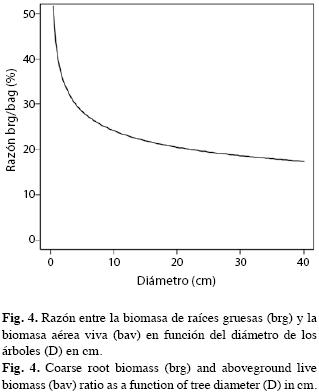
Razón biomasa de las raíces a biomasa aérea: Cuando dividimos las ecuaciones alométricas de las biomasas radicales y aéreas, ecuaciones 2 y 3, respectivamente, obtuvimos la ecuación 10 representada en la Fig. 4.
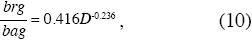
La forma exponencial negativa de la Fig. 4 sugiere que la asignación de recursos fotosintéticos a las raíces es más alta en los árboles pequeños. Para árboles con D=1cm la razón es 41.6% en tanto que para árboles con D=30cm apenas llega a 18%. Como el aumento del diámetro es una función del tiempo, significaría que en los bosques secundarios tempranos se asignaría proporcionalmente más energía a las raíces gruesas que en los más avanzados. Sin embargo, esta función no tiene explícitamente incorporada la edad. Si dividimos la ecuación 5 entre la 4 que representan la Brg y la Bav por hectárea, respectivamente, en función de de la edad, llegamos a la ecuación 11 representada en la Fig. 5.
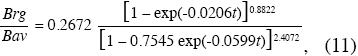
Aquí, a diferencia de lo sucedido con la ecuación 10 y Fig. 4, la asignación de recursos fotosintéticos en las raíces gruesas aumenta su participación a tasas muy elevadas durante los primeros años de la fase de barbecho hasta los 4 años con 25% de Brg en relación con la Bav (Fig. 5), luego la proporción declina lentamente una vez que la sucesión entra a la fase de bosque secundario hasta un mínimo de 18% a los 25 años para luego aumentar constantemente tendiendo asintóticamente a 26.72%. Como en el caso de la biomasa de raíces gruesas la razón Brg/Bav requeriría 217 años para alcanzar 99% del valor asintótico.
Cuando se calcula una regresión entre la razón Brg/Bav de cada parcela en función de la edad t de las parcelas de los bosques secundarios, cuya tendencia y valores corresponden a los puntos de Fig. 5, se obtiene la función exponencial negativa:
Brg/Bav= 0.275e-0.13t, r2 = 0.602 (12)
que decrece para cualquier edad y no habría posibilidad de que, como sucede con la ecuación 11, la curva tuviese tasas positivas en ninguna edad.
Discusión
Ecuaciones de biomasa: La trasformación logarítmica de las funciones alométricas tiene la virtud de eliminar la heterocedasticidad inherente a estos modelos cuya distribución es log-normal (Zapata et al. 2003). No obstante, algunos biometristas aseguran que este procedimiento produce un sesgo que tiende a reducir la biomasa de manera sistemática (Bradu & Mundlak 1970). Por lo tanto, se ha sugerido sumarle al intercepto la mitad del cuadrado medio del error, entre otros factores de corrección (Satoo & Magwick 1982). Zapata et al. (2003) demostraron que los diversos métodos arrojaban correcciones casi idénticas. En este documento optamos por no hacer dicha corrección por dos razones. La primera porque se obtienen estimaciones de la biomasa más conservadoras y, tal vez, más adecuadas para la captura de dióxido de carbono atmosféricas por los bosques secundarios. El efecto, de la corrección de la biomasa no es despreciable por cuanto Zapata et al. (2003) encontraron que la corrección en los bosques primarios de esta misma área aumentaba en 23% la Bav. La otra razón es que, ninguna de las investigaciones revisadas reporta corrección por sesgo, si se hiciese la corrección en este estudio la comparación con otros estudios podría no ser enteramente objetiva y sobre bases similares.
Biomasa de las parcelas: Gran parte de los estudios publicados sobre la recuperación de la biomasa mediante la sucesión secundaria en los trópicos presentan algunas falencias en las estimaciones de la Bav de las parcelas que aquí intentamos superar. Por ejemplo: con frecuencia sólo se tienen en cuenta plantas leñosas desde 2.5cm o más centímetros de diámetro; no se tienen en cuenta las palmas y los bejucos; se emplean ecuaciones de biomasa publicadas en la literatura para otros sitios sin previa validación local; no se tienen en cuenta las primeras etapas sucesionales, en especial, la fase de pastos y de barbecho. La mayoría de los estudios publicados no tienen en cuenta las raíces, o su biomasa se estima con factores de expansión que dejan muchas dudas (Cairns et al. 1997, Johnson et al. 2000, Mokany et al. 2006). En este estudio hemos tratado de superar tales limitaciones midiendo o estimando con regresiones locales casi todos los componentes de la biomasa aérea: plantas leñosas con D≥1cm, la vegetación herbácea y leñosa pequeña (D<1cm), bejucos y palmas con sus correspondientes ecuaciones locales de biomasa (Orrego & del Valle 2003, Sierra et al. 2007). También se tuvieron en cuenta las raíces gruesas cuando ya se han establecido los árboles del bosque secundario. En las fases de pastos y barbecho donde escasean o no existen las raíces gruesas se midió la masa de raíces finas, concepto que integra raíces finas tanto vivas como muertas.
Edad de las parcelas: La coetaneidad de la mayoría de los árboles, especialmente los del dosel, que componen los bosques secundarios hasta cerca de 100 años de edad está ampliamente documentada tanto en el trópico (Terborgh et al. 1997, Finegan 1997, del Valle 2003, Yepes et al. 2010) como fuera de él (Bormann & Likens 1979a, 1979b). Por tanto, en los bosques secundarios del área de estudio datados con menos de 40 años, podemos asumir razonablemente que los árboles del dosel tienen, en esencia, la misma edad que la fase sucesional en que se encuentran.
Para datar las sucesiones empleamos simultáneamente diversos métodos, todos ellos previamente utilizados por otros autores aunque no dentro de una sola investigación: anillos de crecimiento, datación con radiocarbono, sensores remotos y consulta a los habitantes locales. La existencia de anillos de crecimiento anuales en los árboles tropicales es un asunto controvertido (Bormann & Berlyn 1981). Sin embargo, se ha demostrado su existencia desde hace más de cien años en cientos de especies tropicales que crecen en todas las condiciones favorables para el crecimiento de árboles (Roig 2000, Worbes 2002, 2004, Brienen et al. 2009, Lebrija-Trejos 2009, Rozendaal 2010). Entre las especies muestreadas se sabe de la anualidad de los anillos de crecimiento de Myrsine guianensis, Jacaranda copaia, Cedrela odorata, Enterolobium cyclocarpum, Terminalia amazonia, Maclura tinctorea, Triplaris spp, Vochysia spp, Heliocarpus popayanensis y Psidium guajaba (Fahn et al. 1981, Kumar & Singh 1988, Mosquera et al. 2004, Worbes 2002, Tomazello et al. 2004, Brienen et al. 2009, Lebrija-Trejos 2009). Para otras especies la literatura reporta que pueden o no presentar anillos pero sin confirmar su frecuencia (Carothie 1948). De Ochoteraneae colombiana no se encontró ninguna información pero en los cortes pulidos se observan estructuras anulares muy evidentes. De todas maneras, la coincidencia entre las diferentes dataciones (Cuadro 1), solo sería posible si los anillos de todas estas especies fuesen verdaderamente anuales.
En la literatura tropical se han empleado estos métodos para datar las secuencias cronológicas sucesionales: Sierra et al. (2007) y Yepes et al. (2010) emplearon radiocarbono y Horvitz et al. (1999) para datar la sucesión cíclica; Aide et al. (1995) en Puerto Rico y Hartter et al. (2008) en Yucatán emplearon sensores remotos; Brienen et al. (2009) en México emplearon anillos de crecimiento; Terborgh et al. (1997) y del Valle (2003) emplearon los incrementos diamétricos; Vargas et al. (2008) se basaron en la historia de los incendios forestales. El método más empleado para estimar la edad de los bosques tropicales secundarios ha sido la entrevista con miembros de la comunidad local (Uhl et al. 1988, Saldarriaga 1994, Fehse et al. 1999, Hughes et al. 1999, Salimon & Brown 2000, Steininger 2000, Kennard 2002, Vaccaro et al. 2003, Hertel et al. 2003, Neeff & dos Santos 2005, Toledo et al. 2005, Cifuentes-Jara 2008, Fukushima et al. 2008). En este estudio detectamos muchas inconsistencias y grandes diferencias entre los informantes cuando el abandono del uso previo superaba 10 años. Por esta razón acudimos a otras aproximaciones que resultaron satisfactorias logrando dataciones para la secuencia cronológica de hasta 36 años.
Crecimiento de la biomasa: En promedio los bosques tropicales primarios albergan entre 200 y 400t/ha de Bav (Sarmiento et al. 2005, Vargas et al. 2008, Cifuentes-Jara 2008, Yepes et al. 2010). Por tanto, la Bav de los bosques primarios del cañón del río Porce (247t/ha) se encuentra dentro de este rango. Los bosques secundarios acumulan Bav a tasas muy diversas y con tasas máximas, medias y medias ponderadas absolutas y relativas, respectivamente Cuadro 1), de: 4.8 a 26.7 t/ha/año, de 0.42 teniendo en cuenta los bosques enanos de altura (Weaver 1990) o 1.4 en bosques amazónicos (Saldarriaga 1994) a 25.8t/ha/año, 1.4 a 17.2t/ ha/año, de 2 a 15% anual, después del abandono del uso agrícola o ganadero al que se habían dedicado. También el Cuadro 1 muestra que el tiempo para que la biomasa alcance valores similares a los bosques primarios varía desde 32 hasta 247 años y en este estudio correspondió a 87 años; la edad de los ICA máximos y de los IMA máximos varía entre 0 y 60 años y entre 1 y 74 años, respectivamente, y en este estudio a 10 y 30 años, respectivamente. Ello demuestra que la sucesión secundaria de los bosques neotropicales presenta dinámicas ampliamente contrastantes con variaciones entre 6 y 18 veces en las diversas tasas de crecimiento de la biomasa, y entre 8 y 74 veces en las edades a las que estas variables se alcanzan cuando se toman en cuenta solo los pisos basal y premontano secos a pluviales. Lo anterior conduce a considerar la recuperación de la Bav de los bosques de este estudio como similar al de otros bosques del trópico americano cuando la sucesión se produce sobre suelos químicamente pobres o sujetos a erosión, aunque no extremadamente pobres como los Ultisols (Saldarriaga 1994) y Spodosols amazónicos (Jordan 1989, Johnson et al. 2000) en los cuales el avance de la sucesión es significativamente más lento.
La mayoría de los autores han empleado el modelo no lineal asintótico de von Bertalanffy para el estudio de las secuencias cronológicas sucesionales, entre ellos los del Cuadro 4, excepto Weaver (1990), Saldarriaga (1994) y Fehse et al. (1999). Algunos investigadores han encontrado adecuado establecer para el parámetro de forma m=0 en la recuperación de la Bav en función del tiempo sucesional (Fernside & Guimarães 1999, Huhges et al. 1999, Salimon & Brown 2000, Cifuentes-Jara 2008), lo que se conoce como modelo de Weber (Kiviste el al. (2002). Vargas et al. (2008) encontraron m=-0.19 en bosques secos mexicanos. En estos casos la biomasa crece inicialmente de manera explosiva alcanzando sus tasas máximas absolutas instantáneas (ICA, Cuadro 4) en t≈0 años y la biomasa media máxima cerca de t≈1año. Este tipo de crecimiento refleja adecuadas condiciones de fertilidad de los suelos. En estos casos la MPTCR (Cuadro 4) es matemáticamente indeterminada (A/0) o negativa. Hughes et al. (1999) también emplearon el modelo con m=0.6 para la secuencia cronológica más lenta de los bosques húmedos de México, similar al de este estudio (m=0.58). Cifuentes-Jara (2008) encontró m=0.80 en los bosques secos de Costa Rica, y, Neeff & dos Santos (2005) m=1.18 en la Amazonia central, Vaccaro et al. (2003) emplearon el modelo logístico (m=2) y del Valle (2003) un modelo tipo logístico (m=3.8). En el modelo de von Bertalanffy los valores de m≤0 producen curvas de acumulación de la biomasa siempre cóncavas hacia abajo y, en consecuencia, las curvas de IMA e ICA son cóncavas hacia arriba y se maximizan casi en el origen de la curva. Cuando m>0 las curvas de acumulación de la biomasa son sigmoidales y las curvas de IMA e ICA unimodales y alcanzan valores máximos dependiendo, en esencia, del valor de m. En tanto mayor sea el valor de m más lentas son las tasas iníciales del IMA y el ICA y se maximizan a mayores edades. Esto es lo que explica que en este estudio el ICA se maximice a los 10 años, en los bosques secos de Costa Rica a los 16 años (Cifuentes-Jara 2008), en Misiones, Argentina, a los 19 (Vaccaro et al. 2003) y en los humedales turbosos de Colombia (del Valle 2003) a los 60 años (Cuadro 4). Las bajas tasas iniciales de recuperación de la biomasa aparentemente revelan condiciones climáticas o edáficas adversas para el desarrollo sucesional inicial.
Tan grande variabilidad en la forma de las curvas de tasas de crecimiento debidas a su naturaleza no lineal, en las tasas intrínsecas de crecimiento y en las asíntotas no permite comparar el crecimiento de diversas secuencias cronológicas a edades iguales. Esto es precisamente lo que hace tan importante el concepto del cálculo integral del valor medio de una función expresado en las columnas como MPTCA para las tasas medias absolutas y como MPTCR para las tasas medias relativas. Este concepto permite comparar el desempeño total de las funciones desde el origen hasta las asíntotas. Lamentablemente no es usual que los autores empleen este criterio en sus estudios. Los que aparecen en el Cuadro 4 fueron calculados en este estudio más no suministrados por los autores citados.
La estimación de la Bav asintótica y de la edad para aproximarse a ella es muy importante en la modelación de la recuperación de la biomasa mediante la sucesión secundaria. En este estudio se emplearon 33 parcelas de 0.1ha aleatoriamente distribuidas las cuales permiten afirmar que la asíntota de la biomasa de los bosques primarios muestreados es 247t/ha con error menor de ±10% y α=0.05 (Sierra et al. 2007). Algunos autores emplean como asíntota pocas parcelas, no aleatoriamente distribuidas y con poca o ninguna información acerca de su representatividad estadística (Saldarriaga et al. 1994, Hughes et al. 1999, Salimon & Brown 2000, Vaccaro et al. 2003, Cifuentes- Jara 2008). Vargas et al. (2003) emplearon una parcela de 3 000m2 con más de 60 años como bosque “maduro”, pero su secuencia cronológica revela 164 años para aproximarse a la asíntota (Cuadro 4). No obstante Neeff & dos Santos (2005) emplearon 24 parcelas que totalizaron 4.42 ha para obtener la asíntota del bosque primario. Con frecuencia se emplea el término “bosques maduros” (Saldarriaga 1994, Salimon & Brown 2000, Vaccaro et al. 2003, Vargas et al. 2003, Leyva et al. 2009) para la biomasa máxima que alcanzarían los bosques primarios. Esta denominación es confusa pues, en sentido estricto, en los bosques primarios la Bav fluctúa en torno de una media que representa el estado estable o pulsátil. Estos bosques están compuestos por las tres fases de la sucesión cíclica: fase de claros, de construcción y madura (Borman & Likens 1979a, 1979b). Al emplear sólo la fase madura la biomasa se sesga hacia biomasas más altas que las correspondientes a todas las fases en proporción de su área lo cual se consigue con muestreos aleatorios
y no mediante la selección subjetiva de los rodales “maduros”.
Algunos autores estiman linealmente la edad para que los bosques alcancen la biomasa de los primarios o maduros (Saldarriaga et al. 1988, Weaver 1990, Saldarriaga 1994, Fehse et al. 1999. Leyva et al. 2009) encontrando tiempos para la recuperación de la biomasa de los bosques primarios muy inferiores a las que obtendrían si empleasen funciones no lineales asintóticas, más apropiadas para describir la acumulación de la biomasa en función del tiempo. La mayoría de los estudios citados en la literatura se han basado en un reducido número de parcelas: entre 4 y 19 parcelas, excepto del Valle (2003) quien empleó 60 parcelas de tamaño variable según el estadio seral y Neeff & dos Santos (2005) quienes emplearon 54 parcelas. En cuanto a las edades máximas se citan secuencias que alcanzan entre 45 y 82 años (Saldarriaga 1994, Hughes et al. 1999, Fehse et al. 1999, Cifuentes-Jara 2008) que superan ampliamente nuestra secuencia cronológica de 36 años. En todos los casos citados en el Cuadro 1, excepto este estudio y del Valle (2003) quien asumió como biomasa de partida la existente en la sucesión más joven, se supone que al inicio de la sucesión (t= 0), la biomasa es también cero. Tanto desde la perspectiva teórica para ajustar modelos asintóticos como práctica, en especial en proyectos MDL, la biomasa en los puntos extremos en t=0 y en tg→∞ son muy importantes. En la práctica en proyectos MDL, la biomasa en t=0 representa la línea base. Asumir que en el tiempo cero no existe biomasa cuando ello no es así implica subestimación de esta línea. Desde el punto de vista teórico es una extrapolación que fuerza la línea de regresión en una trayectoria que no coincide con la realidad desde el t=0 hasta la edad de las parcelas más jóvenes. Dicha extrapolación alcanzó hasta 11 años en la literatura citada (Hughes et al. 1999). La introducción de la asíntota como constante implica que desde las edades más avanzadas (36 años en este estudio) hasta la asíntota no hay extrapolación, sino interpolación.
Biomasa de las raíces gruesas: No existe criterio unificado acerca del límite de tamaño que separa las raíces gruesas de las finas. En la literatura se encuentran diámetros desde 2mm hasta 5mm haciendo difícil la comparación entre diferentes estudios. En lo sucesivo nos referiremos a artículos que emplearon nuestro mismo criterio a no ser que especifiquemos otro límite. Un estudio llevado a cabo muy cerca del presente modeló la tasa de crecimiento de la Brg (d(Brg)/dt) en función de la Brg con el modelo diferencial de von Bertalanffy. Al integrar esta ecuación obtuvieron la Brg en función de la edad alcanzando como asíntota de 117t/ha (Sierra et al. 2001), casi el doble de las 66t/ha del presente estudio. Saldarriaga (1994) encontró 58t/ha de biomasa viva radical total en los bosques maduros del alto río Negro y en la sucesión más avanzada 30t/ha. Si la acumulación fuese lineal requeriría 155 años para igualar la de los bosques maduros. Como estas tendencias no son lineales sino asintóticas requeriría muchos más años que la optimista estimación lineal. Cuando se observan las curvas de acumulación de la Bav y de la Brg (Fig. 2) se nota que la pendiente de la curva de la Bav es considerablemente más alta que la Brg. Esto se debe a que la tasa intrínseca de crecimiento orgánico de la Bav casi triplica (0.0599/año) la de la Brg (0.0206/año) (ecuaciones 4 y 5). Por esta razón la Brg de la secuencia cronológica requiere dos y media veces más tiempo (217 años) para aproximarse a la Brg de los bosques primarios que la Bav (87 años). Hasta ahora poca atención se ha prestado a la acumulación de la Brg en las sucesiones. Estos resultados sugieren que cuando los bosques secundarios alcanzan Bav cercanas a las de los primarios, la Brg está aún lejos de compararse ellos.
Razón biomasa de las raíces gruesas a biomasa aérea viva: Existe muy poca información sobre la modelación de las ecuaciones alométricas de la razón brg/bav. Sólo encontramos un trabajo previo en un área cercana de la actual (Sierra et al. 2003) pero con resultados opuestos a los nuestros. La proporción resultante aumenta con el tamaño de los árboles. Por el contrario, la pendiente de la razón obtenida en este estudio es siempre negativa (Fig. 4). Algunos autores han encontrado comportamientos similares a los nuestros (Klinge 1973, Rai & Proctor 1986) localizándose proporcionalmente mayor cantidad de energía en las raíces gruesas que en la parte aérea en los árboles más pequeños que en los de mayor tamaño. Klinge (1973) cree que esto se debe a que en los árboles más grandes aumenta el contenido de raíces finas, más importantes para la nutrición de los árboles, que las gruesas que son sólo de soporte. Lo que usualmente calculan los investigadores es la relación Brg/Bav o biomasa radical total (Br)/Bav en parcelas, pero sin expresar una función matemática de esta razón con la edad de la secuencia cronológica. Los estudios de este tipo arrojan resultados muy diferentes: en Cairns et al. (1997) la razón Br/Bav en bosques tropicales y subtropicales es 0.22, mientras que en Mokany et al. (2006) es 0.42. La tendencia de la razón Bav/Brg (ecuación 11 y Fig. 5) es muy diferente de la Fig. 4. La pendiente de la ecuación 11 muestra que durante los primeros 4 años se asignan cantidades muy elevadas de energía a las raíces gruesas, luego la tendencia es decreciente y a partir de 25 años de nuevo aumenta. Pero esto no sucede con la ecuación 12 obtenida (Fig. 5) con los datos de cada parcela de la secuencia cronológica de la sucesión en la que la razón siempre decrece. Fearnside & Guimarães (1996) presentan la evolución de la razón Br/ Bav durante 20 años en una sucesión establecida en antiguas pasturas amazónicas. La razón se redujo de manera similar a la tendencia de la ecuación 12. Saldarriaga et al. (1988) y Saldarriaga (1994) en la Amazonia obtuvieron una razón Br/Bav muy constante (entre 0.19 y 0.23) para edades de 11.5 a 80 años y bosque “maduro”. Nuestros resultados con la ecuación 11 no coinciden con los de Klinge (1973), Rai & Proctor (1986), Saldarriaga et al. (1988) y Fernside & Guimarães (1999). Sin embargo, la tendencia de la ecuación 12 coincide con los anteriores autores, excepto con Saldarriaga et al. (1988), aunque se debe tener en cuenta que todos estos autores estudiaron la biomasa radical total (Br) y no la Brg como en nuestro caso. Klinge (1973) no controló adecuadamente el tamaño de las raíces puesto que su método consistió en arrancar los árboles; suponemos que la mayoría de las raíces finas quedaron dentro del suelo. En la revisión de literatura sobre todos los bosques del mundo Cairns et al. (1997) mencionan acerca de la razón Br/Bav (Root/ shoot ratio en inglés) que los efectos aislados o combinados de edad, textura del suelo, tipo de árboles, razón temperatura/precipitación y precipitación media anual no fueron estadísticamente significativos. Leuchner et al. (2007) encontraron que la razón Brg/Bav aumentó exponencialmente en bosques primarios del Ecuador desde 0.04 a 1 060m de altitud hasta 0.4 a 3 040m de altitud. Cuando se emplea su función para estimar la razón correspondiente a una altitud similar a la de los bosques primarios del presente estudio arroja 0.08, muy inferior a 0.28 de nuestro estudio. La gran variabilidad de la biomasa de las raíces hace que sólo una parcela de 0.16 ha como la empleada por Leuchner et al. (2007) para cada una de sus 5 altitudes no asegure la estabilidad de las tendencias. Jordan (1989) encontró que la razón Br/Bav aumentó desde los bosques tropicales con suelos fértiles hacia los bosques tropicales oligotróficos (Spodsols). Es posible que las diferencias entre los resultados aquí obtenidos con las ecuaciones 11 y 12 se deban a la estructura matemática de la ecuación 11. Este es un tema que ameritaría mayor investigación futura.
La Brg de los bosques secundarios tarda aproximadamente 5 años (ecuación 5) para igualar en peso la masa de raíces finas de las pasturas (7.9t/ha). Debe tenerse en cuenta que la ecuación 4 de Bav se calculó con la restricción de que para t=0, Bav=8.4t/ha, pero la ecuación 5 de Brg se calculó con la restricción en t=0, Brg=0. Es esta razón matemática la que, creemos, explica el comportamiento de la ecuación 11 y de su pendiente durante los primeros 4-5 años, tiempo requerido para que la Brg iguale la Bav inicial (en t=0). Durante este período, al paso que la masa de raíces finas de las pasturas se descompone, se hace el tránsito de pasturas y de barbecho a bosque secundario dominado por las especies de árboles que deben formar aceleradamente sus raíces gruesas. Entre 4-5 años y 25 años la proporción de recursos fotosintéticos asignados a las raíces gruesas se reduce lentamente hasta alcanzar un mínimo en 18%. Hipotéticamente durante estos 25 años los suelos restauran sus propiedades físicas y químicas siguiendo las tendencias propuestas para la razón Br/ Bav por Jordan (1989) en función de la fertilidad y por Fernside & Guimarães (1999) en función del tiempo sucesional hasta unos 20 años. Después de 25 años la razón Brg/Bav aumenta hasta 217 años cuando alcanza 99% de la razón de las asíntotas encontradas en los bosques primarios. Ello posiblemente se puede atribuir al ingreso creciente de especies esciófitas con altas relaciones de brg/bav lo que aumentaría la razón Brg/Bav a partir de los 25 años. El incluir la biomasa de las raíces finas no alteraría sustancialmente la tendencia de la curva de la Fig. 5; por el contrario, la razón Br/Bav sería siempre mayor para cualquier edad que la razón Brg/Bav. Orrego & del Valle (2003) reportan que la suma de raíces gruesas más finas en los bosques primarios es 84t/ha; por tanto, la razón de las asíntotas pasaría a 34.0%.
Este estudio es uno de los pocos existentes sobre recuperación de la biomasa aérea y subterránea en bosques premontanos tropicales: por primera vez se emplean simultánamente diversas técnicas para estimar la edad de los estados sucesionales tropicales y concluye que se requieren 87 años para recuperan la Bav de los bosques primarios pero cerca de dos y media veces más tiempo para recuperar la Brg. El empleo de la razón matemática entre las funciones Brg/Bav aporta información valiosa sobre su evolución que no puede preverse cuando se ajusta una regresión entre los valores de la razón dentro de cada una de las parcelas en función del tiempo sucesional. Se propone emplear el valor medio de una función como una cifra única, sintética, que permite comparar diversas secuencias cronológicas desde su inicio hasta la asíntota. Con este cálculo se encontró que la secuencia cronológica aquí estudiada alcanzó 4.57t/ha/año de tasa de crecimiento absoluto y 10% anual de tasa de crecimiento relativo.
Agradecimientos
Los autores agradecen a las siguientes entidades por la financiación del proyecto: Dirección de Investigaciones de la Universidad Nacional de Colombia sede Medellín (DIME), proyecto 090310002, y Empresas Publicas de Medellín (EPM). Los autores también agradecen la contribución de dos árbitros anónimos cuyas observaciones mejoraron significativamente el documento.
Referencias
Achard, F., H.D. Eva, H.J. Stibig, P. Mayaux, J. Gallego, T. Richards & J.P. Malingreau. 2002. Determination of the deforestation rates of the world’s humid tropical forests. Science 297: 999-1002. [ Links ]
Aide, T.M., J.Z. Zimmerman, H. Herrera, M. Rosario & M. Serrano. 1995. Forest recovery in abandoned tropical pastures in Puerto Rico. Forest. Ecol. Manag. 77: 77-86. [ Links ]
Álvarez, M.J. 1987. Amalfi. Vieco, Medellín, Colombia. [ Links ]
Bormann, F.H. & G. Berlyn.1981. Age and growth rate of tropical trees. Yale University, New Haven, Conecticut, EEUU. [ Links ]
Bormann, F.H. & G.E. Likens.1979a. Catastrophic disturbance and the steady state in northern hardwood forests. Am. Sci. 67: 660-669. [ Links ]
Bormann, F.H. & G.F. Likens. 1979b. Pattern and process in a forested ecosystem. Springer, Nueva York, EEUU. [ Links ]
Bradu, D. & Y. Mundlak. 1970. Estimation in lognormal linear models. J. Am. Stat. Assoc. 65: 198-211. [ Links ]
Brown, S. & A. Lugo. 1990. Tropical secondary forests. J. Trop. Ecol. 6: 1-32. [ Links ]
Brown, S. & A. Lugo. 1982. The storage and production of organic matter in tropical forests and their role in the global carbon cycle. Biotropica 14: 161-187. [ Links ]
Brienen, R.J.W., E. Lebrija-Trejos, M. van Breugel, E.A. Pérez-García, F. Bongers, F.A. Meave & M. Martínez- Ramos. 2009. The potential of tree rings for the study of forest succession in Southern Mexico. Biotropica 41: 186-195. [ Links ]
Cairns, M.A., S. Brown, E.H. Helmer & G.A. Baungardner. 1997. Root biomass allocation in the world´s uplands forests. Oecologia 111: 1-11. [ Links ]
Carothie, H. 1948. Maderas de Venezuela. Caracas, Venezuela. [ Links ]
Chacón, P., H.A. Leblanc & R.O. Russo. 2007. Fijación de carbono en un bosque secundario de la región tropical húmeda de Costa Rica. Tierra Tropical 3: 1-11. [ Links ]
Chazdon, R.L. C.A. Peres, D. Dent, D. Sheil, A.E. Lugo, D. Lamb, N.E. Storck & S.E. Miller. 2009. The potential for species conservation in tropical secondary forests. Conservat. Biol. 23: 146-1417. [ Links ]
Chokkalingam, U., W. de Jong, J. Smith & C. Sabogal. 2001. Secondary forest in Asia: Their diversity,importance, and role in future environmental management. Special Issue. J. Trop. For. Sci. 13: 563-839. [ Links ]
Cifuentes-Jara, M. 2008. Aboveground biomass and ecosystems carbon pools in tropical secondary forests growing in six life zones of Costa Rica. Tesis de Doctorado, Universidad del Estado de Oregón, Corvalis, EEUU. [ Links ]
Clark, D.A., S. Brown, D.W. Kicklighter, J.Q. Chambers, J.R. Thomlinson, J. Ni & E.A. Holland. 2001. Net Primary Production in Tropical Forest: an evaluation and synthesis of existing field data. Ecol. Appl.11: 371-384. [ Links ]
Codazzi, A. 2005. Geografía física y política de la Confederación Granadina. Estado de Antioquia: Antiguas provincias de Medellín, Antioquia y Córdoba. Universidad Nacional de Colombia-Universidad EAFITUniversidad del Cauca. Centro de Publicaciones Universidad EAFIT, Medellín, Colombia. [ Links ]
De Jong, W., U. Chokkalingam, J. Smith & C. Sabogal. 2001. Tropical secondary forest in Asia: introduction and synthesis. J. Trop. Forest Sci. 13: 563-576. [ Links ]
De las Salas, G. 2002. Los bosques secundarios de América tropical: perspectivas para su manejo sostenible. Bois Forêts Trop. 272: 63-73. [ Links ]
Del Valle, J.I. 2003. Crecimiento en biomasa y acumulación de carbono en los sajales del delta del río Patía, p. 281-296. In S.A. Orrego, J.I. del Valle & F.H. Moreno (eds.). Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín-Centro Andino para la Economía en el Medio Ambiente (CAEMA), Bogotá, Colombia. [ Links ]
Denich, M. 1991. A importancia de uma vegetação secundária nova para o incremento da productividade do sostema de produção na Amazônia oriental brasileira. EMBRAPA/CPATU-GTZ, Belén-Pará, Brasil. [ Links ]
Dupuy, B., H.F. Maitre & I. Amsallem. 1999. Tropical forests management techniques: a review of the sustainability of forest management practices in tropical countries. Working paper: FAO/FPIRS/04, Roma, Italia. [ Links ]
El Heraldo de Antioquia. 1935. Se inician los trabajos en varias carreteras departamentales. 9: 1-3. [ Links ]
Espitia, N.C. 1998. Los antiguos pobladores del Valle Medio del río Porce: Aproximación inicial desde el estudio arqueológico del proyecto Porce II. Empresas Públicas de Medellín-Universidad de Antioquia, Medellín, Colombia. [ Links ]
Fehse, J., N. Aguirre, Ch. Paldines, R. Hofstede & J. Sevink. 1999. La productividad de cuatro bosques secundarios en la sierra del Ecuador. Proyecto ECOPAR, Quito, Ecuador. [ Links ]
Fahn, A., J. Burley, K.A. Longman, A. Mariaux & P.B. Tomlinson. 1981. Possible contribution of wood anatomy to the determination of the age of tropical trees, p. 31-54. In F.H. Bormann & G. Berlyn (eds.). Age and growth rate of tropical trees. Yale University, New Haven, Connecticut, EEUU. [ Links ]
FAO-Organización de las Naciones Unidas para la Agricultura y la Alimentación-. 2007. Situación de los Bosques del Mundo. Roma, Italia. [ Links ]
Fearnside, P.M. & W.M. Guimarães. 1996. Carbon uptake by secondary forests in Brazilian Amazonia. For.Ecol. Manag. 80: 35-46. [ Links ]
Finegan, B. 1997. Bases ecológicas para el manejo de bosques secundarios de las zonas de vida húmedas del trópico americano: recuperación de la biodiversidad y producción sostenible de madera, p. 106-119. In E. Elías (eds.). Memorias del taller internacional sobre el estado actual y potencial de manejo y desarrollo del bosque secundario tropical en América latina. TCD, Consejo Centroamericano de Bosques y Áreas Protegidas, GRZ, Ministerio de Cooperación Técnica del Reino de los Países Bajos, IKC. Pucallpa, Perú [ Links ].
Fukushima, M., M. Kanzaki, M. Hara, T. Ohkubo, P. Preechapanya & C. Choocharoen. 2008. Secondary forest succession after the cessation of swidden cultivation in the montane forest area in Northern Thailand. Forest. Ecol. Manag. 255: 1994-2006. [ Links ]
George, S.J., B.M. Mohan-Kumar & G.R. Rajiv. 1991. Nature of secondary succesion on abandoned Eucalyptus plantation of Neiyar (Kerala) in Peninsular India. J. Trop. Forest. Sci. 5: 372-386. [ Links ]
Guariguata, M.R. & R. Ostertag. 2001. Neotropical secondary forest succession: changes in structural and functional characteristics. Forest. Ecol. Manag. 148: 185-206. [ Links ]
Hartter, J., C. Lucas, A.E. Gaughan & L. Lizama. 2008. Detecting tropical dry succession in a shifting cultivation mosaic of the Yucatan Peninsula, Mexico. Appl. Geogr. 28: 134-149. [ Links ]
Herrera, M.A., J.I. del Valle & S.A Orrego. 2003. Biomasa de la vegetación herbácea y leñosa pequeña y necromasa en bosques primarios intervenidos y secundarios, p. 145-168. In S.A. Orrego, J.I. del Valle & F.H. Moreno (eds.). Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín-Centro Andino para la Economía en el Medio Ambiente (CAEMA), Panamericana Formas e Impresos, Bogotá, Colombia. [ Links ]
Hertel, D., C. Leuschner & D. Hölscher. 2003. Size and structure of fine root systems in old-growth and secondary tropical montane forests (Costa Rica). Biotropica 35: 143-153. [ Links ]
Hua, Q. & M. Barbetti. 2004. Review of troposphere bomb 14C data for carbon cycle modeling and age calibration purposes. Radiocarbon 46: 1273-1298. [ Links ]
Hughes, R.F., J.B. Kauffman & V.J. Jaramillo. 1999. Biomass, carbon, and nutrient dynamics of secondary forests in a humid tropical region of Mexico. Ecology 80: 1892-1907. [ Links ]
Horvitz, C.C., L. da Silveira & H.O´R. Sternberg. 1999. 14C dating of tree falls on Barrocolorado Island: A new method to study tropical rain forests gap dynamics. J. Trop. Ecol. 15: 723-735. [ Links ]
Jordan, C.F. 1989. An Amazonian rain forest: The structure and function of a nutrient stressed ecosystem and the impact of slash-and-burn agriculture. The Partenon, Nueva Jersey, EEUU. [ Links ]
Johnson, C.M., D.J. Zarin & A.H. Johnson. 2000. Postdisturbance aboveground biomass accumulation in global secondary forests. Ecology 81: 1395-1401. [ Links ]
Kennard, D.K. 2002. Secondary forest succession in a tropical dry forest: patterns of development across a 50-year crhonosequence in lowland Bolivia. J. Trop. Ecol. 18: 53-66. [ Links ]
Kiviste, A., J.G. Álvarez-González, A. Rojo-Alboreca & A.D. Ruiz-González. 2002. Funciones de crecimiento de aplicación en el ámbito forestal. Ministerio de Ciencia y Tecnología, Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria, Madrid, España. [ Links ]
Klinge, H. 1973. Root mass estimation in lowland tropical rain forest of Central Amazonia, Brazil, II: Coarse root mass of trees and palms in different high classes. An. Acad. Brasl. Ciên. 45: 595-609. [ Links ]
Kumar, N. & V. Singh. 1988. Sensitivity of Mangifera indica and Psidium guajaba plants to SO2 pollution.Natl. Acad. Sci. Lett. 11: 167-172. [ Links ]
Lebrija-Trejos, E. 2009. Tropical dry forest recovery: Process and causes of change. Tesis de Doctorado, Universidad de Wageningen, Wageningen, Países Bajos. [ Links ]
Leyva, J.A., O.J. Rocha, R. Mata & M.V. Gutiérrez-Soto. 2009. Cronología de la regeneración del bosque tropical seco en Santa Rosa, Guanacaste, Costa Rica. II. La vegetación en relación con el suelo. Rev. Biol. Trop. 57: 817-836. [ Links ]
Leuschner, C., G. Moser, C. Bertsch, M. Röderstein & D. Hertel. 2007. Large altitudinal increase in tree root/ shoot ratio in tropical mountain forests of Ecuador. Basic Appl. Ecol. 8: 219-230. [ Links ]
Mokany, K., R.J. Raison & A.S. Prokushkin. 2006. Critical analysis of root:shoot ratios in terrestrial biomes. Glob. Change Biol. 12: 84-96. [ Links ]
Mosquera, B., R. Veiga, L. Mangia, C. Carvalho, E. Estellita, D. Uzeda, A. Facure, B. Biolini & R.M. Anjos. 2004. 137Cs Distribution in guaba tres. Braz. J. Phys. 34: 841-844. [ Links ]
Müller, E. & M. Solis. 1997. Estudio de caso: los bosques secundarios de Costa Rica, p 149-158. In E. Elías (ed.). Memorias del taller internacional sobre el estado actual y potencial de manejo y desarrollo del bosque secundario tropical en América latina. TCD, Consejo Centroamericano de Bosques y Áreas Protegidas-GTZ-Ministerio de Cooperación Técnica del Reino de los Países Bajos, IKC, Pucallpa, Perú [ Links ].
National Academy of Sciences. 1980. Firewood crops: shrubs and tree species for energy production. National Academy, Washington, EEUU. [ Links ]
Neeff, T. & J.R. dos Santos. 2005. A growth model for secondary forest in Central Amazonia. Forest. Ecol. Manag. 216: 270-282. [ Links ]
Núñez, A.M. 1988. Evaluación de comunidades de aves en bosques secundarios restaurados en potreros abandonados ubicados en la cuenca del río Zapotal, Hojancha, Costa Rica. Tesis de Maestría, Centro Agronómico Tropical de Investigación y Enseñanza, Turrialba, Costa Rica. [ Links ]
Orrego, S.A. & J.I. del Valle. 2003. Existencias y tasas de incremento neto de la biomasa y del carbono en bosques primarios intervenidos y secundarios, p. 215-242. In S.A. Orrego, J.I del Valle & F.H. Moreno (eds.). Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín-Centro Andino para la Economía en el Medio Ambiente (CAEMA), Panamericana, Bogotá, Colombia. [ Links ]
Pereira, C.A. & I.C.G. Vieira. 2001. A importância das florestas secundárias e os impactos de sua substituçâo por plantiios mecanizados de grâos na Amazônia. Interciencia 26: 337-341. [ Links ]
Rai, S.N. & J. Proctor. 1986. Ecological studies on four rainforests in Karnataka, India. Jour. Ecol. 74: 439-454. [ Links ]
Reimer, P.J., T.A. Brown & R.W. Reimer. 2004. Discussion, reporting and calibration of post-bomb 14C data. Radiocarbon 46: 1299-1304. [ Links ]
Roig, F.A. 2000. Dendrocronología en América latina. EDIUM, Mendoza, Argentina. [ Links ]
Rozendaal, D.M.A. 2010. Using tree rings to evaluate longterm growth patterns of Bolivian forest trees. Tesis de Doctorado, Universidad de Utrecht, Países Bajos. [ Links ]
Saldarriaga, J.G., D.C. West, M.L. Tharp & C. Uhl. 1988. Long-term chronosequence of forest succession in the upper Río Negro of Colombia and Venezuela. J. Ecol. 76: 938-958. [ Links ]
Saldarriaga, J.G. 1994. Recuperación de la selva de “tierra firme” en el alto río Negro, Amazonia colombianavenezolana. Tropenbos Colombia, Estudios de la Amazonia Colombiana, Santafé de Bogotá, Colombia. [ Links ]
Salimon, C.I & I.F. Brown. 2000. Secondary forests in wester Amazonia: significant sinks for carbon released from deforestation. Interciencia 25: 198-202. [ Links ]
Sánchez, P. 1976. Properties and management of soils in the tropics. Wiley, Nueva York, EEUU. [ Links ]
Sarmiento, G.M. Pinillos & G. Garay. 2005. Biomass variability in tropical America lowland rainforests. Ecotropicos 18: 1-20. [ Links ]
Satoo, T. & H.A.I. Madgwick. 1982. Forest biomass. Martinus Nijhoff/Dr W. Junk, La Haya, Holanda. [ Links ]
Sierra, C.J.I del Valle & S.A. Orrego. 2001. Ecuaciones de biomasa de raíces y sus tasas de acumulación en bosques sucesionales y maduros tropicales de Colombia. Simposio Internacional: Medición y Monitoreo de la Captura de Carbono en Ecosistemas Forestales, 18 al 20 de octubre, Valdivia, Chile. [ Links ]
Sierra, C., J.I. del Valle & S.A. Orrego. 2003. Ecuaciones de biomasa de raíces en bosques primarios intervenidos y secundarios, p 169-188. In S.A. Orrego, J.I. del Valle & F.H. Moreno (eds.). Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín-Centro Andino para la Economía en el Medio Ambiente (CAEMA), Panamericana, Bogotá, Colombia. [ Links ]
Sierra, C.A., J.I. del Valle, S.A. Orrego, F.H. Moreno, M.E. Harmon, M. Zapata, G.J. Colorado, M.A. Herrera, W. Lara, D.E. Restrepo, L.M. Berrouet, L.M. Loaiza & J.F. Benjumea. 2007. Total carbon stocks in tropical forest landscapes of the Porce region, Colombia. Forest. Ecol. Mang. 243: 299-309. [ Links ]
Smith, J., C. Sabogal, W. de Jong & D. Kaimowitz. 1997. Bosque secundarios como recurso para el desarrollo rural y la conservación ambiental en los trópicos de América Latina. CIFOR, Occasinal Paper No 13, Bogor, Indonesia. [ Links ]
Steininger, M.K. 2000. Secondary forest structure and biomass following short and extended land-use in central and southern Amazonia. J. Trop. Ecol. 16: 689-708. [ Links ]
Terborgh, J., C. Flores, P. Mueller & L. Davenport. 1997. Estimating the ages of successional stands of tropical trees from growth increments. J. Trop. Ecol. 14: 833-856. [ Links ]
Toledo, E. 1997. Aspectos políticos e institucionales para el desarrollo de bosques secundarios en la región amazónica, p.128-141. In E. Elías (eds.). Memorias del taller internacional sobre el estado actual y potencial de de manejo y desarrollo del bosque secundario tropical en América latina. TCD, Consejo Centroamericano de Bosques y Áreas Protegidas, GRZ, Ministerio de Cooperación Técnica del Reino de los Países Bajos, IKC. Pucallpa, Perú [ Links ].
Toledo, M., J. Salick, B. Liselle & P. Jørgensen. 2005. Composición florística y usos de Bosques secundarios en la provincia de Guarayos, Santa Cruz, Bolivia. Rev. Bol. Ecol. 18: 1-16. [ Links ]
Tomazello, F.M., C.S. Lisi, N. Hansen & G. Cury. 2004. Características anatómicas das zonas de incremento do lenho de diferentes espécies arbóreas do Estado de São Paulo, Brasil. Sci. For. 66: 45-55. [ Links ]
Uhl, C., R. Buschbacher & E.A.S. Serrão. 1988. Abandoned pastures in eastern Amazonia, I: patterns of plant succession. J. Ecol. 76: 663-681. [ Links ]
Universidad Nacional de Colombia. 2006a. Cambios de la cobertura vegetal en el área de influencia directa del proyecto hidroeléctrico Porce III. Informe para las Empresas Públicas de Medellín-Proyecto Hidroeléctrico Porce III, Contrato 030421027. Departamento de Ciencias Forestales, Universidad Nacional de Colombia sede Medellín, Medellín, Colombia. [ Links ]
Universidad Nacional de Colombia. 2006b. Diagnóstico físico y conservacionista de las cuencas tributarias al embalse Porce III. Contrato 030421227 Universidad Nacional de Colombia sede Medellín-Empresas Públicas de Medellín, Proyecto Hidroeléctrico Porce
III, Medellín, Colombia. [ Links ]
Vaccaro, S., M.F. Arturo, J.F. Goya, J.L. Frangi & G. Piccolo. 2003. Almacenaje de carbono en estadios de la sucesión secundaria en la provincia de Misiones, Argentina. Interciencia 28: 521-527. [ Links ]
Vargas, R., M.F. Allen & E.B. Allen. 2008. Biomass and carbon accumulation in a fire chronosequence of a seasonally dry tropical forests. Global Change Biol. 14: 109-124. [ Links ]
Vilches, B., R.L. Chazdon & V. Milla. 2008. Dinámica de la regeneración natural en cuatro bosques secundarios tropicales de la región de Huetar Norte, Costa Rica: su valor para la conservación o uso comercial. Recursos Naturales y Ambiente No 55: 118-128. [ Links ]
Wadsworth, F.H. 1997. Forest production for tropical America. USDA Forest Service, Agricultural Handbook 170, EEUU. [ Links ]
Weaver, P.L. 1990. Succession in the elfin woodland of the Luquillo Mountains of Puerto Rico. Biotropica 22: 83-89. [ Links ]
Wibowo, D.H. & R.N Byron. 1999. Deforestation mechanism:a survey. Int. J. Soc. Econ. 26: 455-474. [ Links ]
Worbes, M. 2002. One hundred years of tree rings research in the tropics: a brief history and an outlook to future challenges. Dendrochonologia 20:217-231. [ Links ]
Worbes, M. 2004. Tree-ring analysis, p. 586-599. In J. Burley, J. Evans & J.A. Youngquist (eds.). Encypledia of forest sciences. Elsevier, Amsterdam, Holanda. [ Links ]
Yepes, A.P., J.I. del Valle, S.L. Jaramillo & S.A. Orrego. 2010. Recuperación estructural en bosques sucesionales andinos de Porce (Antioquia, Colombia). Rev. Biol. Trop. 58: 427-445. [ Links ]
Zapata, M., G.J. Colorado & J.I del Valle. 2003. Ecuaciones de biomasa aérea para bosques primarios intervenidos y secundarios, p. 87-144. In S.A. Orrego, J.I. del Valle & F.H. Moreno. Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín-Centro Andino para la Economía en el Medio Ambiente (CAEMA), Panamericana, Bogotá, Colombia. [ Links ]
Correspondencia a: Jorge Ignacio del Valle. Universidad Nacional de Colombia sede Medellín, Apartado Aéreo 568, Medellín, Colombia. Telefax 57 (4) 4309343-ext 49178; jidvalle@unal.edu.co
Héctor Iván Restrepo. Grupo de investigación en Bosques y Cambio Climático, Universidad Nacional de Colombia sede Medellín;hirestrepoo@unal.edu.co
Mónica María Londoño. Universidad Nacional de Colombia sede Medellín; monica82villegas@yahoo.es
Recibido 10-VIII-2010. Corregido 16-I-2011. Aceptado 18-II-2011.