Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.59 n.1 San José Mar. 2011
Growth estimation of mangrove cockle Anadara tuberculosa (Mollusca: Bivalvia): application and evaluation of length-based methods
Luis A. Flores
Investigación de Recursos Bioacuáticos y su Ambiente, Instituto Nacional de Pesca, Letamendi 102 y La Ria, Guayaquil, Ecuador. P.O. Box: 09-01-15131; lflores@inp.gob.ec
Dirección para correspondencia
Abstract
Growth is one of the key processes in the dynamic of exploited resources, since it provides part of the information required for structured population models. Growth of mangrove cockle, Anadara tuberculosa was estimated through length-based methods (ELEFAN I y NSLCA) and using diverse shell length intervals (SLI). The variability of L∞, k and phi prime (Φ`) estimates and the effect of each sample were quantified by jackknife techniques. Results showed the same L∞ estimates from ELEFAN I and NSLCA across each SLI used, and all L∞ were within the expected range. On the contrary, k estimates differed between methods. Jackknife estimations uncovered the tendency of ELEFAN I to overestimate k with increases in SLI, and allowed the identification of differences in uncertainty (PE and CV) between both methods. The average values of Φ`derived from NSCLA1.5 and length-age sources were similar and corresponded to ranges reported by other authors. Estimates of L∞, k and Φ` from NSCLA1.5 were 85.97mm, 0.124/year and 2.953 with jackknife and 86.36mm de L∞, 0.110/year de k and 2.914 de Φ` without jackknife, respectively. Based on the observed evidence and according to the biology of the species, NSCLA is suggested to be used with jackknife and a SLI of 1.5mm as an ad hoc approach to estimate the growth parameters of mangrove cockle. Rev. Biol. Trop. 59 (1): 159-170. Epub 2011 March 01.
Key words: growth, length-based methods, von Bertalanffy, uncertainty, Anadara tuberculosa, Ecuador.
Resumen
El crecimiento es uno de los procesos clave en la dinámica de los recursos explotados. En este estudio se estimó el crecimiento de la concha prieta Anadara tuberculosa por medio de métodos basados en tallas (ELEFAN I y NSLCA) y usando distintos intervalos de clase de talla (ICT). La variabilidad de los estimadores para L∞ y k, y el efecto de cada muestra e ICT fueron cuantificados por la técnica de jackknife. ELEFAN I y NSLCA producen una misma estimación de L∞ para cada uno de los ICT. Por el contrario, para k ambos métodos estiman diferentes valores. Las estimaciones con jackknife permitieron detectar que ELEFAN I sobreestima k a medida que se aumenta el ICT, y a definir diferencias en el grado de incertidumbre (EP y CV) entre ambos métodos. Los valores promedio de Φ` derivados de NSCLA1.5 son similares a los de tallaedad y están dentro del rango reportado por otros autores. Las estimaciones de NSCLA1.5 fueron 85.97mm de L∞, 0.124/año de k y 2.953 de Φ` con jackknife y 86.36mm de L∞, 0.110/año de k y 2.914 de Φ` sin jackknife. Basado en las evidencias mostradas y acorde a la biología de la especie se sugiere utilizar el NSCLA conjuntamente con jackknife y un ICT de 1.5mm para estimar los parámetros de crecimiento de la concha prieta.
Palabras claves: crecimiento, métodos indirectos, von Bertalanffy, incertidumbre, Anadara tuberculosa, Ecuador.
Growth is one of the key processes in the dynamic of exploited resources, since it provides part of the information required for structured population models (e.g. size or age). Hence, the estimation of growth parameters is an important topic of study. In the case of bivalves, according to Bayne (1965) and Urban (2002), the von Bertalanffy growth model (VBGM) is valid to represent the growth pattern of the adult stage of many bivalves.
One of the approximations widely used during the past two decades to estimate the VBGM parameters (L∞ and k) are the so called length-based methods (LBM´s) or indirect methods (IM). The extensive application of these methods corresponds to the development of techniques to analyze length data and a higher availability of suitable computational systems (Gulland & Rosenberg 1992, Galindo 2005). In addition, IM represent a useful tool for growth studies in tropical species because tropical systems have less variable climatic conditions and age interpretation or model progression analysis based on length frequency distributions (LFD´s) is more difficult (Lowe- McConell 1987, Leonce-Valencia & Defeo 1997).
The mangrove cockle Anadara tuberculosa (Sowerby 1833) is important harvested species that inhabits mangrove zones (mainly red mangrove, Rhizophora mangle) along the Pacific coast, from Laguna Ballena - Baja California Sur - México to Bahía de Tumbes - Perú (Mora-Sánchez 1990). However, just a few studies have been conducted to quantify its growth (Villalobos & Báez 1983, Mora & Bravo 1992, Franco 1995, Flores 2002, Borda & Cruz 2004, Stern-Pirlot & Wolff 2006, Félix-Pico et al. 2007, Félix-Pico et al. 2009). These studies have used direct methods (DM), IM, culture systems and mark-recapture methods. The application of IM or LBM´s focused on using length data for modal decomposition (Flores 2002, Borda & Cruz 2004). Until now, only the studies of Félix-Pico et al. (2007) and Félix-Pico et al. (2009) have taken advantage of this approach, easily incorporating a big portion of information into LFD´s into the study of mangrove cockle growth.
The length data necessary to create LFD´s are easy to obtain, facilitating the estimation of growth parameters. Among the methods that use LFD´s are the ELEFAN I (Pauly & David 1981), PROJMAT (Shepherd 1987a), SCLA (Shepherd 1987b), NSCLA (Pauly & Arreguín- Sánchez 1995) and NHLCA (Arreguín-Sánchez & Pauly 1996) programs. Recently, the application of the last method has been formalized by Galindo (2005), while ELEFAN I and NSCLA are part of the FISAT I and II softwares (Gayanilo et al. 1995, 2004).
A common characteristic shared by these methods is to assume that species follow a VBGM. However, estimations of parameters are not necessarily the same because of differences in the algorithm used by each method. Besides, uncertainty is generated since most of the information of LFD´s comes from commercial landings, which are influenced by gear selectivity or minimum length of capture. This fact also emphasizes the importance of ssessing the influence of each monthly sample (Leonce-Valencia & Defeo 1997, Nepita & Defeo 2001) and the length interval upon which the LFD´s is built.
Therefore, this study has the following objectives: (1) to estimate the growth parameters in A. tuberculosa applying the length-based methods ELEFAN I and NSLCA, (2) to assess the performance of each method and the effect of diverse length intervals based on uncertainty of parameters and (3) to compare the estimations obtained with previous reports using the growth performance index Φ` (Munro & Pauly 1983, Pauly & Munro 1984).
Materials and methods
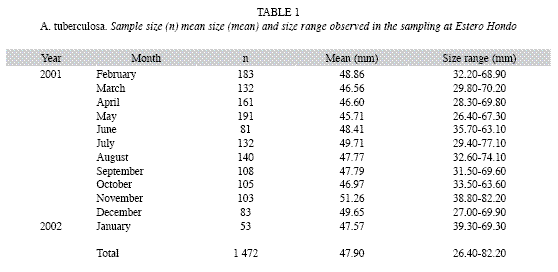
Data sources: I obtained length data for A. tuberculosa from monthly samples taken between February 2001 and January 2002 from unexploited beds in Estero Hondo, Cayapas- Mataje Ecological Mangrove Reserve (REMACAM), NORTHWESTERN Ecuador (1º33´88.8" N - 78º93´0.0" W). Therefore, the possible source of uncertainty due to length selectivity and/or the effect of minimum length capture are eliminated. Shell length (SL) for all mangrove cockles was measured along the anterior-posterior axis with a caliper and a precision of 0.05mm. The total number of individuals sampled per month is displayed in Table 1. The monthly LFD´s were grouped into eight shell length intervals [SLI (0.5mm, 1.0mm, 1.5mm, 2.0mm, 2.5mm, 3.0mm, 3.5mm y 4.0mm)] to estimate the growth parameters and to assess the effect of each SLI over its variability.
Estimation Methods: The ELEFAN I (Pauly & David 1981) and NSLCA (Pauly & Arreguín-Sánchez 1995) methods were used to estimate growth parameters. Detailed algorithms for both ELEFAN I and NSCLA have been reported by some authors (Defeo et al. 1992, Leonce-Valencia & Defeo 1997, De Anda-Montañez et al. 1999, Nepita & Defeo 2001, Escobar 2004, Galindo 2005). Both algorithms are part of the FAO ICLARM Stock Assessment Tools software, FISAT II (Gayanilo et al. 2004, Windows version).
In general, the ELEFAN I program fits the VBGM with a non-parametric function where an optimal curve that crosses most of the modes is selected according to the goodness of fit of the parameters. On the other hand, NSCLA maximizes the score of the non-parametric function similar to previous algorithm. However, this program also fits a circular function to the LDF´s for each sample and, in this process, it computes a total score function for the samples set.
Uncertainty: Jackknife techniques (Efron 1982) were applied to quantify the effect of each sample and shell length interval on growth parameters estimation. A sample was retired (one month out of 12) in a sequential way and with replacement, generating n combinations of growth parameters by method (ELEFAN I and NSLCA) and shell length interval. The percentage error (PE) and the coefficient of variation (CV) were used to evaluate the accuracy and precision of the estimators according to Leonce-Valencia & Defeo (1997). The PE was calculated by the following expression:
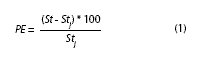
where St is the estimator of the growth parameters (L∞ and k) using all samples (without jackknife) (i.e., 12 months), and Stj is the average estimator of the n jackknife pseudo-values. The PE is optimum when it equals 0, in other words when St is equal to Stj. The CV was calculated by:
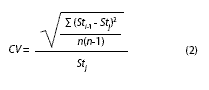
where Sti-1 is the parameter estimator when a sample is omitted and n is the sample size. This procedure has been previously applied to evaluate the influence of each sample (Leonce- Valencia & Defeo 1997, Nepita & Defeo 2001) and it has shown to be useful as an objective criterion to quantify the performance of each method used.
The growth performance index Φ` (phi prime: Munro & Pauly 1983, Pauly & Munro 1984) was used to compare the different growth estimations. This measure has already been used as a growth index in bivalves (Vakily 1990, Defeo et al. 1992, Cardoso & Veloso 2003). This index provides a unified parameter of growth performance based on the L∞ and k values, not showing much variation as in its individual form (Defeo et al. 1992, Leonce- Valencia & Defeo 1997). In addition, its efficiency has been proven for this purpose (Nepita & Defeo 2001). The function that defines the index is:
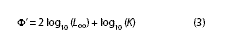
One-way ANOVA was carried out with the Φ` estimates from the resampling technique analysis in order to evaluate statistical differences among each SLI used by each method. If differences were detected, a Newman-Keuls test was performed to identify the SLI that differed. The t-student test was applied to assess statistical differences between methods for each one of the SLI used. In addition, valvebased size-at-age data (Flores 2002) was also used as a comparative basis for the results obtained through LBM´s.
Results
The 1 472 individuals sampled during the year had a mean length of 47.8mm with a minimum and maximum shell length of 26.4 and 82.2mm, respectively (Table 1).
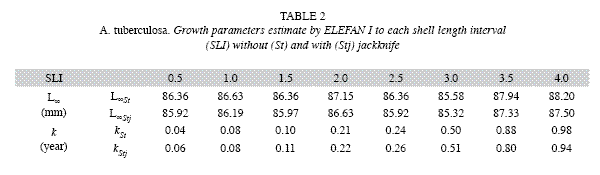
Both LBM´s (ELEFAN I y NSCLA) produced the same initial estimations for L∞ for each one of the SLI used. However, the methods showed different predictions for k. Either for ELEFAN I or NSCLA, L∞ varied between 85.58 and 88.20mm. The estimates of k were less variable using NSCLA (0.10 to 0.35/year) than estimated generated by ELEFAN I (0.04 to 0.98/year) (Table 2, 3).
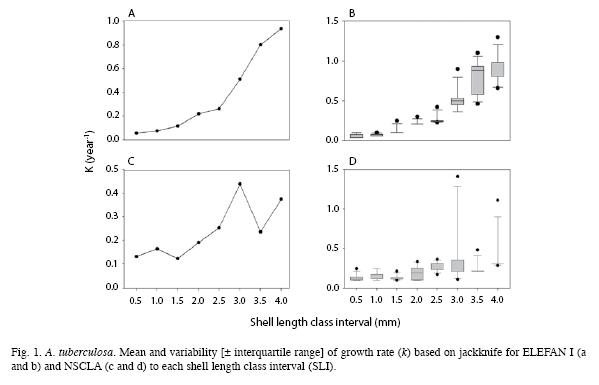
Average estimates of L∞ y k obtained by jackknife techniques were consistent with initial estimations. The jackknife iterations in both methods do not show a direct effect on the L∞ estimation with the change of input data (omitted month). This was observed in all the SLI used, except when the month of November was omitted from the estimation, which showed the maximum cockle sizes in the samples. However, a strong effect of the SLI was found for the k parameter estimation, mainly for ELEFAN I. In ELEFAN I there was a positive correlation between the growth rate and increases in the SLI, while for NSCLA the tendency was irregular (Fig. 1 a, c). Most of the variability was observed in the k (0.11 to 1.41/ year) estimate for NSCLA at a SLI of 3.0mm, followed by the ELEFAN I estimations at SLI of 3.5 and 4.0mm (0.46 to 1.10/year and 0.66 to 1.30/ year) (Fig. 1 b, d).
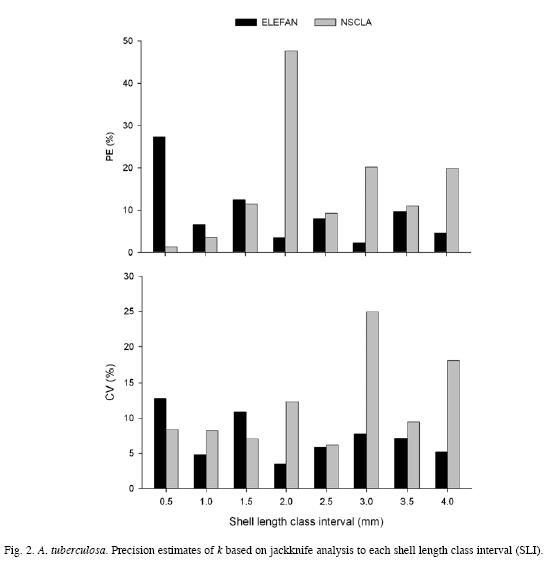
ELEFAN I y NSCLA had the same values of CV and PE for L∞ between 0.31 (3.0mm of SLI) and 0.80 (4.0mm of SLI). On the contrary, the precision estimators PE and CV reflected an important variation of k across the different SLI (Fig. 2). NSCLA generated a wide range of PE between 47.60% (2.0mm SLI) and 1.27% (0.5mm SLI) and it registered the maximum CV value (24.94% at 3.0mm SLI). ELEFAN I showed the minimum CV value (3.45% at 2.0mm SLI). In general, NSCLA tends to be more accurate and precise at SLI lower than 2mm than ELEFAN, which is robust at higher SLI (Fig. 2).
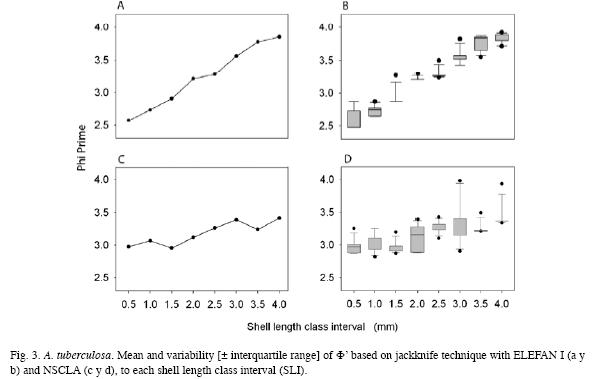
The analysis of Φ` confirms the pattern found for k for each SLI. Because Φ` is more conservative and for that reason does not present much variability like L∞ and k, the pattern observed for ELEFAN I is linear in relation to SLI increases, and almost 98% of its variability was explained by the model (R2=0.975). On the other hand, NSCLA does not show a well defined linear pattern (Fig. 3 a, c). The low variability of Φ` is proven by the reduced standard deviation of each SLI and method taken into account (Fig. 3 b, d).
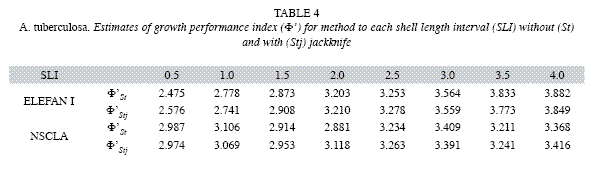
ELEFAN I registered values between 2.58 and 3.85 for Φ`, while the values of NSCLA were between 2.95 to 3.42. The average Φ` for each SLI was not much different from that obtained using the estimated parameters without jackknife techniques (Table 4). Statistical differences for Φ` among each SLI were found within methods (ANOVA F7,88=271.31; p<0.00001 in ELEFAN I and ANOVA F7,88=14.50; p<0.00001 in NSCLA) and among methods in some SLI (0.5, 1.0, 3.5 and 4.0; p<0.05). Comparisons made using the Newman-Keuls test allowed to identify differences among the SLI, finding higher individual variations in ELEFAN I than in NSCLA (Table 5).
Discussion
Of the two length based methods applied and assessed in this study, NSCLA performed better than ELEFAN I, especially when a shell length interval of 1.5mm is used. The decision elements were based on the comparison of the LBM´s results at several SLI and the new analysis of valves-based size-at- age data results; the comparison of the growth performance index (Φ`) and the uncertainty indicators generated (PE and CV).
ELEFAN I was much affected by the shell length interval. As a consequence, it tends to overestimate the growth rate (k) when the SLI increases. In addition, ELEFAN I had problems with convergence during the estimation process. One explanation is that ELEFAN I has been suggested for the study of fast growth species. According to some authors (Villalobos & Báez 1983, Mora & Bravo 1992, Flores 2002, Stern-Pirlot & Wolff 2006) A. tuberculosa is species that grows slowly, a fact that supports the statement by Basson et al. (1988) about the higher performance of NSCLA for growth parameters estimation for long life and slow growing species.
Another possible explanation is related to the algorithm configuration. On one hand, ELEFAN I considers only the mean length for each possible age group without using information about the age distribution identified in the LFD´s. On the other hand, NSCLA uses all the sample information and for that reason it provides better parameter estimates (Leonce-Valencia & Defeo 1998). The use of ELEFAN I, at least at the recommended SLI (1.5mm) should not be completely rejected. This is supported by the absence of significant statistical differences between estimations from both methods in this SLI. Rosenberg & Beddington (1987) justify this, and they mention that a guide to decide which method is the most appropriate does not exist.
SLI is very important in growth parameters estimation, and it has been the focus of some studies that apply simulations to quantify its effects (Isaac 1990, Cabrera-Vásquez & Arreguín-Sánchez 1996, 1999). This study deals with this topic in a simple way by the changing of the SLI in increments of 0.5mm, having the reported value of 4mm by Borda and Cruz (2004) as an upper limit to build the LFD´s. In his simulation experiment without considering individual variability, Isaac (1990) found that ELEFAN I tend to overestimate L∞ and underestimate k when the length interval is increased; while the length interval does not affect the growth estimation in SCLA. In this study the results for NSCLA confirm the reported by Isaac (1990) for SCLA, because both methods use the same algorithm with some modifications. On the contrary, ELEFAN I had a stronger tendency to overestimate k than that found out by Isaac (1990).
The jackknife technique was very useful in quantifying the effect of the several SLI and to establish uncertainty levels. It allows for discrimination and isolation of groups of lower and higher uncertainty, especially for NSCLA. The comparative analysis of Φ` based on the jackknife values confirmed the statement of Nepita & Defeo (2001), since the variability of each one of the SLI decreased in both methods. In addition, the analysis identified statistical differences between SLI and methods (in some cases), confirming the overestimation of the growth rate of A. tuberculosa by ELEFAN I when SLI increases.
The slow growth rates estimated for A. tuberculosa were similar to those reported by other authors (Villalobos & Báez 1983, Mora & Bravo 1992, Flores 2002, Stern-Pirlot & Wolff 2006). This fact is confirmed by in situ observations done in an experiment using shell length intervals between 30.00 to 34.99mm and 35.00 to 39.99mm, which were related to increments of 10.17 to 11.99mm and 8.55 to 10.68mm in one year, respectively (Flores: unpublished data). However, A. tuberculosa is reported as fast growing species by Borda & Cruz (2004) and Félix-Pico et al. (2007). This conclusion could have been affected by the SLI used. Borda & Cruz (2004) used 4mm as SLI and the ELEFAN I method; while Félix-Pico et al. (2007) used 5mm as SLI (J.A. López-Rocha, pers.com.) and both methods, ELEFAN I and NSCLA. Recently, Félix-Pico et al. (2009) again report A. tuberculosa as fast growing species, but they emphasizes that k is probably overestimated. According to this study the value of k estimated by Borda & Cruz (2004) may also be overestimated considering that their study zone was very close to that of Flores (2002).
The values of Φ`estimated by NSCLA were within the range reported in the literature; while ELEFAN I produced some values below the minimum previously reported, especially for lengths smaller than 2mm of SLI (Table 6). This along with the pattern of increasing growth rate (k) when the SLI is increased, make it inadvisable to use the ELEFAN I algorithm to estimate growth parameters for this species.
These analyses highlight the need to carry out more in-depth studies on the growth of A. tuberculosa and other species of the same genus using direct methodologies such as estimates of growth based on the reading of shell growth lines. These studies should employ techniques to validate the frequency of formation of the growth lines and also take into account the effect that different spatial scales can have on the estimate, given the considerable variability previously reported growth parameters (Table 6). My research suggests that, taking into account the biological characteristics of the resource, the performance of the two methods applied and evaluated based on an analysis of the uncertainty generated and the coincidence of Φ` estimates for the study area, it is suggested as an ad hoc approach, to estimate mangrove cockle growth using the jackknife technique together with NSCLA and an SLI of 1.5mm.
Acknowledgments
This paper was prepared during my stay as a graduate student in the Departamento de Oceanografía at the Universidad de Concepción (UDEC). Therefore, I appreciate the support of CONICYT and the Graduate School of UDEC for the Scholarship awarded. The database used in this study is part of my thesis to obtain the title of biologist at the Universidad de Guayaquil (Ecuador), which was conducted with the support of the Instituto Nacional de Pesca (INP) and the Fondo Ecuatoriano Populorum Progressio (FEPP). My gratitude to Yahira Piedrahita (Directora – INP) for her support with funding for the publication of this manuscript. I thank also Jorge Alberto López-Rocha (CICIMAR) and Roberto Licandeo (UDEC) for their valuable recommendations to the initial version of this manuscript. My thanks go to J.A. López-Rocha for providing growth estimation of Anadara from Mexico. Finally, especial thanks to Liliana Alencastro, Nikita Gaibor and Jennifer Nuñez for correction and editing of the English version, and also to the referees for their comments that improved this manuscript.
References
Arreguín-Sánchez, F. & D. Pauly. 1996. The deep structure of Shepherd´s length composition analysis (SLCA) method with a standardized score functions, including oscillatory growth. Documento interno, Centro Interdisciplinario de Ciencias Marinas del Instituto Politécnico Nacional, CICIMAR- IPN, La Paz, B.C.S., México. [ Links ]
Basson, M., A.A. Rosenberg & J.R. Beddington. 1988. The accuracy and reliability of two new methods for estimating growth parameters from length- frequency data. J. Cons. Int. Explor. Mer. 44: 277-285. [ Links ]
Bayne, B.L. 1965. Growth and the delay of metamorphosis of the larvae of Mytilus edulis (L.). Ophelia 2: 1-47. [ Links ]
Borda, C.A. & R. Cruz. 2004. Crecimiento y tasa de mortalidad del bivalvo Anadara tuberculosa (Sowerby, 1833) en el Pacífico Colombiano. Rev. Invest. Mar. 25: 177-184. [ Links ]
Cabrera-Vásquez, M.A. & F. Arreguín-Sánchez. 1996. Determinación del tamaño de intervalo óptimo para el análisis de distribuciones de frecuencias de longitudes de Epinephelus morio. Proc. Gulf Carib. Fish. Inst. 44: 379-390. [ Links ]
Cabrera-Vásquez, M.A. & F. Arreguín-Sánchez. 1999. Cambios en la varianza y tamaño del intervalo en frecuencias de longitudes de Epinephelus morio y su efecto en el comportamiento del método de la matriz de proyección. Proc. Gulf Carib. Fish. Inst. 45: 372-400. [ Links ]
Cardoso, R.S. & V.G. Veloso. 2003. Population dynamics and secondary production of the wedge clam Donax hanleyanus (Bivalvia: Donacidae) on a high-energy, subtropical beach of Brazil. Mar. Biol. 142: 153-162. [ Links ]
De Anda-Montañez, A., F. Arreguín-Sánchez & S. Martínez- Aguilar. 1999. Length-based growth estimates for Pacific Sardine (Sardinops sagax) in the Gulf of California, Mexico. CalCOFI Rep. 40: 179-183. [ Links ]
Defeo, O., F. Arreguín-Sánchez & J. Sánchez 1992. Growth study of the yellow clam Mesodesma mactroides: a comparative analysis of three length-based methods. Sci. Mar. 56: 53-59. [ Links ]
Efron, B. 1982. The Jackknife, the Bootstrap and Other Resampling Plans. Society for Industrial and Applied Mathematics, Filadelfia, Pensilvania. [ Links ]
Escobar, F. 2004. Estimación de los parámetros de crecimiento de Caranx crysos (Mitchill, 1815), Lutjanus synagris (Linnaeus, 1758) y Opisthonema oglinum (Lesueur, 1818) del área de Santa Marta (Caribe colombiano). Comparación de técnicas informáticas de estimación y evaluación de cambios temporales del crecimiento. Memoria de grado de Ingeniero Pesquero. Colombia. [ Links ]
Félix-Pico, E.F., M Ramírez-Rodríguez & O. Holguín-Quiñones. 2009. Growth and fisheries of the bivalve mollusk black ark in Bahia Magdalena, Baja California Sur, Mexico. N. Am. J. Fish. Manage. 29: 231-233. [ Links ]
Félix-Pico, E.F., B.P. Ceballos-Vázquez, M. Ramírez- Rodríguez & J.A. López-Rocha. 2007. Estimación de crecimiento y análisis de las capturas de la almeja pata de mula en Bahía Magdalena B.C.S., México. Memorias de la I Reunión Bianual. "Retos de las ciencias pesqueras y acuáticas en México". 2 a 4 de Mayo. La Paz, B.C.S., México. [ Links ]
Flores, L. 2002. Biometría, Edad y Crecimiento de Anadara tuberculosa (C.B. Adams 1852) y Anadara similis (Sowerby 1833) en Estero Hondo, Reserva Ecológica Manglares Cayapas – Mataje (REMACAM). Esmeraldas. Tesis de Biólogo, Guayaquil, Ecuador. [ Links ]
Franco, L. 1995. Uso y conservación de moluscos del género Anadara (Mollusca: Bivalvia). Evidencia poblacional de un gradiente de explotación humana en el Chocó, Costa Pacífica Colombiana. Tesis de Maestría, Universidad Nacional de Bogotá, INVEMAR, Colombia. [ Links ]
Galindo, G. 2005. Evaluación de tres métodos para estimación del crecimiento basados en el análisis de distribuciones de frecuencias de longitudes. Tesis de Maestría, Centro Interdisciplinario de Ciencias Marinas, CICIMAR, IPN, México. [ Links ]
Gayanilo Jr. F.C., P. Sparre & D. Pauly. 1995. The FAOICLARM Stock Assessment Tools (FISAT) users guide. FAO Computerized Information Series Fisheries, No 8. [ Links ]
Gayanilo Jr. F.C., P. Sparre & D. Pauly. 2004. The FAO-ICLARM Stock Assessment Tools II Windows Version (FISAT II) users guide (Revision I). FAO Computerized Information Series Fisheries, No 8. [ Links ]
Gulland, J.A. & A.A. Rosenberg. 1992. Examen de los métodos que se basan en la talla para evaluar las poblaciones de peces. FAO. Doc. Tec. Pesca. 323. FAO, Roma. [ Links ]
Isaac, V.J. 1990. The accuracy of some length-based methods for fish population studies. ICLARM Tech. Rep. 27. [ Links ]
Leonce-Valencia, C. & O. Defeo. 1997. Evaluation of three length-based method for estimating growth in tropical fishes: the red snapper Lutjanus campechanus of the Campeche Bank (Mexico). Sci. Mar. 61: 297-303. [ Links ]
Leonce-Valencia, C. & O. Defeo. 1998. Estimación de la variabilidad en los parámetros de crecimiento de Lutjanus campechanus del Golfo de México. Proc. Gulf Carib. Fish. Inst. 47: 915-935. [ Links ]
Lowe-McConell, R.O. 1987. Ecological studies in tropical fish communities. Cambridge, Cambridge, London. [ Links ]
Mora-Sánchez, E.M. 1990. Catálogo de bivalvos marinos del Ecuador. Bol. Cient. Tec., Inst. Nacional de Pesca, Guayaquil, Ecuador 10: 1-136. [ Links ]
Mora, E. & Bravo M. 1992. Engorde de concha prieta en una zona de manglar de Bunche. Informe interno INP/PMRC/1992. Guayaquil-Ecuador. 5pp + 9 Tablas + 9 Fig. [ Links ]
Munro, J.L. & D. Pauly. 1983. A simple method for comparison the growth of fishes and invertebrates. Fishbyte 1: 5-6. [ Links ]
Nepita, M.R. & O. Defeo. 2001. Crecimiento del pulpo Octopus maya (Mollusca: Cephalopoda) de la costa de Yucatán, México: un análisis de largo plazo. Rev. Biol. Trop. 49: 93-101. [ Links ]
Pauly, D. & F. Arreguín-Sánchez. 1995. Improving Shepherd´s length composition analysis (SLCA) method for growth parameter estimations. NAGA. ICLARM Q. 18: 31-33. [ Links ]
Pauly, D. & J.L. Munro. 1984. Once more on the comparison of growth in fish and invertebrates. Fishbyte 2: 21. [ Links ]
Pauly, D. & N.C. David. 1981. ELEFAN I, a BASIC program for the objective extraction of growth parameters from length frequency data. Meeresforschung 28: 205-211. [ Links ]
Rosenberg, A.A & J.R. Beddington. 1987. Monte-Carlo testing of methods for estimating growth from lengthfrequency data with general conditions for their applicability, p 283-298. In D. Pauly & G.R. Morgan (eds.). Length-based methods in fisheries research. ICLARM Conf. Proc. 13, Manila. [ Links ]
Shepherd, J.G. 1987a. Towards a method for short-term forecasting of catch rates based on length composition, p. 167-176. In D. Pauly & G.P. Morgan (eds.). Length-based method in fisheries research, ICLARM Conf. Proc. 13, Manila. [ Links ]
Shepherd, J.G. 1987b. A weakly parametric method for the analysis of length composition data, p. 113-19. In D. Pauly & G.P. Morgan (eds.). Length- based method in fisheries research, ICLARM Conf. Proc. 13, Manila. [ Links ]
Stern-Pirlot, A. & M. Wolff. 2006. Population dynamics and fisheries potential of Anadara tuberculosa (Bivalvia: Arcidae) along the Pacific coast of Costa Rica. Rev. Biol. Trop. 54: 87-99. [ Links ]
Urban, H. 2002. Modeling growth of different developmental stages in bivalves. Mar. Ecol. Prog. Ser. 238: 109-114. [ Links ]
Vakily, J.M. 1990. Determination and comparison of growth in bivalves, with emphasis on the tropics and Thailand. Ph.D. Thesis, Christian-Albrechts-Universitat, Germany. [ Links ]
Villalobos, C.R. & A.L. Báez. 1983. Tasa de crecimiento y mortalidad de Anadara tuberculosa (Bivalvia: Arcidae) bajo dos sistemas de cultivo en el Pacífico de Costa Rica. Rev. Lat. Acui. 17: 9-18. [ Links ]
Correspondencia a: Luis A. Flores. Investigación de Recursos Bioacuáticos y su Ambiente, Instituto Nacional de Pesca, Letamendi 102 y La Ria, Guayaquil, Ecuador. P.O. Box: 09-01-15131; lflores@inp.gob.ec
Received 20-I-2010. Corrected 05-VIII-2010. Accepted 01-IX-2010.