Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.57 n.1-2 San José Mar./Jun. 2009
Growth and mortality rates of bigeye tuna Thunnus obesus (Perciformes: Scombridae) in the central Atlantic Ocean
Guoping Zhu1,2, Liuxiong Xu1,2,3, Yingqi Zhou1,2 & Xinjun Chen1,2
1. The Key Laboratory of Shanghai Education Commission for Oceanic Fisheries Resources Exploitation, College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China; gpzhu@shou.edu.cn
2. The Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources (Shanghai Ocean University), Ministry of Education, Shanghai 201306, China.
3. Corresponding author. E-mail: lxxu@shou.edu.cn
Abstract: Age and growth parameters were estimated for bigeye tuna Thunnus obesus Lowe, 1839 sampled
from China longline fisheries in the central Atlantic Ocean from October 2002 to July 2003 and from August 2004 to March 2005. The von Bertalanffy growth parameters were estimated at L8=217.9 cm fork length, k=0.23 year-1, and t0=-0.44 year. The total mortality rate (Z) was estimated to be from 0.82 to 1.02, the fishing mortality (F) and the natural mortality were 0.54 year-1 and 0.39 year-1, respectively. The exploitation ratio (E) was 0.35. This study provides the detailed estimates of growth and mortality rate for bigeye tuna in the central Atlantic Ocean, which can be used as biological input parameters in further stock evaluations in this region. However, age analysis, additional validation of the size composition and stock structure are needed for future studies. Rev. Biol. Trop. 57 (1-2): 79-88. Epub 2009 June 30.
Key words: bigeye tuna, Thunnus obesus, growth, mortality, the central Atlantic Ocean, size frequency analysis, length-weight relationship.
Bigeye tuna (Thunnus obesus Lowe, 1839) are a commercially important species of tunas inhabiting the tropical and subtropical waters of the Atlantic, indian, and Pacific oceans (Sun 2001, Farley et al. 2006). it constitutes an extremely valuable fishery resource intensively exploited by Asian longliners, including China tuna longliners, and targeted as bycatch by US and European purse seiners at various stages of its life cycle (Stéquert and Conand 2000). Little is known about key biological parameters such as its age and growth within the central Atlantic region.
Biological parameters such as age, growth and age (or size) at maturity are vital for accurate stock assessments and management plans to ensure the sustainable development of the fisheries. Age and growth information of bigeye tuna can be obtained from a variety of sources such as (a) length–frequency data (Champagnat and Pianet 1974, Marcille et al. 1978, Weber 1980, Pereira 1985, Fagundes et al. 2001), (b) tagging (Cayré and Diouf 1984, Miyabe 1984, Hallier et al. 2005) and (c) direct aging of calcified tissues such as otoliths (Hallier et al. 2005), scales (Gaikov et al. 1980, Draganik and Pelczarski 1984, Delgado de Molina and Santana 1986) and vertebrae (Alves et al. 1998) (Pauly 1983). Despite this, very few validated age studies have been conducted for large tropical pelagic species like bigeye tuna in the central Atlantic Ocean and the last study of bigeye tuna age and growth was last conducted in the central Atlantic Ocean in later 1980s.
Although the latter two of the above methods are more precise, they are expensive, labor intensive and time consuming. in contrast, length-frequency analysis is inexpensive, easy to apply, and could produce acceptable results (Mytilineou and Sardá 1995). In the present study, data on the age and growth of bigeye tuna in the central Atlantic Ocean are presented. The objective of the present study is therefore to provide the first detailed information on the age and growth of bigeye tuna collected in this area, by using fork length data and the ELEFAN I technique. This will be useful in managing the rapidly developing fishery of bigeye tuna in the Atlantic Ocean.
Materials and methods
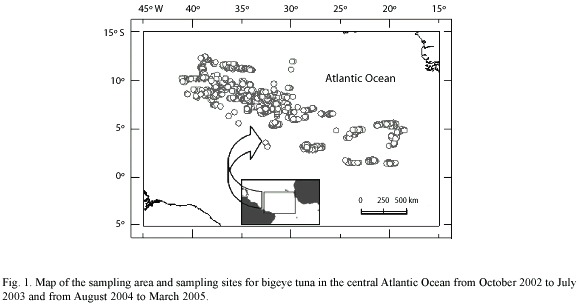
Study area and animal collection: Samples were collected from the central Atlantic Ocean (1º1800"-12º2400" N, 18º3000"41º12 00" W) (Fig. 1) using Chinese longline vessels from October 2002 to July 2003 and from August 2004 to March 2005. Fork length (FL) was measured to the nearest 0.1 cm (and pooled in 5 cm length classes) and round weight (RW) and dressed weight (DW) to the nearest 0.1 kg. The specimens were sexed by inspecting gonad morphology. To examine the temperature experienced by bigeye in the central Atlantic Ocean, using CTD (Conductivity Temperature and Depth sensors, Sea-Bird 37, Sea-Bird Electronics, inc.), daily sea surface temperature (SST) data were obtained from the same Chinese longline vessels in the central Atlantic Ocean at the same periods as above.
Length-weight relationship: The length–weight relationship was calculated by applying exponential regression 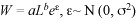 , where W is the round weight (RW) (kg), L the fork length (FL) (cm), a the intercept (initial growth coefficient or condition factor) and b the slope (growth coefficient, i.e., relative growth rate of fish).
, where W is the round weight (RW) (kg), L the fork length (FL) (cm), a the intercept (initial growth coefficient or condition factor) and b the slope (growth coefficient, i.e., relative growth rate of fish).
This equation can also be expressed in its logarithmic form: log W=log a + b log L. The parameters a and b of W–L relationships were estimated by linear regression analysis (leastsquares method) on log-transformed data, and the association degree between variables (W and L) was calculated by the determination coefficient (r2). Regression analysis was employed on log-transformed data for males and females separately and the slopes were tested for significant difference between sexes by means of analysis of covariance (ANCOVA). The hypothesis of isometric growth (Ricker 1975) was tested using the t-test (p < 0.05).
The confidence interval of mean FL was assessed by bootstrapping; 1000 bootstrap pseudo-samples were used.
Growth: The growth process can be described by growth velocity and growth acceleration. Length frequency data were also used o calculate the von Bertalanffy growth rate (k) and the asymptotic length (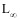 ) by model progression analysis using the program ELEFAN I (Pauly 1987) within the FiSAT program (Gayanilo et al. 1994).
) by model progression analysis using the program ELEFAN I (Pauly 1987) within the FiSAT program (Gayanilo et al. 1994).
Lt = 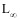 (1-e-(k(t-t0))
(1-e-(k(t-t0))
where Lt = Length at time t; 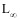 = asymptotic fork length; k=growth constant; t0 = age at length 0, which can be calculated by Paulys empirical equation:
= asymptotic fork length; k=growth constant; t0 = age at length 0, which can be calculated by Paulys empirical equation:
log10(-t0) = -0.3922 - 0.2752log10 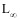 - 1.038log10k
- 1.038log10k
The growth performance index phi-prime 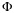 was calculated based on the growth parameter estimates to compare growth parameters obtained in the present work with those reported by other authors because it facilitates the intra and interspecific comparison of the growth performance (Pauly and Munro 1984). This index was calculated by the equation of Pauly and Munro (1984):
was calculated based on the growth parameter estimates to compare growth parameters obtained in the present work with those reported by other authors because it facilitates the intra and interspecific comparison of the growth performance (Pauly and Munro 1984). This index was calculated by the equation of Pauly and Munro (1984):
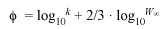
with k = growth constant and 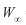 = asymptotic round weight.
= asymptotic round weight.
Mortality: For the calculation of the instantaneous annual mortality rate (Z) the length-converted catch curve (Pauly 1983, Munro 1984) was applied to the pooled length frequency data using the estimated growth parameter. The calculation was done with the FiSAT program (Sparre and venema 1992). The natural mortality was calculated by Paulys empirical equation:
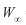 + 0,6757logk+0,4267log T
+ 0,6757logk+0,4267log T
where 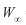 (in kg)= asymptotic round weight; T (in ºC)= the mean annual temperature (in ºC), which is assumed to reflect the sea surface temperature (Pauly, personal communication, Pauly 1980) (in the present paper, T=26.78ºC); M= natural mortality. In order to obtain
(in kg)= asymptotic round weight; T (in ºC)= the mean annual temperature (in ºC), which is assumed to reflect the sea surface temperature (Pauly, personal communication, Pauly 1980) (in the present paper, T=26.78ºC); M= natural mortality. In order to obtain 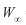 value, the present paper simulated the relationship between dressed weight and round weight using a linear regression analysis. The ANOVA analysis was used to verify if the linear model is appropriate for describing the relationship.
value, the present paper simulated the relationship between dressed weight and round weight using a linear regression analysis. The ANOVA analysis was used to verify if the linear model is appropriate for describing the relationship.
For the calculation of the fishery mortality (F), the above M value was subtracted from the Z value in order to get the fishing mortality (F=Z-M) (Sainsbury 1982, Appeldoom 1984, 1988).
With the known values of F and Z the exploitation rate (E) was calculated according to (Sparre and venema 1992):
E= F (1-e-z)
Z
Results
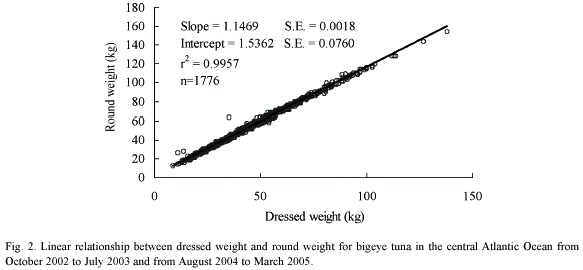
Dressed weight–Round weight relationship: Relationship between dressed weight and round weight was estimated using linear model and led to a determination coefficients (r2 = 0.9957; n = 1776; p<0.001). F value from ANOVA test indicated that the linear model is appropriate for describing the relationship (F = 413911.6; df = 1775; p<0.001) (Fig. 2).
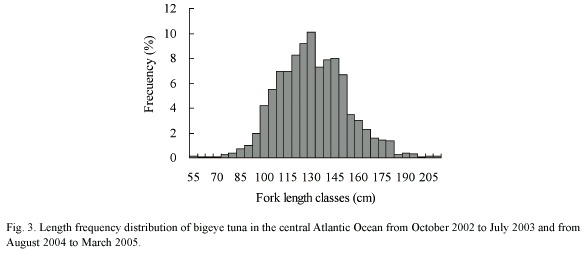
Length–weight relationship: Among 1907 specimens collected, 1772 were used for growth analysis. The length of bigeye tuna ranged between 50 and 206 cm FL and mean FL was 131.3 cm (130.4 – 132.2 cm for the bootstrapped 95% confidence interval) (Fig. 3). The maximum size of males (85-206 cm FL) slightly exceeded that of females (90 - 189 cm FL), while the length of unsexed fish ranged from 50 to 103 cm FL. The mean FL of females and males were 129.9 cm (128.5 -131.3 cm) and 132.3 cm (131.0 - 133.5 cm) respectively.
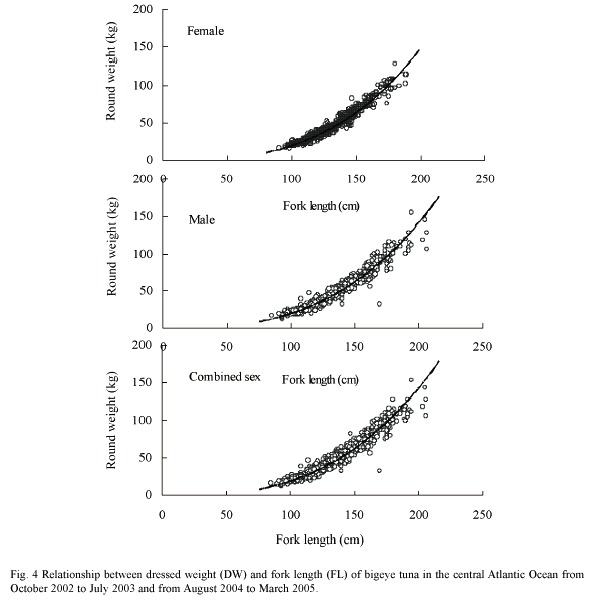
The length-weight relationship was RW=0.00003926FL2.8495 (r2=0.9503, n=1031, S.E.b=0.0203) for males and RW=0.00002601FL2.9362 (r2=0.9567, n=741, S.E.b=0.0230) for females (Fig. 4). The slope was significantly different between sexes (t-test: t=2.826, p<0.001), and significantly lower than the theoretical value of 3 for males (t-test: t=7.414, p<0.001) and females (t-test: t=2.774, p<0.001), indicating negative allometric growth for both sexes. The ANCOVA indicated no significant difference between males and females (p=0.8227>0.05); thus the length-weight relationship with sexes combined was expressed as RW=0.00003376FL2.8813 (r2=0.9526, n=1772, S.E.b=0.0153). The slope was also significantly lower than the theoretical value of 3 for sex combined (t-test: t=7.758, p<0.001).
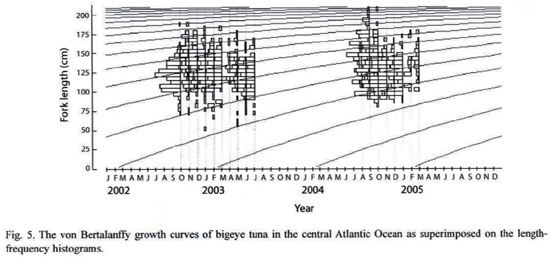
Age and growth: The growth parameters estimated by ELEFAN I routine and the performance index (f) were as follow: 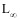 =217.9 cm, k= 0.23 year-1, t0=-0.44, f=0.92. The value of
=217.9 cm, k= 0.23 year-1, t0=-0.44, f=0.92. The value of 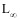 is higher than the maximum observed length (206 cm) (Fig. 5).
is higher than the maximum observed length (206 cm) (Fig. 5).
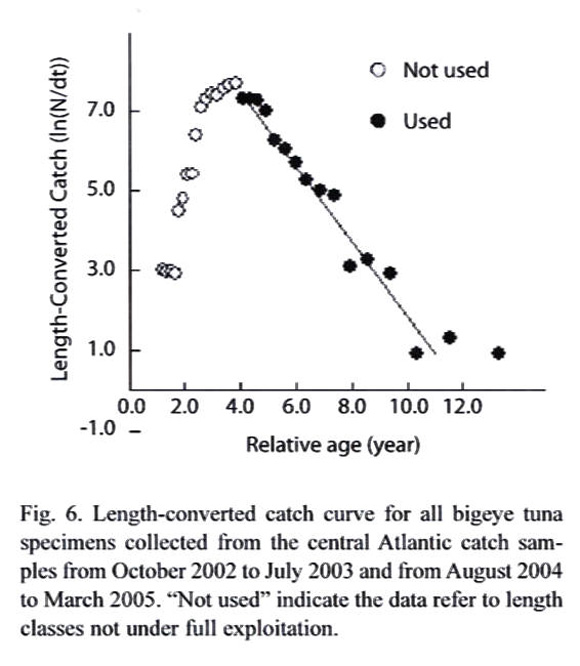
Mortality: The length-converted catch curve is shown in Figure 6. The estimated instantaneous rates of mortality for all fish were Z= 0.92±0.10 year-1, F =0.54 year-1. The instantaneous natural mortality rate (M) obtained using the equation of Pauly (1980) was 0.39 year-1. The reliability of the estimated M was ascertained using the M/K ratio because this ratio has been reported to be within the 1.12 – 2.50 range for most of the fish (Beverton and Holt 1957). The value of M/K ratio was 1.70. The exploitation ratio was E =0.35.
Discussions
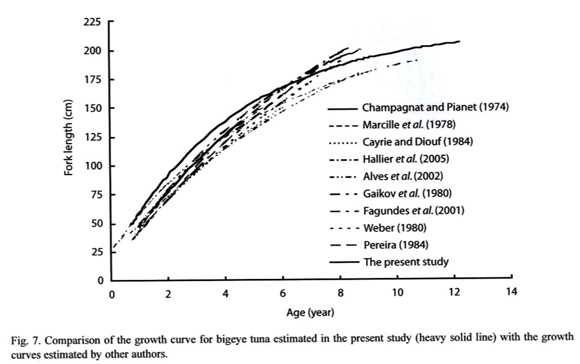
Bigeye tuna growth has been studied by various methods in the Atlantic Ocean (Table 1). Some of these results are illustrated and compared in Figure 7. The study of growth using length-frequency analysis has long been the most frequently used method, even in other oceans, such as the Pacific Ocean (Kume and Joseph 1966, Shomura and Keala 1963, Suda and Kume 1967) and indian Ocean (Marcille and Stéquert 1976).
The size range of the bigeye tuna used in this study was the widest compared with other bigeye tuna growth studies published, and the growth curves estimated from the study agree well with the growth curves estimated earlier by other authors for bigeye tuna using length-frequency analyses and even tagging such as Hallier et al. (2005).To the similar study area, estimations on 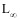 , k and
, k and 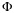 in the present study is close to the results concluded by Draganik and Pelczarski (1984) (
in the present study is close to the results concluded by Draganik and Pelczarski (1984) (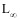 =218.8 cm, k =0.23 year-1 and
=218.8 cm, k =0.23 year-1 and 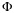 = 0.92), although the latter estimated the growth of bigeye tuna with rays of dorsal fin. Hallier et al. (2005) estimated the growth of bigeye tuna in the Eastern Atlantic Ocean (
= 0.92), although the latter estimated the growth of bigeye tuna with rays of dorsal fin. Hallier et al. (2005) estimated the growth of bigeye tuna in the Eastern Atlantic Ocean (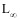 =217.3 cm and k =0.18 year-1), its also near to the result of the present study. Considering results from the published literature, vBGF parameters estimated by different methods and even by the same method, also showed discrepancies for both
=217.3 cm and k =0.18 year-1), its also near to the result of the present study. Considering results from the published literature, vBGF parameters estimated by different methods and even by the same method, also showed discrepancies for both 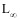 and k values. For example, large difference existed in the results conducted by Weber (1980) (
and k values. For example, large difference existed in the results conducted by Weber (1980) (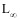 =491.6 cm), Pereira (1985) (
=491.6 cm), Pereira (1985) (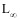 =381.5 cm), and Champagnat and Pianet (1974) (
=381.5 cm), and Champagnat and Pianet (1974) (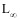 =338.5 cm), lacking of large individuals may be contributed partly to unrealistic high
=338.5 cm), lacking of large individuals may be contributed partly to unrealistic high 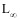 values of Pereira (1985) and Champagnat and Pianet (1974). It is important to understand the consequences of assigning unreliable growth parameters to a fully exploited stock, as predictions of fish populations from models rely heavily on input data, including age and growth (Lessa and Duarte-Neto 2004). According to Potts and Manooch (2002), if samples used in aging studies are not representative of the entire population, model predictions can lead to faulty management decisions.
values of Pereira (1985) and Champagnat and Pianet (1974). It is important to understand the consequences of assigning unreliable growth parameters to a fully exploited stock, as predictions of fish populations from models rely heavily on input data, including age and growth (Lessa and Duarte-Neto 2004). According to Potts and Manooch (2002), if samples used in aging studies are not representative of the entire population, model predictions can lead to faulty management decisions.
Differences in growth patterns can be the result of differences in genetic structure and / or differences in temperature, density of food and diseases (Pauly 1994, Wootton 1998). The comparison of growth performance index of bigeye tuna from the Atlantic Ocean showed that 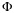 values of bigeye tuna in the Eastern Atlantic Ocean were lower than those in the central Atlantic Ocean (Table 1).
values of bigeye tuna in the Eastern Atlantic Ocean were lower than those in the central Atlantic Ocean (Table 1).
Mortality and exploitation ratio estimates should be taken with caution, as they were estimated from two discontinuous sampling periods and may be biased by annual differences in year class strength. It is rather difficult, and probably unwise, to describe the current position of the stock because of the lack of information on the effect of fishing on the recruitment, behaviour and migration pattern of bigeye tuna in the central Atlantic Ocean.
In conclusion, this study provides the first detailed estimates of growth and mortality rate for bigeye tuna in the central Atlantic Ocean, which can be used as biological input param eters in further stock evaluations in this region. However, age analysis, additional validation of the size composition and stock structure are needed for future studies.
Acknowledgments
We are grateful to the Chinese scientific observers aboard China longline vessels who collected samples. We gratefully acknowledge the captains and crews of the longline vessels "JIN FENG 2 and 3" for permitting the sampling aboard their vessels. Finally, we acknowledge Chen Yong in School of Marine Sciences, University of Maine and two anonymous reviewers for their constructive comments on the manuscript. The present study were sponsored by the Tuna Scientific Observer Program of China grant No. 06472, Shanghai (China) Leading Academic Project grant No. S30702, Special Science and Technology Research Funds for Shanghai Universities and Colleges to Select and Foster Excellent Young Teachers grant No. B-8101-08-0022, innovation Program of Shanghai Municipal Education Commission grant No. 09YZ275 and initial Doctoral Funding of Shanghai Ocean University grant No. B-8202-07-0279.
References
Alves, A., P. de Barros & M.R. Pinho. 1998. Age and growth of bigeye tuna Thunnus obesus captured in the Madeira archipielago. Col. Vol. Sci. Pap. ICCAT 48: 277-283. [ Links ]
Appeldoom, R.S. 1984. The effect of size on mortality of small juvenile conchs (Strombus gigas L. and S. costatus G.). J. shellfish Res. 4: 37- 43. [ Links ]
Appeldoom, R.S. 1988. Age determination, growth, mortality and age of first reproduction in adult queen conch, Strombus gigas L., off Puerto Rico. Fish. Res. 6: 363-378. [ Links ]
Beverton, R.J.H. & S.J. Holt. 1957. On the Dynamics of Exploited Fish Populations. Chapman & Hall, London, UK. 533 p. [ Links ]
Cayré, P. & T. Diouf. 1984. Growth of Atlantic bigeye tuna (Thunnus obesus) according to tagging results. Col. Vol. Sci. Pap. ICCAT 20: 180-187. [ Links ]
Champagnat, C. & R. Pianet. 1974. Croissance du patudo (Thunnus obesus) dans les régions de Dakar et de Pointe Noire. Col. Vol. Sci. Pap. ICCAT 2: 141-144. [ Links ]
Delgado de Molina, A. & J.C. Santana. 1986. Estimacion de la edad y crecimiento del patudo (Thunnus obesus, Lowe, 1933) capturado en las islas Canarias. Col. Vol. Sci. Pap. ICCAT 25: 130-137. [ Links ]
Draganik, B. & W. Pelczarski. 1984. Growth and age of bigeye and yellowfin tuna in the central Atlantic as per data gathered by R/V "Wieczno". Col. Vol. Sci. Pap. ICCAT 20: 96-103. [ Links ]
Fagundes, L., C.A. Arfelli. & A.F. Amorim. 2001. Parâmetros de crescimento e de mortalidade da albacora-bandolim, Thunnus obesus, capturada no litoral sudeste-suldo Brasil (1977-1995). Boletim do Instituto de Pesca, São Paulo 27: 175-184. [ Links ]
Farley, J.H., N.P. Clear, B. Leroy, T.L. Davis & G. McPherson. 2006. Age, growth and preliminary estimates of maturity of bigeye tuna, Thunnus obesus, in the Australian region. Mar. Freshwater Res. 57: 713-724. [ Links ]
Gaikov, V.V., V.N. Chur, V.L. Zharov & P. Yu Fedoseev. 1980. On age and growth of the Atlantic bigeye tuna. Col. Vol. Sci. Pap. ICCAT 9: 294-302. [ Links ]
Gayanilo Jr, F.C., P. Sparre & D. Pauly. 1994. FAO-ICLARM Stock Assessment Tools (FiSAT) User's Guide. FAO Computerized information Series (Fisheries) No 8. FAO, Rome, Italy. 124 p and 3 diskettes. [ Links ]
Hallier, J.P., B. Stéquert, O. Maury & F.X. Bard. 2005. Growth of bigeye tuna (Thunnus obesus) in the eastern Atlantic Ocean from tagging recapture data and otolith readings. Col. Vol. Sci. Pap. ICCAT 57: 181-194. [ Links ]
Kume, S. & J. Joseph. 1966. Size composition, growth and sexual maturity of bigeye tuna, Thunnus obesus (Lowe), from the Japanese longline fishery in the eastern Pacific Ocean. Bull. Inter-Am. Trop. Tuna Comm. 11: 45-99. [ Links ]
Lessa, R. & P. Duarte-Neto. 2004. Age and growth of yellowfin tuna (Thunnus albacares) in the western equatorial Atlantic, using dorsal fin spines. Fish. Res. 69: 157-170. [ Links ]
Marcille, J. & B. Stéquert. 1976. Croissance des jeunes albacores (Thunnus albacares) et patudos (Thunnus obesus) de la côte nord-ouest de Madagascar.Cah. ORSTOM sér. Océanogr. 14: 153-162. [ Links ]
Marcille, J., C. Champagnat & N. Armada. 1978. Croissance du patudo (Thunnus obesus) de locéan Atlantique intertropical oriental. Doc. Sci. Cent. Rech. Oceanogr. Abidjan 9: 73-81. [ Links ]
Miyabe, N. 1984. On the growth of yellowfin and bigeye tunas estimated from the tagging results. Col. Vol. Sci. Pap. ICCAT 20: 117-122. [ Links ]
Munro, J.L. 1984. Yields from coral reef fisheries. Fishbyte 2: 13-15. [ Links ]
Mytilineou, C. & F. Sardá. 1995. Age and growth of Nephrops norvegicus in the Catalan Sea, using length-frequency analysis. Fish. Res. 23: 283-299. [ Links ]
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. ICES J. Mar. Sci. 39: 175-192. [ Links ]
Pauly, D. 1983. Length-converted catch curve. A powerful tool for fisheries research in the tropics (Part I). Fishbyte 1: 9-13. [ Links ]
Pauly, D. 1994. On the Sex of the Fish and the Gender of Scientists: A collection of essays in fisheries science. Chapman & Hall, London, UK. 250p. [ Links ]
Pauly, D. 1987. A review of the ELEFAN system for analysis of length frequency data in fish and invertebrates, p. 7-34. In D. Pauly & G.R. Morgan (eds). Proceedings of the Length-based Methods in Fisheries Research Conference. ICLARM, Manila, Philippines. [ Links ]
Pauly, D. & J.L. Munro. 1984. A simple method for comparing the growth of fishes and invertebrates. Fishbyte 1: 5-6. [ Links ]
Pereira, J. 1985. Observations sur le sex ratio du patudo (Thunnus obesus) aux Acores. Col. Vol. Sci. Pap. ICCAT 23: 237-241. [ Links ]
Potts, J.C. & C.S. Manooch. 2002. Estimated ages of red porgy (Pagrus pagrus) from fishery-dependent and fishery-independent data and a comparison of growth parameters. Fish. Bull. 100: 81–89. [ Links ]
Ricker, W.R. 1975. Computation and interpretation of biological statistics of fish population. Bull. Fish. Res. Board Can. 191: 1-382. [ Links ]
Sainsbury, K.J. 1982. Population dynamics and fishery management of the paua, Holiotis iris I. Population structure, growth, reproduction, and mortality. New Zeal. J. Mar. Fresh.16: 147-161. [ Links ]
Shomura, R.S. & B.A. Keala. 1963. Growth and sexua dimorphism in growth of bigeye tuna (Thunnus obesus), a preliminary report. FAO Fish. Rep. 6: 1409-1417. [ Links ]
Sparre, P. & S.C. Venema. 1992. Introduction to tropical fish stock assessment, part I- Manual. FAO Fish. Tech. Pap. 306: 1-376. [ Links ]
Stéquert, B. & F. Conand. 2000. Preliminary studies of age and growth of bigeye tuna (Thunnus obesus) in the western indian Ocean. IOTC Proceedings 3: 249-255. [ Links ]
Suda, A. & S. Kume. 1967. Survival and recruitment of bigeye in the Pacific Ocean, estimated by the data of tuna longline catch. Nankai Reg. Fish. Res. Lab. Rep. 25: 91-104. [ Links ]
Sun, C.L., C.L Huang & S.Z. Yeh. 2001. Age and growth of the bigeye tuna, Thunnus obesus, in the western Pacific Ocean. Fish. Bull. 99: 502-509. [ Links ]
Weber, E. 1980. An analysis of Atlantic bigeye tuna (Thunnus obesus) growth. Col. Vol. Sci. Pap. ICCAT 9: 303-307. [ Links ]
Wootton, R.J. 1998. Ecology of Teleost Fishes. Kluwer Academic Publishers, Dordrecht, Netherlands. 386p. [ Links ]