Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.50 n.2 San José Jun. 2002
Matthias Wolff
Zentrum für Marine Tropenökologie (ZMT), Fahrenheitstraße 6, D 28359 Bremen, Germany, e- mail: mwolff@uni-bremen.de, fax: ++ 49 421 2380030
Received 01-XI-2000. Corrected 31-V-2002. Accepted 31-V-2002.
Abstract
The present article gives an overview on the leading concepts and modelling approaches for marine ecosystems research including (1) The trophodynamic theory of pelagic ecosystems, (2) Compartment/network models, (3) Mesocosm experiments and (4) Individual based modelling approaches and virtual ecosystems (VE). The main research questions addressed, as well as the potential and limits of each approach, are summarized and discussed and it is shown how the concept of ecosystem has changed over time. Aquatic biomas spectra (derived from the theory of pelagic ecosystems) can give insight into the trophic structure of different systems, and can show how organism sizes are distributed within the system and how different size groups participate in the systems metabolism and production. Compartment/network models allow for a more detailed description of the trophic structure of ecosystems and of the energy/biomass fluxes through the explicit modelling of P/B-and food consumption rates and biomasses for each system compartment. Moreover, system indices for a characterization and comparison with other systems can be obtained such as average trophic efficiency, energy throughput, and degree of connectivity, degree of maturity, and others. Recent dynamic extensions of trophic network models allow for exploring past and future impacts of fishing and environmental disturbances as well as to explore policies such as marine protected areas. Mesocosm experiments address a multitude of questions related to aquatic processes (i.e. primary production, grazing, predation, energy transfer between trophic levels etc.) and the behaviour of organisms (i.e. growth, migration, response to contaminants etc.) under semi-natural conditions. As processes within mesocosms often differ in rate and magnitude from those occurring in nature, mesocosms should be viewed as large in vitro experiments designed to test selected components of the ecosystem and not as an attempt to enclose a multitude of interacting processes. Models that use individual organisms as units can provide insight into the causes of natural variability within populations (growth, phenotype, behaviour) and into the role of intraspecific variation for interspecific processes, succession, and feedback mechanisms. In biological oceanography, interdisciplinary research is increasingly using "Virtual Ecosystems" to simulate non-linear interactions between the dynamics of fluctuating ocean circulation, the physics of air-sea interaction, turbulence and optics, biogeochemistry, and the physiology and behaviour of plankton, which can be compared with real observations. The different approaches available for the analysis of aquatic ecosystems should be seen as complementary ways for the description and understanding of ecosystems. The modern view of marine ecosystems, as has emerged from ecosystem analysis over the last decades, is that of a composite of loosely coupled subsystems of desynchron dynamics which through their combined action maintain the fundamental structure and function of the whole.
Key words: ecosystem analysis, models, concepts, marine, tropics.
"The Problem of Science is to understand
the proper domain of each abstraction rather
than becoming its prisoner"
Levins & Lewontin 1980
The evolution of ecological concepts
Since Darwin, it is widely accepted, that biological phenomena can best be understood from a historical perspective and it seems that the same holds for scientific theories and concepts, including those for the analysis of biological processes and the description of ecosystems. Analogous to the species of an ecosystem, concepts and theories are changing but their renewal is only possible if the old ones are continuously being tested for their validity.
A multitude of expressions such as trophic levels, climax systems, ecological stability, systemss hierarchy, cybernetic control, maximum power principle, succession, holistic etc. have been introduced into ecology at different times in the evolution of this science and it can be recognized that some of these terms are not always used adequately and within the proper context. It seems that different ecologists prefer certain terms (and concepts which stand behind) and avoid or reject others. This is also a reflection of the fact that (marine) ecology, possibly more than other sciences, has branched into many different sub-disciplines (i.e.fisheries biology, biological oceanography, planktology etc.) with high degrees of specialization and little communication between them. If we want to predict ecosystem response to human impact through pollution, overfishing, habitat destruction etc. or to global warming and sea level rise, we need to adopt a synoptic view in order to integrate the findings of the ecological subdisciplines and to ask for the adequacy of available concepts for holistic and quantitative ecosystem studies. As stated by Longhurst (1981): "...one of the principal failures of marine ecologist in recent years has been to become so intellectually involved in the pursuit of processes, and the measurement of rates as to neglect synthesis of their findings into quantitative descriptions of ecosystems".
It seems natural that each scientist and university teacher ultimately uses those terms and studies those aspects of nature which he/she is interested in and it is obvious that there are many ways to describe, study, and analyse ecological phenomena. Since the early days of the marine sciences, traditions or "schools of thoughts" have developed, of which some continue to exist in modern times.
As a result, students of marine ecology in Germany or Chile may be trained to adopt different ecological views. In the first case, they may be told that "relevant ecology" should focus on studying the dynamics of populations and the energy fluxes within ecological systems, while in the latter they might learn that the search for the forces that shape the species structure of living communities is much more relevant, instead. What seems to be missing in many university curricula is to provide students with an overview of leading concepts and their roots.
In the present article this is attempted and those basic concepts and approaches are sketched which, in the opinion of the author, are the most relevant and which have shaped marine ecosystem research over the last decades. Their respective relevance for the understanding of ecosystem function is discussed. The author is aware that the presentation is very condensed and subjective.
The introduction continues with a sketch of the roots of todays ecosystem concepts and with the fundamental problems related to the ecosystem definition. In the following section leading concepts and approaches for marine ecosystem research are described and related research questions are formulated. In the final section of this review a summary is given and those modern concepts are presented that help to explain the functioning and persistence of ecosystems.
The roots of the ecosystem concept - a short look into the past
Ecology emerged as a science strongly founded by Darwinism. While for Darwin the species were the basic units for selection, ecologists also considered the species populations as units for ecological studies. Ecosystems were seen as the result of the evolution of species and their competitive struggle for the niches in the environment. Darwins theory is based on the Malthusian axiom (Malthus 1806) that organisms produce more offspring can survive. This results in the "survival of the fittest" and makes evolution possible. Many ecologists perceived ecosystems as a network of interacting populations, the abiotic environment was seen as the mere background of the action. While early descriptions about ecological interactions between species can be found in Darwin (1859), Haeckel (1866) was the first to create the name Ecology for the science of the interrelationship between species. Considering species populations as discrete units of an ecosystem seemed straightforward and many phenomena (i.e. predation, competition, population growth) can successfully be investigated by this approach.
In Oceanography, the functional trophic relationships between plant and animal populations was emphasized quite early (Möbius 1877) when it became evident that the fishery yield was the result of a chain of processes that involved plants as well as animals. Early quantitative thoughts finally led to the modern processoriented approach of marine ecology. Elton (1927) laid the groundwork for this approach with his "concept of numbers". He showed that the number of organisms decreases with their size and this was related to the fact that energy was flowing from the "small" primary producers to the "large" predators. In his book "The Animal Community" (Elton 1927) he stressed the fundamental importance of size for ecological processes and laid the basis for the modern theory of pelagic ecosystems.
Surprisingly, it almost took half a century until this theory was further elaborated (Platt and Denman 1978). Based on the ideas of Elton, Lindemann (1942) introduced the concept of "trophic levels" which still seems to dominate marine ecology, although some ecologist consider it more as "dead end" for conceptionalizing ecosystems (Cousins 1980) (see further below).
E.P. Odum (1953), based on the ideas of Elton and Lindemann, gave energy flow studies a central importance for the study of ecosystems. Due to his orientation on processes, this functional approach made it also possible to trace the matter transport through the ecosystem and to study feedback processes.
Patten and Odum (1981), and others (Quinlin 1975, Innis 1978) perceived ecosystems as cybernetic self-regulated systems of high organization in which energy, information flux and feedback control mechanisms are essential qualities.
This cybernetic approach leads back to the concept of living communities as "superorganisms" (Clements 1916, Phillips 1934, Thienemann 1918, 1941, von Uexeküll 1921,1928) and organismic terms like growth, maturation and death were introduced into ecosystem ecology. According to Clements, a species community (the word ecosystem as yet did not exist) was a closed unit that reacted uniformly to environmental gradients. This idea was based on plant communities but reappeared later (Elton 1927, Allee et al. 1949). Gleason (1917,1939) was a strict opponent of this concept and emphasized the role of the individual species and its relation to the abiotic environment. He perceived a community as a simple assemblage of species populations with similar abiotic requirements.
The controversy between "Clementsian" and "Gleasoninan" views on the characteristics of communities still exist today and is reflected by the differential use of the terms "community" and "assemblage".
The definition of ecosystem
The most accepted definition of ecosystem dates back to the British botanist Sir Arthur Tansley, who is considered one of the founders of ecosystems ecology. He (Tansley 1935) defines Ecosystem as: "the whole system including not only the organism complex, but also the whole complex of physical factors forming what we call the environment of the biome, the habitat factors in the widest sense. Though the organisms may claim our primary interest, when we are trying to think fundamentally we cannot separate them from their special environment, with which they form one physical system. It is the systems so formed which, from the point of view of an ecologist, are the basic units of nature on the face of the Earth".
This definition does not contain the idea of the "superorganism" and Tansley was indeed considered to be an "Anticlementsian". Nevertheless he uses the term "system" and continues: "The gradual attainment of more complete dynamic equilibrium...is the fundamental characteristic of (ecosystem) development. It is a particular case of the universal process of the evolution of systems in dynamic equilibrium. This equilibrium attained is, however, never quite perfect."
Here, the idea of a predetermined development towards an equilibrium state is clearly expressed. Evans (1956) extended this concept and identified the following essential elements of an ecosystem: (1) the living functional components such as primary producers, destruents, herbivores, predators and parasites that form a complex trophic web and (2) the non-living components which interchange energy and materials through evaporation, precipitation, erosion and sedimentation. He perceived the ecosystem as open to the flux of energy and materials from outside.
Concerning the time-space dimension of ecosystems, different views can be found in the literature. For Bosserman (1979) an assemblage of macrophytes might be an ecosystem, for others a decaying tree or water puddle after a rainfall. A comprehensible definition was given by Weiss (1971): "An ecosystem is a complex unit in space and time, whose sub-units maintain by systematic cooperation its internal structure and function and tend to reestablish it after a destructive perturbation".Weiss knew that the analogy to the organism had only limited value as, contrary to the ecosystem, the organism already contains in the fertilized egg all the plans which define the development of the organism in space and time. Moreover, the relations between its different components (organs, cells) are much more relevant for the maintenance of the organism than the species and communities of an ecosystem.
Following Weiss, but also Tansley, the fundamental attributes of an ecosystem can be summarised as: unity, complexity, self-regulation and the exchange of energy and matter with its external medium. It is evident from the foregoing that ecosystems are by definition dimensionless and therefore represent the least delimited hierarchical level of life. If it were possible to generalize for ecosystem attributes over different scales this would not be such a problem but attributes like biomass, process rates, species richness, and observed variability seem to depend strongly on the scale of observation (Sissenwine 1984 and see Wiens 1989 for a review).
Modern concepts and approaches for marine ecosystem research
1. The trophic theory of pelagic ecosystems ("allometry as universal principle")
Based on Eltons pyramid of numbers (Elton 1927), Platt and Denmann (1978) elaborated a trophodynamic theory of pelagic ecosystems. Elton had already stated that the density (numbers) of organisms declines with increasing organism size, that the prey size is related to that of the predator and that the elementary flow of energy goes from the small organisms to the large ones (this concept does not seem adequate for terrestrial systems, when thinking of little insects that forage on large trees). Eltons main conclusion was that the prey biomass required for the maintenance of a predator was a function of two attributes: the metabolic requirement of the predator and the productivity (generation time) of the prey.
Fenchel (1974) systematically investigated the relationship between size and metabolic activities such as respiration and growth and could show, as others before him (Huxley 1932, Brody 1945, Kleiber 1961), that, within a common body design plan, size was the most decisive attribute for the food requirement, longevity and productivity (generation time) of the organism. This general relationship is given by: y = a Mb . Here, the exponent "b" is the allometric measure that describes the effect of size (M) on the metabolism (y). At the log-log- presentation of the above equation, "b" represents the slope and "a" characterizes the organismic group. The "b" -value remains fairly constant for most groups of organisms, aquatic organisms included (Ikeda 1985), while "a" differs significantly between organisms of different degrees of organization. Warm-blooded animals have much higher "a" values than cold-blooded metazoa due to their additional energy need for thermoregulation. Similar differences can be found between metazoans and protozoans (Wieser 1986).
As "b" is always <1, the mass-specific metabolism (i.e. the metabolism per gram body weight) decreases with body size, which means that populations of small animals use much more energy than those of large ones if both have the same population biomass. It is known that smaller organisms are much more numerous than larger ones and the question arises, how the individual energy use is related to the density of organisms in the system. Damuth (1981) studied this problem for terrestrial herbivores and found population densities to scale to M -0.75 , the direct opposite of the metabolic rate (b = 0.75). This "design constant" (Calder 1985) means, that small and large organisms would use up about the same amount of energy in the system. If this was correct, the population biomass should increase with the weight of the organisms. In the meanwhile these findings of Damuth (1981) were found not to hold generally.
Almost a decade earlier, Dickie (1972) postulated that the size-dependence of ecological processes should be the key for understanding the energy flow within pelagic systems. He proposed to leave Lindemanns (1942) concept of discrete trophic levels and to replace it with that of a continuous biomass spectrum. Sheldon et al. (1972) were the first then to publish particle size spectra of pelagic ecosystems and found them to be more or less flat and continuous. This led the authors to speculate that this flatness of the biomass spectrum is characteristic for the complete size range within the system and that the "standing crop" should be of the same order of magnitude on all trophic levels. They, however, showed that the biomass spectra could well differ between marine areas.
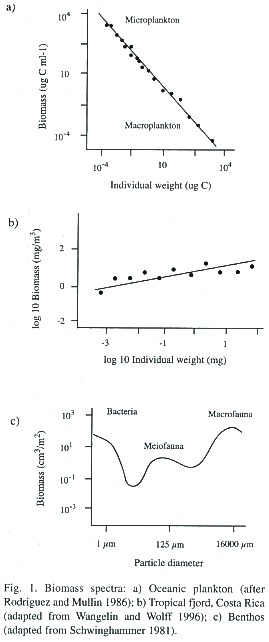
For the construction of the biomass spectrum, the (log) biomass of organisms of a certain weight class is plotted against their (log) individual weight and this is done for a wide range of sizes (weights). This yields a sequence of points in the co-ordinate system which can then be described by a fitted line or curve. From this graph it can be seen whether the biomass spectrum is continuous or discontinuous and whether its slope is positive or negative (Fig. 1a,b and c). Continuous spectra are assumed to reflect a tightly coupled system in which the energy continuously flows from one size group to the other. A positive slope is indicative of a biomass dominance of larger organisms over smaller ones; a negative slope would indicate the opposite. As production and respiration is also a function of body size, the respective contributions by each size class in the system can be determined as well.
The studies of aquatic systems do not seem to confirm the findings of Damuth (1981) in which biomass increases with individual size. Rather, the opposite seems true. Rodriguez and Mullin (1986) showed that biomass in aquatic systems decreases with body size. The literature seems contradictory, however. Gaedke (1992) reports a rather flat biomass spectrum in Lake Konstanz ranging from small bacteria to large crustacea and Rodhouse et al. (1994) observed, in studying the nekton community in the Scottish Sea, an increase of biomass with organism size. Wangelin and Wolff (1996) report similar results for zooplankton- biomass spectra in the tropical Pacific of Costa Rica (Fig. 1b).
Some authors have tried to extend this approach to non-pelagic systems (Fig. 1c.). Warwick (1984) studied the biomass distribution over a range of benthic communities and found maxima around the size (weight) groups of 3.1mg and 0.64 µg, corresponding to a macrofauna and meiofauna peak. He speculated that these peaks represent the result of an evolutionary optimization in which sessile (macro) fauna might best be adapted around this first size at the sediment-water interface, where the sediment is the limiting factor, while the mobile interstitial (meio) fauna living between the sand particles would best be adapted around the other size peak. Schwinghammers (1981) studies confirmed these findings and also found an additional biomass minimum around 10µm, a size at which the small unicellular organisms (bacteria and algae) that live on the surface of sand grains separate from the larger motile interstitial fauna.
The results of the benthic studies show the problems associated with the use of biomass spectra for ecosystem analysis; particular physiological adaptations and other particularities of organisms of certain sizes are not taken into account. Moreover, it is known that the parameter "a" of the allometric equation increases with the degree of organization of the organisms (Wieser 1986) so one should expect a jump in the biomass spectrum from one organization type of organism to the next. Aside from this problem, there is the difficulty of standardization of sampling for the size (weight) determination of organisms. It is always easier to do the respective calculations with small-sized and round-shaped protozoa than for organisms of a complex body form. There is no method available at present that would circumvent these problems (Rodhouse et al. 1994). Some authors state that it would make more sense to construct biomass spectra for individual functional groups than over a range of functional groups (Bahr 1982, Cousins 1980, Rodhouse et al. 1994).
As biomass spectra require relatively easily obtained information and are capable of answering important questions (see also Table 1), they could be constructed as a first step in describing the trophic structure of an ecosystem. As it is also quite cheap, it seems that there is much scope for its use, especially in tropical seas (Wangelin and Wolff 1996).
Concepts and models for marine ecosystem research and related research questions
1. Biomass spectra (trophodynamic theory of aquatic ecosystems)
How are different organism sizes distributed within the system? What sizes dominate the system biomass?
How much does each size group contribute to the system metabolism and productivity?
How does the trophic structure of different pelagic ecosystems differ and why?
How do biomass spectra change after anthropo genetic disturbances (pollution, over fishing) of pelagic systems?
Can they be used as quick methods to detect important changes?
2. Trophic compartment / network models
What are important functional system compartments, their P/B rates, food consumption and production rates?
How are the compartments trophically linked and how much biomass is cycled between them?
What is the average trophic efficiency of the system? How much of the primary production enters the fishery (= fisheries efficiency of the system)? How long are the feeding path lengths?
What is the degree of interconnectivity of the system?
What is the total energy throughput of the system?
What is the systems degree of maturity and robustness against perturbations?
3. Mesocosm experiments
How do different levels of nutrients affect primary production?
How does grazing/ predation affect the productivity of phytoplankton and submerged algae?
How do eutrophication and/or pollution affects aquatic organisms and/or functional system compartments (benthos, plankton)?
How do different groups of organisms behave (grow, feed, swim etc.) under semi-natural conditions of the mesocosm?
How do they trophically interact?
Is species richness of a mesocosm system relating to stability of the system?
4. Individually-based (simulation) models and virtual ecosystems (VE)
What is the natural variability of organisms within a population (growth, phenotype, behaviour) and what are the causal factors?
What is the role of intraspecific variability for interspecific interactions and successions? How do feed- back mechanisms work?
What are the key-role species of the system?
How can smaller scale processes explain large-scale patterns?
How can observations and theory be integrated to realistically simulate complex systems?
2. Trophic compartment ("box") models
These models can be seen as a further development of the above approach. They are based on the "Malthusian axiom" (see above), according to which the "higher" organisms, are the ones that order the ecosystem by consuming the surplus produced at lower trophic levels. The ecosystem is thus defined through the metabolic requirements from above (apex predators) to the lowest level (primary producers) ("top down" concept) (Polovina and Ow 1985, Polovina 1984, Christensen and Pauly 1992,1993). As the fishery is generally using the higher predators, the data base for these compartments is usually better than for the lower trophic levels. The approach was originally developed by fisheries scientists who claimed that the traditional single species modelling of fish resources should be replaced or at least complimented by a holistic and quantitative description of the trophic interrelations within the entire system.
To construct a model, the biotic diversity of the system is reduced by defining functional compartments, into which populations of similar generation times, diet spectra and consumption rates are grouped. In doing so, it is assumed that each ecosystem has a certain redundancy, i.e. several species of the same or similar function.
From the structure of the network and the fluxes of biomass between the model compartments, several ecosystem descriptors can be derived: index on complexity, number of trophic levels, ecological efficiency, relation between system primary production and system biomass, and many others for the characterization of the structure and degree of growth and development of the system (Ulanowicz and Mann 1981, Ulanowicz 1986, Baird and Ulanowicz 1993). This approach allows comparison of ecosystems quantitatively and grouping according to their degree of maturity and capacity for resistance to perturbations (Christensen and Pauly 1993, Rutledge et al. 1976, Wolff 1994a, Wolff et al. 1996). In a way, Odum had already tried this in a qualitative way when he published his 22 attributes for ecosystem maturity (Odum 1969).
These models assume a steady state in which the biomass fluxes within the system are balanced. This assumption requires that the temporal scale for the modelling is adequately chosen.
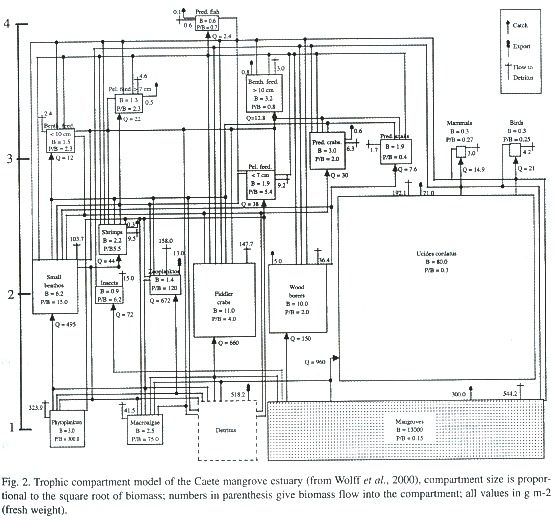
Their great advantage is that a large quantity of data can be integrated to give a holistic description of an entire ecosystem in which the important components (including resources), on one hand, but also the biomass fluxes between them, can be presented. As these models are based on average (usually yearly) rates of consumption and production for organisms along a wide size spectrum, the multiscale problem of ecosystem research is taken care for. All values for compartment biomass and fluxes are given on an area basis, exports (i.e. fishery catch) from and imports to the system are explicitly considered (Fig. 2).
Compared to the biomass spectrum approach, these trophic models seem less reductionistic as not only the size is used as criteria for the species grouping into compartments, but also other important ecological characteristics such as P/B rates, consumption rates, and the diet. Herbivorous and carnivorous fish, for example, would be grouped into different compartments due to their differences in diet as would be penguins and similarsized fish due to their difference in production and consumption rates.
Both approaches focus on the structure of the biomass fluxes in the system and the production characteristics of the system compartments. While system comparisons can be done with these approaches (Baird and Ulanowicz 1993, Christensen and Pauly 1993) their capacity for prediction of system behaviour under conditions of change (natural or anthropogenic perturbations) has been very limited. Recently, however, a new, dynamic version of trophic network models (Ecopath with Ecosim) has been developed (Christensen and Walters 2000) which allows the exploration of past and future impacts of fishing and environmental disturbances. Ecosim models can be replicated over a spatial map grid (Ecospace) to allow exploration of policies such as marine protected areas, while accounting for spatial dispersal/advection effects. Additional inputs are movement rates used to compute exchanges between grid cells, estimates of the importance of trophic interactions (top down vs. bottom up control), and habitat preferences for each of the functional groups included in the model. A key prediction of Ecospace is spatial "cascade" effects, wherein prey densities are low where predators are abundant, for example in protected areas or areas where fishing costs are high (Walters et al. 1999). In using the Ecosim software for the Peruvian upwelling system, Walters et al. (1997) demonstrated that predicted values of fishing mortality to achieve maximum sustainable yield (FMSY) for anchovies were more than twice as high under the assumption of bottom– up control as those predicted under the assumption of top-down control (predator limitation). The alternation of sardine and anchovy in the Humboldt current system was evident under assumptions of top-down control mechanisms, but not so if only resource competition was considered in the simulations.
Over the last decade, trophic network models have increasingly been used, not only for temperate, but especially for tropical systems (Christensen and Pauly 1992, Wolff et al. 1996, 1998, 2000). The insight about the biotic structure, fisheries efficiency and other characteristics of these systems has strongly increased since.
3. Micro/mesocosm- approaches
The basic idea with these approaches is to enclose the ecosystem under study. This normally requires a scaling down of the system and the inclusion of the relevant components in a much smaller space than that in which they normally occur in the wild. The problem lies thus in how to scale the miniature so that it can still function as a reasonable facsimile of the wild ecosystem.
In marine ecological studies, experience has indicated a certain relationship between the amount of water required and the trophic level of the organism of interest (Boyd, 1981). Menzel and Steele (1978) describe this relationship as logarithmic. In all these systems a decision must be made as to the highest trophic level to be investigated.
The pioneering work on large in situ enclosures of seawater (McAllister et al. 1961, Anita et al. 1963) dealt only with phytoplankton and bacterial assemblages. The intent was to estimate primary production from changes in the concentrations of CO2 and O2 . These estimates could then be compared with direct counts of algal numbers and with estimates of the 14C techniques. Results pointed out the importance of the loss of dissolved organic matter by phytoplankton when considering total production, dissolved organic matter, and the substrate of bacterial populations in the seawater. Nutrient depletion was studied in more detail in the tower tank of Scripps Institution of Oceanography (Strickland et al. 1969).
Another attractive use of microcosms is for the examination of trophic interactions of defined populations of phytoplankton and zooplankton. Parsons et al. (1977), after fertilizing enclosures with varying levels of nutrients, followed the production and changes in biomass of phytoplankton, copepods, and ctenophores and showed an inverse relationship between primary production and the efficiency of production at the tertiary level. This and other similar studies (Paffenhöfer 1976, Mullin and Evans 1974, Reeve and Walter 1976) contributed significantly to the understanding of processes occurring at the lower end of the food chain.
Fishes have only occasionally been added to microcosms, perhaps because it has been realized that more fundamental mechanisms of nutrient uptake and the growth of phytoplankton and zooplankton must be better understood before yet another trophic level can be added. Some experiments supported the concept that size of the food particle influences the efficiency of growth in fish (Paloheimo and Dickie 1966, Parsons and LeBrasseur 1970). The complexities inherent in a microcosm containing four trophic levels (phytoplankton, copepods, ctenophores, and fish) (Sonntag and Parsons 1979) are very high. Boyd (1981) points out that the associated difficulties are not much less than those encountered when working in the open sea. Most recent mesocosm studies continue with the research on phytoplankton dynamics as related to nutrient conditions and/or predation.
Several authors (Doering et al. 1986, Porter et al. 1996) have used the microcosm approach to address the bentho-pelagic coupling. Doering et al. (1986), for example, analysed the effect of filter feeding clams on carbon cycling and showed that system production, net and gross sedimentation of carbon and benthic demineralization were all greater in mesocosm enclosures containing clams than in control enclosures. They concluded that the higher production was due to greater fluxes of dissolved inorganic nitrogen from the benthos and found that about 30-46% of the excess biomass produced per day was consumed by clams.
Several recent studies deal with the effect of waste water solids (Costello and Read 1994, Maughan and Oviatt 1993) or other pollutants (Van-Wijk and Hutchinson 1995) on marine organisms including red tide organisms, others involve in situ studies on larval behaviour of invertebrates (Brooke and Mann 1996; Davis et al. 1996), or predation on fish larvae (Brodeur and Bailey, 1994, Cowan and Houde 1991, Houde et al.1994). Baretta-Bekker et al. (1994) used mesocosm experiments to test the microbial loop concept by comparing mesocosm data with results from a dynamic simulation model.
The results of many of these and other studies show that, in spite of attempts to achieve a simulation of nature, processes within micro/mesocosms seem to differ in rate and magnitude from those occurring in nature. One should possibly view microcosms as large, in vitro experiments designed to test selected components of the ecosystem and not as an attempt to enclose a multitude of interacting processes.
So far most microcosm experiments have been conducted in temperate waters. Comparative studies in tropical waters should greatly improve our knowledge about the differences in biotic processes (i.e., plankton growth rates and nutrient uptake, rates of zooplankton grazing, seasonal dynamics etc.) between tropical and temperate regions.
4. The individual-based modelling approach and virtual ecosystems (VE)
Advocates of the individual-based modelling approach try to describe the attributes of each individual and the mechanisms of the interaction between individuals and the environment. They emphasize the fact that abiotic and biotic time-space discontinuities (i.e. light and current conditions for the settlement of algae spores or distribution of prey organisms for a predator) might heavily influence the development of populations and communities.
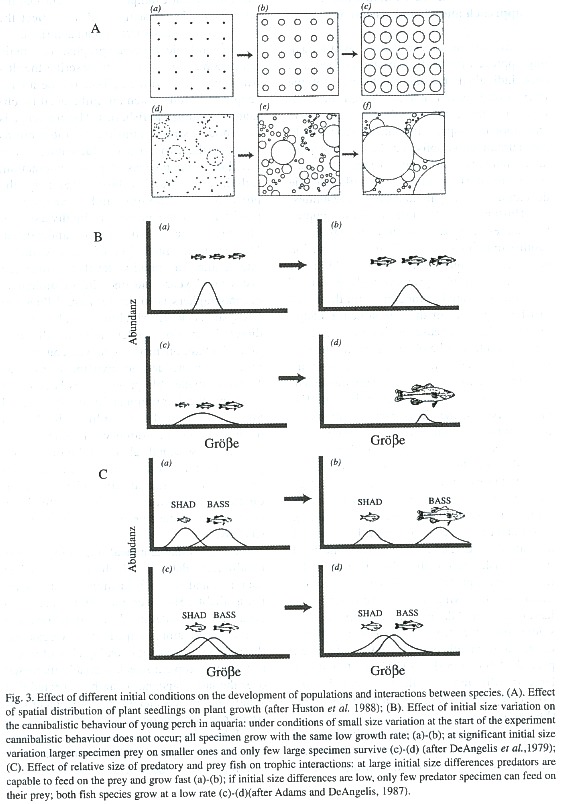
Huston et al. (1988) showed how complex and large-scale patterns in ecosystems can result from simple mechanisms of interaction between individuals on a small-scale. Plant seeds, for example, grow very differently if they are collocated at random, with the result that heterogeneity of the size structure of the growing plants increases with time (Fig. 3A). Similar results can be obtained for marine sessile filter feeders. The resulting size structure of the populations is, thus, strongly dependent on the initial conditions of settlement. For mobile species, the time-space variability of food can have a similar effect. DeAngelis et al. (1979) observed in experiments with bass that, depending on the size variation of fish at the start of the experiment, cannibalism of large over small individuals may or may not occur (Fig. 3B). Neyman (1949), Paloheimo (1971), Beyer and Laurence (1980), and others showed a positive feedback between growth and food intake in fish larvae with high daily food intake increasing the probability of higher food intake during the following days and, consequently, larval survival. Adams and DeAngelis (1987) studied the effect of varying spawning patterns of the large mouth bass (LMB) and its main prey, the "threadfin shad (TS)", and found that large size differences of the LMB could result from quite small initial size differences of TS (Fig. 3C).
It is easy to imagine how mechanisms, as those described above, can strongly determine the succession of communities. In the case of the above plant example, it is evident that the adult plant size structure will also affect the structure of the associated fauna and flora.
In biological oceanography, the main concern has always been to describe the distribution of life with emphasis on the microscopic plankton, which are influenced by climate, pollution and fisheries. The challenge is enormous since non-linear interactions between the dynamics of fluctuating ocean circulation, the physics of air-sea interaction, turbulence and optics, biogeochemistry, the physiology, pathology and behaviour of plankton and the enormous biodiversity of plankton species have to be understood. Mathematical simulation of these complex interactions has rapidly developed over the last several years and one aim of biological oceanographers is to create Virtual Plankton Ecosystems (VPE) which perform better than direct observations in describing the distribution of plankton in the sea, yet contain the information needed to explain it (Woods 1998). Considerable progress has been made
by using the Largrangian Ensemble method (Woods 1998) and the resulting simulations do quite well in describing climatological distributions,seasonal plankton blooms, zooplankton migration or predicting the plankton response to increased atmospheric carbon dioxide ("plankton multiplier effect", a decrease in primary production with a rise in CO 2 (Woods 1998)).
Complex mathematical simulation models require large data sets which in many tropical countries and research institutions, are as yet not available. However, through the access to oceanographic satellite data and to research data of international expeditions (Vargas and Wolff 1996), the quantity and quality of scientific data of tropical seas has greatly increased over the last years and it can be expected that simulation models and VPEs for tropical seas are increasingly gaining in importance.
Table 1 gives a summary of the concepts and approaches presented here with a list of research questions addressed.
Modern concepts of ecosystem function and persistence
Communities and ecosystems have always been subjected to change during the course of evolution but despite these changes, many have remained relatively stable over long geological periods (i.e. coral reefs, rain forests). Over the last decades the rate of change has drastically increased for many systems, however, due to the impact of human activities. Central issues for modern ecosystem research are, therefore, to quantify observed changes, to understand the forces that cause them, and to find out about the capacity of ecosystems to maintain structure and function under conditions of stress or to reestablish both after perturbations.
The problem is that conclusions about the degree of ecosystem damage strongly depend on the ecosystem concepts used by the observer. If studies are focussed on the main ecosystem functions (primary production, respiration, photosynthesis, flux of essential elements) a greater stability is most probably found (even under conditions of perturbations) than if species diversity or population sizes are studied. In short, ecosystem modellers, conservationists, or fisheries ecologists most probably diverge in their opinions when judging the same system.
How do ecosystems manage to persist despite the known perturbations and observed variations at lower hierarchical levels? Several authors have addressed this question.
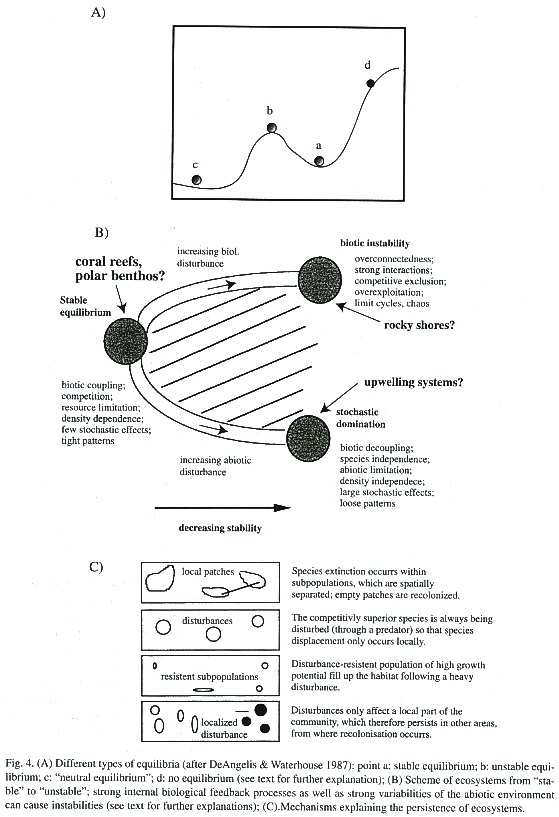
In a classical paper, De Angelis and Waterhouse (1987) try to visualize the related complex problems of stability, equilibrium and scale by a simple theoretical example (Fig. 4A). Each of the balls (c, b and a) represents a different stability point: (a) is of high stability, as it would immediately return to its original position after being moved away from it. Globally, it is not stable, however, as it would not return to its position, once it was taken over the hill (b) or to the point (d). (b) represents an unstable point. Smallest changes would take it away from its position. (c) can be seen as a neutral stability point with no tendency to move back to its position, when moving.
To clarify the problem of scale, the authors suggest Fig. 4A to be under water. Depending if (d) was a pollen grain, sand grain or a pistol bullet, the trajectory would be quite different: in the first case of the pollen grain, nothing would probably happen as the specific weight is so low that it would stay were it is or would float in the water; in the second case, the sand grain would probably fall down the hill and would finally remain in the region of (a); in the third case, the pistol bullet would shoot over the hill (b) to disappear. This example shows, how the equilibrium concept can make sense for a certain spatial scale (in the above example, only in the case of the sand grain) but not for another.
De Angelis and Waterhouse (1987) describe three categories of communities along a gradient from stable equilibrium to non-stable systems (Fig. 4B). According to this concept, there are systems of high stability as a result of strong biotic feedback control through density-dependent effects caused by food and space limitations and competition, and two types of other systems of low stability. In the first, too strong biotic interactions lead to the dominance of a few species and therefore to species exclusions. The other types is systems which are stochastically determined by the great variability of the environmental conditions.
Acoral reef community is often taken as an example for the first type of a stable system of intense biotic coupling through competition, resource limitation, and density dependence. It is assumed that relatively constant environmental conditions (small variations in temperature, light conditions, and nutrient supply) have allowed these systems to evolve to a state of high maturity in which tight biotic patterns maintain a stable equilibrium. As an unstable biotic interactive system we might imagine a rocky shore community, in which the system can switch between ecological states according to the species that happens to dominate the community. This has been reported for kelp-sea urchin communities (Johnson and Mann 1988, Vasquez 1995).
Aclassical example of stochastically dominated systems, in which drastic changes in the physical environment cause respective community changes, are upwelling systems, which may be disturbed by large-scale climatic events like El Niño. Under these conditions, large numbers of cold water-adapted species migrate or die off and are replaced by tropical/subtropical invaders (Wolff 1987,1988, Arntz and Fahrbach 1991). These systems might return, however, to their pre -El Niño species composition (or a similar one) after quite a short time of 2-3 years, however (Wolff 1994b). Fig. 4B also shows that both an increase in "stochastic domination" as well as "biotic instability" is paralleled by a decrease in stability. Systems, which are subjected to stochastic effects and biotic instabilities, are located on the hatched area.
How to explain that even under conditions of instabilities, as described above, natural systems seem to maintain their structure and most of their species richness? The following 4 mechanisms could explain this (following DeAngelis and Waterhouse 1987) (Fig. 4C):
(1) Despite strong biotic interactions, species do not go extinct, because the system consists of loosely coupled subsystems (patches) of different (asynchronic) dynamics. While species might go extinct at the level of the patch, they persist in other patches, from where they might recolonize extinct habitat patches. An example could be a rocky shore community of heterogeneously distributed habitat patches (rocks) of different sizes. Invertebrate predators like crabs could more easily eliminate the sessile fauna on small rocks than on large ones since they are bad swimmers and it takes a longer time to clean larger substrates.
(2) As in the example above, biotic interactions are very strong, but what prevents the extinction of species is not the spatial quasi-isolation of patches but rather a stochastic pattern of biotic disturbances which affects the biotic interactions. Paines research (1969, 1974, 1976) on the key role of sea stars in rocky coastlines is an instructive example. He showed that sea stars, through the permanent elimination of dominant sessile invertebrate species, maintain species diversity in this community.
(3) Strong biological compensatory forces (resistant species of high population growth rates) allow rapid recolonization of a disturbed system. Here, the above example of the upwelling system subjected to an El Niño event could be taken as example. Under conditions of El Niño, a large part of the cold water-adapted species is replaced by intruders or local resistant species of high colonization potential (Arntz and Fahrbach 1991, Wolff 1994a).
(4) The extinction of species does not occur as the disturbance does not affect the whole area occupied by the biological community. Here again the El Niño example can be given; many species have a very large distribution within the eastern Pacific, which exceeds the area of influence of an El Niño event.
The idea of complex, biotic interactive systems that are stabilized by disturbance dates back to Hutchinson (1953), who explained the high diversity of plankton communities by stochastic disturbances which repeatedly interrupted the process of competitive displacement of species. In later studies, the "intermediate disturbance hypothesis" (Connell 1972, Connell 1974, Connell and Slayter 1977) was formulated, which postulates for each system a disturbance regime (intermediate between weak and strong) that maximises diversity. Osman (1977) and Sousa (1979), who studied boulder communities along the Atlantic and Pacific coasts respectively, give examples. The boulders were moved by tidal action with the consequence that the sessile fauna was killed and new space created for successive settlement of invertebrate larvae. The boulder movement (i.e. frequency of disturbance) was directly proportional to boulder size, i.e. the smaller the bolder, the higher the disturbance. The largest boulders were never moved. Those of intermediate size were moved only at spring tides or under extreme weather conditions. Consequently, the small boulders only had the initial rapid settlers, a further succession never took place. The larger boulders were dominated by a few dominant species that had outcompeted other species, while the middle-sized ones had the highest species numbers as a result of succession and limited dominance.
This example also shows that the "ecosystem boulder coast" can be envisioned as a mosaic of community patches of desynchron dynamics. The perception of the ecosystem would vary according to the spatial (and temporal) scale of observation.
The relative constancy of species diversity and ecosystem functioning of an ecosystem thus seems to be the result of desynchron and antagonistic processes (immigration, extinction, and succession) on the level of the mosaic or patch. This is the modern view of ecosystems.
Resumen
Este artículo es una revisión de los conceptos y enfoques predominantes en la modelación e investigación de los ecosistemas marinos, tales como: (1) la Teoría Trofodinámica de ecosistemas pelágicos, (2) modelos de compartimentos/ red (compartment/network models), (3) experimentos de mesocosmos, y (4) modelos basados en enfoques individuales y ecosistemas virtuales. Se resumen y discuten preguntas relevantes para la investigación así como las limitaciones de cada enfoque, y se muestra como el concepto de ecosistema ha cambiado a través del tiempo. El espectro de biomasa acuática (obtenido de la teoría de ecosistemas pelágicos) puede revelar la estructura trófica de los diferentes ecosistemas; puede mostrar como el tamaño de los organismos se distribuyen dentro del ecosistema y como los diferentes grupos, de acuerdo al tamaño, participan en el metabolismo y producción del mismo. Los modelos de compartimentos/redes permiten describir más detalladamente la estructura trófica y el flujo de energía-/ biomasa en los ecosistemas, particularmente, con el modelamiento explícito de P/B y las tasas de consumo de alimento y biomasa de cada compartimento. Además, se pueden obtener índices para la caracterización y comparación entre sistemas, como por ejemplo la eficiencia trófica promedio, el rendimiento energético, los grados de conectividad y de madurez, y otros. Novedosas ampliaciones dinámicas de los modelos tróficos de red, permiten explorar los impactos pasados y futuros de las pesquerías y de las perturbaciones ambientales, así como sondear políticas de manejo como por ejemplo, las áreas marinas protegidas. Los experimentos de mesocosmos tratan con una multitud de preguntas relacionadas con procesos acuáticos (i.e. producción primaria, pastoreo, depredación, paso de energía entre niveles tróficos, etc.) y el comportamiento de los organismos (i.e. crecimiento, migración, reacción a los contaminantes, etc.) bajo condiciones seminaturales. Como los procesos dentro del mesocosmos frecuentemente difieren de los naturales en tasa y magnitud, éstos deberán ser considerados como grandes experimentos in vitro, diseñados para probar selectos componentes del ecosistema y no como intentos de abarcar múltiples procesos interactivos. Los modelos que utilizan organismos individuales como unidades, pueden revelar las causas de la variabilidad natural dentro de las poblaciones (crecimiento, fenotipo, comportamiento) y del papel de la variación intraespecífica de los procesos interespecíficos, de la sucesión y de los mecanismos retroactivos. Los ecosistemas virtuales están siendo utilizados ampliamente en la investigación interdisciplinaria dentro de la oceanografía biológica para simular interacciones no lineares entre las fluctuaciones dinámicas de la circulación oceánica, la física de las interacciones aire- mar, turbulencia y óptica, biogeoquímica, y en la fisiología y comportamiento del plancton. Todos estos aspectos pueden ser comparados con observaciones reales. Los diferentes enfoques disponibles para el análisis de ecosistemas acuáticos deberán ser considerados como medios complementarios para la descripción y comprensión de los ecosistemas. La perspectiva actual de los ecosistemas marinos es el resultado del análisis de ecosistemas durante las últimas décadas, y es la de un compuesto de subsistemas poco acoplados de dinámicas desincronizadas que mantienen la función y estructura fundamental del todo a través de la acción combinada.
References
Adams, S.M. & D.L. DeAngelis. 1987. Indirect effects of early bass-shad interactions on predator population structure and food web dynamics, pp. 103-117. In W.C. Kerfood & A. Sih (eds.). Predation in aquatic ecosystems. University of New England, Hannover. [ Links ]
Allee, W.C., A.E. Emerson, O. Park,. T. Park & K.P. Schmidt. 1949. Principles of animal ecology. W.B. Saunders, Philadelphia. [ Links ]
Anita, N.J., C.D. McAllister, T.R. Parsons, K. Stephens & J.D.H. Strickland. 1963. Further measurements of primary production using a large volume plastic sphere. Limnol. Oceanogr. 8: 166-183. [ Links ]
Arntz, W.E. & E. Fahrbach. 1991. El Niño-Klimaexperiment der Natur. Birkhauser, Basel, Boston, Berlin. 264 p. [ Links ]
Bahr, L.M. 1982. Functional taxonomy: An immodest proposal. Ecol. Model. 15: 211- 233. [ Links ]
Baird, D. & R.E. Ulanowicz. 1993. Comparative study on the trophic structure, cycling and ecosystem properties of four tidal estuaries. Mar. Ecol. Prog. Ser. 99: 221-237. [ Links ]
Baretta-Bekker, J.G., B. Riemann, J.W. Baretta & E. Koch-Rasmussen. 1994. Testing the microbial loop concept by comparing mesocosm data with results from a dynamical simulation model. Mar. Ecol. Prog. Ser. 106: 187-198. [ Links ]
Beyer, J.E. & G.C. Laurence. 1980. A stochastic model of larval fish growth. Ecol. Model. 8: 109-132. [ Links ]
Bosserman, R.W. 1979. The hierarchical integrity of Utricula-Periphyton microecosystems. Ph.D. thesis, University of Georgia. 266 p. [ Links ]
Boyd, C.M. 1981. Microcosms and experimental planktonic food chains, pp. 627-649. In A.R. Longhurst (ed.). Analysis of marine ecosystems. Vol. 2.Academic, London. [ Links ]
Brodeur, R.D. & K.M. Bailey. 1994. Predation on the early life stages of marine fish: A case study on walleye pollock in the Gulf of Alaska, pp. 245-260. In Y. Yoshiro, Y. Yamashita & Y. Oozeki (eds.). Proceedings of the workshop in survival strategies in early life stages of marine resources. Watanabe, Brookfield, VT-USA, Balkema. [ Links ]
Brody, S. 1945. Bioenergetics and growth. Reinhold, New York. 1023 p. [ Links ]
Brooke, S. & R. Mann. 1996. Use of mesocosms for in situ culture of marine invertebrate larvae. J. Shellfish Res. 15: 491-492. [ Links ]
Calder, W.A. 1985. Size and metabolism in natural systems, pp. 65-75. In R.E. Ulanowicz & T. Platt (eds.). Ecosystem theory for biological oceanography. Can. Bull. Fish. Aquat. Sci. 213. [ Links ]
Christensen, V. & D. Pauly. 1992. ECOPATH II-a software for balancing steady state ecosystem models and calculating network characteristics. Ecol. Model. 61: 169-185. [ Links ]
Christensen, V. & D. Pauly (eds.). 1993. Trophic models of aquatic ecosystems. ICLARM Conf. Proc. 26. 390 p. [ Links ]
Christensen, A. & C.J. Walters. 2000. Ecopath with Ecosim: Methods, capabilities and limitations. In D. Pauly & T.J. Pitcher (eds.). Methods for asessing the impact of fisheries on marine ecosystems of the North Atlantic. Fish. Cent. Res. Rep. 8(2): (in press). [ Links ]
Clements, F.E. 1916. Plant succession: An analyisis of the development of vegetation. Wash., Carn. Inst. Publ. 242 p. [ Links ]
Connell, J.H. 1972. Community interactions on marine rocky intertidal shores. Ann.Rev.Ecol.Syst. 3: 169- 192. [ Links ]
Connell, J.H. 1974. Field experiments in marine ecology, pp. 21-54. In R.N. Mariscal (ed.). Experimental Marine Biology. Academic , New York. [ Links ]
Connell, J.H. & R.O. Slatyer. 1977. Mechanisms of succession in natural communities and their role in community stability and organization. Amer. Natur. 111: 1119-1144. [ Links ]
Costello, M.J. & P. Read. 1994. Toxicity of sewag sludge to marine organisms: A review. Mar. Environ. Res. 37: 23-46. [ Links ]
Cousins, S.H. 1980. A trophic continuum derived from plant structure, animal size and a detritus cascade. J. Theor. Biol. 82: 607-618. [ Links ]
Cowan, J.H. & E.D. Houde. 1991. Size-dependent predation on fish larvae by ctenophores, scyphomedusae and planktivorous fish. ICES La Rochelle (France), 26 Sep-4 Oct 1991. 19 p. [ Links ]
Damuth, J. 1981. Population density and body size in mammals. Nature 290: 699-700. [ Links ]
Darwin, C. 1859. On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murrey, London. 123 p. [ Links ]
Davis, M., G.A., Hodgkins & A.W. Stoner. 1996. A mesocosm system for ecological research with marine invertebrate larvae. Mar. Ecol. Prog. Ser. 130: 97- 104. [ Links ]
DeAngelis, D., D.C. Cox & Coutant. 1979. Cannibalism and size dispersal in young-of-the-year largemouth bass: Experiments and model. Ecol. Model. 24: 133- 148. [ Links ]
De Angelis, D. & J.C. Waterhouse. 1987. Equilibrium and nonequilibrium concepts in ecological models. Ecol. Monogr. 57: 1-21. [ Links ]
Dickie, L.M. 1972. Food chains and fish production. Int. Commis. Northwest Atlantic Fish. Spec. Pub. 8: 201-219. [ Links ]
Doering, P.H., C.A. Oviatt & J.R. Kelly. 1986. The effects of the filter-feeding clam Mercenaria mercenaria on carbon cycling in experimental marine mesocosms. J. Mar. Res. 44: 839-861. [ Links ]
Elton, C. 1927. Animal ecology. Macmillan, New York. 207 p. [ Links ]
Evans, F.C. 1956. Ecosystem as the basic unit in ecology. Science 123: 1127-1128. [ Links ]
Fenchel, T. 1974. Intrinsic rate of natural increase: The relationship with body size. Oecologia 14: 317-326. [ Links ]
Gaedke, U. 1992. The size distribution of plankton biomass in a large lake and its seasonal variability. Limnol. Oceanogr. 37: 1202-1220. [ Links ]
Gleason, H.A. 1917. The structure and development of the plant association. Bull. Torrey Bot. Club 43: 463-481. [ Links ]
Gleason, H.A. 1939. The individualist concept of the plant association. Amer. Midl. Natur. 21: 92-110. [ Links ]
Haeckel, E. 1866. Generelle Morphologie der Organismen. Vol. 2. Berlin. [ Links ]
Houde, E.D., J.C. Gamble, S.E. Dorsey & J.H. Cowan, Jr. 1994. Drifting mesocosms: The influence of gelatinous zooplankton on mortality of bay anchovy, Anchoa mitchilli, eggs and yolk-sac larvae. ICES - J. Mar. Sci. 51: 383-394. [ Links ]
Huston, M., D. DeAngelis & W. Post. 1988. New computer models unify ecological theory. BioScience 38: 682-691. [ Links ]
Hutchinson, G.E. 1953. The concept of pattern in ecology. Proc. Nat. Acad. Sci. 50: 221-246. [ Links ]
Hutchinson, G.E. 1978. An introduction to population ecology. Yale University, New Haven. [ Links ]
Huxley, J.S. 1932. Problems of relative growth (1972 reprint). Dover, New York. 312 p. [ Links ]
Ikeda, T. 1985. Metabolic rates of epipelagic marine zooplankton. Mar. Biol. 85: 1-11. [ Links ]
Innis, G.S. (ed.). 1978. Grassland simulation model. Ecological studies. Vol. 26. Springer, New York. [ Links ]
Johnson, C.R. & K.H. Mann. 1988. Diversity, patterns of adaptation, and stability of Nova Scotian kelp beds. Ecol. Monogr. 58: 129-154. [ Links ]
Kleiber, M. 1961. The fire of life. Wiley, New York. 453 p. [ Links ]
Levins, R. & R. Lewontin. 1980. Dialectics and reductionism in ecology, pp. 107-138. In E. Saarinen (ed.). Conceptual issues in ecology. Dordrecht. [ Links ]
Lindemann, R.L. 1942. The trophic-dynamic aspect of ecology. Ecology 23: 399-418. [ Links ]
Longhurst, A.R. (ed.). 1981. Analysis of marine ecosystems. Academic, London. [ Links ]
Malthus, T.R. 1806. An essay on the principle of population, as it affects the future improvement of society, with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers. J. Johnson, London. [ Links ]
Maugham, J.T. & C.A. Oviat. 1993. Sediment and benthic response to waste water solids in a marine mesocosm. Water. Environ. Res. 65: 879-889. [ Links ]
McAllister, C.C., T.R. Parsons, K. Stephens & J.D.H..Strickland. 1961. Measurement of primary production in coastal sea water using a large volume plastic sphere.Limnol.Oceanogr. 6: 237-258. [ Links ]
Menzel, D.W. & J.H. Steele.1978. The application of plastic enclosures to the study of pelagic marine biota: Rapp. P.V. Reun. Cons. int. Explor. Mer. 173: 7-12. [ Links ]
Möbius, K. 1877. Die Auster und die Austernwirtschaft. Berlin. [ Links ]
Mullin, M.M. & P.M. Evans. 1974. The use of a deep tank in plankton ecology. II. Efficiency of a planktonic food chain. Limnol. Oceanogr. 19: 902-911. [ Links ]
Neyman, J. 1949. On the problem of estimating the number of schools of fish. Univ. Calif.Publ.Statis.1:21-36. [ Links ]
Odum, E.P. 1953. Fundamentals of Ecology. Saunders, Philadelphia. 384 p. [ Links ]
Odum, E.P. 1969. The strategy of ecosystem development. Science 164: 262-270. [ Links ]
Osman, R.W. 1977. The establishment and development of marine epifaunal community. Ecol. Monogr. 47: 37- 63. [ Links ]
Paffenhöfer, G.A.,1976. Continuous and nocturnal feeding of the marine planktonic copepod Calanus helgolandicus. Bull.Mar.Sci. 26: 49-58. [ Links ]
Paine, R.T. 1969. The Pisaster-Tegula interaction: prey patches, predator food preference, and intertidal community structure. Ecology 50: 950-961. [ Links ]
Paine, R.T. 1974. Intertidal community structure. Experimental studies on the relationship between a dominant competitor and its principal predator. Oecologia 15: 93-120. [ Links ]
Paine, R.T. 1976. Size-limit predation: An observational and experimental approach with the Mytilus-Pisaster interaction. Ecology 57: 858-878. [ Links ]
Paloheimo, J.E. 1971. Astochastic theory of search: implications for predator-prey situations. Math. Biosci. 12: 105-132. [ Links ]
Paloheimo, J.E. & L.M. Dickie.1966. Food and growth of fishes.II. Effects of food and temperature on the relation between metabolism and body weight. J. Fish. Res. Bd. Canada 23: 869-908. [ Links ]
Parsons, T.R. & R.J. LeBrasseur. 1970. The availability of food to different trophic levels in the marine food chain. pp. 325-343. In: J.H. Steele (ed.). Marine Food Chains. Oliver and Boyd, Edinburgh. [ Links ]
Parsons, T.R., K. von Bröckel, P. Koeller & M. Takahashi.1977. The distribution of organic carbon in a marine planktonic food web following nutrient enrichment. J. Exp. Mar. Biol. Ecol. 26: 235-247. [ Links ]
Patten, B.C. & E.P. Odum. 1981. The cybernetic nature of ecosystems. Am. Nat. 118: 886-895. [ Links ]
Pella, J.J. & P.K.Tomlinson.1969. Ageneralized stock production model. Bull. Inter-Am. Trop. Tuna Comm. 13: 419-496. [ Links ]
Phillips, J. 1934. Succession, development, the climax and the complex organism. J. Ecol. 22: 554-571. [ Links ]
Platt, T. & K. Denman. 1978. The structure of pelagic ecosystems. Rapp. P.-V. Reun. Cons. Int. Explor. Mer. 173: 60-65. [ Links ]
Polovina, J.J. 1984. Model of the coral reef ecosystem. Part I. The ECOPATH model and its application to French frigate shoals. Coral Reefs. 3: 1-11. [ Links ]
Polovina, J.J.,Ow, M.D.,1985: An approach to estimating an ecosystem box model. Fish.Bull.NOAA/NMFS, 83: 457-460. [ Links ]
Porter,E.T., R.I.E Newell & L.P. Sanford, 1996. Physical and biological scaling of benthic-pelagic coupling in coastal ecosystems: The role of bivalve suspension feeders J. Shellfish. Res.: 490-491. [ Links ]
Quinlin, A.V. 1975. Design and analysis of mass conservative models of ecodynamic systems. Ph.D. thesis. MIT, Cambridge. [ Links ]
Reeve, M.R. & M.A. Walter. 1976. A large-scale experiment on the growth and predation potential of ctenophore populations. p. 187-199. In: G.O. Mackie (ed). Coelenterate Ecology and Behaviour. Plenum, New York,. [ Links ]
Rodhouse, G.P., U. Piatkowski, E.J. Murphy, M.G. Withe & D.G. Bone. 1994. Utility and limits of biomass spectra: the nekton community sampled with the RTM 25 in the Scotia Sea during austral summer. Mar. Ecol. Prog. Ser. 112: 29-39. [ Links ]
Rodriguez, J. & M.M. Mullin.1986. Relation between biomass and body weight of plankton in a steady state oceanic ecosystem. Limnol. Oceanogr. 31: 361-370. [ Links ]
Rutledge, R.W, B.L. Basore & R.J. Mulholland.1976. Ecological stability: an information theory viewpoint. J. Theor. Biol. 57: 355-371. [ Links ]
Sheldon, R.W., A. Prakash & W.H. Sutcliffe-Jr.1972. The size distribution of particles in the ocean. Limnol. Oceanogr. 17: 327-340. [ Links ]
Schwinghammer, P. 1981. Characteristic size distributions of integral benthic communities. Can. J. Fish. Aquat. Sci. 38: 1255-1263. [ Links ]
Sissenwine, M.P. 1984. The uncertain environment of fisheries scientists and managers. Mar. Res. Econ. 1: 1-30. [ Links ]
Sonntag, N.C. & T.R. Parsons. 1979. Mixing an enclosed, 1300m3 water column: effects on the planktonic food web. J. Plankton Res. 1: 85-102. [ Links ]
Sousa, W.P. 1979. Experimental investigations of disturbance and ecological succession in a rocky intertidal algal community. Ecol. Monogr. 49: 227-254. [ Links ]
Strickland, J.D.H., O. Holm-Hansen, R.W. Eppley & R.J. Linn. 1969. The use of a deep tank in plankton ecology. I. Studies on the growth and composition of phytoplankton crops at low nutrient levels. Limn.Oceanogr.14:23-34. [ Links ]
Tansely, A.G. 1935. The use and abuse of vegetational concepts and terms. Ecology 64: 284-307. [ Links ]
Thienemann, A. 1918. Lebensgemeinschaft und Lebensraum. Naturwissenschaftl. Wochenschrift. N.F. 17: 282-290. [ Links ]
Thienemann, A. 1941. Leben und Umwelt. Bios. Band 12 Joh. Ambr. Bart. Leipzig. [ Links ]
Uexküll, J. von. 1928. Theoretische Biologie, II. Auflage, Berlin. [ Links ]
Uexküll, J von, 1921. Umwelt und Innewelt der Tiere. 2 Auflage, Springer, Berlin. [ Links ]
Ulanowicz, R. E. 1986. Growth and Development. Ecosystems Phenomenology. Springer, Berlin. 203 p. [ Links ]
Ulanowicz, R.E. & K.H. Mann.1981. Ecosystems under stress. pp. 133-137 In: K.H. Mann, & R.E.
Ulanowicz (eds.). Mathematical Models in Biological Oceanography. UNESCO, Paris.
Van-Wijk, D.J. & T.H. Hutchinson.1995. The ecotoxicity of chlorate to aquatic organisms: A critical review. Ecotoxicol. Environ. Saf. 32: 244-253. [ Links ]
Vargas, J.A. & M. Wolff (eds.) 1996. Pacific coastal ecosystems of Costa Rica with emphasis on the Golfo Dulce and adjacent areas: a synoptic view based on the RV Victor Hensen expedition 1993/1994 and previous studies. Rev. Biol. Trop. 44. (Suppl. 3): 238p. [ Links ]
Vasquez, J.A. 1995. Ecological effects of brown sea weed harvesting. Mar. Biol. 38: 251-257. [ Links ]
Verhulst, P.F. 1838. Notice sur la loi que la population suit dans son accroissement. Corresp. Matherm. Phys. 10: 113-121. [ Links ]
Walters, C., V. Christensen & D. Pauly. 1997. Structuring dynamic models of exploited ecosystems from trophic mass -balance assessments. Rev. Fish. Biol. Fisher. 7: 139-172. [ Links ]
Walters, C., D. Pauly & V. Christensen. 1999. Ecospace: Prediction of mesosclae spatial patterns in trophic relations ships of exploited ecosystems, with emphasis on the impacts of marine protected areas. Ecosystems 2: 539-554. [ Links ]
Wangelin, M. von & M. Wolff. 1996. Comparative biomass spectra and species composition of the zooplankton community of the Golfo Dulce and Golfo de Nicoya ecosystems. Rev. Biol. Trop. 44 (Suppl. 3): 135-155. [ Links ]
Warwick, R. M. 1984. Species size distributions in marine benthic communities. Oecologia 61: 32-41. [ Links ]
Weiss, P.A. (ed).1971. Hierarchically Organized Systems in Theory and Practice. Hafner, New York. [ Links ]
Wiens, J.A. 1989. Spatial scaling in Ecology. Funct.Ecol. 3: 385-397. [ Links ]
Wieser, W.,1985. A new look at energy conversion in ectothermic and endothermic animals. Oecologia 66: 506-510. [ Links ]
Wieser, W.1986. Vom Werden zum Sein. Naturwissenschaften 73: 543-549. [ Links ]
Wolff, M. 1987. Population dynamics of the Peruvian scallop Argopecten purpuratus during the El Niño Phenomenon 1983. Can. J. Fish. Aquat. Sci. 44: 1684-1691. [ Links ]
Wolff, M. 1988: Spawning and recruitment in the Peruvian scallop Argopecten purpuratus. Mar. Ecol. Prog. Ser.42: 213-217. [ Links ]
Wolff, M. 1994 a: Atrophic model for Tongoy Bay - a system exposed to suspended scallop culture (Northern Chile). J. Exp. Mar. Ecol. Biol. 182: 149-168. [ Links ]
Wolff, M.,1994 b: Population dynamics, life histories and management of selected invertebrates of the Southeast Pacific upwelling system. Habilitationsschrift, Universität Bremen, 210 p. [ Links ]
Wolff, M,. H.J Hartmann & V. Koch.1996. A trophic pilot model for Golfo Dulce, a fjordlike tropical embayment, Costa Rica. Rev. Biol. Trop. 44 (Suppl. 3): 215-231. [ Links ]
Wolff, M., V. Koch, J.B.,Chavarria, & J. Vargas. 1998. A trophic flow model of the Golfo de Nicoya, Costa Rica. Rev. Biol. Trop. 46 (Suppl. 6): 63-79. [ Links ]
Wolff, M., V. Koch & V. Isaac. 2000. A trophic flow model of the Caeté mangrove estuary (North Brazil) with considerations for the sustainable use of its resources. Est. Coast. Shelf Sci. 50: 789- 803. [ Links ]
Woods, J. 1998. Virtual Plankton Ecology. A new strategy for biological oceanography. Biological Oceanography 1., 58p. [ Links ]