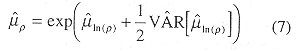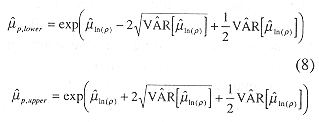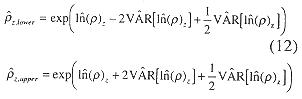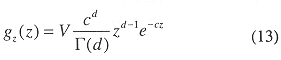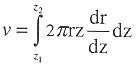Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.48 n.2-3 San José Jun. 2000
John Hedgepeth1 Vincent F. Gallucci2 Jorge Campos3 4 and Moises Mug3
Received 26-II-1999 Corrected 12-VIII-1999 Accepted 4-II-2000.
Abstract
A stratified sampling design was used for a hydroacoustic survey of the inner parts of the Gulf of Nicoya in 1987 and 1988. The bottom topography of the inner Gulf was modeled by introducing the concept of a topographical basin model, as the basis for the projection of the sample survey estimates to the entire inner gulf. The bottom depth contours and volumes for the basin model were constructed from nautical charts. The estimates of sample abundance were made for the fish in the inner Gulf using the acoustic methods, EMS (Expectation Maximization and Smoothing) and echo integration. The estimates of population were made by the multiplication of the topographic model's estimate of water volume and a model of fish density dependent on bottom depth. The results showed a general decrease in fish density biomass with bottom depth, and a simultaneous tendency for maximum concentrations over bottom depths of about four meters. The four meter bottom depth includes a broad expanse of the inner Gulf located south of Isla Chira. Overall estimates of volumetric density (0.269 fish/m3) and of areal densities (1.88 fish/m2) are comparable to other estuarine shallow water environments.
Key words
Gulf of Nicoya, hydroacoustics, tropical fisheries, biomass estimation, estuaries.
Estimation of fish biomass in shallow water is always a challenge, especially so for acoustics equipment. The difficulty is due primarily to reverberation noise and poor resolution close to the bottom. Other problems include the difficulty of the resolution of abundance counts into species or species groups, especially in tropical environments, and fish behaviors which may lead either to gear avoidance or attraction.
Species identification is usually accomplished by coordinating trawl transects with the acoustic transects. Acoustics estimates are often an improvement over trawl estimates, including superior area coverage per person hour, depth-fish abundance profile information without changing trawl gears and general ease of operation. Furthermore, trawl gear selectivity and species catchability are unnecessary for acoustics estimation.
The Gulf of Nicoya is one of the most productive embayments on Central America's Pacific Coast (Madrigal 1985). It is a shallow embayment that supports an important artisanal gillnet fishery focused on the larger fish species (Lai et al. 1994). Of the over 100 harvested species, the Sciaenidae dominate with over 30 species, 15 of which contribute most to the bioproduction. The preferred species in the harvest are Cynoscion albus (corvina reina), C. squamipinnis (corvina aguada), Micropogonias altipinnis (corvina agria), and C. phoxocephalus (corvina picuda) (Mug-Villanueva et al. 1994).
Despite a history of data collection on the artisanal corvina fisheries, relatively little is known about the actual abundance and biomass of the fish resources in the Gulf. The linkage between fish habitat and harvested fish species was explored by Madrigal (1985) who produced, for three corvinas, regression relationships between landed weight and the physical variables of salinity, dissolved oxygen, nitrate and phosphorus. Donato (1988) found that distributions of both non-commercial and commercial species are associated with zones that can be characterized by physical factors like temperature, salinity, oxygen, and depth. Bartels et al. (1983) also found that depth and temperature were associated with species presence and added distance to the ocean. In addition, Szelistowski and Garita (1989) suggest that sciaenid resources are susceptible to pollution induced mortality.
In a more general sense, the fish in the Gulf have been examined by several investigators. Peterson (1956) investigated the baitfish resources of the Gulf and noted the abundance of engraulids and clupeids. León (1973) used semi-balloon trawls and found that the inner Gulf is dominated by a non-commercial sciaenid, sea catfish, engraulids and clupeids. Bartels et al. (1983) found similar results except that engraulids and clupeids were less important. Hedgepeth and Thorne (1989) used acoustics, a midwater trawl and gillnets and concluded that engraulids and clupeids were the most numerous fish groups in the inner Gulf.
This paper describes the use of a single-beam acoustic transducer in the mangrove-surrounded Gulf of Nicoya in Costa Rica and it presents new conceptual methodology to resolve some of the above noted physical limitations upon the use of acoustics in this environment. It is the first acoustic estimate of the fish biomass in the Gulf, primarily in the upper or inner part where the acoustic transects were placed, an area of about one third of the Gulf's 1530 km2. It extends a preliminary analysis (Hedgepeth et al. 1990). We developed a model for estimating fish biomass by taking advantage of known depth contours and acoustic information about expected fish density relative to bottom depth. We used a simple research echosounder with a single-beam transducer. A single-beam transducer system has the advantage of simplicity and the disadvantage of being unable, by itself, to measure acoustic size (or target strength). However, if the density is not too high and the EMS (Expectation Maximization and Smoothing) computational method (Wilson 1989) is used, single-beam systems can estimate acoustic size and abundance. When single fish targets cannot be resolved by the acoustic system, then the computational method called echo integration (EI) will estimate density, but not acoustic size which, as noted, is found when the EMS method is used. Although this paper is not about the EMS or EI methods, readers should be aware of computational method(s) in order to evaluate the limitations of an acoustics report. More sophisticated and expensive multi-beam systems will estimate both of these quantities.
Materials and Methods
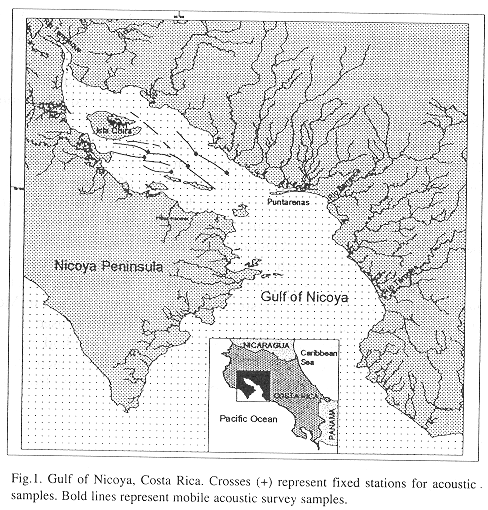
The Gulf of Nicoya covers about 1530 km2 and is the largest Pacific Ocean gulf of Costa Rica (10°N, 85°W) (Fig. 1). The inner or northern Gulf is shallower, with depths typically from 4 to 10 meters.
A single-beam transducer Simrad EYM echosounder was used in 1987 and 1988. Analog voltage from the echosounder was recorded on beta video tape. When fish density was low enough deconvolution analysis was used to estimate average acoustic backscattering cross sections and density, and echo integration was used when fish density was large (Hedgepeth et al. 1990). Stanton's (1985a) criterion was used to calculate the critical density to decide between the deconvolution or echo integration methods. The deconvolution method represents the transducer beam as an analytical probability density function (pdf). A parameter sensitivity analysis showed the deconvolution method to be robust to errors in the beam pdf for estimation of the acoustic size but not for the estimation of abundance. Furthermore, the deconvolution method sometimes produces artifactual modes in the density. Therefore, the EMS method was also used to estimate backscattering cross section.
The inner Gulf is heavily utilized by artisanal fishermen, who use a variety of gear, the gillnet being the most common. The 1987 and 1988 acoustic surveys were coordinated with individual fishing boats in order to use gillnet fishermen's catch as an indication of fish species recorded by acoustic transducer. A large fraction of fish detected by the acoustic gear was not retained by fishermen's gillnets, which was not suprising since gillnets are highly size selective. The 1988 survey included the use of a midwater trawl in a survey sampling design with the acoustics gear.
Estimation: The Expectation-Maximization-Smoothing method (EMS), in which intermediate estimates are smoothed to avoid highly fluctuating results, can be applied when fish densities are low enough to permit echo counting (Hedgepeth 1994). In this study, EMS was applied to all of the acoustic data collected from the inner Gulf of Nicoya during August and September, 1988. EMS provided abundance estimates in low densities and scaled the echo integration results in high densities. The EMS scalars came from depths adjacent to the areas of high density. Echo integration is used in high density areas because more precision estimates result than with counting methods such as EMS (Ehrenberg 1973).
Methods: A and B below, were used to estimate mean density, population abundance and 95 % confidence intervals. Both regress a function of fish density against bottom depth. An exponential model relates acoustic density estimates from EMS and echo integration to mean bottom depth along the acoustic transect. If the acoustic density is (z) and z is the mean depth over the transect, the model is
where . A lognormal transformation yielded a linear model and stabilized the variance,
where a' = ln(a).
Parameters a' and b were estimated by standard methods (Sokal and Rolf 1969). Density in (2) was estimated from the relationship between the normal and lognormal probability distributions (Mood et al. 1974),
where µ and are the mean and variance of the normally distributed log density (ln
).
Method A (Cochran 1977, Scheaffer et al. 1986) provides estimates of mean density, confidence limits of the mean and, by multiplication with volume, number of fish. Pairs of density with bottom depth and an estimate of mean bottom depth from the inner Gulf are required.
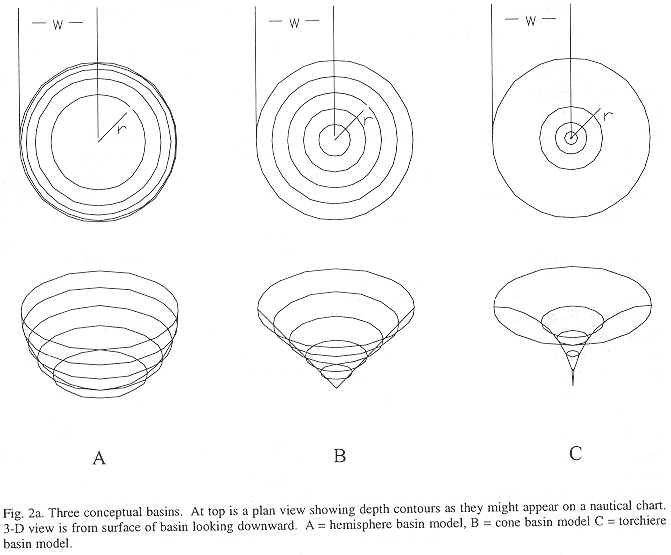
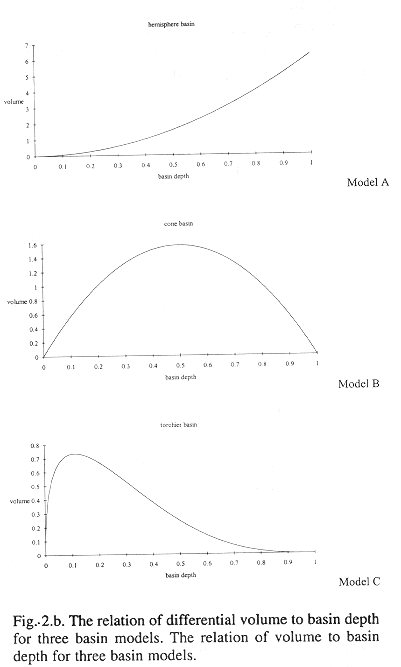
Method B regresses fish density on bottom depth to establish a functional relation between density and depth. A basin model for the inner Gulf is used to relate volume to depth. Volume-at-depth multiplied by density-at-depth estimates abundance of fish-at-depth. Fig. 2 shows three idealized basin models and Appendix I shows the equations used to find the volume for each model. Total fish abundance is estimated by integrating abundance at depth.
Methods A and B both reduce the uncertainty in estimated density r by using additional bottom depths from a chart (Instituto Geográfico de Costa Rica C.R. 006-U.S. Defense Mapping Agency 21544). The chart was digitized. The coast, 2 m, 5 m, 10 m and 20 m bottom contours were digitized using polyline commands to compute the surface area bounded by each contour. Volume was estimated by multiplying area by average depth within contours for use in Method B. The average of all depths is used in Method A.
Method A: The regression estimator (3) presents increased precision over alternative estimators from auxiliary information, viz., depth. The regression estimator of the population mean log density, µln (), utilizes the mean depth of the samples, z, and the mean depth of the area where the population estimate is made, µz,
where µz was estimated from nautical chart, CR006.
The estimator for the variance of in (4) is
from which the approximate 95% confidence interval is
Estimates of the mean density were made by transforming log estimates using the formula given for the expected value of a lognormal random variable (Mood et al. 1974):
The confidence interval for the density was similarly formed
Fish population estimates were made by multiplying density estimates by the volume of water in the inner Gulf of Nicoya.
Method B: Density and fish abundance in the inner Gulf are estimated using the functional relationship between fish density and bottom depth and on a model of the bottom depth distribution, viz., a "basin model". The method uses the linear regression (2)
where a', b and the total, regression and residual sums of squares follow from Sokal and Rholf (1969). The variance estimator of the estimate of log density, used to construct confidence intervals, given by
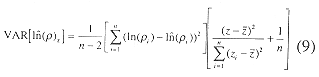
The 95% confidence limits follow from (9)
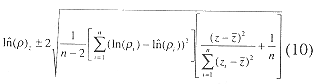
Equation (2) produced a functional relationship between log density and depth for depths of interest in the inner Gulf, i.e. less than 25 m. The functional relationship between density and depth was found by transforming (2) using (3).
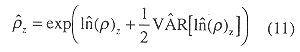
The confidence interval for density was found from.
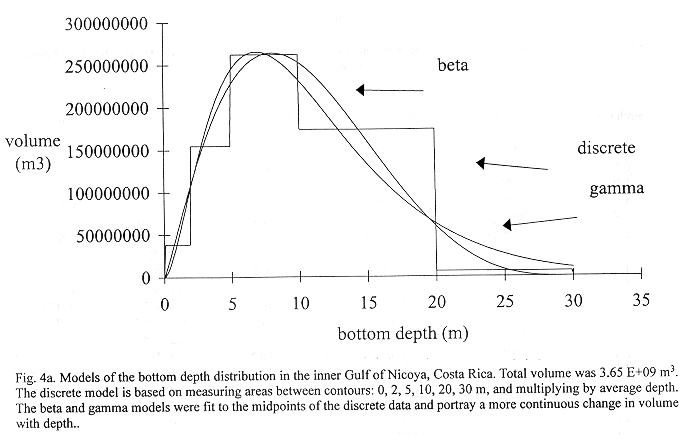
Basin Models: The basin model is formed from a volume v and bottom depth z, relationship, i.e. vz. Multiplication of vz with the estimated z produces estimates of numbers of fish at depth. The 0-2, 2-5, 5-10,10-20, and 20-30 m depth contour intervals and average depths in those intervals are multiplied to estimate a volume step function. Gamma and beta distributions (Mood et al. 1974) replace the step function to represent the continuous nature of bottom depth. These functions are fit at the midpoints of the steps.
The gamma distribution's volume to depth relationship is
where V = total volume of the inner Gulf. The beta distribution was fit between 0 and 30 meters bottom depth to obtain
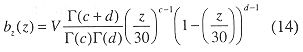
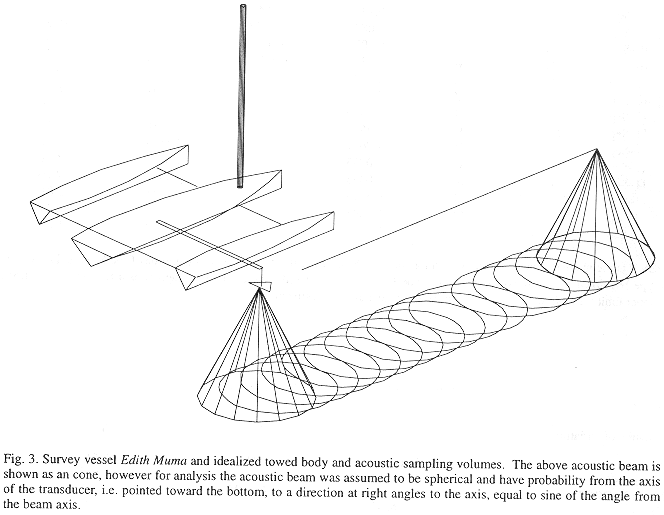
Sampling: The inner Gulf was sampled from 25 August to 12 September, 1988, primarily with mobile surveys (a 9 m auxiliary outboard powered trimaran, Edith Muma, Fig. 3) supplemented with several tidal drift surveys and one stationary transducer sample. Navigation was by hand-bearing compasses using known points of land. Field positions were confirmed using the depth to the bottom. A two-stage sampling design was initially used in which the region was divided into a number of strips in the first stage. Two randomly placed transects were allocated to each strip in the second stage. Each transect was approximately three nautical miles in length (Fig. 1).
Species identification with underwater video or SCUBA was not possible due to turbidity so we relied on midwater trawl and gillnet catches to partition the estimates from the single-beam echosounder into species and size groups Since our trawl design was selective for fishes under 20 cm, we also used gillnet catches from a 3 inch stretch mesh X 100 feet from a 4.5 m outboard powered boat. We sampled with nets at least once during each three nautical mile acoustic transect.
The trawl net had a mouth opening of 4 m across and 3 m deep. It was pulled with a 7 m boat. The net mouth was spread open by horizontal and vertical bars. The net depth was adjusted by attaching variable length lines with "Polyform" plastic floats to the ends. The estimated towing speed using this configuration was 2 knots. At the end of a tow the net was hauled up to the side of the vessel and the cod-end emptied onto the deck of the acoustic sampling vessel, where the catch was enumerated and recorded. Subsampling was done when catches were large. When time was short, samples were placed into plastic bags and counted later.
Data include species, total number and weights and lengths of the entire catch. Fish density was estimated from trawls by the area swept method, i.e. volume = area of the trawl opening times speed times time. Densities from trawl surveys were compared to estimates from acoustic transects.
Results
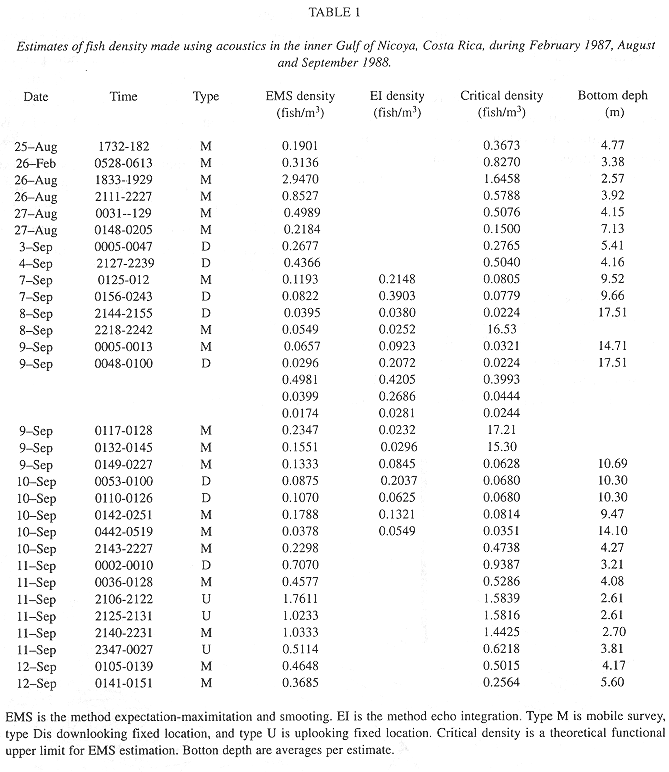
Estimates of density (Table 1) were made from 16 attempted transects in the inner Gulf of Nicoya (Fig. 1) using the EMS and echo integration methods. Thirty density estimates were used for a regression analysis. More estimates than transects were available because transects were often split to allow trawl sample processing. Uplooking or downlooking data was collected from several anchor points. When both EMS and echo integration estimates were made from a collection fish echoes, the echo integration estimate from Table 1 was selected for the regression analysis because the single-target EMS method is more likely to be in error when used with data from higher fish densities. Parameters of the regression model were fit by minimizing the sum of squared deviations of the estimated log density and observed log density,
The analysis of variance of the partitioned sums of squares of the log density data is shown in Table 2.
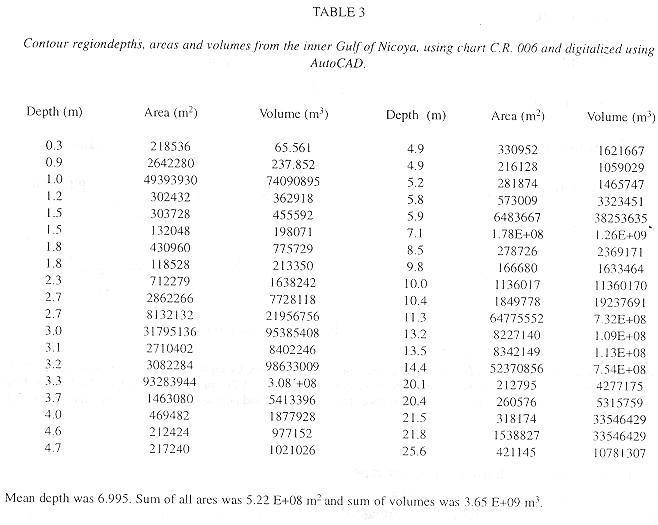
Table 3 shows the average depth, area and volume computations for 23 contour regions digitized in the inner Gulf of Nicoya. The total volume of the inner Gulf of Nicoya was estimated as 3.65 E+09 m3, and the surface area was 5.22 E+08 m2.
Method A: The regression estimators for (4) and (5) are computed as
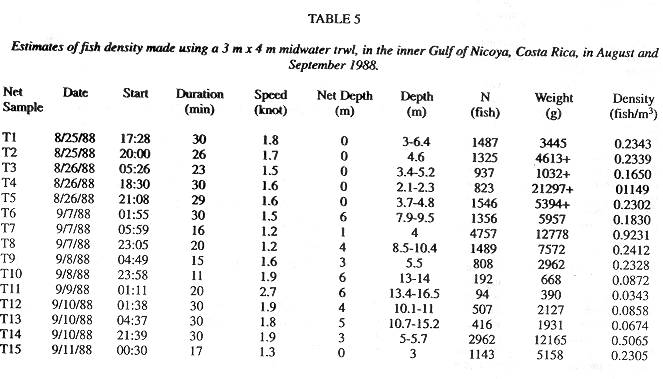
Inverse transformations (6) and (7) give a density estimate of 0.330 with a 95% confidence interval 0.258 to 0.422 in terms of fish/m3, respectively. Multiplication by the total volume of the inner Gulf of Nicoya, 3.65 E+09 m3, gives an estimate of fish population of 1.20 E+09, with approximate 95% confidence interval of 9.42 E+08 to 1.54 E+09 fish.
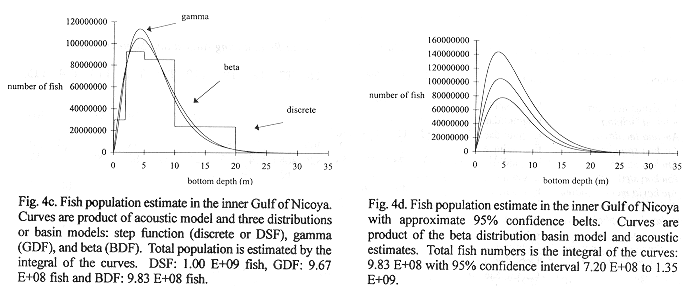
Method B: Figure 4a shows three basin models relating volume and bottom depth relationships for the Gulf from data in Table 1. A discrete step function (dsf), a gamma distribution (gdf) and beta distribution (bdf) were fit to these data. The step function model used steps at 0-2, 2-5, 5-10,10-20, and 20-30 m depth intervals where average depths in those intervals were multiplied to compute volume. The beta distribution model was chosen for use with densities because it modeled the step function results better than the gamma distribution. The total volume of the inner Gulf of Nicoya was estimated as 3.65 E+09 m3.
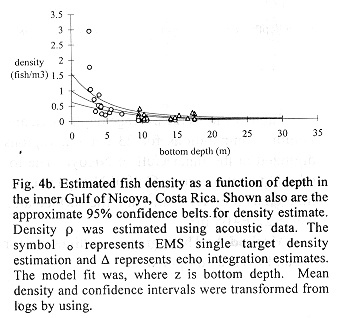
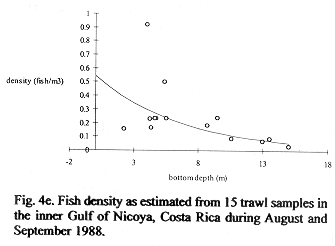
Fig. 4b shows 30 density estimates superimposed on the regression line (15) inverse transformed using (11). Method B estimated total fish numbers by multiplying the densities at depth from the transformed regression by volume at depth. The dsf, gdf, and bdf functions gave estimates of 1.00 E+09, 9.67 E+08, 9.83 E+08 fish, respectively (Fig.3c). The bdf was used in confidence interval computations by multiplying the limits shown in Fig. 4b by the bdf shown in Fig. 4a. The result is shown in Fig. 4d and numerically integrated resulting in a 95% confidence interval, 7.20 E+08 to 1.35 E+09 fish. This interval corresponds to 0.197 to 0.369 fish/m3 after dividing by the volume of the inner Gulf.
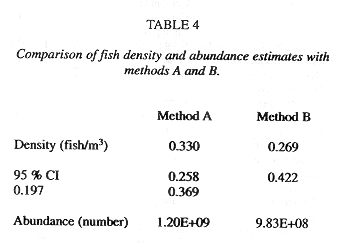
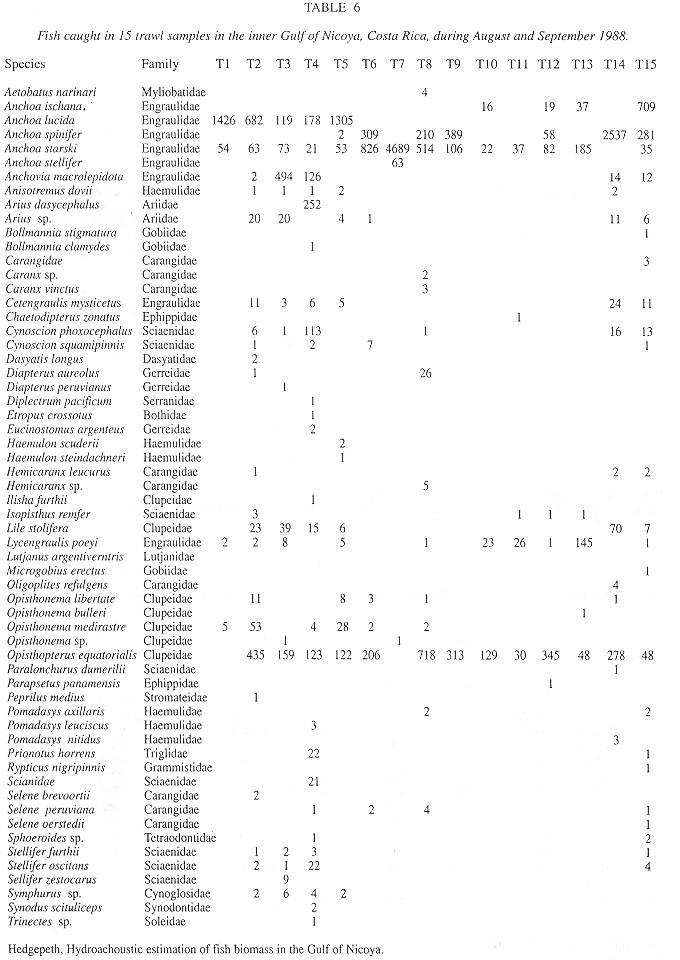
Summary of Method A and Method B results: Trawl Comparisons: A total of 15 trawl hauls were made during the time of the acoustic transects. A total of 19843 fish, representing 65 species, were caught. A total weight in excess of 87.5 kg can be interpreted as 4.4 g/fish. Trawl catches were used to estimate fish density by the area swept method, the trawl mouth being 3m x 4m. The calculations and density estimates are shown in Table 5, with the time, date and duration of trawl. Estimated densities ranged from 0.0343 to 0.9231 fish/m3. The densities may also be related to depth, as in the acoustic survey. The results are shown in Fig. 4e. The 65 species captured are shown in Table 6, with number caught in each haul.
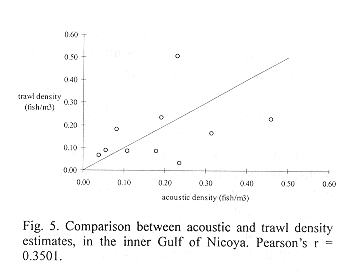
A comparison between trawl and acoustic estimates produced a Pearson's r of 0.3501 (Fig. 5). In shallow water, the trawl estimates were slightly lower than the acoustic estimates.
Discussion
The Gulf of Nicoya supports an important artisanal fishery, targeting relatively few but capturing many of the species in the Gulf. Our primary interest was in the estimation of abundance and the locations of the targeted fish stocks but the limitations and strengths of simple acoustic equipment in shallow bays fostered a wider interest in the distribution of fish numbers over the inner Gulf.
The acoustic estimates reported here for all species would be partitioned using the trawl data to represent the fraction harvested of a specific species or species complex.
For fisheries where catch is sampled with error (20 % C.V. or larger) the use of independent abundance data such as that provided from acoustics, produces noticeable improvements in estimation of stock abundance. If the results of a hydroacoustics survey are to be used for quantitative stock assessment, a mathematical model that incorporates such results would be used. In this case, the catch-at-size analysis (CASA) (Sullivan et al. 1990) method would then be used to reconstruct abundance and other population parameters using a time series of the landed fish length frequencies and acoustic estimates of total population size, as auxiliary data.
The abundance estimates for all fish species given in Tables 1, and 5 can be compared with abundances for other bay environments. For methods A and B, our estimates of volumetric density were 0.330 and 0.269 fish/m3 and of areal densities of 2.30 and 1.88 fish/m2, respectively. Reina-Hervas and Serrano (1987) report 4.0 fish/m2 in Malaga Bay, Spain, in two areas, one with depths from 1-10 m and the other with depth of 15 m. From the Spanish Ria Arosa, Chesney and Iglesias (1979) and Iglesias (1981) measured 0.22 to 1.0 fish/m2. Nash and Gibson (1982) reported 0.045-0.47 fish/m2 along the west coast of Scotland. Allen and Herbinson (1991) reported trawl estimates from southern California bays and nearshore waters. Over 0.5 m depths there were 2.93 fish/m2, over 1 m depths there were 0.826 fish/m2 and over 13 m depths there were 0.114 fish/m2.
Open ocean estimates of standing biomass are often lower. For example, Kalish et al. (1986) used nets to estimate fish density in deep scattering layers off Oregon and measured 0.00016 and 0.0167 fish/m3 during day and night. Polovina (1986) used a catch-removal method to estimate exploitable bottom fish stocks on a south Pacific reef of 0.00296 fish/m2. Gordea and Duarte (1991) report a daytime high of 1.0 fish/m2 for hake off Africa. DeMartini and Roberts (1990) showed fish densities near Macrocystis beds of 0.1 to 1.0 fish/m2, as a logarithmic function of Macrocystis density.
Volumetric density estimates can be made when bottom depth information is given. The Malaga Bay estimates are on the order of 0.4 fish/m3, which are only slightly higher than those found for the inner Gulf of Nicoya. Allen and Herbinson (1991) found 1.46, 0.826, and 0.00877 fish/m3 over 0.5, 1.0 and 13.0 m depths. These densities, comparable with the results shown in Fig. 4b, represent 43 bay species and 60 nearshore ocean species of fish. Rudstam et al. (1987) used acoustics to estimate 0.00862 fish/m3 using acoustics in a Wisconsin lake with average depth of 18 m.
Many literature sources do not provide comparable estimates in terms of individual fish, but report biomass only in weight. For example, Brandt et al. (1992) reported fish (prey) densities of 1.88, 1.3, and 3.0 g/m3 in the Chesapeake Bay. Sullivan (1991) showed a density dependence on depth for north Pacific walleye pollock with densities up to about 20 g/m2. Mathisen et al. (1978) reported an overall mean nekton biomass of 57.70 g/m2 in an upwelling area off western Africa. Using an estimate of mean weight of 4.4 g/fish, fish biomass in the inner Gulf of Nicoya is roughly 1.3 g/m3 or 9 g/m2, or about 4400 MT.
This paper developed a basin model concept as a step in the estimation of abundance of fish in the inner Gulf of Nicoya. Although the alternate regression estimator gave similar estimates in terms of total abundance and mean fish density, the basin model has the advantage of providing a perception of where to find the most fish.
The basin model approach allowed an analysis in terms of the variable bottom depth. Other variables might be investigated to estimate numbers of fish: temperature, salinity, distance from shore, distance to an aggregation device, combinations of these, and so on. If two variables such as bottom depth and distance from shore were used, a three dimensional picture could locate optimal fish habitat. When more are used then other techniques can be employed such as multiple figures or statistical descriptions of fish preference.
Figs. 4c and 4d show that fish are concentrated over bottom depths of approximately four meters. The four meters bottom depths include a broad expanse of the inner Gulf of Nicoya, south of Isla Chira (Fig. 1) known as the Chira flats. Fishermen use drift gillnets carried along by currents which fish essentially from the surface to the bottom over the area. Personal experience observing fishing concentrations at 4 m bottom depth indicates that the results using acoustic-basin model is a good method of predicting fishing success. Other evidence which supports this view are the number of fish sales tickets showing the frequency of occurrence of the description "Chira", which most likely refers to the Chira flats, and capture points on the Chira flats shown by Madrigal (1985).
Geostatistical concepts are rapidly expanding the scope of survey sampling applications. The use of a topographical depth model to introduce a dependency on depth is a one-dimensional version of the geostatistical approach. The technique has the advantage of being relatively simple and could allow the classification of embayments by different bottom depth and volume relationships.
Acknowledgments
Field work in the Gulf of Nicoya during 1987-1988 was supported by the U.S. Agency of International Development under the Collaborative Research Support Program (CRSP) in the Fisheries Stock Assesment, and the University of Costa Rica project 808-86-106. We thank the master and crew of CIMAR RV Edith Muma for their help during the cruises.
Resumen
Se utilizó un diseño muestral estratificado para llevar a cabo una evaluación hidroacústica de la sección interior del Golfo de Nicoya. La topografía submarina fue modelada introduciendo el concepto topográfico de la cuenca, como una forma de proyectar los estimados del muestreo a todo el Golfo interno. Las isobatas y volúmenes de la cuenca del Golfo fueron construidos a partir de cartas náuticas. Los estimados de abundancia en las muestras se hicieron para los peces en la parte interna del Golfo utilizando los métodos acústicos conocidos como EMS (Expectation, Maximitation and Smoothing) y ecointegración. Los estimados de población se obtuvieron a partir de la multiplicación de los estimados del modelo topográfico de volúmen acuático y un modelo de densidad de peces dependiente de la profundidad. Los resultados muestran una disminución general en densidad de peces al aumentar la profundidad y una tendencia simultánea hacia la acumulación máxima en profundidades cercanas a los cuatro metros. Las áreas de fondo marino de aproximadamente cuatro metros incluyen extensas zonas de la parte interna del Golfo localizadas al sur de la Isla de Chira. Los estimados globales de densidad por volumen (0.269 peces/m3) y de densidad por área (1.88 peces/m2) son comparables con otros ambientes estuarinos someros.
References
Allen, M. J. & K. T. Herbinson. 1991. Beam-trawl survey of bay and nearshore fish of the soft-bottom habitat of southern California in 1989. CalCOFI Rep. 32: 112-127. [ Links ]
Amjoun, B., H.-L.Lai & V.F. Gallucci. 1990. User's guide to program CASA, a catch-at-size analysis. Release 1.0. Management Assistance for Artisanal Fisheries. Center for Quatitative Science, School of Fisheries, University of Washington. [ Links ]
Bartels, C.E., K. S. Price, M.I. Lopez & W. A. Bussing. 1983. Occurrence, distribution, abundance and diversity of fishes in the Gulf of Nicoya, Costa Rica. Rev. Biol. Trop. 31: 75-101. [ Links ]
Brandt, S. B., D. M. Mason & E. Patrick. 1992. Spatially-explicit models of fish growth rate. Fisheries 17: 23-35. [ Links ]
Chesney, E. J. Jr. & J. Iglesias. 1979. Seasonal distribution, abundance and diversity of demersal fishes in the inner Ria de Arosa, Northwest Spain. Estuar. Coast. Mar. Sci. 8: 227-239. [ Links ]
Cochran, W. G. 1977. Sampling Techniques. Chapter 7. Regression estimators. 189: 204. Wiley, New York. [ Links ]
Conquest, L., R. Burr, R. Donnelly, J. Chavarria & V. Gallucci. 1996 Sampling problems in artisanal fisheries. p. 179-225. In V. Gallucci, S. Saila, D. Guftafson & B. Rothschield (eds.) Stock Assessment: Quantitative Methods and Applications for Small Scale Fisheries. Lewis, New York. [ Links ]
DeMartini, E. E. & D. A. Roberts. 1990. Effects of giant kelp (Macrocystis) on the density and abundance of fishes in a cobble-bottom kelp forest. Bull. Mar. Sci. 46: 287-300. [ Links ]
Donato, F. 1988. Distribución, abundancia y diversidad de peces en el Golfo de Nicoya, Costa Rica. Tesis de Maestría en Zoología. Universidad de Costa Rica, San José. 86 p. [ Links ]
Ehrenberg, J. E. 1973. Estimation of the intensity of a filtered Poisson process and its application to acoustic assessment of marine organisms. University of Washington. 135 pp. [ Links ]
Gordea, A. & C.M. Duarte. 1991. Size-dependent spatial distribution of hake (Merluccius paradoxus) in Namibian waters. Can. J. Fish. Aquat. Sci. 48: 2095-2099. [ Links ]
Hedgepeth, J B. & R. E. Thorne. 1989. Hydroacoustic assessment of fish stocks in the Gulf of Nicoya, Costa Rica. From Oceans '89 Proceedings. IEEE Publications. 4: 1039-1045. [ Links ]
Hedgepeth, J. B., R.E. Thorne & V.F. Gallucci. 1990. Hydroacoustic assessment of fish stocks in the Gulf of Nicoya, Costa Rica. Collaborative Research Support Program.Working paper 65. [ Links ]
Hedgepeth, J B. 1994. Stock Assessment with hidroacoustic estimates of abundance via tuning and smoothed EM estimation. PhD. Disertation for the University of Washington. Washington. [ Links ]
Hedgepeth, J.B., V.F. Gallucci, R.E. Thorne & J. Campos. 1996 The application of some acoustic methods for the assessment of tropical artisanal fisheries. p. 271-353. In V. Gallucci, S. Saila, D. Guftanson & B. Rothschield (eds.) Stock Assessment: Quantitative Methods and Applications for Small Scale Fisheries. Lewis, New York. [ Links ]
Iglesias, J. 1981. Spatial and temporal changes in the demersal fish community of the Ria de Arosa (NW Spain). Mar. Biol. 65: 199-208. [ Links ]
Kalish, J. M, C.F. Greenlaw, W. G. Pearcy & D. V. Holliday. 1986. The biological and acoustical structure of sound scattering layers off Oregon. Deep-Sea Res. 33: 631-653. [ Links ]
Lai, H.-L., M. Mug & V. F. Gallucci. 1994. Management strategies for the tropical corvina reina Cynoscion albus in a multi-mesh gillnet artisanal fishery. p. 82-178. In G. Cruse, D. Eggers, R. Marasco, C. Pautzke, and T.J. Quinn II (eds.). Proceedings of the International Symposium on Management Strategies for Exploited Fish Populations. Achorage, Alaska. USA. [ Links ]
León, P. E. 1973. Ecología de la ictiofauna del Golfo de Nicoya, Costa Rica, un estuario tropical. Rev. Biol.Trop. 21: 5-30. [ Links ]
Madrigal, E. 1985. Dinámica pesquera de tres especies de Sciaenidae (corvinas) en el Golfo de Nicoya, Costa Rica. Tesis de Maestría en Zoología, Universidad de Costa Rica, San José. [ Links ]
Mathisen, O. A., R.E. Thorne, R. J. Trumble & M. Blackburn. 1978. Food consumption of pelagic fish in an upwelling area. p.111-123. In R. Boje & M. Tomczak (eds.) Upwelling Ecosystems. Springer-Verlag, Berlin. [ Links ]
Mood, A. M., F.A. Graybill & D. C. Boes. 1974. Introduction to the theory of statistics. McGraw-Hill. New York. 564 p. [ Links ]
Mug-Villanueva, M., V. F. Gallucci & H.-L. Lai. 1994. Age determination of corvina reina (Cynoscion albus) in the Gulf of Nicoya, Costa Rica, based on examination and analysis of hyaline zones, morphology and microstructure of otoliths. J. Fish Biol. 45: 177-191. [ Links ]
Nash, R. D.M. & R. N.Gibson. 1982. Seasonal fluctuations and compositions of two populations of small demersal fishes on the west coast of Scotland. Estuar. Coast. Shelf. Sci. 15: 485-496. [ Links ]
Peterson, C.L. 1956. Observations on the taxonomy, biology and ecology of the engraulid and clupeid fishes in the Gulf of Nicoya, Costa Rica. Bull. Inter-Amer.Trop.Tuna Comm. 1: 139: 280. [ Links ]
Polovina, J J. 1986. A variable catchability version of the Leslie model with application to an intensive fishing experiment on a multispecies stock. Fish. Bull. 84: 423-428. [ Links ]
Reina-Hervas, J. A. & P.Serrano. 1987. Structural and seasonal variations of inshore fish population in Malaga Bay, southeastern Spain. Mar. Biol. 95: 501-508. [ Links ]
Rudstam, L.G., T. Lindem & S. Hansson. 1988. Density and in situ target strength of herring and sprat: a comparison between two methods of analyzing single-beam sonar data. Fish. Res. 6: 305-315. [ Links ]
Scheaffer, R.L., W. Mendenhall & L. Ott. 1986. Elementary Survey Sampling. Chapter 6. Ratio, regression, and difference estimation. Duxbury, Boston, Massachussettes. 125-167 p. [ Links ]
Sokal, R. R. & F.J. Rohlf. 1969. Biometry. W. H. Freeman, San Francisco. 776 p. [ Links ]
Stanton, T. K. 1985a. Volume scattering: echo peak PDF. J. Acoust. Soc. Am. 77: 1358-1366. [ Links ]
Stanton, T. K. 1985b. Density estimate of biological sound scatterers using sonar echo peak PDFs. J. Acoust. Soc. Am. 78: 1868-73. [ Links ]
Sullivan, P.J., H.-L. Lai & V. F. Gallucci. 1990. A catch-at-length analysis that incorporates a stochastic model of growth. Can. J. Fish. Aquat. Sci. 47: 184-198. [ Links ]
Szelistowski, W.A. & J. Garita. 1989. Mass mortality of sciaenid fishes in the Gulf of Nicoya, Costa Rica. Fish. Bull. U.S. 87: 363-365. [ Links ]
Wilson, J. D. 1989. A smoothed EM algorithm for the solution of Wicksell's corpuscle problem. J. Statist. Comput. Simuln. 31: 195-221. [ Links ]
Three idealized basin models; hemisphere, cone, and torchiere.
Figure 2a shows three conceptual basins which produce different volume versus depth relations. The following relations can be shown for radius r at basin depth, z, given the maximum depth, h, and the surface radius, w:
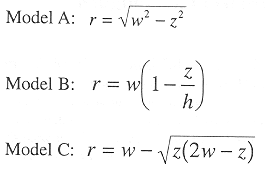
The volume of the hollow cylinder bounded y the contours for depth z1 and z2 is
where r is found above and for the three models is:
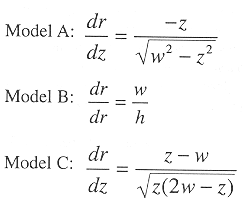
The teorical differential volumes (i.e. ) for the three models are presented in Figure 2b. In practice, the basin model determined by the digitizing the contours and measuring areas from a nautical chart. Volumes were estimated from the product of area by mean depth, which is analogous to the integral approach above. A grid of bottom depths is sampled from this surface to obtain an empirical depth frequency distribution. This is also analogous to integration between depth contours. An alternative is to fit surface to bottom depths with a terrain modeling package.
1 BioSonics. 4027 Leary Way NW. Seattle, Washington. 98107. USA.
2 School of Fisheries and School of Marine Affairs. University of Washington. UW Box. 357980. Seattle, Washington. 98195. USA. E-mail: gallucci@fish.washington.edu
3Centro de Investigación en Ciencias del Mar y Limnología (CIMAR). Universidad de Costa Rica, 2060 San José, Costa Rica
4Escuela de Biología. Universidad de Costa Rica, 2060, San José, Costa Rica.
3, 4 E-mail: promarco@sol.racsa.co.cr