Introducción

En las ciencias naturales se realizan diferentes tipos de estudios, que se pueden clasificar en estudios observacionales y estudios experimentales (^{Shaffer y Johnson 2008}). En general, los estudios experimentales son mayoritariamente comparativos, ya que se comparan tratamientos (^{Vargas-Rojas 2021}). En experimentación agrícola, después de definir los tratamientos, estos se asignan aleatoriamente a las unidades de acuerdo con el diseño experimental que mejor se ajusta al estudio en cuestión. Posteriormente, se registran una o varias variables de respuesta. Finalmente, mediante el uso de técnicas de análisis estadístico, se estiman las medias de la variable de respuesta para cada tratamiento y se realizan pruebas de hipótesis con el objetivo de compararlas.

Para realizar la comparación, cuando la variable respuesta es cuantitativa y se asume que se distribuye normal, se recurre al análisis de varianza (ANDEVA), el cual se basa en el estadístico F (^{Robledo 2015}). El ANDEVA consiste en el contraste de una hipótesis nula ( H 0 ) o de no efecto de tratamientos contra una hipótesis alternativa (𝐻 𝐴 ) que indica la existencia de efectos no nulos (^{Mesquida et al. 2023}). En este contraste de hipótesis se pueden cometer dos tipos de errores; tipo I y tipo II. El error tipo I es el error que se comete al rechazar la hipótesis nula cuando es verdadera, y tiene una probabilidad asociada, que es el nivel de significancia de la prueba. El error tipo II ocurre cuando no se rechaza la hipótesis nula y esta es falsa; la probabilidad de cometer este error se denota como β, que es la probabilidad de no encontrar diferencias cuando realmente existen (^{Montgomery 2019}).

El estudio de la potencia estadística se basa en la estimación de la probabilidad de cometer error tipo II. Se busca minimizar esta probabilidad, con el objetivo de maximizar su complemento, la potencia estadística (^{Lapeña et al. 2011}, ^{Kinney et al. 2020}). Autores como ^{Brysbaert y Stevens (2018}) y ^{Cohen (1988}) sugieren que se debe establecer una potencia de prueba de al menos el 0,80 (80%) para detectar un efecto, bajo el supuesto de que dicho efecto existe en la población estudiada. Aunque este valor de 0,80 es comúnmente utilizado y se considera un umbral mínimo aceptable, otros autores como ^{Lenth (2001}) indican que la potencia de prueba debe ser mayor a 0,85 o 0,90. La idea subyacente es asegurar una probabilidad razonable de detectar el tamaño de efecto especificado.

La estimación de la potencia depende de cinco elementos interrelacionados: 1) nivel de significancia, 2) tamaño del efecto, 3) variabilidad residual, 4) número de repeticiones y 5) diseño del experimento (^{Brandmaier et al. 2018}). El nivel de significancia es controlado por el investigador (^{Kotrlik et al. 2011}), mientras que el diseño depende de las condiciones del experimento. Por lo tanto, la potencia de la prueba para un nivel de significancia está determinada por el número de repeticiones, el tamaño de efecto deseado entre los tratamientos y una variabilidad dada (^{Gbur et al. 2012}). El tamaño del efecto se refiere a la diferencia mínima que el investigador considera importante entre las medias de la variable respuesta de un par de tratamientos (^{Kuehl 2001}). La variabilidad es la varianza residual del experimento y el número de repeticiones es la cantidad de unidades experimentales independientes por tratamiento, necesarias para alcanzar cierto nivel de potencia (^{Cohen 1992}).

La importancia de estimar la potencia de prueba de manera prospectiva radica en que, mediante esta estimación, es posible asegurar a priori la capacidad de distinguir un tamaño de efecto específico de la variación inherente de la variable respuesta, de naturaleza aleatoria (^{Gent et al. 2018}). Sin embargo, a pesar de que el número necesario de repeticiones es una pregunta común entre los investigadores, su estimación no forma parte de la planificación de experimentos en el ámbito agrícola (^{González-Lutz 2008}). Por tanto, es común encontrar investigaciones donde se concluye que no existen diferencias significativas entre tratamientos, pero al no fijar una potencia de prueba, la falta de significancia puede deberse a un número de repeticiones inadecuado para detectar un tamaño de efecto (^{Williams et al. 2023}), lo que conlleva a resultados erróneos o inconclusos (^{Cohen 1990}, ^{Kozak y Piepho 2017}).

Para poder estimar la potencia de la prueba, es necesario conocer la varianza residual del experimento, empero, esta solo se conoce después de obtener las observaciones y ajustar el modelo de ANDEVA. Por consiguiente, para realizar estimaciones de la potencia de la prueba, se puede utilizar un aproximado de la varianza residual. Según ^{Dale y Fortin (2014}), el primer paso importante es conocer las características de un sitio antes de diseñar el experimento. Para ello, se requiere un estudio piloto o un ensayo de uniformidad. Estos últimos han sido utilizados para estimar el tamaño de la unidad experimental, comparar la eficiencia de distintos diseños experimentales, estudiar la variabilidad del suelo y realizar simulaciones de campos aleatorios (^{Fagroud y Van Meirvenne 2002}, ^{Richter y Kroschewski 2012}).

En adición a lo anterior, se debe considerar que la definición del tamaño del efecto no es un asunto arbitrario. Desde un punto de vista teórico es poco probable que la diferencia numérica entre dos medias sea exactamente cero (^{Nakagawa y Cuthill 2007}). Es decir, en la mayoría de los casos será un valor distinto de cero. Sin embargo, no siempre una diferencia no nula es relevante para el investigador, sino que depende de lo que implica esta diferencia en términos de rendimiento o producción. A manera de ejemplo, un investigador puede definir el tamaño del efecto en relación con el beneficio financiero que puede derivarse de una práctica de manejo, como el uso de variedades. Así, si un aumento del rendimiento del 10% debido al uso de una nueva variedad resulta en rédito económico, este tamaño del efecto sería de interés. Por lo tanto, en la etapa de planificación del experimento, se debe definir el tamaño del efecto de forma que tome en cuenta criterios biológicos, físicos, económicos, científicos y/o prácticos (^{Apuan 2014}).

Para cuantificar el tamaño del efecto, se han identificado más de 61 estadísticos, tanto estandarizados como no estandarizados. Entre los más utilizados se encuentran la diferencia esperada entre dos medias (una medida no estandarizada) y la “d” de Cohen (una medida estandarizada). Siempre que sea interpretable, es preferible utilizar la diferencia no estandarizada entre las dos medias (^{Nakagawa y Cuthill 2007}), para obtener una estimación de esta magnitud se puede recurrir a resultados de estudios de metaanálisis (^{Krupnik et al. 2019}).

En el contexto de la investigación agrícola en Costa Rica, la mayoría de los estudios se centran en pruebas paramétricas (por ejemplo, ANDEVA o regresión), y rara vez abordan la potencia estadística desde una perspectiva prospectiva (^{Vargas-Rojas 2021}). Así, el objetivo de este estudio fue analizar cómo varía la potencia de prueba en función de la variabilidad y el tamaño del efecto, para que los investigadores comprendan la importancia de estos elementos y mejoren la estimación del número de repeticiones utilizados en sus experimentos agrícolas.

Materiales y métodos

Elementos considerados para la estimación de la potencia estadística de la prueba

Se estableció un nivel de significancia de 0,05 como un valor comúnmente utilizado como umbral de error tipo I en experimentos agrícolas (^{Kozak y Piepho 2017}). También se supuso que el campo experimental es razonablemente homogéneo, por lo que se empleó un diseño completamente aleatorizado (DCA). A continuación, se detallan los procedimientos empleados para determinar el tamaño del efecto, la varianza residual y el número de repeticiones.

Estimación de la varianza residual

Para este trabajo, se partió del supuesto de que no se conocía la varianza residual y no se pudo obtener de otros estudios. Por lo tanto, se utilizaron los resultados de la investigación realizada por ^{Vargas-Rojas (2021}), quien estudió la correlación espacial de la variable rendimiento (kg) en un ensayo de uniformidad en el cultivo de arroz en Bagaces, Costa Rica. Este autor reportó que el modelo de correlación espacial esférica, sin efecto “nugget”, fue el que mejor se ajustó a los datos. Además, estimó los valores del "sill" y el "range" en 0,0091 y 1,44, respectivamente. Con base en esos parámetros, se simularon 10 000 campos aleatorios, denominados de aquí en adelante como simulaciones de ensayo de uniformidad. Cada simulación correspondió a una cuadrícula de 24 m × 16 m (384 m²), con un espacio entre puntos de 1 m × 1 m. Cada punto de la grilla representaba una realización de la variable aleatoria, en este caso, el rendimiento en kilogramos. El procedimiento se realizó con el paquete geoR versión1.9-4 (^{Ribeiro y Diggle 2001}) del lenguaje de programación R versión 4.3.3 (^{R Core Team 2024}).

En cada una de las 10 000 simulaciones del ensayo de uniformidad, se formaron 16 unidades experimentales (UE) de 3 m de largo por 8 m de ancho (24 m²). Este tamaño se seleccionó según la recomendación de ^{Vargas Rojas y Navarro Flores (2019}), quienes lo definieron como adecuado para ensayos de rendimiento en arroz. Una vez conformadas las unidades experimentales, la producción de cada una en kilogramos (kg UE^-1) se obtuvo mediante la suma de los rendimientos simulados en los puntos de la grilla de 24 m × 16 m, lo que permitió la conformación de 10 000 conjuntos de 16 unidades experimentales. Luego, en cada conjunto, se definieron dos tratamientos ficticios con efecto nulo (A y B) y se asignaron de manera aleatoria, lo que permitió obtener ocho unidades experimentales para cada tratamiento. Posteriormente, se ajustó el modelo de análisis de varianza para un diseño completamente aleatorizado (DCA) que se presenta en la Ecuación 1.

Donde 𝑦 𝑖𝑗 es el rendimiento del i-ésimo (i = 1, 2) tratamiento en la j-ésima unidad experimental (j = 1,…, n); 𝜇 es la media general del rendimiento; 𝜏 𝑖 : es el efecto fijo del i-ésimo tratamiento y 𝑒 𝑖𝑗 representa el error residual, se supone que esta normalmente distribuido con media cero y varianza 𝜎 2 , además se supone que la cov ( 𝑒 𝑖𝑗 , 𝑒 𝑖'𝑗' )=0 Ɐ ij ≠ i'j´.

A partir del modelo de la Ecuación 1, y dado que no se aplicaron tratamientos reales que generaran desviaciones con respecto a la media general, se estimó la media general y la varianza residual para cada uno de los 10 000 conjuntos de unidades experimentales. Para evidenciar cómo afecta el aumento de la varianza residual en la estimación del número de repeticiones, se definieron dos escenarios. En el escenario A, se utilizó la varianza residual promedio del conjunto de 10 000 unidades experimentales, que fue de 0,53; mientras que en el escenario B se usó el cuantil 95 de la varianza residual del conjunto de 10 000 unidades experimentales, que correspondió a un valor de 0,71. Además, el valor de la media general promedio fue de 10,74 kg UE^-1 (4,48 t ha^-1).

Definición del tamaño del efecto

Para definir el tamaño del efecto en este trabajo se emplearon los hallazgos de ^{Ibrahim y Saito (2022}) quienes realizaron un metaanálisis para cuantificar el aumento del rendimiento en arroz debido a prácticas agronómicas. Estos autores encontraron que, la diferencia entre el rendimiento de tratamientos con prácticas agronómicas mejoradas y el tratamiento testigo fue en promedio de 1,60 t ha^-1. Este valor se tomó como base para definir el tamaño del efecto, que resultó ser un 15% de la media general estimada con los datos de las simulaciones del ensayo de uniformidad.

También se definieron dos tamaños de efecto en los que se redujo la diferencia a 5% y 10%; para considerar escenarios donde las prácticas agrícolas generen tamaños de efecto menores. De manera que los porcentajes definidos corresponden a diferencias de 0,54 kg UE^-1 (0,22 t ha^-1), 1,07 kg UE^-1 (0,45 t ha^-1) y 1,61 kg UE^-1 (0,67 t ha^-1), para efectos de 5%, 10% y 15%, respectivamente. Es necesario indicar que, para las estimaciones de potencia, se utilizaron las diferencias absolutas y no los porcentajes.

Número de repeticiones

Bajo el enfoque de ANDEVA, la hipótesis nula ( 𝐻 0 ) se evaluó con el uso del estadístico F. Este estadístico tiene una distribución 𝐹 𝑔𝑙𝑛,𝑔𝑙𝑑,𝜆 , donde gln son los grados de libertad del numerador, gld son los grados de libertad del denominador y 𝜆 es el parámetro de no centralidad. Cuando la hipótesis nula es verdadera, 𝜆 es igual a 0; en el caso contrario, 𝜆 tomará valores mayores a 0. Luego, la potencia quedó determinada como P 𝐹 𝑔𝑙𝑛,𝑔𝑙𝑑,𝜆 > 𝐹 𝑐𝑟í𝑡𝑖𝑐𝑎 , donde el lado izquierdo de la inecuación corresponde a una F no central, mientras que el lado derecho es el cuantil (1- 𝛼) de una F central para un nivel de significación 𝛼 determinado.

Los pasos para la estimación de la potencia fueron:

Se calculó el valor crítico (𝐹 (𝑐𝑟í𝑡𝑖𝑐𝑎] ) para el estadístico F como el cuantil 1- 𝛼 de una 𝐹 𝑔𝑙𝑛,𝑔𝑙𝑑,0 .

Se estimó 𝜆, cuyo cálculo consideró la estructura del diseño, la varianza residual utilizada y el efecto de tratamiento que se quieren detectar. Para este trabajo, se definió como los tamaños del efecto que se evaluaron: 5%, 10% y 15% con respecto a la media de la producción. A partir de estos valores, se calculó la potencia de la prueba para una diferencia entre pares de medias igual o mayor al tamaño del efecto supuesto, lo que estableció una cota inferior para 𝜆 (^{Vargas-Rojas 2021}, ^{Vargas-Rojas y García 2022}).

Una vez obtenidos 1 y 2 se calculó la potencia como: P 𝐹 𝑔𝑙𝑛,𝑔𝑙𝑑,𝜆 > 𝐹 𝑐𝑟í𝑡𝑖𝑐𝑎 . La estimación de la potencia se hizo desde dos hasta 15 repeticiones para cada tamaño de efecto y para cada escenario de varianza.

Todos los procedimientos se realizaron con el lenguaje de programación R (^{R Core Team 2023}). El código de R utilizado para estimar la potencia estadística se compartirá por solicitud al correo electrónico del autor para correspondencia.

Resultados

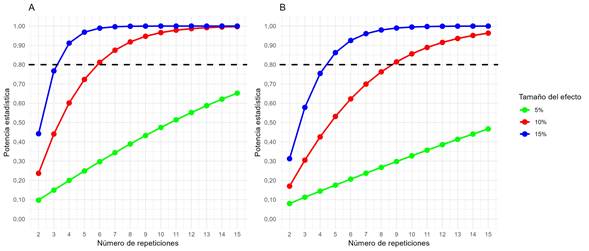
La Figura 1 resume los resultados de las simulaciones para ambos escenarios. Para una varianza residual de 0,53 con cuatro repeticiones se alcanzó una potencia del 0,91 para detectar un tamaño de efecto del 15%, mientras que se necesitaron seis repeticiones para lograr una potencia de 0,81 y detectar un efecto del 10% (Figura 1 A). Cuando la varianza residual aumentó a 0,71 (Figura 1 B), para detectar un efecto del 15% se necesitaron cinco repeticiones para alcanzar una potencia de 0,86. Por otro lado, si el efecto es del 10% y se quiere mantener una potencia superior a 0,80; fueron necesarias nueve repeticiones (Figura 1 B). Finalmente, para detectar un tamaño de efecto del 5%, la potencia estadística con las varianzas residuales definidas apenas alcanzó valores entre 0,40 y 0,60 con 15 repeticiones. Es decir, para que diferencias más pequeñas sean significativas se necesita aumentar el número de repeticiones.

De forma general, en la Figura 1 se puede observar que mientras mayor fue el tamaño del efecto a detectar y menor fue la varianza residual, se necesitan menos repeticiones para alcanzar el umbral de potencia de prueba de 0,80.

Discusión

Los resultados (Figura 1) muestran que si la varianza residual se mantiene constante, a medida que el tamaño del efecto a detectar disminuye, se requiere un mayor número de repeticiones. Este resultado concuerda con lo expuesto por ^{Burmeister y Aitken (2012}), quienes mencionan que, de forma general, entre menor sea el tamaño del efecto, es decir, cuanto menor sea la diferencia entre tratamientos que se desea detectar, mayor será el número de repeticiones requerido para alcanzar una potencia dada.

De manera que cuando se planifica un estudio experimental la estimación del número de repeticiones se debe realizar en función del tamaño del efecto que se quiere detectar. En este sentido, ^{Lenth (2001}) destaca que un experimento debe contar con repeticiones suficientes para detectar diferencias significativas que también sean relevantes desde una perspectiva científica. Al mismo tiempo, el autor advierte que se debe tener cuidado en no diseñar un experimento con muchas repeticiones donde un efecto de poca importancia científica sea detectable estadísticamente. Por lo tanto, la importancia del número de repeticiones no se limita solo a la perspectiva científica, sino que también tiene un componente económico. Un experimento con un número insuficiente de repeticiones puede resultar en un desperdicio de recursos, ya que no produce resultados útiles, mientras que un experimento con un número excesivo de repeticiones consume más recursos de los necesarios (^{Baguley 2004}).

En ese sentido, resulta determinante contar con una estimación del tamaño del efecto. Para ejemplificar la obtención del tamaño del efecto, en este trabajo se utilizaron los resultados disponibles en una publicación previa, lo cual es una práctica común (^{Vargas-Rojas 2021}). También es posible obtener esta información de estudios piloto (^{Anderson et al. 2017}). Sin embargo, no siempre es factible utilizar datos de publicaciones anteriores o de estudios piloto. En tales casos, el investigador debe determinar la magnitud del efecto en función de su importancia dentro del contexto de la investigación (^{Baguley 2004}).

Lo anterior pone en evidencia lo relevante que es el tamaño del efecto en un experimento. En algunas disciplinas como medicina, psicología y ciencias del comportamiento y cognitivas, se ha adoptado la práctica de reportar e interpretar el tamaño del efecto en los artículos científicos (^{Gignac y Szodorai 2016}). Sin embargo, en los experimentos en ciencias agrícolas, la estimación del tamaño del efecto es un aspecto que a menudo se omite (^{Apuan 2014}). Por ejemplo, algunos protocolos para evaluar variedades vegetales a nivel de campo establecen que el experimento debe tener tres o más repeticiones para asegurar la confiabilidad estadística del ensayo, que miden con los grados de libertad del error, pero esto no garantiza una potencia adecuada para detectar un tamaño de efecto definido. Lo anterior podría generar que se descarten materiales o tratamientos que podrían ser promisorios (^{Bono y Arnau 1995}, ^{Anderson et al. 2017}).

Por consiguiente, la formulación de recomendaciones generales resulta inapropiada. Al planificar un experimento agrícola no es suficiente plantear un análisis de varianza, enumerar las fuentes de variación o indicar que se utilizará una prueba de separación de medias. También se debe considerar que, para determinar el número adecuado de repeticiones que garantice una potencia estadística suficiente en la prueba de hipótesis, se deben tener en cuenta el tamaño del efecto, la varianza, el nivel de significancia y la estructura de tratamientos. Estos elementos pueden variar de un experimento a otro según los objetivos y las condiciones específicas de la investigación (^{Stroup 1999}).

De igual forma, los resultados obtenidos en el presente trabajo (Figura 1) indican que, a medida que aumenta la variabilidad residual, se requiere un número mayor de repeticiones para detectar el mismo tamaño de efecto con una potencia dada. Cuanta más variabilidad pueda haber en un experimento, mayor será el número de repeticiones necesarias para detectar estas diferencias de manera confiable (^{Woodcock et al. 2016}). Sin embargo, obtener una medida de variabilidad antes de realizar el experimento es un tema complejo, ya que esta información no siempre está disponible. Al igual que el tamaño del efecto, es posible recurrir a medidas de variabilidad previamente conocidas de estudios anteriores (^{Quesada y Figuerola 2010}), pero existe la limitación de que en muchas revistas científicas no se proporciona información sobre la variabilidad residual del experimento, sino solo sobre las medias ajustadas y su diferencia (^{Stroup 2002}).

Finalmente, lo analizado en este trabajo pretende poner en evidencia la necesidad de que exista un diálogo entre los investigadores y los estadísticos, de manera que los primeros comuniquen sus necesidades y los segundos las puedan trasladar a los términos estadísticos correspondientes. Esta práctica ayudaría a dejar claro los objetivos y el verdadero alcance de una investigación. En esta línea, ^{Quinn y Keough (2002}), argumentan una de las ventajas del análisis de potencia de forma prospectiva radica en la necesidad de definir tanto la hipótesis alternativa (es decir, el tamaño del efecto) como el modelo estadístico que se utilizará en el análisis. Esta especificación del modelo implica una reflexión sobre el análisis antes de la recolección de estos, lo cual se considera una práctica recomendable.

Conclusiones

En el análisis de los dos escenarios de variabilidad presentados en este trabajo quedó en evidencia que, en el escenario con mayor varianza residual, se requirió un mayor número de repeticiones para alcanzar la potencia deseada. Además, se demostró que, independientemente del escenario de variabilidad, a medida que disminuye el tamaño del efecto que se quiere detectar en un análisis de varianza, se incrementa el número necesario de repeticiones para lograr la potencia deseada.

Por lo tanto, para planificar experimentos con una potencia suficiente, es fundamental disponer de una estimación aproximada de la varianza residual y del tamaño del efecto de interés para el experimento en cuestión.