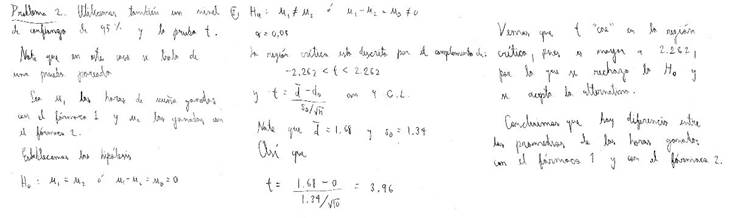Introducción
Recientemente, en los currículos de diversos países (e.g., Australia, México, Costa Rica y Chile) existe una mayor presencia de la probabilidad y estadística desde la educación básica. Esto se debe a la importancia que tiene hoy en día la formación de una ciudadanía crítica, con capacidad de interpretar el mundo en el que se desenvuelve. En el currículo chileno, para tercero y cuarto medio, podemos observar que también se espera que el estudiantado pueda realizar inferencias aplicando procedimientos de intervalos de confianza o de pruebas de hipótesis (Mineduc, 2019), tópicos que anteriormente se habían privilegiado para los cursos universitarios. Sin embargo, nos preguntamos si los estudiantes, y sobre todo el profesorado, se encuentran preparados para afrontar este reto.
En diversas investigaciones se han identificado dificultades que presentan tanto estudiantes como profesores al trabajar inferencia, por ejemplo, sobre la comprensión del nivel de significancia, tipo de error, la lógica de las pruebas de hipótesis, el planteamiento de las hipótesis estadísticas y las distribuciones muestrales (e.g., Batanero, Vera y Díaz, 2012; Garfield y Ben-Zvi, 2008; Garfield y Ben-Zvi, 2008; Harradine, Batanero y Rossman, 2011; Sotos, Vanhoof, Van den Noortgate y Onghena, 2007). Estas dificultades pueden llevar al estudiante a enfocarse más en los algoritmos que en comprender realmente las nociones involucradas para llevar a cabo la inferencia. No obstante, de acuerdo con Rossman (2008), además de la conclusión, la inferencia debe incluir la evidencia y el razonamiento sobre los cuales se realiza; es decir, los desarrollos algorítmicos no son suficientes para realizar inferencias.
Como respuesta a dichas dificultades se han realizado investigaciones, por una parte, sobre cómo aproximarnos a la inferencia desde una perspectiva informal, denominada razonamiento inferencial informal -RII(e.g., Makar & Rubin, 2009; Zieffler, del Mas,Garfield & Reading, 2008) y, por otra parte, sobre cómo construir sobre ese RII un razonamiento inferencial formal -RIF(e.g., Jacob & Doerr, 2014; Makar & Rubin, 2018; Pfannkuch, Arnold & Wild, 2015; Weinberg, Wiesner & Pfaff, 2010). Respecto a esta última perspectiva, dichas investigaciones enfatizan la necesidad de introducir la inferencia por etapas, en otras palabras, promover progresivamente el razonamiento inferencial formal en los estudiantes. Pfannkuch, Arnold y Wild (2015) indican algunos conceptos fundamentales, tanto para la inferencia informal como para la inferencia formal, que se pueden trabajar de forma transversal en el currículo escolar; además, presentan algunas actividades de aprendizaje sobre la comparación de diagramas de caja y el uso de software que ayudan a explicar cada uno de los conceptos fundamentales. Sin embargo, aún sigue abierta la discusión sobre cómo podemos construir un RIF sobre las bases que se han desarrollado del RII.
Una de las bondades principales de las pruebas con el estadístico t-Student es que pueden ser utilizadas con muestras pequeñas, muestras de este tipo son muy frecuentes tanto en estudios del área industrial, farmacéutica y agronómica como en los de carácter social. Sin embargo, realizar inferencias basados en pruebas con este estadístico requiere una comprensión profunda de las nociones que se encuentran relacionadas con el estadístico t-Student, ya que aunque los profesores y futuros profesores pueden realizar los procedimientos aparentemente de forma adecuada cuando resuelven un problema guiado del libro texto, pueden tener dificultades para comprender o conectar las nociones estadísticas involucradas, lo cual podría llevar a no saber identificar el tipo de datos, elegir el estadístico y la distribución o la prueba necesaria para resolver un problema real (Batanero, 2013).
Con base en lo expuesto anteriormente, el presente artículo tiene como objetivo caracterizar el razonamiento inferencial (RI) de una muestra de profesores de matemáticas de enseñanza media cuando resuelven problemas sobre la t-Student; esto con la finalidad de estudiar los elementos (representaciones, conceptos/definiciones, propiedades, procedimientos, argumentos) que utilizan en sus prácticas y si dichos elementos permiten asociarlas a distintos niveles de razonamiento inferencial. Así mismo, este estudio pretende explorar empíricamente, si los niveles de RI para el estadístico t-Student propuestos a nivel teórico por Lugo-Armenta y Pino-Fan (2021a), son predictores del nivel de razonamiento inferencial que los profesores ponen en juego al resolver problemas sobre este estadístico.
Marco teórico
En las investigaciones sobre educación estadística podemos encontrar referencia al razonamiento, a la alfabetización y al pensamiento estadístico, con definiciones o usos que frecuentemente ligan estas posturas. Ben-Zvi y Garfield (2004) presentan definiciones sobre tales nociones, rescatando las diferencias que existen entre ellas; por ejemplo, la alfabetización estadística incluye las habilidades básicas para comprender la información estadística o resultados de la investigación, mientras que el razonamiento estadístico lo definen como “la forma en que las personas razonan ideas estadísticas y dan sentido a la información estadística” (p. 7). Entonces, razonar es comprender y ser capaz tanto de explicar los procesos estadísticos como de interpretar sus resultados. En cuanto al pensamiento estadístico, los mismos autores señalan que implica comprender por qué y cómo se llevan a cabo las investigaciones estadísticas, la naturaleza del muestreo, cómo utilizamos modelos para simular fenómenos aleatorios, cómo, cuándo y por qué las herramientas inferenciales pueden usarse, el contexto de un problema y utilizarlo para sacar conclusiones y comprender el proceso que involucra; así mismo, ser capaz de criticar y evaluar los resultados de un estudio estadístico.
Nuestro posicionamiento de razonamiento recurre a una visión pragmatista sobre la construcción del conocimiento matemático, así como del conocimiento matemático escolar; es decir, que para hablar de razonamiento recurrimos a una visión integrada y transdisciplinar, que involucra pensamiento, razonamiento y alfabetización estadística, pues cada uno de estos enfoques de la estadística escolar se desarrolla desde las perspectivas psicológica, epistémica y semiótica, respectivamente. Entonces, asumimos razonamiento como un “macroproceso social y epistémico” que involucra poner en juego tanto objetos matemáticos primarios (representaciones, conceptos/definiciones, propiedades/proposiciones, procedimientos y argumentos) como procesos matemáticos para la solución de una situación-problema. En otras palabras, para decir que un sujeto “comprende” la t-Student debemos observar que en el razonamiento asociado a sus prácticas (para resolver distintos tipos de situaciones/problemas), emerjan de manera gradual, sistemática y progresiva, objetos matemáticos primarios y procesos vinculados a los significados de esta noción (Lugo-Armenta y Pino-Fan, 2021a). Así, al considerar el razonamiento en términos de prácticas, objetos y procesos matemáticos utilizados en ellas, se transita en cierto sentido por las definiciones dadas por Ben-Zvi y Garfield (2004).
Para definir las prácticas, objetos y procesos matemáticos recurrimos al enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS), el cual es un enfoque teórico inclusivo de la educación matemática que tiene supuestos teóricos antropológicos y semióticos (Godino, Batanero y Font, 2007; 2019; Presmeg, 2014). El EOS reconoce la doble naturaleza de las matemáticas, como sistema de objetos y de prácticas. La noción de práctica tiene un rol fundamental y se entiende como “toda actuación o expresión (verbal, gráfica, etc.) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o generalizarla a otros contextos y problemas” (Godino y Batanero, 1994, p. 334). De los sistemas de prácticas, operativas o discursivas, emergen los objetos matemáticos primarios que dan cuenta de su organización y estructura: elementos lingüísticos, situaciones/problemas, conceptos/definiciones, propiedades/proposiciones, procedimientos y argumentos (Godino, Batanero y Font, 2007; 2019). Estos objetos matemáticos primarios pueden ser analizados desde la perspectiva proceso-producto, por lo que debemos considerar los procesos: comunicación, problematización, definición, enunciación, algoritmización y argumentación (Godino, Font, Wilhelmi y Lurduy, 2011). Otros procesos que permiten comprender la naturaleza compleja y progresiva de los objetos matemáticos son: generalización, particularización, idealización, materialización, representación, significación, reificación, descomposición y modelización (Pino-Fan, Godino y Font, 2016; Font y Rubio, 2017).
Para el desarrollo de este estudio utilizamos una propuesta teórica de niveles de razonamiento inferencial sobre el estadístico t-Student, la cual está fundamentada sobre las nociones teóricas que hemos descrito y en la literatura de investigación de educación estadística (Lugo-Armenta y Pino-Fan, 2021a). En dicha propuesta se vinculan diversas perspectivas sobre el razonamiento inferencial informal y los objetos y procesos matemáticos identificados con un estudio de tipo histórico-epistemológico sobre estadístico t-Student. El estudio histórico-epistemológico se realizó desde una perspectiva intuitiva, preformal y formal. En el Anexo A se resume la propuesta de niveles de razonamiento inferencial para el estadístico t-Student (a partir del estudio de Lugo-Armenta y Pino-Fan, 2021a), y en la Tabla 1 describimos brevemente la esencia de los cuatro niveles de dicha propuesta.
Tabla 1 Niveles de razonamiento inferencial para el estadístico t-Student.
| Nivel 1 |
|---|
| Los indicadores de este nivel corresponden a un razonamiento inferencial informal, estos van más allá de simples interpretaciones de los gráficos o cálculos de medidas; dichos indicadores están enfocados en que el estudiante razone inferencialmente y realice conjeturas a partir de los datos. Los argumentos que apoyan las conjeturas están basados en la variación interna de los datos. |
| Nivel 2 |
| En este nivel se encuentran indicadores que corresponden a un nivel de tipo pre-formal, donde se pueden identificar rasgos del RII tales como la forma en que se utiliza (define) la probabilidad, como una medida de certidumbre asociada a un evento sin compararla con un nivel de significancia o un límite preestablecido, y cómo se observa implícita la hipótesis en el problema. |
| Nivel 3 |
| Los indicadores que se encuentran en este nivel se consideran pre-formales, pero con un mayor grado de formalidad que en el nivel anterior, dado que se tiene una visión más amplia de las posibilidades para trabajar con las pruebas t-Student, hacia la generalización de estas pruebas. Los aspectos que marcan cierto grado preformal son, por ejemplo, el lenguaje utilizado para plantear las hipótesis y la forma de trabajar y comprender la significancia. |
| Nivel 4 |
| Los indicadores que se presentan en este nivel corresponden a un razonamiento inferencial formal. Se espera que el estudiante pueda tomar decisiones basadas en las técnicas estadísticas de la metodología de las pruebas de hipótesis y sea capaz de analizar críticamente sus desarrollos estadísticos. |
Nota: Fuente propia de la investigación.
Metodología
Este estudio se encuentra enmarcado en el paradigma cualitativo (Cohen, Manion y Morrison, 2011), ya que busca analizar las prácticas matemáticas que realizan los profesores al resolver problemas que involucran al estadístico t-Student y, con base en ello, determinar el nivel de razonamiento que se pone de manifiesto con dicha práctica matemática. Dicha caracterización se realiza mediante los niveles de razonamiento inferencial sobre el estadístico t-Student descritos en la sección anterior (ver también Anexo A).
Los sujetos que participaron en este estudio son 59 profesores en ejercicio y 22 profesores en formación. Los profesores en ejercicio se inscribieron a un taller de razonamiento estadístico organizado por una universidad chilena y dirigido a profesores de enseñanza media de matemáticas de Chile; este taller tuvo una duración de una semana y se llevó a cabo de forma virtual con modalidad sincrónica y asincrónica. Los profesores en ejercicio eran de distintos colegios (municipales, subvencionados y particulares) con distintas características, en su mayoría, de una región al sur de Chile, y algunos de otras regiones. Durante la semana, los profesores tuvieron la oportunidad de resolver actividades y discutir sus soluciones con sus pares y los formadores que impartieron el taller (ambos autores de este artículo).
Se propusieron actividades de carácter individual y algunas actividades para resolver en equipos. La conformación de los equipos fue de forma aleatoria. En este artículo presentamos el análisis de las prácticas desarrolladas por tres de los seis equipos conformados (1, 4 y 6); consideramos estos equipos dado que las prácticas que se mostraron y discutieron representaban el tipo de prácticas desarrolladas en las actividades grupales e individuales.
Por su parte, los profesores en formación que participaron en este estudio eran de diversas universidades de Costa Rica y se inscribieron en un taller de razonamiento estadístico, con duración de una semana de forma virtual y con modalidad asincrónica, y fue organizado por dos universidades de dicho país. En este taller los participantes resolvieron actividades sobre el estadístico t-Student y tuvieron oportunidad de interactuar con sus pares y con el formador (primer autor de este artículo) por medio de un foro y videos. Más detalles sobre cómo se desarrollaron los talleres se pueden ver en Lugo-Armenta y Pino-Fan (2021b).
En el caso de los profesores en formación, por la naturaleza de la modalidad del curso, las actividades se resolvieron individualmente y en este artículo presentamos el análisis de las prácticas desarrolladas por cinco participantes (2, 8, 9, 12 y 20) debido a que fueron representativas de las prácticas desarrolladas por todos los participantes.
En el Anexo B se presentan las actividades que resolvieron de forma grupal los profesores en ejercicio; por motivo de espacio no se discuten todas las actividades en este artículo, pero sus características eran similares, pues permitían que los profesores pudieran resolverlas con prácticas que admitían rasgos de alguno de los cuatro niveles de RI para la t-Student. Cabe destacar que estas mismas actividades también fueron resueltas por los profesores en formación, pero de forma individual por la modalidad del taller.
Con las actividades se esperaba que los participantes realizaran prácticas matemáticas las cuales: (1) podían ser de carácter intuitivo, como realizar conjeturas sobre la problemática planteada utilizando gráficos (e.g., ojiva y boxplot) o medidas estadísticas como los cuartiles, media, desviación estándar, así como reflexionar sobre la dispersión, la simetría y la importancia del cero en el contexto de la actividad.
(2) Podían indicar algunas características de los datos proporcionados, como el tipo de variable, muestra o muestras pequeñas, varianza poblacional desconocida; también hacer referencia a la hipótesis implícita en el problema, algunas propiedades como el estadístico t-Student y los grados de libertad, mientras que en los argumentos podían utilizar la probabilidad en el contexto, por ejemplo, de que el fármaco no incremente las horas de sueño. (3) Además de lo indicado en el punto anterior, podían expresar las hipótesis en lenguaje natural, identificar si existe desigualdad de varianzas y de tamaños muestrales, así como dependencia de las muestras y las implicaciones que esto tiene en la prueba t-Student; también establecer un límite de desviación significativo y utilizarlo para argumentar su inferencia.
(4) En una práctica del último nivel podían indicar y justificar un nivel de significancia, declarar las hipótesis en lenguaje simbólico, realizar la prueba con el estadístico t-Student, tomar una decisión basada en la prueba de hipótesis y ser capaz de argumentar estadísticamente su decisión, así como de analizar críticamente la eficiencia de su inferencia estadística.
Análisis de las prácticas de los profesores
A continuación, analizamos las prácticas desarrolladas por los profesores en ejercicio y en formación, a propósito de la solución de las actividades 1 y 2. Destacamos que para este análisis utilizamos la propuesta de niveles de razonamiento inferencial sobre la t-Student (Tabla 1 y Anexo A) y la noción de práctica matemática y configuración de objetos y procesos, descrita en la sección de marco teórico.
Prácticas asociadas a la actividad 1
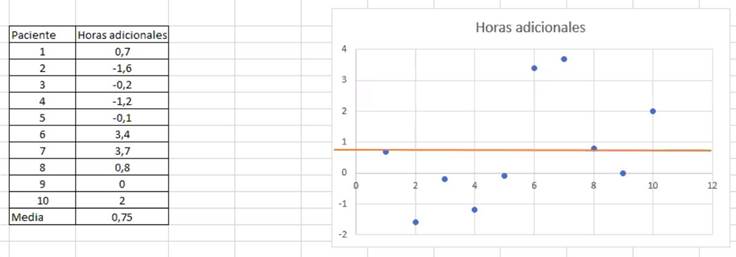
La actividad 1 (ver Anexo B) trata de un experimento con un fármaco para dormir, donde interesa conocer si realmente existe un aumento en las horas de sueño cuando se utiliza el fármaco. A continuación, presentamos las prácticas que desarrollaron los profesores en ejercicio sobre esta actividad. El primer tipo de práctica característica para la actividad 1 se ejemplifica con los desarrollos del equipo 4 (Figura 1).
Los profesores de este equipo señalaron que graficaron los datos sobre el incremento de horas de sueño que se proporcionaban en el problema para observar cuán dispersos estaban los datos entre sí, también calcularon la media y la dibujaron
en el mismo gráfico; ellos indicaron que a partir de lo anterior podían ver qué tan dispersos están los datos en relación con la media. Además, visualizaron en el gráfico que solo hay cuatro personas con incremento de hora de sueño por encima de la media, aunque una de ellas se encuentra casi en el valor de la media; a partir de esto, señalaron que en realidad solo hay tres personas en la muestra a quienes les hace efecto de forma significativa el fármaco (por lo alejados que se encuentran de la media) y que entonces no existe un aumento en las horas de sueño con este fármaco.
En la práctica que realizaron los profesores podemos observar conceptos/definiciones como los de dispersión y significancia (aunque con una acepción más intuitiva), propiedades/proposiciones como la media, procedimientos tales como el cálculo de la media y elaboración del gráfico de puntos, los argumentos estuvieron basados en el número de personas que ellos consideraron que tuvieron un aumento significativo. También observamos el papel central que adquirió la representación gráfica para que los profesores visualizaran los datos y tomaran una decisión. La mayoría de estos elementos pertenecen al nivel 1, sin embargo, nos llama la atención el uso que dan a la significancia; para ellos “es significativo si se encuentra muy alejado de la media”, pero al preguntarles ¿qué tan alejado?, ellos indicaron que no lo cuantificaron, “simplemente que se pueda visualizar lejos de la media”. Con respecto al concepto/definición significancia, como un límite significativo a partir de cierto valor de probabilidad, en los niveles de razonamiento inferencial sobre el estadístico t-Student se encuentra en el nivel 3, aunque en las prácticas de los profesores no fue posible observar esta definición de significancia.
Podemos observar que la práctica que desarrolla el equipo 4 guarda relación con lo que se espera en la primer tarea para promover el RII del marco propuesto por Zieffler et al. (2008), pues los profesores realizaron conjeturas basados en las características del gráfico. Para una práctica con elementos más complejos del nivel uno, los profesores podrían haber calculado, además de la media, otras medidas estadísticas como los cuartiles. Los cuartiles les podrían ayudar a analizar la variación interna del conjunto de datos, tal y como lo propone Galton (1875), y basar su conclusión tanto en la visualización del gráfico como en la dispersión de los intervalos que ha calculado. Los aspectos anteriormente mencionados se abordan en el nivel 1.2 de los niveles propuestos en Lugo-Armenta y Pino-Fan (2021a).
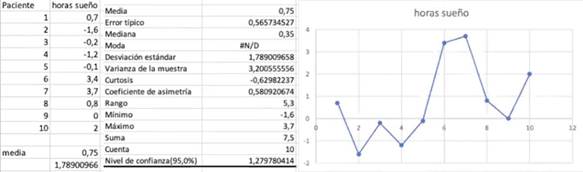
Una segunda práctica característica para esta actividad se ejemplifica con los desarrollos del equipo 1. Los profesores de este equipo se auxiliaron de Excel para resolver el problema, con el cual utilizaron algunas medidas estadísticas, que se pueden observar a la izquierda y al centro de la Figura 2, y un gráfico para representar el incremento de las horas de sueño de cada uno de los participantes.
Los profesores en ejercicio del equipo 1, indicaron que lo primero en que pensaron para resolver el problema fue obtener la media y la desviación estándar, y después en realizar un gráfico para poder visualizar la dispersión. Posteriormente, también realizaron un análisis de los datos con diversas medidas enfocadas a estudiar la dispersión, de las cuales destacaron la curtosis; a partir de este análisis, argumentaron que “como lo observamos con la media, desviación y el gráfico, hay una gran dispersión de los datos y debido a dicha dispersión no existe realmente un aumento en las horas de sueño”. Podemos observar que los profesores aluden principalmente al concepto de dispersión, y propiedades/proposiciones tales como la media, desviación estándar, error típico o error estándar, varianza, curtosis, entre otros. Los procedimientos realizados atienden a las propiedades indicadas y otras, que se pueden ver en la Figura 2, con el uso de Excel. En esta práctica logramos observar que, a pesar de obtener diversas medidas estadísticas, los profesores argumentaron sus conclusiones con la media, desviación estándar y la dispersión que lograron visualizar por medio del gráfico. Estos objetos matemáticos primarios y los procesos que se encuentran asociados a ellos pertenecen al nivel 1 de razonamiento inferencial sobre el estadístico t-Student.
Un aspecto por destacar en esta práctica, es que los profesores utilizan la fórmula de Excel para obtener un intervalo de confianza para la t-Student y lo etiquetan como ‘Nivel de confianza (95,0 %)’, pero no forman el intervalo. Lo anterior evidencia que identifican que se trata de una prueba t-Student, pero no son capaces de realizar los procedimientos para resolver el problema por pruebas de hipótesis o por intervalos de confianza. Este aspecto es el único indicador de práctica del nivel dos que observamos.
En esta práctica, a diferencia de la práctica desarrollada por el equipo 4, podemos observar una implementación más completa de los elementos que se consideran en el nivel uno, pues su conjetura se basa tanto en la visualización del gráfico como en las diversas medidas estadísticas que han calculado para analizar la dispersión de los datos. Como hemos señalado, este equipo parece percatarse de que se puede realizar una prueba t-Student, no obstante, no la lleva a cabo. Para que la práctica de estos profesores progrese a una de nivel dos, una vez que comprendan las características de las diversas pruebas con el estadístico t-Student, podrían identificar la hipótesis que se encuentra implícita en el problema. La hipótesis es el primer componente del ciclo de investigación estadística (PPDAC) de Wild y Pfannkuch (1999), además diversos estudios han reportado las bondades de trabajar inicialmente con hipótesis a través de preguntas o conjeturas (e.g., Bakker, Ben-Zvi y Makar, 2017; Pfannkuch y Wild, 2004; Pfannkuch, et al., 2016). También podrían apoyarse en recursos tecnológicos para realizar actividades con simulaciones, que permitan promover la comprensión de la distribución t-Student. Este tipo de actividades se han documentado en investigaciones como las de Bakker y Gravemeijer (2004), Reading y Reid (2006) y Rossman (2008). Además, de acuerdo con Konold et al. (2011), es necesario que primero se fomente un razonamiento probabilístico básico para que los estudiantes o profesores puedan realizar inferencias informales, en este caso preformales. En este sentido, en el nivel dos de nuestra propuesta se propone utilizar la probabilidad como una medida de certidumbre asociada a un evento, antes de compararla con un límite preestablecido (nivel 3) o un nivel de significancia (nivel 4).
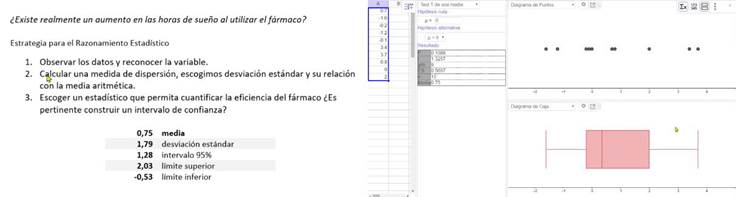
Un tercer tipo de práctica utilizada para resolver la actividad se ejemplifica con la desarrollada por el equipo 6. Los profesores establecieron ciertas estrategias como se enumeran en la parte izquierda de la Figura 3.
Con respecto a la estrategia 1, los profesores detallaron que al observar los datos se percataron de que se trataba de una variable continua la cual adquiere valores tanto positivos como negativos y que, por lo tanto, fue necesario definir qué significa el cero para esta variable; además, definir la variable cobra relevancia en el contexto del problema porque indica que no hay un aumento en las horas de sueño con el fármaco. Los profesores explicaron que realizaron un gráfico de puntos con papel y lápiz para observar cuán lejos o cerca se encontraban los valores del cero, gráfico que posteriormente obtuvieron con el uso de Geogebra (Figura 3). También señalaron que podían utilizar un boxplot para observar cuánto se extienden los datos. Con la segunda estrategia buscaban observar la dispersión de los datos, para lo cual decidieron explorar la relación de la desviación estándar con la media aritmética, auxiliándose de Excel para realizar los cálculos. Los profesores indicaron que la parte que les generó más dificultad y discusión, entre los miembros del equipo, fue la estrategia tres, pues debían escoger un estadístico que permitiera cuantificar la eficiencia del fármaco y pensaban que debía ser uno que utilizara la relación de la desviación estándar y la media aritmética; finalmente, indicaron que decidieron optar por el estadístico t-Student y aplicar una prueba t para una muestra (ver parte derecha de la Figura 3) y construyeron un intervalo de confianza del 95 % (parte de la izquierda de la Figura 3). Una vez que obtuvieron los límites inferior y superior del intervalo, los profesores destacaron la importancia de haber reconocido la variable y definido al cero como la no eficacia o no aumento de horas de sueño, e indicaron que “como el cero se encuentra dentro del intervalo no se tiene un verdadero aumento en las horas de sueño”. En la primera parte de la práctica (estrategia uno y dos) que realizaron los profesores podemos identificar su interés por observar el comportamiento de los datos y la visualización por medio de gráficos para realizar una conjetura, aspectos que son característicos del nivel 1. Algunos de los objetos matemáticos primarios que se identificaron en la práctica son conceptos/definiciones como variable y dispersión, propiedades/proposiciones tales como media y desviación estándar, los procedimientos sobre la media, desviación estándar y los límites del intervalo (los cuales fueron realizados con el apoyo de Excel). Cabe destacar que estos objetos matemáticos primarios que caracterizan la práctica son propios del nivel 1 de razonamiento inferencial.
En la segunda parte de la práctica (estrategia tres) se identificaron elementos que son representativos del nivel 4. Por ejemplo, conceptos/definiciones como nivel de confianza, muestra y probabilidad, propiedades/proposiciones tales como el estadístico t-Student, grados de libertad, error estándar, hipótesis nula y alternativa, límites inferior y superior y la regla de decisión; los procedimientos para llevar a cabo la prueba de hipótesis t-Student para una muestra los realizaron con el recurso tecnológico Geogebra y para formar el intervalo de confianza utilizaron las funciones de Excel. Por su parte, los argumentos estuvieron basados en que el cero se encuentra dentro del intervalo de confianza y, por lo tanto, “no se tendría un verdadero aumento en las horas de sueño”.
Es importante destacar que, a diferencia de las prácticas anteriores, en la desarrollada por el equipo 6, los profesores se preocuparon por comprender el tipo de datos con los que estaban trabajando, por ejemplo, el tipo de variable. Además, dieron un significado al cero, aspecto que fue clave para la prueba de hipótesis, la formación del intervalo y para desarrollar el argumento sobre su inferencia. Sin embargo, cuando se les preguntó por qué optaron por utilizar un nivel de confianza del 95 %, los profesores indicaron que era “el porcentaje que siempre utilizan”, lo cual pone de manifiesto la falta de comprensión sobre algunas nociones que utilizaron. Es decir, los profesores pueden operar con ellas algorítmicamente, pero les falta comprender con mayor profundidad algunas nociones tales como el nivel de confianza y otras que se encuentran relacionadas con dicha noción (e.g., nivel de significancia y los tipos de error). Aunado a comprender las nociones anteriormente mencionadas, los profesores podrían trabajar con la potencia de la prueba para una movilización integral del nivel cuatro, esto daría cuenta de un razonamiento inferencial formal. De acuerdo con Cohen (1992), podemos comprender la potencia de la prueba como un índice de la validez de los resultados estadísticos; también es importante considerar la prueba estadística (en este caso la t-Student), el nivel de significancia, el tamaño del efecto y el tamaño de la muestra como los factores que determinan a la potencia de la prueba (Lipsey y Aiken, 1990).
Con respecto a los profesores en formación, debemos señalar que las prácticas que desarrollaron para resolver la actividad 1 fueron similares a las que acabamos de analizar. No obstante, es de interés analizar algunas prácticas que se destacaron, como la que se muestra en la Figura 4.
El profesor en formación etiquetado con el número 8 (PF8), señaló que decidió aplicar una prueba t-Student debido a que con la información proporcionada se desconoce la varianza poblacional; también planteó las hipótesis nula y alternativa en lenguaje natural, y aplicó la prueba, para lo cual decidió utilizar un nivel de confianza de 95 %.
En esta práctica podemos identificar el uso de conceptos/definiciones como varianza poblacional, media poblacional, población, muestra, hipótesis y nivel de confianza; también propiedades/proposiciones, tales como, la media de la muestra, desviación estándar, tamaño muestral, estadístico t-Student, grados de libertad, estadístico teórico y las reglas para la toma de decisión. Los procedimientos realizados por el futuro profesor consisten en el planteamiento de las hipótesis, el nivel de significancia, el cálculo del estadístico t-Student, de los grados de libertad, obtener el valor del estadístico teórico y del valor de la probabilidad para el estadístico de prueba y, finalmente, decidir si se rechaza la hipótesis nula. Los argumentos que realizó estuvieron basados en los criterios para la toma de decisión; es decir, como el valor del estadístico de prueba es menor que el del estadístico teórico, entonces no se rechaza la hipótesis nula. Los elementos lingüísticos que utiliza son lenguaje natural y simbólico.
En la práctica que realizó PF8, se encuentran presentes elementos o criterios característicos de los niveles tres, como el realizar el planteamiento de las hipótesis en lenguaje natural, y cuatro, como el uso del nivel de significancia.
Queremos resaltar el siguiente argumento que desarrolla el profesor, el cual se puede observar en la Figura 4, “la diferencia entre el estadístico t y el estadístico teórico no es grande y, por lo tanto, no es significativo”, pues aunque el profesor ha realizado adecuadamente los procedimientos, este argumento deja de manifiesto que tal vez algunas de las propiedades/proposiciones o conceptos/definiciones que está utilizando necesitan ser comprendidas con mayor profundidad y de manera integral. Podría ayudar a dicha comprensión sí estableciera las regiones de rechazo y no rechazo, y se formulara preguntas como ¿qué significa el valor crítico que he establecido a partir del estadístico teórico?, ¿cómo en estas regiones están presentes los niveles de significancia y de confianza, y la relación que existe entre ellos?, y ¿cómo podría interpretar el nivel de confianza en términos de la hipótesis nula?; reflexionar sobre estos aspectos le permitirá al PF8 que su práctica transite al nivel cuatro.
También podemos observar en la práctica del PF8, que comete un error cuando va a trabajar con el criterio de decisión del valor-p, por consiguiente, podría iniciar la comprensión del valor-p con una aproximación informal, auxiliándose de software para simulaciones o para el cálculo de la probabilidad del estadístico t-Student, y con ello apoyar su inferencia (Rossman, 2008).
En la Figura 5 podemos observar la práctica que realizó el profesor en formación 2 (PF2) respecto a la actividad 1. Inicialmente, el profesor indicó que debido a que se trata de una muestra de 10 pacientes (muestra pequeña) y se desconoce la varianza poblacional se puede realizar una prueba t-Student; además, estableció las hipótesis nula y alternativa con lenguaje simbólico y las explicó en lenguaje natural, calculó el estadístico t-Student, obtuvo el p-valor y concluyó en términos del problema. En esta práctica podemos identificar que los elementos lingüísticos que utilizó son lenguaje
natural y lenguaje simbólico, algunos conceptos/definiciones son población, varianza poblacional, media poblacional, muestra e hipótesis, mientras que las propiedades/ proposiciones son la media de la muestra, desviación estándar, tamaño muestral, estadístico t-Student, grados de libertad, alfa y la regla para la toma de decisión. Los procedimientos que realizó fue calcular el estadístico t-Student, obtener el p-valor y compararlo con el valor de alfa para tomar la decisión de rechazar o no la hipótesis nula. Finalmente, argumenta su conclusión indicando que como el p-valor es mayor que el alfa, la diferencia no es significativa. En síntesis, la práctica que desarrolla es característica del nivel cuatro.
Para que el PF2 desarrolle una práctica de nivel cuatro más robusta, podría trabajar con los errores tipo I y tipo II y comprender las relaciones entre dichos errores. Para promover dicha comprensión puede auxiliarse de software y representaciones gráficas de forma similar a lo propuesto por Rossman (2008) para la distribución o el valor-p. Además, el PF2 podría validar su inferencia haciendo uso de la potencia de la prueba, tal y como sugerimos al PF8. En este sentido, para aproximarse a los errores tipo I y tipo II, y la potencia de la prueba, Vera y Díaz (2013) proponen primero explorar con profundidad la idea de probabilidad condicional mediante applets, pues esto les permitirá a los profesores experimentar diferentes posibilidades de forma visual.
Los recursos que, en general, utilizaron los profesores en formación fueron Excel, R, Geogebra, calculadoras en línea, lápiz y papel para cálculos manuales, y tablas de probabilidad.
Prácticas asociadas a la actividad 2
Como se puede observar en el Anexo B, la actividad 2 trata sobre un experimento con dos fármacos para dormir, y se desea conocer si existe diferencia entre las horas de sueño que se ganan con el fármaco 1 y 2.
A continuación, presentamos prácticas referentes a la actividad 2.
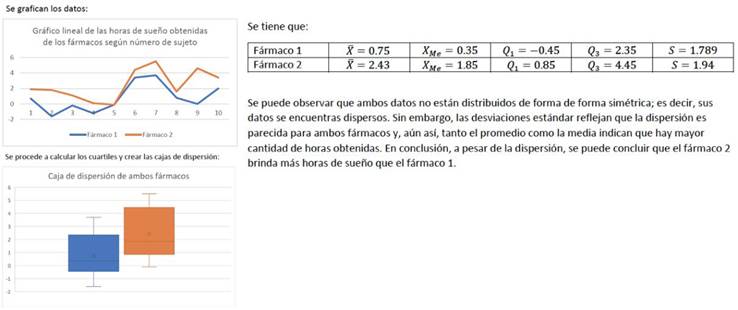
Como se puede apreciar en la Figura 6, el profesor en formación doce (PF12) primeramente realizó un gráfico de líneas sobre las horas de sueño ganadas por cada paciente; después realizó boxplots para observar la dispersión en ambas muestras y finalmente concluyó que el fármaco dos brinda más horas de sueño que el fármaco uno, basándose en la media, los cuartiles y la visualización en los gráficos.
En la práctica del PF12 podemos identificar objetos matemáticos primarios, dentro de los que distinguimos los elementos lingüísticos representaciones gráficas, lenguaje natural y simbólico; algunos conceptos/definiciones como muestra, simetría y dispersión; mientras que las propiedades/ proposiciones son media, desviación estándar, mediana y cuartiles uno y tres. Los procedimientos que realizó fueron el gráfico de líneas basado en la información proporcionada en la tabla de la actividad y posteriormente el cálculo de los cuartiles para construir dos boxplots con el uso de Excel, también calculó la media y desviación estándar. Para argumentar sobre la conclusión que realiza, recurre principalmente a la dispersión, media y mediana. Todos los objetos primarios que hemos identificado en la práctica matemática del PF12 corresponden al nivel 1 de razonamiento inferencial sobre el estadístico t-Student.
Además de la práctica desarrollada por el PF12 para esta actividad, el profesor podría analizar la variación interna de ambas muestras mediante el método de fluctuación (Edgeworth, 1885), que se entiende como una medida de la variación de una serie de datos con respecto a otra serie. De acuerdo con Stigler (2017), la idea de la comparación en términos de la variación interna de los datos fue retomada por Gosset y Fisher para proponer nuevos métodos; por ello, en nuestra propuesta de niveles de razonamiento inferencial se considera este método en el nivel uno, como una versión intuitiva, de este tipo de prueba, que pueda apoyar las conjeturas o inferencias informales.
En la Figura 7 podemos observar la práctica del profesor en formación nueve (PF9), la cual es característica, principalmente, del nivel dos.
El PF9 declaró en su práctica que el problema puede ser abordado mediante una prueba de hipótesis para dos medias (promedios) y que se puede utilizar la distribución t-Student, debido a que asumió que los datos siguen una distribución normal e identificó que se desconoce la desviación estándar de la población. Planteó las hipótesis en lenguaje natural, aunque utilizó la simbología para indicar cuál es la nula y alternativa. También identificó el tamaño de las muestras y obtuvo la media y desviación estándar de cada muestra. A partir de las desviaciones estándar, calculó la varianza agrupada, utilizando esta propiedad/ proposición para cuando se trabaja con dos muestras independientes y con desigualdad del tamaño muestral. Además, indicó que asumió que las desviaciones poblacionales son iguales, y para realizar la prueba utilizó el estadístico t-Student y el valor-p como la probabilidad a partir de la distribución t, para lo cual recurrió a los grados de libertad; asumió un nivel de significancia e identificó que se trata de una prueba con dos colas iguales.
En la práctica que realizó el PF9 identificamos conceptos/definiciones tales como hipótesis, muestra y población.
Las propiedades/proposiciones que destacan son distribución normal, distribución t-Student, tamaño muestral, media, desviación estándar, varianza agrupada, estadístico t-Student para muestras independientes con diferente tamaño muestral, grados de libertad y valor-p. Los procedimientos que aplicó fueron, calcular las medias y desviaciones estándar a partir de los datos de la actividad, varianza agrupada, estadístico t-Student, grados de libertad, establecer el nivel de significancia y encontrar la probabilidad mediante la distribución t-Student. Finalmente, concluye que existe una diferencia entre las horas de sueño que se ganan con el fármaco 1 y 2, y lo argumenta con base en la comparación que realiza del valor-p con respecto del nivel de significancia. Es importante destacar que, aunque el
PF9 identifica que puede aplicar una prueba t-Student para resolver el problema, a partir de las características previamente descritas, no identifica que se trata de dos muestras dependientes y utiliza las propiedades/ proposiciones del estadístico t-Student y varianza agrupada para cuando se está trabajando con muestras independientes con diferente tamaño muestral. Otro aspecto que resalta en su práctica es que asume que las desviaciones poblacionales son iguales, al parecer como justificación para su uso de la varianza agrupada en el estadístico; esto y los otros aspectos de su práctica que hemos
caracterizado nos permite percatarnos de que el profesor tiene algunas nociones sobre el estadístico t-Student, su distribución y de las características de las pruebas de hipótesis. Sin embargo, presenta errores y dificultades al resolver la actividad, que inician con la identificación del tipo de datos que está trabajando y la selección apropiada del estadístico t-Student.
Para que el PF9 logre desarrollar una práctica de nivel tres a partir de la práctica que ha realizado, es necesario que primeramente reconozca el tipo de datos con los que se encuentra trabajando, así como la lógica y restricciones de las pruebas t-Student. En este caso, es esencial que comprenda las implicaciones que tiene en el estadístico t-Student al estar trabajando con muestras dependientes, estos aspectos se pueden observar en el nivel tres de la propuesta de niveles de razonamiento inferencial. También, el profesor podría abordar el nivel de significancia de forma preformal, es decir, trabajar con el concepto/definición de significancia como límite de desviación significativo, a partir de este límite se considera seriamente que sí es probable que exista una diferencia; esta aproximación fue trabajada por Fisher (1925) y concuerda con la propuesta de Rossman (2008) para introducir algunas ideas sobre inferencia.
Un tercer tipo de prácticas interesante de analizar,se ejemplifica con la respuesta del profesor en formación 20 (PF20), la cual se presenta en la Figura 8. En dicha práctica, podemos ver que el futuro profesor identificó que se tienen muestras pareadas y puede aplicar una prueba t-Student para este tipo de muestras. Indicó que µ1 y µ2 son las horas de sueño ganadas con el fármaco 1 y 2, respectivamente, a partir de esto estableció las hipótesis estadísticas en lenguaje simbólico. También, estableció un valor de alfa, obtuvo la región crítica, indicó la propiedad/proposición sobre el estadístico t-Student y lo calculó. Para concluir si existe una diferencia entre las horas de sueño que se ganan con ambos fármacos, comparó el valor que obtuvo del estadístico con la región crítica y señaló que como “cae en la región crítica” rechaza la hipótesis nula y acepta la alternativa. Lo anterior lo llevó a concluir que “hay diferencia entre los promedios de las horas ganadas con el fármaco 1 y con el fármaco 2”.
La práctica de este profesor es característica del nivel 4, debido a que podemos observar diversos criterios de dicho nivel que se encuentran vinculados con los siguientes objetos primarios: los elementos lingüísticos presentes son lenguaje natural y simbólico, algunos conceptos/definiciones son muestra, población, muestras pareadas,
nivel de confianza, nivel de significancia, hipótesis y región crítica. También observamos propiedades/proposiciones tales como estadístico t-Student para muestras pareadas, media y desviación estándar de la diferencia de las muestras, regla de decisión con el estadístico y región crítica. Los procedimientos que realizó el profesor se enfocaron en la obtención de los grados de libertad, la región crítica (dos colas iguales) mediante la distribución t-Student para nueve grados de libertad y un nivel de confianza de 0.05, el cálculo del estadístico t-Student y en aplicar la regla de decisión para concluir. Los argumentos que formuló versaron sobre que el estadístico calculado ‘cae en la región crítica’ por lo cual se rechaza la hipótesis nula, en otras palabras, argumentó basándose en la regla o criterio para la toma de decisión sobre el valor crítico. A partir de los objetos matemáticos primarios y los procesos (e.g., comunicación, definición, enunciación, algoritmización, argumentación y generalización) que se identificaron en la práctica del PF20, podemos percatarnos de que para su desarrollo se involucra un razonamiento inferencial de tipo formal. Este tipo de razonamiento le permitió al PF20 tomar decisiones basado en técnicas de inferencia estadística, concretamente, en la metodología de las pruebas de hipótesis. Al igual que en las prácticas del PF2 y los profesores del equipo 6 para la actividad uno, para que el PF20 fortalezca su razonamiento inferencial formal podría profundizar en su comprensión del nivel de significancia y de confianza, así como abordar los errores tipo I y tipo II, y la potencia de la prueba.
Las prácticas anteriores son ejemplares del tipo de prácticas que realizaron tanto los profesores en formación como los profesores en ejercicio para resolver la actividad 2. A continuación, la Figura 9 presenta otra práctica que se destacó en el grupo de profesores en ejercicio.
Los profesores en ejercicio del equipo 6 indicaron, en la clase sincrónica, que primero buscaron observar la diferencia entre las horas ganadas entre el fármaco 2 y 1, y determinaron que al parecer existía una diferencia positiva de horas de sueño con el fármaco 2. También comentaron que, al observar los datos proporcionados en la actividad, advirtieron que se trataba de una variable continua que admite valores positivos y negativos. Otro aspecto que resaltaron es el significado que tiene el cero en esta variable y su importancia para determinar si existe diferencia alguna entre el aumento de las horas de sueño con los fármacos. Posteriormente, señalaron que podían resolver el problema con un intervalo de confianza del
95 % basado en la t-Student. Una vez que obtuvieron los límites inferior y superior del intervalo, los profesores destacaron la importancia que tiene el significado del cero, como su diferencia entre las horas de sueño que se ganan con ambos fármacos, para establecer una conclusión en términos del problema. Finalmente, indicaron que como el cero no se encuentra dentro del intervalo, entonces existe una diferencia estadísticamente significativa entre las horas de sueño que se ganan con los medicamentos.
Podemos separar la práctica del equipo 6 en dos partes, en la primera observamos que los profesores utilizan un razonamiento inferencial informal para realizar un análisis de los datos basado en las diferencias de las horas de sueño que se observó en cada uno de los pacientes con cada fármaco; este tipo de práctica se puede caracterizar en el nivel uno debido a que la conjetura que realizan se basa en un análisis de la variación de los datos de ambas muestras; a partir de este análisis obtuvieron que 9 de los 10 pacientes presentaron un aumento mayor de las horas de sueño con el fármaco 2. En cambio, la segunda parte de la práctica se considera de nivel cuatro, debido a que podemos identificar criterios representativos de dicho nivel. Los mencionados criterios se encuentran relacionados con los siguientes objetos primarios que observamos en la práctica de los profesores. Los elementos lingüísticos identificados son representación tabular y lenguaje natural y simbólico, mientras que algunos conceptos/definiciones son muestras dependientes, intervalo de confianza y nivel de confianza; propiedades/proposiciones tales como media y desviación estándar de la diferencia de las muestras, estadístico t-Student, límite inferior y superior del intervalo de confianza y distribución t-Student. Los procedimientos para llevar a cabo el intervalo de confianza los realizaron con los recursos tecnológicos Excel; y los argumentos estuvieron basados en que el cero se encuentra fuera del intervalo de confianza y, por lo tanto, se tendría una diferencia significativa en el aumento de las horas de sueño de ambos fármacos.
Como podemos observar, existe un salto abrupto entre las dos partes de la práctica de los profesores del equipo 6. Por un lado, en la primera parte, los profesores llevan a cabo un análisis de las diferencias de horas de sueño y a partir de este análisis realizan una conjetura; en esta parte como hemos visto, por el tipo de análisis e inferencia (conjetura), se pone en juego un razonamiento inferencial informal. Por otro lado, en la segunda parte, podemos percatarnos que los mismos profesores desarrollan una práctica que se asocia a un razonamiento inferencial formal, esto es debido a que utilizaron objetos matemáticos primarios, y sus procesos asociados, que son propios de inferencia estadística, específicamente, por intervalos de confianza. Si bien, los intervalos de confianza no se encuentran contemplados en los niveles de razonamiento inferencial sobre el estadístico t-Student, debido a que el desarrollo desde lo informal a lo formal de estos niveles se ha conceptualizado con las pruebas de hipótesis, los elementos que han surgido en la práctica de estos profesores pertenecerían al nivel cuatro. Pfannkuch, Arnold y Wild (2015) han desarrollado una propuesta para trabajar con los intervalos de confianza desde ideas intuitivas hasta formales, este estudio puede ser un punto de partida para proponer niveles progresivos de razonamiento inferencial pormenorizados sobre los intervalos de confianza.
En las prácticas asociadas al nivel cuatro de los profesores en ejercicio, a diferencia de las prácticas de los profesores en formación, no se plantean las hipótesis nula y alternativa en lenguaje natural o simbólico, en vez de ello, las hipótesis parecieran estar implícitas, pues realizan directamente la prueba de hipótesis o el intervalo de confianza y centran su conclusión en términos del problema. Diversas investigaciones (e.g., Pfannkuch y Wild, 2004; Stohl, Angotti y Tarr, 2010) han reconocido la importancia del planteamiento de hipótesis y sugieren la introducción de una hipótesis en forma de pregunta y después ir evolucionando como se ha planteado en la propuesta de niveles de razonamiento inferencial.
Reflexiones finales
En este estudio realizamos una caracterización del razonamiento inferencial que evidencian los profesores de matemáticas de enseñanza media (bachillerato) en sus prácticas al resolver problemas sobre el estadístico t-Student, tanto para identificar los objetos matemáticos primarios que los profesores utilizan en sus prácticas, y si estos se pueden asociar a los distintos niveles de razonamiento inferencial, así como para ilustrar empíricamente si los niveles de razonamiento inferencial sobre el estadístico t-Student (Lugo-Armenta y Pino-Fan, 2021a) se pueden considerar como predictores del razonamiento inferencial que los profesores de matemáticas exhiben en sus prácticas sobre dicho estadístico.
Encontramos que tanto los profesores en ejercicio como los profesores en formación desarrollaron prácticas similares, en las cuales se identificaron elementos (representaciones, conceptos/definiciones, propiedades, procedimientos, argumentos) que se asocian a los diversos niveles de razonamiento inferencial sobre el estadístico t-Student, tal como se ha logrado evidenciar en el apartado anterior. Además, hemos discutido cómo la práctica de los profesores podría ser más robusta dentro del mismo nivel o transitar al siguiente nivel. Sobre las prácticas de cada nivel que desarrollaron los profesores podríamos decir que, en las asociadas al nivel uno se destacó el uso de representaciones gráficas y de diversas medidas estadísticas como la media y desviación entandar para interpretar la dispersión de los datos. Mientras que en las prácticas de los niveles 2 y 3 se enfatizó el uso del planteamiento de las hipótesis en lenguaje natural, el uso del estadístico y la distribución t-Student. En las prácticas que dan cuenta del nivel cuatro encontramos el planteamiento de las hipótesis con lenguaje simbólico, el estadístico y la distribución t-Student, reglas para la toma de decisión, nivel de confianza, nivel de significancia, muestras dependientes, entre otros. Sin embargo, no fue posible observar en las prácticas algunos elementos de los niveles de razonamiento inferencial, como aquellos relacionados con los criterios sobre el error tipo I y II, y la potencia de la prueba del nivel cuatro, la acepción de significancia del nivel tres, el uso de la probabilidad del nivel dos y la intercomparación y fluctuación del nivel uno.
A continuación, destacamos aspectos que hemos observado en las prácticas de los profesores y que se han reportado en la bibliografía de educación estadística como errores frecuentes y dificultades en inferencia estadística, y cómo los niveles de razonamiento inferencial propuestos podrían ayudar con dichas dificultades.
En las prácticas de los profesores en ejercicio encontramos que no se plantearon las hipótesis nula y alternativa, aspecto que es fundamental en las pruebas de hipótesis, pero como han evidenciado diversos estudios (e.g., Batanero, 2013; López-Martín, Batanero y Gea, 2019; Sotos et al., 2007; Vallecillos, 1997) las hipótesis nula y alternativa son de las principales dificultades que presentan tanto profesores como estudiantes en inferencia. Por ello, en los niveles de razonamiento inferencial sobre el estadístico t-Student se plantea trabajar en tres momentos con las hipótesis: en un primer momento, se identifica la hipótesis que se encuentra implícita en el problema y se hace explicita por medio de un lenguaje natural; en un segundo momento, se plantean las hipótesis nula y alternativa en lenguaje natural; y en un tercer momento, se trabaja con las hipótesis nula y alternativa en lenguaje simbólico, que es como solemos encontrarlas en los estudios estadísticos. Trabajar las hipótesis en estos tres momentos permitiría a los estudiantes comprender la naturaleza y diferencias entre ambas hipótesis de forma progresiva. Respecto a las hipótesis, también resaltamos que en las prácticas de los profesores en formación se identificaron ambas hipótesis planteadas en lenguaje natural (e.g., PF8 y PF9), en dichas prácticas se identificaron dificultades que presentan los profesores, como en la interpretación de los resultados, el nivel de significancia o el reconocimiento del tipo de datos. Estas dificultades brindan una pauta para percatarnos tanto de la necesidad de una comprensión más profunda y holística de los diversos conceptos y propiedades que se encuentran involucradas en las pruebas de hipótesis, como de la presencia de un nivel de razonamiento preformal.
Tanto los profesores en ejercicio como los profesores en formación no analizan la potencia de la prueba y los errores tipo I y tipo II. Yates (1951) ya nos venía advirtiendo que esto sucedía con los científicos y en los artículos de revistas especializadas, pues así como los profesores hoy en día, en aquella época los científicos se centraban en el resultado de las pruebas de hipótesis y dejaban de lado la magnitud del efecto, la potencia de la prueba y los errores. Que en la inferencia estadística dejemos de lado el tamaño del efecto, la potencia o la probabilidad de cometer los errores tipo I y tipo II podríamos considerarlo como una visión determinista de la inferencia o de la prueba de hipótesis que estamos realizando (Batanero, 2018). En los niveles de razonamiento inferencial sobre el estadístico t-Student podemos encontrar indicadores asociados con los errores tipo I y tipo II, y la potencia de la prueba. La progresividad dentro del mismo nivel cuatro manifiesta que los criterios referentes a los tipos de error y la potencia de prueba presentan una complejidad mayor a la toma de decisión basada en el criterio de selección (valor-p o valor crítico), dicha complejidad puede ser la causa de que en las prácticas analizadas no se hayan identificado elementos relacionados con ellas.
Otro aspecto que es importante resaltar, refiere a los criterios de decisión del nivel cuatro, específicamente abordaremos la dificultad que parecen tener los profesores con el valor-p, esta dificultad se ejemplifica con la práctica del PF8. Cuando el PF8 realiza la conclusión de la actividad, indica que como alfa menor que 1.39 no puede rechazar la hipótesis nula. Como podemos ver, el profesor parece comprender erróneamente al valor-p, ya que en realidad está trabajando con el valor del estadístico t-Student, pero consideramos que no es una simple equivocación, pues si el profesor realmente comprendiera esta noción entendería que está trabajando con un valor de probabilidad (que no puede ser mayor a uno). Diversas investigaciones han identificado dificultades y errores de estudiantes y de profesores respecto al cálculo e interpretación del valor-p (e.g., Inzunza y Jiménez, 2013; López-Martín, Batanero y Gea, 2019), incluso algunas refieren a métodos informales (e.g., Biehler, Frischemeier y Podworny, 2015). En los niveles de razonamiento inferencial que utilizamos en este artículo, se proponen tres momentos, en los niveles 2, 3 y 4 respectivamente, para trabajar progresivamente el valor-p y otras nociones relacionadas como el nivel de significancia. En el nivel dos se trabaja con el concepto tradicional de probabilidad, en el nivel tres se relaciona el concepto de significancia con la probabilidad y una regla intuitiva para la toma de decisión, mientras que en el nivel cuatro se hace uso del criterio de decisión con el nivel de significancia y el valor-p. Consideramos que realizar dicha progresión, que es propuesta en los niveles de razonamiento inferencial, puede ayudar en la comprensión tanto del el valor-p como de las nociones relacionadas.
De acuerdo con Batanero (2013), el mayor número de interpretaciones incorrectas y de errores en inferencia estadística se relacionan con el contraste de hipótesis. Por un lado, algunos conceptos que se suelen comprender erróneamente son el nivel de significancia, las hipótesis nula y alternativa, las distribuciones muestrales y los errores tipo I y tipo II. Por otro lado, se suele comprender erróneamente la lógica de las pruebas de hipótesis y realizar interpretaciones incorrectas de los resultados. A estas dificultades de tipo conceptual podemos añadir las dificultades didácticas, aunque hoy en día los cálculos han sido sustituidos por diversos softwares, como se ha evidenciado en las prácticas analizadas, la enseñanza de la inferencia y el razonamiento inferencial son más complejos. Es por ello, y por lo que hemos analizado y discutido a lo largo de este artículo, que consideramos que los niveles de razonamiento inferencial sobre el estadístico t-Student pueden ser utilizados como predictores del razonamiento inferencial en diversos momentos de la enseñanza y, además, se prevén como una herramienta útil para los profesores en su planeación de clases y para los formadores en el diseño de tareas que permitan promover un razonamiento inferencial de forma progresiva, desde lo informal a lo formal, para el estadístico t-Student.
Financiamiento
Esta investigación ha sido desarrollada en el marco del Proyecto Fondecyt 1200005, financiado por la Agencia Nacional de Investigación y Desarrollo (ANID) de Chile.
Declaración de la contribución de los autores
Todos los autores afirmamos que se leyó y aprobó la versión final de este artículo.
El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente:
J.G.L.A. 60 % y L.R.P.F. 40 %.
Declaración de disponibilidad de los datos
Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente (J.G.L.A.), previa solicitud razonable.
Ver anexo a28v36n1-s1