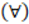Introduction
Proofs are relevant in mathematics and school mathematics. In mathematics, the discovery and prove of new theorems is at the highest level of research, yet there is no generalized definition accepted within the mathematical community. In general, there are two main conceptualizations, one approaching the realm of logic that considers proofs as a sequence of mathematical propositions and the other close to the practice of mathematicians, where semantic and informal aspects have more relevance, thereby considereing proofs more as arguments to convince experts of the validity of a theorem by emphasizing on the explanation of veracity (Cabassut et al., 2012; Hanna and De Villiers, 2012; Tall et al., 2012).
In school mathematics there exists also the debate between the logic-syntactic and semantic aspects of proofs. In some countries, mathematical proving appears in the curriculum as explicit teaching content, while in others as a process standard that must be addressed in the different topics. There is international consensus on its importance in the training of students at all educational levels, because it favors the understanding of mathematics and the processes to develop, establish and communicate mathematical knowledge. In particular, it is advocated to propose tasks to students in which exploration, validation and interpretation generate the need for comprehension, in addition, it is considered important that they confront unexpected results, presenting ambiguities and contradictions to provoke in them the urgency for mathematical proving (Cabassut et al., 2012; Durand-Guerrier et al., 2012a; Mariotti, 2006; NCTM, 2003; Stylianides, 2007; Stylianides et al., 2017; Zaslavsky et al., 2012).
In the case of secondary education in Costa Rica, the mathematics curriculum contemplates the process of “reasoning and argumentation” in students. Mathematical proving is considered as a formal phase of argumentation and plays a relevant role in the formulation of conjectures (Ministerio de Educación Pública, 2012).
To address mathematical proving in the secondary education curriculum, as content or as a process, this topic matter must be part of the knowledge required by mathematics teachers for their teacher performance. In addition to apprehending the contents and their relationships, teachers must know how mathematical knowledge and the syntactic rules of the discipline are produced (Flores-Medrano et al., 2016). In the case of mathematical proofs, teachers must possess specific knowledge that includes knowing about their nature, about their logic and syntactic aspects and; about mathematical aspects, as well as being aware of the role that mathematical proving plays in the discipline of mathematics. Furthermore, teachers must hold specific pedagogical knowledge for the teaching of proving, that is, knowledge of all the elements that enable this topic matter to be tough in school mathematics (Buchbinder and McCrone, 2018; Cabassut et al., 2012; Durand-Guerrier et al., 2012b; Knuth, 2002; Lin et al., 2012; Lo and McCrory, 2009; Pietropaolo and Campos, 2009; Tabach et al., 2009).
Nonetheless, in some investigations it has been detected that mathematics teachers exhibit complex and different conceptions about proofs (Montoro, 2007). All studies point to the importance of mathematical proofs in mathematics (Ayalon and Even, 2008; Ramos et al., 2015; Viseu et al., 2017), however, there are different points of view regarding their role in school mathematics (Crespo and Ponteville, 2005; Ramos et al., 2015). Likewise, some teachers show a reduced vision on the nature of proofs, exhibit deficiencies in the involved mathematical knowledge (Martínez-Recio, 1999; Knuth, 2002; Vicario and Carrillo, 2005), present empirical arguments as if they were proofs (Flores, 2007; Stylianides and Stylianides, 2009) and base their conviction on external entities rather than their own knowledge (Lin et al., 2012).
Along this line, the objective of the present study is to characterize the knowledge of mathematics teachers in initial training (i.e., MTITs), belonging to the undergraduate program Bachillerato y Licenciatura en la Enseñanza de la Matemática (translated as Bachelor and Licentiate Program in Mathematics Teaching) at the Universidad Nacional (UNA) in Costa Rica, on the mathematical practice of proving. Since mathematical proving knowledge can encompass several components, and the research subjects (i.e., participants, MTITs) are at a final stage in their formative program and, therefore, have little professional experience, this research was limited to “mathematical knowledge”, specifically, to knowledge on the logic-syntactic and mathematical aspects involved in the evaluation of mathematical arguments.
The present work is contextualized within the line of research on the training of mathematics teachers and is part of the greater research group “FQM 193. Didactics of Mathematics. Numerical Thinking”. The work specifically deals with the topic of mathematical knowledge evidenced by MTITs regarding the mathematical practice of proving from the perspective of teacher performance. Its contribution to this area of research lays in providing inputs that can favor the manner in which mathematical proving is approached in the curricular plan of MTITs at the Universidad Nacional in Costa Rica, and similar initial training plans elsewhere, and realizes a theoretical contribution in the construction of gauging components for the study of the state of knowledge of MTITs regarding mathematical proving, particularly through the use of knowledge indicators for logic-syntactic and mathematical aspects.
Theoretical framework
The study of the professional knowledge evidenced by mathematics teachers is a focus of interest in research in Mathematics Education. Notable works conducted in the eighties are those of Elbaz (1983) and Shulman (1986), the investigations carried out by the International Group for the Psychology of Mathematics Education (IGPME) (Ponte and Chapman, 2006), and the theoretical perspectives on knowledge, as well as beliefs within teaching and teacher performance of mathematics teachers described in the The Handbook of Mathematics Teacher Education (Sullivan & Wood, 2008).
To study the specialized knowledge on mathematical proving possesed by mathematics teachers, interest centers then around knowledge on mathematical tasks, that is to say, the way in which knowledge is produced in mathematics (Carrillo et al., 2018; Flores-Medrano et al., 2016). Thus, to carry out the present research, it was considered pertinent to have a theoretical model of the knowledge evidenced by mathematics teachers that would include mathematical proving within a category of knowledge. The Mathematics Teacher’s Specialized Knowledge (MTSK) model considers this type of knowledge as part of mathematical knowledge owned by mathematics teachers and assigns a subdomain within it, denominated Knowledge of Practices in Mathematics (KPM)(Carrillo et al., 2018).
The model takes an analytical approach with the purpose of obtaining information about the teacher’s knowledge, particularly about the elements that compose it and their interactions. For this, two domains are considered: (1) mathematical knowledge and (2) pedagogical content knowledge (Carrillo et al., 2018). The object of practice in the context of the present research is mathematics itself and, therefore, the interest is focused on its operation and not on the process of its teaching. Mathematical practice is understood in the sense indicated by Carrillo et al. (2018) as any mathematical activity carried out in a systematic way, that is fundamental in the creation of mathematical knowledge and that posseses a logic basis that allows the derivation of rules.
According to Carrillo et al. (2018), “Knowledge of Practices in Mathematics (KPM)” can be general or topic specific. General “mathematical practice” refers to the teacher’s knowledge on how mathematics is developed in a generic manner and independent of particular topics. “Specific mathematical practice” is a particular case of ), “Knowledge of Practices in Mathematics (KPM)” and is associated with the particularities of the mathematical topic in question. In this research, it is considered that knowledge of the logic and syntactic aspects of mathematical proving is attended by general mathematical practice since, as indicated by Carrillo et al. (2018), it encompasses the knowledge of the meaning of the necessary and sufficient conditions, the type of proof to guarantee the veracity of a mathematical statement, the various argumentative practices, among others. Likewise, knowledge about the mathematical aspects of proving is considered by specific mathematical practice, since not only is general logic-syntactic knowledge required, but it also considers the mathematics involved in the propositions and their proofs.
To characterize the knowledge on logic and syntactic aspects of mathematical proving evidenced by MTITs at the Universidad Nacional in Costa Rica, three elements of logic validity have been considered, which were specified based on the conceptual analysis of mathematical proofs (Alfaro, Flores and Valverde, 2019): (1) type of proof, (2) type of quantifier and (3) the type of logic connective. Regarding the mathematical aspects of proving, it must be considered that mathematical theories are hypothetical and are made up of propositions of the “if - then” form which means that mathematical proving requires rigor. The axioms, hypotheses, definitions and theorems involved must be understood and applied in their exact meanings (Cabassut et al., 2012). In a formal theory or mathematical system, three fundamental elements are distinguished: (1) axioms, (2) definitions and (3) theorems (Cabassut et al., 2012; Garrido, 1991; Patterson, 1950; Roberts,2010).
Methodology
The present work is positioned in the interpretive paradigm and has a qualitative approach because the object of interest is the interpretation of the meanings that the subjects (i.e., participants, MTITs) attribute to their actions (Bryman, 2012; Cohen, Manion and Morrison, 2007; Rodríguez, 2003; Sandín, 2003). It consists of two empirical phases aimed at characterizing the knowledge of MTITs at the Universidad Nacional, regarding: (1) the logic and syntactic aspects of mathematical proving, which correspond to the “logic validity” of mathematical proofs and (2) the mathematical aspects of proving, which correlate to the “mathematical validity” of proofs.
The undergraduate program in Mathematics Teaching at the Universidad Nacional is a joint program, the School of Mathematics offers the mathematical component and the Division of Educology provides the pedagogical component. Upon completion of a 4-year academic curriculum, students obtain the degree of Bachelor extendable to an optional Licentiate degree upon achievement of three additional semesters and the preparation of a final graduation project. In phase 1 of the study, 25 MTIT subjects participated, of which 18 were enrolled in the fourth and final year of the bachelor program and were thus denominated Bachelor Group (BG); 7 subjects were enrolled in the optional licentiate program and were identified as the Licentiate Group (LG). Both groups constituted the entire population of enrolled and active students at the corresponding academic levels during the second semester of 2018. In phase 2 of the study, 19 MTIT subjects participated, 12 were enrolled in the fourth year (BG) and 7 in the fifth year (LG), similarly, both groups corresponded to the entire enrolled and active student body at the corresponding academic levels during the first semester of 2019. Of the 12 subjects enrolled in the fourth year, 11 participated in phase 1. All 7 subjects enrolled in the fifth year had previously participated participated in phase 1 of the study. Subjects were coded using the letter “S” to indicate that they were undergraduate students; “B” bachelor or “L” licentiate; letters “M” and “W” designate man and woman, respectively; bachelor subjects were numbered 01 to 19 and licentiate from 01 to 07. All research subjects have approved the academic courses contempleted in the program’s curriculum thus demonstrating proficiency in mathematical propositions.
Information gathering
For collecting information in phases 1 and 2, two questionnaires were elaborated. Questionnaire 1 denominated “logic validity in the evaluation of mathematical arguments” was applied in September and October 2018 and questionnaire 2, “mathematical validity in the evaluation of mathematical arguments”, was applied in the months of May and June 2019, both with an approximate duration of one hour. In each case, subjects completed the questionaires individually during the schedules assigned to the enrolled courses. Prior to their application, questionnaires were reviewed by three Mathematics Education specialists who were chosen for their training in mathematics and mathematics didactics, in addition to their extensive knowledge of the educational context of the research subjects (MTITs).
The creation of both questionnaires contemplated elements from the theoretical framework of logic and mathematical validity knowledge involved in mathematical proving. In the case of questionnaire 1, research subjects had to evaluate the way to proceed in proving proposition P: Any real number satisfies that, if it is positive, then the sum of it and its multiplicative inverse is greater than or equal to two (Winicki-Landman, 1998). This proposition was used by Knuth (2002) in his research with 16 mathematics teachers where he presented them with an argument that proved the reciprocal predicate. In questionnaire 1, in addition to the argument on the reciprocal, three additional arguments were included, one considers a particular case and the other two present a direct proof and proof by reduction to absurdity. In this way, the questionnaire consists of four tasks. In addition, the veracity of said proposition was indicated. Table 1 provides each of the mathematical arguments presented with the tasks.
Table 1 Mathematical arguments involved in the tasks of questionnaire 1

Note: Own source from the present investigation.
Questionnaire 2 consists of four tasks. In each of them, a mathematical proposition and a mathematical argument are presented to guarantee their validity. The first three arguments have errors with respect to mathematical aspects, specifically, in the first task, an inappropriate use is made of the “hypothesis” of the mathematical proposition; in the second, the improper use of an “axiom” and in the third, the improper use of “definitions”. In the event that subjects (i.e., MTITs) would detect errors, they were asked to indicate what modifications they would apply to the argument to convert it to a mathematical proof. Table 2 provides each of the mathematical propositions and mathematical arguments presented in the tasks.
Methodological aspects of information analysis
Information collected from both questionnaires was examined by content analysis which is a scientific research technique for making replicable and valid inferences from texts (or other meaningful matter) to the contexts of their use (Cohen, Manion, y Morrison, 2007; Krippendorff, 2004).
To analyze the responses of the subjects of questionnaire 1, the syntactic structure of the given proposition was considered and for each argument an a priori analysis of the elements of knowledge on the logic validity that could be studied was made. Based on the latter, four categories were considered: (1) proof by a particular case, (2) proof of reciprocal, (3) direct proof of the universal implication, and (4) proof of the universal implication by reduction to absurdity. Based on the study of each of the four arguments, knowledge indicators were generated which are phrases to ascertain evidence of knowledge in the subjects’ responses. Such indicators are presented in Table 3. The responses of each subject were thoroughly reviewed, and coded 1 or 0 for presence or absense of knowledge indicators, respectively. Additionally, the responses, and a synthesis of them, that could not be classified by such indicators were recorded. The procedure followed for coding subject responses that gave rise to the results is illustrated for Task 1―proof by a particular case. The responses of subject SBW12 for tasks 1 and 2 are presented.
Table 3 Knowledge indicators generated for the universal implication of questionnaire 1

Note: Own source from the present investigation.
Based on the analysis of Figure 1 , it is certain that the subject evidences in his response the following knowledge indicator defined for task 1 (see table 3): “the argument is not a proof because it is considered a particular case”. Thus, such response is coded as 1 for this particular indicator.

Translation of task statement and response (justification) provided by the subject
Figure 1 Response of subject SBW12 for task 1
Based on the analysis of Figure 2, it is certain that the subject evidences in his response the knowledge indicator defined for task 2 (see table 3): “the argument is not a proof because it is considered the reciprocal of the predicate, that is, the consequent 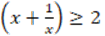 is assumed to be true and the veracity of antecedent
is assumed to be true and the veracity of antecedent 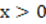 is guaranteed”, therefore, 1 is assigned. To analyze the responses of the subjects in questionnaire 2, four categories were established based on the elements of mathematical validity raised in the theoretical framework: “(1) partial use of the non-negative discriminant hypothesis” present in task 1, “(2) improper use of the axiom of existence of the multiplicative inverse” present in task 2, “(3) improper use of the definitions of odd and even integer” present in task 3 and “( 4) proper use of hypotheses, axioms, definitions and theorems in the proof of the theorem of the sum of the measures of the interior angles of a triangle in Euclidean geometry” present in task 4.
is guaranteed”, therefore, 1 is assigned. To analyze the responses of the subjects in questionnaire 2, four categories were established based on the elements of mathematical validity raised in the theoretical framework: “(1) partial use of the non-negative discriminant hypothesis” present in task 1, “(2) improper use of the axiom of existence of the multiplicative inverse” present in task 2, “(3) improper use of the definitions of odd and even integer” present in task 3 and “( 4) proper use of hypotheses, axioms, definitions and theorems in the proof of the theorem of the sum of the measures of the interior angles of a triangle in Euclidean geometry” present in task 4.

Translation of task statement and response (justification) provided by the subject
Figure 2 Response of subject SBW12 for task 2
For each of the tasks, the researchers analyze a priori the mathematical elements that are consider could be taken into account in the evaluation of the arguments involved. This process is illustrated in task 1, where the argument is not a mathematical proof because the non-negative discriminant hypothesis 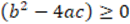 is partially used by assuming that
is partially used by assuming that 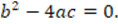 Based on this, a knowledge indicator was proposed for the explanation that the argument is not a mathematical proof, namely: “Manifests that the argument is not a proof because the hypothesis
Based on this, a knowledge indicator was proposed for the explanation that the argument is not a mathematical proof, namely: “Manifests that the argument is not a proof because the hypothesis 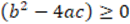 is partially used”. To effectuate the modification of the argument to make it a proof, it was considered that the hypothesis
is partially used”. To effectuate the modification of the argument to make it a proof, it was considered that the hypothesis 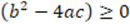 must be used and, based on it, exhibit in the correction at least one of the following real numbers
must be used and, based on it, exhibit in the correction at least one of the following real numbers 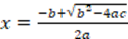 o
o 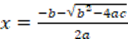 . Thus, two knowledge indicators were raised: “Manifests that the hypothesis
. Thus, two knowledge indicators were raised: “Manifests that the hypothesis 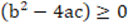 must be considered for correcting the argument, however, it does not exhibit any of the real numbers that satisfy existence” and “Manifests that the hypothesis
must be considered for correcting the argument, however, it does not exhibit any of the real numbers that satisfy existence” and “Manifests that the hypothesis 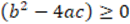 must be considered in order to exhibit any of the real numbers
must be considered in order to exhibit any of the real numbers 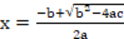 or
or 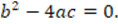 in the argument’s correction”. Table 4 presents the knowledge indicators associated with the tasks of questionnaire 2.
in the argument’s correction”. Table 4 presents the knowledge indicators associated with the tasks of questionnaire 2.
Table 4 Knowledge indicators developed for the analysis categories of questionnaire 2

Note: Own source from the present investigation.
For each subject, an exhaustive review of their responses was carried out in a similar manner as was done for questionnaire 1. In this way, the presence or absence of the defined knowledge indicators were assigned as 1 or 0, respectively. Additionally, the responses, and a synthesis of them, that could not be classified by such indicators were recorded.
Results
This section presents the results on the knowledge of mathematics teachers in initial training (MTITs) relative to the evaluation of mathematical arguments. In the first section, the logic-syntactic aspects are considered followed by mathematical aspects.
Results of empirical phase 1: specialized knowledge about the logic validity of the mathematical proof
The results are presented considering the four categories generated when evaluating mathematical arguments to prove proposition P: any real number satisfies that, if it is positive, then the sum of it and its multiplicative inverse is greater than or equal to two: (1) proof by a particular case, (2) proof of reciprocal, (3) direct proof of the universal implication and (4) proof of the universal implication by reduction to absurdity. For each argument, it is presented the number of subjects who considered the argument to be a proof and who evidenced knowledge of the proposed indicators in their responses. In addition, and when appropriate for each argument, it is presented the synthesis of the responses that could not be classified by the defined indicators and that evidenced knowledge of the logic-syntactic aspects of the proof.
Argument 1: Proof by a particular case
In the evaluation of this argument, 23 of the 25 subjects considered the argument did not to correspond to a mathematical proof of the given proposition and all of the subjects were aware that this was due to the fact that the argument only considered a particular case. A representative response follows:
As it is a proposition that applies to all the elements of the set
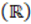 , it is not possible to demonstrate it by means of a specific example with one particular element, instead, one must initiate by considering a generic element from the set, the generic element being representable of any element of that set, and prove with it that the property is satisfied (SBM10).
, it is not possible to demonstrate it by means of a specific example with one particular element, instead, one must initiate by considering a generic element from the set, the generic element being representable of any element of that set, and prove with it that the property is satisfied (SBM10).
A group of six subjects considered that the argument would be a mathematical proof if the proposition had an existential quantifier, which evidences knowledge about how to prove a proposition with said quantifier by exhibiting a concrete element of the universe. A representative response follows:
Argument 2: Proof of reciprocal
In the evaluation of this argument, 23 of the 25 subjects considered that it did not correspond to a mathematical proof of the given proposition and 19 subjects evidenced knowledge that this was due to the fact that the argument considered the reciprocal of the predicate. Some representative responses are as follows:
Because the proposition has an implication form
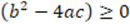 one must assume the antecedent to be true and seek to prove the consequent, not vice versa, since this would not be the logic structure (SBM16).
one must assume the antecedent to be true and seek to prove the consequent, not vice versa, since this would not be the logic structure (SBM16).Because the proposition P is
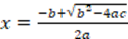 (expressed symbolically) and in the given argument, the reciprocal is proved, that is,
(expressed symbolically) and in the given argument, the reciprocal is proved, that is, 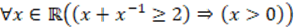 (SLW07).
(SLW07).
Argument 3: Direct proof of the universal implication
In the evaluation of this argument, 22 of the 25 subjects considered that it corresponded to a mathematical proof of the given proposition and all subjects manifested to possess knowledge. Table 5 presents the number of subjects whose responses displayed evidence of the knowledge indicators defined for the direct proof of the universal implication.
Table 5 Number of subjects evidencing knowledge indicators for the direct proof of the universal implication.

Note: Own source from the present investigation.
As can be seen in the previous table, most of the subjects evidence knowledge about how to proceed in the direct proof of the universal implication, that is, they know that the antecedent must be assumed to be true and, subsequently, the veracity of the consequent must be guaranteed. Nonetheless, very few subjects made explicit reference to the selection of an arbitrary element of the universe set, which is precisely what supports the way of proceeding in directly proving the implication. Likewise, none of the subjects expressed the validity of the property for all the elements of the universe set by virtue of the fact that it was guaranteed for a generic element. Some representative responses include:
Because the proposition has an implication form, it is assumed that
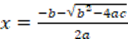 is true and it must be verified that the sum of the number and its multiplicative inverse is true, as shown in the box. Besides, verification is performed for an arbitrary but fixed value of
is true and it must be verified that the sum of the number and its multiplicative inverse is true, as shown in the box. Besides, verification is performed for an arbitrary but fixed value of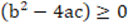 (SBM16).
(SBM16). It starts correctly, according to the given quantifier, by providing any element that is real. Then, implication is correctly used with the hypothesis that
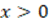 and mention is made of the consequent (what needs to be proved). The consequent is then proved from the operation
and mention is made of the consequent (what needs to be proved). The consequent is then proved from the operation 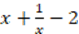 , which is utilized out of convenience, whilst already knowing that its equivalent expression is greater than or equal to zero, thus the expression is also greater than or equal to zero and manages to prove the consequent of the implication (SLM02).
, which is utilized out of convenience, whilst already knowing that its equivalent expression is greater than or equal to zero, thus the expression is also greater than or equal to zero and manages to prove the consequent of the implication (SLM02).
Argument 4: Proof of the universal implication by reduction to absurdity
In the evaluation of this argument, 21 of the 25 subjects considered that it corresponded to a mathematical proof of the given proposition and 16 of them manifested knowledge of the three proposed indicators. In addition, four subjects affirmed that the argument was a proof, although their responses did not evidence any indicator as was the case for the four subjects who declared that it was not a mathematical proof.
Table 6 presents the number of subjects whose responses displayed evidence of the knowledge indicators defined for the proof of the universal implication by reduction to absurdity.
Table 6 Number of subjects evidencing knowledge indicators for the proof of the universal implication by reduction to absurdity

Note: Own source from the present investigation.
Some representative responses of the subjects who evidenced knowledge include:
Based on the results presented in this section, it can be seen that a large majority of future mathematics teachers possess knowledge to discriminate whether or not an argument is a mathematical proof of an arithmetic property such as the one proposed. Their knowledge allows them to recognize perverse justifications that cannot be considered proofs, such as the proof by a particular case, or that of the reciprocal theorem; their insight also allows them to recognize when the precise steps have been followed to prove the proposition. Nonetheless, the number of subjects who identify the steps when a reduction to absurdity proof is proposed decreases considerably.
Results of empirical phase 2: Specialized knowledge on the mathematical validity of the proof
The results are presented considering the four categories defined in this second phase to analyze the responses provided by research subjects regarding their indication of whether the argument corresponded to a mathematical proof of the given proposition, explaining the reasons for their choice and, in the case that the provided argument was not deemed a mathematical proof, indicate the modifications they would realize to the mathematical argument to make it a mathematical proof. For each category is presented the number of subjects who considered the proposed argument to be a proof and whose responses evidenced knowledge of the proposed indicators. In addition, and when appropriate, it is presented the synthesis of the responses that were not contemplated by the indicators and that evidence knowledge of the mathematical aspects of proving.
Category 1: Partial use of the non-negative discriminant hypothesis
In the evaluation of this argument in task 1, 17 of the 19 subjects considered that it did not correspond to a mathematical proof of the given proposition and 15 subjects displayed evidenced of at least one of the defined knowledge indicators. Additionally, two subjects manifested that the argument was a proof, but did not evidence any indicator as did two other subjects who manifested that it was not a mathematical proof. Table 7 presents the number of subjects whose responses displayed evidence of the knowledge indicators defined for this category.
Table 7 Number of subjects evidencing category 1 knowledge indicators: Partial use of the non-negative discriminant hypothesis.

Note: Own source from the present investigation.
Representative responses provided by two subjects are presented. Both manifested that the argument was not a proof due to the partial use of the hypothesis, subject SLM06 completes his assessment by exhibiting a real number to satisfy existence, while subject SBW12 does not:
Explanation: It is only shown that the mathematical proposition is valid for the case when 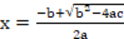 , it would be necessary to prove it for the case when
, it would be necessary to prove it for the case when  . It uses a particular case. Correction: For the case when
. It uses a particular case. Correction: For the case when  . It suffices to consider the real number
. It suffices to consider the real number  . Then
. Then 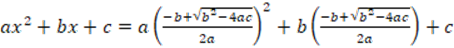
Thus, the real number 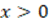 satisfies existence (SLM06).
satisfies existence (SLM06).
Explanation: In the hypothesis it is stated that 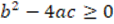 , but when the proof is performed, only the case where
, but when the proof is performed, only the case where 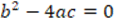 is taken into account without considering the case for greater than zero, thus, the proof is not entirely correct. Correction: I would consider both cases,
is taken into account without considering the case for greater than zero, thus, the proof is not entirely correct. Correction: I would consider both cases, 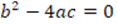 and
and 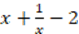 . Therefore, it will be necessary to search for an
. Therefore, it will be necessary to search for an  that fulfills the second case (SBW12).
that fulfills the second case (SBW12).
Category 2: Improper use of the axiom of existence of the multiplicative inverse
In this argument, present in task 2, only seven subjects appreciated the abusive quality of the reasoning, manifesting that it was not a mathematical proof and, of them, five evidenced the reason by means of one of the proposed indicators. Table 8 presents the number of subjects whose responses displayed evidence of the knowledge indicators defined for this category.
Table 8 Number of subjects evidencing category 2 knowledge indicators: improper use of the axiom of existence of the multiplicative inverse
Note: Own source from the present investigation.
As can be seen in the previous table, five subjects manifested that the argument was not a proof due to the improper use of the multiplicative inverse axiom and, of them, four evidenced in their argument corrections of the need to consider two cases: when 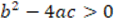 and
and 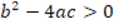 . Presented are representative responses of two subjects who manifested that the argument was not a proof due to the improper use of the multiplicative inverse axiom, one belongs to subject SBM02 whose correction argument makes reference to the consideration of cases to utilize the multiplicative inverse while the response of subject SBM03 does not:
. Presented are representative responses of two subjects who manifested that the argument was not a proof due to the improper use of the multiplicative inverse axiom, one belongs to subject SBM02 whose correction argument makes reference to the consideration of cases to utilize the multiplicative inverse while the response of subject SBM03 does not:
Explanation: Because it is generalized for any 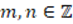 and initiates from the fact that
and initiates from the fact that 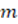 divides
divides 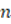 and
and 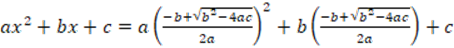 divides
divides 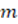 , although if one of them is zero for them to be divisible with each other, both must be zero. To avoid
, although if one of them is zero for them to be divisible with each other, both must be zero. To avoid 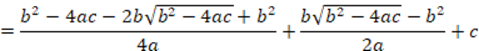 which is undefined in the case when it is zero. Correction: Considering
which is undefined in the case when it is zero. Correction: Considering 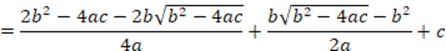 Case I as was done. Separately Case II for
Case I as was done. Separately Case II for 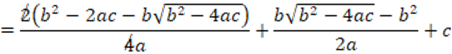 and
and 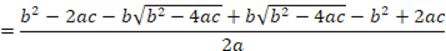
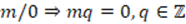 and since
and since 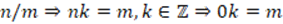
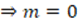 . Therefore
. Therefore 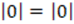 . Thus by case I and case II
. Thus by case I and case II 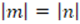 (SBM02).
(SBM02).
Explanation: The proof is incomplete, the definition that one number is divisible by another is used correctly, and all the rest of the steps are correct. However, it seems adequate to include the case
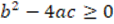 or
or 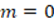 , because in one step we are multiplying both sides of the inequality by
, because in one step we are multiplying both sides of the inequality by 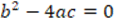 , but it is clear that
, but it is clear that 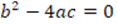 will not be equal to
will not be equal to , or else the hypothesis that
, or else the hypothesis that  and
and 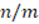 would be contradicted, as we end up with
would be contradicted, as we end up with 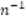 and
and 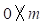 . The same would occur if
. The same would occur if 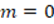 . For
. For 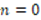 to be satisfied, both
to be satisfied, both 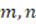 must be
must be 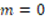 . Corrección: If
. Corrección: If 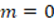 ,
, 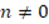 ,
, 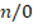 and
and 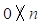 ¡! contradicts the hypothesis. If
¡! contradicts the hypothesis. If 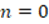 ,
, 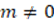 ,
, 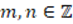 and
and 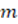 ¡! contradicts the hypothesis. If
¡! contradicts the hypothesis. If 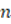 and
and 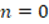 ,
, 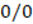 and
and 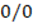 , the theorem holds since
, the theorem holds since 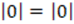 (SBM03).
(SBM03).
Regarding the 12 subjects who manifested that the argument was a mathematical proof, none of them evidenced any of the proposed indicators. However, three of them made reference to the multiplicative inverse in their explanation. Subject SBW11 stated that it was unnecessary for 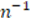 to be an integer, but without specifying that its existence would not be guaranteed in the event that
to be an integer, but without specifying that its existence would not be guaranteed in the event that 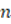 was zero. Subjects SBW05 and SBM16 manifested that
was zero. Subjects SBW05 and SBM16 manifested that 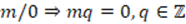 exists when
exists when 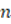 is different from zero, however, they evidenced knowledge on the concept of divisibility that implied that
is different from zero, however, they evidenced knowledge on the concept of divisibility that implied that 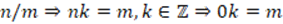 was different from zero. Following, the three responses:
was different from zero. Following, the three responses:
Explanation:
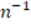 does not need to be an integer, so it would not affect us at any time. In addition, it is initiated from the definition to conclude with a truth value (SBW11).
does not need to be an integer, so it would not affect us at any time. In addition, it is initiated from the definition to conclude with a truth value (SBW11).Explanation: The arguments are correct. It is clear that if
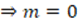 and
and 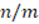 ,
, 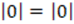 and
and 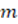 cannot be zero. It would then be appropriate to specify that
cannot be zero. It would then be appropriate to specify that 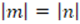 exists. Hypotheses are separated, translation is performed correctly, and properties are adequately applied. Clearly draws a conclusion in which it is evidenced what needed to be proved (SBW05).
exists. Hypotheses are separated, translation is performed correctly, and properties are adequately applied. Clearly draws a conclusion in which it is evidenced what needed to be proved (SBW05).Explanation: The only problem that the argument could present is when it is multiplied by
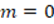 in the equality, however, due to the hypothesis
in the equality, however, due to the hypothesis 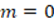 ; then
; then 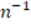 and since
and since 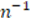 then
then 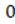 , thus
, thus 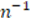 is perfectly defined. Because of this, all reasonings thereafter, make perfect sense, and also all the gaps that could remain are covered, the only thing that can be added is that the substitution can be carried out in any of the two equations resulting from the definition of
is perfectly defined. Because of this, all reasonings thereafter, make perfect sense, and also all the gaps that could remain are covered, the only thing that can be added is that the substitution can be carried out in any of the two equations resulting from the definition of 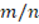 and
and 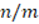 (SBM16).
(SBM16).
The previous answers demonstrate that subjects SBW05 and SBM16 considered the argument as a proof due to inaccuracies in their knowledge about divisibility, however, they evidence knowledge that a real number has a multiplicative inverse if it is different from zero.
Category 3: Improper use of the definitions of odd and even integer
In this argument, present in task 3, 16 of the 19 subjects manifested that it was not a mathematical proof and, of them, 14 evidenced some of the proposed indicators. In addition, three subjects stated that the argument was a proof, but did not evidenced any indicator, as did two other subjects who manifested that it was not a mathematical proof. Table 9 presents the number of subjects whose responses displayed evidence of the knowledge indicators defined for this category.
Table 9 Number of subjects evidencing category 3 knowledge indicators: improper use of the definitions of odd and even integer

Note: Own source from the present investigation.
As can be seen in the table above, 13 subjects manifested that the argument was not a demonstration due to the improper use of the definitions of even and odd integer and all of them evidenced the correct use of the definitions in the correction of the argument. There was a subject, SBM02, who did not evidenced the first indicator in his explanation, however, in the correction of the argument, he manifested knowledge of the second indicator.
Representative responses from three subjects who manifested that the argument was not a proof are presented. Following, the response of the SBM02 subject mentioned in the previous paragraph and the responses of SBW12 and SLM02 who evidenced knowledge of the two raised indicators:
Explanation:
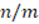 is considered in line 3, clearly
is considered in line 3, clearly 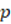 is taken as an even number. Thus
is taken as an even number. Thus 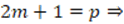
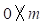 and
and 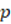 is even, then
is even, then 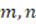 is odd, so
is odd, so 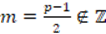 since
since 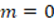 . The same rationale applies for
. The same rationale applies for 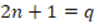 . Correction: Consider
. Correction: Consider 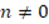 and
and 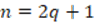 in line 3. Then,
in line 3. Then, 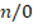 . Where
. Where 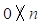 . Take
. Take 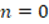 . Thus,
. Thus, 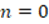 which is the definition of an even integer. Guaranteeing that
which is the definition of an even integer. Guaranteeing that 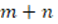 is even (SBM02).
is even (SBM02).Explanation: By stating that
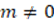 , it is guaranteed that
, it is guaranteed that 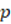 is odd, however, it does not guarantee that
is odd, however, it does not guarantee that 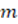 is odd, since if
is odd, since if 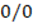 is even or odd the same is true. On the other hand, it is arrived at
is even or odd the same is true. On the other hand, it is arrived at 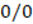 guarantees that
guarantees that 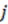 , but not
, but not 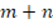 , is even, the latter sum could be odd but when it is multiplied by 2,
, is even, the latter sum could be odd but when it is multiplied by 2, 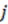 becomes an even number. Correction: It is best to take the definitions for
becomes an even number. Correction: It is best to take the definitions for 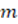 and
and 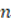 , as
, as  and
and 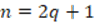 , so that when they are added the result is
, so that when they are added the result is 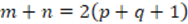 thereby ensuring that
thereby ensuring that 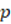 is even (SBW12).
is even (SBW12).Explanation: The values of
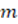 and
and 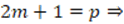 are defined incorrectly as integers, also they should be inverted, that is, the value of
are defined incorrectly as integers, also they should be inverted, that is, the value of 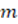 should be flipped for
should be flipped for 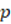 , and likewise
, and likewise 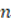 for
for 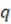 . Correction: Since
. Correction: Since 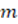 and
and 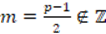 are odd, they satisfy that:
are odd, they satisfy that: 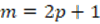 and
and 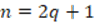 , with
, with 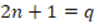 . Then
. Then 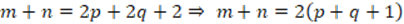 , with
, with 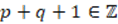 . Thus,
. Thus, 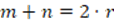 , with
, with 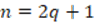 and
and 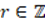 having the form of an even number
having the form of an even number 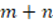 (SLM02).
(SLM02).
Category 4: Proper use of hypotheses, axioms, definitions and theorems in the proof of the theorem of the sum of the measures of the interior angles of a triangle in Euclidean geometry
In this argument, present in task 4, all 19 subjects stated that it was a mathematical proof, however, most subjects limited themselves to a mere statement since only nine subjects showed any of the proposed knowledge indicators. Table 10 presents the number of subjects whose responses displayed evidence of the defined knowledge indicators for this category.
Table 10 Number of subjects evidencing category 4 knowledge indicators: proper use of hypotheses, axioms, definitions and theorems in the proof of the theorem of the sum of the measures of the interior angles of a triangle in Euclidean geometry

Note: Own source from the present investigation.
Based on the previous table, it can be noted that, despite the fact that all future mathematics teachers identified as valid the proof of the property of the sum of the measures of the interior angles of a triangle, none made reference to the fact that the proposition is a general statement, which stems from the hypothesis that any triangle in Euclidean geometry was to be considered. However, two subjects evidenced knowledge about the use of the parallel postulate, definitions and theorems, simultaneously; four subjects only evidenced the use of the parallel postulate; and three subjects only evidenced the use of mathematical theorems in the argument. To illustrate this, three responses are presented: that of subject SBW12 evidences the use of the parallel postulate, definitions and theorems; that of subject SBM02 refers only to the parallel postulate; and that of the subject SBW05 refers only to the use of theorems:
For the 10 research subjects who indicated that the argument was a proof of the given proposition, but who did not evidence any of the proposed indicators, in their answers we found inaccuracies to justify the validity of a correct mathematical argument, basing their answers on generalities such as: the presence of an adequate logic structure, that is, starting from a true proposition and generating true partial conclusions that lead to the conclusion, the consideration of all the possibilities and their corresponding justification, the use of previous results from Euclidean geometry and the clarity of the argument.
Based on the results presented in this section, it can be seen that all future mathematics teachers evidence knowledge to determine when an argument constitutes a mathematical proof of a proposition, although few subjects provide the justifications for it. Likewise, the vast majority evidence knowledge to discriminate if an argument does not correspond to a mathematical proof based on mathematical aspects such as the partial use of the hypothesis and the improper use of definitions. However, there is a significant decrease in subjects that identify the improper use of the multiplicative inverse axiom.
Regarding the correction of the arguments that do not correspond to a mathematical proof, there is a decrease in the number of subjects who consider in their proposals to modify the argument, the mathematical aspects that invalidated it: (1) in argument 3, 14 of 19 subjects suggested that the definitions of odd and even number should be modified, (2) in argument 1, 7 of 19 subjects indicated that the complete hypothesis of the non-negative discriminant should be used and exhibited some real number to satisfy existence, while 8 of 19 subjects only made reference to the use of the complete hypothesis and (3) in argument 2, 4 of 19 subjects manifested that two cases must be considered for the number in question, when it was zero and when it was different from zero to be able to use the multiplicative inverse axiom.
Conclusions
Most of the mathematics teachers in initial training (MTITs) evidenced knowledge of the logic-syntactic aspects in the evaluation of the four mathematical arguments proposed in questionnaire 1 for universal implication, corresponding to the mathematical proposition P: any real number satisfies that, if it is positive, then the sum of it and its multiplicative inverse is greater than or equal to two.
For the first two arguments, the majority of the subjects manifested that they did not correspond to a proof, appreciating that, in the first argument, the proof alluded to a particular case and that in the second, the reciprocal of the predicate was proved. For the third and fourth arguments, the majority of subjects indicated that they did correspond to proofs. In the case of the third argument, regarding the direct proof of the universal implication, the majority of subjects evidenced knowledge that the antecedent had to be assumed to be true and subsequently, guarantee the veracity of the consequent. However, only a minority evidenced knowledge about the consideration of a generic element of the universe and none made reference to the fact that the property was valid by virtue that it had been guaranteed for a generic element that represents any element of the universe. These results coincide with those obtained by Durand-Guerrier et al. (2012b). In the fourth argument, regarding the proof by reduction to absurdity of the universal implication, the majority of subjects displayed evidence of knowledge of the three proposed indicators, namely, that the negation of the given proposition should be assumed, that a contradiction should be generated and once generated, it could be concluded that the original proposition was true.
The proposition of questionnaire 2 was used by Knuth (2002) in his research with 16 mathematics teachers where he presented them with an argument that proved the reciprocal predicate. According to this researcher, 10 teachers considered it as a proof and focused on correcting the algebraic manipulations more than on validity aspects. In our study, the majority of mathematics teachers in initial training (MTITs) focused on logic correction rather than on the mathematics employed in each argument, which allows us to observe adequate knowledge of the logic-syntactic aspects involved in proving by universal implication. Specifically, MTITs evidence knowledge to discern that the consideration of a particular case does not constitute mathematical proving, and they appreciate the argument that uses this fallacy. Also, they have demonstrated to possess knowledge on how to proceed in direct and reduction to absurdity proving.
The study of knowledge regarding the mathematical aspects of proving is complex, since, in addition to logic-syntactic elements, concepts and their meanings intervene in the mathematical theory in which proofs are inserted. In this sense, Mariotti (2006) points out that, contrary to what happens within a formal theory, in the practice of mathematical deduction there exists dependence on the comprehension and prior assimilation of the meaning of the concepts from which certain properties are followed logically. The mathematical aspects considered in this investigation such as hypotheses, axioms, definitions and theorems could have presented different levels of difficulty in understanding a proof.
In the case of the first argument, corresponding to the category denominated “partial use of the non-negative discriminant hypothesis” (in a second degree equation in a real variable), the hypothesis appears explicitly in the proposition to be proved. The vast majority of the research subjects evidenced that it was not a proof due to this partial use. In correcting the argument, a minority of the subjects evidenced knowledge regarding the fact that the hypothesis of the discriminant must be considered in its entirety and also sought and proposed a real number that would comply with existence.
In the remaining three arguments, the definitions, axioms and theorems employed are not necessarily explicit in the proposition to be proved and, therefore, the subjects are required to know them in depth in order to evaluate their use during proving. In the second argument corresponding to the category denominated “improper use of the axiom of existence of the multiplicative inverse” (to demonstrate the equality in absolute value of two integers divisible by each other), very few subjects evidenced knowledge about the argument not being a proof due to the improper use of the multiplicative inverse. Likewise, very few subjects, in their suggested argument correction, manifested that the number in question must be considered to be non-zero in order to use its multiplicative inverse.
In the third argument corresponding to the category denominated “improper use of the definitions of even and odd integers” (to demonstrate the parity of the sum of two odd numbers), the majority of subjects evidenced that it was not a proof due to the inappropriate use of definitions. In correcting the argument, most subjects evidenced knowledge of the algebraic conditions that characterize odd and even numbers, possibly because they have used them frequently in undergraduate courses. However, the ignorance of all the conditions of the definitions could lead to the subjects misjudging an argument. For example, in the second argument, two subjects considered that in the definition of divisibility the numbers involved are necessarily non-zero, therefore, existence of the multiplicative inverse was justified for them, which implied that they considered the argument to be a proof.
In the fourth argument corresponding to the category denominated “proper use of hypotheses, axioms, definitions and theorems in the proof of the theorem of the sum of the measures of the interior angles of a triangle in Euclidean geometry”, the totality of the subjects manifested that the argument was a mathematical proof. However, only a minority evidenced knowledge of the proposed indicators. This fact suggests that it is easier to explain when a mathematical argument has errors than to justify its correctness.
According to Mariotti (2006), traditionally, the mathematical proof is considered in itself possible of being separated from the proposition which it supports and from the theoretical framework within which such support makes sense. In the present research it has been evidenced that the vast majority of research subjects (MTITs) took notice that in a proof all these elements are involved simultaneously and it is impossible to comprehend the meaning of a mathematical proof without linking the proposition to which it refers and the mathematical theory in which it is inscribed. In this way, in mathematical practice the truth values of propositions are proved, but the term “truth” must always be understood in relation to a particular theory.
The results obtained support the appreciation of Cabassut et al. (2012) in which they affirm that the mathematical proof does not establish facts, but rather guarantees the validity of propositions of the type “if-then”, this implies that the hypotheses, axioms, theorems and definitions must be understood and applied in their precise meanings within a mathematical theory. It is thus considered that the mathematical aspects of proving can contribute to the specialized knowledge of mathematics teachers to understand that mathematical results are not universal truths. For example, when it is stated that the sum of the measures of the interior angles of any triangle is 180 degrees, the knowledge about the mathematical validity of the proof allows us to understand that in a certain theory this result can be derived.
Acknowledgements
This work is part of the Project «Conocimiento Didáctico del Profesor y Aprendizaje de Conceptos Matemáticos Escolares» (EDU2015-70565-P) (translated as “Teacher didactic knowledge and learning of school mathematical concepts” of the National Plan for R+D+I (MICIN) and the Andalusian Plan for Research, Development and Innovation (Group FQM-193, Didactics of Mathematics. Numerical Thinking). In addition, it had the support of project PCG2018-095765-B-I00 of the National Plan for R+D+I (MICIN) and the Andalusian Plan for Research, Development and Innovation (Group FQM-193, Didactics of Mathematics. Numerical Thinking) and the School of Mathematics of the Universidad Nacional in Costa Rica.
Informed consent
The authors declare that the participants (subjects) of this study were informed about the treatment of the information.











 text in
text in