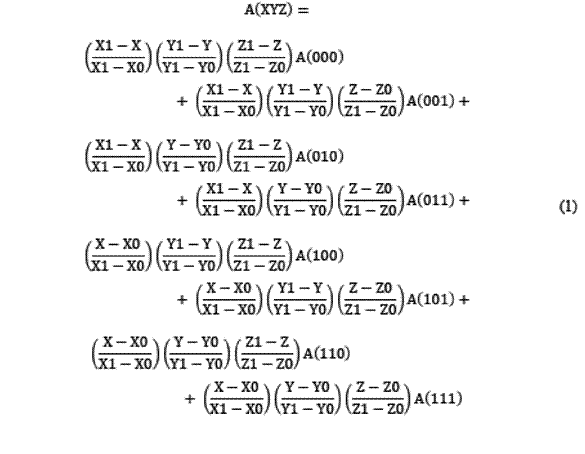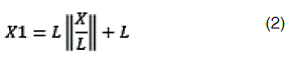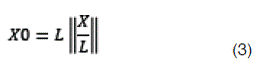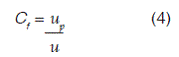Introducción
En ingeniería, es común conocer un conjunto de datos discretos, obtenidos a través de mediciones de algún fenómeno, como los campos escalares de temperaturas o presiones en un espacio determinado y en puntos definidos. Para conocer los valores de las variables en puntos intermedios, la interpolación es un método ampliamente usado. Hoy día los métodos de interpolación proveen de herramientas que pueden ser utilizadas en áreas muy diversas como lo son las imágenes médicas [1], métodos de renderizado tridimensional [2] y modelado en geología [3], entre otros. De modo que la interpolación permite generar información nueva a partir de la estimación sobre datos conocidos. Vale resaltar la diferencia entre la interpolación y la regresión, siendo la primera una técnica que genera una función única que contiene estrictamente todos los datos medidos y se emplea cuando estos se conocen con elevada precisión; mientras que la segunda entrega una función que representa la tendencia de los datos, sin contenerlos necesariamente, y se emplea en casos que el error experimental sea significativo [4].
En cuanto a la interpolación, la versión en una dimensión busca encontrar los valores intermedios a partir de muestras discretas, cuando se estudia un fenómeno que depende de una sola variable. El valor buscado estará encerrado entre dos puntos, los cuales incidirán en el valor buscado [5]. Por ejemplo, si en un sistema se monitorean los niveles de temperatura cada hora, y se sabe el valor a las 2:00 pm y a las 3:00 pm, pero se desea saber el valor de la variable a las 2:20 pm se puede recurrir a interpolar para estimarla.
La interpolación en dos dimensiones es un método utilizado para obtener los valores no medidos o no conocidos en un fenómeno que dependa de dos variables. Un ejemplo es la estimación de los niveles de contaminación en una región geográfica, donde las muestras se toman en los vértices de una cuadrícula en la vista de planta de la región [6]. Entonces, el nivel de contaminación por estimar en cualquier punto desconocido, estará influenciado por los valores en los cuatro vértices de las muestras que lo rodean. Por tanto, en este caso el grado de contaminación dependerá de dos variables. (Dos coordenadas espaciales en la región geográfica, en la vista de planta, a un nivel de altura previamente definido).
La interpolación en tres dimensiones trata con fenómenos que dependan de tres variables. Por ejemplo, en una habitación donde se quiere saber la humedad en algún punto específico. Para ubicar este punto son necesarias tres coordenadas en el espacio. Las muestras tomadas de humedad en la habitación se pueden ubicar en una malla cúbica, en donde cada punto tiene un valor de humedad asociado. Entonces, los valores desconocidos estarán encerrados por los 8 vértices de un cubo dentro de la malla.
A diferencia de los métodos en una y dos dimensiones, en cuanto a interpolación en tres dimensiones la literatura no brinda mucha información. Se indica que se puede derivar de los métodos anteriores, pero no se explicita ningún procedimiento o ejemplo para resolver este tipo de problemas [4].
En el caso de soluciones por software, Matlab de MathWorks Inc., posee una función llamada interp3 la cual permite solucionar el problema de interpolar en tres dimensiones [7]. Esta función requiere como entrada una matriz cúbica que posea los valores de la variable de interés en cada vértice, además, solicita los puntos en los cuales se desea encontrar el valor en cuestión. Con estos datos, la función entrega el valor interpolado en las coordenadas requeridas. No obstante, sus ventajas en velocidad de cálculo y simplicidad de aplicación, tiene la limitación de que la malla de entrada debe ser perfectamente cúbica y es indispensable conocer el valor de la variable dependiente en todos los vértices de dicha malla. Además, el usuario no tiene posibilidad de conocer en detalle o modificar el funcionamiento interno de la función, por lo que no es posible desarrollar ajustes para casos especiales, por ejemplo, adaptaciones necesarias para mallas no cúbicas o espacios no isotrópicos donde la velocidad de propagación del fenómeno sea dependiente de la dirección de propagación.
Con este panorama, en el presente estudio se detalla el algoritmo de la interpolación tridimensional en campos escalares, de modo que sea posible conocer el valor de una variable en un campo continuo, a partir de valores medidos en el espacio de manera discreta.
Metodología
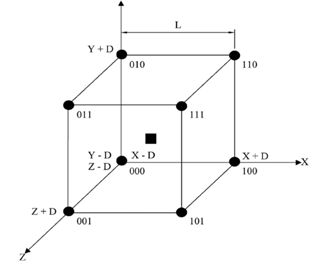
El método propuesto para interpolación tridimensional se plantea con una malla tridimensional cúbica. De modo que cualquier punto posee ocho vecinos ubicados en los vértices, como se muestra en la Figura 1. Cada vértice representa un valor dado, lo que permite interpolar. El método toma en cuenta el acercamiento con los puntos conocidos, es decir, un punto que se encuentre más cerca del punto de interés tendrá mayor influencia en el resultado de la interpolación.
La identificación de los puntos vecinos en la Figura 1 se realiza de dos maneras. La primera es en forma binaria, de manera que el primer, segundo y tercer número representan al eje “x”, “y” y “z” respectivamente. El número 0 representa que la coordenada está por detrás del punto de interés y el número 1 indica que está por delante. También se utiliza la nomenclatura con una diferencia D; cuando D se suma representa lo mismo que un 1, y cuando se resta representa un 0 . Por ejemplo, el punto 010 está ubicado en las coordenadas (X - D, Y + D, Z -D ).
Suponiendo que se tienen una cantidad finita de puntos, y que cada uno tiene asignado un valor para cierta variable A; si se deseara conocer el valor de A en un lugar cualquiera (X, Y, Z) que difiera de los puntos conocidos, entonces, se debe realizar una interpolación tridimensional y obtener así A(XYZ).
Para esto, se deben ubicar los ocho puntos más cercanos al sitio requerido y aplicar la ecuación (1), donde; por ejemplo, las coordenadas del punto 111 son X1, Y1 y Z1 y las coordenadas del punto 010 son X0, Y1 y Z0, de modo similar el resto de puntos [8].
En la ecuación anterior, el valor de A en cada uno de los ocho puntos es multiplicado por un factor que es el que da el valor de proximidad relativa con el punto (X, Y, Z) de estudio. Ese valor está en el rango entre 0 y 1. Por la estructura propuesta, se garantiza que la contribución relativa de todos los puntos complete la unidad.
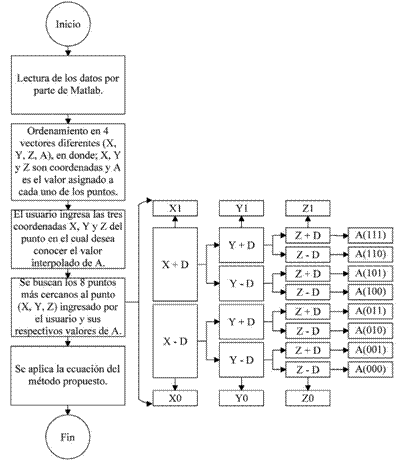
La generalización del método se implementa mediante código, en particular desarrollado en Matlab. El método funciona según se detalla en la figura 2. Se presenta en forma de diagrama de flujo, para que pueda ser implementado en cualquier lenguaje de programación.
En la Figura 2 se explica el código de manera gráfica, el cual empieza con una lectura de los datos ingresados por el usuario. Posteriormente se hace un ordenamiento de los datos en X, Y, Z y el valor del campo escalar A.
El usuario ingresa los valores de las coordenadas donde desea conocer el valor de A. El código realiza un filtrado en todos los puntos que existan para encontrar los 8 puntos más cercanos al punto (X, Y, Z) ingresado por el usuario.
Dicho filtrado busca primero el punto (X1, Y1, Z1) asociados al valor A(111), luego el valor A(000) encontrado en el punto (X0, Y0, Z0), y a partir de estos, se pueden realizar más filtrados para llegar a los otros 6 valores y sus respectivos valores asignados.
En el filtrado se debe considerar la distancia entre los puntos. Es decir, la distancia “L” del cubo. Para ello se aplica la ecuación (2), de este modo se encuentra el punto inmediatamente posterior a cada uno de los valores del punto requerido (X, Y, Z). Para esta ecuación; X1 es el valor superior que se debe encontrar según sea el filtrado correspondiente y L es la medida de la arista del cubo de la Figura 1. Las dobles líneas en la fracción indican que se toma la parte entera de la división. La expresión para Y1 y Z1 es totalmente análoga.
En la Figura 2 se detalla la realización del filtrado. Lo primero es encontrar X1, para esto, es necesario buscar en la lista de valores en X todos aquellos que sean iguales a X1 aplicando la ecuación (2). Ese es el valor de X1, sin embargo, en este nivel del código hay una gran cantidad de puntos que cumplen con tener la coordenada X1, por lo tanto es necesario realizar un segundo filtrado para encontrar el punto Y1. De los puntos seleccionados mediante X1, se realiza la búsqueda de todos los valores en Y que sean iguales a Y1 considerando la ecuación (2), pero reemplazando las X por Y. De esta manera se reducen los puntos, sin embargo, resulta necesario un filtro adicional para encontrar el valor Z1. Se realiza una última búsqueda de manera análoga, pero esta vez en Z. Esto da como resultado el primer punto (X1, Y1, Z1), el cual tiene asociado el valor A(111).
Luego se realiza el mismo filtrado, pero, para encontrar el punto (X0, Y0 y Z0). El proceso se realiza según se explicó anteriormente, pero se utiliza la ecuación (3) para encontrar el valor de X0, que corresponde al punto inmediatamente inferior al requerido, los valores de Y0 y Z0 se encuentran de forma análoga reemplazando la X por Y o Z según corresponda.
Con esto se obtiene el punto (X0, Y0, Z0), el cual tiene un valor asociado A(000). A partir de estos dos puntos se pueden obtener los restantes, por ejemplo, para encontrar el valor de A(010) es necesario el punto (X0, Y1, Z0). De esta manera, se encuentran los otros seis valores: A(001), A(010), A(011), A(100), A(101) y A(110), asociados cada uno a un vértice distinto del cubo que encierra al punto de interés.
Con esta información, se aplica la ecuación (1) del método propuesto y tal como se mencionó anteriormente, se obtiene el valor interpolado. En la sección de aplicación se presenta un ejemplo para una mejor comprensión del método.
Aplicación
Para aplicar la solución propuesta se plantea un ejemplo de ingeniería que permite visualizar el uso de la interpolación tridimensional en campos escalares [9]. El problema planteado y la solución se presentan a continuación.
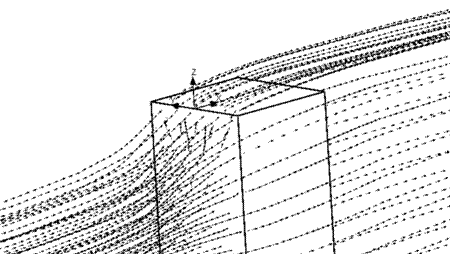
Se tiene, en una ciudad, una corriente de viento con un perfil de velocidad incidente u, como el que se muestra en la Figura 3. Cuando el flujo pasa alrededor de algún edificio, este se distorsiona y su perfil se convierte en u p en los alrededores del edificio de interés.
El factor de concentración, denotado como C f (equivalente a A en la sección de metodología, donde se explica el método propuesto), permite cuantificar la concentración de flujo y se define según se muestra en la ecuación (4):
El problema de ingeniería por resolver es lograr conocer el valor de C f en un punto cualquiera (X, Y, Z), dentro de un dominio tridimensional. En el caso particular es un volumen cúbico de 20 m de arista, con el sistema de coordenadas ubicado como se muestra en la Figura 3.
Para conocer el valor del C f en las coordenadas (X, Y, Z), es necesario realizar la interpolación tridimensional en campos escalares que se propone en este artículo. Usando como datos de entrada la magnitud de la velocidad del viento dentro del dominio de interés. La aplicación de la solución se implementa, tal como se indicó anteriormente, en un código en Matlab.
En el ejemplo que se desarrolla, L = 1 m, por lo que se tienen 213 = 9261 puntos de medición, cada uno con un valor C f asociado.
Dado el valor de L, se buscará en los vectores de cada eje coordenado valores iguales a la parte entera de cada una de las coordenadas dadas por el usuario, más una unidad, y con esto se obtiene (X1, Y1, Z1). Para definir el punto (X0, Y0, Z0) entonces se realizará con la parte entera únicamente, sin sumar la unidad. Esto según las ecuaciones (2) y (3) respectivamente.
Un ejemplo concreto de lo anterior es tener como coordenadas de interpolación el punto (6,92, -8,56, 0,87). Entonces la parte entera más la unidad (7, -8, 1) es igual a (X1, Y1, Z1). De forma similar la parte entera (6, -9, 0) corresponde a (X0, Y0, Z0). Con esta información se construye la Cuadro 1, que muestra las 8 posibles permutaciones, para cada una de ellas existe un único valor de C f , el cual en este caso es tomado de un conjunto de datos que se emplearán posteriormente para validar el método propuesto.
Con la información del Cuadro 1 y la ecuación (1) del método propuesto, se obtiene para el punto de interés el factor de concentración, C f = 0,4576.
Cuadro 1 Ejemplo de los ocho puntos vecinos de (6,92, -8,56, 0,87).
| Punto | [101]Coordenadas (X, Y, Z) | [102]Cf |
| 000 | [105](6, -9, 0) | [106]0,000 |
| 001 | [109](6, -9, 1) | [110]0,579 |
| 010 | [113](6, -8, 0) | [114]0,000 |
| 011 | [117](6, -8, 1) | [118]0,449 |
| 100 | [121](7, -9, 0) | [122]0,000 |
| 101 | [125](7, -9, 1) | [126]0,580 |
| 110 | [129](7, -8, 0) | [130]0,000 |
| 111 | [133](7, -8, 1) | [134]0,458 |
Validación
El método propuesto se valida mediante la función de Matlabinterp3. En la cual se deben ingresar 7 entradas: las primeras 3 son los vectores en los ejes “x”, “y” y “z” detallados en el cuadro 2, que contienen todas las posiciones cartesianas de los puntos donde se conocen los valores posibles para el campo escalar de interés, en el ejemplo en cuestión, el campo C f . Las últimas 3 entradas son las coordenadas del punto donde se quiere conocer el valor interpolado.
La cuarta entrada requiere de especial atención, es propiamente una matriz de tres índices, con los valores del campo escalar, en el caso particular C f . Esta matriz es de tamaño n por m por p, donde cada una de estas letras representa la cantidad de puntos en los ejes “y”, “x” y “z” respectivamente. Vale destacar que en esta matriz hay tres restricciones importantes: i) Se intercambian las coordenadas “y” y “x” respecto de lo acostumbrado, es decir, el primer índice se refiere al eje “y” y el segundo índice al eje “x”. ii) Debe existir estrictamente un valor para cada espacio en el arreglo, de modo que la ausencia de alguna medición en los vértices de la malla imposibilita utilizar esta función. iii) La malla de datos debe tener un espaciamiento uniforme, en caso de una distribución de datos irregular, la función interp3 no puede emplearse.
Esta última característica también la posee el código propuesto. Sin embargo, dado que el código está desarrollado de forma explícita, es posible modificarlo y adecuarlo para otro tipo de mallas con cualquier tipo de forma o estructura.
En la matriz tridimensional C f , cada entrada es propiamente un valor del campo de concentración de flujo, y tal como se indicó anteriormente, cada uno de sus índices hace referencia a cada una de las coordenadas “x”, “y” y “z” del punto. Para el caso particular en estudio, el Cuadro 2 presenta los rangos y coordenadas en cada uno de los ejes cartesianos.
De modo que, en el caso en estudio, el valor de C f (5, 10, 10) será el valor de C f en el punto con las coordenadas cartesianas (4, -1, 9). Así, se almacena la información de manera compacta, pues para 21 posiciones de datos por eje, se tienen entonces tres vectores de 21 entradas y una matriz de 21x21x21 = 9261 datos, en lugar de asignar cada punto de manera independiente en vectores, lo que implicaría generar 4 vectores de 9261 entradas cada uno.
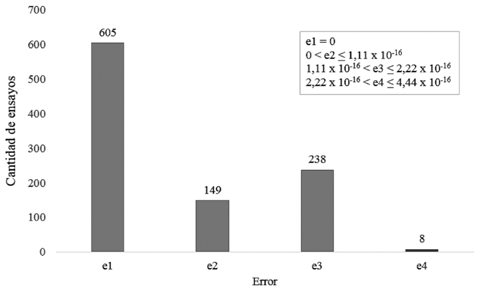
Una vez ingresados los datos de entrada a la función interp3, se hace un ciclo de pruebas con 1000 puntos, elegidos de forma aleatoria, dentro de los rangos de interés, para validar el valor de C f que entrega el método propuesto, frente al que arroja la función interp3 de Matlab. La Figura 4 muestra el valor del error absoluto de estos 1000 ensayos.
Cuadro 2 Rangos de valores en cada eje de coordenadas.
| Posición | [148]rango x | [149]rango y | [150]rango z |
| 1 | [153]0 | [154]-10 | [155]0 |
| 2 | [158]1 | [159]-9 | [160]1 |
| 3 | [163]2 | [164]-8 | [165]2 |
| 4 | [168]3 | [169]-7 | [170]3 |
| 5 | [173]4 | [174]-6 | [175]4 |
| 6 | [178]5 | [179]-5 | [180]5 |
| 7 | [183]6 | [184]-4 | [185]6 |
| 8 | [188]7 | [189]-3 | [190]7 |
| 9 | [193]8 | [194]-2 | [195]8 |
| 10 | [198]9 | [199]-1 | [200]9 |
| 11 | [203]10 | [204]0 | [205]10 |
| 12 | [208]11 | [209]1 | [210]11 |
| 13 | [213]12 | [214]2 | [215]12 |
| 14 | [218]13 | [219]3 | [220]13 |
| 15 | [223]14 | [224]4 | [225]14 |
| 16 | [228]15 | [229]5 | [230]15 |
| 17 | [233]16 | [234]6 | [235]16 |
| 18 | [238]17 | [239]7 | [240]17 |
| 19 | [243]18 | [244]8 | [245]18 |
| 20 | [248]19 | [249]9 | [250]19 |
| 21 | [253]20 | [254]10 | [255]20 |
El promedio del error de los 1000 ensayos de la figura 4 es 6,9575 x 10-17 y el épsilon del computado empleado es 2,22 x 10-16. Dado lo anterior y que el error máximo es del orden de 10-16, se puede asegurar la confiablidad del método propuesto, pues las diferencias encontradas son atribuibles a la precisión finita de la aritmética del computador y no al método propuesto.
Conclusiones
Al desarrollar e implementar un método para resolver el problema de la interpolación tridimensional en un campo escalar, se encuentran las siguientes conclusiones:
La utilización de una matriz de tres índices, para el almacenamiento de la información de un campo escalar en tres dimensiones, resulta sumamente compacta e implica un ahorro significativo en memoria computacional.
El método propuesto de interpolación tridimensional puede generalizarse a una malla que no sea uniforme, lo cual lo hace más flexible que las funciones existentes en los programas comerciales de simulación numérica.
El método desarrollado concuerda, de manera confiable, con los resultados entregados por Matlab.
Estas conclusiones garantizan la validez del método propuesto y a la vez abren nuevas oportunidades de desarrollo e investigación, como lo es la extensión de esta solución a volúmenes irregulares o dependientes del tiempo, así como modelos no lineales u otros tipos, aplicables a espacios no isotrópicos.