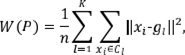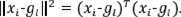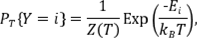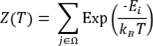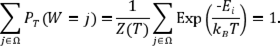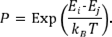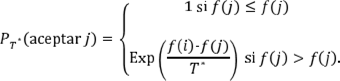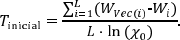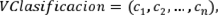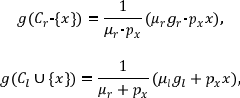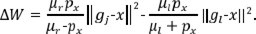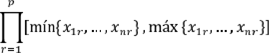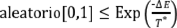Introducción
El particionamiento de datos corresponde a un problema de optimización combinatoria en el que se desea efectuar una distribución de individuos en grupos, regido por algún criterio mínimo de costo, el cual se fundamenta en el grado de similitud que presenten los individuos asignados a un mismo grupo.
Primero se considera el conjunto de individuos X ={ x 1, ..., x n } y se quiere construir un agrupamiento de dichos objetos en K grupos, K conocido a priori. Dicho agrupamiento se denomina una partición P ={ C 1 , ..., C K } del conjunto X , la cual debe satisfacer que C l ⊂ X y C l ≠ Ø para cada l=1, ..., n ; l ≠ l’ ⇒ C l ∩ C l’ = Ø y X = ∪ K l=1 C l . Se parte de la tabla de datos de tamaño nxp, caracterizada por n individuos y p variables cuantitativas independientes, tal como se muestra en el cuadro 1.
La fila
i
del cuadro 1 contiene las entradas del
i -
ésimo individuo que puede interpretarse como un vector en 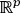 . Cada individuo se asume con peso constante
. Cada individuo se asume con peso constante 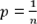 , y xij corresponde al valor que toma xi en la j- ésima variable cuantitativa υj .
, y xij corresponde al valor que toma xi en la j- ésima variable cuantitativa υj .
Cuadro 1 Tabla de datos de tamaño nxp
| Ind/Var | υ1 | υ2 | ... | υp |
|---|---|---|---|---|
| x1 | x11 | x12 | … | x1p |
| x2 | x12 | x22 | … | x2p |
| · · · | · · · | · · · | · · · | · · · |
| xn | xn1 | xn2 | … | xnp |
Si se considera el conjunto X={x1, ..., xn} como representación matricial de la cuadro 1, con 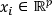 y P una partición de
X
en
K
clases
C
1, ...,
C
K
, entonces el problema de particionamiento de los individuos
x
1
, ...,
x
n
en
K
clases puede formularse como la minimización de la función
y P una partición de
X
en
K
clases
C
1, ...,
C
K
, entonces el problema de particionamiento de los individuos
x
1
, ...,
x
n
en
K
clases puede formularse como la minimización de la función
donde ||·||2 corresponde a la norma inducida por la métrica euclídea clásica, tal que
La función W(P) se denomina la inercia intraclases asociada a la partición P y permite cuantificar el agrupamiento de los individuos en todas las clases a la vez. Cuanto menor sea el valor de W(P) , los individuos pertenecientes a una misma clase están más agrupados entre sí, indicando, por ende, una mayor similitud a lo interno de las clases. Lo anterior en contraposición de la disimilitud que presentan los individuos pertenecientes a clases diferentes.
Sobrecalentamiento simulado (SS)
La heurística de sobrecalentamiento simulado (SS) (llamado en inglés simulated annealing) también denominada recocido simulado, es una técnica de búsqueda y optimización propuesta por primera vez en 1983 por Kirkpatrick, Gellat y Vecchi, relacionando los campos de la optimización combinatoria y la estadística termodinámica (Kirkpatrick et al., 1983).
Este método está basado en la idea de un proceso de metalurgia denominado annealing, que está conformado por dos etapas. En la primera, un sólido es calentado a altas temperaturas hasta que se funde. De esta manera, las partículas que conforman la materia se mueven y se reorganizan en forma aleatoria. En la segunda etapa, la materia recalentada y deformada entra en un enfriamiento. Para ello, la temperatura suministrada al sólido empieza a disminuir lentamente, de modo que este encuentre un estado de equilibrio para cada paso de dicho decrecimiento (Babu & Murty, 1994). El objetivo de este proceso es generar materiales, como el caso del vidrio, de mayor dureza.
El equilibrio térmico del sistema, cuando la temperatura es T, se rige mediante la distribución de Boltzmann (Moyano, 2011; Pauling, 1988). Según esta distribución, si Ω es un espacio de probabilidad que posee todos los estados de la sustancia y si Y es una variable aleatoria sobre Ω que indica el estado actual de la sustancia, entonces la probabilidad de que Y=i está dada por:
donde E i denota la cantidad de energía del estado i y sometido a una temperatura T , k B es una constante física conocida como constante de Boltzmann, que relaciona temperatura absoluta y energía, y Z T es una constante de normalización calculada por la relación:
y denominada función de partición canónica. Además, se cumple que P T (W=i) ≥ 0 y
Por lo que P T (Y=i) es una función de densidad de probabilidad para Y . De este modo es notorio, para cualquier temperatura T , la existencia de estados en Ω con probabilidad positiva de ocurrir. Así, cuando la temperatura T es cercana a cero, los estados con probabilidad positiva serán aquellos de muy baja energía (Bertsimas & Tsitsiklis, 1993; de los Cobos et al., 2010).
Mediante la técnica de Monte Carlo para la simulación de variables aleatorias es posible simular el proceso físico del annealing, generando así una secuencia de estados de la materia calentada a una temperatura T . Si la materia calentada se encuentra en el estado i con energía E i , es posible generar un nuevo estado j mediante una perturbación causada por la transferencia o desplazamiento de una partícula de la materia. La energía de este nuevo estado es E j . De esta manera, si E i -E i ≤ 0 , el estado j se acepta como el estado actual. En caso contrario, la aceptación del estado j se hace solo bajo la probabilidad (Abbass et al., 2002; Babu & Murty, 1994; de los Cobos et al., 2010)
Este método se conoce como el criterio de aceptación de Metropolis. El valor k B T puede verse como una sola cantidad, que en el algoritmo de SS se le denomina parámetro de control o simplemente temperatura. Este valor se debe ajustar para cada problema por resolver y se denotará con T* .
Sobrecalentamiento simulado en optimización combinatoria
Si se considera un problema de optimización combinatoria en el que se quiere determinar el valor que minimice la función objetivo ƒ dentro del espacio de búsqueda, el algoritmo de SS puede verse como una iteración del algoritmo de Metropolis, si se toman valores decrecientes del parámetro de control T* (de los Cobos et al., 2010), donde el estado i corresponde a una solución factible y la energía E i es el valor de la función objetivo en dicho estado, es decir, E i = ƒ (i ) .
El criterio de aceptación de Metropolis establece la regla para aceptar la solución j dada la solución i , la cual indica que la probabilidad de aceptación está dada por (Aarts, 1990):
Al igual que en el proceso de annealing en metalurgia, el éxito del algoritmo depende de la velocidad del enfriamiento (control del parámetro temperatura). Existen muchas formas de realizar el enfriamiento, algunas de ellas pueden ser consultadas en Talbi (2009) y Osman y Christofides (1994). En particular, la fórmula más usada para realizar la actualización de la temperatura para la iteración k +1 es la fórmula geómetrica dada por T* k +1 = α T*k , donde α ∈]0,1[. Se recomienda un valor para α cercano a uno, debido a que valores altos de α generan un decreciento más lento del modelo geométrico y, por ende, el sistema tendrá más oportunidad de alcanzar un equilibrio en cada uno de los estados de la temperatura. Este modelo fue el seleccionado para el presente trabajo.
En el algoritmo de SS, el sistema debe alcanzar su estabilidad térmica para cada valor de la temperatura T* , antes de hacer que esta decrezca por alguno de los modelos de enfriamiento. Por lo tanto, se torna necesario la inserción de un nuevo parámetro LongCade que representa un largo de truncamiento de la cadena de Markov (Mesa, 2007). Este parámetro indica el número de soluciones generadas para una temperatura T* fija. Como consecuencia, en la implementación del algoritmo, para un estado de la temperatura se ejecuta un ciclo de longitud LongCade, que corresponde a la longitud tomada para la cadena de Markov. Finalizada dicha cadena, se enfría el sistema (se pasa a un nuevo estado) para proceder nuevamente con la ejecución del ciclo correspondiente. Se mantiene este comportamiento de manera sucesiva hasta que el sistema se haya enfriado lo suficiente. El algoritmo completo de SS se muestra en el Algoritmo 1, y en particular en la línea 6 se puede observar el ciclo asociado a la cadena de Markov.
ALGORITMO 1 Sobrecalentamiento simulado
Entrada: ParámetrosT f (temperatura final), M (número máximo de iteraciones) y LongCade.
1: s ← Solución inicial generada aleatoriamente.
2: T* ← Tinicial · 3: k ← 0.
4: MIENTRAS No se dé el criterio de parada HACER 5: k ← k + 1 .
6: PARA j ← 1 HASTA LongCade HACER
7: s' ← Se genera una nueva solución mediante una perturbación de s .
8: ∆E ← f (s’)-f (s) .
9: SI ∆E ≤ 0 ENTONCES
10: s ← s’ .
11: SI NO
12: SI aleatorio [0,1] ≤ Exp 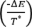 ENTONCES
ENTONCES
13: s ← s’ .
14: FIN SI
15: FIN SI
16: FIN PARA
17: T* ← g (T*) , con g la función de enfriamiento.
18: FIN MIENTRAS
19: Retornar: La mejor solución encontrada en el proceso.
Para el caso del valor de
T
inicial
(temperatura inicial), existen muchas referencias en la literatura sobre formas de cómo definir este parámetro para la ejecución del algoritmo de SS. Por ejemplo, pueden consultarse Kirkpatrick et al. (1983), Talbi (2009), Yang (2010) y Ben-Ameur (2004). Para efectos de la implementación se siguió una estrategia similar a la propuesta en Ben-Ameur (2004) que se basó en la regla de aceptación de Metropolis. En particular, la probabilidad de aceptación en el caso que
f(j) > f(i)
, se implementa mediante la comparación del valor de 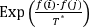 con un número aleatorio generado con una distribución uniforme en el intervalo ]0,1[ (Aarts & Korst, 1990). Dicho número aleatorio se puede interpretar como una tasa de aceptación χ0 (Trejos & Murillo, 2004), con 0 < χ0 < 1, y visualizarlo como el porcentaje que se quiere para aceptar (bajo una probabilidad) las primeras soluciones en el algoritmo de sobrecalentamiento simulado. En síntesis, si
f(j) > f(i)
y dada una tasa de aceptación χ0, se tiene que
con un número aleatorio generado con una distribución uniforme en el intervalo ]0,1[ (Aarts & Korst, 1990). Dicho número aleatorio se puede interpretar como una tasa de aceptación χ0 (Trejos & Murillo, 2004), con 0 < χ0 < 1, y visualizarlo como el porcentaje que se quiere para aceptar (bajo una probabilidad) las primeras soluciones en el algoritmo de sobrecalentamiento simulado. En síntesis, si
f(j) > f(i)
y dada una tasa de aceptación χ0, se tiene que 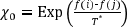 . Así, despejando T* en la igualdad anterior se obtiene
. Así, despejando T* en la igualdad anterior se obtiene 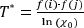 Por lo tanto, para el cálculo de la temperatura inicial se generaron de manera aleatoria L soluciones factibles del problema de optimización y a cada una de ellas se le construyó un vecino (la generación de vecinos se tratará en detalle en la siguiente sección) tal que tuviera una inercia intraclases mayor que la inercia de la solución factible a partir de la cual se generó. Es decir, si Wi denota la inercia intraclases de la i-ésima solución generada y WVec(i) denota la inercia intraclases de su vecino, para i = 1,...,L , entonces debe darse que WVec(i) > Wi . Finalmente, se promediaron las diferencias positivas WVec(i) -Wi y se dividió entre la expresión In (χ0). Por lo tanto,
Por lo tanto, para el cálculo de la temperatura inicial se generaron de manera aleatoria L soluciones factibles del problema de optimización y a cada una de ellas se le construyó un vecino (la generación de vecinos se tratará en detalle en la siguiente sección) tal que tuviera una inercia intraclases mayor que la inercia de la solución factible a partir de la cual se generó. Es decir, si Wi denota la inercia intraclases de la i-ésima solución generada y WVec(i) denota la inercia intraclases de su vecino, para i = 1,...,L , entonces debe darse que WVec(i) > Wi . Finalmente, se promediaron las diferencias positivas WVec(i) -Wi y se dividió entre la expresión In (χ0). Por lo tanto,
En este estudio se seleccionó χ0=0,96, con el objetivo de favorecer una alta variabilidad para el cálculo de la temperatura inicial.
Implementación en particionamiento
Para efectos de la implementación computacional del problema de particionamiento con el algoritmo de SS se construyó un vector, denominado VClasificacion (vector de clasificación), que representa la forma en la que se manejan las posibles particiones de X. Dicho vector posee entradas enteras y es de dimensión 1 x n. Además, tiene la forma
de tal manera que la i-ésima entrada, ci , de VClasificacion satisface que ci ∈ {1,2,...,K} y denota la clase a la que se asigna el individuo xi de X. Por lo tanto, se quiere determinar la combinación de entradas enteras para VClasificacion que minimice el valor de la inercia intraclases W(P) y que represente de manera computacional la partición P buscada. Por lo anterior, en la implementación se entiende como una solución factible del problema a cada combinación posible tomada por VClasificacion. Los algoritmos diseñados parten de una solución inicial generada de manera aleatoria. Esto es, una combinación dada sobre VClasificacion, en la que cada entrada de dicho vector es seleccionada de manera aleatoria del conjunto {1,2,...,K}.
En el presente estudio se analizan y comparan dos variantes del algoritmo de SS. Dichas variantes consisten en dos metodologías alternativas para la construcción de los vecinos en el algoritmo de SS (refiérase a la línea 7 del Algoritmo 1). La primera de ellas, que se denotará SS-T, representa la metodología clásica de construcción de vecinos mediante las transferencias de objetos entre las clases. En efecto, se entiende como vecino de la solución factible presente en una determinada iteración del algoritmo (SolActual) a otra clasificación, denotada Vecino, generada al cambiar la entrada ck de SolActual a un valor cj, respetando las condiciones cj ∈ {1,2,...,K}, cj ≠ ck De la definición de VClasificacion se nota que esta forma de generar un vecino corresponde a la transferencia del individuo xi de X de la clase i a la clase j.
Para efectos de mejorar el rendimiento del algoritmo SS-T, en términos de los tiempos de ejecución, se utilizaron las fórmulas de actualización que se enuncian y demuestran en Trejos et al. (2014), que indican la forma en la que varían los centros de gravedad y la inercia intraclases, al realizar la transferencia de un objeto de una clase a otra. En este sentido, al hacer la transferencia de x de la clase Cr a la clase Cl , los centros de gravedad se modifican de la siguiente manera:
donde px es el peso del individuo x. Además, la inercia intraclases presenta la variación
Por otra parte, la segunda metodología consiste en generar un vecino mediante el movimiento del centroide de una de las clases que conforman la partición generada en SolActual. En este algoritmo, que se denotará SS-CG, cada solución factible de la forma (c1 , c2 ,..., cn) del problema de optimización tratado tiene asociada la estructura (g1 , g2 ,..., gK) , que corresponde a la matriz de centros de gravedad de la partición P = {C1 , C2 ,..., CK} y relativa a dicha solución factible. De tal manera que gl representa el centro de gravedad de la clase Cl , para l ∈ {1,2 ,...,K} y, en caso de que se asuman todos los individuos en X con el mismo peso 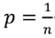 , se define como
, se define como 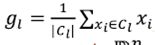 . Así, los centros de gravedad, al igual que los individuos xi , corresponden a vectores de
. Así, los centros de gravedad, al igual que los individuos xi , corresponden a vectores de 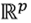 y, por ende, tienen la forma
g
l
= (g
l1
, g
l2
,..., g
lp
)
, para
l
∈ {1,2
,...,K
). A partir de lo anterior, en el algoritmo SS-CG se siguen los siguientes pasos para la construcción de un vecino:
y, por ende, tienen la forma
g
l
= (g
l1
, g
l2
,..., g
lp
)
, para
l
∈ {1,2
,...,K
). A partir de lo anterior, en el algoritmo SS-CG se siguen los siguientes pasos para la construcción de un vecino:
De manera aleatoria se selecciona cuál de los K centroides (centros de gravedad artificiales) relativos a la solución actual será el que se moverá de posición.
De las p posiciones del centroide seleccionado, se escoge aleatoriamente la posición que se variará.
Si se ha seleccionado el centroide l, con l ∈ {1,2
,...,K
}, y la posición
r
, con
r
∈ {1,2
,...,p
}, entonces la posición (
l,r
) de dicho vector se actualiza para generar el nuevo centroide asociado a la clase l del vecino, como
g
*
lr
=g
lr
+ 2 · σ
r
o
g
*
lr
=
g
lr
-2 · σ
r
. Esto es, se suma o resta (bajo una probabilidad) el tamaño de paso 2 · σ
r
, donde σ
r
denota la desviación estándar de los valores que toman los n individuos de X en la variable número
r
. El movimiento realizado siempre respeta las condiciones
g
lr
± ∆
r
≥ mín {x
1r
,..., x
nr
} y
g
lr
± ∆
r
≤ máx {x
1r
,..., x
nr
}. Es decir, se restringe el que los movimientos en la dimensión
r
se realicen entre el valor máximo y el valor mínimo que toman los individuos por clasificar en la variable r. Esta estrategia lo que hace es delimitar el espacio de búsqueda, que en un principio es 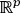 , al hiperrectángulo dado por el producto de intervalos
, al hiperrectángulo dado por el producto de intervalos
Teniendo actualizada la matriz de centroides, debido al movimiento generado en una única dimensión de uno de sus centroides, se recalculan las entradas de VClasificacion. Esto es, se reasignan los n individuos de X al centroide más cercano, para generar nuevamente la partición que será representada computacionalmente en VClasificacion. En este punto culmina la generación del vecino para este algoritmo.
En ambos algoritmos se utilizó como complemento la técnica de k- medias, la cual corresponde a un algoritmo de búsqueda local que en términos globales consta de tres etapas (Trejos et al., 2014):
Se recorren secuencialmente los n individuos de X y cada uno de ellos se asigna a la clase más cercana (en el contexto del artículo se entiende como la menor distancia en el sentido euclídeo). Esto es, el individuo xi se asigna a la clase Cr , si el centro de gravedad gr de dicha clase satisface que el valor de ||xi -gr || sea mínimo, para r ∈ {1,2,..., K}.
Posteriormente al proceso de transferencias, se calculan de nuevo los centros de gravedad de las clases.
Se repiten los dos primeros pasos hasta que haya convergencia del algoritmo.
Se utilizó el parámetro KM para controlar la aplicación respectiva de esta técnica. El Algoritmo 2 muestra la adaptación realizada en la investigación al algoritmo de SS para estudiar el problema de particionamiento con las dos variantes de generación de vecinos ya explicadas. En la línea 12 se indica el punto en el que se construye el vecino. Si se hace hace referencia al algoritmo SS-T, este proceso se ejecuta mediante la transferencia de un individuo de una clase a otra. Por su parte, en el caso de SS-CG se realiza mediante el movimiento de un centroide, tal y como se explicó previamente. En la línea 13 se indica la condición bajo la cual se desarrolla la aplicación del algoritmo de k-medias. En la línea 32 se muestra el uso de la fórmula geométrica como modelo de enfriamiento. Como estrategia de aceleración se determinó abortar el bucle PARA asociado a un valor de la temperatura, si ha transcurrido más del 50% de iteraciones en ese bucle, sin que se haya presentado una mejora de la mejor solución que el algoritmo ha encontrado hasta ese momento (ver líneas 28 y 29). Por último, con el objetivo de favorecer la exploración del espacio de soluciones factibles y evadir la optimalidad local, se implementó la idea de reiniciar aleatoriamente SolActual si se han realizado 10 enfriamientos consecutivos en los que el algoritmo no ha reportado ninguna mejora (refiérase a las líneas 8 y 9).
Análisis del parámetro α
Es bien conocido la alta sensibilidad que tienen las heurísticas, y los algoritmos en general, ante la selección que se realice para los parámetros propios de cada algoritmo. Por ejemplo, el parámetro α que se utiliza para controlar el modelo geométrico de enfriamiento en sobrecalentamiento simulado influye en el rendimiento de este algoritmo para poder encontrar buenas soluciones.
ALGORITMO 2 SS en particionamiento
Entrada: Parámetros Tƒ , M, LongCade, α (para decrecer la temperatura) y KM.
1: SolActual ← Solución inicial generada aleatoriamente.
2: TempActual ← Tinicial
3: Iteraciones ← 0
4: ContadorSinMejoras ← 0
5: MIENTRAS TempActual >Tƒ y Iteraciones < M HACER 6: Iteraciones ← Iteraciones +1.
7: ContadorSinMejoras ← ContadorSinMejoras +1 8: SI ContadorSinMejoras mod 10 = 0 ENTONCES 9: Reiniciar la solución actual.
10: FIN SI
11: PARA j ← 1 HASTA LongCade HACER
12: Vecino ← Generar vecino de SolActual
13: SI j mod KM = 0 ENTONCES 14: Vecino.AplicarKMedias.
15: FIN SI
16: ∆E ← Vecino.Inercia - SolActual.inercia
17: SI ∆E ≤ 0 ENTONCES 18: SolActual ← Vecino.
19: SI SolActual.inercia < MejorSolucion.inercia ENTONCES 20: MejorSolucion ← SolActual.
21: ContadorSinMejoras ← 0
22: FIN SI
23: SI NO
25: SolActual ← Vecino.
26: FIN SI
27: FIN SI
28: SI ContadorSinMejoras > 0,5 · LongCade ENTONCES 29: Abortar cadena actual (abortar el PARA).
30: FIN SI
31: FIN PARA
32: TempActual ← α ⋅ TempActual.
33: FIN MIENTRAS
34: Retornar: MejorSolucion.
Si se escoge un valor muy cercano a la unidad, como, por ejemplo, α = 0,999, entonces el sistema se enfriará de manera muy lenta, generando, en términos computacionales, tiempos de ejecución muy elevados. Recíprocamente, si se selecciona, por ejemplo, α = 0,5, entonces el sistema se enfría tan rápidamente que el algoritmo no tiene la oportunidad de explorar adecuadamente el espacio de soluciones factibles en búsqueda de buenas soluciones. Como consecuencia, se hace necesario buscar un equilibrio en los valores asignados a cada parámetro.
Para soporte del proceso se generaron experimentalmente dos tablas de datos, que se denominarán T105 ( n = 105, que es la cantidad de objetos por clasificar) y T525 ( n = 525), siguiendo una distribución normal de números pseudoaleatorios. El agrupamiento se desarrolló, en cada tabla, considerando K = 7 (número de clases), tal que seis clases tienen varianza σ2 = 1 y la clase restante tiene varianza σ2 = 3. Además, T105 fue construida con una clase “grande” de cardinalidad 51 y las seis clases restantes con cardinalidad 9. De manera similar, T525 tiene una clase de tamaño 261 y las seis restantes de 44 objetos. Dado que el diseño es controlado, se pudo determinar a priori el valor de W (P) (inercia intraclases) que representa, en cada caso, el agrupamiento de referencia en 7 clases. Esto con el objetivo de controlar la respuesta del algoritmo ante tablas experimentales. El cuadro 2 muestra los valores de referencia de W (P) para T105 y T525.
Posteriormente, se realizó un proceso de calibración del parámetro α. Para ello se tomó como base lo expuesto en Talbi (2009) y Trejos y Murillo (2004), en cuanto a que valores de α cercanos a la unidad generan mejores resultados. Por lo tanto, en el análisis se consideró variar α desde 0,9 hasta 0,99 a paso de 0,1, habiendo analizado entonces 10 posibles valores para este parámetro. Después del análisis se decidió tomar α = 0,99 para la comparación de los algoritmos.
Datos utilizados y resultados
Para la prueba de los algoritmos se utilizaron ocho tablas extraídas de repositorios internacionales disponibles en http://archive.ics.uci.edu/ml/ (University of California) y http://cs.joensuu.fi/sipu/ datasets/ (University of Eastern Finland), las cuales se describen a continuación.
Tabla de los Iris de Fisher
Tabla de 150 objetos (150 flores de tres especies: Iris setosa, Iris versicolor e Iris virginica), que son caracterizadas en cuatro variables cuantitativas: largo y ancho del sépalo y largo y ancho del pétalo.
Tablas de Wine Quality
Constan de dos tablas sobre las variantes roja y blanca del vinho verde (vino producido en Minho, zona al noroeste de Portugal). La primera, winequality-red (WQ-red), consta de 1599 muestras de vino rojo caracterizadas en 11 atributos cuantitativos. Por su parte, la tabla winequality-white (WQ-white) se compone de 4898 muestras de vino blanco, descritas en esos mismos atributos.
Tabla Glass
Está compuesta por 214 instancias, que corresponden a muestras de 6 clases de vidrios caracterizadas en 9 atributos cuantitativos (cantidad presente en cada muestra de Mg, K, Ca, Ba, entre otros elementos químicos).
Tablas de S-Sets
Corresponde a un conjunto de cuatro tablas de datos sintéticos, denominadas S1, S2, S3 y S4. Cada tabla tiene 5000 individuos y 15 clases. La diferencia entre ellas es el grado de solapamiento entre las clases.
El cuadro 3 resume las principales características de los conjuntos de datos anteriores. En particular, se indica el número n de individuos, el número p de variables, el número K de clases y el valor W (P) de mínima inercia intraclases que se logró determinar para cada tabla, y que se tomó como valor de referencia para calcular los porcentajes de atracción.
Cuadro 3 Características de las tablas de datos.
| Tabla | n | p | K | W(P) referencia |
|---|---|---|---|---|
| Iris | 150 | 4 | 3 | 0,5214 |
| WQ-red | 1599 | 11 | 3 | 247,2075 |
| WQ-white | 4898 | 11 | 3 | 560,4186 |
| Glass | 214 | 9 | 6 | 1,5704 |
| S1 | 5000 | 2 | 15 | 1783523123,37346 |
| S2 | 5000 | 2 | 15 | 2655821898,14594 |
| S3 | 5000 | 2 | 15 | 3377914369,87141 |
| S4 | 5000 | 2 | 15 | 3140628447,25202 |
El cuadro 4 muestra los resultados obtenidos al aplicar los algoritmos de SS a las tablas de datos. En ambos casos se consideró un número máximo de iteraciones M = 400, KM = 5 y T ƒ = 0,001. En cada caso, los porcentajes indicados representan la proporción de veces que el algoritmo atinó el valor de referencia para la inercia intraclases, de un total de 500 ejecuciones. En cada corrida se registró el tiempo en segundos, y en el cuadro 4 se reportan los tiempos promedios para cada caso. Además, también se muestra el valor del parámetro LongCade, que se utilizó en las diferentes corridas.
Finalmente, el equipo utilizado para las pruebas corresponde a una computadora de escritorio HP Compaq Elite 8300 MT, con procesador Intel(R) Core(TM) i7-3770 CPU @3.40 GHz, con memoria RAM instalada de 8 GB.
Conclusiones
En función de los resultados expuestos en el cuadro 4, se muestra un claro dominio del algoritmo SS-T sobre el algoritmo SS-CG. Excepto para la tabla WQ-red, los tiempos promedio en todos los demás casos son menores para SS-T y los porcentajes de atracción son mayores o iguales que los generados por SS-CG.
Por otra parte, con base en el experimento se reforzó la intuición de que el solapamiento entre las clases es un factor que incide significativamente para poder determinar la clasificación óptima de un conjunto de datos. En particular, la tabla S4 tiene un alto grado de intersección entre las clases y, por ende, resultó ser la tabla más complicada de analizar.
Además, otro aspecto relacionado con la complejidad de los datos, que se pudo ver como parte del análisis, es que el número K de clases tiene mayor influencia en el hecho de que una tabla de datos sea difícil de analizar, en comparación con otras características como el número n de individuos y el número p de variables. Por ejemplo, se pueden comparar las tablas WQ-white y S1, las cuales tienen casi el mismo número de individuos, y además WQ-white tiene 11 variables cuantitativas, en contraposición a S1 que son solo 2. Sin embargo, la diferencia en la cantidad de clases es lo que provoca que para S1 se genere un aumento drástico en el tiempo promedio y una disminución en la calidad del rendimiento de los algoritmos, medido en términos de los porcentajes de atracción.
Cuadro 4 Tiempos promedio en segundos y porcentajes de atracción de los algoritmos.
| Tabla | SS-T | SS-CG | ||||
|---|---|---|---|---|---|---|
| % | Tiempo en segundos | LongCade | % | Tiempo en segundos | LongCade | |
| T105 | 100% | 0,078 | 30 | 100% | 0,488 | 100 |
| T525 | 92% | 3,181 | 300 | 11% | 3,507 | 150 |
| Iris | 100% | 0,017 | 10 | 100% | 0,168 | 60 |
| WQ-red | 93% | 3,558 | 100 | 100% | 1,924 | 30 |
| WQ-white | 100% | 1,778 | 10 | 98% | 5,758 | 30 |
| Glass | 100% | 0,071 | 10 | 100% | 0,498 | 45 |
| S1 | 78% | 22,159 | 40 | 0% | - | - |
| S2 | 100% | 10,841 | 40 | 0% | - | - |
| S3 | 93% | 7,998 | 40 | 0% | - | - |
| S4 | 32% | 37,328 | 300 | 0% | - | - |