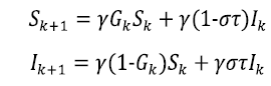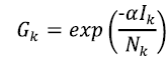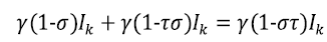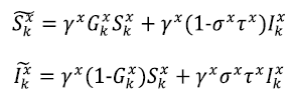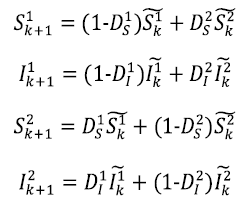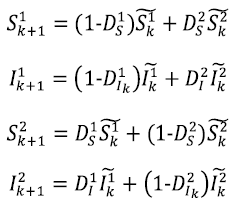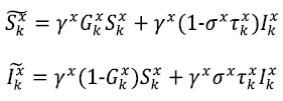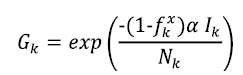Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
Introducción
La simulación a través de modelos matemáticos permite explorar el impacto de la aplicación de una o varias medidas de control en la dinámica de la transmisión de enfermedades infecciosas, proporcionando información valiosa para la toma de decisiones con el objetivo de controlarlas o erradicarlas.
Según Welte et al. (2010), hay dos maneras de lograr la eficacia general de un programa para controlar el brote de una enfermedad: un análisis retrospectivo de datos y la simulación utilizando modelos matemáticos. Diversas investigaciones demuestran que el uso de modelos matemáticos para describir la dinámica de transmisión de las enfermedades infecciosas son una herramienta necesaria para realizar un buen análisis de la relación costo-eficacia en la aplicación de medidas de control en la propagación de una enfermedad (Kretzschmar & Wallinga, 2010 y González et al., 2011).
La historia y eventos recientes demuestran que las enfermedades contagiosas constituyen una amenaza para la población mundial. Los países están cada vez más interconectados gracias a los modernos sistemas de transporte. Surgen enfermedades nuevas o reaparecen otras viejas que pueden atravesar fronteras y propagarse rápidamente por varias poblaciones. Así lo demostró la pandemia de gripe AH1N1, cuyo brote se detectó en abril de 2009 en México y al cabo de un mes se había extendido a 24 países (WHO, 2009). De estas y otras experiencias se puede concluir que un factor determinante en la propagación de una enfermedad es la movilidad intensa y rápida de la población. Es por esa razón que para este análisis se decidió usar un modelo discreto SIS metapoblacional. Conviene utilizar modelos en tiempo discreto, ya que los datos reales son dados de manera discreta y eso permite comparar los resultados (Brauer et al., 2014).
La propagación de enfermedades infecciosas y sus medidas de control han sido objeto de diversos estudios, la mayoría lo han hecho en modelos para la dinámica en una población. El objetivo de este trabajo es utilizar modelos metapoblacionales, estos modelos permiten conocer la influencia de los flujos migratorios en la propagación de una enfermedad y comprender las características de la propagación en subpoblaciones, cada una con su propia dinámica pero conectadas por el movimiento de personas entre sí.
Modelo SIS metapoblacional
Los modelos SIS (susceptible-infectado-susceptible) son modelos epidemiológicos de compartimentos, que se definen a partir de clases y subclases. Como indican Brauer et al. (2014), las tasas de transición entre las clases para estos modelos se estiman a partir del conocimiento cualitativo y evidente en la historia natural de la enfermedad.
Para este estudio se eligió un modelo discreto metapoblacional de transmisión de enfermedades SIS. En este tipo de modelos, la población se divide en dos grupos de personas: las que han sido infectadas por la enfermedad y son infecciosas y las que son susceptibles de ser infectadas por la enfermedad.
Los modelos SIS se usan para enfermedades en las que no hay inmunidad, pues, una vez que las personas infectadas se recuperan, pasan a ser de nuevo susceptibles. Por lo tanto, la progresión de la enfermedad desde el punto de vista de un individuo es susceptible-infectadosusceptible.
El modelo SIS utilizado en este caso es una variante del planteado en Castillo-Chavez y Yakubu (2002) y además se ha considerado la aplicación de un tratamiento (Alpízar, 2012). En este modelo, la población se dividió en dos parches que, según Arino y Driessche (2006), pueden representar ciudades, regiones geográficas o comunidades que están interconectadas por los procesos de inmigración y emigración. Se trabajó con el siguiente modelo SIS:
donde
es la probabilidad de seguir siendo susceptible en el tiempo
k
a
k+1
y α es una constante que pondera el papel de la prevalencia de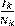 
en la transmisión de la enfermedad en el momento
k
, I
k
son los infectados en el tiempo
k
y N
k
es la población total en el tiempo
k
.
Supongamos que la población es constante N k =S k +I k en cada momento k , es decir, no se considera la dinámica demográfica de la población. Por lo tanto, el cambio en el grupo de personas infectadas siempre es igual al cambio en el grupo de susceptibles.
Si γ es la probabilidad de sobrevivir a la enfermedad, entonces, γG k S k es el grupo de personas que siguen siendo susceptibles en k+1 y γ(1-G k )S k es la cantidad de personas que dejan de ser susceptibles y pasan a pertenecer al grupo de infectados.
Si (1-σ) es la probabilidad de recuperación natural (sin tratamiento) y (1-τ) es la probabilidad de recuperación con tratamiento efectivo, entonces γστI k es el grupo de personas que siguen siendo infectadas en el tiempo k+1 y γ (1−σ) I k son los infectados que pasan a ser susceptibles por recuperación natural y γ(1-τσ) es la cantidad de personas que no se recuperaron naturalmente pero sí por la aplicación del tratamiento; así, los infectados que pasan a ser susceptibles en k+1 están dados por
Ahora consideremos una población con dos parches acoplados en donde la dinámica de cada uno de ellos está descrita por el modelo SIS anterior. Si denotamos con
x
cada parche, entonces
x
∈{1,2}. Sea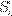 
el grupo de susceptibles y I
x
k
el grupo de infectados en el tiempo
k
y del parche
x
. En el parche
x
las personas sobreviven con probabilidad γ
x
, mientras que los infectados se recuperan naturalmente con probabilidad (1−σ
x
). Los susceptibles empiezan a ser infectados con probabilidad 1-G
k
x
. Supongamos que una fracción (1−τ
x
) de los individuos infectados que no se recuperó de forma natural es tratada y vuelve a la clase susceptible. En primer lugar, las ecuaciones que describen la dinámica de la enfermedad dentro de cada parche están dadas por
Ahora, se considera la dispersión de individuos entre los parches: D s y D I son las fracciones de individuos susceptibles e infectados de cada población que se intercambian en cada paso del tiempo, se les asignan superíndices para distinguir las fracciones asociadas a cada parche. Así, el sistema SIS para una metapoblación con dos parches se define como sigue:
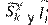representa la dinámica local de cada parche.
El control de una enfermedad infecciosa se hace mediante la intervención directa o la reducción de la susceptibilidad de una población. Al analizar el modelo anterior, observamos que se puede ejercer control sobre varios parámetros que representen la aplicación de estrategias para un control óptimo de la enfermedad. Se puede controlar el flujo de personas infectadas entre las dos poblaciones, capturado por los parámetros D 1 y I D 2 I . Se puede tomar como variable de control τ x , donde 1-τ x es la proporción de la población a la que se le aplicará algún tipo de tratamiento en el parche x . El impacto de las medidas de intervención directa, como el distanciamiento social, produce cambios en el valor de α. Más precisamente, se define α x = (1-ƒ x )α como el parámetro de transmisión dentro del grupo x después de que las estrategias de intervención se han aplicado para reducir la transmisión, que se mide por el parámetro ƒ x . Después de introducir estos controles, las ecuaciones para cada parche son:
donde la dinámica local de cada parche estaría dada por el sistema
Interesa estudiar los efectos de la aplicación de algunas medidas de control en la propagación de la enfermedad. Particularmente, se consideran tres medidas:
Aplicar tratamiento: sea un programa de vacunación o un determinado fármaco. Si hay recursos suficientes, todas las personas infectadas pueden ser tratadas, de lo contrario, la finalidad del tratamiento es reducir al mínimo el total de infectados (Rowthorn et al., 2009).
En ausencia de un tratamiento o vacuna, se puede utilizar el aislamiento de los individuos diagnosticados -al que se le llamará distanciamiento social- para controlar la propagación de la enfermedad. En el distanciamiento social, la persona enferma se separa de las que no están enfermas y puede ser atendida en un centro médico o en su hogar. Algunas medidas potencialmente eficaces, según WHO (2005), son las restricciones de las actividades sociales, por ejemplo, la cancelación de eventos públicos masivos (conciertos, deportivos, cine, obras de teatro, festivales), el cierre temporal de instalaciones de recreación (restaurantes, piscinas, clubes sociales, gimnasios), cierre de oficinas, escuelas y sistemas de transporte público.
Restricciones sobre la dispersión: la imposición de controles sobre los parámetros que regulan el flujo migratorio entre los parches de una metapoblación, limitando la tasa de dispersión de individuos infectados, lo que sería equivalente a controles de frontera entre los parches (Rowthorn et al., 2009). Aunque tal vez en la realidad no sea posible restringir en su totalidad el flujo de personas infectadas entre los parches, sí es posible aplicar algún tipo de limitación. Para enfrentar el impacto de la dispersión en el desarrollo de la enfermedad se puede establecer mayor vigilancia en los puestos fronterizos con el fin de detectar individuos infectados, adoptar medidas tales como la inspección visual, aplicación de cuestionarios, medición de la temperatura (utilizando arcos térmicos), uso de imágenes térmicas y pruebas de laboratorio rápidas, entre otros métodos de inspección (Ali & Keil, 2007).
En resumen, se ejercerá control sobre los parámetros 1-τ x k , ƒ x k y D x Ik , en cada uno de los parches, que representan: la proporción de la población a la que se le aplicará tratamiento médico, la proporción de la población a la que se le aplicará distanciamiento social y proporción de individuos infectados que se dejarán pasar de un parche a otro, respectivamente.
Resultados numéricos
Para las simulaciones se trabajó con las siguientes cotas para los controles: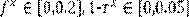 
(tomado de González et al., 2011)
Se asignó arbitrariamente una cota inferior para D considerando que lograr una restricción I completa en el flujo de personas de un parche a otro es realmente imposible. Además, se consideró D x s como el mayor valor que puede tomar D x I .
El valor para los demás parámetros del modelo se presenta en el cuadro 1.
Consideremos una las siguientes poblaciones iniciales para la clase de susceptibles
S 1 1 =S 2 1 =1000, además I 1 1 =100 y I 2 1 =0 suponiendo que se detecta el brote de la enfermedad en el parche 1 y se quiere ejercer control para evitar que se inicie un brote en el parche 2.
Cuadro 1 Valor de los parámetros del modelo SIS metapoblac
| Parámetro | Valor | Definición | Fuente |
|---|---|---|---|
| T | 60 | Días transcurridos | |
| γ | 1 | Probabilidad de sobrevivir a la enfermedad | |
| β | 1.94 | Tasa de transmisión | González et al., 2011 |
| 1-σ x | 1 7 | Fracción de recuperados naturalmente | González et al., 2011 |
| Dx s | 0.03 | Fracción de susceptibles que emigran del parche x. | Herrera-Valdez et al., 2011 |
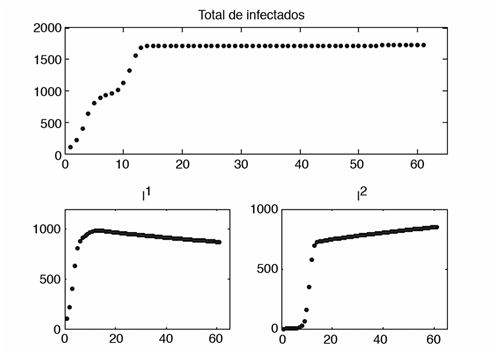
Lo que se quiere saber en la mayoría de los casos es la cantidad de personas infectadas que habrá en un período determinado de tiempo, suponiendo que no se aplica ninguna medida de control. Los resultados se muestran en la figura 1, donde se observa que en menos de 20 días se tienen más de 500 personas infectadas en el parche 2, aunque al finalizar los 60 días el total de infectados es mayor en la población en la que se inició la enfermedad.
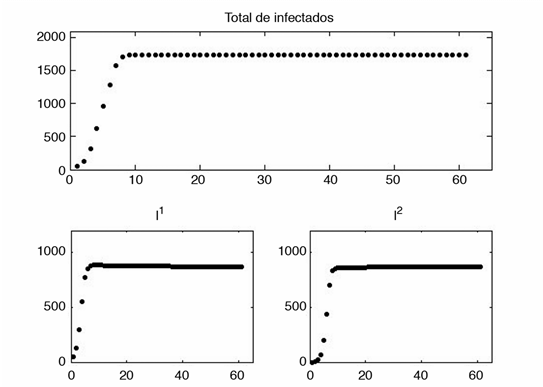
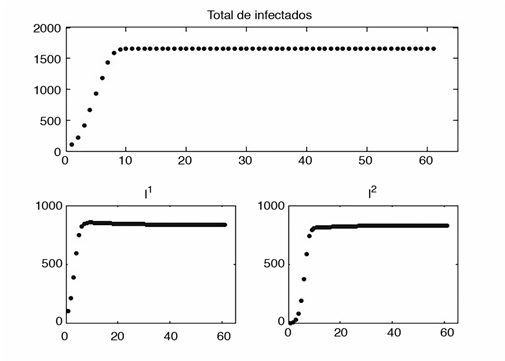
Supongamos que se aplique el máximo control para ƒ x y 1-τ x , es decir, se aplicará distanciamiento social al 20% de la población y el tratamiento al 5% de la población. Para los valores anteriores consideremos dos casos, primero, que no se aplica ninguna restricción en el flujo de personas (figura 2), y segundo, que se aplica la máxima restricción, sin lograr la restricción total, para el flujo de personas (figura 3). Comparando estos dos casos, se puede observar que, aunque el número de infectados es similar, la aplicación de restricciones retrasa el máximo de enfermos al día 15; mientras que si no se aplica restricción alguna, el máximo se alcanza en el día 10. Además, aplicar alguna medida de control que regule el paso de personas de una población a otra produce una pequeña segunda ola de infectados.
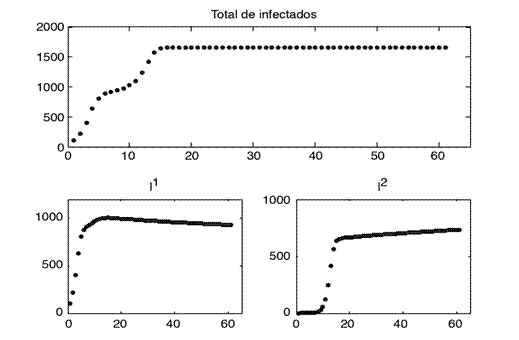
En la figura 4 se ha considerado el caso de aplicar el máximo para las tres medidas de control en la población 1 y en la población 2 solamente la restricción máxima en el flujo de personas, es decir, no se ha aplicado distanciamiento social ni tratamiento en la población 2. La dinámica es muy similar al caso de la figura 3, pero se nota un aumento en el total de infectados de la población 2.
Hay que recordar que, aunque se está aplicando máxima restricción en el flujo de personas, se consideró una cota inferior diferente de cero para el mínimo en el flujo, dado que en la realidad es imposible la restricción total.
Conclusiones
Se ha demostrado una vez más que las simulaciones con modelos matématicos proporcionan información útil sobre las medidas de control que se deben tomar para lograr controlar una enfermedad a tiempo y evitar consecuencias desastrosas. Esta información pueden usarla los profesionales en salud para la planeación de programas de salud pública. Además, el modelo se puede utilizar para la evaluación de programas de control, trabajando otras simulaciones, constituyendo una opción económica y efectiva.
En los resultados obtenidos se hace evidente que el propósito principal de las restricciones en el flujo de personas infectadas es retrasar la propagación de la enfermedad hasta que se puedan desarrollar y aplicar otras intervenciones, o bien se pueden combinar con otras medidas de control (Herrera-Valdez et al., 2011). Ese retraso puede ser de gran ayuda en el desarrollo de la conciencia pública, la aplicación del distanciamiento social y la preparación de los centros de atención y de las medidades de prevención. Todo tiempo adicional que permita prepararse es una oportunidad para reducir los efectos potenciales de varias enfermedades.
