Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.59 n.4 San José Dec. 2011
Estudio del crecimiento de Prioria copaifera (Caesalpinaceae) mediante técnicas dendrocronológicas
Jorge Andrés Giraldo Jiménez1 & Jorge Ignacio del Valle Arango1
1. Grupo de Bosques y Cambio Climático, Universidad Nacional de Colombia Sede Medellín, Departamento de Ciencias Forestales. Apartado Aéreo No 568, Medellín, Colombia; jagiral1@bt.unal.edu.co, jidvalle@unal.edu.coAbstract
A growth study of Prioria copaifera (Caesalpinaceae) using dendrochronological techniques. The Cativo (Prioria copaifera) forms very homogeneous forests called cativales in the flooded plains of some rivers from Costa Rica to Colombia. For over 70 years Cativo has been the main base of the timber industry in the Colombian Darien area. Because of high productivity and high-dominance of Cativo trees, they represent one of the most prone tropical forests for sustainable forest management. The objective of this research is to model diameter and timber volume growth and growth rates (absolute, mean and relative) of Cativo as a function of age, using tree ring data derived from dendrochronologycal techniques. We evaluated the annual nature of the tree rings by radiocarbon analysis and crossdating techniques. Besides, the diameter and volume growth was modeled using von Bertalanffy’s model. As of our results, we estimated the life span of Cativo in 614 years as the time required to reach 99% of the asymptotic diameter. By the mean value we have found that the mean rate of diameter growth is 0.31cm/y. The species requires 90 years to reach 40cm in diameter, the regulated cut diameter in Colombia. We find that Cativo reaches maximum current annual increment (ICA) in diameter at 40 years and in volume at 90 years with rates of 0.5cm/y and 0.032m3/y per tree, respectively. The maximum diameter mean annual increments (MAI) are achieved at 80 years and for the volume at 140 year, with growth rates of 0.45cm/y and 0.018m3/y per tree, respectively. The generated information is useful for the sustainable management of Cativo forests. Rev. Biol. Trop. 59 (4): 1813-1831. Epub 2011 December 01.
Key words: annual rings, tropical trees, flooded forest, dendrochronology, Prioria copaifera, radiocarbon dating, life span.
Resumen
El cativo (Prioria copaifera G.) forma bosques dominados por la especie llamados cativales. Durante más de 70 años el cativo ha sido la base principal de la industria maderera en el Darién colombiano, siendo, por su alta productividad y dominancia uno de los bosques tropicales más fáciles de ordenar sosteniblemente. El propósito de esta investigación es modelar el crecimiento del diámetro y el volumen del cativo en función de la edad así como las tasas instantáneas, medias y relativas, empleando anillos de crecimiento. La anualidad de los anillos se demostró usando el efecto de las bombas nucleares y mediante cofechado. Con base en los anillos de crecimiento radiales se modelo el crecimiento del diámetro y del volumen. Esta especie alcanza 40cm de diámetro en 90 años y presenta crecimiento medio de 0.31cm/año. El lapso vital de la especie es de aproximadamente 614 años. El incremento corriente anual máximo del volumen a los 90 años es 0.033m3/año, e iguala al incremento medio a los 145 años con 0.018m3/año. La tasa media de crecimiento absoluta es 0.021m3/año. Los resultados aquí obtenidos sirven como base técnica para el manejo sostenible de los cativales.
Palabras clave: anillos anuales, árboles tropicales, bosques inundables, dendrocronología, datación por radiocarbono, lapso vital.
Los gobiernos buscan encontrar equilibrio entre el desarrollo económico, social y ambiental. A esta armonía se le denomina sostenibilidad, cuya finalidad es satisfacer las necesidades de la sociedad sobre la base del manejo sostenible de los recursos naturales; esto es especialmente cierto en cuanto a los servicios y productos que aportan los bosques y su biodiversidad (Davey et al. 2003). Existen dos posiciones contrastantes muy marcadas acerca del manejo de los bosques y su biodiversidad. Una de ellas es la protección estricta, en la cual, a veces como excepción, se permite la investigación de la biodiversidad. La otra línea, aún por construir en gran parte de los países tropicales, se caracteriza por permitir un manejo más flexible en virtud del cual se extrae productos en forma sostenible de los bosques naturales o se emplean sus servicios ambientales sin afectar la base natural de generación de esos bienes o servicios.
El manejo sostenible de la producción maderable de los bosques tropicales es un asunto complejo que depende tanto de factores económicos, sociales y políticos como técnicos. En cuanto a estos últimos, se requiere al menos información acerca de: existencias maderables de las especies que se someterán al manejo, tasas de regeneración y mortalidad e información sobre tasas de crecimiento y relaciones entre las dimensiones de los árboles y su edad (Schöngart 2008).
En Colombia no existe aún ordenación forestal sostenible de los bosques naturales a pesar de que cubren cerca del 50% de su territorio continental (más de 50 millones de hectáreas). Un tipo de bosque especialmente importante en Colombia es el catival. Este bosque se desarrolla en las llanuras periódicamente inundables de los ríos Atrato y León, departamentos Chocó y Antioquia, que vierten sus aguas al golfo de Urabá, Darién colombiano. Los cativales sobresalen por conformar comunidades de varias especies de árboles entre las cuales el cativo (P. copaifera Grisebac) es dominante. Allí se encuentran los cativales más extensos existentes en América, su área original cubría 363 000ha (González et al. 1991). Durante más de 70 años el cativo ha sido la base principal de la industria maderera en el bajo Atrato. Los cativales se clasifican de acuerdo con la duración del período de inundación, en tipo A1, el de mayor duración de la inundación (más de séis meses), catival A2, permanece inundado entre tres y séis meses y catival A3 permanece inundado menos de tres meses al año (González et al. 1991). La dominancia del cativo decrece desde el tipo A1 al A3.
El estudio del crecimiento es de gran importancia para ecólogos y silvicultores por cuanto permite conocer aspectos de la dinámica de los bosques y estimar los turnos, ciclos de corta sostenibles y tamaño de la cosecha de un bosque o rodal. El crecimiento y la edad de los árboles tropicales usualmente se estudia con la información obtenida de parcelas permanentes y el ajuste de esos datos a ecuaciones diferenciales y simulaciones complejas (Del Valle 1979, 1986, 2002. 2003, Lieberman & Lieberman 1985, Lieberman et al. 1985, Condit et al. 1993, 1995b, González 1995, Clark & Clark 1999, Baker 2003, Grauel 2004, Bullock et al. 2004). Hoy son crecientes las investigaciones que emplean los anillos de crecimiento o bien, la combinación de anillos de crecimiento y radiocarbono (Worbes 1985, Worbes & Junk 1989, Worbes et al. 2003, Fichtler et al. 2003, Soliz 2010).
El cativo ha sido estudiado por algunos investigadores con el fin de estimar el crecimiento del diámetro en función de la edad usando información proveniente de parcelas permanentes (Del Valle 1979, 1986, Linares 1987, 1988, González et al. 1991, Condit et al. 1993, 1995b, González 1995, Grauel 2004). No obstante, debido al empleo de parcelas permanentes los datos obtenidos solo representan pequeñas fracciones de la vida de los árboles. La dendrocronología estudia los anillos de crecimiento de los árboles para extraer la señal ambiental contenida en ellos, pero también para estudiar su crecimiento (Roig 2000). Los anillos de crecimiento se definen como bandas de células producidas por el cámbium vascular en un período de tiempo (Kaennel & Schweingruber 1995). En los trópicos la formación de anillos se atribuye a períodos alternos de sequía y lluvia o en árboles que crecen sobre llanuras inundables, a las condiciones hipóxicas durante el período de inundación (Mariaux 1967, Worbes 1995, 1999, 2002, Schöngart et al. 2002, 2004). No obstante, Fichtler et al. (2003), encontraron especies con anillos anuales en La Selva, Costa Rica, un bosque ecuatorial sin meses ecológicamente secos, por cuanto sugieren que los estudios dendrocronológicos se pueden extender a todo el trópico sin excepción. La existencia de los anillos en los árboles pudiera ser entonces de origen genético, aunque las condiciones ambientales pueden influir en la intensidad de sus características. Igual que muchos árboles tropicales el cativo forma anillos de crecimiento visibles a simple vista (Kukachka 1965); McKenzie (1972) demostró su anualidad.
No existe en la literatura publicada antecedentes acerca del estudio del crecimiento de árboles tropicales en Colombia mediante técnicas dendrocronológicas. Aún en todo el trópico estos estudios son escasos. Esta investigación se propone demostrar la frecuencia de formación de los anillos de crecimiento del cativo y modelar su crecimiento en diámetro y volumen empleando anillos de crecimiento.
Materiales y métodos
Área de estudio: Los árboles se muestrearon en un catival A1 en el caño Pedeguita sobre la llanura aluvial del río Atrato que vierte sus aguas al golfo de Urabá, Darién colombiano, 27km al sur-este del la ciudad de Riosucio (7°15’4.40" N-76°58’42.39" O), a pocos metros sobre el nivel del mar. En el momento de la toma de las muestras el catival estaba siendo explotado y, de acuerdo con la información de la empresa Maderas del Darién, no había sido intervenido previamente. El clima es ecuatorial pues no presenta meses ecológicamente secos. La precipitación media anual es de aproximadamente 3 600mm con régimen básicamente unimodal (Eslava 1993). La precipitación supera 100mm en todos los meses alcanzando su máximo en julio con 430mm. La muestra consistió de 11 discos de sendos árboles cortados aproximadamente a la altura del pecho.
Preparación de las muestras: Las secciones transversales se secaron al aire bajo techo y se pulieron con lija de grano grueso (No. 30), disminuyendo gradualmente a grano fino (No. 600). En cada sección transversal se trazaron entre dos y tres radios sobre los cuales se le midieron los anillos y se tomaron fotografías para describir las características anatómicas de los anillos de crecimiento.
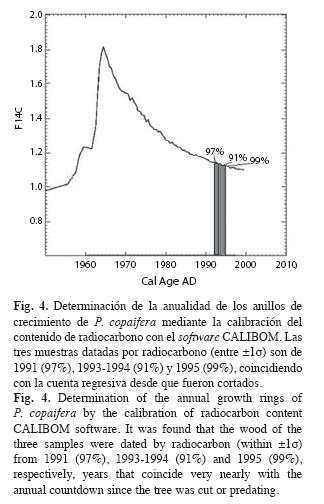
Análisis de radiocarbono: Se empleó el llamado "efecto de las bombas nucleares" en el aumento de la concentración de C14 en el CO2 atmosférico (Worbes & Junk 1989, Worbes 1995) que es un marcador isotópico para datar la fecha de formación de productos orgánicos como la madera posteriores a 1955 (Stuiver et al. 1981, Worbes & Junk 1989). Bajo el supuesto de anualidad de los anillos se predató el año de formación de tres anillos en tres secciones transversales de cativo; esto es, si los árboles se apearon en 2009 y se contaron desde la periferia hacia el centro anatómico del árbol 17 anillos; supuestamente este último anillo se formó en 1991, si fuesen anuales (predatación). A cada anillo se le extrajeron unos 20g de madera con una broca. Las muestras se enviaron al Radioanalytical Laboratory of the Marzeev Institute of Hygiene and Medical Ecology de Kiev, Ucrania. Los análisis de C14 se calibraron con el programa CALIBOM de uso libre en la revista Radiocarbon (Hua & Barbetti 2004, Reimer et al. 2004). Si el año predatado coincide con el que arroja la calibración, es una evidencia muy convincente de la anualidad de los anillos.
Obtención de las series: Se denomina series a los anchos de los anillos medidos a lo largo de un radio. A cada sección transversal se le midieron los anillos siguiendo la dirección de los radios (previamente marcados) en una plataforma Velmex, con precisión de 0.001mm observando los anillos en el monitor mediante una cámara Microcap. Los valores observados se almacenaron con el software Mesure J2X, en formato ".raw".
Cofechado, medición y ajuste de los anillos: Este proceso permite realizar el control de calidad de cada serie eliminando los errores de medición, para ello se usó el software COFECHA (Holmes 1983). El programa detecta anillos faltantes o falsos anillos, así como los anillos que presentan patrones anómalos respecto de la serie maestra (Grissino-Mayer 2001).
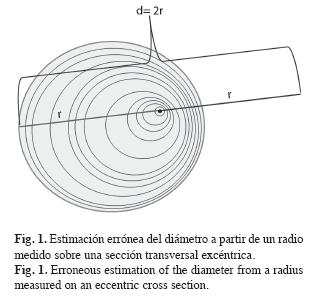
Los anillos de crecimiento medidos se suman uno a uno para así obtener sucesivos radios los cuales se duplican para obtener diámetros. Este procedimiento tiene errores de sobre o subestimación cuando el centro anatómico de una sección transversal no coincide con el centro geométrico correspondiente a un círculo perfecto (Fig. 1). Cuando esto sucede el ancho de los anillos medidos a lo largo de un radio (serie) debe ajustarse antes de hacer estimaciones del diámetro. Para ello cada ancho se ajustó mediante la siguiente fórmula:
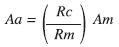
dónde: Aa, ancho ajustado; Rc, radio del círculo perfecto (perímetro de la sección transversal/2П); Rm, longitud del radio sobre el que se midieron los anchos de los anillos; Am, ancho del anillo medido.
Modelación del crecimiento diamétrico: Con los pares de datos, diámetro y edad, se estimó una función de crecimiento no lineal. La información obtenida de las trayectorias tienedos problemas estadísticos: i) los diámetros en función de la edad tienden a ser heterocedásticos por cuanto la varianza se incrementa violando el principio de homogeneidad de la varianza; ii) existe autocorrelación temporal entre el diámetro de un año con el de años anteriores; luego los diámetros no son observaciones independientes. En este estudio se empleó la medida remedial citada por Lema (2003). Primero se calcula el modelo con los diámetros no corregidos, luego de verificar la presencia de heterocedasticidad, se calcula una regresión simple que busca relacionar los residuales estudentizados elevados al cuadrado (ei 2), y la variable a predecir en este caso el diámetro (D),
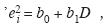
con lo que la ponderación queda Wi = 1/êi2 para cada Di, donde cada Wi es la ponderación incluida en el modelo para remediar la heterocedasticidad. Para resolver el segundo problema se tomó del conjunto original de datos de edad-diámetro (N=2 654) una muestra aleatoria de 240 datos con los cuales se ajustaron los estimadores paramétricos del modelo de crecimiento. Se empleó el modelo de von Bertalanffy (Vanclay 2003) por su origen teórico, versatilidad y amplio uso en silvicultura:
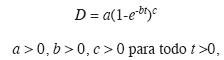
donde: D, el diámetro a la altura del pecho (cm); a, la asíntota (cm); b, la tasa intrínseca de crecimiento; c, parámetro de forma; t, edad en años y e la constante de Euler. También se calculó el incremento corriente anual (ICA) o tasa de crecimiento absoluto, el incremento medio anual (IMA) o tasa de incremento medio y la tasa de incremento relativo (IR) del diámetro (Assman 1970).
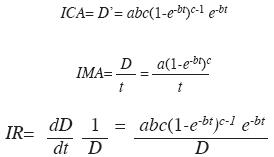
Validación: Para validar el modelo se tomó una muestra aleatoria de 50 pares de datos diámetro-edad diferentes de los 240 con los que se estimaron los parámetros del modelo y se aplicó una prueba de χ2 con el fin de determinar si existían diferencias estadísticas entre los diámetros de esta muestra y los estimados con el modelo.
Lapso vital y tasa de crecimiento: El lapso vital se estimó calculando el tiempo requerido para que el diámetro de los árboles alcance 99% del valor asintótico (Del Valle 2002).
Con el fin de obtener una tasa de crecimiento medio que involucre toda la forma de la curva y no dependa de la edad, se empleo el valor medio de una función (Del Valle 2002) para lo cual se escribió la ecuación de von Bertalanffy en forma derivada:
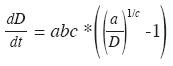
Valor medio del crecimiento absoluto o ICA,
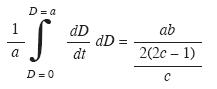
Valor medio del crecimiento relativo IR,
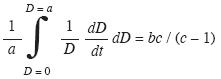
Volumen aserrable: Con base en 1 126 cativos cuyo volumen aserrable se estimó por suma de secciones cubicadas en el campo (Romero 1965) para árboles con D entre 35 y 135cm y diámetro superior del árbol hasta 30cm se ajustó por mínimos cuadrados ordinarios la función alométrica linealizada del volumen aserrable:
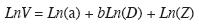
donde: ln, logaritmo natural; V, volumen aserrable de un árbol (m3) hasta 30cm de diámetro superior; D, diámetro a la altura del pecho (cm); a y b, parámetros; Z, término multiplicativo del error o factor de corrección (Zapata et al. 2001). Para el modelo de crecimiento dimétrico se emplearon los mismos 240 diámetros previamente obtenidos aleatoriamente; pero ahora para estimar sus volumenes. Estos, a su vez, se emplearon para ajustar el modelo de crecimiento del volumen en función de la edad de los árboles.
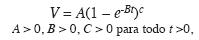
donde: A, la asíntota de volumen por árbol (m3), B tasa intríseca de crecimiento de volumen; C, parámetro de forma de la ecuación de volumen. También se calcularon el ICA, el IMA el IR y las tasas promedias absolutas y relativas mediante el valor medio de una función de la ecuación de volumen, tal como con el diámetro. El modelo se validó con 50 volúmenes aleatoriamente seleccionados y no empleados en el ajuste de la regresión.
Resultados
Descripción de los anillos: Los anillos de crecimiento son visibles a simple vista en las secciones transversales pulidas; se observan definidos por líneas de parénquima marginal más claras que la madera de fondo (Fig. 2). Los poros visibles a simple vista poseen parénquima paratraqueal vasicéntrico, en ocasiones aliforme, romboidal-confluente en tramos de dos a tres poros de tamaño mediano (de 100 a 200μm de diαmetro), radios apenas visibles a simple vista (de 50 a 100μm) (Vαsquez & Ramírez 2005).
Patrones de crecimiento: Comparados los anchos de anillos de todos los árboles se encontró que si un individuo crece mucho respecto del año anterior los demás individuos también tenderán a presentar crecimientos altos ese año. Por ejemplo, entre los años 1972-1974, 1987-1988 existen crecimientos altos. Este patrón se repite en los años de menor crecimiento (Fig. 3). Es decir, existe un patrón de crecimiento común en todos los anillos. Es de esperar que los años con picos altos de crecimiento correspondan a condiciones ambientales favorables. Una sincronización como la observada en la (Fig. 3) durante más de 150 años en su conjunto aporta evidencias adicionales acerca de la anualidad de los anillos. Los resultados del software COFECHA indican que la correlación entre cada serie y la cronología maestra oscila entre 0.337 y 0.613, la correlación interserial (correlación media) es de 0.476. Todas las correlaciones fueron significativas con nivel de confianza del 99% (α=0.01).
Anualidad de los anillos de crecimiento: Los siguientes son los resultados de porcentaje de C14 moderno (%C14M±% error): 112.9±0.6, 120.7±0.7 y 110.0±0.7. La calibración con CALIBOMB (Fig. 4) arrojó probabilidades entre 91 y 99% de que estos anillos correspondían con el año predatado. Esta evidencia per se, además de la sincronización de los crecimientos máximos y mínimos (Fig. 2) y el cofechado, permiten afirmar que los anillos de crecimiento de P. copaifera son anuales.
Crecimiento diamétrico: En la Fig. 5 (A) se muestran las trayectorias de las series de los árboles sin corrección y en la Fig. 5 (B) las trayectorias de las series corregidas. Obsérvese que las trayectorias corregidas de una misma sección transversal convergen todas al mismo valor final debido al factor de corrección. Las edades de los árboles variaron desde 46 hasta 154 años. No se observan diferencias importantes en estas trayectorias debido a que en P. copaifera el centro anatómico no se encuentra muy distante del centro geométrico.
Modelación del crecimiento diamétrico: El modelo de crecimiento diamétrico del cativo en la zona de estudio es
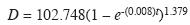
En este modelo R2=0.9342. El estimador Durbin & Watson (D-W) 1.953 y la autocorrelación de primer orden 0.023 muestran que no existe autocorrelación temporal significativa, solo ruido blanco de origen aleatorio. Luego de aplicar la medida correctiva se encontró que los residuales son razonablemente homocedásticos (residuales no mostrados).
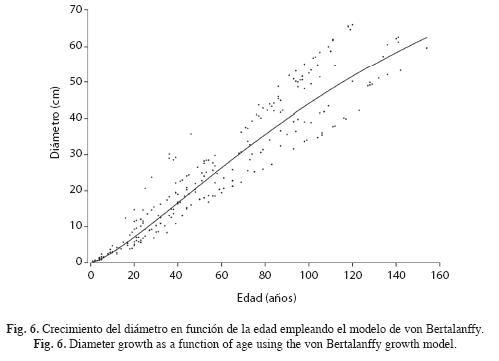
Para alcanzar 40cm, diámetro de corta legal en Colombia, se requieren 88 años (Fig. 6). Las tasas ICA, IMA e IR de crecimiento diamétrico se presentan en la Fig. 7 y corresponden, respectivamente, a las ecuaciones:
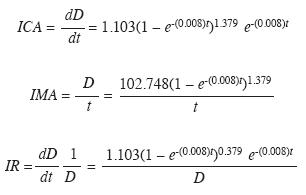
El ICA se maximiza cerca de los 40 años con 0.49cm/año. No obstante, a esta edad los árboles solo tienen 17cm de D (Figs. 6 y 7). El máximo ICA se presenta a los 73 años, punto en el cual el ICA=IMA con tasas de 0.44cm/año. A esta edad el D es de 30.7cm (Figs. 6 y 7). La trayectoria del IR muestra que las tasas de crecimiento decrecen abruptamente hasta aproximadamente los 20 años de edad cuando los árboles alcanzan unos 7cm de D. A partir de allí el IR continúa decreciendo pero a tasas menores (Fig. 7). Empleando el valor medio de una función se encontró que la tasa media del ICA es 0.31cm/año y la del IR es 2.9% anual. El lapso vital de la especie es 614 años.
En la validación del modelo de crecimiento diamétrico se encontró que los diámetros predichos no difieren significativamente de los observados con nivel de confianza del 95% (α=0.05) y 49 grados de libertad, el valor tabulado (χ2(0.05,49)) fue superior al calculado: 66.33>54.86.
Ecuación de volumen: La ecuación del volumen de madera aserrable del cativo es:
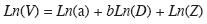
En esta ecuación R2=0.9248 y el error estándar de la estimación (EEE) 0.2098; el estadístico D-W=1.629 y la autocorrelación de primer orden 0.181. Todos estos estadísticos revelan ajustes adecuados. Haciendo la corrección por sesgo; esto es, agregándole al término independiente ½(EEE) se llega a la ecuación de volumen aserrabe con corrección por sesgo:
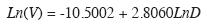
La Fig. 8 muestra la forma logarítmica de la ecuación con la nube de puntos de los datos empleados para dicho cálculo. A pesar de haber graficado el modelo ajustado con y sin corrección por sesgo, no es perceptible la diferencia debido a la escala. Al utilizar las ecuaciones que modelan el volumen a los 1 126 cativos empleados para la regresión se encontró que la no corrección por sesgo solo afecta en 2.2% el volumen, menos de 2x10-3 m3 por árbol.
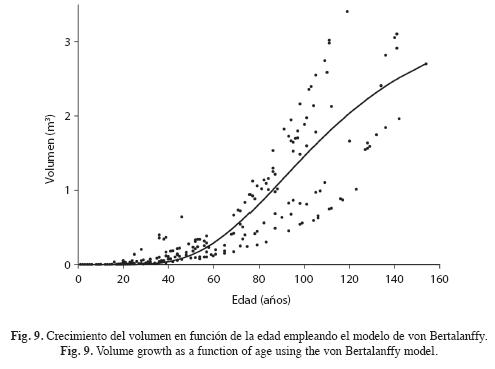
Modelo de crecimiento del volumen aserrable: Luego de corregir la heterocedasticidad, tal como se hizo con la ecuación de crecimiento diamétrico, se obtuvo la ecuacion de crecimiento del volumen aserrable por árbol (Fig. 9):
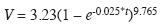
El ajuste del modelo es estadísticamente aceptable luego de la corrección por heterocedasticidad:
R2=0.99 EEE=0.4256, D-W=1.980
y autocorrelación de primer orden 0.0112 sugiriendo que no existe autocorrelación significativa de errores. El alto valor de R2 se debe atribuir al efecto de la ponderación aplicada para corregir la heterocedasticidad de los residuales cuya figura no se muestra.
Durante los primeros 40 años el crecimiento del volumen aserrable es muy lento (Fig. 9). Ello se debe a que hasta que los árboles no superen los 30cm de D no empiezan a acumular volumen aserrable, pues la ecuación alométrica del volumen aserrable se estimó para árboles con diámetros de 30cm en la parte superior y más delgada del tronco (Véanse los métodos). Luego de 40 años el volumen acumulado incrementa notablemente en forma sigmoidal alcanzando cerca de 1m3 por árbol a los 90 años, hasta alcanzar la asíntota de 3.23m3 cuando t→∞. Las siguientes ecuaciones expresan las tasas de incremento de volumen ICA, IMA e IR:
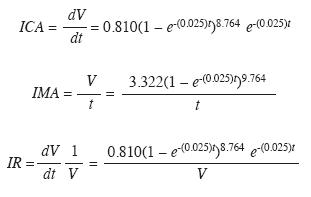
El ICA alcanza el máximo valor los 90 años con 0.033m3/año por árbol (Fig. 10). A esta edad los árboles tienen 41cm de D. El IMA alcanza su máximo a los 143 años con 0.018m3/año por árbol. A esta edad los árboles tienen 60cm de D. Como se observa en la Fig. 10 en este punto IMA=ICA. El llamado turno biológico de los forestales o del máximo rendimiento sostenible anual del volumen es precisamente el punto donde se maximiza el IMA; esto es 143 años. El IMA medio del volumen es 0.021m3/año por árbol y el IR 2.8% anual. El IR desciende muy rápidamente hasta aproximadamente 30 años cuando los árboles alcanzan unos 12cm de D, a partir de esta edad continúa decreciendo aunque a tasas menores.
Al comparar los volumenes aserrables predichos con los observados se encontró que no difieren estadísticamente con nivel de confianza del 95% (α=0.05) y 48 grados de libertad (χ2(0.05,48): 65.17 > 10.57). Este resultado valida estadísticamente el modelo.
Discusión
La modelación del crecimiento del diámetro y el volumen de los árboles es una herramienta técnica indispensable en la ordenación y el manejo sostenible de los bosques por cuanto permiten determinar los turnos de corta, las dimensiones y la producción esperada así como el momento en que las tasas de crecimiento se maximizan (Vanclay 2003, Schöngart 2008).
Igual que muchos árboles tropicales el cativo forma anillos de crecimiento visibles a simple vista. Sus anillos están definidos por bandas de parénquima marginal y porosidad difusa. Estas características habían sido descritas previamente por otros autores (Kukachka 1965, Mckenzie 1972). Este tipo de anillos es característico de las leguminosas (Worbes 2002).
Previamente McKenzie (1972) había demostrado que los anillos del cativo eran anuales empleando el método de marcado del cambium con alfileres y observando el tejido formado un año más tarde. Linares (1988) y Grauel (2004), sin aportar evidencias, no creen en ello y González et al. (1991) consideran insuficiente el conocimiento de los anillos en los árboles tropicales como para aplicarlos para esta especie. Este es un claro ejemplo de la necesidad de hacer ciencia en esta área del conocimiento. Los resultados de esta investigación confirman los resultados de McKenzie (1972). En primer lugar, la sincronización observada durante más de 150 años aporta evidencia acerca de la naturaleza anual de los anillos y de la respuesta a una señal ambiental común (Stalhe 1999) como podría ser el pulso anual de ciclos de inundación y estiaje. El cofechado tanto dentro como entre los árboles aporta también evidencia en este mismo sentido. Finalmente, los resultados de la datación con radiocarbono son una prueba adicional, más allá de cualquier duda razonable, de la anualidad de los anillos del cativo.
En el estudio de crecimiento de los árboles tropicales se han empleado métodos indirectos y simulaciones basadas en la información obtenida de parcelas permanentes (Del Valle 1979, 1986, 2003, Lieberman & Lieberman 1985, Lieberman et al. 1985, Vogel et al. 1986, González 1995, Condit et al. 1993, 1995b, Grauel 2004). Muy pocos en el trópico han empleado anillos de crecimiento y la mayoría desde hace pocos años (Návar et al. 2001, Brienen & Zuidema 2003, 2006, Brienen 2005, Schöngart 2008, Rozendaal 2010). Algunos científicos se quejan de la dificultad de estudiar la dinámica de las selvas tropicales porque, según ellos, los árboles no tienen anillos anuales (Schweingruber 1988, Lamprecht 1990). No obstante, una muestra de más de 600 árboles del Brasil demostró la existencia de anillos en cerca de la mitad de ellos (Alves & Angyalosy-Alonso 2000); también en Medellín, de 63 especies cuya madera se comercializa en la ciudad, 62% resultaron con anillos visibles a simple vista (Vásquez & Ramírez 2005). Las pruebas de anualidad en muchos árboles tropicales son hoy tan abundantes que siempre que ellos existan la hipótesis a probar debería ser que son anuales. El estudio del crecimiento de los árboles tropicales con anillos de crecimiento, cuando se ha demostrado su anualidad, es quizá la mejor opción posible desde diferentes puntos de vista, como se trata de demostrar a continuación.
El empleo de parcelas permanentes tiene estas limitaciones para el estudio del crecimiento de los árboles: i) el establecimiento, marcado inicial y posteriores remediciones necesarias para disponer de tasas de crecimiento del diámetro es muy costoso pues requiere regresar al bosque durante varios años para acopiar las mediciones; ii) toma mucho tiempo, usualmente no menos de cinco años antes de disponer de mediciones relativamente confiables; iii) con frecuencia existen pocos especímenes impidiendo disponer de una muestra adecuada para la mayoría de las especies; iv) con relativa frecuencia las especies que se desea estudiar son heliófitas y pertenecen a cohortes coetáneas; esto es, son producto de claros formados en la selva en los cuales se regeneró la especie antes del establecimiento de la parcela y, por lo regular, solo se encuentran especímenes de edades similares. Los métodos que no emplean anillos de crecimiento parten de la hipótesis de que los árboles más grandes tienen mayor edad, cuando pueden ser de similar edad lo que produce resultados contraevidentes; v) arrojan resultados sesgados debido a que por muy prolongado que sea el período de medición éste difícilmente reflejaría las condiciones ambientales durante el lapso vital de cada árbol; vi) existen multitud de factores que llevan a que las mediciones del diámetro en los árboles de las parcelas permanentes, a pesar del cuidado que se tenga al efectuarlas, no sean de tan alta calidad debido a la precisión de los instrumentos y a que no se está midiendo solo la actividad del cámbium vascular sino también del cortical, amén de dilataciones y contracciones que presentan los árboles aun durante un mismo día. A todos estos factores se deben las enormes variaciones encontradas en el crecimiento del cativo y de otras especies de las selvas tropicales cuyas tasas de crecimiento diamétrico varían desde ampliamente negativas (Clark & Clark 1999, Condit et al. 1993, 1995b) hasta 40 mm/año (Condit et al. 1993, 1995b, Grauel 2004). De los sesgos y errores existentes en las mediciones en parcelas permanentes dan cuenta estos ejemplos con cativo: con base en la curva media para los censos de 1982 y 1985 las proyecciones de Condit et al. (1995b) en la Isla Barrocolorado (IBC) indican que el cativo requiere 130 años para pasar desde 1cm hasta 60cm de D. Con base en los mismos árboles pero para los censos de 1985 y 1990 el resultado fue de 180 años, 38.5% superior. En la parcela río Balsas en el sitio Casarete en censos de 1997 y 1998 Grauel (1999) reporta 310 años para que el cativo pase desde 10cm hasta 60cm de D; para el mismo sitio y censos de 1997 y 2001 solo requiere 200 años (Grauel 2004), 110 años menos.
Por el contrario, si los árboles tienen anillos de crecimiento anuales: i) los costos se minimizan por cuanto sólo se requiere viajar al área de estudio en una sola ocasión para recoger las muestras y durante menos tiempo que el requerido para el establecimiento y medición de una parcela permanente; una vez en el laboratorio, el trabajo se puede ejecutar en menos de un año; ii) dado que los árboles aportan toda la información de su crecimiento durante todo su lapso vital no existe riesgo de sesgo debido a condiciones más o menos favorables; iii) no importa si los árboles son o no de la misma edad; tampoco si pertenecen o no a una cohorte determinada; iii) el tamaño de la muestra no está constreñido por los estrechos límites de una parcela; ésta se puede acopiar de un área de estudio mucho mayor. iv) estas mismas muestras podrían servir para estudios acerca de la dinámica y la competencia en los bosques así como para estudios dendroclimáticos, dendrohidrológicos y dendroquímicos lo que no es tan claro en la información procedente de los datos de tasas de crecimiento diamétricas acopiadas en las parcelas permanentes; v) Los incrementos se pueden medir con precisión de milésima de milímetro; vi) el crecimiento se mide exclusivamente como producto de la actividad del cambium vascular, en muestras secas y más estables a los cambios de dimensión; vii) no pueden existir crecimientos negativos.
El crecimiento diamétrico del cativo ha sido estudiado en parcelas permanentes por diversos autores, pero hasta ahora ningún autor reporta el crecimiento del volumen. Las tasas de crecimiento del D hasta 60cm de todas las fuentes disponibles consistentes en 12 cifras (Del Valle 1979, 1986, González et al. 1991, González 1995, Condit et al. 1993, 1995b, Grauel 1999, 2004), excepto Linares (1987, 1988), arrojan cifras que oscilan entre 0.19 y 0.77cm/año con media de 0.41cm/año, cercana a los 0.43cm/año de este estudio.
Aunque la mayoría de las parcelas del estudio de Grauel (2004) se establecieron en bosques previamente explotados, tal vez donde más se nota el efecto de la explotación de la madera es en una parcela en la que se estimó en 80 años el tiempo requerido para que los árboles pasaran desde 4cm hasta 60cm de D (0.70cm/año). Cuando se comparan los datos de Condit et al. (1993,1995b), cuya parcela se encuentra en bosques sin inundaciones anuales, con los de los otros autores también revelan que no parece haber diferencias entre las tasas de crecimiento del cativo entre bosques inundables y de tierra firme.
Las cifras previamente citadas contrastan con las de Linares (1987,1988) quien, a diferencia de Grauel (2004), trabajó en bosques sin intervenciones previas. Linares (1987) afirma que en cativales A2 esta especie alcanza 60cm de D en 55 años (1.09cm/año) y en cativales A1 en 60 años (1.00cm/año). En otro estudio (Linares 1988) afirma que en bosques no intervenidos el cativo alcanza 60cm en 38 años (1.60cm/año) pero que este tiempo se puede reducir "significativamente con técnicas de manejo". Tasas medias de crecimiento tan altas son poco creíbles; más aun, sus sitios de trabajo fueron los mismos de González et al. (1991) y González (1995), quienes encontraron tasas sustancialmente inferiores y se extrañan de los resultados de Linares (González et al. 1991). Para especies con maderas con densidad similar a la del cativo se puede esperar que las técnicas silviculturales apropiadas aumenten las tasas de crecimiento de tal manera que se alcance hasta 1.0cm/año en promedio, tal como lo hizo De Graaf (1986) mediante refinamientos que implican una drástica reducción del área basal, no en selvas tropicales húmedas sin intervención alguna.
Las tasas de crecimiento del cativo no son, como podría pensarse, bajas cuando se comparan con las de otros árboles de las selvas húmedas tropicales no sometidas a intervenciones recientes. Manokaran & Swaine (1994) presentan los resultados de las tasas de crecimiento diamétrico de los árboles emergentes y del dosel en tres parcelas permanentes de dos hectáreas cada una en los bosques húmedos de Malaysia medidas durante 37, 36 y 13 años. En las tres parcelas las tasas medias de crecimiento diamétrico fueron del orden de 0.25 a 0.30cm/ año, similares a las del cativo en esta investigación. Lamentablemente pocos investigadores calculan las tasas de crecimiento medias absolutas y relativas durante todo el lapso vital de los árboles (desde D=0 hasta D=asíntota) que es un criterio mucho más objetivo pues sintetiza el desempeño total de una especie, lo que no se logra con la comparación en edades o diámetros fijos debido a que estas son funciones no lineales de formas muy diversas. La tasa absoluta de crecimiento diamétrico medio de 0.31cm/año aquí encontrada resultó más de dos veces inferior a 0.67cm/año calculada con los datos de Del Valle & Lema (1999) para Campnosperma panamense en bosques intervenidos sobre pantanos de turba del Pacífico sur colombiano. En cuanto al crecimiento relativo (IR) la situación es la misma: 4.1% y 2.9% anual para sajo y cativo de este estudio, respectivamente, Los resultados para cativo de Del Valle (1986) muestran que la tasa relativa es menor (1.8% anual, versus 2.9% anual), pero la tasa absoluta mayor (0.50cm/año versus 0.31cm/ año) que los encontrados en esta investigación.
En los bosques inundables amazónicos Schöngart (2008) clasificó de rápido crecimiento las especies con densidad de madera baja (0.23-0.57g/cm3) que alcanzan 50cm de D en 50 o menos años. Especies de crecimiento lento y alta densidad (0.65-0.94g/cm3) que alcanzan ese mismo diámetro entre 100 y 150 años. Las especies de crecimiento intermedio se encuentran entre estos dos límites; tal sería el caso del cativo cuya densidad es 0.46g/cm3 y requiere 112 años para alcanzar 50cm de Condit et al. (1995a) encontraron que el lapso vital del cativo es 1100 años. Este cálculo se basó en estimar con la tasa de mortalidad exponencial el tiempo requerido para que sobreviva solo el 1‰ de una cohorte. Cuando se emplean los datos de la tasa intrínseca de mortalidad de Condit et al. (1995a) no para 1‰ sino para 1% los resultados son similares a los aquí encontrados: 614 años versus 760 años. Además, si los cálculos de lapso vital en este estudio no se basaran en 99% de la asíntota sino en 99.9%, se obtendrían 902 años, similares a los 1 100 años de Condit et al (1995a). Pareciera mejor emplear 99% de la asíntota por cuanto los resultados concuerdan con Worbes & Junk (1999) a quienes la lectura de anillos de crecimiento les sugieren edades máximas de 700 años para árboles de la Amazonia. No obstante, existe una gran polémica acerca de la longevidad de los árboles tropicales. Algunos afirman que existen árboles con edades entre 800 y cerca de 1400 años (Chambers et al. 1998). Probablemente los métodos más confiables son los directos tales como el conteo de anillos de crecimiento y radiocarbono. Las proyecciones basadas en tasas de crecimiento o de mortalidad parecen menos confiables; por ejemplo Condit et al (1995a) encontraron lapsos vitales hasta de 2000 años para Swartzia simples en Panamá.
La teoría del manejo sostenible desarrollada con animales pero ampliamente aplicada también para plantas prevé que la cosecha máxima que se puede extraer sin afectar la capacidad de recuperación del sistema corresponde al IMA máximo (Odum & Barret 2006). Esta teoría se basa en la ecuación logística que es solo un caso particular de la de von Bertalanffy. Por tanto, en nuestro caso sería, de acuerdo con la Fig. 10, 0.033m3/año por árbol a los 90 años (Fig. 10). Sin embargo, la teoría desarrollada por los forestales centroeuropeos a finales del siglo XVII y principios del XVIII (Assman 1970) estipula que el rendimiento máximo sostenible no corresponde al ICA máximo sino al IMA máximo que se presenta a edades mayores y con extracciones sustancialmlente inferiores. En nuestro caso, de acuerdo con la Fig. 10, ello sucedería a los 145 años y se producirían solo 0.018m3/año por árbol. Esto significa que tan primigenia idea de sostenibilidad era más conservadora que ideas posteriores, ampliamente divulgadas en los textos de ecología.
Este estudio confirma que, como lo encontró McKenzie (1972), Prioria copaifera tiene anillos de crecimiento anuales. También aporta evidencias de la utilidad y ventajas de los anillos de los árboles tropicales para los estudios epidométricos, superando ampliamente el empleo de modelos de simulación basados en información de parcelas permanentes. De nuevo, el modelo de crecimiento de von Bertalanffy resultó apropiado para el estudio del crecimiento orgánico. El lapso vital de la especie es de unos 600 años y las tasas medias de crecimientos diamétrico y del volumen aserrable son 0.31cm/año y 0.021m3/año por árbol, respectivamente. Las tasas medias relativas de crecimiento del diámetro y del volumen aserrable son 2.9% y 2.8%, respectivamente.
La especie alcanza tasas de crecimiento promedias cuando se compara con otras especies tropicales. La información aquí presentada es muy importante en el manejo sostenible de los cativales existentes en su área de distribución que en el continente se extiende desde Costa Rica hasta el Darién colombiano.
Agradecimientos
Los autores agradecen a las siguientes entidades y personas: Gobernación del departamento de Antioquia por la financiación parcial del proyecto en el marco del macroproyecto Expedición Antioquia 2013, a la Universidad Nacional de Colombia sede Medellín por el tiempo concedido al coautor para la investigación y a la Dirección de Investigaciones (DIME) quien cofinanció parte de la investigación, al Laboratorio de Bosques y Cambio Climático de la Universidad Nacional de Colombia sede Medellín por el empleo de su infraestructura y equipos. Un agradecimiento muy especial debemos a Luis Alfredo Moreno de la empresa Maderas del Darién por su invaluable colaboración en el trabajo de campo.
Referencias
Alves, E.S. & V. Angyalosy-Alonso. 2000. Ecological trends in the wood anatomy of some Brazilian species, I. Growth rings and vessels. IAWA J. 21: 3-30. [ Links ]
Assman, E. 1970. The principles of forest yield study: studies in the organic production, structure, increment and yield of forest stands. Pergamon, Oxford, Reino Unido. [ Links ]
Baker, P.J. 2003. Tree age estimation for the tropics: A test from the Southern Appalachians. Ecol. Appl. 13: 1718-732. [ Links ]
Brienen, R. & P.A. Zuidema. 2003. Anillos de crecimiento de árboles maderables de Bolivia: Su potencial para el manejo de bosques y una guía metodológica. Programa Manejo de Bosques de la Amazonía Boliviana (PROMAB). Instituto de Geología y Medio Ambiente de la Universidad Mayor de San Andrés (IGEMA). Informe Técnico No7, Bolivia. [ Links ]
Brienen, R. 2005. Tree rings in the tropics: A study on growth and ages of Bolivian rain forest trees. Programa Manejo de Bosques de la Amazonía Boliviana (PROMAB), Scientific Series 10. Riberalta, Bolivia. [ Links ]
Brienen, R. & P.A. Zuidema. 2006. The use of tree rings in tropical forest management: Projecting timber yields of four Bolivian tree species. Forest Ecol. Manag. 226: 256-267. [ Links ]
Bullock, S.H., R.M. Turner, R. Hastings, M. Escoto-Rodriguez, Z. Ramirez & J.L. Rodriguez-Navarro. 2004. Variance of size-age curves: Bootstrapping with autocorrelation. Ecology 85: 2114-2117. [ Links ]
Clark, D. & D. Clark. 1999. Assessing the growth of tropical rain forest trees: issue for forest modeling and management. Ecol. Appl. 9: 981-997. [ Links ]
Condit, R., S.P. Hubbell & R.B. Foster. 1993. Mortality and growth of a commercial hardwood "el cativo", Prioria copaifera, in Panama. Forest Ecol. Manag. 62:107-122. [ Links ]
Condit, R., S.P. Hubbell & R.B. Foster. 1995a. Mortality rates of 205 neotropical tree and shrub species and the impact of a severe drought. Ecol. Monogr. 65: 419-439. [ Links ]
Condit, R., S.P. Hubbell & R.B. Foster. 1995b. Demography and harvest potential of Latin American timber species: Data from a large, permanent plot in Panama. J. Trop. For. Sci. 74: 599-622. [ Links ]
Chambers, J.Q., N. Higuchi & J.P. Schimel. 1998. Ancient trees in Amazonia. Nature 39: 135-136. [ Links ]
Davey, S.M., J.R.L. Hoare & K.E. Rumba. 2003. La ordenación forestal sostenible y el enfoque por ecosistemas: Una perspectiva australiana. Unasylva 64: 5-13 [ Links ]
De Graaf, N.R.1986. A silvicultural system for natural regeneration of tropical rain forest in Surimame. Tesis de Ph.D., Wageningen Agricultural University, Países Bajos. [ Links ]
Del Valle, J.I. 1979. Curva preliminar del cativo (Prioria copaifera) en un bosque virgen empleando el método de los tiempos de paso. Rev. Fac. Nal. Agr. 32: 19-26. [ Links ]
Del Valle, J.I. 1986. La ecuación de crecimiento de von Bertalanfy en la determinación de la edad y el crecimiento de árboles tropicales. Rev. Fac. Nal. Agr. 39: 61-74. [ Links ]
Del Valle, J.I. & A. Lema. 1999. Crecimiento de cohortes de árboles coetáneos en rodales espacialmente dispersos. El caso de Campnosperma panamense. Rev. Acad. Colomb. Cienc. 23: 249-260. [ Links ]
Del Valle, J.I. 2002. Mortality as a mathematical function of organic growth and diameter structure. Plant. Biosyst. 136: 217-222. [ Links ]
Del Valle, J.I. 2003. Crecimiento en biomasa y acumulación de carbono en los sajales del delta del río Patía, p 281-296. In S.A. Orrego, J.I. del Valle & F.H. Moreno. Medición de la captura de carbono en ecosistemas forestales tropicales de Colombia: Contribuciones para la mitigación del cambio climático. Universidad Nacional de Colombia, Sede Medellín. Centro Andino para la Economía en el Medio Ambiente (CAEMA), Panamericana Formas e Impresos, Bogotá, Colombia. [ Links ]
Eslava, J.A. 1993. Climatología, p. 136-147. In P. Leyva. Colombia Pacifico, Tomo I. Fondo Editorial para la Protección del Medio Ambiente José Celestino Mutis-Fondo Editorial FEN-Colombia, Santafé de Bogotá, Colombia. [ Links ]
Fichtler, E., D.A. Clark & M. Worbes. 2003. Age and long-term growth of trees in an old-growth tropical rain forest based on analyses of tree rings and 14C. Biotropica 35: 306-317. [ Links ]
González, H., H.D. Gómez & F. Arteaga. 1991. Aspectos estructurales de un bosque de cativo en la región del bajo Atrato, Colombia. Rev. Fac. Nal. Agr. 44: 3-50. [ Links ]
González, H. 1995. Análisis del crecimiento diamétrico de Prioria copaifera en condiciones naturales por medio de un modelo matemático determinístico. Crónica Forestal y del Medio Ambiente 10: 101-120. [ Links ]
Grauel, W.T. 1999. Species diversity and stand dynamics of Cativo (Prioria copaifera Griseb.) forest in the Darien Province, Panama, p. 69-78. In C. Kleinn & M. Köhl. Long-term observation and research in forestry. Proceedings of the IUFRO S4.11 International Symposium, Turrialba, Costa Rica. [ Links ]
Grauel, W.T. 2004. Ecology and management of wetland forest dominated by Prioria copaifera in Darien, Panama. Ph.D. Thesis, University of Florida, EEUU. [ Links ]
Grissino-Mayer, H. 2001 Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree-Ring Res. 57: 205-221. [ Links ]
Holmes, R.L. 1983. Computer assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 43: 69-78. [ Links ]
Hua, Q. & M. Barbetti. 2004. Review of troposphere bomb 14C data for carbon cycle modeling and age calibration purposes. Radiocarbon 46: 1273-1298. [ Links ]
Kaennel, M. & F.H. Schweingruber. 1995. Multilingual glossary of dendrochronology. Swiss Federal Institute for Forest Snow and Landscape Research, WSL/FNP, Paul Haupt, Berna, Suiza. [ Links ]
Kukachka, B.F. 1965. Cativo, Prioria copaifera Gris. U.S Forest Service Research Note. Forest Service, Forest Product Laboratory, Madison, Wisconsin, EEUU. [ Links ]
Lamprecht, H. 1990. Silvicultura en los trópicos. Cooperación Técnica República Federal de Alemania, Echborn, Alemania. [ Links ]
Lema, A. 2003. Elementos estadísticos de dasometría y medición forestal. Silvano, Medellin, Colombia. [ Links ]
Lieberman, D., M. Lieberman, G. Hartshorn & R. Peralta. 1985. Growth rates and age-size relationships of tropical wet forests trees in Costa Rica. J. Trop. Ecol. 1: 97-109. [ Links ]
Lieberman, M. & D. Lieberman. 1985. Simulation growth curves from periodic increment data. Ecology 62: 632-635. [ Links ]
Linares, R. 1987. Estudio del catival en Colombia, p. 54-66 In R. Solano. Reunión Nacional de Silvicultura. Memoria: Impacto de la Investigación Silvicultural Tropical en el Desarrollo Económico Forestal Colombiano. Serie Documentación No 9. Corporación Nacional de Investigación y Fomento Forestal. Bogotá, Colombia. [ Links ]
Linares, R. 1988. Estudio preliminar de la asociación catival en Colombia. Serie Documentación 17, Corporación Nacional de Investigación y Fomento Forestal, Bogotá, Colombia. [ Links ]
Manokaran, N. & M.D. Swaine. 1994. Population dynamics of tree species in dipterocarp forests of Peninsular Malaysia. Forest Research Institute Malaysia, Malayan Forestry Records No 40, Kuala Lumpur, Malaysia. [ Links ]
Mariaux, A. 1967. Les cernes dans les bois tropicaux africains, nature et periodicité. Bois For. Trop. 113: 3-14. [ Links ]
McKenzie, T.A. 1972. Observations on growth and technique for estimating annual growth in Prioria copaifera. Turrialba 22: 353-354. [ Links ]
Návar, J., J. Nájera & E. Jurado. 2001. Preliminary estimates of biomass growth in the Tamaulipan thornscrub in north-eastern Mexico. J. Arid. Env. 47: 287-290. [ Links ]
Odum, E.P. & G.W. Barret. 2006. Fundamentos de ecología. Thompson, México. [ Links ]
Reimer, P.J., Th.A. Brown & R.W. Reimer. 2004. Discussion: Reporting and calibration of post-bomb14C data. Radiocarbon 46: 1299-1304. [ Links ]
Roig, F.A. 2000. Dendrocronología en América Latina. EDIUNC, Mendoza, Argentina. [ Links ]
Romero, A. 1965. Tabla para el cálculo del volumen de madera aserrable de la especie cativo (Prioria copaifera Griseb). Tesis de Ingeniero Forestal, Universidad Nacional de Colombia Sede Medellín, Colombia. [ Links ]
Rozendaal, D.M. 2010. Looking backwards: Using tree rings to evalueate long-term growth patterns of Bolivian forest trees. Programa Manejo de Bosques de la Amazonía Boliviana (PROMAB). Scientific Series 12. Riberalta, Bolivia. [ Links ]
Schweingruber, F.H. 1988. Tree-rings: Basics and application of dendrochronology. D. Reidel, Dordrecht, Holanda. [ Links ]
Schöngart, J., M.T. Piedade, S. Ludwigshausen, V. Horna & M. Worbes. 2002. Phenology and stem-growth periodicity of tree species in Amazonian floodplain forest. J. Trop. Ecol. 18: 581-597. [ Links ]
Schöngart, J., W. Junk, M.T. Piedade, J.M. Ayress, A. Huttermann & M. Worbes. 2004. Teleconecction between tree growth in the Amazonian floodplains and the El Niño-Southern oscillation effect. Glob. Change Biol. 10: 683-692. [ Links ]
Schöngart, J. 2008. Growth-Oriented Logging (GOL): A new concept towards sustainable forest management in Central Amazonian várzea floodplains. Forest Ecol. Manag. 256: 46-58. [ Links ]
Soliz, C.C. 2010. Shedding light on tree growth: ring analysis of juvenile tropical trees. Promab Scientific Series 13, Riberalta, Bolivia. [ Links ]
Stuiver, M., A. Luca, J.C. White & W. Broecker. 1981. Isotopic indicators of age/growth in tropical trees. In F.H. Bormann & G. Berlyn (eds.). Age and growth rate of tropical trees: new directions for research: 75-82 (Bull. 949). Yale University, New Haven, EEUU. [ Links ]
Stahle, D.W. 1999. Useful strategies for the development of tropical tree-ring chronologies. IAWA Journal 20: 249-253. [ Links ]
Vanclay, J. 2003. Growth modelling and yield prediction for sustainable forest management. Malaysian Forester 66: 58-69. [ Links ]
Vásquez, A.M. & A.M. Ramírez. 2005. Maderas comerciales del Valle de Aburrá. Área Metropolitana del Valle de Aburrá, Medellín, Colombia. [ Links ]
Vogel, J.C., A. Fuls, H. Visser & B. Berckner. 1986. Radiocarbon fluctuations during third millenium BC. Radiocarbon 28: 935-938. [ Links ]
Worbes, M. 1985. Estructural and others adaptations to long-term flooding by trees on Central Amazonia. Amazoniana 9: 459-484. [ Links ]
Worbes, M. & W. Junk. 1989. Dating tropical trees by means of 14C from bomb test. Ecology 70: 503-507. [ Links ]
Worbes, M. 1995. How to measure growth dynamics in tropical trees a review. IAWA J. 16: 337-351. [ Links ]
Worbes, M. 1999. Annual growth rings, rainfall dependent growth and long-term growth patterns of tropical trees from the Caparo forest reserve in Venezuela. J. Ecol. 87: 391-403. [ Links ]
Worbes, M. & W. Junk. 1999. How old are tropical trees? The persistence of a myth. IAWA J. 20: 255-260. [ Links ]
Worbes, M. 2002. One hundred of tree-ring research in the tropics-a brief history and outlook to future challenges. Dendrochronología 20: 217-231. [ Links ]
Worbes, M., R. Staschel, A. Ruloff & W.J. Junk. 2003. Tree rings analysis reveals age structure, dynamics and wood production of a natural forest stand in Cameroon. Forest Ecol. Manag. 173: 105-123. [ Links ]
Zapata, M., J.I. del Valle & S.A. Orrego. 2001. Corrección por sesgos en modelos log-normales alométricos linealizados utilizados para la estimación de la biomasa aérea. Simposio internacional medición y monitoreo de la captura de carbono en ecosistemas forestales, 18 al 20 de octubre. Valdivia, Chile. [ Links ]
Correspondencia a: Jorge Andrés Giraldo Jiménez & Jorge Ignacio del Valle Arango. Grupo de Bosques y Cambio Climático, Universidad Nacional de Colombia Sede Medellín, Departamento de Ciencias Forestales. Apartado Aéreo No 568, Medellín, Colombia; jagiral1@bt.unal.edu.co, jidvalle@unal.edu.co
Recibido 03-IX-2010. Corregido 09-II-2011. Aceptado 10-II-2011.