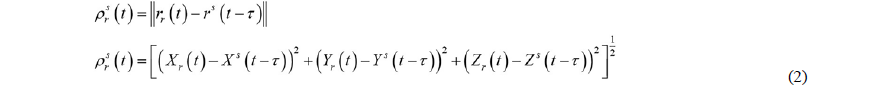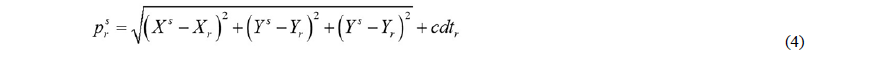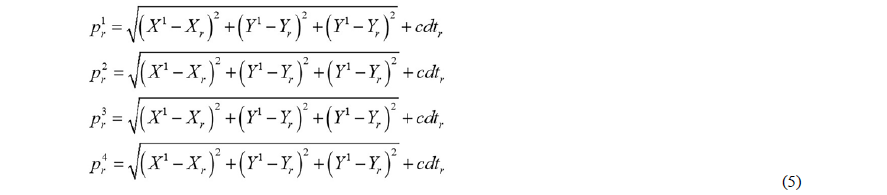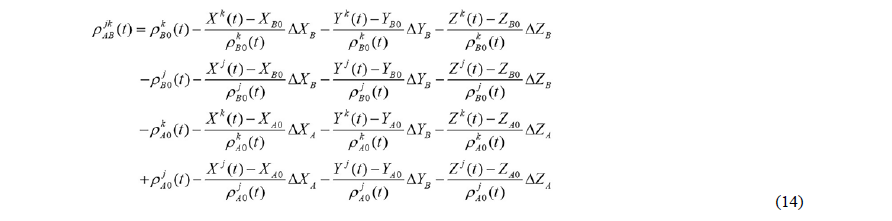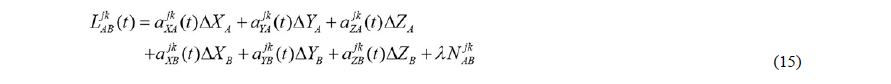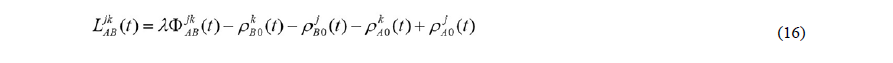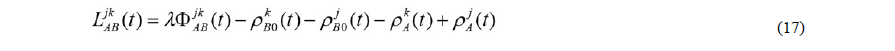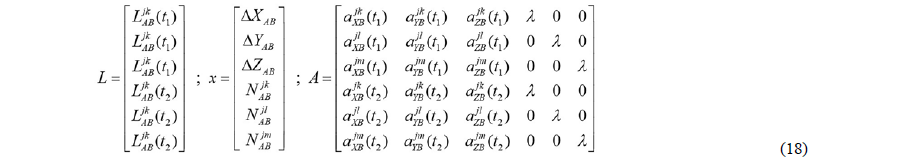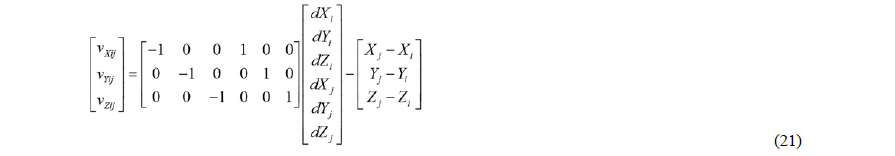1. Introdcción
La referencia geodésica oficial de Costa Rica, denominada como CR-SIRGAS, corresponde con un marco geodésico moderno el cual contempla observaciones diarias GNSS tomadas en las estaciones que lo conforman, el procesamiento semanal de estos datos como parte del mantenimiento de la red SIRGAS-CON y, por supuesto, las soluciones semanales finales de coordenadas geocéntricas, las cuales responden a las variaciones físicas que se producen en la superficie terrestre. La época de referencia, el cambio en las coordenadas geocéntricas semanales del marco y su influencia en los procesamientos de datos GNSS fueron aspectos que se tomaron en consideración en este artículo. La primera determinación del marco geodésico nacional CR-SIRGAS se redujo a la época 2014,59 y consideró como referencia internacional el IGb2008 [3], mientras que su más reciente actualización está referida a la época 2019,24 vinculado al marco internacional IGS2014 [1]. Ambas versiones de CR-SIRGAS están sustentadas sobre ocho estaciones GNSS de operación continua, las cuales son administradas por el Instituto Geográfico Nacional de Costa Rica (IGNCR), representando actualmente la mejor base geodésica que ha tenido el país. A pesar de ellos, existe una serie de consultas por parte de los profesionales sobre el traslado a las diferentes épocas de referencia a partir de la época de observación y potenciales metodologías relacionadas con el proceso de georreferenciación dentro de CR-SIRGAS. Aunque se pueden aplicar distintos métodos matemáticos para efectuar dicho proceso, como el de transformación de similaridad o bien una migración generalmente lineal por medio de parámetros de velocidad, siempre se dependerá de la información que se tenga inicialmente y sobre todo hacia dónde se quiere hacer el traslado [4]. Adicionalmente, no se debe olvidar la influencia que tienen las coordenadas de las estaciones que se usarán como vínculo o referencia para los distintos procesos de ajustes, así como también las épocas de observación y referencia.
2. Marco teórico
A. Principio de la medición GNSS
El principio de la medición GNSS es relativamente sencillo cuando se descartan una serie de factores físicos e instrumentales. Partiendo de que se cuenta con una constelación de satélites (SV) cuyas órbitas y, por lo tanto, sus coordenadas en función del tiempo son conocidas y que están transmitiendo constantemente señales con ciertos códigos y portadoras, el trabajo del receptor en tierra consiste en identificar primeramente cuáles satélites está captando. Luego, por medio de la generación interna de una réplica del código de cada satélite, el receptor hace una comparación de estos dos códigos continuamente hasta encontrar la misma secuencia, es decir, hasta estar sincronizados [9] y [10]. Adicionalmente la diferencia de tiempo entre el momento de la emisión ts de la señal desde el satélite y el momento tr de su recepción, multiplicada por la velocidad de la luz en el vacío c, dará como resultado la distancia r entre el satélite s y el receptor r (ver ecuación (1) [5].
B. Posicionamiento puntual por pseudodistancias
Si se asume, por un momento, que el reloj del receptor está sincronizado con el reloj de satélite, que no hay influencia de la ionósfera ni la tropósfera y que no se tiene la influencia de otras fuentes que afectan aleatoriamente la medición, la ecuación (1) tomará la forma presentada en la ecuación (2) [5].
Donde el vector rr=[XrYrZr]T representa la posición de la antena del receptor, es decir las incógnitas, mientras que el vector rs=[XsYsZs]T contiene las coordenadas de los satélites que son conocidas. Generalmente, ambos vectores se expresan dentro de un marco tridimensional coordenado, el cual está centrado y fijo a la Tierra conocido generalmente como Earth-centered, Earth-fixed (ECEF) [5]. En la práctica, sin embargo, cuando un receptor GNSS cambia de un satélite a otro, su reloj interno no está sincronizado con respecto a los relojes de los satélites, por lo tanto, la medición de la distancia entre el receptor y el satélite estará afectada por esa falta de sincronización en los relojes del receptor y del satélite dtr y dts, respectivamente, y de ahí su denominación como pseudodistancias. Lo anterior implica que la distancia geométrica p entre el satélite y el receptor será igual a la pseudodistancia más una distancia producto de la influencia de los relojes (ver ecuación (3)) [8], [9] y [10].
Aunque los relojes en los satélites sean monitoreados constantemente en la relación con la escala de tiempo propia de cada sistema, y que esa información se conoce en el mensaje de navegación, se mantiene la falta de sincronización en los relojes de los receptores dtr , implicando así que la ecuación (3) adquiera la forma que se presenta en la ecuación (4), es decir, en función de las coordenadas del satélite, las coordenadas del receptor más una distancia resultado del producto de la falta de sincronización del reloj del receptor por la velocidad de la luz en vacío.
En la ecuación anterior, hay un total de cuatro incógnitas, las tres coordenadas (Xr, Yr, Zr) de la posición de la antena y la falta de sincronización en el reloj del receptor dtr, conocida como estado del reloj del receptor. Su solución matemática necesita conocer al menos un total de cuatro pseudodistancias. Se tendrá, ahora, un sistema de ecuaciones de tamaño 4 x 4 similar al presentado en el conjunto de ecuaciones (5) y que requiere ser linealizado [5] y [8].
En la ecuación 6, se presentan los coeficientes diferenciales del conjunto de ecuaciones (5), agrupados en la matriz de configuración, generalmente denominada como matriz A.
El planteamiento de los sistemas de ecuaciones tendrá, generalmente, una mayor cantidad de datos que incógnitas por lo que, si se cuenta con una cantidad m de satélites en vista (m > 4), la estimación de las coordenadas del receptor y del estado de reloj estará dado por la ecuación (7). Donde P es la matriz de pesos de las observaciones de tamaño m × m, la matriz A tendrá ahora tamaño m × 4, y la matriz Qxx será la matriz de cofactores de las incógnitas de tamaño 4 × 4. El proceso de solución será iterativo, sin embargo, si la posición inicial es muy cercana a la real, probablemente no se requiera de más de una sola iteración.
C. Exactitud de la posición puntual
Los parámetros que permiten estimar la exactitud de las coordenadas del receptor se obtienen por medio de la matriz de cofactores Qxx del vector solución x. Considerando, inicialmente, una matriz de pesos P identidad, la correspondiente matriz de cofactores Qxx estará dada por la relación (ATA)-1 . La diagonal de esta matriz tendrá las varianzas de las coordenadas del receptor y del estado del reloj, mientras que los elementos fuera de la diagonal, las covarianzas, representan el grado de correlación entre las incógnitas como se muestra en la ecuación (8).
Una serie de elementos estocásticos presentes en la medición de cada distancia, desde el satélite hasta el receptor, se agrupan en el factor denominado UERE (User Equivalent Range Error) que se envía en el mensaje de navegación, el cual, en combinación con el parámetro DOP (Dilution Of Precision), permite hacer una estimación de la exactitud en el posicionamiento de un punto. El DOP es un escalar indicador de la calidad del proceso de ajuste ligado a la geometría de los satélites que se tuvieron en vista. Un valor bajo de DOP representa una buena geometría, es decir, con satélites bien distribuidos en el horizonte, mientras que un valor alto implicará una geometría deficiente. Este factor es llamado, generalmente, pérdida de la precisión geométrica (GDOP), el cual brindará información de la posición al no considerar el término qtt e informará sobre el parámetro de tiempo si solamente se considera dicho término [8] y [10]. Los diferentes parámetros DOP se calculan tal como se muestra en el conjunto de ecuaciones (9).
Las relaciones anteriores están ligadas a coordenadas cartesianas geocéntricas, sin embargo, si se requiere de la matriz de covarianza Qneuen un sistema topocéntrico, se debe contemplar la correspondiente matriz de rotación cuyo planteamiento se puede consultar en [8]. Tanto el UERE como el DOP son indicadores que dependen de la geometría de los satélites y de los errores en las pseudodistancias y son solamente una aproximación que limita la propagación aleatoria de los errores [8].
D. Ampliación de la ecuación de pseudodistancias
En los apartados anteriores, se presentaron las relaciones generales con las cuales se puede obtener una posición puntual a partir de mediciones GNSS tomando en cuenta una serie de supuestos. Sin embargo, es conocido que la realidad es muy diferente y que las señales en su tiempo de viaje sufren una serie de afectaciones que, posteriormente, deben ser contempladas para obtener una posición con la suficiente exactitud como para ser empleada en proyectos geodésicos. Desde esta perspectiva, la ecuación (3) para la pseudodistancia obtenida por código deberá ampliarse, considerando una serie de factores adicionales (ver ecuación (10)) [5]. En la misma, Tsres el retraso provocado por la atmósfera neutra (tropósfera), Isr es el retaso producto de la ionósfera y esr representa una serie de errores no modelados como el multicamino, el ruido en el receptor y otros efectos menores.
Considerando ahora las fases de las portadoras, la ecuación para pseudodistancia está dada en la ecuación 11) donde l es la longitud de onda de la portadora, Msr son las ambigüedades enteras de las portadoras en ciclos y los retrasos en las fases del receptor y los satélites, por último εsr representa los errores no modelados en la fase entre los cuales están el multicamino, el ruido en el receptor y otros efectos menores [5].
E. Posicionamiento relativo
Dentro de las posibilidades que se ofrecen en las metodologías de levantamiento GNSS, está la denominada estática relativa por medición de fase en la cual el principio básico consiste en tener al menos dos receptores que estén observando simultáneamente a un mismo conjunto de satélites durante un determinado tiempo. La relación directa entre ambos receptores está dada, de manera geométrica, por la denominada línea base, que es un vector espacial calculado a partir del procesamiento de las mediciones GNSS en ambos puntos. Por ejemplo, si se tienen dos puntos A y B, y se asume inicialmente A como fijo, se requiere de los incrementos de coordenadas entre ambos. En la ecuación (12), se presenta el caso concreto para dos puntos A y B [8]-[10].
El objetivo es determinar dichos incrementos entre los dos puntos considerados, asumiendo uno de ellos como fijo. Estas componentes pueden indistintamente expresarse también como observaciones elipsoídicas de azimut α, distancia s y diferencia de altura Δh relativa entre los puntos. Este método de momento continúa siendo el que brinda los mejores resultados en el posicionamiento, ya que el hecho de hacer las diferencias de las ecuaciones de observación elimina una serie de errores propios del sistema y otros de origen físico.
Si bien actualmente es posible calcular dicho vector en tiempo real, el enfoque que se abordará en este documento considera el cálculo del vector producto de un post procesamiento por medio de la combinación de la medida de fase de la portadora. Los métodos de combinación son altamente conocidos, así como los procedimientos que permiten la resolución de las ambigüedades, por lo que se recomienda al lector consultar, entre otros, [5]-[10] para mayores detalles.
F. Cálculo de líneas base o vectores
Este apartado se desarrollará partiendo de la relación final de las dobles diferencias, debido a que se cancela el parámetro del estado del reloj del satélite y receptor. De esta manera, para dos puntos A y B observando dos satélites j y k toma la forma que se presenta en el conjunto de ecuaciones de (13) [7],[8].
Si se multiplica la ecuación anterior por λ, el primer término de la derecha representa las pseudodistancias medidas desde los dos satélites a los dos puntos y cada una de estas tres ecuaciones debe ser linealizada. El resultado de este proceso se presenta en la ecuación (14), donde los subíndices cero se refieren a la aplicación de la serie de Taylor la cual requiere de valores aproximados de las incógnitas [8].
Sustituyendo la ecuación (14) en la ecuación (13) se tendrá ahora la ecuación de observación linealizada. El lector deberá notar que, por simplicidad en la notación, se han sustituido los cocientes de diferencias de coordenadas en X, Y, Z de los satélites j y k y las coordenadas aproximadas del receptor en los puntos A y B entre su correspondiente pseudodistancia por los términos a, tal como se muestra en la ecuación (15) [8].
En la ecuación anterior, el término que está a la izquierda del signo igual quedará expresado según la ecuación (16) [8].
Si se considera ahora, por ejemplo, que el punto A es fijo, es decir, se conocen sus coordenadas, se reduce el número de incógnitas en tres porque ΔXA = ΔYA = ΔZA = 0 implicando que la ecuación (16) tomará la forma de la ecuación (17) donde desaparece el cero en las pseudodistancias al punto A[8].
Si se toman ahora, por ejemplo, cuatro satélites j, k, l, m en dos instantes de tiempo t1 y t2, se tiene en el conjunto de ecuaciones (18), la forma del vector de observaciones L, del vector de incógnitas x y de la matriz de configuración A[8].
G. Posicionamiento relativo
De acuerdo con la teoría del ajuste por mínimos cuadrados aplicada a las componentes de una línea base entre los puntos i y j, estas se pueden considerar como observaciones. La forma linealizada de esta relación se puede ver en la ecuación (19) [9], [10].
Sin embargo, para tener consistencia con la formulación del procedimiento, se deben incluir los residuos a las observaciones, tal como se muestra explícitamente en la ecuación (20) en cada una de las componentes del vector.
El modelo funcional linealizado del ajuste v = Ax – l se presenta ahora en la ecuación (21).
La adecuación de los tamaños de las matrices y vectores se hará dependiendo de la cantidad de puntos y líneas base que se consideren entre ellos, respetando la regla de r – 1, con r igual a la cantidad de receptores midiendo de forma simultánea.
3. Metodología
A. Fuentes de datos
Para la realización de este estudio, se usó un total de tres fuentes de datos. La primera corresponde a los archivos de observación de las ocho estaciones que sustentan actualmente el marco geodésico nacional CR-SIRGAS [1], administradas por el IGNCR. Los archivos de observación de dichas estaciones se pueden descargar de manera gratuita en el enlace: https://gnss.rnp.go.cr/SBC. La segunda fuente la conforma un grupo de archivos de datos pertenecientes a un conjunto de estaciones GNSS de operación continua, ubicado principalmente en el sector occidental de Costa Rica y son parte de un proyecto de investigación desarrollado por UNAVCO en colaboración con el Observatorio Vulcanológico y Sismológico de Costa Rica (OVSICORI) [11]. Los archivos de observación de esta fuente se descargan gratuitamente en: https://data.unavco.org/archive/gnss/rinex/. Finalmente, la tercera fuente de datos consultada fue el conjunto de archivos de observación solicitado directamente vía correo electrónico al OVSICORI. En el CUADRO I, se presentan las coordenadas geodésicas aproximadas de las treinta y dos estaciones usadas, la fuente de datos consultada y el tipo de punto. En este estudio, las ocho estaciones de CR-SIRGAS se consideraron fijas y las veinticuatro estaciones restantes se tomaron como nuevas.
B. Establecimiento de las épocas de observación y referencia
Se definió como época de observación ti el martes 13 de julio de 2021 correspondiente con el día del año DOY = 194, semana 2166 y día de la semana 2, época 2021,53. Sin embargo, para la estación EART, no se contó con el archivo respectivo por lo que se usó el DOY = 200, que corresponde con lunes 19 de julio de 2021, semana 2167, día de la semana 1, época 2021,55. Además, se consideraron las épocas t0 = 2019,24 y tk = 2014,59, correspondientes a las dos versiones oficiales de CR-SIRGAS [1].
Cuadro I Coordenadas aproximadas y clasificación puntos de la red de estaciones GNSS de operación continua con base en la fuente de los datos y el tipo. En la columna “Fuente” la O, la U y la I se refieren a OVSICORI, a UNAVCO y a IGNCR, respectivamente; y las letras F y N de la columna “Tipo” se refieren a las categorías fijo y nuevo
| Estación | Latitud Norte [°] | Longitud Oeste [°] | Altura [m] | Fuente | Tipo | Estación | Latitud Norte [°] | Longitud Oeste [°] | Altura [m] | Fuente | Tipo |
| BATA | 10,097 | 83,376 | 33,84 | O | N | LEPA | 9,945 | 85,031 | 20,94 | U | N |
| BIJA | 9,749 | 84,576 | 555,62 | U | N | LIBE | 10,631 | 85,438 | 163,83 | I | F |
| CABA | 10,237 | 85,343 | 26,93 | U | N | LIMN | 9,993 | 83,026 | 25,04 | I | F |
| CCOL | 8,407 | 82,973 | 83,27 | O | N | LMNL | 10,267 | 85,053 | 102,93 | U | N |
| CDME | 9,553 | 83,763 | 3483,40 | O | N | NEIL | 8,644 | 82,944 | 66,52 | I | F |
| CDTO | 8,573 | 82,872 | 100,04 | O | N | NYCO | 10,144 | 85,455 | 155,56 | I | F |
| CIQE | 10,323 | 84,431 | 680,65 | I | F | PNE2 | 10,195 | 85,828 | 19,66 | U | N |
| CNKC | 9,592 | 82,978 | 105,85 | O | N | PUJE | 10,113 | 85,272 | 29,16 | U | N |
| COVE | 10,719 | 84,401 | 99,02 | O | N | PUMO | 10,064 | 84,966 | 17,95 | U | N |
| CTCR | 8,890 | 82,764 | 1490,68 | O | N | PUNT | 9,980 | 84,832 | 23,66 | I | F |
| EART | 10,212 | 83,594 | 45,37 | O | N | RIDC | 9,920 | 84,049 | 1212,16 | I | F |
| EPZA | 10,140 | 85,568 | 668,61 | U | N | RIFO | 10,317 | 83,922 | 116,17 | O | N |
| HUA2 | 10,017 | 85,351 | 594,24 | U | N | SAGE | 9,373 | 83,704 | 723,17 | I | F |
| IND1 | 9,864 | 85,502 | 75,25 | U | N | SAJU | 10,067 | 85,710 | 73,78 | U | N |
| IRZU | 9,966 | 83,897 | 2964,91 | O | N | SRBA | 9,232 | 83,360 | 940,01 | O | N |
| LAFE | 9,807 | 84,960 | 65,29 | U | N | VRAI | 9,924 | 83,190 | 438,34 | U | N |
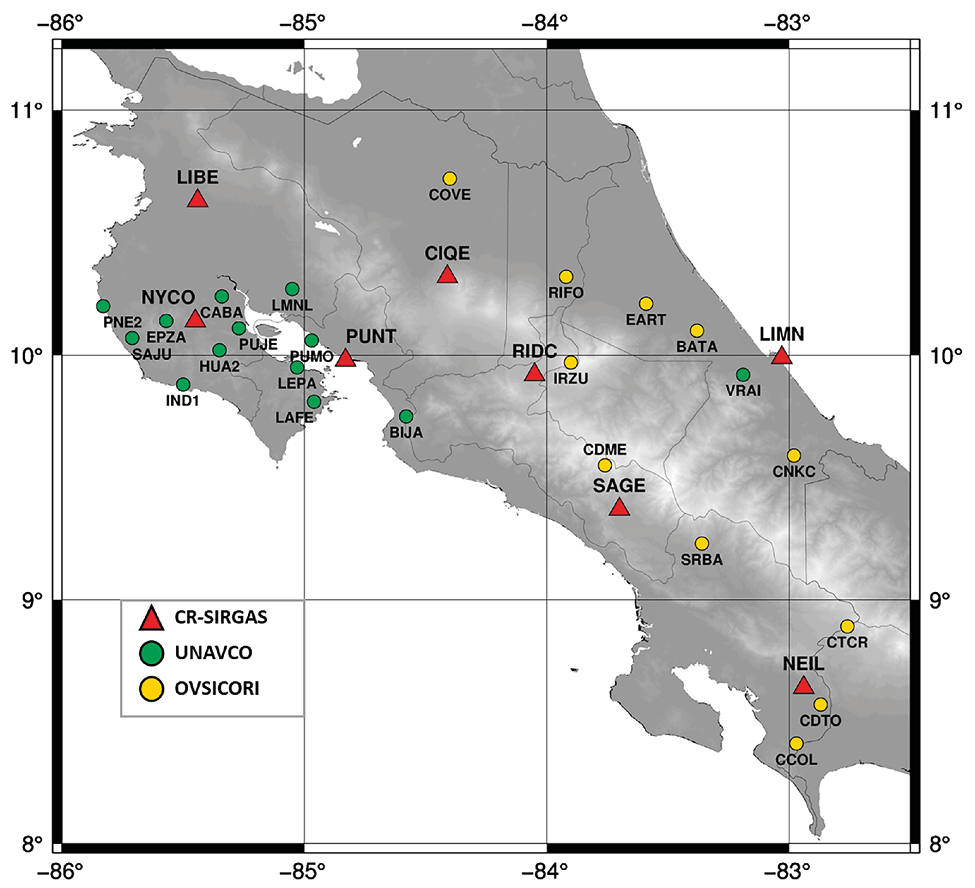
La distribución espacial de los puntos se presenta en la Fig. 1, donde las estaciones fijas CR-SIRGAS se identifican con un triángulo de color rojo, y las estaciones nuevas con círculos de color verde y amarillo, dependiendo de la fuente de datos.
C. Determinación de las líneas base
La red de puntos seleccionados para este estudio está conformada por un total de veinticuatro puntos nuevos que permiten calcular un total de veintitrés líneas base o vectores independientes. Sin embargo, se implementó una metodología que tomó los archivos de cada una de las estaciones de manera independiente como si se tratara de mediciones aisladas en un día particular, asumiendo que dicha medición se realiza para el establecimiento de un punto con enlace al marco de referencia CR-SIRGAS. Al respecto, se establecieron los siguientes criterios para el cálculo de las coordenadas de los puntos nuevos:
1) Cada punto fue procesado de manera individual con un archivo de 24 h de observación y sin formar ninguna figura con los restantes puntos nuevos;
2) cada punto debería ser intersecado por un máximo de cuatro estaciones de referencia CR-SIRGAS, teniendo, para cada proceso de ajuste, un total de doce observaciones;
3) La elección de las estaciones de vínculo se basó en el criterio de proximidad al punto nuevo, es decir, aunque, en principio, cada punto nuevo puede formar vector con las ocho estaciones de referencia, solamente se escogieron las cuatro más cercanas.
En la Fig. 2, se presenta, de manera esquemática, el criterio de selección usado en la escogencia de las estaciones de vínculo para cada uno de los puntos nuevos. Los triángulos de color rojo representan estaciones GNSS de operación continua (estaciones fijas CR-SIRGAS) y los círculos representan las estaciones nuevas. La codificación de las líneas contempló vectores de tamaño “corto” en color negro, los vectores de longitud “media” en color azul y los vectores de longitud “larga” en color verde. Las comillas en los adjetivos anteriores se colocaron solamente para clasificar distancias en esas tres categorías y solo con ese efecto ya que el término corto, medio y larga puede tener diferentes connotaciones. Por ejemplo, el punto PN1 se enlazó a las estaciones conocidas EB6, EB2, EB5 y EB4 en donde se aprecian dos vectores de longitud media y dos de longitud larga. En el caso del punto PN2, se enlazó a las estaciones EB2, EB3, EB1 y EB5 que tiene tres vectores de longitud media y uno de longitud corta. Finalmente, en el caso de PN3, se vinculó a las estaciones EB7, EB3, EB2 y EB8 en las que hay dos vectores cortos y dos vectores de longitud larga.
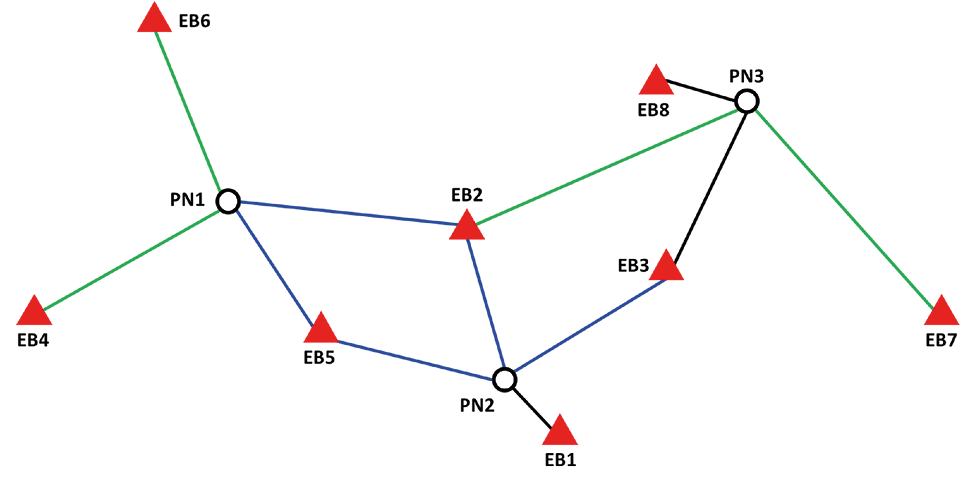
Fuente: elaboración propia
Fig. 2 Fig. 2. Representación de la selección de estaciones fijas representadas por triángulos de acuerdo con el criterio de proximidad a la estación nueva representada un círculo. Los colores de los vectores están dispuestos de acuerdo con su longitud.
El procesamiento de las líneas base se realizó con el software comercial Trimble Bussines Center (TBC) versión 5.2 con licencia de la Escuela de Topografía, Catastro y Geodesia (ETCG) de la Universidad Nacional (UNA). Por un lado, en la parte superior de la Fig. 3, se representa el vínculo entre la estación fija y la estación nueva con los cuadros de color azul; en la parte inferior a la izquierda se muestra el porcentaje de ocasiones en las que la estación fija fue considerada por cada punto nuevo. Por otro lado, a la derecha de la figura, se tiene el porcentaje respecto a la totalidad de las líneas base usadas. En total, se procesaron noventa y seis vectores contemplando, para las ocho estaciones CR-SIRGAS, los archivos de coordenadas semanales finales SIRGAS disponibles en: https://www.sirgas.org/en/weekly-solutions/, así como archivos de órbitas finales del International GNSS Service (IGS), los cuales se pueden descargar en: https://igs.org/products-access/.
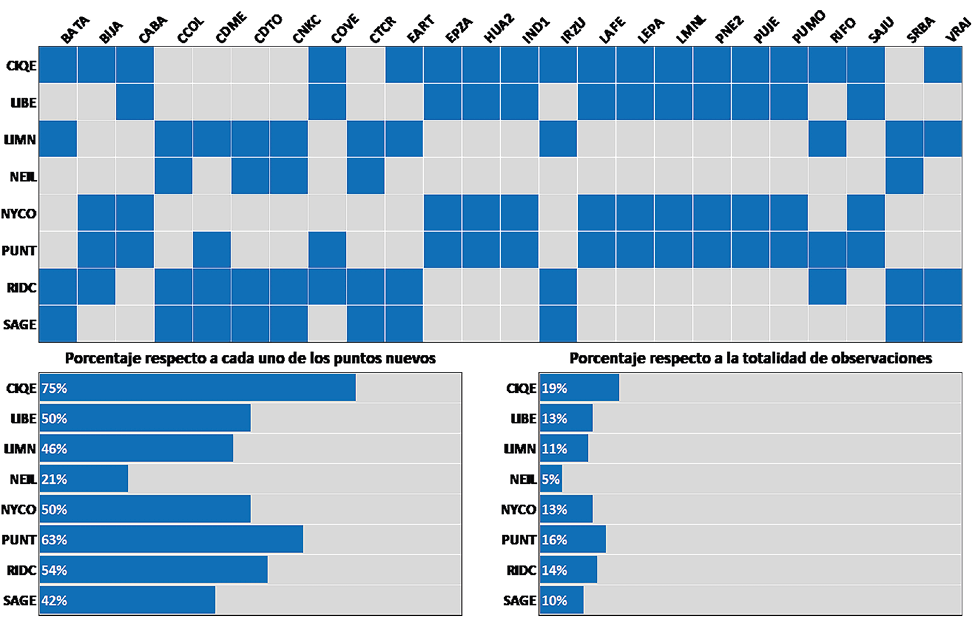
Fuente: elaboración propia
Fig. 3 En la parte superior los cuadros azules representan los puntos extremos de cada una de las líneas base y, en la parte inferior se presentan, por medio de barras horizontales el porcentaje de estaciones CR-SIRGAS usadas respecto a los puntos nuevos y a la totalidad de las observaciones.
Con el fin de dar una idea del valor de la magnitud de las componentes elipsoídicas de cada uno de los vectores, en la Fig. 4, se presenta una matriz que reúne la clasificación por magnitud de cada uno de los tres tipos de componente del vector (α, s y Δh). La codificación de colores se tiene en la parte de la derecha en la cual cada una de las magnitudes debe leerse considerando los intervalos en los que se encuentra la observación. En el caso de los azimuts α, se establecieron cuatro rangos: valores menores o iguales a 90º en color rojo, valores entre 90º y 180º en color amarillo, valores entre 180º y 270º en color verde y valores mayores a 270º y menores que 360º en color azul. En lo que respecta a las distancias s y a las diferencias de altura Δh, el color azul representa magnitudes mayores a los 125 km y 2000 m, respectivamente. En el caso de las diferencias de altura, se tomó el valor absoluto de la observación para facilitar la interpretación.
D. Ajuste de las redes
Una vez calculados los vectores entre cada una de las estaciones de amarre y el punto nuevo se realizaron veinticuatro procesos de ajuste con un total de cuatro vectores por punto, que generaron un total de n = 12 observaciones para resolver u = 7 incógnitas, las tres coordenadas geocéntricas de la estación nueva, más cuatro parámetros de transformación determinados entre la red original y la solución [14]. De esta manera, cada uno de los ajustes se logró con un total de f = 5 grados de libertad y pruebas estadísticas al 95 % de probabilidad [14]. Las variantes aplicadas en bloque de ajustes contemplaron, fundamentalmente, los diferentes conjuntos de coordenadas para las estaciones de amarre, es decir, las diferentes épocas consideradas. Las variantes que se implementaron fueron las siguientes:
1) Ajuste en la época de observación ti = 2021,53. Este primer bloque de ajustes para los veinticuatro puntos nuevos contempló como coordenadas de amarre los valores de las soluciones semanales finales de SIRGAS para la semana 2166. Las coordenadas ajustadas de los puntos nuevos, por lo tanto, son válidas a esta época de observación. Los resultados de las coordenadas ajustadas se presentan en el Anexo 1. En este documento, los resultados de los ajustes se denominaron 2021,53;
2) ajuste en la época de referencia de CR-SIRGAS t0 = 2019,24. Los resultados de las líneas base determinadas en el paso anterior fueron usados como observaciones para determinar las coordenadas ajustadas de los puntos de la red en esta época de referencia. Se usaron como coordenadas de amarre de las estaciones CR-SIRGAS para la semana 2046. Dentro de este documento los resultados de este ajuste se denominaron 2019,24;
3) ajuste en la época de referencia de CR-SIRGAS t0 = 2019,24. A diferencia del paso anterior se tomaron en estos procesos las observaciones correspondientes con esta época, específicamente el día 86 del año 2019 además de los archivos de órbitas finales del IGS y las coordenadas semanales finales para la semana 2046. Es decir, resultados en CR-SIRGAS versión 2. Las coordenadas ajustadas se presentan en el Anexo 2. En este documento los resultados de estos ajustes se denominaron CR-SIRGAS;
4) de conformidad con [1], se aplicaron los parámetros oficiales de transformación entre la época t0 = 2019,24 y tk = 2014,59. Los resultados se pueden consultar en el Anexo 3. Este cálculo no responde a un proceso de ajuste. En este documento, los resultados de la transformación se denominaron 2014,59T y no requieren mayor detalle, debido a que son el resultado de aplicación de un proceso conocido.
4. Resultados
El modelo matemático del ajuste por mínimos cuadrados contempla dos partes denominadas modelo funcional y modelo estocástico. El primero establece las relaciones funcionales entre las observaciones y las incógnitas, el segundo, considera la matriz P de pesos de las observaciones que es la inversa de la matriz de factores y cofactores de las observaciones originales denominada QLL y esta depende del inverso de un factor denominado varianza de referencia teórica σ20 , el cual consiste en un valor adimensionado de referencia establecido inicialmente y que se aplica como un escalar a la matriz de varianza-covarianza ΣLL[6],[8]. La situación descrita se presenta en el conjunto de ecuaciones (22).
Luego, a partir de los residuos vi de las observaciones, la cantidad de observaciones n y el número de incógnitas o parámetros u, se hace una estimación de la varianza de referencia por medio de la varianza empírica s20, como se presenta en la ecuación (23).
Es común que el valor teórico de la varianza de referencia se asuma unitario y, por lo tanto, el valor a posteriori o empírico brindará información sobre dicha estimación inicial, permitiendo, adicionalmente, una cuantificación e interpretación rápida sobre el proceso de cálculo en general. En la Fig. 5 se presentan los resultados de las desviaciones estándar empíricas de la unidad de peso para los tres conjuntos de ajustes realizados.
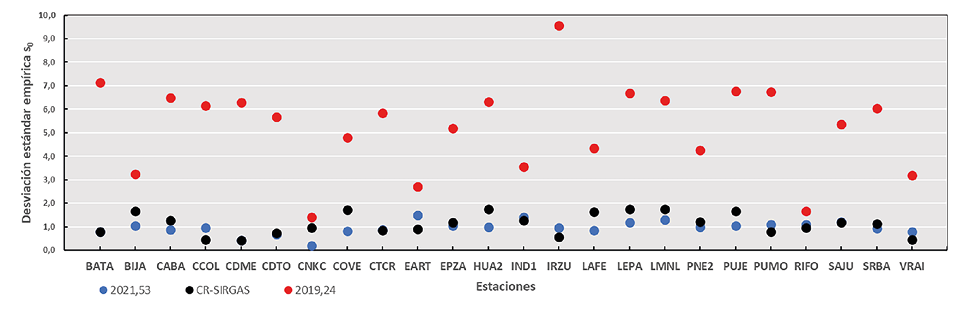
Fuente: elaboración propia
Fig. 5 Comportamiento del valor de desviación estándar empírica s0 obtenidos en los procesos de ajuste en una de las tres épocas consideradas.
Se aprecia cómo los resultados de este parámetro estadístico para el caso del ajuste en la época 2019,24 con observaciones realizadas en 2021,53 (círculo de color rojo) son mayores que los logrados en los dos procesos en los que se usó correspondencia de observaciones y coordenadas. Estos valores estuvieron comprendidos en un rango entre 1,5 y 9,5 explicando que a los ajustes realizados en esta época se les aplicó un equilibrio de varianzas. Es decir, este factor aumentó la varianza de referencia inicial para lograr la aceptación del modelo matemático, lo que implicó una reducción en la calidad de los resultados, como se verá en los siguientes apartados.
A. Cinemática de las estaciones CR-SIRGAS
CR-SIRGAS es un marco geodésico que puede ser catalogado como semicinemático y los cambios en las coordenadas de sus estaciones pueden usarse para calcular coordenadas en diferentes instantes [15], [16]. De esta manera, las variaciones semanales en las coordenadas de vínculo como respuesta a la cinemática del país, es un aspecto que indudablemente influirá en los resultados de observaciones tomadas en diferentes épocas de observación ti[4]. Las variaciones en las coordenadas de las estaciones del marco nacional CR-SIRGAS se obtienen a partir de los archivos de coordenadas semanales finales de SIRGAS. A partir de estas, se presentan, en la Fig. 6, sus series temporales entre la época 2019,25 y la 2021,53. Concomitantemente, el CUADRO II muestra el rango de variación por coordenadas para cada una de esas estaciones en el intervalo de tiempo considerado.
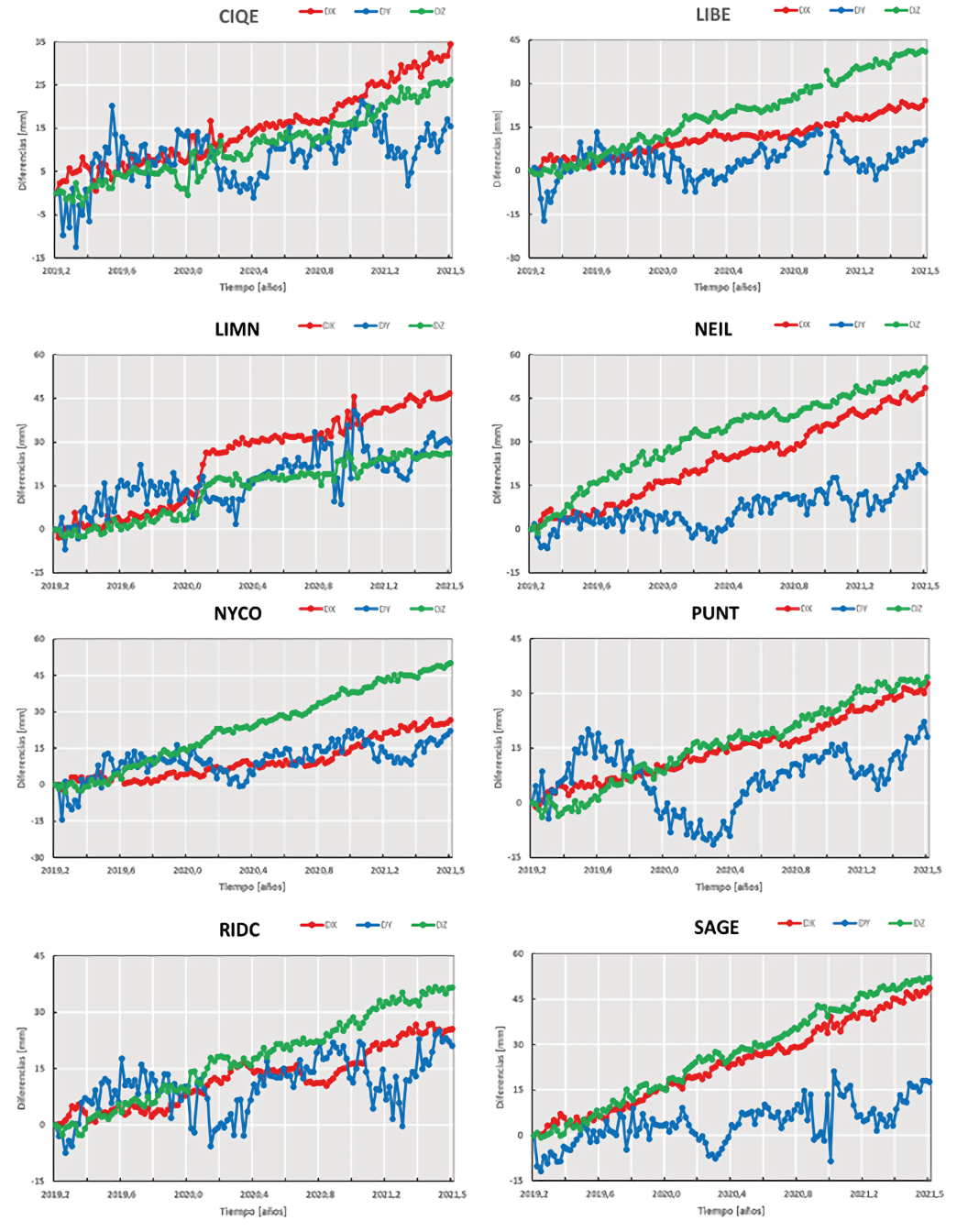
Fuente: elaboración propia a partir de las soluciones semanales SIRGAS
Fig. 6 Series temporales en coordenadas cartesianas geocéntricas para las ocho estaciones CR-SIRGAS desde la época 2019,24 hasta la época 2021,53.
Cuadro II Cuantificación del rango de variación en coordenadas geocéntricas cartesianas para cada una de las ocho estaciones CR-SIRGAS para el intervalo de estudio
| Rango | CIQE | LIBE | LIMN | NEIL | NYCO | PUNT | RIDC | SAGE |
| X [mm] | 34,5 | 25,2 | 49,7 | 48,6 | 28,8 | 33,8 | 26,9 | 48,7 |
| Y [mm] | 33,8 | 31,3 | 47,8 | 28,7 | 37,3 | 33,7 | 32,5 | 33,0 |
| Z [mm] | 28,9 | 43,6 | 29,6 | 56,7 | 53,1 | 38,4 | 39,6 | 52,8 |
Los resultados anteriores confirman y cuantifican los cambios en las coordenadas de las ocho estaciones CR-SIRGAS, lo cual repercute directamente en la época de observación. Por ejemplo, viendo la Fig. 6, si se realizaran mediciones en una época tm = 2020,30 y se tomara como referencia la estación SAGE, pero considerando sus coordenadas en la época de referencia t0 = 2019,24, habría discrepancias entre los +15 mm y +30 mm en las coordenadas X y Z, mientras que, en la coordenada Y, se tendría una variación aproximada de -10 mm solo por el dinamismo del propio marco. Estos cambios producirían efectos en los resultados de los ajustes en la época de observación.
B. Coordenadas ajustadas de los puntos nuevos
La salida del programa de procesamiento brinda tres tipos de coordenadas ajustadas para los puntos nuevos: coordenadas cartesianas geocéntricas (X, Y, Z), coordenadas geodésicas elipsoídicas (φ, λ, h) y coordenadas cartográficas planas (N, E), en este caso, en la proyección nacional Costa Rica Transversa Mercator (CRTM05), acompañada de una estimación de la altura nivelada (H) del punto obtenida por medio de la diferencia entre la altura geodésica h y el valor de la ondulación del geoide N para el punto según el modelo EGM2008 [17]. En el CUADRO III, se presentan los resultados de las diferencias en coordenadas cartesianas geocéntricas entre las tres épocas consideradas. Se nota, en la comparación CR-SIRGAS y 2019,24, que los valores de las diferencias son menores respecto a las otras dos comparaciones. Esto se debe a que se usó la misma época y a que las coordenadas obtenidas en 2019,24 están ajustadas, es decir, el algoritmo de ajuste por mínimos cuadrados genera una solución de coordenadas sacrificando, en este caso particular, la geometría de la red y la exactitud de las coordenadas. Esta situación debe complementarse con el análisis de los residuos y las exactitudes de las observaciones ajustadas.
Cuadro III Cuantificación de las diferencias en coordenadas cartesianas geocéntricas obtenidas para cada una de las épocas consideradas y sus los valores mínimo, máximo y rango
| Estación | (2021,53 – CR-SIRGAS) | (2021,53 – 2019,24) | (CR-SIRGAS – 2019,24) | ||||||
| X [cm] | Y [cm] | Z [cm] | X [cm] | Y [cm] | Z [cm] | X [cm] | Y [cm] | Z [cm] | |
| BATA | 3,2 | 1,7 | 2,0 | 3,8 | 2,5 | 3,4 | 0,6 | 0,8 | 1,4 |
| BIJA | 3,7 | -0,1 | 1,7 | 2,8 | 2,1 | 3,7 | -1,0 | 2,2 | 2,1 |
| CABA | 3,1 | 1,4 | 5,3 | 2,6 | 1,9 | 4,1 | -0,5 | 0,5 | -1,3 |
| CCOL | 6,3 | 2,5 | 5,6 | 5,6 | 1,6 | 5,7 | -0,7 | -1,0 | 0,1 |
| CDME | 4,0 | 2,6 | 4,7 | 4,0 | 2,0 | 3,7 | 0,0 | -0,6 | -1,0 |
| CDTO | 4,5 | 3,1 | 4,6 | 5,1 | 1,9 | 5,7 | 0,6 | -1,2 | 1,2 |
| CNKC | 2,4 | 4,4 | 1,9 | 4,1 | 2,1 | 4,4 | 1,7 | -2,3 | 2,5 |
| COVE | 3,7 | 0,9 | 2,2 | 3,4 | 0,1 | 3,6 | -0,2 | -0,8 | 1,5 |
| CTCR | 5,0 | 0,4 | 3,7 | 4,6 | 1,3 | 5,4 | -0,4 | 0,9 | 1,7 |
| EART | 3,7 | 5,0 | 2,0 | 3,5 | 2,1 | 3,6 | -0,2 | -3,0 | 1,6 |
| EPZA | 2,5 | 4,2 | 3,9 | 2,4 | 2,5 | 4,7 | 0,0 | -1,8 | 0,8 |
| HUA2 | 3,0 | 4,9 | 4,5 | 2,2 | 2,5 | 4,0 | -0,8 | -2,3 | -0,5 |
| IND1 | 4,7 | 4,1 | 6,1 | 1,5 | 2,8 | 4,5 | -3,2 | -1,3 | -1,6 |
| IRZU | 3,9 | 3,6 | 3,0 | 3,7 | 2,1 | 3,2 | -0,2 | -1,5 | 0,2 |
| LAFE | 3,3 | 2,4 | 3,9 | 2,7 | 2,4 | 3,6 | -0,6 | 0,0 | -0,3 |
| LEPA | 3,8 | 1,2 | 4,5 | 2,5 | 2,4 | 3,2 | -1,2 | 1,2 | -1,2 |
| LMNL | 3,3 | 0,3 | 4,4 | 2,8 | 1,5 | 3,7 | -0,5 | 1,2 | -0,7 |
| PNE2 | 1,8 | 2,5 | 4,7 | 2,3 | 3,0 | 4,9 | 0,5 | 0,5 | 0,3 |
| PUJE | 3,6 | 0,7 | 3,7 | 2,3 | 2,1 | 3,9 | -1,3 | 1,5 | 0,2 |
| PUMO | 3,3 | 0,3 | 4,6 | 2,7 | 2,1 | 3,4 | -0,6 | 1,8 | -1,3 |
| RIFO | 3,6 | -0,9 | 2,5 | 3,3 | 1,8 | 3,3 | 0,4 | 0,4 | 0,5 |
| SAJU | 3,2 | 1,7 | 4,5 | 2,0 | 2,8 | 4,6 | -1,3 | 1,1 | 0,2 |
| SRBA | 4,8 | 2,2 | 5,6 | 4,5 | 2,6 | 4,8 | -0,2 | 0,4 | -0,8 |
| VRAI | 3,6 | 2,2 | 2,9 | 4,0 | 2,5 | 3,3 | 0,4 | 0,4 | 0,5 |
| Mínimo | 1,8 | -0,9 | 1,7 | 1,5 | 0,1 | 3,2 | -3,2 | -3,0 | -1,6 |
| Máximo | 6,3 | 5,0 | 6,1 | 5,6 | 3,0 | 5,7 | 1,7 | 2,2 | 2,5 |
| Rango | 4,5 | 5,9 | 4,5 | 4,1 | 2,9 | 2,5 | 4,9 | 5,2 | 4,1 |
Fuente: elaboración propia
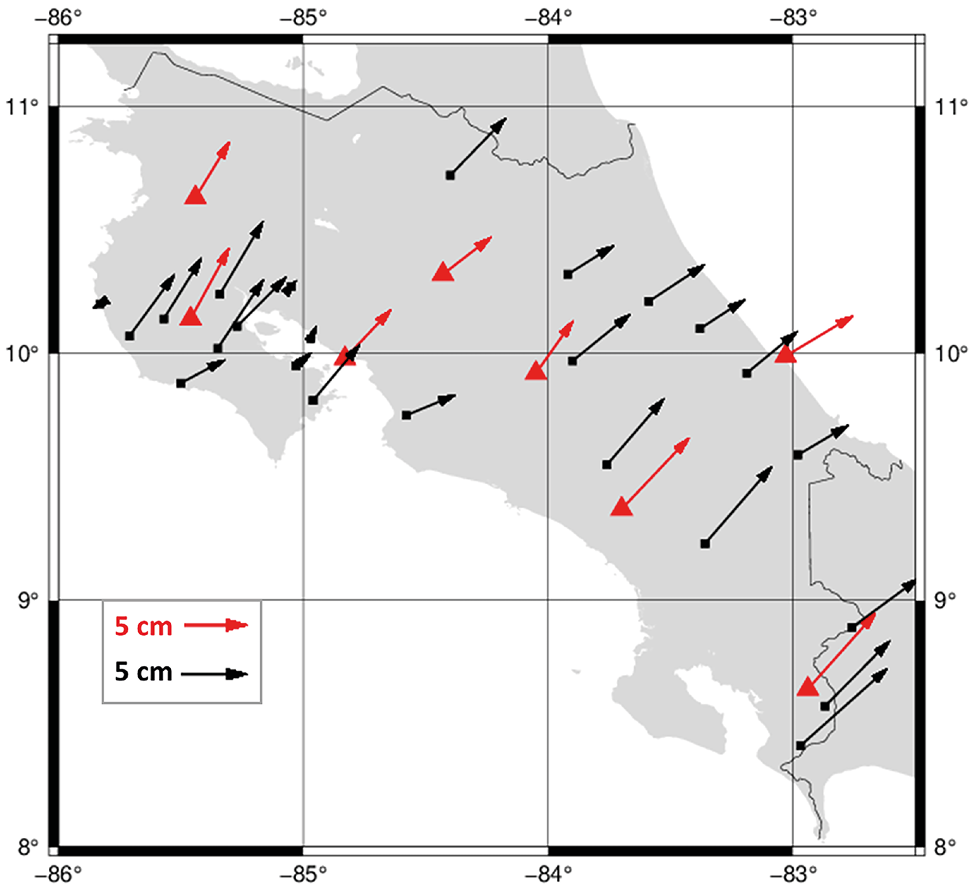
Con el objetivo de visualizar principalmente la magnitud y la dirección, debido a la diferencia de coordenadas entre CR-SIRGAS y 2021,53, en la Fig. 7, se presenta los vectores desplazamientos calculados con base en coordenadas cartográficas.
Fuente: elaboración propia
Fig. 7 Vectores de desplazamiento determinados con base en coordenadas cartográficas entre la época 2021,53 y 2019,24. Mapa compilado con Generic Mapping Tools (GMT) versión 6.0.0 [12].
Se nota cómo la dirección y magnitud de los vectores responde efectivamente con el movimiento esperado que sigue el país al estar ubicado sobre la Placa Caribe e influenciado por la Placa Cocos [18]. En este proyecto particular, se tuvo un desplazamiento promedio 4,82 cm que representan unos 2,1 cm por año en un azimut promedio de 55° para los puntos nuevos, mientras que las estaciones CR-SIRGAS tuvieron una magnitud de 5,75 cm es decir unos 2,5 cm por año en un azimut promedio de 42° [4] y [18].
C. Exactitud en las coordenadas ajustadas
Uno de los parámetros más importantes, y que generalmente la mayoría de los usuarios revisa inmediatamente luego del proceso de ajuste, es la exactitud de las coordenadas ajustadas de los puntos nuevos. Estos resultados se obtuvieron configurando las pruebas estadísticas del programa de procesamiento para trabajar con un 95 % de probabilidad. Los resultados mínimo, máximo y promedio de las exactitudes para cada una de las tres variantes de ajuste se presentan en el CUADRO IV.
Cuadro IV Valores mínimo, máximo y promedio de las exactitudes obtenidas en cada una de las tres épocas consideradas
| Época | 2021,53 | CR-SIRGAS | 2019,24 | ||||||
| Exactitud | sX [mm] | sY [mm] | sZ [mm] | sX [mm] | sY [mm] | sZ [mm] | sX [mm] | sY [mm] | sZ [mm] |
| Mínimo | 1,3 | 6,1 | 1,6 | 2,1 | 9,7 | 2,2 | 8,3 | 40,9 | 10,7 |
| Máximo | 9,2 | 49,8 | 11,2 | 10,9 | 84,3 | 18,1 | 23,3 | 135,7 | 29,4 |
| Promedio | 3,0 | 16,7 | 3,8 | 5,8 | 31,1 | 6,8 | 14,5 | 81,0 | 18,9 |
Fuente: elaboración propia
En el conjunto de gráficos de la Fig. 8, se presentan por medio barras verticales, la exactitud en las coordenadas geocéntricas para cada uno de los veinticuatro puntos nuevos. Se aprecia que en el caso de las coordenadas X y Z, para los resultados de 2021,53, los valores son menores a ± 5 mm. En el caso de la coordenada Y, como es de esperar, se tienen valores menores a los ± 25 mm, excepto en los puntos EART, IND1 y RIFO. En los resultados del ajuste CR-SIRGAS, el comportamiento general de la exactitud en las coordenadas X y Z se mantiene en ± 10 mm, exceptuando el punto COVE, mientras que en la coordenada Y los valores están por debajo de los ± 50 mm, con excepción en los puntos COVE e IND1. En el caso de los resultados en 2019,24, las barras de color rojo presentan valores elevados (ver CUADRO IV) respecto a los casos 2021,53 y CR-SIRGAS, llegando a ± 25 mm para CCOL en X, más de ± 125 mm en IND1 para la coordenada Y, y casi ± 30 mm en Z para la misma estación IND1.
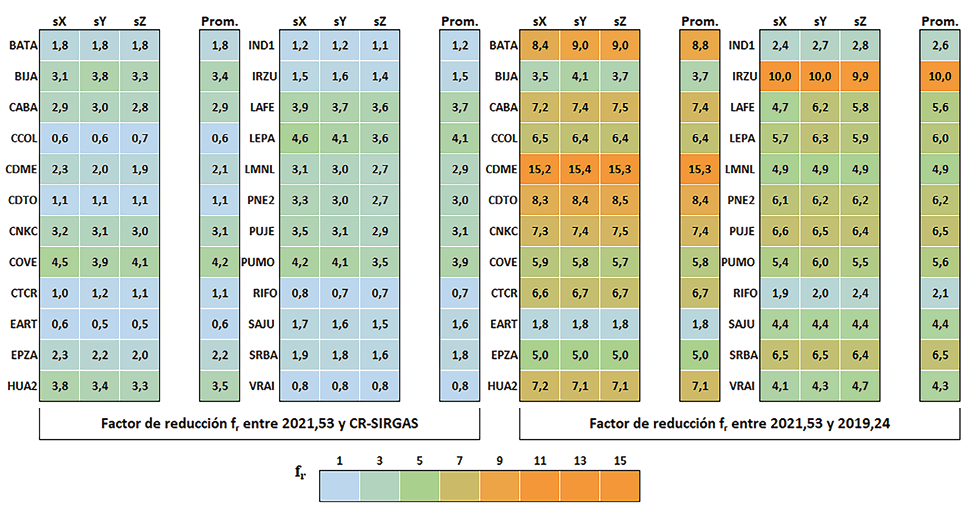
El efecto de las discrepancias entre las exactitudes de las coordenadas ajustadas obtenidas de los resultados de los procesamientos de CR-SIRGAS y 2019,24 respecto a 2021,53, se cuantificó utilizando un factor de reducción fr , el cual tendrá valores menores, iguales o mayores que la unidad representando incremento, igual o pérdida de exactitud respectivamente. Estos valores se presentan en la Fig. 9 donde se hizo una codificación de colores para facilitar la identificación del fr y en la cual, adicionalmente, se calculó el promedio de este factor. Se nota en el bloque de la izquierda que el promedio del fr se encuentra entre 0,6 y 4,2, mientras que en el bloque de la derecha el promedio aumenta a un rango entre 1,8 y 15,3. En esta figura, se evidencia también un elemento sistemático en cada una de las comparaciones por cada una de las coordenadas. el cual puede ser atribuido precisamente a que el marco CR-SIRGAS es cinemático y, por lo tanto, las coordenadas de sus estaciones presentaron variaciones constantes de este estudio.
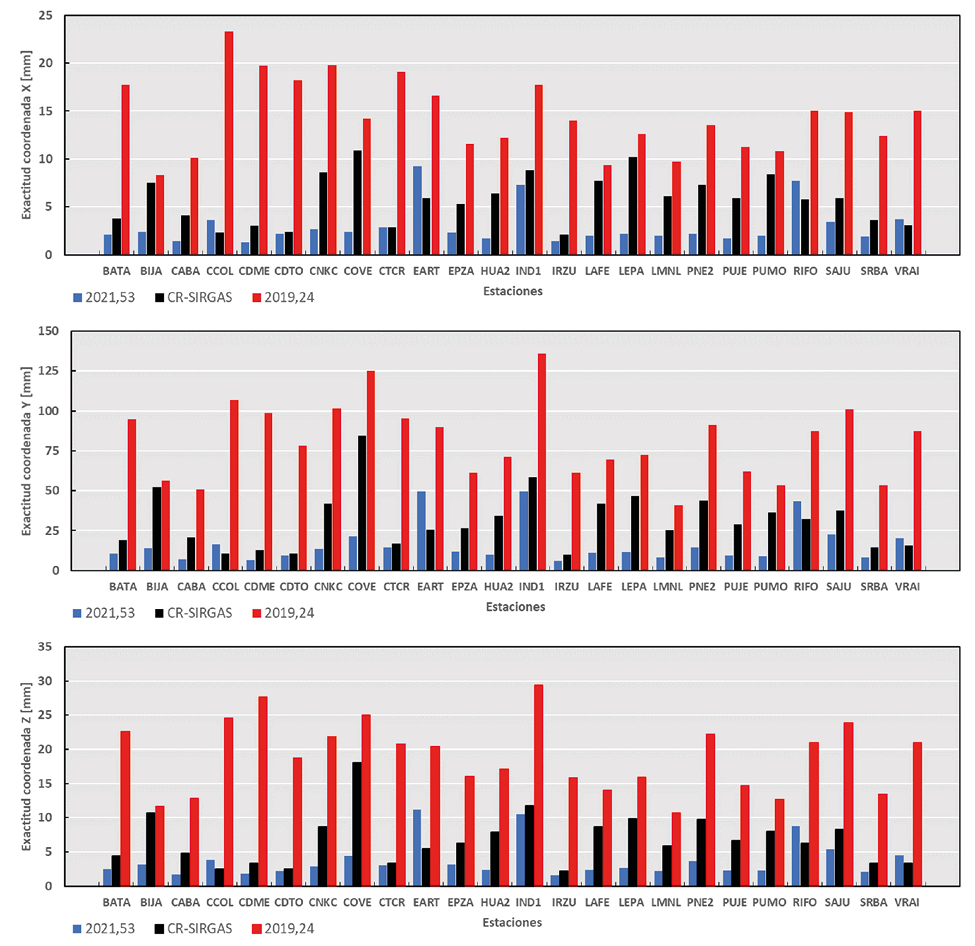
Fuente: elaboración propia
Fig. 8 Comparación de la exactitud en cada una de las tres coordenadas cartesianas geocéntricas para todos los puntos nuevos.
D. Elipses absolutas de confianza
El programa de cálculo TBC también ofrece, dentro de sus salidas, los tres parámetros de las elipses absolutas de confianza: semieje mayor a, semieje menor b y azimut θ del semieje mayor. Estas regiones de confianza, al depender de los coeficientes de la matriz de factores y cofactores de las incógnitas y de la cantidad de grados de libertad del ajuste, estarán relacionadas precisamente con los resultados de la exactitud y, considerando la configuración geométrica, brindan información sobre la calidad de los puntos.
En los apartados anteriores, se ha expuesto que la exactitud de las coordenadas ajustadas de los puntos nuevos en el ajuste 2019,24 baja considerablemente respecto a dos resultados. En las tres determinaciones, la excentricidad promedio de las elipses fue 0,588, sin embargo, el aumento en los ejes para las elipses en el ajuste 2019,24 estuvo entre 1,5 y 15. La representación de estas regiones de confianza se presenta en la Fig. 10, donde a la derecha se presentan en conjunto las elipses obtenidas de los ajustes 2021,53 y CR-SIRGAS dibujadas aumentadas en un factor 250, y, a la derecha, se agregan, en color rojo, las elipses del ajuste 2019,24 y se mantuvo la escala para destacar las diferencias. El azimut del semieje mayor prácticamente se mantuvo invariable en los tres casos.
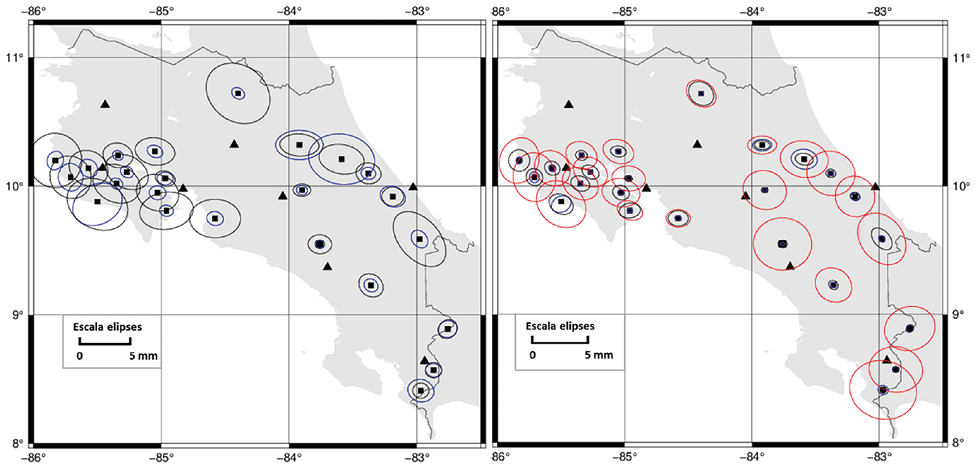
Fuente: elaboración propia
Fig. 10 A la derecha comparación de las elipses absolutas de confianza, épocas 2021,53 y CR-SIRGAS (color negro y azul respectivamente), a la derecha se agregan las correspondientes elipses de la época 2019,24 (color rojo). Mapa compilado con Generic Mapping Tools (GMT) versión 6.0.0 [12].
E. Observaciones ajustadas
Las observaciones ajustadas son el resultado de la suma de las observaciones originales y los respectivos residuales siguiendo el principio de mínimos cuadrados. El programa de procesamiento brinda, como parte de las salidas, las componentes elipsoídicas de cada uno de los vectores calculados, así como su residual y error. Una primera forma para analizar el comportamiento de las observaciones ajustadas y sus exactitudes se presenta en esta Fig. 11, donde se muestra la matriz de correlación respectiva determinada para cada una de las tres épocas de referencia.
En la misma Fig. 11, se puede observar, por un lado, que las componentes ajustadas de cada uno de los vectores en las tres épocas son prácticamente independientes con un coeficiente de correlación promedio de -0,02, sin embargo, las componentes de distancia y diferencia de altura entre las distintas épocas están totalmente correlacionadas, así como la componente de azimut solamente entre las épocas 2021,53 y 2019,24. Por otro lado, se observa que las exactitudes en las componentes de distancia y diferencia de altura están altamente correlacionadas en las tres épocas, llegando a un valor promedio de +0,82. Se ve, además, que las exactitudes en la componente angular están medianamente relacionadas con las respectivas exactitudes en distancia y diferencia de altura solamente en la época 2021,53. Este comportamiento no se repite para CR-SIRGAS ni 2019,24. Luego, las correlaciones entre los grupos de datos tienen diferentes valores, destacándose la relación inversa entre las distancia s y la exactitud azimutal sa con un promedio de correlación de -0,65 en todas las épocas.
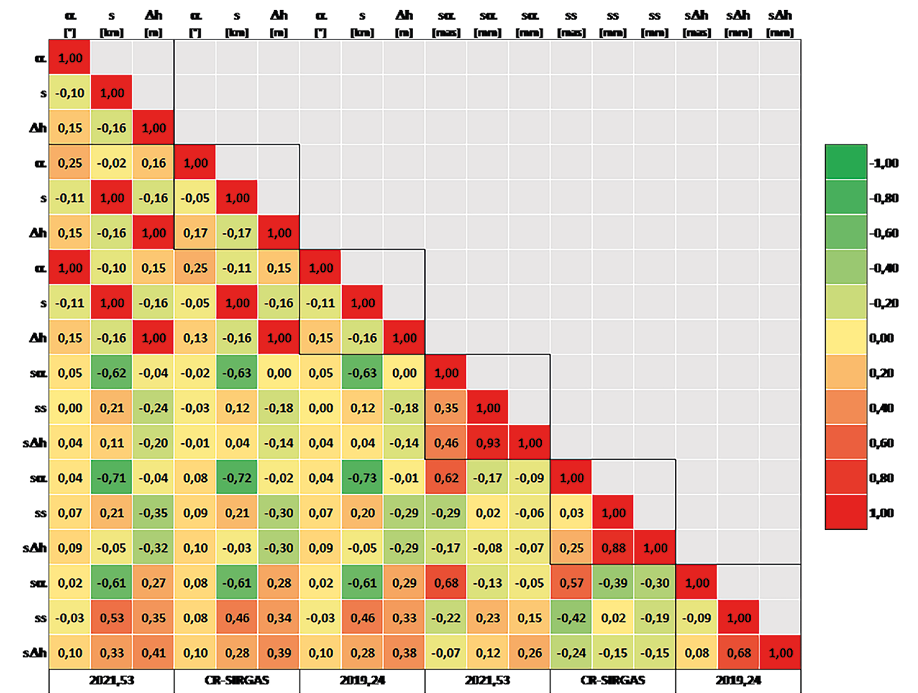
Fuente: elaboración propia
Fig. 11 Matriz de correlación para los conjuntos de observaciones ajustadas obtenidas en cada una de las tres épocas consideradas.
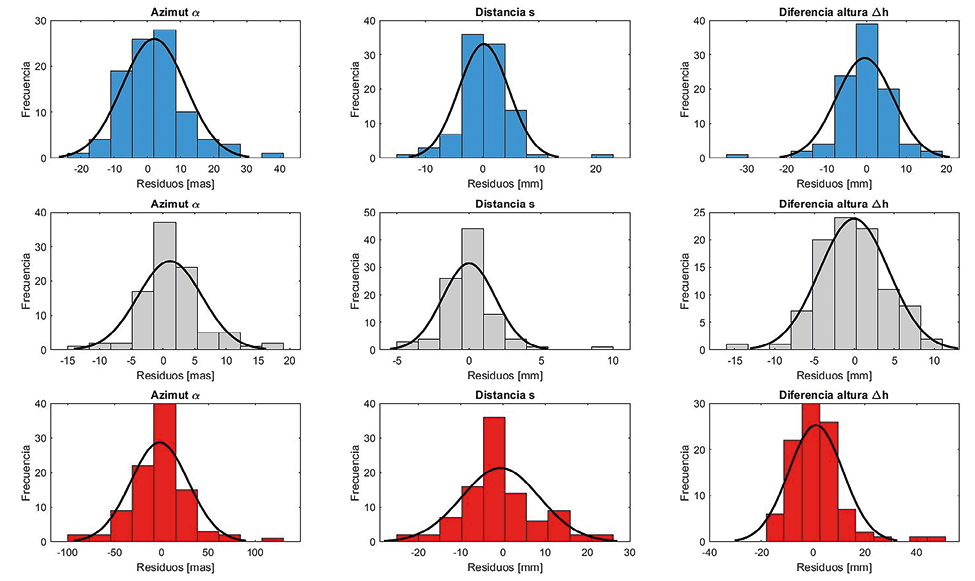
Los residuales son las correcciones que proporciona el algoritmo de ajuste a las observaciones originales. En el conjunto de gráficos de la Fig. 12, se presenta su distribución por época de ajuste y su tipo de magnitud. Superpuesta, se grafica la curva de la función de densidad en color negro. En las filas de arriba hacia abajo, se muestran los resultados generados por los ajustes relativos a 2021,53, CR-SIRGAS y 2019,24 y, en las columnas de izquierda a derecha, se presentan las componentes elipsoídicas de azimut, distancia y diferencia de altura, respectivamente. En los gráficos de la figura, se observa, evidentemente, que los residuos son aleatorios y que se distribuyen de una manera prácticamente normal. Además, se nota que, en el caso del ajuste CR-SIRGAS, las tres componentes tienen una dispersión menor, aproximadamente la mitad al compararla con el ajuste 2021,53. Sin embargo la dispersión de los residuales en el ajuste 2019,24 es mucho mayor en todas las componentes, lo cual implica que se tuvieron valores individuales que se alejan del valor central. Debe también indicarse que, en todos los setenta y dos procesos de ajuste realizados, no hubo evidencia estadística de observaciones groseras.
Fuente: elaboración propia
Fig. 12 Distribución de los residuos para cada una de las componentes geodésicas de las líneas base ajustadas.
La exactitud de las observaciones ajustadas no siempre es considerada importante por los usuarios, sin embargo, ofrece valiosa información cuando se analizan los resultados de un proceso de ajuste. En observaciones GNSS, una primera evaluación se da, por ejemplo, al usar la exactitud nominal de los receptores en las componentes horizontal y vertical y en los respectivos modos estático y cinemático. Ahora bien, probablemente esta estimación inicial teórica de los errores sea aplicada solamente para contar con información general que permita a los usuarios conocer la incertidumbre en la longitud de las potenciales líneas base a medir y en muy pocos casos se le prestará atención a la componente vertical y la estimación en la parte angular será prácticamente nula.
En el conjunto de gráficos de la Fig. 13 se presentan las exactitudes obtenidas de los procesos de ajuste respecto a las tres épocas analizadas. En el eje vertical, se tiene la magnitud de la exactitud y, en el eje horizontal, los valores de cada una de las líneas base ordenadas de manera ascendente. El objetivo es mostrar el comportamiento de la exactitud en función de su componente respectiva.
Fuente: elaboración propia
Fig. 13 Comparación de las exactitudes en observaciones ajustadas ordenadas ascendentemente de acuerdo con las magnitudes geodésicas de las líneas base ajustadas.
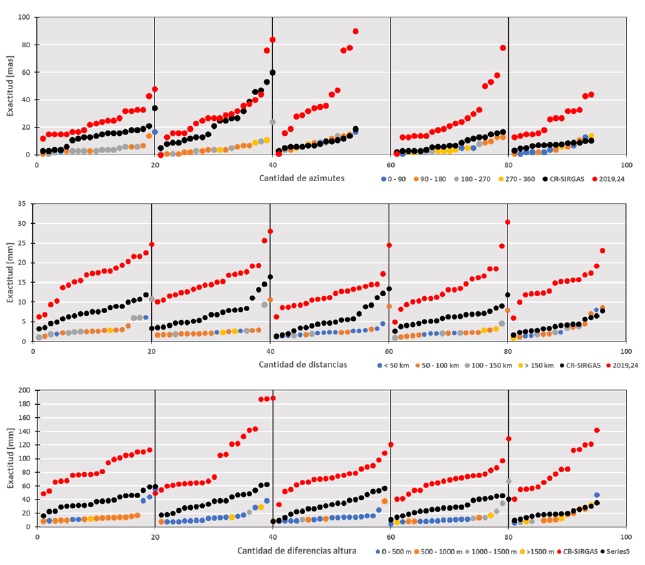
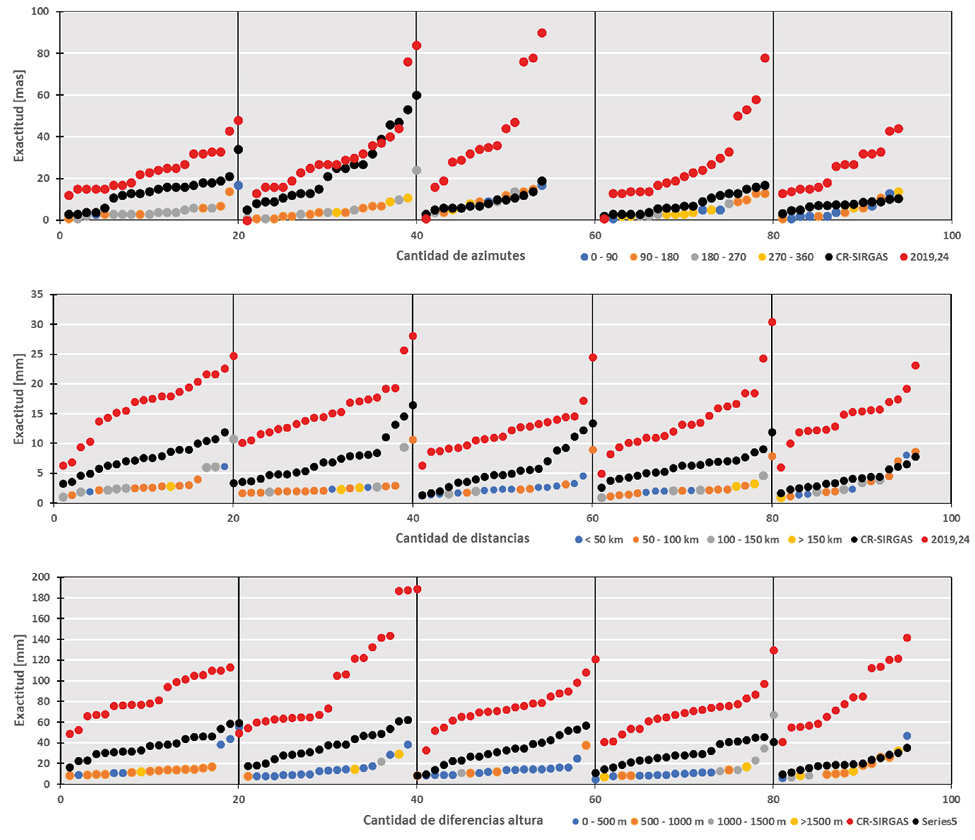
De forma complementaria a la información presentada anteriormente, en el conjunto de gráficos de la Fig. 14 se presenta, en el eje vertical, la exactitud de las observaciones ajustadas separadas en sus compontes de azimut, distancia y diferencia de altura y en el eje horizontal, la cantidad de observaciones de cada componente separadas en rangos de veinte observaciones. Los puntos en cada uno de los segmentos representan los valores de exactitud ordenados ascendentemente e identificados por colores azul, naranja, gris y amarillo, de acuerdo con el rango de la observación para la época 2021,53. Adicionalmente, el conjunto de puntos de color rojo representa la exactitud de las observaciones ajustadas en la época 2019,24.
La idea general de la Fig. 14 es mostrar el comportamiento de la exactitud en cada componente independientemente del valor de la observación. Se nota que la exactitud en el ajuste 2019,24 es visiblemente más baja con respecto a los valores logrados en 2015,53 y en CR-SIRGAS. Particularmente la componente azimutal en esta época presentó valores que superaron los ±100 mas (10-3 segundos) de exactitud. Fue, por esta razón, que se decidió eliminar esas observaciones del gráfico con lo cual se logró que en la escala vertical se aprecien los valores del resto de observaciones. Se recalca el hecho de que, aunque la exactitud en algunos azimuts fue superior a los ±100 mas, estadísticamente no se catalogaron como observaciones groseras. Aun así, se notan observaciones en el bloque de las veinte a las ochenta observaciones cuya exactitud decrece a más de ±60 mas. Se aprecia, además, cómo las exactitudes obtenidas en 2021,53 y CR-SIRGAS prácticamente coinciden en el bloque de las cuarenta a las noventa y seis observaciones, mientras que en los dos primeros bloques se tiene un comportamiento aleatorio para CR-SIRGAS y 2019,24 respecto a 2021,53. En el caso de las distancias elipsoídicas, los resultados de la exactitud tienen un comportamiento que se catalogó como similar en los primeros cuatro bloques y,, en el quinto bloque, 2021,53 y CR-SIRGAS prácticamente coinciden y quedando por debajo de los ± 10 mm. En todos los bloques de observaciones, se evidencia la disminución de la exactitud en 2019,24 con valores que alcanzan los ± 30 mm. Las observaciones de diferencias de altura elipsoídicas se graficaron calculando el valor absoluto de la observación para facilitar la interpretación del gráfico. Se evidencia que estas observaciones en 2021,53 se mantienen por debajo de los ± 20 mm con una alta coincidencia en el último bloque de observaciones. Con respecto a CR-SIRGAS, la exactitud estuvo en los ± 20 mm y los ± 60 mm. Sin embargo, la exactitud vertical de 2019,24 alcanza un rango entre los ± 60 mm y los ± 140 mm con tres observaciones que superan los ± 180 mm.
Discusión y conclusiones
El post-procesamiento correcto de observaciones GNSS requiere contemplar, indiscutiblemente, archivos de coordenadas finales de las estaciones que se tomarán como vínculo y de los archivos de órbitas finales, cuando se ocupe garantizar un nivel de exactitud subcentimétrico necesario para diferentes aplicaciones como la georreferenciación de información espacial. Los resultados presentados en este artículo se refirieron principalmente a cuantificar la disminución de la calidad en los resultados de ajustes GNSS por influencia de la época de observación y referencia.
El actual marco geodésico de referencia nacional, CR-SIRGAS, brinda la información necesaria que cuantifica, de manera general, los cambios físicos del país. Estos cambios repercuten en la cinemática propia de ese marco dando como resultado, dentro del período de este estudio (2,3 años), que los cambios en las coordenadas cartesianas geocéntricas estuvieran entre los 25 mm y los 57 mm (ver Figura 6). En otras palabras, las coordenadas de referencia de las estaciones CR-SIRGAS válidas en la época t0 = 2014,59 variaron significativamente con el tiempo en concordancia con el movimiento general del país.
Se realizó un análisis de todos los parámetros que se ofrecen en las salidas del programa de procesamiento TBC. En primer lugar, la varianza de referencia inicial se vio aumentada, lo que implicó una disminución en la calidad de los restantes parámetros estadísticos (ver Fig. 5). La clara disminución en el peso inicial de las observaciones es un aspecto que no se había cuantificado y que evidentemente influye de forma negativa en los resultados. La cuantificación del equilibrio de la varianza inicial estuvo entre 1,5 y 9,5. En el caso concreto de este estudio, se evidenció que mediciones de 24 h, tomadas en la época de observación ti = 2021,53, brindaron resultados con una alta exactitud cuando fueron debidamente procesados, es decir, contemplando coordenadas de amarre y órbitas finales en la respectiva época de observación (ver CUADRO IV). Sin embargo, este mismo conjunto de mediciones, al ser procesado en la época de referencia t0 = 2019,24, presentó una disminución en la calidad de los resultados de coordenadas y observaciones ajustadas (ver CUADRO IV y Fig. 10, 13 y 14).
Se determinó la matriz de correlación de las observaciones ajustadas obtenidas para cada una de las épocas consideradas. Esta matriz muestra que, dependiendo del tipo de magnitud y de la época respectiva, el coeficiente de correlación puede ser significativo; además, como parte del análisis global, se mostró el comportamiento de los residuales, su función de distribución (ver Fig. 12) y el comportamiento de las componentes geodésicas de las líneas base ajustadas (ver Fig. 13 y 14).
Se lograron también cuantificar las diferencias en las coordenadas ajustadas obtenidas con observaciones registradas en la épocas 2019,24 y 2021,53 y llevadas estas últimas a la época 2019,24. Los resultados demostraron que la diferencia en las coordenadas cartesianas geocéntricas ajustadas en 2019,24 está entre los 4,1 mm y 5,2 mm (CUADRO III); aunque la diferencia es pequeña, la misma debe ser analizada en concordancia con la exactitud en las coordenadas ajustadas, la cual disminuye presentando valores entre ± 8 mm y ± 136 mm (CUADRO IV y Fig. 8) y con la respectiva disminución de la exactitud de las observaciones ajustadas (ver Fig. 13 y 14).
Se cuantificó la afectación en la exactitud de las coordenadas cartesianas geodésicas ajustadas (Fig. 9) por medio del denominado factor de reducción fr , que tomó valores extremos entre 2 y 15, afectando fuertemente a las estaciones CDME e IRZU y, en menor grado, a las estaciones EART y RIFO.
Se presentó el comportamiento de las elipses absolutas de confianza al 95 % de probabilidad (Fig. 10), en las que se evidenció un aumento de los semiejes en los resultados 2019,24 y, sin embargo, se mantiene una orientación azimutal prácticamente invariable en las tres épocas. Esto es producto de la misma configuración en las redes, pero con repercusión de la época de observación. Es decir, el aumento en el tamaño de las regiones de confianza no se debe a la configuración de las redes, sino producto de la referencia temporal.
El usuario deberá tener claro que el ajuste de un conjunto de observaciones GNSS estará ligado a su época de referencia, por lo que, necesariamente, tendrá que considerar órbitas finales y coordenadas de vínculo a la misma época. Además, se debe señalar que cuando el traslado a una época diferente a la de observación sea posible, los resultados perderán calidad en cuanto a su exactitud, tal como se expuso en este documento.
Cabe, entonces, la pregunta de si una transformación de coordenadas podría generar mejores resultados. No necesariamente. Este proceso depende de la calidad de los puntos y de los propios valores de los parámetros: si estos fueron locales o contemplan todo el país y, además, de toda una serie de posibilidades. No obstante, la transformación de coordenadas es un procedimiento tan válido como el traslado entre épocas. Queda a criterio del usuario una u otra aplicación. Consecuentemente, es necesario advertir, además, que este estudio trabajó con observaciones de 24 h por lo que la emulación de la metodología presentada, considerando mediciones con tiempos menores y diferente cantidad de estaciones de vínculo, probablemente brinden resultados de una calidad menor a la presentada en este artículo.
Se recomienda a los profesionales, cuyos proyectos tengan finalidades catastrales, ser consistentes con la época de observación y los datos relativos a ella, sin dejar de lado las tolerancias oficiales para los procesos de georreferenciación. Se sabe que la actualización de los diferentes insumos catastrales usados por las autoridades no puede darse con la misma periodicidad con la que se obtienen las coordenadas del marco y de ahí que lo ideal sería brindarle a la administración los mejores resultados posibles vistos como una contribución particular al desarrollo nacional.
Este trabajo brinda tres anexos con los resultados de las coordenadas para las épocas 2021,53, CR-SIRGAS y 2014,59, que se pueden usar como referencia para diferentes aplicaciones topográficas, catastrales y cartográficas. Obviamente, estos resultados de las coordenadas se deben trabajar considerando adicionalmente los objetivos y finalidades específicas de cada proyecto. Se aclara que, aunque los resultados de coordenadas ajustadas fueron obtenidos con la mejor exactitud posible que ofrece el programa de procesamiento, estos valores, de momento, no son oficiales, ya que no cuentan el aval por parte del Instituto Geográfico Nacional de Costa Rica.