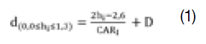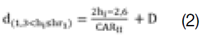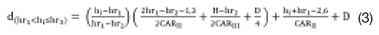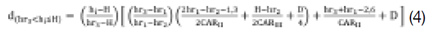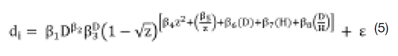Introdução

A quantificação de multiprodutos em povoamentos florestais permite delinear o melhor aproveitamento possível da madeira, principalmente, com um cenário favorável à tomada de decisões frente às oscilações do mercado de produtos madeireiros. Para isso, é fundamental conhecer o perfil do fuste das árvores a fim de realizar o sortimento dos diferentes usos desejáveis. Tal exigência, demanda o emprego de uma equação de taper estimada a partir de dados de cubagem que, geralmente, é realizada em árvores-amostra abatidas. Também, em algumas situações, a cubagem pode ser feita com a árvore em pé, como em (¹) onde foram cubadas 110 árvores de Anadenanthera peregrina empregando-se um Pentaprisma de Weller.

Independentemente, de abater ou não as árvores-amostra para cubagem, esta atividade acomoda um grande número de dados, como se observa em (²), que acumularam 802 diâmetros medidos ao longo do tronco de 86 árvores de pinus. Também, em (³), que mediram 283 diâmetros do tronco em 35 árvores cubadas de Corymbia citriodora. Já, como em (⁴), onde coletaram um total 1.695 dados de cubagem de 78 árvores de pinus. Porquanto, em (⁵) obtiveram 2.412 dados de cubagem de 201 árvores de P. brutia. Nessas situações caracterizadas, se pode empenhar esforços visando reduzir a massa de dados de cubagem sem prejudicar a confiabilidade das equações de taper geradas.

Destaque pode ser dado ao método da altura relativa (¹), que possibilita a descrição do perfil do fuste de árvores sem o emprego de uma grande base de dados de cubagem. As medições podem ser coletadas com as árvores em pé, pois exige apenas os diâmetros do fuste situados à 0,1 m, 1,3 m, altura total (H) e em um ponto relativo a H, definido como altura relativa (hr). Aliás, o problema está apenas em hr que pode ser resolvido pelo emprego de um pentaprisma de Weller ou Relascópio de Bitterlich, porque em 0,1 m e 1,3 m a medição do diâmetro do fuste é feita sem dificuldades técnicas operacionais, e em H o mesmo tem valor igual a zero para a espécie em análise.

Se apercebe, então, que o Método da Altura Relativa (Método hr) consiste de uma metodologia promissora para constar em atividades de inventários florestais, porque permite que os diâmetros em 0,1 m, 0,3 m e em hr sejam tomados de forma simultânea às demais variáveis medidas em parcelas de inventário (⁶). Também, nesta metodologia, o volume do fuste pode ser obtido por meio de uma cubagem simulada com as equações de taper geradas resultando em boa acuracidade, como se observa em (⁷), (⁸).

Outra alternativa no desenvolvimento do Método hr é o ajuste de modelos de taper, ou de volumes, empregando-se dados de cubagem simulada com as equações que compõem a metodologia (¹), (⁷). Por exemplo, em (⁷) se realizou o ajuste de modelos de volumes para avaliar o crescimento inicial de eucalipto e acácia em uma integração de lavoura, pecuária e floresta e também em monocultivo.

Por outro lado, em (¹) foi avaliado o emprego de dados de A. peregrina no ajuste do modelo de taper de Kozak (1988), evidenciando acurácia em níveis aceitáveis com emprego tanto de medições diretas do diâmetro do fuste (cubagem de árvores abatidas) quanto de diâmetros obtidos pelo Método hr (cubagem de árvores em pé).

Dentre os trabalhos com enfoque no Método hr, feitos em espécies de eucalipto, acácia, mogno africano e pinus, não se observam trabalhos feitos com dados de Corymbia citriodora. Por isso, dada à importância desta espécie para a produção de diferentes produtos madeireiros (carvão vegetal, lenha, mourões, madeira serrada, dentre outros), se conduziu este trabalho com o objetivo de comparar o ajuste de equações de taper empregando-se dados de cubagem obtidos por meio de medições diretas ao longo do fuste e indiretamente por meio do Método hr.

Material e métodos

O estudo foi realizado utilizando-se dados coletados em um plantio seminal de Corymbia citriodora localizado próximo ao município de Gurupi, estado do Tocantins, Brasil. Este plantio, implantado no espaçamento inicial de 3m X 2 m, tinha a idade de 67 meses na época da coleta de dados que se referem à cubagem feita em 24 árvores abatidas.

Em cada árvore abatida, foram feitas medições diretas do diâmetro ao longo do fuste nas posições: 0,2 m; 0,4 m; 0,7 m; 1,3 m; 2,7 m e, sucessivamente, de 2 m em 2 m até um diâmetro em torno de 3 cm. Também, se mediu a altura total (H) e o diâmetro em hr = (H − 2) / 2 exigido para o desenvolvimento do Método hr que incluiu, ainda, os diâmetros em 0,2 m, 1,3 m e H. Com estes dados, se obteve as seguintes equações de taper (1, 2, 3, 4 e 5):

Em que: d_{(0,0≤hi≤H)}= diâmetro obtido ao longo do fuste empregando-se geometria analítica (cm); CAR_I, CAR_II e CAR_III= coeficiente angular da reta entre 0,2 a 1,3m, 1,3m a hr e hr a H, respectivamente; h_i=i-ésima altura no fuste onde se deseja obter o diâmetro d_i (m); D=DAP (cm); H=altura total (m); hr1= (H-1.7)/1.7 (m), hr2= (H-1.4)/1.4 (m) e hr3= (H-1.1)/1.1 (m).

Empregando-se as equações de 1 a 4, nas mesmas posições em que se fez medições diretas de diâmetros do fuste com as árvores abatidas (cubagem real), se realizou uma cubagem supondo-se as 24 árvores em pé (cubagem hr). Dessa forma, se obteve as informações necessárias ao ajuste de modelos de taper empregando-se dados da cubagem real e cubagem hr. Para isso, utilizando-se o programa estatístico R For Windows 3.6.2 (⁹), procedeu-se ao ajuste do modelo de taper de Muhairwe (¹⁰) que tem a seguinte conformação eq.5:

Em que: d_i= diâmetro do tronco na i-ésima altura h_i de cubagem (cm); z=hi/Hb, b= coeficientes da regressão à serem estimados; e= erro aleatório do modelo; demais já foram definidos anteriormente.

Para avaliar as equações de taper, geradas com dados de cubagem real e cubagem hr, foi adotada a validação cruzada que consistiu no uso de dois bancos de dados, sendo um reservado para gerar equações e outro para aplicação destas e vice-versa. Nessa condição, conforme feito por (³), adaptou-se as informações da cubagem das 24 árvores utilizando-se, para o primeiro banco de dados (BD1), as posições: 0,2 m; 0,7 m; 4,7 m e a cada 4 m até a última posição no fuste. Já, para o segundo banco de dados (BD2), utilizou-se as posições: 0,4 m; 2,7 m e a cada 4 m até a última posição no fuste que não foi utilizado no BD1.

Empregando BD1 e BD2, em uma validação cruzada, foi possível avaliar a predição dos diâmetros do fuste por meio das equações de taper estimadas a partir do modelo de Muhairwe empregando-se dados de cubagem real e cubagem hr. Neste caso, para avaliar os valores preditos de diâmetros do fuste, foram adotados os critérios estatísticos: resíduo médio (RM), Bias (B), correlação linear entre valores preditos e real (r), desvio padrão dos resíduos (DPR), exatidão de predição obtida pelo teste de qui-quadrado ao nível de 5% de significância (Ex) e raiz quadrada do resíduo médio (RQRM), além da análise gráfica da distribuição dos resíduos (AGR), em cujas formulações e procedimentos de análises podem ser vistos em (³) e (¹¹).

A análise também foi feita na quantificação do volume do fuste das 24 árvores aplicando-se a fórmula de Huber nos dados da cubagem real e cubagem hr. Como a divisão em dois bancos de dados resultaria em baixo número de indivíduos, a análise do volume foi feita com uma validação com dados dependentes adotando-se os mesmos critérios estatísticos da avaliação de equações de taper.

Resultados e discussão

Inicialmente, aplicando-se o método da altura relativa nas 24 árvores cubadas de C. citriodora, se descreveu o perfil do fuste utilizando-se as mesmas posições em que se efetuou às medições diretas nestas mesmas árvores abatidas. Como mostra a Figura 1, há uma tendência de sobreposição da dispersão da cubagem hr com a cubagem real evidenciando a viabilidade de emprego desses dados no ajuste de modelos de taper, como se faz com os dados da cubagem real (³), (¹¹), (¹²).

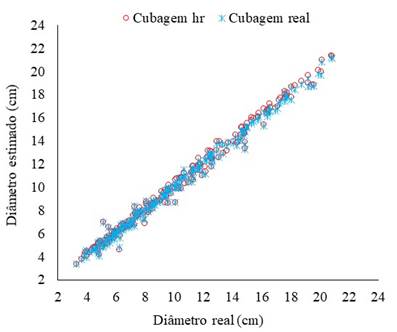
Figura 1 Dispersão de diâmetro do fuste de Corymbia citriodora empregando cubagem hr e cubagem real. 

Figure 1. Stem diameter dispersion of Corymbia citriodora using real and hr cubing.

Diante disso, utilizando-se os dados obtidos em BD1 (n=106) e BD2 (n=91) com a cubagem real (CR) e cubagem hr (Chr), se procedeu ao ajuste do modelo de Muhairwe (¹⁰) gerando-se duas equações de taper para cada banco de dados (Tabela 1). Em seguida, por meio da aplicação em BD2 das equações geradas por BD1 e vice versa, se obteve uma inexpressiva superioridade das equações geradas por CR, porque os resultados são bem próximos (Tabela 2). Exceção se faz com os critérios RM e B por não resultarem em valores muito próximos entre CR e Chr, porém, se apresentam em níveis aceitáveis de acurácia expressando erros inferiores à ± 2 %.

Tabela 1 Coeficientes estimados do modelo de Muhairwe empregando-se dados obtidos pela cubagem real e cubagem hr. 

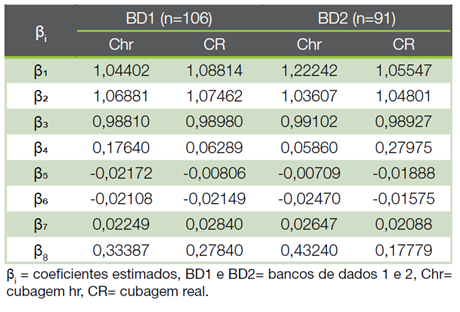
Tabela 2 Critérios estatísticos adotados na validação cruzada das equações de taper geradas a partir do ajuste do modelo de Muhairwe empregando-se dados de cubagem real e cubagem hr. 

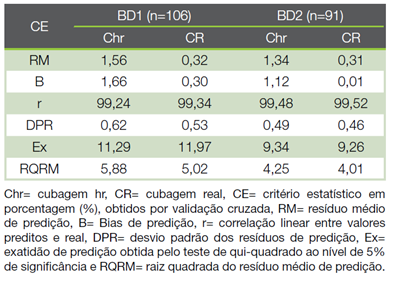
Quanto à correlação r acima de 0,992, se observam resultados expressando altíssimo índice entre valores reais e preditos como em (³), que resultou em r=0,994 para o modelo em estudo. Valores estes muito parecidos devido à, principalmente, se tratar da mesma espécie apesar de os dados serem coletados em plantios diferentes. Também, este resultado de r>0,992, é melhor ao r=0,942 obtido por (¹¹), sendo o único trabalho que se procedeu igualmente a este estudo, mas utilizando-se o modelo de Kozak (¹³).

Pelo critério Ex, os diâmetros estão sendo preditos com erros inferiores à 12% com 95% de probabilidade, tendo uma exatidão com valores muito próximos para as equações geradas empregando-se dados de CR e Chr. Valores, também, melhores aos obtidos por (¹) com Ex de 22,5% para Chr e de 23,7% para CR. Resultados estes, tanto de r=0,942 como Ex, tiveram qualidade inferior ao presente estudo, provavelmente, por se tratar de uma base de dados de cubagem que se refere à uma espécie florestal amostrada no ambiente de mata nativa (Floresta Atlântica).

Por outro lado, quanto à distribuição dos resíduos (Figura 2), se observa no uso de BD1 que os resíduos se distribuem de forma homogênea e bem equilibrada ao longo do eixo 0 cm de resíduo com ±1,5cm, tanto em relação ao diâmetro predito quanto à altura ao longo do fuste, tendo melhor comportamento para CR. Houve uma tendência em ocorrer resíduos negativos na predição de diâmetros do fuste acima de 15 cm para Chr, sendo tal tendência não detectada para os resíduos em relação de hi que foi igual para ambos CR e Chr.

No uso de dados BD2 (Figura 2), a distribuição de resíduos foi desejável para ambos dados de cubagens CR e Chr com efeito bem menos indesejável com o que foi detectado com BD1. Já, nos histogramas dos resíduos, houve uma tendência de haver distribuição normal destes para ambos dados de cubagens CR e Chr com uma melhor distribuição para CR.

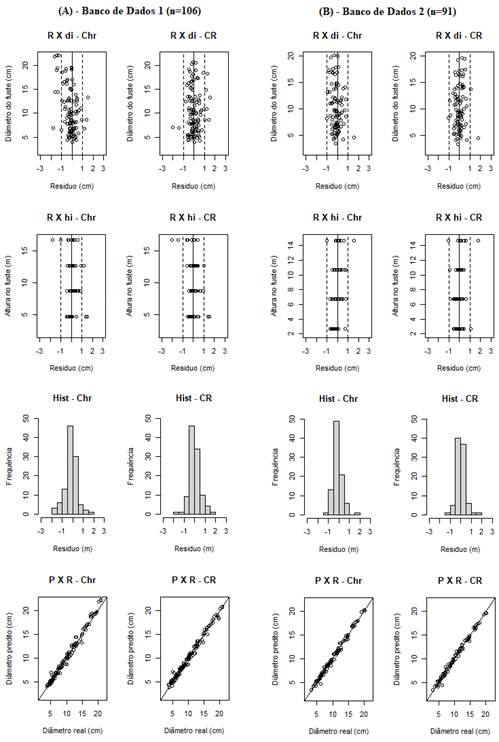
Figura 2 Distribuição de residuos para o modelo de Muhairwe obtido na validação cruzada. R= resíduo, di= diâmetro do fuste, hi= altura no fuste, Hist= histograma, P= predição, Chr e CR= cubagem hr e CR. 

Figure 2. Residual distribution of the Muhairwe model obtained in the cross-validation. R= residue, di= stem diameter, hi= stem height, Hist= histogram, P= prediction, Chr and CR= cubing hr and CR.

As análises feitas com o ajuste do modelo de Muhairwe, evidenciaram haver níveis de acurácia aceitáveis e muito próximos nas equações de taper geradas, tanto com o emprego de CR quanto com Chr. Com isso, se pôde inferir que: usar dados de cubagem obtidos por Cr e Chr no ajuste de uma equação de taper, se pode gerar equações diferentes em níveis aceitáveis de acuracidade. Isso, aliado ao fato de o método da altura relativa possibilitar a coleta de dados com a árvore em pé, se torna bastante vantajoso porque a viabiliza ser feita junto com as medições nas parcelas de inventário (⁶), o que proporciona redução no tempo e custos na coleta de dados de cubagem.

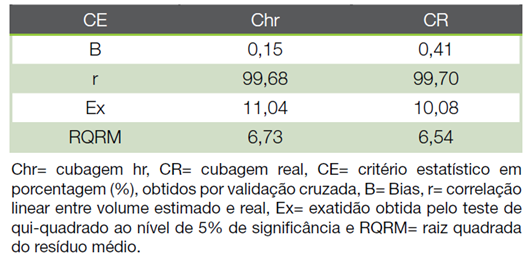
A avaliação também foi feita aplicando-se a formula de Huber nos dados obtidos por CR e Chr resultando no volume individual das 24 árvores. Se utilizou de uma validação com dados dependentes, porque a separação em dois lotes de dados iria resultar em baixo número de árvores para ajuste e validação. Como resultado, se obteve para Chr um B=0,15% melhor que CR, sendo nos critérios estatísticos r, Ex e RQRM obtido um resultado favorável ao uso de CR com valores de 99,7%, 10,08% e 6,54%, respectivamente (Tabela 3).

Tabela 3 Critérios estatísticos utilizados para avaliar o volume a partir das equações do modelo de Muhairwe ajustado com dados de cubagem real e hr. 

Os resultados obtidos por Chr são próximos aos obtidos pelo emprego de CR (Tabela 3), proporcionando um nível de acurácia na quantificação do volume também em níveis aceitáveis, o que evidencia o mesmo resultado da análise das equações de taper. Além disso, a análise da distribuição de resíduos (Figura 3), comprova os resultados estarem diferentes de forma a não destacar um uso preferencial por CR. Se observa no histograma dos resíduos, uma amplitude entre ±15% para CR e uma amplitude de ±10% para Chr. Portanto, se pode inferir que é possível também utilizar o método da altura relativa para obter o volume individual de árvores de C. citriodora, com ressalvas de não haver a necessidade de abater árvores-amostra para cubagem.

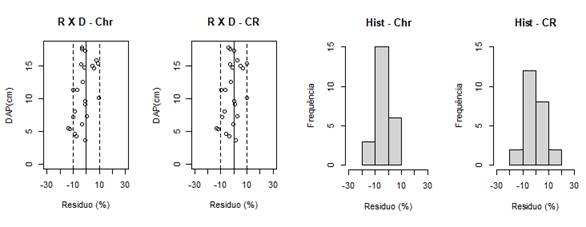
Figura 3 Distribuição de resíduos do volume obtido pelas equações do modelo de Muhairwe empregando-se a cubagem hr (Chr) e real (CR). R= resíduo, D=diâmetro do tronco em 1,3 m (DAP), Hist= histograma. 

Figure 3. Residual distribution of the volume obtained by the Muhairwe model using the cubing hr (Chr) and real (CR). R= residual, D= stem diameter in 1.3 m (DHB), Hist= histogram.

Conclusão

De acordo com os resultados obtidos neste estudo, concluiu-se que o ajuste de um modelo de taper, empregando-se dados de cubagem simulados pelo Método hr, resulta em um nível de acurácia aceitável, inexpressivamente inferior ao obtido com o uso de dados reais de cubagem de C. citriodora, inclusive na quantificação do seu volume. Também, que o emprego do Método hr, possibilitará significativa redução de tempo e custos dos procedimentos técnico-operacionais envolvidos na coleta de dados, uma vez que exige a medição de diâmetros do fuste em apenas quatro posições sem o abate de árvores-amostra, possibilitando que sejam feitas em simultâneo com as medições das parcelas de inventário.