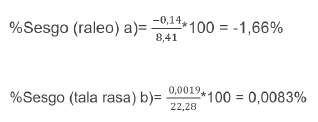Introducción
Las plantaciones forestales han sido parte importante en el uso de la tierra desde hace varias décadas y seguirán aumentando en los próximos años, tanto para la producción de madera con fines industriales como para la generación de servicios ambientales (Prado, 2015). El fin último de las plantaciones forestales es alcanzar los objetivos máximos de producción que permitan obtener la mejor rentabilidad para el productor, en concordancia con buenas prácticas de manejo (Sotomayor, Helmke y García, 2002) y un aprovechamiento forestal sostenible. En el sector forestal se han utilizado por muchos años los modelos de regresión para estimar la tasa de producción de una plantación y para predecir la producción de los diferentes métodos de aprovechamiento forestal.
La principal función de los modelos de regresión es tratar de explicar el comportamiento de una variable conocida como “dependiente”, en función de una o más variables llamadas “independientes”. En plantaciones forestales han sido utilizados para medir la biomasa, estimar el crecimiento de los árboles, predecir el volumen y medir la respuesta a tratamientos silviculturales (FAO, 1980; Ortiz-Malavasi, 2006). Según la FAO (1980), un modelo de regresión consiste en un conjunto de ecuaciones o gráficos que muestran las relaciones cuantitativas que existen entre las variables en estudio. Normalmente, los modelos de regresión son ajustados mediante los análisis de regresión y la escogencia del mejor modelo va a depender, entre otras variables, del Coeficiente de determinación (R2), el Coeficiente de determinación ajustado (R2-ajust) y del Error estándar de la muestra (Syx) (Ortiz-Malavasi, 2006).
El objetivo principal de esta investigación fue desarrollar las ecuaciones de regresión de mejor ajuste para predecir la producción (m3/h) de la operación de arrastre de madera en troza proveniente de plantaciones de Gmelina arborea con búfalos de agua, para lo cual se plantearon dos hipótesis: hipótesis del investigador: existe al menos un modelo de estimación que pueda utilizarse con confiabilidad y precisión en la estimación de la producción de madera en troza en la labor de arrastre con búfalos de agua y la hipótesis estadística: no existe ningún modelo de estimación que pueda utilizarse con confiabilidad y precisión en la estimación de la producción de madera en troza en la labor de arrastre con búfalos de agua.
Material y métodos
Sitio de muestreo
La evaluación de la operación de arrastre se realizó en cinco fincas pertenecientes a pequeños productores de la región Huetar Caribe de Costa Rica. Específicamente las fincas se encuentran en la zona de Sahara de Bataán, en la provincia de Limón y pertenecen a productores cuya principal actividad económica es la agricultura. Según datos del Instituto Meteorológico Nacional (2015), la provincia de Limón presenta una temperatura media anual de 25,86 °C y una precipitación media mensual de 298,25 mm. El mes de setiembre es el más seco y el de diciembre el más lluvioso (142 mm y 443 mm anuales respectivamente).
Análisis de los datos
En cada una de las 5 fincas evaluadas se recolectaron datos de dos tratamientos silviculturales que generaron dos condiciones de aprovechamiento: raleo y tala rasa, de dos métodos de arrastre empleados: sulky y cadenas, así como de dos búfalos: Búfalo 1 (4 años de edad) y Búfalo 2 (13 años de edad); con la finalidad de analizarlos estadísticamente para verificar si existía o no diferencia entre los grupos de datos obtenidos. Para realizar la recolección de datos se desarrolló un estudio de tiempos (T) y movimientos (M) utilizando la metodología del muestreo propuesta por Cordero (1988).
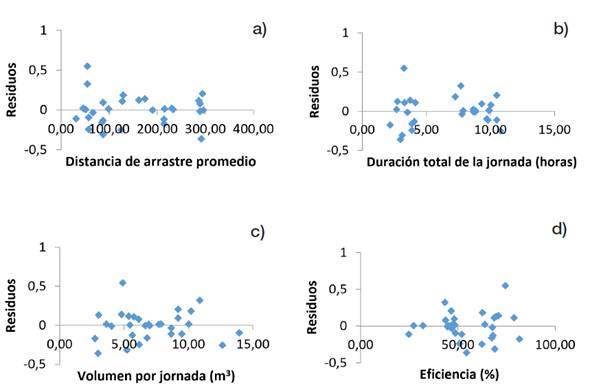
Se construyeron dos tablas en hojas electrónicas de Excel (versión 2013), la primera con los ciclos evaluados (viaje vacío, amarre de la troza, viaje cargado y soltar la troza) y la segunda con las jornadas de trabajo. Se consideró como la variable dependiente la producción de madera (m3/h) y las variables independientes fueron: distancia de arrastre en metros (D), número de fustes arrastrados (N), duración total de la jornada en horas (T), duración efectiva de la jornada en horas (Te), volumen en metros cúbicos (V) y eficiencia en porcentaje (E). Para identificar la curva de mejor ajuste que guiara el desarrollo y escogencia de las mejores ecuaciones de regresión, se depuró la base de datos en forma objetiva y se crearon gráficos de dispersión.
Para el análisis estadístico de los datos se recurrió al programa Infostat (versión 10.0) con un 95 % de confianza (a= 0,05). Se realizó la prueba de normalidad Shapiro-Wilks en la que se plantearon dos hipótesis: Ho: los datos siguen una distribución normal y Ha: los datos no siguen una distribución normal. Para probar la homogeneidad de las varianzas de cada una de las variables se recurrió a un análisis de varianza (ANDEVA), el cual buscó probar las siguientes hipótesis: Ho: las varianzas de los datos son iguales y Ha: las varianzas de los datos son diferentes. Para probar si existía o no diferencias entre: a) condición de aprovechamiento, b) método de arrastre utilizado y c) búfalo utilizado para el arrastre, se empleó la prueba de Tukey para datos con distribución normal y la prueba de Bonferroni para datos cuyo comportamiento no fue normal.
Modelos de regresión
Para la construcción de los modelos de regresión que estimen la producción de madera se procedió a utilizar la metodología propuesta por Hughell (1990), con la ayuda del programa estadístico IBM SPSS Statistics Base (versión 22.0). Se utilizaron los promedios de los datos de cada uno de los ciclos de trabajo en cada una de las jornadas trabajadas; para cada una de las condiciones de aprovechamiento: raleo y tala rasa (cuadro 1).
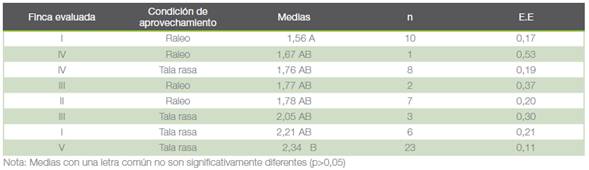
Cuadro 1 Prueba de Bonferroni para los datos de producción (m3/h) obtenida por finca durante el arrastre de madera de plantaciones forestales, Limón, Costa Rica en el 2016.
Para medir la calidad del ajuste del modelo escogido se consideraron aspectos como el coeficiente de variación, el coeficiente de determinación R2, el coeficiente de determinación ajustado y el error estándar de la muestra. Una vez generados y escogidos los modelos, se verificaron los supuestos de la regresión lineal múltiple (De la Fuente, 2011). Las hipótesis de linealidad, homocedasticidad e independencia fueron probadas a través de análisis gráficos que enfrentaron los valores de los residuos del modelo contra los valores ajustados. Mientras que la hipótesis de normalidad se comprobó mediante una prueba de Shapiro-Wilks realizada a los residuos para probar la normalidad o no de la distribución de los datos.
Como paso final se ejecutó la validación de cada uno de los modelos con un 25 % de los datos recolectados seleccionados al azar y que no fueron utilizados para la construcción de los modelos (5 jornadas en el caso del raleo y 10 jornadas en tala rasa). Para la validación se utilizó la fórmula del % de sesgo que establece que su resultado debe de encontrarse en un intervalo de +/- 2 % (Jiménez, 2012), de la siguiente manera:
Además, se realizó una prueba de Wilcoxon mediante el programa Infostat (versión 10.0) con el objetivo de verificar las siguientes hipótesis: Ho: la Σ de los valores observados es igual a la Σ de los valores estimados y Ha: la Σ de los valores observados es diferente a la Σ de los valores estimados.
Se eligieron los modelos que predijeron de forma confiable los datos de producción en cada una de las condiciones de aprovechamiento.
Resultados y discusión
Sitio de muestreo
El estudio se realizó en 5 fincas ubicadas en la región Huetar Caribe de Costa Rica, específicamente en la localidad de Bataán, provincia de Limón, entre las coordenadas 83°20’32”O y 10°05’09”N. Las plantaciones forestales fueron cosechadas en el período de abril 2015 a febrero 2016; se obtuvo un volumen promedio por árbol de 0,291 m3, un diámetro promedio de 25,27 cm y una altura comercial promedio de 10,98 cm.
Análisis de los datos
Se evaluaron un total de 1208 ciclos de arrastre durante el estudio de 60 jornadas o días de trabajo, 20 jornadas (527 ciclos) de la condición de aprovechamiento raleo y 40 jornadas (681 ciclos) de la condición de aprovechamiento tala rasa. El análisis se realizó con los datos promedios de las jornadas evaluadas.
Se probó la normalidad de todos los datos provenientes de las jornadas de trabajo por medio de la prueba Shapiro-Wilks la cual arrojó un p-value de 0,0061 con lo que se rechaza la Ho y se concluye que los datos no siguen una distribución normal, esto como consecuencia de la alta variabilidad que muestran las variables.
Se determinó si existió o no diferencia estadística entre: 1) condición de aprovechamiento, 2) método de arrastre y 3) búfalo utilizado para el arrastre de madera (cuadro 2 y 3).
Cuadro 2 Prueba de Bonferroni para los datos de producción (m3/hora) mediante dos métodos de extracción durante el arrastre de madera de plantaciones forestales ubicadas en Sahara de Bataán, Limón, Costa Rica en el 2016.

Cuadro 3 Prueba de Bonferroni para los datos de producción (m3/hora) mediante la utilización de dos búfalos durante el arrastre de madera de plantaciones forestales ubicadas en Sahara de Bataán, Limón, Costa Rica en el 2016.

1) Condición de aprovechamiento.
Se ejecutó un análisis de varianza de manera que se pudiera comprobar la homogeneidad de las varianzas de ambos grupos de datos. Se obtuvo p-value de 0,0096 lo que indica que las varianzas son diferentes. Utilizando estadística no paramétrica se realizó una prueba de Kruskal-Wallis coincidiendo con los resultados obtenidos en el ANDEVA (p-value: 0,0212), lo que sugiere que sí existe diferencia entre las fincas evaluadas. Como último paso se corrió una prueba de Bonferroni (Cuadro 1) con el objetivo de identificar entre cuales de las fincas existía diferencia.
Los resultados mostrados en el cuadro 1 sugieren que la Finca V con la condición de aprovechamiento tala rasa y la Finca I con la condición de aprovechamiento raleo fueron las fincas donde se presentó mayor variabilidad y entre el resto de las fincas existió diferencia pero no relevante. Además, se observó que precisamente las Finca I (raleo) y V (tala rasa) son las de menor y mayor producción (m3/hora) respectivamente, debido a que en la Finca I (raleo) se arrastró una menor cantidad de fustes durante todas las jornadas evaluadas, mientras que en la Finca V (tala rasa) la cantidad de fustes y los diámetros obtenidos fueron mayores, lo que generó un aumento en la producción. Otro aspecto influyente fue que el estudio inició con el aprovechamiento de la Finca I (raleo), y concluyó, año y medio después, con el aprovechamiento de la Finca V (tala rasa).
Por otro lado los datos de las medias sugieren la formación de dos grupos con características similares: el primero con las fincas en las que se aplicó raleo y el segundo con las fincas en las que se ejecutó la tala rasa. Los datos de mayor producción fueron los de tala rasa.
2) Método de arrastre.
Se realizó una prueba F para igualdad de varianzas basada en dos muestras en la que se obtuvo un p-value de 0,0723 lo que demuestra que las varianzas de ambos grupos de datos son iguales; esto fue corroborado con una prueba de Kruskal-Wallis (p-value de 0,7136). Por último se corrió una prueba de Bonferroni de manera que se lograran visualizar la poca diferencia entre las medias de ambos grupos de datos (Cuadro 2).
Los datos sugieren que estadísticamente no existió diferencia entre la utilización de uno u otro método de arrastre, ya que las condiciones casi planas de terreno, plantación y clima fueron muy homogéneas originando poca variabilidad entre los métodos utilizados. Sin embargo Guzmán y Zambrana (2009) mencionan que la utilización del sulky podría conllevar grandes beneficios para el animal cuando las distancias de arrastre son largas, ya que eleva la troza del suelo, disminuyendo la fricción al momento del arrastre.
3) Búfalos de agua utilizados para el arrastre.
Los datos fueron recolectados con dos animales distintos: Búfalo 1 y Búfalo 2. La prueba F para igualdad de varianzas mostró un p-value de 0,9368 lo que señala que ambos grupos de datos poseen varianzas iguales. Se recurrió a la prueba no paramétrica de Kruskal-Wallis (p-value 0,2698) con lo que se corroboró los datos de la prueba paramétrica F. El cuadro 3 muestra los resultados de la prueba de Bonferroni en donde se observa que las medias de ambos grupos son estadísticamente iguales.
El búfalo más utilizado fue el Búfalo 1. Este animal presentó un peso de 900 kg, una edad de 13 años y una experiencia aproximada en el arrastre de madera de 10 años, mientras que el Búfalo 2 se caracterizó por ser un animal joven de 4 años, un peso aproximado de 600 kg y una experiencia en el arrastre de madera de 2 años. Las diferencias físicas entre ambos búfalos no se visualizaron en la prueba de Bonferroni debido a que la fuerza que presentó el Búfalo 1 al arrastrar madera, fue equilibrada con la velocidad que mostró el Búfalo 2. Un animal tan pesado como el Búfalo 1, arrastró trozas de mayor volumen, pero en un gran lapso de tiempo; el Búfalo 2 por su parte, arrastró trozas con menos metros cúbicos en un lapso de tiempo corto, por lo que al final de la jornada la cubicación de la madera puesta en el patio de acopio fue similar para ambos animales.
Cuadro 4 Resumen de estadísticos para las ecuaciones con mejor ajuste al predecir la producción (m3/h) de la condición de aprovechamiento raleo, durante la operación de arrastre con búfalos en un aprovechamiento de plantaciones forestales. Limón, Costa Rica.

Los resultados obtenidos del análisis estadístico realizado anteriormente guían la búsqueda del modelo de regresión ya que se exponen las variables y las agrupaciones adecuadas para el mejor ajuste de los modelos. Durante el desarrollo del modelo de regresión fue necesario la agrupación de los datos obtenidos para cada uno de las condiciones de aprovechamiento utilizadas, no así para los métodos de arrastre ni para los búfalos utilizados en donde se sugirió desarrollar el modelo sin hacer alguna distinción.
Modelos de regresión
El desarrollo de los modelos de regresión se realizó por medio del programa IBM SPSS Statistics (versión 20.0). Se determinó el mejor modelo para el conjunto de datos de producción obtenidos durante el raleo (a) y se definió otro modelo para el conjunto de datos de producción obtenidos durante la tala rasa (b).
a) Generación de un modelo de regresión para un conjunto de datos obtenidos del aprovechamiento de un raleo.
Se seleccionaron los dos mejores modelos que predijeron con mayor exactitud la producción (m3/h). En el primer modelo seleccionado las variables “eficiencia” y “distancia de arrastre” resultaron no significativas a pesar de que el R2 fue mejor que en la segunda ecuación, por lo que se excluyó la variable “eficiencia” y se volvió a correr el modelo para verificar los resultados. El cuadro 4 muestra los estadísticos calculados para las dos ecuaciones que presentaron mejor ajuste, siendo la ecuación número 2 la mejor y más representativa.
La ecuación 2 fue la que presentó mejor ajuste para los datos de esta condición de aprovechamiento. Un 93,2 % de la variabilidad de la producción es explicado por variables como el volumen, la distancia y la duración total de la jornada, consideradas de fácil medición dentro del sector forestal si se toma en cuenta que son básicas dentro del estudio de plantaciones forestales; mientras que el restante 6,8 % es explicado por variables externas como el clima, el peso e incluso el ánimo del animal y factores propios de la operación de aprovechamiento entre otras.
Se verificó cada uno de los supuestos de la regresión. Los residuos de las variables que conforman la ecuación seleccionada fueron graficados. En los 3 casos (figura 1) los datos de residuos presentaron comportamientos constantes, sin ninguna formación de patrones que pusiera en riesgo el modelo seleccionado. Las tres variables independientes presentaron varianza constante con los valores distribuidos de manera homogénea a lo largo de la muestra.
Se aplicó la prueba de normalidad a los residuos obteniendo un p-value de 0,1385 señalando que los residuos de las variables son normales, cumpliendo con el tercer supuesto de los modelos de regresión.
b) Generación de un modelo de regresión para un conjunto de datos obtenidos del aprovechamiento de una tala rasa.
Se eligieron los dos modelos de regresión con mejor ajuste, los cuales se muestran en el cuadro 5. Durante el análisis del primer modelo se observó que la variable independiente “fustes arrastrados” fue no significativa, lo que quiere decir que no aportó nada al modelo por lo que se eliminó y se volvió a correr el programa. Los resultados del segundo modelo expusieron un R2 ajustado más bajo, sin embargo, todas las variables incluidas resultaron altamente significativas, lo que indica que la producción está correlacionada altamente con el volumen, la distancia de arrastre, la duración total de la jornada y con la eficiencia de la misma y que las variables antes mencionadas explicaron en un 86,7 % el comportamiento de la producción.
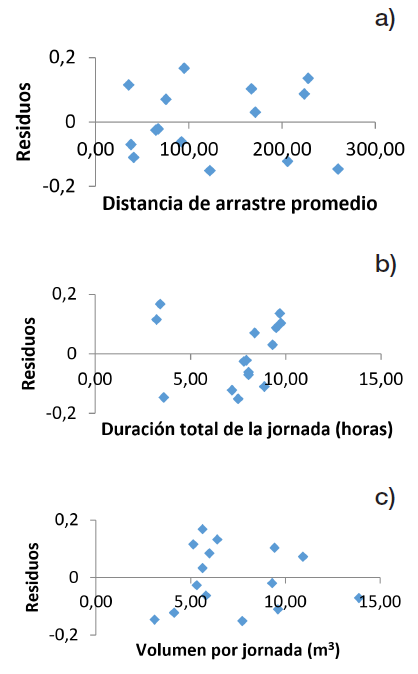
Figure 1 Residual values of production (m3/ h) for the variables of a) volume per day, b) distance of trawling and c) total duration of the day, during the operation of trawling with buffalo in an exploitation of forest plantations. Limón, Costa Rica in 2016.
Se aplicó la prueba de normalidad a los residuos obteniendo un p-value de 0,1385 señalando que los residuos de las variables son normales, cumpliendo con el tercer supuesto de los modelos de regresión.
a) Generación de un modelo de regresión para un conjunto de datos obtenidos del aprovechamiento de una tala rasa.
Se eligieron los dos modelos de regresión con mejor ajuste, los cuales se muestran en el cuadro 5. Durante el análisis del primer modelo se observó que la variable independiente “fustes arrastrados” fue no significativa, lo que quiere decir que no aportó nada al modelo por lo que se eliminó y se volvió a correr el programa. Los resultados del segundo modelo expusieron un R2 ajustado más bajo, sin embargo, todas las variables incluidas resultaron altamente significativas, lo que indica que la producción está correlacionada altamente con el volumen, la distancia de arrastre, la duración total de la jornada y con la eficiencia de la misma y que las variables antes mencionadas explicaron en un 86,7% el comportamiento de la producción.
La ecuación 2 fue la que indicó la mejor correlación entre las variables para el conjunto de datos obtenidos mediante la condición de aprovechamiento tala rasa.
La varianza de cada una de las variables (figura 2) fue constante, de igual manera el supuesto de normalidad de los residuos también se cumplió (p-value de 0,7671).
Las ecuaciones seleccionadas en cada uno de las condiciones de aprovechamiento resultaron estadísticamente confiables. No obstante, en ambos casos la segunda ecuación presentó un R2 más bajo que la primera, según Toro et al (2010) un buen ajuste resulta más difícil en la medida que aumenta el número de datos y disminuye el número de variables utilizadas; tal y como sucedió en este trabajo la primera presentó una variable más que la segunda por lo que el R2 fue mejor, sin embargo, alguna de las variables fue no significativa y se excluyó del modelo.
Variables como eficiencia, duración de la jornada y distancia de arrastre presentaron signo negativo dentro de las ecuaciones seleccionadas, lo cual representa un resultado inversamente proporcional a la producción: a mayor distancia y mayor duración, menor será la producción obtenida. En cuanto a la eficiencia, el signo negativo señala una eficiencia indirecta, es decir, la eficiencia pudo haber sido alta sin necesidad de que el búfalo estuviera arrastrando más madera. El estudio de tiempos y movimientos realizado para este trabajo señaló que el movimiento productivo “viaje vacío” tuvo casi el mismo porcentaje que el movimiento “viaje cargado”, lo que indica que, a pesar de estar realizando un movimiento productivo, lo cual aumenta la eficiencia, el animal va vacío, por lo que no necesariamente aumenta la producción.
Cuadro 5 Estadísticos resumen obtenidos para las ecuaciones con mejor ajuste al predecir la producción (m3/h) durante la operación de arrastre con búfalos en un aprovechamiento de plantaciones forestales. Limón, Costa Rica en el 2016.

Validación
La construcción de los modelos finalizó con la validación de las ecuaciones de mejor ajuste. La importancia de la validación radica en determinar si un modelo de regresión verdaderamente representa de uno u otro modo la realidad. Según Arango, Rivera y Granobles (2000), la validación es la aprobación, a través de procedimientos estadísticos adecuados, de un nivel aceptable de confianza, de tal modo que las interpretaciones para el sistema real efectuadas a partir de las inferencias obtenidas con el modelo de simulación, sean correctas. La validación se realizó con un conjunto de datos escogidos al azar, según se explicó en el capítulo de materiales y métodos.
Se verificó el porcentaje de sesgo tanto para a) el modelo escogido para los datos de raleo como para b) el modelo generado a partir de los datos de tala rasa, los cuales se muestran a continuación:
Los porcentajes obtenidos en ambos casos se encuentran dentro del intervalo permitido de sesgo (-2 %, +2 %) para poder decir con confianza que un modelo predice de manera correcta una variable. El signo negativo, mostrado en el resultado del primer modelo, indica que se estaría sobreestimando la producción en un 1,66%, ya que la suma de los valores estimados fue mayor que la suma de los valores observados, sin embargo, si se visualizan los resultados del modelo desarrollado para los datos de tala rasa, se puede decir que el modelo es muy bueno y que subestima los cálculos de producción en apenas un 0,008 %.
Además, se realizó la prueba de Wilcoxon la cual refuerza la validez de ambos modelos, obteniendo en ambos casos un p-value de 0,99, lo que señala que la suma de los valores observados es estadísticamente igual a la suma de los valores estimados.
Conclusiones
Los modelos de estimación en este estudio se basaron en datos obtenidos en la evaluación de la etapa de arrastre con búfalos de agua, al ser un ser vivo se genera heterogeneidad en las variables evaluadas.
El mejor modelo encontrado para la estimación de la producción basado en variables de fácil medición, obtuvo un R2 de 93,2 % para el caso de la condición de aprovechamiento raleo y 86,7 % para datos obtenidos del aprovechamiento de una tala rasa.
Los modelos obtenidos durante la evaluación de este trabajo son específicos para la zona de estudio ya que concentra características de clima y terreno muy particulares. Su utilización con otros datos deberá restringirse a plantaciones que cuenten con las características similares a las mencionadas en este trabajo.
Los modelos de producción, una vez validados, se convierten en una herramienta importante para el estudio y la caracterización de aspectos económicos, productivos y técnicos de un sistema de producción de madera reforestada.
Recomendaciones
Debido a que cada plantación presenta características distintas incluso estando establecidas en la misma zona de vida, se recomienda tener precaución al utilizar las ecuaciones desarrolladas para estimar la producción de madera reforestada durante este trabajo, al ser aplicadas en cada una de las plantaciones de interés.