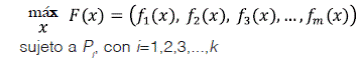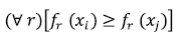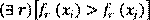Optimización multiobjetivo

En la optimización multiobjetivo, cada una de las funciones objetivo representa una aptitud o un costo a optimizar, las cuales dependen de n parámetros. Sin pérdida de generalidad, en el resto del artículo se mencionan problemas de optimización de aptitudes dejando claro que los principios y resultados también son validos para problemas de optimización de costos. En particular, la r-ésima aptitud está dada por una función y la función evaluadora del problema a optimizar está compuesta por dichas funciones de aptitud. Suponiendo que se deben optimizar m aptitudes, la función a optimizar es de la forma y el problema general está dado por:

donde 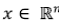y la i-ésima restricción está dada por la proposición P _i . En la búsqueda de la solución óptima del problema general, se trabaja sobre un espacio de posibles soluciones en , donde todas satisfacen un criterio multiobjetivo de optimalidad.

En otras palabras, el objetivo es optimizar de manera simultánea todas las funciones objetivo, puesto que en la mayoría de los problemas no es posible encontrar un solo valor óptimo para todas ellas, ya que el óptimo de una función no necesariamente lo es para las demás (^{Zitzler et al., 2003}).

Para comparar dos elementos del espacio solución se establece el concepto de dominancia de Pareto como un orden parcial sobre elementos en R ⁿ , en el que una solución x _i domina a otra solución x _j si se cumplen las siguientes dos condiciones:

x _i no es peor que x _j en todas las aptitudes

x _i es mejor que x _j en al menos una de las aptitudes

y se denota con x _i > x _j . Si alguna de las condiciones anteriores no se cumple, se dice que x _i no domina a x _j .

Una solución es Pareto óptima si y solo si no es dominada por ninguna otra solución, en ese caso todas las soluciones Pareto óptimas forman el conjunto de soluciones óptimas de Pareto denotado por 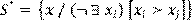y al conjunto 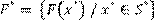se le llama

Frente de Pareto (^{Parmee et al., 2000}; ^{Ngatchou, 2008}).

Métodos clásicos adaptados

Estos métodos se derivan del desarrollo en series de Taylor de la función objetivo y se clasifican de acuerdo con la cantidad de términos que utilizan de dicha serie. Por ejemplo, el Steepest Descent (Gradient Descent) usa una aproximación de primer orden y el método de Newton una aproximación de segundo orden; ambos métodos realizan la búsqueda del óptimo por medio de direcciones de descenso, lo que acelera la convergencia a la solución si dicha aproximación es lo suficientemente cercana a la función real (Fliege & Svaiter, 2008).

Usualmente, los métodos clásicos se usan para resolver problemas uniobjetivo; sin embargo, existen adaptaciones para utilizarlos en problemas multiobjetivo. Por ejemplo, ^{Fliege et al. (2006}) adaptaron el método de Newton a problemas de optimización multiobjetivo con funciones convexas, formando el conjunto de soluciones óptimas de Pareto a partir de puntos llamados puntos críticos o estacionarios (^{Ortega & Rheinboldt, 2000}), donde 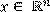es un punto crítico si .

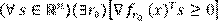A pesar de su exactitud, este tipo de métodos tiene la desventaja de que su comportamiento y convergencia dependen del tipo de función con la que trabajen. Por ejemplo, se requiere que la función sea derivable y convexa, condiciones no siempre garantizables en problemas de ingeniería.

Además, considerando que se trabaja con funciones cuya evaluación tiene un alto costo computacional y que la evaluación numérica de sus derivadas utiliza al menos dos llamadas de esa función, el costo total para evaluar dichas derivadas y gradientes es aún más alto; de manera que este tipo de métodos no es adecuado para esa clase de problemas.

Métodos heurísticos de optimización

Las heurísticas o métodos heurísticos son algoritmos construidos de manera intuitiva. Algunos autores denominan metaheurística a aquellos casos en los que el algoritmo de optimización utiliza a su vez subprocesos heurísticos, pero esta es una distinción no generalizada (^{Schweickardt, 2009}).

Entre las heurísticas más populares están Colonia de hormigas (AC: Ant Colony), Recocido Simulado (SA: Simulated Annealing), Búsqueda Tabú (TS: Tabu Search), Enjambre de Partículas (PS: Particle Swarm) y los algoritmos evolutivos (EA: Evolutionary Algorithm). Los EA se inspiran en conceptos de la evolución biológica tales como la reproducción, mutación, recombinación y selección (Vasunhara et al., 2015); además, balancean la exploración y explotación del espacio de búsqueda de manera exhaustiva con pocas evaluaciones. En contraste, AC, SA y TS son los métodos más antiguos y tienden a realizar más llamadas a la función evaluadora (^{Eskandari & Geiger, 2008}).

Los algoritmos genéticos (GA: Genetic Algorithm) son parte de los algoritmos evolutivos y utilizan técnicas aleatorias y estocásticas para simular la evolución por medio de la selección de individuos con características prometedoras (^{Gen & Cheng, 2000}; ^{Reeves & Rowe, 2003}). Nondominated Sorting in Genetic Algorithm II (NSGA-II) y Strength Pareto Evolutionary Algorithm 2 (SPEA2) son dos de los algoritmos más utilizados en los EA. NSGA-II es un algoritmo genético que implementa una técnica de capas o rangos para clasificar en distintos niveles de dominancia a la población completa. Además, utiliza torneos binarios de selección con reemplazo y una distancia de aglomeración para conservar la diversidad en los elementos de la población (^{Chen & Chiang, 2014}). SPEA2 es un algoritmo evolutivo que, a partir de un valor de bondad, conserva en una población o archivo externo a los mejores individuos para tomar de allí a los padres de los descendientes. Para la selección de padres utiliza un procedimiento de truncamiento basado en un torneo binario y en las distancias entre los individuos del archivo externo (^{Zitzler et al., 2001}; ^{Dastfan et al., 2014}).

Por otro lado, los métodos híbridos combinan las heurísticas con los métodos clásicos para acelerar el proceso de búsqueda. En la mayoría de los casos, estos métodos están adaptados a problemas particulares que hacen que la combinación trabaje de manera adecuada.

S-Metric Selection Evolutionary Multiobjective Algorithm (SMS-EMOA) es un algoritmo que combina los GA con métodos como Newton y Gradiente Conjugado para realizar una búsqueda local (^{Koch et al., 2009}). Por medio de una mutación polinomial y un cruzamiento binario simulado, SMS-EMOA genera una cantidad fija de descendientes, analiza probabilísticamente cada objetivo de manera independiente y, con base en los resultados, realiza búsquedas locales en algún objetivo específico por medio de alguno de los métodos clásicos.

^{Gutiérrez-Méndez (2011}) toma en cuenta el comportamiento social para la selección de los individuos a los que se les aplicarán los operadores genéticos, de manera similar a PS. También, como parte de la búsqueda de óptimos globales, aplica búsquedas locales en ciertos sectores del espacio de búsqueda o en individuos con características particulares previamente definidas para refinar la búsqueda con candidatos prometedores. Las búsquedas locales en general se realizan por medio de procesos iterativos o algún método clásico.

El éxito de las heurísticas se debe a que encuentran soluciones satisfactorias en la mayoría de los problemas. Sin embargo, requieren de muchas evaluaciones para garantizar buenas soluciones globales como, por ejemplo, en problemas de 10 dimensiones se requieren alrededor de 1000 evaluaciones (^{Müller & Shoemaker, 2014}), un aspecto que contribuye al aumento del costo computacional del proceso de optimización con funciones objetivo caras.

Modelos gaussianos estocásticos

Autores como ^{Ong et al. (2003}) y ^{Zhang et al. (2009}) mencionan que los modelos basados en procesos gaussianos estocásticos se consideran los más eficientes para tratar problemas caros de optimización uniobjetivo. Estos asumen que la función objetivo es un proceso gaussiano estocástico, donde los valores de la función objetivo para un punto nuevo se pueden estimar a través de los datos obtenidos en búsquedas anteriores y un factor de calidad, como la mejora esperada y la probabilidad de mejora, lo cual guía la decisión de cuáles puntos evaluar.

Efficient Global Optimization (EGO) es un conjunto de algoritmos diseñados para problemas uniobjetivo que buscan soluciones de tal manera que se maximice la mejora esperada al menor costo posible, encontrando respuestas con alto potencial para mejorar el costo mínimo con un valor de predicción bajo. Así, en la búsqueda de algoritmos evolutivos para problemas multiobjetivo que reduzcan el costo computacional, surgen los llamados ParEGO como una extensión de EGO (^{Zhang et al., 2009}). ParEGO predice el siguiente punto a evaluar a partir de un subconjunto del espacio de búsqueda; sin embargo, no hace distinción entre un óptimo local y uno global.

ParEGO genera un número de soluciones en un hipercubo y, a partir de un modelo gaussiano, encuentra la probabilidad de que una solución particular mejore la solución general del problema, maximizando dicha probabilidad por medio del método Down Hill Simplex (^{Knowles & Hughes, 2005}). La principal idea es recolectar datos de los candidatos previamente evaluados que puedan ser utilizados durante el proceso de evolución para construir y refinar el modelo de aproximación y a través de ellos evitar las evaluaciones de los candidatos menos prometedores. Las funciones serán evaluadas solo en los miembros más prometedores de la población, disminuyendo considerablemente el costo computacional (^{Ong, 2003}). ParEGO requiere de una cantidad mínima de evaluaciones de la función original (cientos), de lo contrario, no converge al frente de Pareto real.

^{Eskandari y Geiger (2008}) implementaron un algoritmo para tratar problemas con funciones de alto costo computacional llamado Fast Pareto Genetic Algorithm (FastPGA), que usa una técnica de clasificación basada en la información acerca de la dominancia de Pareto a través de soluciones y relaciones de nichos. Su desarrollo es similar al de NSGA-II e incluye algunas de las técnicas de ParEGO. Por medio de NSGA-II, optimiza las mejoras esperadas de todos los objetivos de manera independiente y así localiza el siguiente candidato a ser evaluado, sin utilizar toda la información dada por el modelo gaussiano estocástico, lo cual reduce la eficiencia (^{Deb et al., 2002}).

Por otro lado, Multiobjective Evolutionary Algorithm/Descomposition (MOEA/D) descompone el problema en varios subproblemas uniobjetivo, obtenidos a partir de escalarizaciones del problema original definidas por una combinación lineal de las funciones que conforman la función objetivo general. Los subproblemas se relacionan entre sí por medio de las distancias entre los vectores peso de cada combinación lineal, donde dos subproblemas cercanos deben generar soluciones similares (^{Zhang & Li, 2007}).

Así, Multiobjective Evolutionary Algorithm Descomposition with Gaussian Process Model (MOEA/D-EGO) combina MOEA/D con modelos gaussianos estocásticos. En cada iteración se construye un modelo gaussiano para cada subproblema a partir de los datos obtenidos en las búsquedas anteriores y las mejoras esperadas son optimizadas simultáneamente. Por medio de MOEA/D, este método genera nuevos candidatos y se usa un modelo basado en subconjuntos para mejorar la calidad de la predicción sin aumentar el costo computacional. En cada iteración se construye una distribución de predicción para cada objetivo de manera individual (^{Zhang et al., 2009}).

Aproximación de funciones

Recientemente se han propuesto técnicas de optimización para funciones costosas basadas en modelos sustitutos que aproximan a la función original. En vez de usar modelos computacionales costosos durante la optimización, se utilizan métodos que trabajan con una réplica de la función reduciendo la cantidad de evaluaciones de la función original a cientos en vez de miles, lo que produce resultados con un alto grado de exactitud a un costo menor (^{Müller & Shoemaker, 2014}).

Las primeras propuestas de aproximación construían metamodelos que actuaban sobre la mayor parte del espacio de búsqueda, trabajando con un modelo para cada objetivo, pero eso requiere de evaluaciones en todo el espacio de búsqueda, cuando en realidad lo que interesa son los puntos cerca del frente de Pareto y no los puntos en el interior (^{Voutchkov & Keane, 2010}). Debido a esto, ahora se trabaja con modelos localizados, eficientes en regiones de interés y no en el espacio completo.

Para minimizar la cantidad de evaluaciones que se le realizan a la función objetivo original, se usan modelos de aproximación en los que se toma una muestra de puntos y su respectiva evaluación en la función original, a partir de los cuales se crea una función sustituta que se utiliza en la mayoría de las evaluaciones para guiar el proceso. La función original se evalúa únicamente para actualizar los datos de la muestra y así el modelo utilizado en cada iteración (^{Haanpää, 2012}).

Las superficies de seudorespuesta (PRS: Pseudo Response Surface) o métodos de superficie de respuesta (RSM: Response Surface Methods) evalúan solo puntos cercanos a la región Pareto óptima realizando un mínimo de evaluaciones a las funciones objetivo originales, pero para ello se requiere una estrategia de muestreo predeterminada. RSM utiliza modelos de predicción basados en redes neuronales para aproximar la superficie y predecir cuál o cuáles puntos es mejor evaluar (^{Messac & Mullur, 2008}).

Los modelos más utilizados en la construcción de funciones sustitutas son interpolación, regresión, funciones de base radial (RBF: Radial Basis Functions) y funciones krigeanas (KF: Kriging Function). Sobresalen, entre estos, RBF y KF, porque el error es mínimo cerca de los puntos de muestra, requieren pocas muestras y funcionan adecuadamente en problemas con dimensión mayor a 25 (^{Müller & Shoemaker, 2014}). Sin embargo, con el aumento en la cantidad de datos y variables del problema se incrementa la cantidad de evaluaciones y, en consecuencia, también el costo computacional (^{Voutchkov & Keane, 2010}).

La eficiencia de estos métodos depende directamente de la muestra tomada. En algunos casos, la solución podría aproximarse a mínimos locales y en otros a óptimos globales. Es así como modelos del tipo Local Optima through Metamodels (LOOM) buscan todos los óptimos locales en un número reducido de llamadas a la función objetivo real, con base en repetidas búsquedas locales por medio de un metamodelo de esta. Dado que la mayor dificultad en los problemas de optimización es el costo de evaluar el desarrollo de cada solución en un espacio de búsqueda grande, LOOM trabaja de manera esparcida respecto al número de llamadas a la función objetivo, gracias al uso del metamodelo (^{Rivieri et al., 2013}).