INTRODUCCIÓN

Las investigaciones que examinan la contribución de diversas variables escolares asociadas al aprendizaje del estudiantado provienen de los estudios que se abocan a la función de producción educacional (^{Varas et al., 2013}). A partir de la publicación del informe ^{Coleman (Coleman et al., 1966}) de los Estados Unidos, estos estudios dieron un salto cualitativo. En el informe se revela el escaso peso atribuido a las variables escolares en la explicación de las desigualdades halladas (explicaban menos del 10% de la varianza) y la gran importancia del origen social para el rendimiento estudiantil (^{Álvarez y Martínez, 2016}). Sin embargo, el informe dejó algunas preguntas abiertas: ¿estos hallazgos son replicables a otros países?, ¿según el grado de desarrollo del país, la escuela impactará de manera diferente?

^{Heyneman y Loxley (1982}) dan respuesta a estas preguntas presentando los resultados de un estudio internacional en el cual participaron 18 países, algunos de ellos de bajo ingreso per cápita, tales como Chile, Irán, India y Tailandia. Los resultados revelan que en los países de bajos ingresos el porcentaje de varianza explicada por las variables escolares es dos a tres veces más que el que se encuentra en los países de altos ingresos, y que cuanto más pobre es el país en términos económicos mayor es el impacto de la calidad de la escuela y del profesorado en el rendimiento escolar. Con base en este hallazgo, ellos concluyen que hay evidencia suficiente para mostrar que el impacto de la calidad de la escuela y del profesorado es mayor en los países de bajos ingresos. Surge entonces una pregunta importante: ¿Qué conocimientos requiere el profesorado para que su enseñanza sea efectiva?

^{Shulman (1986}) es pionero en clasificar el conocimiento que el profesorado necesita para que su práctica profesional sea efectiva, a saber: Conocimiento del Contenido (CC), Conocimiento Pedagógico del Contenido (CPC) y conocimiento curricular. Él identifica el CC como la cantidad y la organización del conocimiento del contenido per se en la mente del profesorado. El CPC implica la comprensión de cómo representar el contenido de manera adecuada para que el estudiantado lo comprenda. El trabajo de ^{Shulman (1986}) atrajo la atención de los investigadores y los condujo a especificar y a esclarecer aún más el CC y el CPC. En el campo de la educación matemática, ^{Ball et al. (2008}) introdujeron el constructo conocimiento matemático para la enseñanza y describieron varios componentes asociados al CC: cono- cimiento común del contenido, conocimiento del horizonte matemático y conocimiento especializado del contenido. Contribuyendo a precisar este constructo, ^{Hill et al. (2008}) describieron componentes asociados al CPC de Shulman: conocimiento de la enseñanza del contenido, conocimiento del currículo y conocimiento del estudiantado y el contenido matemático.

Algunos investigadores han elaborado instrumentos válidos y confiables para medir el CC y el CPC con la finalidad de estimar el efecto que tiene el conocimiento del profesorado en el aprendizaje del estudiantado. ^{Hill et al. (2005}) fueron pioneros en mostrar que el CC y el CPC inciden en el rendimiento en matemáticas. En el estudio participan personas estudiantes de primer grado y de tercer grado y el profesorado en escuelas de los Estados Unidos. Las pruebas administradas al estudiantado incluyen

preguntas acerca de números, operaciones o pre-álgebra y álgebra. Las pruebas aplicadas al profesorado incluyeron preguntas relativas a números, operaciones y geometría. Posteriormente, otros investiga- dores han reportado resultados similares (^{Baumert et al., 2010}; ^{Kelcey et al., 2019}; ^{Tchoshanov et al., 2017}; ^{Yang et al., 2020}). Sin embargo, en países en desarrollo faltan estudios que estimen en qué medida el CC y el CPC contribuyen al logro de aprendizaje del alumnado (^{Cueto et al., 2017}). Además, estos estudios no se centran en el tema de las fracciones. Analizar un tema en profundidad puede permitir detectar las debilidades y fortalezas que manifiestan tanto el profesorado como el estudiantado.

El tema de las fracciones es un componente crítico en el plan de estudios de matemáticas en las escuelas primarias y secundarias de todo el mundo. El conocimiento de las fracciones predice el aprendizaje del álgebra y, por lo tanto, sienta las bases para la adquisición de conceptos más avanzados (^{Azid et al., 2020}; ^{Barbieri et al., 2021}; ^{Braithwaite y Siegler, 2021}; ^{Soni y Okamoto, 2020}; ^{Stelzer et al., 2021}; ^{Zhang et al., 2021}). Sin embargo, numerosas investigaciones han informado que la fracción es una de las nociones matemáticas más difíciles de entender por el estudiantado (^{Deringöl, 2019}; ^{Lenz et al., 2019}; ^{Xu et al., 2022}).

El concepto de fracción es complejo porque no comprende un solo constructo sino varios subconstructos, tales como parte-todo, operador, cociente, razón y medida (^{Jiang et al., 2020}). Por ejemplo, 3/4 se puede concebir como parte-todo (tres de cuatro partes iguales de un todo), como una medida (una suma de tres unidades de medida 1/4), como una razón (tres es a cuatro), como cociente (tres dividido por cuatro) y como operador (3/4 de una cantidad). ^{Kieren (1976}) fue el primero en separar el concepto de fracción en subconstructos: parte-todo, razón, operador, cociente y medida. Posteriormente, ^{Behr et al. (1983}) proponen un modelo teórico que relaciona los subconstructos parte-todo, razón, operador, cociente y medida con la equivalencia de fracciones, las operaciones de adición y multiplicación de fracciones y con la resolución de problemas.

Sustentados en los trabajos de ^{Kieren (1976}) y ^{Behr et al. (1983}), diversos investigadores han examinado las dificultades que presenta el alumnado en fracciones. Los estudios revelan que las personas estudiantes obtienen mejores resultados en tareas relativas al subconstructo parte-todo y desarrollan poco conocimiento en los otros subconstructos (^{Charalambous y Pitta-Pantazi, 2007}; ^{Ramadianti et al., 2019}; ^{Wijaya, 2017}). La comprensión del subconstructo medida resulta ser más difícil (^{Jiang et al., 2020}).

Por otro lado, hay investigaciones que muestran que el profesorado en formación y en servicio presentan una comprensión limitada de las fracciones (^{Avcu, 2019}; ^{Copur-Gencturk, 2021}; ^{Reeder y Utley, 2017}; ^{Van Steenbrugge et al., 2014}). Una persona docente que comprende un tema matemático puede ser capaz de brindar una instrucción de alta calidad, pero si no comprende el tema es casi seguro que no realizará una instrucción de calidad (^{Siegler y Lortie-Forgues, 2017}). En consecuencia, resulta pertinente estudiar la contribución del conocimiento del profesorado en el aprendizaje del alumnado en fracciones.

Para efecto de este trabajo, el conocimiento de las fracciones forma parte del CC del profesorado de primaria y se define como un conocimiento conceptual y conectado en el sentido de ^{Ma (2010}), el cual involucra la comprensión de los subconstructos parte-todo, operador, cociente y medida (^{Behr et al., 1983}; ^{Kieren, 1976}). El conocimiento sobre la enseñanza de las fracciones forma parte del CPC del profesorado de primaria y se define como el conocimiento didáctico que las personas docentes tienen respecto de los errores típicos, de las dificultades y de las estrategias utilizadas por el estudiantado (^{Hill et al., 2008}). Atendiendo a los antecedentes expuestos, este estudio tiene por objetivo examinar en qué medida el conocimiento del profesorado sobre las fracciones y su enseñanza, en asociación con las variables: conocimientos previos del estudiantado, Nivel Socioeconómico (NSE) y el nivel de conocimientos en matemáticas de la escuela medido a través de las pruebas SIMCE (Sistema de Medición de la Calidad de la Educación), contribuye al avance de aprendizaje del estudiantado en fracciones. Se plantean los siguientes objetivos específicos:

MATERIALES Y MÉTODOS

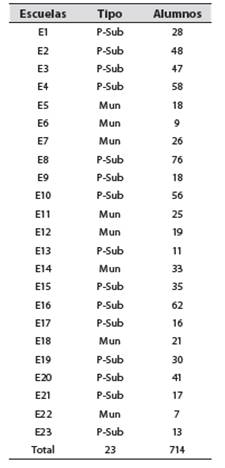
Esta investigación fue desarrollada desde un enfoque cuantitativo con un diseño ex post facto, siendo los instrumentos del estudio pruebas estructuradas con preguntas cerradas aplicadas al estudiantado y al profesorado. En el estudio participaron 714 personas estudiantes de 4.° grado y 23 personas docentes de 23 establecimientos escolares (8 municipales y 15 subvencionados) de la conurbación de La Serena- Coquimbo; correspondiente al 15% de la población de establecimientos. Las personas docentes tienen el título de profesor o de profesora de enseñanza básica, de los cuales 22 son generalistas, lo cual quiere decir que dictan clases de todas las asignaturas incluyendo matemáticas y una de las personas docentes tiene una mención en matemáticas. Los datos fueron tomados durante el año escolar 2016 (ver Tabla 1).

Tabla 1 Tipos de escuela y alumnos por escuela 

Los grupos se obtuvieron de un muestreo proporcional con participación voluntaria y corresponden a un grupo de escuelas que dista en ½ desviación estándar de la media poblacional (p < .01). Del total de personas docentes, 20 son mujeres y 3 hombres, y en promedio tienen 13 años de experiencia, con un mínimo de 2 años y un máximo de 42 años. Los 23 establecimientos de la muestra constituyen una cifra estimada como suficiente para llevar adelante el análisis estadístico. Efectivamente, ^{Maas y Hox (2005}) afirman que si se está interesado en los efectos fijos del modelo, 10 grupos de 30 individuos en el segundo nivel son suficientes para llevar adelante el estudio.

Para la recopilación de datos, se utilizó una prueba sobre las fracciones para el alumnado de cuarto grado que constó de 22 ítems de opción múltiple organizados de acuerdo a una matriz de especificaciones enmarcada en los contenidos curriculares (^{Ministerio de Educación (Mineduc), 2013}) de la unidad de “Fracciones” (ver Tabla 2). La prueba se aplicó a 714 personas estudiantes al inicio del año escolar como pretest y al final del año como postest. Esta prueba fue validada por jueces expertos en el tema de didáctica de las fracciones y se aplicó a una muestra piloto de 300 estudiantes de cuarto grado. La prueba mostró una confiabilidad de ,77 según el coeficiente alfa de Cronbach.

Tabla 2 Matriz de Especificaciones Prueba para los Alumnos 

Además se utilizó una prueba de conocimiento sobre las fracciones y su enseñanza para el profesorado que constó de 10 ítems correspondientes al conocimiento sobre las fracciones enmarcadas en los contenidos curriculares (^{Mineduc, 2013}) y 14 ítems sobre la enseñanza de las fracciones. Esta prueba fue validada por jueces expertos en el tema de didáctica de las fracciones y se aplicó a una muestra piloto de 80 personas docentes de primaria. La prueba mostró una confiabilidad de .75 según el coeficiente alfa de Cronbach.

En el presente estudio se consideraron las siguientes variables contextuales:

NSE: Nivel socioeconómico medio de las familias del estudiantado que anualmente rinden las pruebas SIMCE en el país. Los puntajes NSE son públicos y están disponibles en línea.

SIMCE: Puntaje promedio desde el 2012 al 2016, obtenido por la escuela en las pruebas de matemáticas anuales SIMCE (Sistema de Medición de la Calidad de la Educación) realizadas en el país, que evalúan el logro de aprendizaje en la asignatura de matemáticas, abarcando una muestra representativa de los contenidos de tercer y cuarto grado (^{Mineduc, 2013}). Los puntajes de la prueba SIMCE se encuentran disponibles en línea.

En la literatura, ha sido ampliamente reportado que el NSE influye en la calidad de vida del alumnado y en el contexto en que se desarrolla la actividad pedagógica. El NSE promedio del estudiantado es diferente para cada escuela, las diferencias observadas tanto en el pretest como en el postest del alumnado de distintas escuelas podrían estar explicadas en parte por las diferencias en el NSE. En Chile, se ha reportado que el estudiantado con un menor NSE obtiene puntajes SIMCE significativamente más bajos que los de mayor NSE.

Para aplicar las pruebas al estudiantado, se solicitó autorización a las personas docentes, personas directoras, apoderados y apoderadas. Las pruebas fueron aplicadas por una persona ayudante de investigación del proyecto, en las primeras horas de clases, dando 60 minutos de tiempo. La prueba aplicada al profesorado fue administrada en conjunto a todos en una sala dando 60 minutos de tiempo.

Los datos se analizan siguiendo la metodología de modelos multinivel, expuesta por ^{Pardo et al. (2007}). El análisis incluyó variables a nivel de escuela, SIMCE, NSE y C_Profesorado (Conocimiento del Profesorado), y variables a nivel del estudiantado, pretest y avance. La variable avance es la variable dependiente y se obtiene al calcular la diferencia entre el postest y el pretest. Esta variable se considera como medida de avance de aprendizaje del estudiantado de cuarto grado en el tema de las fracciones. El análisis inferencial comenzó con las asociaciones lineales entre las variables a través de la estimación de correlaciones de Pearson, a continuación se examinaron distintos modelos multinivel, en los cuales las escuelas constituyen una variable categórica que contribuye a explicar las variaciones en la variable dependiente avance. Los análisis multinivel se inician con el Modelo ANOVA de un Factor de Efectos Aleatorios (AEA), seguidos por los Modelos Regresión con Medias como Resultado (RMR) y ANCOVA de un Factor de Efectos Aleatorios (ACEA).

DISCUSIÓN DE RESULTADOS

El principal hallazgo de este estudio fue que el conocimiento del profesorado, solo o en combinación con otros factores, explicó alrededor del 6% de la variabilidad total del avance del alumnado, con una significación al 5%. Este resultado está en consonancia con el estudio de ^{Hill et al. (2005}), quienes encontraron que dada la gran cantidad de variabilidad dentro de las escuelas, solo una pequeña cantidad se podría atribuir al profesorado, esto es aproximadamente el 8% para primer grado y un 2% para tercer grado.

En este estudio, las variables de nivel 1: avance y pretest, se midieron a nivel del alumnado. Las variables del nivel 2: C_Profesorado, NSE y SIMCE, se midieron a nivel de escuela, y se asignaron el mismo valor al alumnado de la respectiva escuela (ver Tabla 3).

Tabla 3 Estadísticos descriptivos 

Se estudiaron las correlaciones entre las variables (ver Tabla 4). Se observó que la correlación más alta se presentó entre NSE y SIMCE. La correlación entre el conocimiento del profesorado y el avance de aprendizaje del alumnado fue positiva, débil pero significativa. Resultados similares fueron reportados en la literatura sobre la asociación entre el conocimiento del profesor y el rendimiento del estudiantado en matemáticas (^{Cueto et al., 2017}; ^{Hill et al., 2005}; ^{Tchoshanov et al., 2017}).

Tabla 4 Correlaciones entre las variables inter escuela 

Nota: Correlación Pearson bilateral; ** p < ,01

La Tabla 5 muestra la escuela, el tipo de escuela, el número de estudiantado por escuela, la media del avance de aprendizaje y la desviación típica del avance.

Tabla 5 Estadísticos Descriptivos por Escuela 

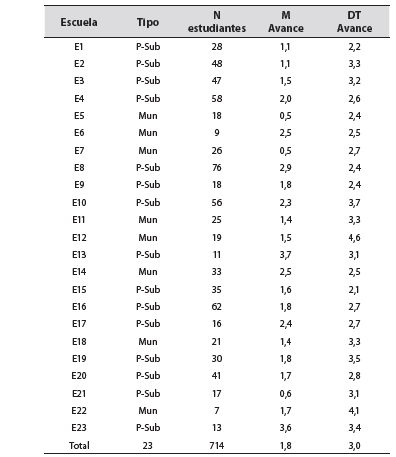
Nota: P-Sub: escuela particular subvencionada y Mun: escuela municipal

La Tabla 6 muestra la diferencia en el estadístico -2LL asociada a los modelos Inicial y AEA, la diferencia de 9.1 se distribuyó según chi cuadrado con 1 grado de libertad (p < .01), por lo que se rechazó la hipó- tesis de que el efecto del factor Escuela sea nulo. Se observó que el modelo RMR no superó al AEA dado que las diferencias no fueron significativas. El modelo ACEA que incluyó el efecto Profesorado y pretest superó a los modelos anteriores.

Tabla 6 Criterios de Información 

Nota: *** p < ,001; ** p < ,01

En la Tabla 7, RMR mostró que el SIMCE y el NSE no se asociaron significativamente con el avance del estudiantado (p= 0,91, p= 0,22). El conocimiento del profesorado se asoció significativamente con el avance de aprendizaje del estudiantado (p = 0,02). Estudios previos mostraron resultados similares (^{Cueto et al., 2017}; ^{Hill et al., 2005}; ^{Tchoshanov et al., 2017}).

Tabla 7 Estimaciones de los Parámetros de Efectos Fijos 

Nota: *** p < ,001; ** p < ,01

En la Tabla 8, el estadístico Wald otorgó la significación del efecto del procedimiento MIXED del SPSS, en este estudio se usó el estadístico -2LL, el cual es más fiable para muestras pequeñas. Según estas estimaciones, la variabilidad entre las escuelas representó el 4% de la variabilidad total del avance. El 96% de la varianza fue explicada por las diferencias dentro de cada escuela. Los modelos ACEAs mostraron que la estimación de la variabilidad entre las escuelas aumentó con respecto al modelo RMR y la varianza de los residuos pasó de 8,97 en el modelo AEA, a 7,18 en el modelo ACEA, similarmente para las tres covariables: SIMCE_c, NSE_c y C_Profesorado_c. Por tanto, al corregir el resultado en el avance mediante las puntuaciones en el pretest, la variabilidad dentro de cada escuela fue reducida en un 20%. Al comparar el modelo AEA y el modelo RMR, se conoció la proporción de varianza explicada en el nivel 2. El 8% fue atribuible al NSE, el -10% al SIMCE y 26% al conocimiento del profesorado. El SIMCE no se mostró relevante en el modelo estudiado. Por lo tanto, el conocimiento del profesor solo o en combinación con otros factores explicó alrededor del 6% de la variabilidad total del avance del alumnado, con una significación al 5%. El resultado del estudio está en línea con los hallazgos de diversas investigaciones sobre el efecto del CC y CPC en el aprendizaje del estudiantado en matemáticas (^{Baumert et al., 2010}; ^{Kelcey et al., 2019}; ^{Tchoshanov et al., 2017}).

Tabla 8 Estimaciones de los Parámetros de Covarianza 

*** p < ,001; ** p < ,01

Los resultados de las pruebas aplicadas en el estudio fueron los siguientes:

Prueba sobre las fracciones para el alumnado (n=714). La mayoría de las personas estudiantes respondió correctamente las preguntas relativas al subconstruto parte-todo (80%), las preguntas que resultaron más difíciles (20% a 50%) fueron las relativas al subconstructo medida, tales como ubicar fracciones en la recta numérica y comparar fracciones con distinto denominador. Estos resultados fueron similares a los reportados en la literatura (^{Charalambous y Pitta-Pantazi, 2007}; ^{Ramadianti et al., 2019}; ^{Wijaya, 2017}).

Prueba sobre las fracciones y su enseñanza para el profesorado (n=23). Respecto de la dimensión conocimiento sobre las fracciones, las preguntas que resultaron más fáciles de responder correctamente por el profesorado fueron las relativas al subconstructo parte-todo y las preguntas que resultaron más difíciles fueron las relativas al subconstructo medida. Respecto de la dimensión conocimiento sobre la enseñanza asociada al conocimiento didáctico de la matemática, las preguntas que resultaron más fáciles de responder correctamente fueron las relativas a identificar estrategias y dificultades comunes del estudiantado y las preguntas que resultaron más difíciles fueron las relativas al conocimiento de errores comunes del alumnado.

Estos resultados mostraron que el profesorado presentó una comprensión limitada respecto de las fracciones y su enseñanza, coincidente con lo reportado en la literatura (^{Avcu, 2019}; ^{Copur-Gencturk, 2021}; ^{Reeder y Utley, 2017}).

CONCLUSIONES

En este trabajo se constató que el conocimiento del profesor, solo o en combinación con otros factores, explica alrededor del 6% de la variabilidad total del avance del alumnado, con una significación al 5%. Este estudio se suma a un grupo de investigaciones que estiman el efecto del conocimiento del profesor en los logros de aprendizaje del estudiantado en matemáticas (^{Baumert et al., 2010}; ^{Hill et al., 2005}; ^{Kelcey et al., 2019}; ^{Tchoshanov et al., 2017}). No obstante, se diferencia de estudios previos porque se centra en las fracciones, un tema de gran interés para la matemática educativa. En consecuencia, el trabajo constituye un aporte a la investigación sobre el efecto del conocimiento del profesorado en el alumnado.

En este estudio se evidencia que la varianza entre escuelas estaría explicada en un 8% por el nivel socioeconómico. En la literatura se ha reportado que el NSE alto se relaciona con mejores condiciones (vivienda, acceso a salud, entre otras) que tienden a contribuir al logro de aprendizaje del alumnado. Se ha observado que en países en desarrollo, el alumnado con NSE bajo difícilmente alcanza rendimientos comparables con el alumnado de NSE alto.

Respecto de las pruebas aplicadas al estudiantado, se observa que las preguntas más fáciles de responder son relativas al subconstructo parte-todo y las más difíciles son las relativas al subconstructo medida. En general, en los textos escolares, el subconstructo parte-todo se representa utilizando figuras geométricas divididas en partes iguales. Estas representaciones son familiares para el estudiantado, por lo tanto, le resultan fácil de comprender (^{Charalambous y Pitta-Pantazi, 2007}). Sin embargo, más adelante esta idea se convierte en un obstáculo para la compresión del subconstructo medida, la comparación de fracciones y otras ideas que determinan el sentido numérico. En consecuencia, aparecen errores típicos como, por ejemplo, al resolver tareas de comparación de fracciones, el alumnado se equivoca al señalar que 1/4 > 1/2, argumentando que 4 es mayor que 2. Esto sugiere que aunque parte-todo puede ser la base para comprender los otros subconstructos, no es suficiente por sí mismo para una comprensión profunda de las fracciones (^{Reeder y Utley, 2017}).

Por otra parte, el subconstructo medida a menudo se representa por medio de rectas numéricas, este modelo resulta ser menos intuitivo que los utilizados para representar parte-todo y por ende más difícil de entender (^{Jiang, 2020}). No obstante, la literatura señala que la enseñanza centrada en el subconstructo medida sería clave para el aprendizaje de las fracciones (^{Siegler y Lortie-Forgues, 2017}). Asimismo, se observa que las preguntas con mayor dificultad para el profesorado fueron relativas al subconstructo medida. Algunos estudios sugieren que el aprendizaje de las fracciones por parte del estudiantado puede verse limitado por la comprensión de las fracciones por parte del profesorado. Las instituciones formadoras de las personas docentes tienen un rol clave en la solución del problema, se sugiere que estas instituciones refuercen este conocimiento (^{Avcu, 2019}; ^{Copur-Gencturk, 2021}; ^{Van Steenbrugge et al., 2014}).

La dificultad en la comprensión de las fracciones es una constante en todos los sistemas educativos. Por lo tanto, reconocer aquellos factores que predicen el aprendizaje de fracciones se convierte en un tema clave (^{Stelzer et al., 2021}). El presente estudio entrega pistas para continuar la investigación res- pecto de los conocimientos que requiere el profesorado de manera que el estudiantado pueda avanzar en el aprendizaje de las fracciones. La investigación futura podría incluir otras variables, por ejemplo: relacionadas con aspectos socio-afectivos del alumnado, características del contexto escolar y factores actitudinales del profesorado hacia el aprendizaje del alumnado