Introducción

Las redes de carreteras y ferrocarriles, por lo general, se encuentran separadas físicamente, por lo que las interacciones entre ellas suelen ser relativamente pocas, sin embargo, estas interacciones se dan en los cruces ferroviarios. Cuando los vehículos de estos dos distintos sistemas se aproximan, se presenta la posibilidad de que los choques ocurran y aunque son eventos poco frecuentes, ocurren (Guadamuz-Flores y Agüero Valverde, 2017a)^[1].

Debido principalmente a la gran diferencia entre las masas de los vehículos de estos sistemas, los usuarios de las carreteras, tanto de vehículos como peatones, tienen una vulnerabilidad mucho mayor que los vehículos de ferrovías y, por tanto, la probabilidad de sus daños como consecuencia del accidente es mayor (Guadamuz-Flores y Agüero Valverde, 2017b)^[2].

La infraestructura ferroviaria actual de Costa Rica es deficiente, más allá de los aspectos meramente funcionales y operativos propios del sistema ferroviario, también impacta negativamente en las interacciones con el sistema de carreteras en su eficiencia, comodidad y seguridad, siendo este último de especial interés para esta investigación.

Aunque la infraestructura ferroviaria actual está muy rezagada y es necesario implementar la infraestructura adecuada para la realidad nacional en gran cantidad de puntos (Guadamuz, 2014; FWHA, 2007)^{[3] [4]}, difícilmente se cuenta con todos los recursos necesarios para intervenir toda la red de forma simultánea, por lo que se debe priorizar la inversión de las mejoras.

El objetivo de esta investigación es realizar una identificación de los sitios con promesa de mejora, así como una clasificación que pueda servir como insumo inicial para un programa de inversión de recursos por parte de las entidades gubernamentales responsables del tema, a saber, el Consejo de Seguridad Vial (COSEVI) del Ministerio de Obras Públicas y Transportes (MOPT) y el Instituto Costarricense de Ferrocarriles (Incofer).

En la experiencia internacional, es usual encontrar estudios seguridad vial para ferrocarriles. A manera de ejemplo, se pueden mencionar Saccomanno et al. (2003)^[5], Miranda-Moreno (2006)^[6], Åhrén y Parida (2009)^[7], Eluru et al. (2012)^[8], Russo (2013)^[9] y Hamilton y Clarke (2017)^[10].

Enfocado directamente en Costa Rica, los estudios en el tema son escasos, por ejemplo, Guadamuz (2014)^[3] realizó una investigación acerca de la seguridad vial en ferrovías en la Gran Área Metropolitana, sin embargo, los análisis se limitaron meramente a estadísticas descriptivas, sin un modelo estadístico propiamente diseñado para estimar cruces con promesa de mejora.

En línea con esta investigación, en 2017 se realizó una investigación enfocada en generar modelos espaciales para determinar la frecuencia de choques ferroviarios (Guadamuz-Flores y Agüero Valverde, 2017a)^[1], por lo que este estudio se convierte en un insumo de gran importancia para realizar la clasificación de cruces con mayor potencial de mejora.

Adicional a este estudio, también en 2017 se efectuó otra investigación enfocada a Costa Rica, pero esta vez para estimar la severidad resultante de los accidentes de tránsito, donde se evidencia la vulnerabilidad de los usuarios de las carreteras, especialmente de los peatones (Guadamuz-Flores y Agüero Valverde, 2017b)^[2].

Con respecto a los métodos Bayesianos y espaciales aplicados, la mayor parte de la investigación ha utilizado distintos métodos, y se han enfocado en carreteras o sus usuarios más vulnerables, por ejemplo, los trabajos de Agüero-Valverde y Jovanis (2008)^[11], Mitra (2009)^[12], Guo et al. (2010)^[13], Lord y Miranda-Moreno (2008)^[14] y Siddiqui et al. (2012)^[15] y la referencia espacial más importante, Cressie (1993)^[16].

Uno de los principales retos para esta investigación se resume en la falta de datos disponibles para los análisis, esto también queda reflejado en la escasa investigación que se ha realizado en el país relacionada con ferrovías y más aún con la seguridad vial de este modo de transporte. A pesar de esto, los resultados de los análisis realizados son claros acerca de los sitios que requieren atención más urgente.

El principal objetivo de esta investigación es determinar los cruces ferroviarios que tienen mayor excedente de choques con el fin de que se prioricen sus inversiones en infraestructura. Para esto, se hace uso de métodos estadísticos avanzados que mejoran las estimaciones.

Descripción de los datos

Por la naturaleza propia del fenómeno, los choques viales son eventos poco frecuentes y para cruces ferroviarios la ocurrencia es todavía menor. Este aspecto aunado a un serio problema de falta de datos de calidad y un protocolo para la recolección estandarizada de los datos, generan dificultades importantes para poder resolver el problema de fondo de una manera más sencilla.

A pesar del problema anterior, los datos utilizados son suficientemente útiles para determinar estadísticamente los sitios con mayor concentración de choques y excedente considerable de frecuencia con respecto a cruces con condiciones similares, por tanto, permite identificar estos cruces para atenderlos prioritariamente.

Los datos utilizados corresponden a la Gran Área Metropolitana de Costa Rica, donde opera principalmente un sistema de transporte de pasajeros de baja velocidad durante horas pico. En esta región se encuentran 134 cruces ferroviarios a nivel, con características variadas, por ejemplo, desde cruces con carreteras nacionales de alto tránsito y velocidad, hasta entradas a condominios residenciales. De estas intersecciones, 52% no tuvieron ningún choque en el período de análisis.

Los datos utilizados se obtuvieron de los registros del Incofer entre 2010 y 2013. En este período ocurrieron 154 choques. Se utilizaron variables geométricas de la infraestructura como el ángulo entre la carretera y la ferrovía, el número de carriles de la carretera, el ancho total de la carretera, la presencia de curva en la carretera antes del cruce, la presencia de curva en la ferrovía antes del cruce, la existencia de ferrovía paralela la carretera sin separación física. Estas características se obtuvieron con imágenes satelitales y sistemas de información geográfica.

Debido a la alta disparidad entre tipos de cruces, el tráfico promedio diario (TPD) no estaba disponible para una cantidad significativa de cruces, por lo que fue necesario utilizar el tipo de carretera como una variable proxy del TPD. Después de realizar distintas pruebas de homogeneidad, el tipo de carretera a ser utilizado en los modelos fue clasificado en tres categorías homogéneas: a) rutas nacionales (categoría base), b) vías cantonales de cuadrante, y c) otras vías cantonales. La velocidad del tren se midió con el uso de dispositivos GPS dentro de los trenes. Las estadísticas descriptivas de las variables utilizadas en el estudio se presentan en el Table 1.

Metodología

Los choques viales son comúnmente modelados como procesos Poisson-lognormal o Poisson-gamma (i.e. binomial negativa) debido a la naturaleza del fenómeno(Aguero-Valverde y Jovanis, 2008^[11]; Guo y et al., 2010^[13]; Miranda-Moreno, 2006^[13]). Para esta investigación se encontró que los modelos Poisson-lognormal mostraban mejores resultados; esto es consistente con estudios previos (Aguero-Valverde y Jovanis, 2008^[11]; Siddiqui et al., 2012^[15]; Lord y Miranda-Moreno, 2008^[14]). Es importante señalar que los modelos Poisson-lognormal han sido considerados como una mejor forma para manejar valores bajos de media y tamaños de muestra pequeños (Lord y Miranda-Moreno, 2008)^[14].

El proceso Poisson es descrito como en (Guadamuz-Flores y Agüero Valverde, 2017a)^[1]:

donde Y_i es la cantidad de choques observados para el cruce i y \theta_i es la tasa esperada de choques para el cruce . Esta relación es definida como la relación matemática entre predictores que siguen una distribución log-normal (Ecuación (2)).

donde

\beta_0= intercepto

\beta_k= coeficiente para el k - ésimo predictor

x_{ik}= valor del k - ésimo predictor para el cruce i

v_i= heterogeneidad entre cruces no explicada por el modelo

A su vez, vi es definida con una distribución normal como se muestra en las ecuaciones (3) y (4).

Se observa que los efectos aleatorios tienen una distribución inicial normal centrada en cero y con un parámetro de precisión que controla la sobre-dispersión por heterogeneidad (Guadamuz-Flores y Agüero-Valverde 2017a)^[1].

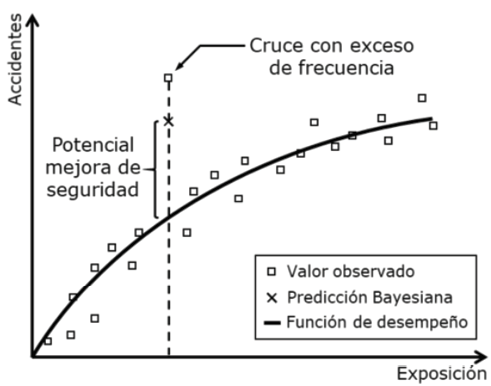
Este primer modelo permite determinar la función de desempeño de las intersecciones con características similares, pero es necesario un paso adicional para determinar los cruces con mayor exceso de frecuencia de choques. No es deseable obtener esta diferencia entre lo observado y lo estimado con la función de desempeño directamente como la diferencia con los coeficientes estimados, ya que, al utilizar estadística Bayesiana, cada iteración es independiente. Esta diferencia se calcula como se indica en la ecuación (5).

Con esto lo que se determina es la diferencia entre la observación y la estimación para cada cruce (i) y en cada iteración, luego el promedio de todas las iteraciones. Es decir, \delta_i es el promedio de las diferencias y no la diferencia de los promedios, que es lo que normalmente se obtendría con estadística frecuentista al no existir la posibilidad de simular el evento una cantidad finita pero muy grande de veces.

Figure 1 Potencial de mejora en la seguridad vial de cruce con exceso de frecuencia 

El modelo anterior fue estimado utilizando mediante métodos Bayesianos a través de OpenBUGS 3.2.3 (Lunn et al., 2009)[17]y se realizaron 1 000 iteraciones que fueron descartadas antes de tomar las muestras de los resultados. Adicional a las iteraciones anteriores, se simularon 110 000 iteraciones para cumplir que el error de las cadenas Markov Monte Carlo (MCMC) sea menor que el 5% del error estándar del parámetro siendo estimado, como medida de rendimiento para la convergencia de las simulaciones (Aguero-Valverde y Jovanis, 2008^[11]; Guadamuz-Flores y Agüero Valverde, 2017a^[1]).

Los métodos Bayesianos requieren de distribuciones y valores iniciales, por lo que para obtener dichos valores se modelaron previamente las estimaciones (Poisson log-normal y binomial negativa) en el paquete estadístico R 3.5.1 y su interfaz gráfica RStudio 1.1.447 y además se estimaron las variables significativas.

Se aclara que las distancias utilizadas para estos análisis espaciales se obtuvieron mediante el uso de Sistemas de Información Geográfica (SIG), donde se utilizó la distancia real a través de la red ferroviaria y no distancias aéreas o euclidianas, que son apenas aproximaciones de la distancia real, por lo que las distancias utilizadas ayudan a representar de mejor manera la realidad que se busca modelar.

Luego se ordenan los cruces descendentemente por el valor de su exceso (\delta_i) y se seleccionan los diez más críticos, que son los que tendrían mayor potencial de mejora si se les interviene adecuadamente.

Análisis de resultados

Variables seleccionadas finalmente para el modelo, fueron aquellas, donde se encontró que eran significativas para un intervalo de credibilidad del 95% o que se consideró que su justificación técnica prevalecía sobre el resultado estadístico, por ejemplo, la variable categórica “Curva en carretera” que se refiere a la existencia de una curva en la vía antes del cruce ferroviario, permanece en el modelo a pesar de que el intervalo de credibilidad incluye el cero, debido a que es significativa para el modelo de sólo efectos espaciales (sólo CAR), pero que por brevedad no se muestran sus resultados y que sí es significativa con un intervalo de credibilidad del 80%.

En una investigación previa (Guadamuz-Flores y Agüero Valverde, 2017a^[1]) se demuestra cómo el modelo CAR-2 es el mejor modelo espacial de acuerdo a las medidas de rendimiento Bayesianas utilizadas, así que, por brevedad, se muestran los resultados de las distribuciones posteriores para cada parámetro estimado solamente para esta configuración de modelo.

Los coeficientes obtenidos del modelo CAR-2 son intuitivos en el signo obtenido, por ejemplo, la media estimada para la cantidad de carriles es de 0,411 y dada la función de enlace de Poisson, se interpreta como un cambio porcentual en la cantidad de accidentes:

Es decir, para un cruce en general, un carril adicional en la carretera implica un aumento en promedio de 51% en la cantidad de choques estimados, manteniendo el resto de variables constantes.

Otro resultado interesante es como la existencia de una curva en la carretera antes del cruce ferroviario implica un aumento en promedio de 48% en la cantidad de choques comparado con una carretera sin curva, manteniendo el resto de variables constantes. Este tipo de interpretaciones se puede aplicar a otros coeficientes, que por brevedad se omiten.

Para el tráfico de trenes, la tasa de cambio no es constante, sino que depende de las condiciones particulares.

Por ejemplo, al pasar de 10 a 20 trenes por día en un cruce específico, es decir, duplicar desde 10 trenes, se esperaría un aumento promedio de 157% choques, manteniendo el resto de variables constantes. Estos aumentos en choques muestran lo crítico que puede acarrear un cambio que inicialmente parece inocente, si no se aplican las contramedidas necesarias para mitigar dicho cambio y esta es la línea de pensamiento crítico que busca promover esta investigación.

Luego, para el orden de priorización de los cruces con mayor excedente de choques entre lo esperado y observado se obtuvo lo mostrado en el Table 3. Ahí se muestran deltas de casos mediante un modelo CAR-2, que se interpreta como el exceso de accidentes del cruce comparado con cruces con condiciones similares.

Al inicio del Table 3 se observan los cinco cruces más críticos por exceso de choques, donde para estos primeros cinco lo que se observa es que presentan una cantidad mayor de accidentes que choques similares y se utiliza un intervalo de credibilidad del 80%, que es más flexible que el utilizado para los coeficientes del modelo, debido a que la poca disponibilidad de datos para este tipo de fenómenos provoca que no se pueda concluir con tanta confianza para cruces específicos.

De esta forma se observa que, para el cruce del Mercado de Mayoreo en la Sabana, el Río Pirro en la entrada a Heredia y un cruce cerca del Museo Nacional tienen una cantidad de choques significativamente mayor, por lo que son necesarias intervenciones para reducir estos excesos y tienen una alta promesa de mejora. Para los cruces del Ministerio de Agricultura y Ganadería (MAG) y MACOPA se concluye que, aunque el intervalo de credibilidad del 80% no es completamente contundente lo es muy cercano, es decir, es evidente que no está centrado en cero, sino que el intervalo apenas roza con el origen, por lo que estos crucen también merecen cierta consideración para la priorización de las medidas para mejorar la seguridad vial.

Los cinco cruces al final del cuadro mostrado se refieren más bien a cruces que tienen muy pocos choques, es decir, a pesar de sus condiciones similares a otros cruces que sí presentan mayor incidencia, son los peor ranqueados, por lo que, desde otra óptica del manejo de los recursos, estos presentan un riesgo muy alto para los usuarios de la infraestructura de carretera, pero que no se ve reflejado en choques como tal, por condiciones que no fueron incluidas en el modelo, como por ejemplo, un posible mayor cuidado de los conductores al transitar por dichos cruces. Aunque en este caso se observa que se tienen desviaciones estándar muy altas, por lo que los resultados no son tan concluyentes y sería necesario ahondar más en el tema en futuras investigaciones.

Para mostrar de una forma más natural la clasificación de los cruces se presenta la Figure 2, donde se observan de acuerdo al color y tamaño del punto del cruce su clasificación de acuerdo al exceso de choques.

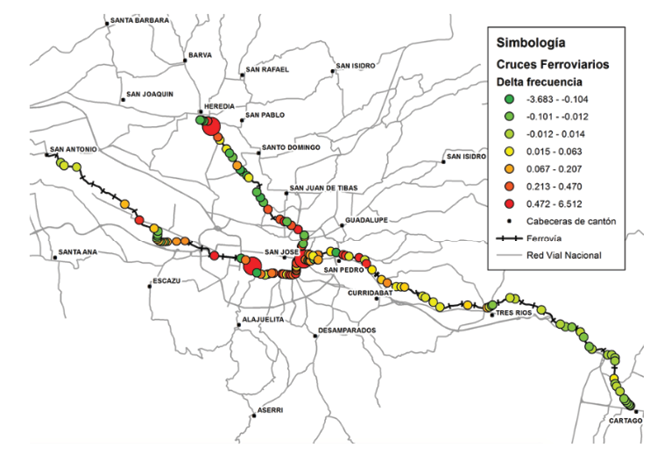
*los deltas significativos se muestran en círculos de mayor tamaño

Figure 2 Ubicación de cruces con exceso y escasez de frecuencia de choques. 

Nuevamente, se hace hincapié en que la recomendación técnica es intervenir los cruces en la priorización que se muestra en el Table 3, de manera que se optimice la asignación de los recursos y atención de las necesidades de infraestructura vial segura y adecuada.

Para cada uno de los cruces más críticos, se deben plantear las medidas de mitigación necesarias, siguiendo las mejores prácticas posibles, donde el manual para cruces carretera-ferrovía a nivel (FHWA, 2007)^[4] ofrece criterios suficientes para la aplicación de mejoras. Estos cruces, junto con otros, fueron estudiados desde una óptica más técnica que la estadística por Guadamuz ^[3], por lo que es conveniente que el lector consulte dicha investigación acerca de las mejoras puntuales necesarias en cada cruce con prioridad de inversión. Entre las recomendaciones se pueden citar mejorar la señalización de los cruces e implementar medidas de seguridad activa como semáforos peatonales y agujas.

Dichas inversiones son de bajo costo por lo que deberían ser implementadas a la mayor brevedad y considerar mejoras reales más costosas a la hora de implementar proyectos ambiciosos, como lo pueden ser la implementación de un sistema eléctrico de trenes para transporte de pasajeros que incluyan un completo rediseño del sistema o ampliaciones de las carreteras que incluyan los cruces señalados.

Nótese que esta investigación no toma en cuenta aspectos de eficiencia del sistema, como por ejemplo el cruce de circunvalación en San Pedro, a la altura del restaurante Taco Bell, que, aunque no presenta exceso de choques, a todas luces es un cruce que no debe existir a nivel debido a las características del alineamiento y uso tanto de la carretera como de la ferrovía.

Conclusiones

La priorización de cruces más críticos permite administrar de mejor manera los recursos para las mejoras de infraestructura. Como es evidente de los resultados, los cruces con mayor exceso de frecuencia de choques deberían ser intervenidos de forma prioritaria pues estos cruces son los que presentan mayor promesa de mejora si son intervenidos adecuadamente en su infraestructura.

Los métodos espaciales Bayesianos permiten estimar de mejor manera la cantidad de choques en los distintos cruces, comparado con modelos estadísticos clásicos, debido a que se cuenta con una frecuencia de choques baja y un tamaño de muestra relativamente bajo. Los métodos Bayesianos en general, y espaciales en particular, están mejor equipados para hacer frente a los problemas de baja frecuencia y tamaño de muestra. El mejor modelo Bayesiano espacial resulta ser el modelo condicional autoregresivo de segundo orden de vecinos (CAR-2).

La priorización por exceso de velocidad basada en el modelo CAR-2 resulta en los siguientes cruces con mayor exceso de choques: 1) Mercado de Mayoreo (Sabana), 2) Río Pirro (Heredia), 3) MAG (Sabana), 4) MACOPA (Calle Blancos) y 5) Cerca de Museo Nacional (San José).

Otros cruces presentan menores choques que cruces con condiciones similares, lo cual se traduce en un riesgo mayor que no es evidenciado mediante choques como tal.