Introducción
El módulo resiliente es una medida de la capacidad los materiales para almacenar o absorber energía sin deformación permanente, es decir, es una propiedad dentro del límite proporcional del material (Popov, 1990)[1]. Se determina mediante un ensayo de respuesta dinámica basado en la deformación recuperable bajo cargas repetidas y se define como (Ecuación (1)) (Huang, 2004)[2]:
donde:
M_R= módulo resiliente
\sigma_d = esfuerzo desviador
\epsilon_r = deformación unitario recuparable (resiliente)
Cuando un material se somete a un ensayo de carga repetida, al inicio de la aplicación de carga, se da una deformación permanente y al mismo tiempo una deformación recuperable, conforme aumenta el número de repeticiones carga, la deformación plástica va disminuyendo y la deformación pasa a ser prácticamente toda recuperable (Huang, 2004)[2] Figure 1.
El módulo resiliente se realiza en materiales cohesivos y granulares mediante un ensayo triaxial de carga repetida, que simula los estados de esfuerzos que experimenta el material por el tránsito de los vehículos. El ensayo consiste en la aplicación de un pulso de carga haversiana de magnitud fija, con una duración de carga de 100 ms y un periodo de reposo de 900 ms, sobre un espécimen de ensayo cilíndrico (102 mm de diámetro y 203 mm de altura, generalmente). Durante el ensayo, la muestra se somete a un esfuerzo cíclico de manera dinámica y esfuerzo de confinamiento de forma estática proporcionado por medio de una cámara de presión triaxial. La respuesta total de la deformación axial resiliente (recuperable) de la muestra se mide y se utiliza para calcular el módulo resiliente, según la norma de ensayo AASHTO T 307 (AASHTO, 2019)[3]. El ensayo se ejecuta para varios estados de esfuerzo, de manera que se pueda calcular un modelo de módulo resiliente para el material que se está analizando, Ecuaciones (2, 3 y 4) (NCHRP, 2004)[4].
donde:
M_R= módulo resiliente
\theta = invariante de esfuerzos (sumatoria de esfuerzos principales)
\sigma_1, \sigma_2, \sigma_3= esfuerzos principales
P_a= presión atmosférica
\tau_{oct}= esfuerzo cortante octaédrico
k_1, k_2, k_3= parámetros de regresión normalizados log-log
El módulo resiliente se utiliza en el análisis elástico multicapa, y junto con el módulo de Poisson, es una variable indispensable para predecir la respuesta mecánica de los materiales como los esfuerzos, deformaciones y deflexiones dentro de un pavimento flexible (Jiménez, 2009)[5]. Su valor es un parámetro de entrada para el diseño empírico y mecánico-empírico de pavimentos.
Al ser un ensayo costoso por los equipos que implica, no todos laboratorios de materiales convencionales disponen de este ensayo. Muchos diseñadores de pavimentos optan por el uso de correlaciones o nomogramas para determinar el valor aproximado del módulo resiliente. Con los nomogramas se estima el módulo resiliente según los resultados de otros ensayos básicos de caracterización (AASHTO, 1993)[6]. Otra forma, es mediante ecuaciones empíricas como la que propusieron Heukelom y Klomp (Heukelom y Klomp, 1962)[7] (Ecuación (5)).
donde:
M_R= módulo resiliente, psi
CBR = índice de soporte California, %
>El valor de 1500 de la Ecuación (5) puede variar de 750 a 3000 con un factor de 2. Provee mejores resultados con CBR menores a 20, es decir, con suelos de grano fino o subrasantes (Huang, 2004)[2]. Ninguna de estas formas de estimar el módulo resiliente da un resultado cercano al valor real que podría experimentar el material dentro de la estructura del pavimento, ya que, por ejemplo, no toma en consideración el comportamiento esfuerzo-dependiente, es decir, en condiciones reales de carga el material no exhibe un único valor de módulo resiliente, sino que esto va a depender del estado de esfuerzos bajo el cual este sometido en el pavimento.
El objetivo principal de la investigación, es la estimación de un modelo universal de módulo resiliente para materiales granulares, que considere variables relacionadas con los estados de esfuerzos y las características básicas de los materiales. Para lograr esto, se tomó una base datos con 13 materiales granulares diferentes con resultados de ensayo de módulo resiliente y caracterización básica. Con esta información, se generó un modelo de regresión lineal mediante mínimos cuadrados ordinarios (MCO). El modelo se validó mediante diferentes indicadores estadísticos y se obtuvo una bondad de ajuste aceptable.
Metodología
Para el desarrollo del modelo de predicción del módulo resiliente de materiales granulares, se analizaron 13 muestras provenientes de diferentes zonas de Costa Rica compuesta por 8 bases, 2 subbases y 3 préstamos; de las cuales se tienen datos de ensayo de: módulo resiliente, granulometría, densidad-humedad (Próctor modificado) e índice de soporte California (CBR). Para el análisis se seleccionaron inicialmente las variables mostradas en la Tabla 1. En esta misma tabla se indican los rangos de datos de cada variable para las muestras analizadas.
Table 1 Variables para análisis de regresión
Se generó la matriz de coeficientes de correlación Pearson con el objetivo de determinar el grado de asociación lineal entre pares de variables. Este análisis estadístico se utilizó como criterio para descartar variables explicativas que estuvieran correlacionadas (esto se detalla posteriormente en la Tabla 2).
Con las variables definidas se aplicó un modelo clásico de regresión lineal mediante el método de mínimos cuadrados ordinarios (MCO) para determinar el modelo de predicción. Para que los parámetros o predictores de la regresión sean consistentes (no sesgados) y eficientes (varianza mínima) se deben cumplir los siguientes supuestos:
Los residuos tienen una media de cero.
Todos los predictores no están correlacionados con los residuos.
Los residuos no están correlacionados entre sí.
Los residuos tienen una varianza constante (homocedasticidad).
Ninguna variable predictora está correlacionada perfectamente (r = 1) con otra variable predictora (multicolinealidad).
Los residuos están distribuidos normalmente.
Los supuestos se verificaron con el análisis de gráficos de residuos, histogramas e inferencia por medio de pruebas de hipótesis. Para considerar el no cumplimiento del supuesto de varianza constante de las perturbaciones se realizó una corrección de White de los errores estándar por heterocedasticidad con el fin de tener una inferencia robusta. Para garantizar la linealidad de las variables se aplicó una transformación logarítmica ya que algunas variables tienen un comportamiento no lineal.
Se evaluó la bondad de ajuste del modelo, es decir, el grado en que las variables independientes analizadas explicaban la variable dependiente (módulo resiliente) por medio del coeficiente de determinación ajustado.
En la Figure 2 se muestra el esquema que se siguió para validar el modelo de regresión.
Resultados y análisis
Linealidad
Para garantizar la linealidad del modelo se realizó una transformación de variable de tipo logarítmica, debido a que el módulo resiliente con respecto al invariante de esfuerzos o el esfuerzo desviador, puede variar de forma no lineal. Por lo tanto, el modelo no lineal propuesto inicialmente se indica en la Ecuación (6). Los β corresponden a los coeficientes de regresión.
Aplicando la transformación de variable (log-log) el modelo lineal sería (7):
Correlación Lineal entre Variables
Para seleccionar de la Table 1 las variables independientes a ser incluidas en el análisis de regresión, se calcularon los coeficientes de correlación entre todas las variables (Table 2). Un coeficiente de correlación mayor a 0,70, se considera como una correlación significativa entre variables (Holicky, 2013)[8].
Table 2 Coeficientes de correlación Pearson entre variables
Se puede observar que las variables de esfuerzo desviador y esfuerzo de confinamiento están correlacionadas con el invariante de esfuerzos de forma positiva, esto se debe a que el invariante de esfuerzos es la suma de esfuerzos principales y estos incluyen al esfuerzo desviador y el esfuerzo de confinamiento. La densidad máxima seca y el contenido óptimo de humedad están correlacionadas de forma negativa, esto es esperable ya que una es función de la otra. Con respecto a las variables granulométricas todas entre ellas están correlacionadas positivamente. Esto es razonable ya que los porcentajes pasando son sumas acumuladas y el tamaño por el que pasa el 60%, es dependiente de los porcentajes pasando. El índice de soporte California se correlaciona negativamente con el porcentaje pasando el tamiz N°4 y positivamente con el tamaño por el que pasa el 60%, esto es esperable, ya que, a mayor contenido de partículas gruesas, mayor valor de CBR.
Con respecto a la correlación del módulo resiliente con las demás variables, este tiene una correlación alta positiva con respecto el esfuerzo desviador, el esfuerzo de confinamiento y el invariante de esfuerzos, siendo este último el que tiene mayor coeficiente de correlación. Se observa una correlación menor del módulo resiliente con las restantes variables.
Entre las variables asociadas al ensayo de Próctor modificado, el contenido óptimo de humedad tiene una mayor correlación con el módulo resiliente. Entre las variables granulométricas, el porcentaje pasando el tamiz N°200 es el que tiene mayor coeficiente de correlación. El índice de soporte California tiene un bajo coeficiente de correlación con el módulo resiliente.
Del análisis realizado se seleccionaron para generar el modelo de regresión las variables independientes: invariante de esfuerzos, contenido óptimo de humedad y porcentaje pasando el tamiz N°200. Con esta selección, se elimina la multicolinealidad entre las variables explicativas.
Generación de Modelo
Con las variables independientes escogidas y bajo el cumplimiento de los supuestos, se realiza el modelo de regresión lineal múltiple con el método de mínimos cuadrados ordinarios. En la Table 3 se presenta un resumen con los resultados obtenidos del análisis de regresión lineal múltiple realizado con el software Microsoft Excel.
Table 3 Resumen de resultados de regresión lineal múltiple
Análisis de Residuales
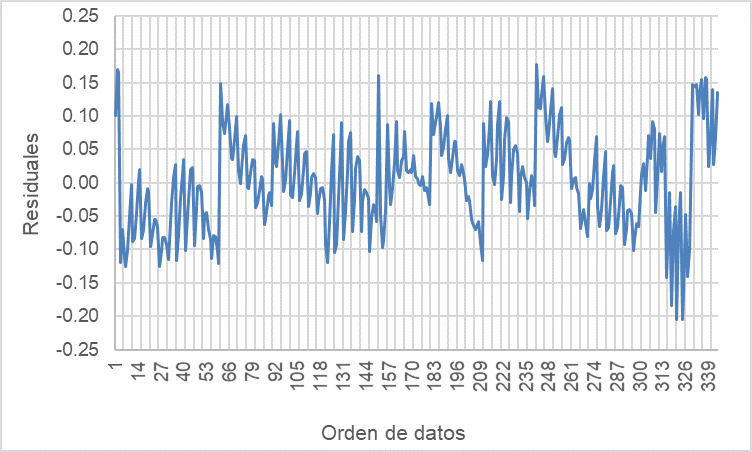
Se verificaron los supuestos que especifican el comportamiento de los residuos (diferencia entre los valores observados y los predichos): no correlación, normalidad y varianza constante para todas las observaciones (homocedasticidad). En la Figure 3, se muestra el gráfico de residuos vs los valores ajustados, se puede apreciar que inicialmente se cumple el supuesto de homocedasticidad ya que los residuos se ubican de forma aleatoria a ambos lados del cero, con patrones no detectables en los puntos. A su vez, en la Figure 4 se observa la variación de los residuos con el orden de los datos, se puede ver que no hay tendencias o patrones cuando se muestran en orden cronológico los residuales, esto indica que se cumple con el supuesto de independencia entre residuos (Montgomery & Runger, 2003)[9].
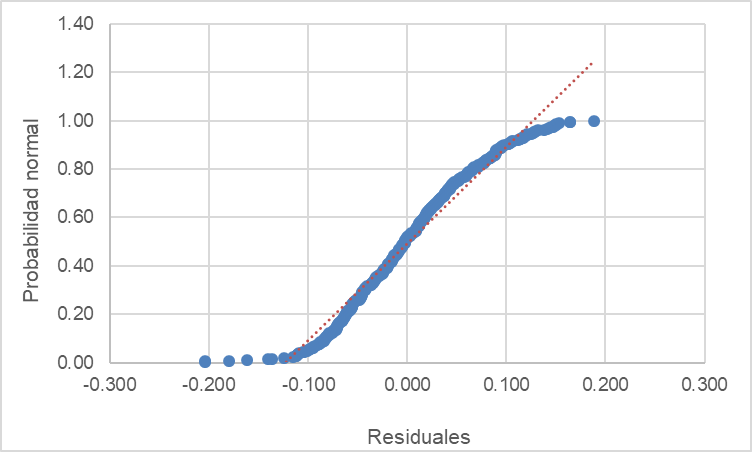
Para verificar que los residuos están distribuidos normalmente, se elaboró un histograma de frecuencias y un gráfico de normalidad. En la Figure 5 se observa que los residuales tienden a seguir una distribución normal por la forma simétrica de campana de Gauss, que muestra la distribución de frecuencias. Sin embargo, en la Figure 6 se advierte que los residuos no están distribuidos normalmente puesto que no todos los puntos caen sobre la línea recta, el gráfico tiene forma de S que implica una distribución colas, esto puede indicar que existen pocas o demasiadas observaciones en las colas de la distribución.
La no normalidad de los residuos no implica que los estimadores MCO no sean insesgados (consistentes) y de varianza mínima (eficientes) (Gujarati & Porter, 2009)[10]. Con respecto a la inferencia, los estadísticos t y F tienen distribuciones que son aproximadamente distribuciones t y F, cuando las muestras son de tamaño grandes (n - k > 30) (Benavente, Otero, & Vásquez, 2007)[11]; es decir, que si se cumple con esta condición, la inferencia estadística sigue siendo confiable, a pesar del no cumplimiento de la normalidad de los residuos3.
Análisis de Estimadores
El intercepto tiene un coeficiente de regresión mayor que el de las variables explicativas, esto implica que una porción importante del modelo está siendo explicado por intercepto. Esto podría indicar que modelo se podría mejorar incorporando otras variables explicativas. El invariante de esfuerzos tiene un coeficiente positivo, lo cual es esperable, ya que conforme aumenta el invariante de esfuerzos aumenta el módulo resiliente. El coeficiente del contenido óptimo de humedad tiene signo negativo. Esto también es razonable, ya que se espera que el módulo resiliente disminuya conforme mayor sea el contenido de humedad óptimo del material. De igual manera, el coeficiente del porcentaje pasando el tamiz N°200 tiene signo negativo, este comportamiento es aceptable, ya que se espera que un material con mayor porcentaje pasando el tamiz N°200 tenga un menor módulo resiliente.
Los valores de t-student calculados para cada estimador, son mayores al valor crítico de 1,96 para un nivel de confianza del 95%, esto quiere decir, que se rechaza la hipótesis nula H0 de que alguno de los estimadores sea igual a cero. De igual forma, los p-value menores al nivel de significancia α = 0,05 indican que estadísticamente ninguno de los estimadores considerados en el modelo sea igual a cero. El valor de F calculado es mayor que el crítico, lo que indica que se rechaza la hipótesis nula H0 de que todas pendientes del modelo son iguales a cero.
Análisis de Bondad de Ajuste
La suma de cuadrados de la regresión (SSR) es mayor a la suma de cuadrados de errores (SSE), esto implica que la varianza de la variable dependiente se explica en su mayor parte por las desviaciones de las variables independientes y no por las desviaciones de los residuos. Este comportamiento es el deseado, y es por esto, que el coeficiente de determinación R2 es cercano a 1. El R2 ajustado brinda un valor más confiable de la bondad de ajuste del modelo ya que el R2 tiende a sobreestimar el poder predictivo del modelo, aunque las variables no sean significativas.
En la Figure 7 se presenta un gráfico donde se comparan los módulos resilientes estimados vs los medidos, si los puntos pasan por la línea a 45°, implica que el modelo propuesto es efectivo prediciendo la variable dependiente y no presenta un sesgo; el modelo propuesto se ajusta satisfactoriamente a los datos medidos, no así la correlación de la Ecuación (5) comúnmente utilizada para estimar el módulo resiliente (Heukelom & Klomp, 1962)[7], que presenta un sesgo importante y tiende a sobreestimar su valor.
Corrección por Heterocedasticidad
Suponiendo que no se cumpliera el supuesto de homocedasticidad (varianza constante de los residuos), se realizó una corrección de heterocedasticidad de White de los errores estándar para las inferencias estadísticas fueran asintóticamente válidas (es decir, para muestras grandes), sobre los verdaderos valores de los parámetros (Gujarati & Porter, 2009)[10]. En la Table 4 se resumen los resultados.
Table 4 Resumen de resultados de regresión lineal múltiple con corrección de White
Los valores t student calculados son menores al t crítico igual a 1,960 para un nivel de confianza del 95%, por lo tanto, hay suficiente evidencia estadística para rechazar la hipótesis nula de que uno de los estimadores β sea igual cero. Los t student calculados de 3 comparados con los de la Table 4 (sin corrección de White), no son apreciablemente diferentes, por lo tanto, el supuesto de homocedasticidad se puede confirmar nuevamente.
Conclusiones y recomendaciones
De los datos analizados y de la validación del modelo de regresión propuesto para el módulo resiliente se obtuvo que:
Para la base de datos y las variables consideradas inicialmente en el estudio, se determinó que las variables más significativas estadísticamente y que mejor describen el modelo de módulo resiliente son: el invariante de esfuerzos (q), el contenido óptimo de humedad (%Opt) y el porcentaje pasando el tamiz N°200 (PasN°200).
Se verificaron los supuestos y cumplimientos para la regresión por mínimos cuadrados ordinarios, excepto la normalidad de los residuos, sin embargo, esto no afecta la consistencia y eficiencia, ni tampoco la inferencia del estimador al tener una muestra grande. Este efecto sobre la normalidad de los residuos se puede mitigar aumentando el tamaño de la muestra.
El modelo final propuesto se muestra en la Ecuación (8):
El modelo que se propone posee una bondad de ajuste satisfactoria, y se puede verificar con base en la muestra analizada que la correlación MR = 1500 × CBR, presenta un sesgo importante y tiende a sobrestimar los valores de módulo resiliente y no toma en cuenta el comportamiento esfuerzo-dependiente del material.
Se recomienda aumentar la base de datos con más materiales para ampliar el espectro de materiales que incluye el modelo y así mejorar su confiabilidad.
Aunque no se incluyó en el análisis debido a que algunas muestras carecían del dato, sería importante evaluar variables como límites de consistencia, compresión inconfinada y parámetros de resistencia al corte, entre otras variables que puedan describir mejor el modelo.
El módulo resiliente varía según el contenido de humedad, por lo tanto, se recomienda evaluar esta variable de tal manera que el modelo contemple cambios de humedad a los que podría estar expuesto el material durante su tiempo de servicio.