Introducción
En Costa Rica el sistema educativo está organizado en tres grandes secciones: Educación Preescolar (EP), Educación General Básica (EGB) y la Educación Diversificada (ED). La EGB se subdivide en I Ciclo (incluye primero, segundo y tercero de Educación Primaria), II Ciclo (incluye cuarto, quinto y sexto de Educación Primaria) y III Ciclo (incluye el sétimo, octavo y noveno de Educación Secundaria).
La institución objeto de estudio es un complejo educativo privado que ofrece servicios desde educación preescolar hasta educación diversificada. Además, esta se enmarca en las regulaciones del Ministerio de Educación Pública (MEP) de Costa Rica; pero posee libertad para ampliar y modificar la malla curricular de las asignaturas.
Esta investigación longitudinal (ver Poveda-Vásquez y Zumbado-Castro, 2023) se enfoca en el I y II Ciclo de la EGB y dentro de ella se enmarcan los resultados que se mostrarán en este artículo.
Desde el año 2016, en la institución se realizó una reforma curricular en matemáticas que ha estado acompañada de la indagación para establecer planes de acción. La resolución de problemas se incluyó como la estrategia metodológica principal de manera análoga a la propuesta del MEP (2012). Está concebida en dos etapas: la primera, el aprendizaje del saber; la segunda, la aplicación y movilización de los aprendizajes. A su vez, el proceso de aprendizaje se subdivide en cuatro momentos: el planteamiento de un problema, el trabajo estudiantil independiente, la discusión interactiva y el cierre o clausura; esta estrategia metodológica concuerda con el plan académico institucional que le permite al estudiantado aprender a conocer, hacer, convivir y ser.
Los diseños curriculares de la institución se plantearon originalmente para clases presenciales y matemáticas no fue la excepción. La situación provocada por el virus SARS-CoV-2 o Covid-19 ocasionó la suspensión de clases presenciales de manera abrupta en el año 2020 y para el año 2021 las lecciones se vislumbraban para una alternancia entre sesiones virtuales y presenciales.
A nivel país, en el área de matemáticas, el MEP tomó decisiones para recortar conocimientos y habilidades específicas, inclusive la anulación de las áreas de geometría para I Ciclo, medidas para II Ciclo y estadística y probabilidad para ambos ciclos de la Educación Primaria (Poveda-Vásquez y Manning-Jara, 2021).
Sin embargo, a nivel institucional, a finales del año 2020, a través de un taller con docentes, se estableció la priorización curricular según los dos escenarios para el año 2021: presencialidad parcial o total. La delimitación curricular permitió establecer un perfil de salida del estudiantado de la institución. Sin embargo, era necesario conocer el nivel de avance de la reforma curricular institucional en el escenario de pandemia y postpandemia, con la intención de tomar decisiones de forma inmediata para el curso lectivo 2022. Para esto se diseñó, aplicó y analizó una prueba diagnóstica, que se efectuó en el mes de noviembre del año 2021 a todos los niveles educativos de primaria. Este artículo presenta únicamente los resultados de cuarto año para la asignatura de Matemáticas con estudiantes cuyas edades oscilan entre los 9 y 10 años.
Marco teórico
Evaluación diagnóstica
Esta evaluación establece las condiciones del estudiantado para iniciar nuevos procesos de enseñanza y aprendizaje. Ella aporta las bases para la planificación porque establece los puntos reales de partida y permite establecer una estrategia para atender las necesidades evidentes del estudiantado (MEP, 2010; Santamaría, 2005).
La evaluación diagnóstica determina presencia, ausencia y gradualidad en elementos como conocimientos previos, formas de representación, estrategias de aprendizaje, entre otros (MEP, 2010).
Según Mayorga, Gallardo y Jimeno (2015), una evaluación diagnóstica para matemáticas debe mostrar en qué medida la persona estudiante logra usar los objetos matemáticos y sus propiedades. Estos autores señalan la importancia de hacerlo en ''escenarios reales y diversos de su vida cotidiana''(p. 49).
El diagnóstico sobre el uso que hace el estudiantado de las matemáticas debe considerar diversos elementos: contenidos matemáticos, la intervención de las capacidades cognitivas superiores, la presencia e intervención con contextos reales o abstractos y los niveles de complejidad de las actividades de evaluación (Caraballo, Rico y Lupiáñez, 2011; Ruiz, 2018).
Además, la prueba diagnóstica debe poseer características psicométricas que aporten evidencias de confiabilidad y validez, de manera que las calificaciones asignadas al estudiantado sean fieles a las habilidades que posee y, por ende, se puedan tomar decisiones adecuadas para cada estudiante.
Para efectos de la investigación realizada, las habilidades matemáticas específicas trabajadas durante cuarto año en el 2021 fueron el centro de atención del diagnóstico con el propósito de planificar la intervención para atender las necesidades del alumnado a partir del 2022 y que serán citadas posteriormente.
Áreas matemáticas de diagnóstico
De acuerdo con Chin, Chew y Lim (2021), es fundamental en la elaboración de una prueba diagnóstica la revisión del Currículo de Matemáticas vigente en el país o institución y aquellas ideas que a nivel institucional establezcan los estándares del año escolar en cuestión.
Las áreas matemáticas: números, medidas, geometría, relaciones y álgebra, así como estadística y probabilidad organizan la malla curricular nacional y se replica en el diseño del currículo institucional.
La institución asume del MEP (2012) las perspectivas para las áreas matemáticas. Es importante señalar que estas son coherentes con estándares internacionales como los establecidos por la Organización para la Cooperación y el Desarrollo Económico (OCDE). A continuación, se detallan las perspectivas.
Respecto al área de números, con ella se pretende durante la primaria integrar los números, las operaciones y el cálculo, con énfasis en el vínculo entre representaciones numéricas y operaciones. Además, el cálculo mental, la estimación y el sentido numérico deberán ser fortalecidos. Las propiedades de los números, las operaciones y la relación entre ellas son prioritarias. Durante el I Ciclo se enfatiza el trabajo en los números naturales y el II Ciclo en fracciones y decimales (MEP, 2012).
El área de medidas posee un estrecho vínculo con el área de números, la estimación se considera fundamental para la comparación de las mediciones. Además, esta área será un recurso para la introducción de procedimientos relacionados con objetos matemáticos. Las unidades de medida son fundamentales en esta área, la manipulación vinculada con situaciones reales se prioriza (MEP, 2012).
Respecto a geometría, ella será orientada hacia la realidad para favorecer la visualización espacial y construcción de figuras abstractas con sólidas bases adquiridas mediante la intuición, la manipulación, la visualización de objetos concretos y paulatinamente avanzar hacia objetos abstractos (MEP, 2012), para lo anterior es fundamental conocer las características básicas de las figuras planas.
Para el área de relaciones y álgebra, el pensamiento funcional y algebraico es prioritario. Él será introducido de manera paulatina durante la primaria. Los patrones, sucesiones, las relaciones y representaciones serán esenciales.
Respecto a estadística y probabilidad, esta área ''tiene un gran potencial para implementar en el aula la resolución de problemas en contextos reales''(Chaves, 2020, p. 56). Las nociones básicas de esta área se introducen de manera intuitiva y paulatina. En la siguiente Tabla 1 se ofrece una síntesis.
A pesar de que existen estas perspectivas por áreas matemáticas, Poveda-Vásquez y Zumbado-Castro (2023), en un estudio previo en esta misma institución educativa, al analizar los planeamientos y evaluaciones aplicadas por docentes, así como los cuadernos de estudiantes, encontraron que el personal docente dedica mucho tiempo al área de números, descuidando el desarrollo de habilidades en las otras áreas matemáticas.
Destrezas para la resolución de problemas
La estrategia metodológica asumida por la institución utiliza el problema como
Tabla 1 Síntesis de la perspectiva por área matemática en la Educación Primaria
| Área Matemática | Perspectiva |
|---|---|
| Números | • Integrar los números, las operaciones y el cálculo |
| • Enfatizar en el vínculo entre representaciones numéricas y operaciones | |
| • Fortalecer el cálculo mental, la estimación y el sentido numérico | |
| • Priorizar las propiedades de los números, las operaciones y la relación entre ellas | |
| • Enfatizar en: | |
| a) I Ciclo: el trabajo en los números naturales | |
| b) II Ciclo: el trabajo con fracciones y decimales | |
| Medidas | • Promover la estimación en la comparación de las mediciones |
| • Utilizar las situaciones reales para el uso de unidades de medida | |
| Geometría | • Caracterizar las figuras planas básicas |
| • Favorecer la visualización espacial en contextos reales | |
| • Emplear la intuición, la manipulación, la visualización de objetos concretos hasta llegar a los objetos abstractos | |
| Relaciones y álgebra | • Priorizar el pensamiento funcional y algebraico |
| • Introducir ambos pensamientos de manera paulatina | |
| • Utilizar los patrones, las sucesiones, las relaciones y las representaciones | |
| Estadística y probabilidad | • Introducción intuitiva y paulatina de las nociones básicas. |
| • Emplear problemas en contextos reales. |
Nota: Fuente propia de la investigación.
su recurso didáctico. El problema se entiende como la situación que ofrece uno o más retos, que hace pensar y que también ofrece la oportunidad de movilizar conocimientos recientemente aprendidos. El estudiantado con su uso aprende a pensar matemáticamente y utiliza sus conocimientos previos (Zumbado et al., 2021).
Según Jaramillo y Puga (2016), existen múltiples operaciones metacognitivas durante la resolución de problemas matemáticos y en ellos participan de manera inevitable los conocimientos matemáticos específicos. Los conocimientos pueden ser de un área o de varias áreas matemáticas de manera simultánea.
Existen factores externos que el estudiantado enfrenta en la resolución de problemas contextualizados, entre ellos: (1) la comprensión del contexto, (2) el vínculo que pueda establecer con su realidad y (3) la motivación generada por la situación problematizada. De acuerdo con Ruiz (2018), la resolución de problemas en contextos reales es básica para generar capacidades cognitivas superiores, debido a la exigencia que implica enfrentar una situación real o que parezca real.
Metodología
El tipo de investigación es inferencial-exploratoria, por tanto, es de enfoque cuantitativo. Las 51 personas estudiantes que conformaban los tres grupos de cuarto año de la institución participaron del diagnóstico.
El instrumento empleado fue una prueba escrita constituida por seis ítems de selección única, 11 preguntas de respuesta breve y dos preguntas de desarrollo. Para efectos del análisis de la información los ítems fueron enumerados de 1 a 19. La prueba fue confeccionada con base en dos fuentes: (1) la priorización establecida por docentes en el taller efectuado con ese propósito y (2) los planeamientos empleados por el cuerpo docente que incluyen los problemas, los ejemplos y los ejercicios de práctica utilizados durante el desarrollo de las lecciones.
Además, para recolectar las evidencias de validez y confiabilidad de los resultados de la prueba diagnóstica en matemáticas se aplicó la teoría clásica de los test (TCT) (Chin et al., 2021; Martínez, Hernández y Hernández, 2014). Los software utilizados para el análisis de datos fueron: SPSS 28.0.1.0; el lenguaje de programación y el entorno R.
Para la elaboración de la prueba se seleccionaron por área las habilidades que se muestran en la Tabla 2.
En la Tabla 2 se observa la distribución de los ítems, por área matemática y según las habilidades que fueron empleadas para diagnosticar. Estos valores se emplearon para balancear la prueba según el tiempo asignado por la docente de matemática de cuarto año, según los planeamientos analizados. Además, se indican los puntajes respectivos a cada ítem.
La aplicación se realizó de forma simultánea a los tres grupos de este nivel educativo el lunes 22 de noviembre del 2021 durante un periodo de 60 minutos. La prueba escrita fue aplicada de manera presencial e individual y su administración estuvo a cargo de personas externas a la institución (una persona del equipo investigador y dos asistentes). Se solicitó que la docente a cargo del grupo según el horario lectivo estuviera durante los 60 minutos, para que atendiera cualquier situación particular con alguna persona estudiante.
Además, durante la aplicación se realizaron indicaciones generales tales como: (1) se podían dejar respuestas en blanco, (2) se podían aclarar consultas, en caso de que no se entendiera alguna pregunta o instrucción,
Tabla 2 Distribución de puntaje por área matemática y habilidades en la prueba diagnóstica para cuarto año
| Área matematica | Item | Habilidades Especificas | Puntaje |
| Números | 1 | Identifica las fracciones como parte de la unidad o parte de una colección de objetos | 1 |
| Analiza las fracciones propias. | |||
| 4 | Multiplica un número con o sin expansión decimal por 10, 100 y por 1000. | 1 | |
| 9 | Compara y ordena números en su representación decimal. | 3 | |
| 10 | Compara números naturales menores que un millón utilizando los símbolos <, > o =. | 2 | |
| 7 y 8 | Calcula los resultados de sumas, restas, multiplicaciones y divisiones. | 4 | |
| 11 y 12 | Aplica correctamente el algoritmo de la división de números naturales. Comprende la relación entre la multiplicación y la división. | 4 | |
| 19 | Resuelve y plantea problemas contextualizados donde se requiera el uso de la suma, la resta y la multiplicación de números naturales. | 4 | |
| Relaciones y álgebra | 2 | Identifica el número que falta en una expresión matemática, una figura o en una tabla. | 1 |
| 3 | Analiza patrones en sucesiones con figuras, representaciones geométricas y en tablas de números naturales menores que 1 000 000. | 1 | |
| 15 | Analiza patrones en sucesiones con figuras, representaciones geométricas y en tablas de números naturales menores que 1 000 000. | 2 | |
| Probabilidad y estadística | 5 | Determina eventos más probables, igualmente probables y menos probables de acuerdo con la frecuencia de sus resultados simples. | 1 |
| 16 | Interpreta información que ha sido resumida en dibujos, diagramas, cuadros y gráficos en diferentes contextos. | 2 | |
| Medidas | 6 | Mide el tiempo utilizando años, meses, semanas, horas, minutos y segundos. | 1 |
| 18 | Reconoce las monedas y billetes de Costa Rica. | 3 | |
| Establece la relación bancaria entre las monedas y billetes de todas las denominaciones. | |||
| Aplica el uso de cantidades monetarias en diversas situaciones reales. | |||
| Geometría | 13 y 14 | Identifica diversos elementos de los cuadriláteros (lado, vértice, ángulo, base, altura, diagonal). | 4 |
| Reconoce propiedades de cuadriláteros referidas a los lados, los ángulos y las diagonales. | |||
| Reconoce en dibujos u objetos del entorno polígonos regulares e irregulares. | |||
| 17 | Clasifica triángulos de acuerdo con las medidas de sus lados. | 3 | |
| Estima, por observación, si un triángulo es equilátero, isósceles o escaleno | |||
| Puntaje total de la Prueba | 37 |
Nota: Fuente propia de la investigación.
(3) cada estudiante debía revisar sus respues-tas antes de entregar el diagnóstico.
Al finalizar la ejecución de las pruebas, los instrumentos fueron recolectados y siste-matizados mediante matrices en Microsoft Excel, SPSS y el lenguaje de programación y el entorno R. Los datos fueron analizados mediante estadística descriptiva e inferencial.
Análisis y resultados
Prueba diagnóstica
La TCT mostró que la prueba presenta un alfa de Cronbach de 0.79 y se encuentra en el rango aceptado en investigaciones de esta índole (Frías-Navarro, 2021; Montero y Jiménez, 2013). Respecto al análisis del índice de dificultad del ítem la información se presenta en la Tabla 3.
Tabla 3 Distribución de la dificultad por ítem en la prueba diagnóstica para cuarto grado
| Índice de dificultad (escala de 1 a 100) | Dificultad del ítem | Ítems de la prueba |
|---|---|---|
| (0-20) | Muy difícil | 15, 17, 19 |
| (20-40) | Difícil | 4, 9, 14, 18 |
| (40-60) | Intermedio | 1, 3, 5, 7, 8, 11,12, 13,16 |
| (60-80) | Fácil | 6, 10, |
| (80-100) | Muy fácil | 2 |
Los resultados de la aplicación de la prueba indican que hay tres ítems muy difíciles y uno muy fácil, por lo tanto, para futuras aplicaciones se debe prestar atención al comportamiento de estas preguntas y complementar la información de manera que se pueda determinar por qué se ubicaron en esos rangos. Además, se realizó el análisis de la discriminación y la desviación estándar, dentro de los resultados se destaca que los ítems 2, 17 y 19 poseen valores de discriminación menores a 0.3 lo que refuerza la necesidad
de un análisis más profundo (Chin et al., 2021). El ítem 17 posee la menor des-viación estándar y merece en este documen-to un análisis más detallado.
En la Figura 1 se muestra el ítem 17, ella integra dos habilidades específicas: la clasificación de triángulos de acuerdo con las medidas de sus lados y la estimación por observación. La interrogante que surge es si la dificultad está asociada con: (1) recordar los nombres asociados con la clasificación de triángulos por la longitud de sus lados o (2) su esti-mación, sin embargo, esta respuesta sobre-pasa los alcances de esta investigación, pero este asunto es valioso para una posible línea de investigación.
Continuando con el análisis, es importante señalar que 15 de los 19 ítems se ubican entre los rangos de fácil y difícil que se considera idóneo.
Respecto a las calificaciones, estudiantes de cuarto año obtuvieron un promedio de 47.6. La mediana se ubicó en 45.95. Por lo tanto, la asimetría es positiva
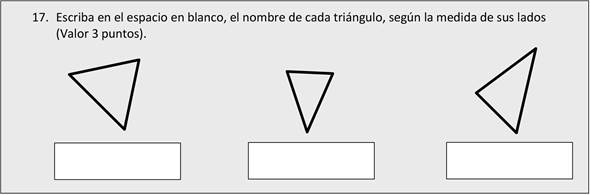
Fuente propia de la investigación
Figura 1 Ítem 17 de la prueba diagnóstica aplicada en la institución.
y significa que las calificaciones más altas afectaron la distribución, como se muestra en la siguiente Gráfica 1.
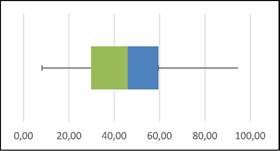
Nota: Fuente propia de la investigación
Gráfica 1 Distribución de las calificaciones del estudiantado de cuarto año en la institución
Al entregar los resultados de las notas del estudiantado a la institución, se planteó una reunión con la docente de cuarto grado y con la docente que daría quinto grado en el año siguiente, con el objetivo de analizar aquellos casos de estudiantes cuyas notas se encontraban en el primer cuartil.
Áreas matemáticas
Tal y como se explicó anteriormente, la prueba diagnóstica se diseñó considerando los planeamientos de docentes y las áreas matemáticas que están presentes en el diseño curricular: números, relaciones y álgebra, medidas, geometría, así como estadística y probabilidad.
El dominio de las habilidades por parte del estudiantado se analizó, de acuerdo con los resultados por cada ítem asociado a cada área matemática, tal y como se mostró en la Tabla 1. En la Gráfica 2 se presenta el porcentaje de dominio por área matemática.
Al ser contenidos trabajados durante el año lectivo, se esperaba que este se ubicara entre un 80 % y 100 %.
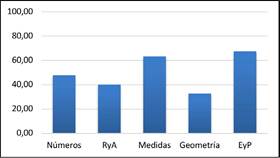
Notas: Fuente propia de la investigación, RyA: Relaciones y álgebra; EyP: Estadística y probabilidad.
Gráfica 2 Porcentaje de dominio de cada área matemática, según el diagnóstico aplicado a cuarto año en la institución, noviembre del 2021
La Gráfica 2 anterior muestra que, de acuerdo con la prueba diagnóstica, el estudiantado de cuarto año tiene mayor dominio de las áreas de medidas y estadística y probabilidad; sin embargo, el porcentaje de dominio apenas supera el 60 %, mientras que geometría es el área matemática con menor dominio. Una posible causa de este bajo porcentaje en geometría podría estar asociada al nivel de dificultad del ítem 17, que se analizó anteriormente.
En la misma gráfica se visualiza que las áreas de números y relaciones y álgebra se ubican entre el 40 % y 50 % de dominio.
Este análisis por ítem y por área permitió identificar los conocimientos matemáticos que el cuerpo docente debe retomar y reforzar en el año lectivo posterior. En la Tabla 4 se muestran estos conocimientos, según el área matemática.
Tabla 4 Conocimientos, por área matemática, que se deben reforzar, de acuerdo con la prueba diagnóstica aplicada al estudiantado de cuarto año
| Área matemática | Conocimientos |
|---|---|
| Números | Concepto de fracción y su representación gráfica. |
| Multiplicación y división abreviada. | |
| Composición y descomposición de números a través de | |
| la suma. | |
| Orden de los números con decimales | |
| Operaciones con números naturales en problemas de | |
| contexto real | |
| Medidas | Monedas y sus conversiones |
| Relaciones y álgebra | Sucesiones |
| Geometría | Características de polígonos y cuadriláteros. |
| Clasificación de triángulos según la medida de sus lados. |
Nota: Fuente propia de la investigación.
Resolución de problemas
Otro de los aspectos básicos del diseño curricular de matemáticas de la institución es la resolución de problemas en contextos reales y debe estar presente en: (1) la mediación pedagógica durante las clases de matemática, (2) la movilización de los conocimientos (práctica) y (3) la evaluación de aprendizajes.
En la prueba diagnóstica para cuarto año se plantearon dos preguntas de desarrollo. La primera evaluaba la integración del área de medidas con números, mediante un problema que implicaba la combinación de monedas nacionales para determinar un monto de dinero, lo que implicaba el uso simultáneo de habilidades de ambas áreas.
La segunda pregunta evaluaba el concepto de la multiplicación y suma de números en un problema de contexto real debido a su importancia en los diagnósticos de Maet al., 2015).
A continuación, el segundo problema contextualizado de la prueba diagnóstica.
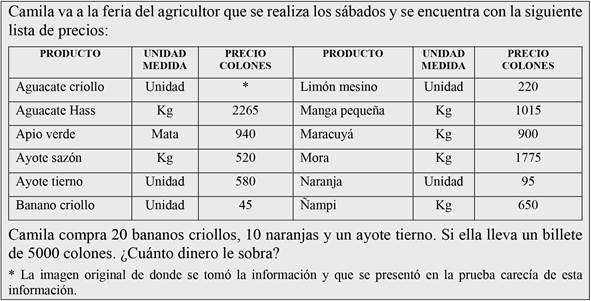
Fuente propia de la investigación
Figura 2 Segundo problema de desarrollo de la prueba diagnóstica para cuarto año.
El ítem poseía un valor de cuatro puntos y en caso de no llegar a la respuesta esperada se asignaron créditos parciales de 0, 1, 2 o 3 puntos de acuerdo con la resolución efectuada por cada estudiante.
Tal y como se observa en la Gráfica 3, el 14 % (aproximadamente) de estudiantes de cuarto año obtuvo el puntaje máximo asigna do al ítem y un poco más del 40 % obtuvo un puntaje de cero en la pregunta de resolución de problemas, mostrada en la Figura 1.
Dentro de las posibles causas de estos porcentajes están: (1) la dificultad de entender lo que plantea el contexto, (2) la dificultad de comprender la pregunta por responder, (3) la dificultad de plantear las operaciones respectivas para la resolución del problema y (4) los errores al realizar las operaciones respectivas.
Conclusiones
Este estudio fue trascendente porque recolectó evidencias científicas mediante la prueba diagnóstica sobre conocimientos, debilidades y fortalezas del estudiantado de cuarto año participante; lo anterior con miras al siguiente año escolar. Esto permitió a la institución tomar estas decisiones:
En números, trabajar en el fortalecimiento de la multiplicación abreviada, porque es una actividad matemática muy importante para ese año lectivo y los posteriores, y se ob-servó que el estudiantado no maneja bien dichos procedimientos.
En geometría, buscar estrategias metodológicas para la enseñanza de los conceptos geométricos, de tal manera que el estudiantado no se los aprendan solamente para una prueba, como sucedió el tema de clasificación de triángulos de acuerdo con la medida de sus lados, sino que el conocimiento le quede a lo largo del año.
En el área de relaciones y álgebra, en el tema de las sucesiones, trabajar con problemas cuyo patrón no sea solo lineal, sino otro tipo de patrones como los propuestos en los ítems 3 y 15 de la prueba diagnóstica, porque implican un mayor grado de análisis porque involucra figuras o valores que implican centenas.
En estadística y probabilidad, no es necesario hacer ajustes porque se notó que el estudiantado sabe leer información de una gráfica dada.
En general, trabajar bastante la resolución de problemas en el aula, pues es aquí donde el personal docente se puede percatar sobre las debilidades del estudiantado. Por ejemplo, el elegir la información necesaria para la resolución permitió a la institución tomar estas decisiones:
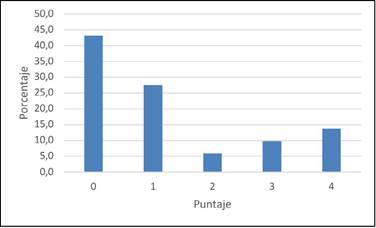
Nota: Fuente propia de la investigación.
Gráfica 3 Porcentaje de puntos asignados al segundo problema de desarrollo de la prueba diagnóstica aplicada a cuarto año en la institución, noviembre del 2021
de un problema y descartar aquella que no es importante, es un proceso que se debe trabajar en la mediación pedagógica para que luego esta se vea reflejada en los ítems de desarrollo.
La evaluación diagnóstica realizada fue fundamental para conocer el alcance y desarrollo de las habilidades matemáticas en el estudiantado (Mayorga, Gallardo y Jimeno, 2015); sin embargo, este tipo de evaluación se vuelve más importante en el momento histórico de la pandemia y postpandemia, pues es necesario analizar si las diferentes estrategias empleadas por las escuelas y los colegios en general han sido suficientes para el logro de los objetivos educativos, como se lo propuso la institución objeto de esta investigación
En el diagnóstico aplicado no solo se consideraron las habilidades y conocimientos y matemáticos, sino que se usaron otros elementos curriculares (Ruiz, 2018), tales como: (1) la resolución de problemas, (2) la integración de habilidades matemáticas, (3) los contextos reales; entre otros, lo que permitió una visión más integral del análisis.
Diferentes estudios, desde hace más de 40 años han planteado que las reformas curriculares deben evaluarse constantemente (Ibarrola y Glazman, 1978; Taba, 1974; Tyler, 1973). Poveda-Vásquez y Zumbado-Castro (2023) presentan un primer estudio en esta institución educativa sobre la implementación curricular en matemáticas. La investigación aquí expuesta permite dar un seguimiento a lo que sucede en la institución, en el área de matemáticas.
Por otro lado, esta investigación está totalmente relacionada con la mediación pedagógica, pues es necesario tomar acciones, de acuerdo con los resultados. Por esto, las reuniones con las autoridades de la institución y con la docente que estaba a cargo (en el año 2021) y la docente que estaría a cargo de esta población el año siguiente (en 2022), fueron fundamentales para la toma de decisiones, ya sea de carácter individual (considerando los resultados por estudiante) o de manera más general.
Agradecimiento
Agradecimientos a la administración de la institución, a su personal docente, administrativo y al estudiantado.















