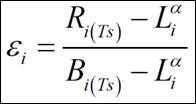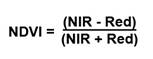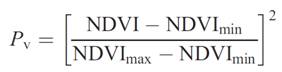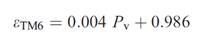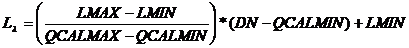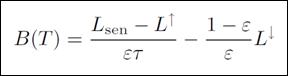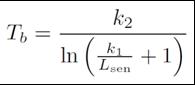Introducción
La teledetección espacial ha experimentado un renovado impulso en las últimas décadas, con nuevos sensores y plataformas que han permitido la obtención de magnitudes o variables geofísicas de enorme valor geográfico. Dentro del amplio abanico de dichas variables, la temperatura terrestre es el principal objeto de estudio de la teledetección térmica. De hecho, la temperatura superficial es una fuente fundamental de información, tanto cualitativa como cuantitativa, acerca de los procesos que ocurren en la superficie terrestre, permitiendo por tanto su caracterización, análisis y modelización (Quattrochi y Luvall, 2000).
Las imágenes en infrarrojo térmico de media resolución permiten, además, estimar otras variables como la evapotranspiración a partir de la ecuación de balance energético, de gran utilidad en la gestión del recurso hídrico.
La puesta en órbita en 1982 del sensor Thematic Mapper (TM) a bordo de la plataforma Landsat-4 y posteriormente (en 1984) con la plataforma Landsat-5, ha permitido el acceso a una base histórica de más de 25 años de imágenes térmicas. El lanzamiento en 1999 de la plataforma Landsat-7 con el sensor Enhanced Thematic Mapper plus (ETM+) permitió el acceso a imágenes térmicas con una resolución de 60 metros, aunque un fallo técnico del sensor limitó severamente su uso, por lo que fue sustituido en 2013 por los instrumentos OLI y TIRS de la plataforma Landsat 8.
Marco conceptual
Teledetección térmica es un término que hace referencia a las medidas obtenidas por un sensor ubicado a bordo de una plataforma (un avión o satélite) que capta la radiación electromagnética emitida por la superficie terrestre en la región del infrarrojo térmico, típicamente entre los 8 y 14 µm (Sobrino, et al. 2000).
En el intervalo espectral comprendido entre 8 y 14 μm (infrarrojo térmico) se produce el 80 % de la emisividad de la superficie terrestre. En dicho intervalo es donde, además, la transmisividad atmosférica es más elevada y por tanto, donde se ubican las medidas que diferentes sensores toman a bordo de las misiones de los satélites (Pérez y Muñoz, 2002).
La atenuación de la señal en dicha región del espectro se debe a la absorción de aerosoles, pero se trata de una cantidad despreciable debido a que las concentraciones de vapor de agua (H2O) ozono (O3) y dióxido de carbono (CO2) se encuentran en menor proporción (Prata et al., 1994).
Sin embargo, la transmisión atmosférica de la radiación se ve afectada por el vapor de agua cinco veces más que por el resto de los gases juntos, absorbiendo la radiación de onda larga del infrarrojo térmico y onda corta en la región de las microondas (desde los 22 μm a 1 mm). En cuanto al dióxido de carbono, este absorbe fuertemente la radiación en la región del infrarrojo lejano del espectro electromagnético, mientras que el ozono lo hace para longitudes de ondas más cortas y energéticas (Atkins & Jones, 2006).
En consecuencia, la estimación de la temperatura superficial está condicionada, principalmente, por el contenido de vapor de agua de la atmósfera (especialmente sensible en la zona intertropical) y la emisividad de la superficie estudiada. Por todo ello, una correcta estimación de la temperatura superficial implica necesariamente la consideración y corrección de estos factores.
La radiación emitida por una superficie a una determinada longitud de onda, dentro del rango infrarrojo térmico, es función no sólo de su temperatura, sino que depende también de su emisividad. Es por ello, un parámetro crítico para el estudio del balance radiativo terrestre. La ecuación de la emisividad está representada como la energía emitida por una superficie eficiente (Valor y Caselles, 1996) y viene dada por:
Ecuación 1. Ecuación de la emisividad (Valor y Caselles, 1996)
Siendo ε i la emisividad de una superficie (considerando la transmisividad e irradiancia de la atmósfera), R i(Ts) la radiancia espectral emitida por un cuerpo a una determinada longitud de onda y temperatura, B i(Ts) la radiancia emitida por un cuerpo negro a una temperatura dada, medida en campo, y por último L i ∞ la irradiancia atmosférica.
Se suele definir un cuerpo negro como un emisor perfecto, es decir, con una emisividad de 1; sin embargo, la vegetación tiene valores de emisividad menores, entre 0,97 - 0,985, debido a que parte de la energía incidente es reflejada, absorbida y transmitida en proporciones diferentes, según la longitud de onda (Rubio et al., 2003). Su valor es altamente dependiente de la composición de la superficie, sobre todo con su contenido de humedad, rugosidad y tamaño de sus partículas (Barreto, et al. 2009).
También varía con la longitud de onda en la cual es medida, la resolución y ángulo de observación, dando una idea de la complejidad que representa su estimación. Algunas de las técnicas que se han utilizado para estimar la emisividad de la superficie son:
Método de emisividad normalizada (NEM) propuesto por Gillespie et al., (1985).
El índice Independiente de la Temperatura (TISI) propuesta por Becker y Li, (1990).
La separación de emisividad (TES) propuesta por Gillespie et al. (1999).
El método basado en índice de vegetación (NDVI) propuesto por Valor y Caselles, (1996) que fue el utilizado en el presente estudio.
El canal térmico (6 para Landsat TM-ETM+) convertido a radiancia se puede transformar a temperatura de brillo efectiva por medio de la ecuación de cálculo de la temperatura superficial a partir de los valores de brillo de la imagen térmica, que requiere de dos constantes de calibración como muestra el cuadro 1:
Cuadro 1 Constantes de calibración de la banda térmica del satélite Landsat
| Satélites | Bandas | K1 | K2 |
| (W/m-2/sr-1/μm-1) | Kelvin | ||
| Landsat 4 | 6 | 671,62 | 1284,30 |
| Landsat 5 | 6 | 607,76 | 1260,56 |
| Landsat 7 | 6 | 666,09 | 1282,71 |
| Landsat 8 | 10 | 774,89 | 1321,08 |
| 11 | 480,89 | 1201,14 | |
Fuente: Chander et al., 2009.
Por otra parte, el uso de la banda térmica en el estudio de la temperatura superficial de la Tierra requiere de la eliminación de los efectos atmosféricos en dicha longitud de onda. Además, la emisividad de un objeto en el terreno es igualmente atenuada y aumentada por la atmósfera. Por todo ello, resulta imprescindible un conocimiento apropiado de la atmósfera para la estimación de la transmitancia, la radiancia ascendente y la radiancia descendente. Cuando se conocen los valores de estas 3 variables, se puede convertir la radiancia medida en el espacio a la radiancia emitida por una superficie (Barsi et al., 2003).
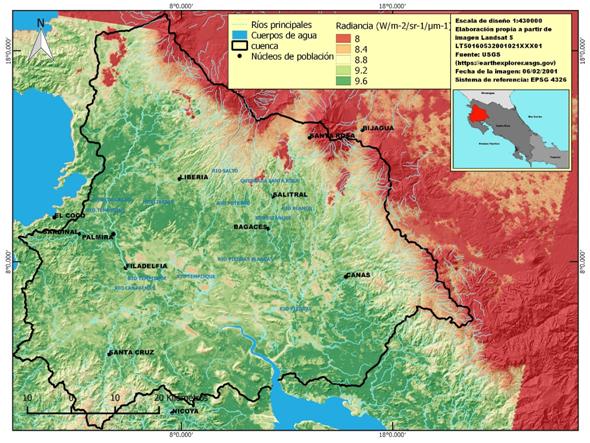
Área geográfica de estudio
La cuenca del río Tempisque-Bebedero, en el noroeste de Costa Rica, cubre en total 5455 km² en la provincia de Guanacaste. La cuenca se encuentra situada 10º 58’ 25’’ de latitud norte, 10º 06’ 41’’ de latitud sur, 85º 46’ 59’’ oeste y 84º 49’ 40’’ este. El clima predominante en la cuenca es de tipo tropical con una prolongada estación seca, que va de finales de noviembre a principios de mayo. La estación de lluvias comienza en mayo y se prolonga hasta noviembre. Existe por tanto una fuerte estacionalidad en las precipitaciones, con un valor promedio anual de 1900 mm. En cuanto a las temperaturas, no existe la marcada estacionalidad que se da en las precipitaciones, con un promedio anual de 28 ºC. Sin embargo, es habitual en plena estación seca que la temperatura promedio ascienda hasta los 34 ºC de promedio, con máximos puntuales de hasta 40 ºC. Desde un punto de vista geomorfológico se trata de una zona de origen predominantemente sedimentario, y por ello reciente. El complejo Nicoya configura la red de drenaje en virtud de colinas calizas que constituyen un espacio formado fundamentalmente a partir del Mioceno (Denyer, Montero & Flores, 2014). La existencia de espacios abiertos, llanuras inundables, cultivos y pastizales facilita la obtención de temperatura superficial del suelo, tanto por la homogeneidad de los pixeles obtenidos por el satélite como por la existencia de suelo sin cobertura forestal densa.
Materiales y métodos
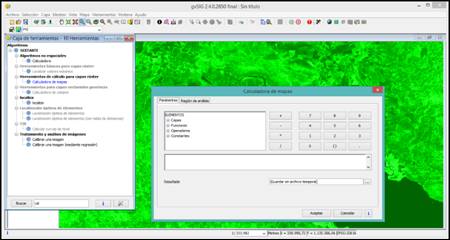
Para el presente trabajo se utilizaron exclusivamente recursos libres online y software de código abierto. Todo el procesamiento de imágenes que sustenta la presente metodología se realizó con la herramienta “calculadora de mapas” de GvSIG 2.4 (figura 1).
El problema fundamental con la estimación de la temperatura superficial de la Tierra a partir de datos de satélite es la necesidad de corregir en los mismos, los efectos debidos a la absorción atmosférica y a la emisividad de la superficie medida. Para la producción del mapa de emisividad, por tanto, se parte del modelo presentado por (Valor y Caselles, 1996). Pero previamente, es conveniente la realización de una corrección DOS1 a las bandas roja e infrarroja de Landsat5, para remover el efecto de la dispersión atmosférica.
Seguidamente, calculamos el índice de vegetación diferencial normalizado, o NDVI (como se muestra en la figura 2) a partir de las bandas 3 y 4, ya corregidas atmosféricamente. La fórmula del NDVI es:
Ecuación 2. Índice de vegetación diferencial normalizado
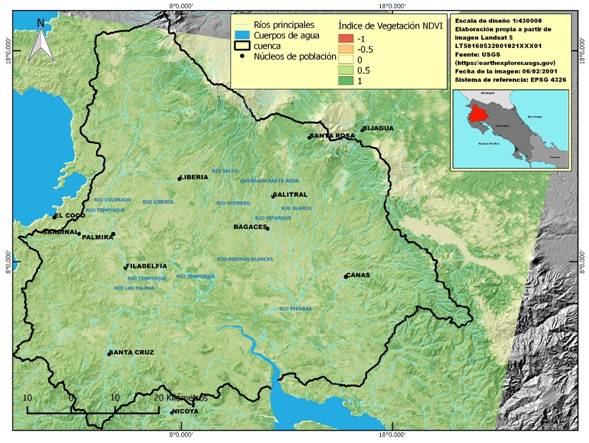
Figura 2 Índice de Vegetación Diferencial Normalizado o NDVI de la cuenca del Río Tempisque-Bebedero, Costa Rica
Una vez obtenido el NDVI, se puede utilizar este directamente para calcular la emisividad de los pixeles, o bien se puede generar un PV (Proportion of Vegetation). La ventaja de esta segunda opción es que permite aislar la emisividad de las diferentes cubiertas, tomando como referencia la de la vegetación que puede ser calculada a partir de este índice (Carlson & Ripley, 1997) mostrado en la ecuación 3.
Ecuación 3. Proporción de vegetación
Fuente: Carlson & Ripley, 1997.
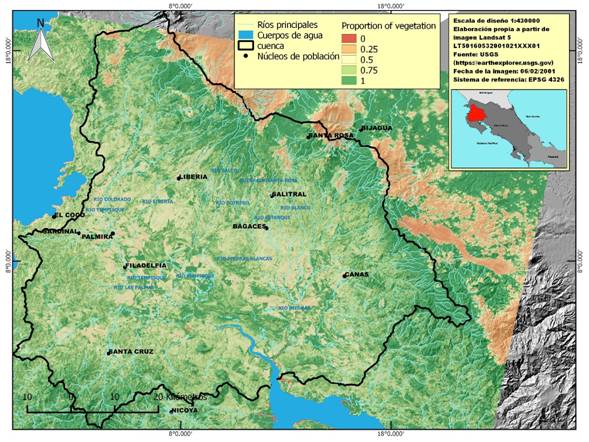
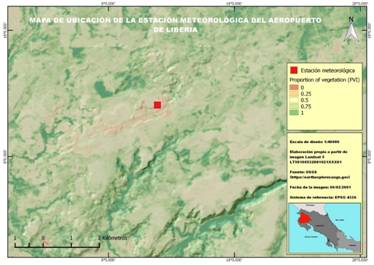
Figura 3 Índice de Proporción de Vegetación o PV, de la cuenca del Río Tempisque-Bebedero, Costa Rica
En la figura 3 se puede constatar que la cantidad de superficie cubierta por vegetación es sensiblemente menor en el PVI que en el NDVI.
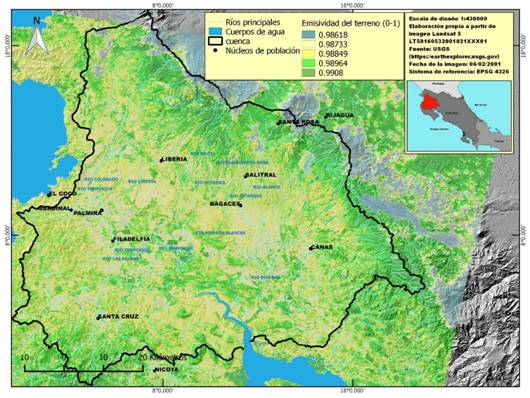
Seguidamente, se procede a mapear la emisividad de los pixeles a partir de la vegetación, como se muestra en la figura 4. Asumiendo que el valor típico de la emisividad en el térmico es de 0.99 para la vegetación, escoger un valor típico de emisividad para el suelo puede ser algo más complejo. Una posibilidad es tomar como referencia el valor propuesto a partir de las 49 muestras de la biblioteca espectral de Aster (http://asterweb.jpl.nasa.gov). En tal caso el valor medio es de 0.973, con una desviación estándar de 0.004 y la expresión final para calcular la emisividad en el monocanal térmico sería la correspondiente con la ecuación 4:
Ecuación 4. Cálculo de emisividad a partir de la proporción de vegetación o Pv
Fuente: Sobrino, Jiménez-Muñoz & Paolini, 2004.
Se va a tomar como referencia el valor de emisividad del pixel correspondiente a la estación meteorológica de Liberia (figura 5) con coordenadas UTM 16 N 1172043 X / 660453 Y
Se calculó la temperatura superficial a partir del método monocanal, basado en la ecuación de transferencia radiativa de Coll, Galve, Sánchez y Caselles (2010). Para ello, se tuvieron en cuenta los aportes de Valor y Caselles (1996) y Chander et al. (2009).
En primer lugar, se realizó una calibración radiométrica para llevar los valores digitales a radiancia espectral (W/m-2/sr-1/μm-1) como muestra la figura 6. La calibración radiométrica o transformación a valores de radiancia es un paso esencial para poder comparar datos o información de múltiples sensores y plataformas en una escala radiométrica común.
La radiancia se calcula de acuerdo a los metadatos del archivo MTL de la banda 6, a través de la ecuación 5:
Ecuación 5. Cálculo de radiancia
Donde L λ es la radiancia espectral de la banda térmica que va a ser calculada; LMAX y LMIN son los valores de radiancia máxima y mínima para la banda 6; QCALMAX y QCALMIN son los valores máximo y mínimo de la radiancia calibrada, es decir, modificados a escala en unidades de números digitales (en función de la resolución radiométrica del sensor) y DN son los niveles digitales (la banda 6 en este caso).
A diferencia de imágenes anteriores, los valores de radiancia más elevados (en verde) se dan en zonas de escasa cobertura vegetal.
Para calcular la temperatura superficial se consideró la siguiente ecuación de transferencia radiativa de C. Coll, J. M. Galve, J. M. Sánchez y V. Caselles (2010):
Ecuación 6. Ecuación de transferencia radiativa
Fuente: Coll, Galve, Sánchez y Caselles, 2010.
Donde; L sen es la radiancia medida por el sensor (W/m-2/sr-1/μm-1), ε es la emisividad de la superficie, B es el parámetro derivado de la Ley de Planck calculado a partir de la ecuación de cálculo de temperatura de la superficie terrestre (°K), L ↓ : radiancia atmosférica descendente (W/m-2/sr-1/μm-1), τ: transmisividad atmosférica y L ↑: radiancia atmosférica ascendente (W/m-2/sr-1/μm-1).
La transmisividad de la atmósfera, y la radiancia ascendente y descendente no son parámetros presentes en los metadatos de una imagen satelital. Para su obtención se recurrió a una herramienta operativa en línea de corrección atmosférica que permite calcular la temperatura superficial con un sesgo inferior a 0.5 ± 0.8ºK (Barsi y otros, 2003). La herramienta se denomina Atmospheric Correction Parameter Calculator y está disponible en el sitio web; https://atmcorr.gsfc.nasa.gov/.
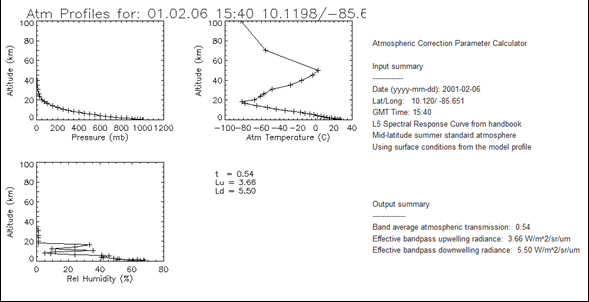
Figura 7 Para la fecha de la escena Landsat (6 de febrero de 2001) se obtuvieron unos valores de transmisividad atmosférica de 0,54, una radiancia ascendente de 3,66 (W/m-2/sr-1/μm-1) y una radiancia descendente de 5,50 (W/m-2/sr-1/μm-1).
Fuente: https://atmcorr.gsfc.nasa.gov/
Barsi y otros (2003) afirman que los valores de temperatura superficial pueden ser estimados con un error de ±2ºK cuando la atmósfera está relativamente despejada y se conoce la emisividad de la superficie. Esta herramienta utiliza perfiles atmosféricos del National Center for Environmental Prediction (NCEP) interpolados a una posición, fecha y hora dadas y el modelo MODTRAN 4 (Berk et al. 1999).
Seguidamente, se aplicó la ecuación 7 de transferencia radiativa propuesta por Coll, Galve, Sánchez y Caselles (2010). El error que introduce esta ecuación se incrementa con el ancho de longitud de onda, la humedad atmosférica y las variaciones de emisividad de la superficie (Coll et al, 2010).
El siguiente paso consistió en aplicar la ecuación 7 de cálculo de temperatura de brillo:
Ecuación 7. Cálculo de la temperatura a partir de los valores de brillo de la imagen (Chander, 2009)
Donde k 2 y k 1 son los coeficientes de calibración, con valores de 1260,56 y 607,76 (W/m-2/sr-1/μm-1), respectivamente, (Chander et. al. 2009) mientras que L sen es el ráster de radiancia corregida obtenido en el paso anterior. El resultado se obtiene en grados kelvin, que fueron transformados en Celsius.
Conclusiones
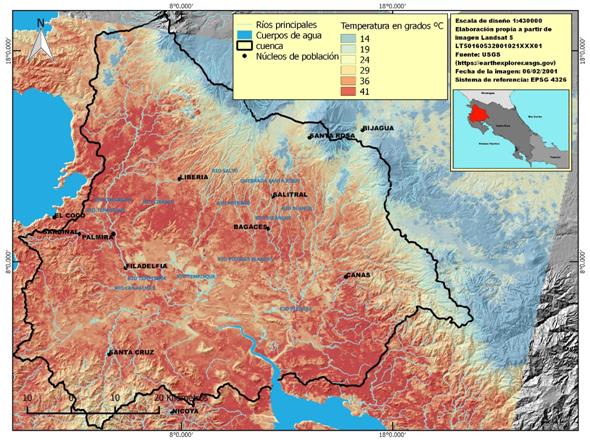
La temperatura finalmente obtenida para el aeropuerto de Liberia fue de 44,379 ºC a las 15:40 del 6 de febrero de 2001. De acuerdo con la información proporcionada por el Instituto Meteorológico Nacional de Costa Rica, la temperatura máxima en el aeropuerto de Liberia ese día fue de 34,1ºC. La obtención de la temperatura sin tomar en cuenta parámetros como la emisividad, la transmisividad y la radiancia bidireccional (es decir, aplicando la ecuación 8 directamente sobre la radiancia) genera valores de temperatura más bajos, y por tanto más parecidos a la temperatura del aire a la sombra y a cierta distancia del suelo. Concretamente, en el caso del pixel correspondiente a la estación meteorológica del aeropuerto de Liberia, la temperatura obtenida con este método fue de 32ºC. Considerando la presencia de suelo asfaltado y el hecho de que la temperatura superficial puede superar ampliamente a la temperatura medida a la sombra y a un metro del suelo, la diferencia de 12ºC parece más que plausible. Por otra parte, cuanto menor es la irradiancia solar y mayor es la velocidad del viento, menores diferencias existen entre estas temperaturas, y por ello más próxima es la temperatura del aire a la temperatura superficial medida desde satélite. Además, estas diferencias también disminuyen a mayor proporción de cobertura vegetal y cuando no existe estrés hídrico (Niclós, et al, 2010).
La existencia de correlaciones entre temperatura del aire y temperatura superficial en diferentes tipos de coberturas de la zona intertropical y en zonas con diferentes relieves debe ser estudiada con mayor profundidad. También se requiere analizar y validar la introducción de nuevos parámetros en las ecuaciones propuestas, con objeto de obtener un algoritmo general que permita estimar la temperatura del aire a partir de la observación desde satélite.
La principal desventaja que presenta esta metodología deriva del hecho de que el valor de emisividad que se incorpora a la ecuación 5 proviene de un pixel del terreno (no de un valor promedio de la imagen) por lo que la estimación del valor de temperatura superficial de la imagen sólo tendría una precisión de ±2ºK en el pixel del cual se tomó el respectivo valor de emisividad.
Finalmente, la utilidad de esta metodología monocanal de obtención de temperatura superficial permite aproximaciones históricas (como la presente, del año 2001) muy precisas acerca de cómo contribuían las coberturas artificiales en la formación de islas de calor urbano en el pasado.