Introdução
O detalhamento e a qualidade de informações biométricas são essenciais para um adequado planejamento e prognóstico do crescimento e produtividade florestal. A busca por alternativas que forneçam estimativas exatas e reduzem o tempo das medições em campo são constantes, exigindo-se de mais pesquisas sobre o processamento de dados biométricos (1).
A altura total de uma árvore se refere à distância linear do nível do solo até o ápice da copa. Trata-se de uma variável biométrica amplamente utilizada em cálculos volumétricos de fustes e de seus múltiplos sortimentos, classificação produtiva de sítios, caracterização de crescimento e orçamentos de carbono (2). Por outro lado, sua medição é mais dispendiosa e demorada em comparação com aquela do diâmetro. A fim de se otimizar a mensuração em povoamentos equiâneos, é comum medir a altura de uma parte das árvores da parcela e adotar a modelagem hipsométrica para a estimativa de altura dos demais indivíduos, que tiveram somente o diâmetro medido.
A modelagem hipsométrica por sua vez, é uma técnica para o estabelecimento de relação funcional com vistas à estimativa da altura individual de árvores, processada frequentemente via regressão linear. A estimação da variável mais laboriosa em função daquela correlacionada de mais fácil e rápida medição, permite uma sensível redução nos custos e melhoria operacional de amostragem (3).
Os modelos hipsométricos podem ser classificados em duas categorias distintas de acordo com a aplicabilidade, tradicional (local) ou generalistas (geral). Modelos tradicionais são os mais simples, dependentes apenas do diâmetro e indicados para o ajustamento por talhão ou para um pequeno conjunto de talhões análogos e homogêneos em termos de capacidade produtiva. A forte correlação entre a altura e o diâmetro justifica o uso desta como variável preditora em modelos tradicionais. Contudo, diversos aspectos estão relacionados com a expressão do crescimento vegetal. É preciso a compreensão de que as árvores se encontram em contínuo estado de competição em um povoamento florestal, sendo o crescimento influenciado por aspectos genéticos, edáficos, fisiográficos, climáticos e demais mecanismos relacionados à complexidade de ecossistemas (4), (5).
A inclusão de características do povoamento aumenta a qualidade preditiva e realismo biológico dos modelos hipsométricos, tornando a equação adaptável a vários sítios (1), (6), (7), (8). O modelo generalista mais conhecido no setor florestal brasileiro é o de (9), que se baseia no uso de dados diamétricos e logaritmizados da altura dominante como variáveis preditoras. Todavia, a coleta de dados é um entrave para o uso desse modelo, que requer a identificação e medição da altura de mais árvores em campo, especificadamente, daquelas dominantes.
Na busca de alternativas mais eficientes para a estimativa da altura de árvores, adaptações em modelos hipsométricos clássicos podem ser adotadas para a melhoria do desempenho da modelagem sem intensificar a mensuração em campo. Apesar de incipiente, a inclusão de variáveis preditoras obtidas em nível de parcela tem sido pesquisada em substituição a altura dominante, como o diâmetro médio quadrático, diâmetro máximo, diâmetro dominante, média aritmética do diâmetro e outras (2), (10), (11). Outra alternativa promissora, é a inclusão de informações competitivas individuais da própria árvore como variável preditora para a estimativa de sua altura.
A competitividade entre árvores pode ser resumida na forma de índices ou expressões matemáticas que refletem o grau de supressão/dominância de cada árvore em relação àquelas competidoras (12), (13), (14), (15), (16). Os índices de competição independentes da distância é uma representação numérica do efeito cumulativo de todo o conjunto de características e interações bióticas e abióticas inerentes a uma árvore ou grupo de indivíduos ao longo do tempo, desconsiderando a posição espacial relativa de árvores dentro da unidade amostral (15), (17), (18).
Embora o uso de índices de competição seja comum em modelagens do crescimento e produção em nível de árvore individual (19), (20), investigações científicas sobre sua aplicação na modelagem hipsométrica são escassas e podem subsidiar a quantificação de recursos florestais. Mediante exposto, o objetivo do presente trabalho foi avaliar alternativas para a modelagem hipsométrica generalista de eucalipto via regressão linear, com a inclusão de índices de competição independentes da distância como variáveis preditoras.
Material e métodos
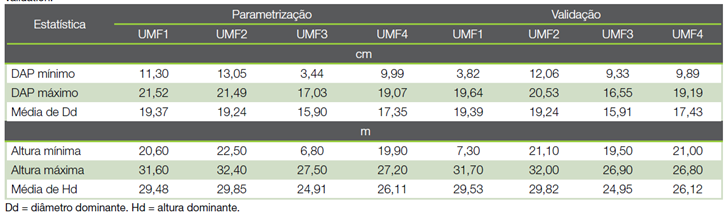
O trabalho foi realizado com informações de 34 parcelas distribuídas aleatoriamente em povoamentos clonais de Eucalyptus urophylla S. T. Blake pertencentes a uma empresa florestal, localizados na região central de Minas Gerais. O clima da região é do tipo Cwa pelo sistema internacional de classificação de Köppen (21). Foram estabelecidas quatros unidades de manejo florestal (UMF) com médias de temperatura e precipitação de: 22,7ºC e 1.259 mm para a UMF1 (87,91 ha); de 23,4ºC e 1.043 mm para a UMF2 (42,74 ha); de 23,4ºC e 1.043 mm para UMF3 (77,21 ha) e; de 23,0ºC e 1.189mm par UMF4 (85,57 ha), respectivamente.
Realizou-se o inventário florestal na idade de 72 meses, sendo lançadas: 11 parcelas na UMF1; 6 parcelas na UMF2; 10 parcelas na UMF3 e 7 parcelas na UMF4. A área útil de cada parcela e o espaçamento de plantio foram 400 m2 e 3,0 × 2,5 m, respectivamente. Foram mensurados o diâmetro com casca à altura do peito (DAP - à altura de 1,30 m do solo, cm) de todos os fustes. Em cada parcela, tomaram-se a altura total (Ht, m) das 15 primeiras árvores e de quatro árvores dominantes (Hd, m), conforme conceito de (22), equivalente a uma árvore dominante a cada 100 m2. Assumindo a idade índice de 72 meses, a capacidade produtiva de UMF1 a UMF4 foram de: S = 29,26 m; S = 29,81 m; S = 24,94 m e; S = 26,12 m, respectivamente.
Calcularam-se sete índices de competição independentes da distância conhecidos no setor florestal (Quadro 1). Os índices IC1, IC2 e IC3 representam a competição bilateral e assumem que os recursos de crescimento são disputados por todas as árvores vizinhas. Os demais índices (IC4 a IC7) assumem como árvores competidoras aquelas de diâmetro maior que a árvore objetivo e, portanto, representam a competição unilateral, ou seja, árvores maiores não são afetadas por aquelas vizinhas menores.
Os dados foram divididos aleatoriamente em grupos de parametrização (70,0 % das amostras) e de validação (30,0 % das amostras), mutualmente exclusivos, empregando método randômico de amostragem sem reposição (método holdout). Nessa divisão, todas as parcelas foram contempladas com árvores em ambos os grupos (Quadro 2).
Quadro 2 Descrição de dados utilizados no ajuste hipsométrico de eucalipto aos 72 meses de idade, separados em grupos de parametrização e validação.
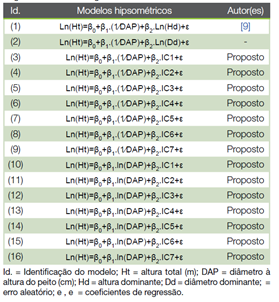
Ajustaram-se 16 modelos hipsométricos generalistas (Quadro 3), sendo dois modelos rotineiramente adotados no setor florestal baseados em informações de fustes dominantes e 14 propostos, de dupla entrada (DAP e índice de competição). Os modelos propostos foram estabelecidos a partir dos modelos tradicionais de (23) e de (24), que possuem saída hipsométrica logaritmizada e se diferem em termos de variável preditora; o primeiro inclui o inverso de DAP e o segundo, o logaritmo neperiano de DAP. Todos os modelos foram ajustados a todo conjunto de dados do grupo de parametrização, isto é, sem estratificação. O método dos Mínimos Quadrados Ordinários (MQO) foi adotado nas análises de regressão.
Quadro 3 Modelos hipsométricos generalistas testados para a estimativa da altura de eucalipto aos 72 meses de idade.
A fim de se avaliar a presença de multicolinearidade dos modelos, calculou-se o Valor de Inflação da Variância (VIF). Os pontos que extrapolaram a tendência geral dos dados não foram eliminados das análises estatísticas a fim de se verificar a capacdade da modelagem em lidar com outliers ou ruídos. Para diagnóstico de efeito estatístico, empregou-se 5% de significância em todas as análises. Estas foram efetuadas com auxílio do software R versão 3.5.2 (25).
Resultados
Os coeficientes e a qualidade de ajuste dos modelos hipsométricos generalistas para eucalipto aos 72 meses de idade se encontram no Quadro 4. O valor de inflação da variância de todos os ajustes realizados foi baixo (VIF < 9). Todos os coeficientes das equações foram significativos (p ≤ 0,05), exceto para a equação (10). Esta equação foi descartada da análise gráfica subsequente. Em geral, as equações apresentaram poucos desvios (baixos valores de RQEM e MDA) e altas correlações (r ≥ 0,90 na fase de parametrização e r ≥ 0,89, na validação). Tomando-se como referência a fase de parametrização, a RQEM e MDA aumentaram em torno de 1,27 a 8,38% e de 0,35 a 8,64% na fase de validação. Notou-se pequeno aumento do coeficiente de correlação na fase de validação somente para a equação (2), de 0,06%.
Quadro 4 Coeficientes e qualidade de ajuste dos modelos hipsométricos generalistas para eucalipto aos 72 meses de idade.
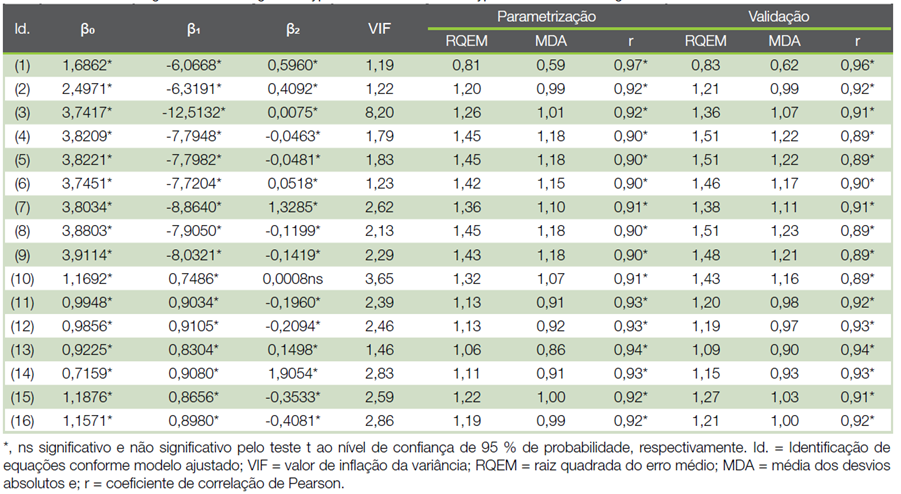
No que se refere às estatísticas de qualidade de ajuste, a equação (2) tendeu a oscilar menos entre fases de parametrização e validação. O modelo de (9) ajustado, ou modelo (1), exibiu as maiores correlações e os menores valores de RQEM e MDA nas fases de parametrização e validação.
Dentre os modelos propostos (Quadro 3), as equações (13) e (14) tiveram os menores valores de RQEM (≤ 1,15) e MDA (≤ 0,93), além da maior correlação (≥ 0,93), durante parametrização e validação. Estas duas equações se basearam no modelo de (24) e a inclusão dos índices de competição IC4 e IC5 como preditores, respectivamente. Uma característica em comum destes índices é a inclusão do atributo área basal das árvores vizinhas competidoras na expressão matemática. Ambas as equações foram selecionadas para as análises de inspeção gráfica subsequentes (Figura 1).
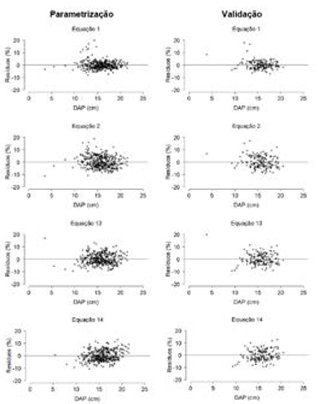
Figura 1 Distribuição de resíduos percentuais das equações hipsométricas generalistas obtidas para eucalipto aos 72 meses de idade.
Figure 1. Distribution of percentage residuals of general hypsometric equations obtained for eucalyptus at 72 months of age.
Apenas para fins de visualização gráfica, foram omitidos os resíduos percentuais da equação (14) referentes aos valores de 46,55% (DAP = 3,44 e IC5 = 0,24) e 47,39% (DAP = 3,82 e IC5 = 0,23) nas fases de parametrização e validação, respectivamente. A distribuição dos resíduos percentuais das equações selecionadas tendeu à homocedasticidade, exceto na equação (14). As equações (1) e (13) exibiram resíduos mais próximos ao eixo das abcissas, especialmente, no intervalo entre -10 a 10%.
Discussão
Todas as equações hipsométricas geradas foram biologicamente consistentes, com coeficientes negativos associados ao inverso de DAP e positivos para as demais relações diretas com atributos biométricos (Quadro 4). É conveniente salientar que as estatísticas apresentadas neste quadro não retratam o desempenho dos modelos hipsométricos, tratam-se apenas, das médias das variações das estimativas totais ou indicativo da qualidade de ajuste (26). Portanto, fez-se necessária a validação e análise gráfica de resíduos.
A inclusão da altura dominante na modelagem hipsométrica tem sido exaustivamente utilizada para ampliar o potencial de generalização das equações até talhões com diferentes potenciais produtivos. O modelo de (9) ajustado apresentou a melhor qualidade de ajuste e desempenho estatístico para representar a relação hipsométrica de E. urophylla (Quadro 4 e Figura 1). Enfatiza-se que este modelo se difere do modelo de (23) pela inclusão da altura dominante em sua expressão e possui, como limitação, a necessidade de informações de árvores dominantes durante a amostragem, tornando o inventário florestal mais dispendioso e laborioso.
Por outro lado, a inclusão de índice competição como variável preditora, independentes da distância e baseados em aspectos da estrutura horizontal, influenciou o desempenho preditivo dos modelos ajustados. Nas circunstâncias cuja amostragem não tenha abrangida a identificação e/ou coleta de informação hipsométrica de árvores dominantes, índices de competição podem ser analisados para a definição de equações generalistas para a estimativa da altura. Verificou-se que a inclusão de índices de competição favorece, em algumas ocasiões, a qualidade de ajustamento, reduzindo os desvios e ampliando o desempenho preditivo da modelagem generalista. Esta característica possui grande importância prática no processamento de dados, pois facilita a aplicação da equação hipsométrica para amplas áreas de cultivo e diminui a quantidade de estratificações e ajustes hipsométricos.
Os modelos generalistas propostos se fundamentaram em características competitivas individuais das próprias árvores. Embora a competição seja um fenômeno de alta complexidade biológica (12), (14), (27) e tenha sido sintetizada na forma de índice, a precisão do ajuste desses modelos foi considerada satisfatória. As equações provenientes dos modelos (11) a (14), baseadas na expressão do modelo de (24), exibiram qualidade de ajuste um pouco melhor em relação àquela que se baseou na inclusão do diâmetro dominante como variável preditora.
Apesar de que o ajuste do modelo (10) tenha resultado em coeficiente de regressão não significativo e, em comparação aos demais ajustes, poucos desvios ((Quadro 4) não se verificou a presença de multicolinearidade, haja vista que, VIF acima de 10 é um indício claro de multicolinearidade (28). Ressalta-se que diante de eventual presença da multicolinearidade, os coeficientes da regressão deixam de refletir os efeitos inerentes de particular variável independente sobre aquela dependente, representando parcialmente seu real efeito. Também, não se observou problemas de sub ou sobreparametrização nas equações obtidas, o que levaria a discrepâncias na qualidade de ajuste entre as fases de validação e parametrização. A validação é uma importante etapa para a escolha de um modelo hipsométrico livre de vieses e resíduos heterogêneos.
O uso indiscriminado de modelos hipsométricos deve ser visto com bastante cautela, pois dificuldades relacionadas a inconsistência biológica são comuns durante o processamento estatístico. A escolha apropriada de um modelo hipsométrico permite a obtenção de estimativas não enviesadas de altura e, consequentemente, do volume. A inclusão do índice de competição IC4 como variável preditora em modelos hipsométricos mostrou que pode ser uma alternativa viável em substituição ao uso de informações biométricas de árvores dominantes, reduzindo soma de quadrado dos resíduos e a intensidade de fustes amostrados para a modelagem hipsométrica generalista em povoamento equiâneos. Este índice representou a competição unilateral, aquela que implica em concorrência especialmente por radiação luminosa (29), que é comum em povoamentos cuja competição já se encontra estabelecida, em idades próximas a colheita florestal.
A modelagem hipsométrica é uma etapa fundamental para a estimativa da altura de árvores e quantificação volumétrica em inventários florestais de povoamentos equiâneos. Os resultados obtidos fornecem subsídios importantes para o desenvolvimento de futuras pesquisas sobre a hipsometria em povoamentos florestais empregando, particularmente, modelos de regressão lineares, facilmente ajustados e interpretados. A inclusão de preditores que representam aspectos relacionados as interações bióticas e abióticas na modelagem hipsométrica, como índices de competição, mostrou potencial para a melhoria preditiva sem comprometer a amostragem em campo e o realismo biológico.
Conclusões
A inclusão de índices de competição independentes da distância em modelos hipsométricos ampliam a capacidade de generalização de equações para talhões de eucalipto com distintas capacidades produtivas. O índice de competição IC4, que representa à área basal de árvores vizinhas competidoras, favorece a qualidade de ajuste e desempenho preditivo da modelagem hipsométrica nos sítios estudados. Diante da ausência de informações da altura de árvores dominantes, a modelagem generalista pode ser melhor viabilizada com a inclusão desse índice como variável preditora no modelo de (24).















