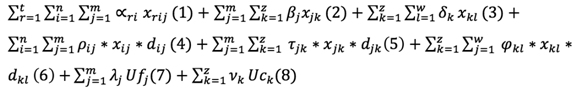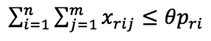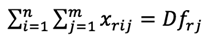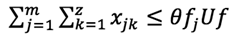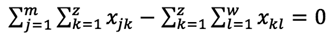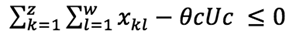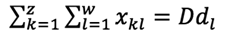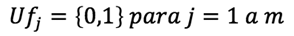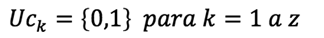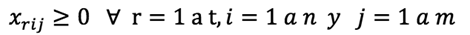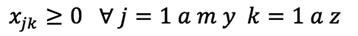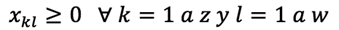Introducción
El aumento en la producción, transporte, almacenamiento y consumo de bienes estimulado por la globalización ha provocado importantes problemas ambientales, entre ellos, el cambio climático, ocasionado por el aumento de gases de efecto invernadero, que se ha constituido en una peligrosa amenaza para el planeta [1]. La configuración de la cadena de suministros comprende, entre otros, la ubicación de las fábricas y de los centros de distribución o almacenes, así como la cantidad y capacidad de sus instalaciones. La configuración de la cadena de suministros es una decisión de tipo estratégico y de largo plazo por lo que tiene importante impacto en el tiempo. Además, define en gran medida aspectos más operativos como los medios de transporte, sus características y capacidades. Por demás, el enfoque de la ecología industrial con miras a lograr el desarrollo sostenible incluye las cadenas de suministros [2].
El análisis de la cadena de suministros que involucra a todos sus actores ofrece una importante oportunidad para la reducción de emisiones, por cuanto las principales emisiones de algunos productos se generan en los procesos para extraer las materias primas; las de otros, en los procesos de transformación, mientras que las de otros finalmente, en las operaciones de logística. Por otra parte, la cadena de suministros debe satisfacer requisitos como el cumplimiento de las demandas de los clientes, bajo limitaciones como la capacidad de entrega de los proveedores, de producción de las fábricas y de almacenamiento de los centros de distribución. Esto hace que se requiera el procesamiento complejo de una gran cantidad de variables que, para llegar a resultados óptimos, obliga a recurrir a la vía de la modelación matemática, tanto para acelerar el proceso como para asegurar una precisión adecuada.
La carencia actual de modelos no permite responder a los frecuentes cuestionamientos sobre los beneficios de la implementación de una administración verde en los negocios [3]. Mediante la revisión de literatura se encontró una diversidad de planteamientos y consideraciones en las investigaciones que han propuesto modelos matemáticos para la sostenibilidad en la cadena de suministros. Una gran parte se han enfocado en las condiciones e intereses particulares de algunos tipos de industrias y productos. A diferencia de las anteriores, en esta investigación se desarrolla un modelo de optimización para la configuración de la cadena de suministros que es más general que particular, con el fin de poder analizar condiciones comunes a varios productos. El modelo está dirigido a la reducción de las emisiones de carbono mediante el análisis de condiciones importantes de la configuración, como el aprovisionamiento de materiales y la ubicación de las fábricas y de los centros de distribución.
Revisión de literatura
En primer lugar, es importante definir el concepto de cadena de suministros. Según Chase y Jacobs [4], la cadena de suministros refiere al traslado de información y material, con origen y destino en los procesos de manufactura, entre ellos los procesos de logística y almacenamiento. El suministro refiere al despacho de artículos y servicios tanto para las fábricas y almacenes, en un extremo de la cadena, como para los clientes, en el otro extremo.
La gestión de la cadena de suministros implica la toma de variadas decisiones. Las decisiones de estructura se refieren a la ubicación de las fábricas y los centros de distribución o almacenes, a la cantidad y capacidad de las facilidades, a la capacidad que subcontratar o expandir, y al medio de transporte que utilizar [5]. El resultado de las decisiones de estructura se conoce como la configuración de la cadena de suministros. La configuración de la cadena de suministros es en sí una variable de decisión crítica, pues las decisiones que implica, como la ubicación de los centros de distribución, las políticas de conexión entre ellos y los niveles de inventario son de suma importancia para los sistemas de distribución de las empresas [6].
La cadena de suministros produce una huella de carbono. A lo largo de la cadena de suministros se generan emisiones de gases de efecto invernadero por parte de los proveedores, la logística de suministro a las fábricas, las fábricas, la logística de distribución de las fábricas a los clientes, y los clientes por el mismo uso de los productos [7]. Los proveedores y fábricas generan emisiones propias de sus procesos. Las operaciones de logística hacia o desde la fábrica generan emisiones por el almacenamiento y transporte. Por ende, las características de un producto y su particular cadena de suministros son los condicionantes para un estudio de huella de carbono tal y como se concluye en [8].
Referente a los modelos de optimización para la cadena de suministros, un diseño de la configuración de una cadena de suministros que incorpora consideraciones ambientales se presenta en [9]. El modelo desarrollado para establecer balances o acuerdos entre los costos y el impacto sobre el medioambiente consiste en una configuración compuesta por proveedores, fábricas y clientes. Con él, se estudió la influencia de los procesos de manejo de materiales y transporte en las emisiones de gases de efecto invernadero y en los costos. Sin embargo, no se contempló el posible almacenamiento intermedio en centros de distribución; tampoco, el desglose de los materiales que las fábricas requieren de los proveedores. El modelo incluye una variable que denominaron nivel de protección ambiental de la instalación y que denota la inversión en tecnologías sofisticadas con una menor emisión de carbono. Entre los resultados, se determinó que al aumentar la capacidad y cantidad del suministro, tanto las emisiones como el costo total podían bajar. Se resolvió el modelo desarrollado de optimización multi objetivo no lineal utilizando Solver del ILOG CPLEX 9.0
En [10] se presenta un modelo de optimización multiobjetivo para el diseño de la configuración de una cadena de suministros de ciclo cerrado. La configuración modelada abarca desde proveedores hasta centros de recolección del producto. Sin embargo, no incluye el almacenamiento intermedio en centros de distribución a los clientes. En la función objetivo se minimizan conjuntamente los costos totales y las emisiones de carbono equivalentes. Las variables de decisión son la ubicación de los actores y el transporte tanto de materiales como del producto terminado, y del retornado para cerrar el ciclo. Las demandas y tasas de producto retornado se estudiaron con incertidumbre, por lo que se examinaron escenarios discretos. Se encontró que el factor de peso utilizado para analizar cada uno de los dos objetivos, económico y ambiental, tiene un gran impacto en los resultados, por lo que se sugiere estimar su valor con cautela. Para la solución se utilizó LINGO 13.0.
En [11] se presenta un modelo de optimización para el diseño de una cadena de suministros que fue resuelto con programación lineal entera mixta. La configuración modelada abarca desde los proveedores hasta los clientes, pero no incluye centros de distribución. En el modelo se analiza el efecto del medio de transporte y de la cantidad de traslados. Las variables de decisión son la localización de las instalaciones, así como los medios y la cantidad de los traslados ejecutados. Como función objetivo se formula una de los costos totales y otra de las emisiones de carbono. En la función de emisiones de carbono se consideró un límite máximo de emisiones que permitir en la cadena. Se encontró que conforme el interés por la conservación ambiental es menor, se efectúan más recorridos a distancias más lejanas. Al usar la programación por metas se encontró una solución equilibrada entre los costos y el ambiente. Se utilizó CPLEX para su solución.
Planteamiento de un modelo para una cadena de suministros sostenible
En esta investigación se desarrolla un modelo matemático que apoya la toma de decisiones referentes a la configuración de la cadena de suministros de una empresa de manufactura. La configuración estudiada está conformada por proveedores, fábricas, almacenes o centros de distribución y clientes o detallistas, así como por los aspectos operativos de la logística requerida para el traslado de los materiales y productos entre ellos.
En el modelo se analiza un conjunto definido de proveedores, considerando el hecho de que los fabricantes suelen adquirir materias primas de proveedores aprobados por sus características de calidad y precio. En cuanto a las instalaciones de fabricación, así como a los centros de distribución, se hace una consideración distinta, pues de ellos se requiere determinar cuáles poner en operación, además del volumen de producción o almacenamiento..
Para establecer las emisiones de carbono de las instalaciones, se registraron las variaciones el en consumo energético, tanto eléctrico como de combustible, así como las descargas de refrigerantes. Para los traslados se identificó el tipo y la cantidad de combustible utilizado. Se hizo uso de factores de emisión para convertir el consumo energético y de combustible en emisiones de carbono. Se utilizaron los valores del potencial de calentamiento global del Panel Intergubernamental del Cambio Climático (IPCC) a 100 años para convertir las emisiones en carbono equivalente.
Notación utilizada en el modelo
M representa el conjunto de materiales, indexados por r, una cantidad r=1 a t
P representa el conjunto de proveedores, indexados por i, una cantidad i=1 a n
F representa el conjunto de fábricas, indexadas por j, una cantidad j=1 a m
C representa el conjunto de centros de distribución, indexados por k, una cantidad k=1 a z
D representa el conjunto de detallistas, indexados por l, una cantidad l=1 a w
Las variables de decisión que corresponden al flujo a lo largo de la configuración son las siguientes:
xrij cantidad de material r de proveedor i a fábrica j
para i =1 a n, j =1 a m, y r =1 a t
xjk cantidad de producto de fábrica j a centro de distribución k
para j =1 a m y k =1 a z
xkl cantidad de producto de centro de distribución k a detallista l w
para k =1 a z y l =1 a w
Los parámetros de entrada son los siguientes:
a ri precio de venta de cada material r del proveedor i
b j costo de producción de cada fábrica j (costo variable)
lj costo fijo de operación de cada fábrica j
dk costo de almacenamiento en el centro de distribución k (costo variable)
n k costo fijo de operación de cada centro de distribución k
Df rj demanda de material r de cada fábrica j (toneladas)
Dd l demanda de producto de cada detallista l (toneladas)
qf j capacidad de producción de cada fabrica j (toneladas)
qp ri capacidad de suministro de material r de cada proveedor i (toneladas)
qc k capacidad de almacenamiento de cada centro de distribución k (toneladas)
EEpri consumo energético eléctrico (kWh) de material en proveedor i
EEfj consumo energético eléctrico (kWh) de producto en fábrica j
EEck consumo energético eléctrico (kWh) de producto en centro de distribución k
FEpri litros de combustible por material r en cada proveedor i
FEfj litros de combustible por producto en cada fábrica j
FEck litros de combustible por producto en centro de distribución k
REpri descarga de refrigerante (kg) por material r en proveedor i
REfj descarga de refrigerante (kg) por producto en fábrica j
REck descarga de refrigerante (kg) por producto en centro de distribución k
EFEEpi factor de emisión de energía eléctrica de cada proveedor (kgCO2/kWh)
EFEEfj factor de emisión de energía eléctrica de cada fábrica (kgCO2/kWh)
EFEEck factor de emisión de energía eléctrica de cada centro (kgCO2/kWh)
EFFEpi factor de emisión de otras fuentes de energía en cada proveedor (kgCO2/l)
EFFEfj factor de emisión de otras fuentes de energía en cada fábrica (kgCO2/l)
EFFEck factor de emisión de otras fuentes de energía en cada centro distribución (kgCO2/l)
w j emisión fija de cada fábrica (kgCO2e)
s k emisión fija de cada centro de distribución (kgCO2e)
d ij distancias proveedor i a fábrica j (km)
d jk distancias fábrica j a centro distribución k (km)
d kl distancias centro distribución k a detallista l (km)
r ij costo por tonelada-kilómetro del proveedor i a la fábrica j
t jk costo por tonelada-kilómetro de fábrica j a centro de distribución k
f kl costo por tonelada-kilómetro de centro de distribución k a detallista l
Tfpi factor de emisión de transporte en kgCO2e/t-km, de proveedor i a fábrica j
Tffj factor de emisión de transporte en kgCO2e/t-km, de fábrica j a centro de distribución k
Tfck factor de emisión de transporte en kgCO2e/t-km, de centro distribución k a detallistas l
El costo operativo de la configuración de la cadena de suministros contempla los elementos de dos fuentes, una correspondiente a los costos operativos y otra a los costos de los traslados. Los costos operativos se generan en el interior de cada nodo o actor de la cadena, en tanto que los costos de traslados son los correspondientes al traslado de los productos entre los actores (nodos) de la cadena. Los costos operativos tienen un componente fijo y otro variable. Así, la función de costo económico de la configuración se compone de los siguientes sumandos:
Costo = precio de materiales de los proveedores (1) + costos operativos de las fábricas (2) + costos operativos de los centros de distribución (3) + costos del traslado de proveedores a fábricas (4) + costos del traslado de fábricas a centros de distribución (5) + costos de traslado de centros de distribución a detallistas (6) + costos fijos de las fábricas seleccionadas (7) + costos fijos de los centros de distribución seleccionados (8).
En la siguiente ecuación se presenta la función de costo de la cadena de suministros (los números entre paréntesis refieren a los componentes del costo indicados anteriormente):
Costo =
Las emisiones de carbono de la configuración de la cadena de suministros se contabilizaron de dos fuentes, a saber, de las operaciones y procesos productivos internos de proveedores, fábricas y centros de distribución, así como de las debidas a los traslados entre ellos. La función de las emisiones de carbono equivalentes de la cadena de suministros es la siguiente:
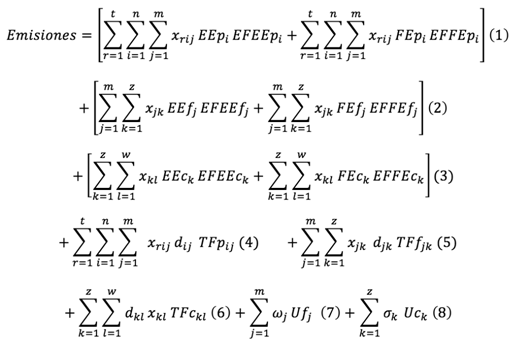
Emisiones de carbono equivalente (E) = emisiones operativas de los proveedores (1) + emisiones operativas de las fábricas (2) + emisiones operativas de los centros de distribución (3) + emisiones por traslado de proveedores a fábricas (4) + emisiones por traslado de fábricas a centros de distribución (5) + emisiones por traslado de centros de distribución a detallistas (6) + emisiones fijas de las fábricas seleccionadas (7) + emisiones fijas de los centros de distribución seleccionados (8)
La siguiente ecuación presenta la función de emisiones de carbono de la cadena de suministros (los números entre paréntesis refieren a los componentes indicados):
Para emular las condiciones reales de una cadena de suministros, el modelo contiene las siguientes restricciones:
La ecuación 1 garantiza que los proveedores no exceden su capacidad de suministrar cada material r. La ecuación 2 establece las restricciones referentes a las demandas de las fábricas. La ecuación 3 establece las restricciones referentes a la capacidad de las fábricas. El producto que envía cada fábrica j no puede exceder su capacidad de producción. La ecuación 4 garantiza el balance entre la mercadería que ingresa y la que sale de cada centro de distribución. La ecuación 5 impide que cada centro de distribución sobrepase su capacidad. La ecuación 6 establece restricción sobre el cumplimiento de la demanda de producto de cada detallista l. La ecuación 7 se refiere a que cada fábrica puede ser o no seleccionada como parte de la configuración; el valor Ufj es 1 cuando la fábrica se selecciona y 0 cuando no. La ecuación 8 se refiere a que cada centro de distribución puede ser o no seleccionado como parte de la configuración; el valor Uck es 1 cuando se selecciona y 0 cuando no. Las ecuaciones 9, 10 y 11 satisfacen las restricciones de no negatividad sobre las variables de flujo a lo largo de la cadena de suministros.
Solución del modelo matemático
Para la solución del modelo, se utilizó la programación por metas. Las metas que se examinaron fueron dos: una que se denominó ambiental, ya que comprendía las emisiones de carbono, y otra que se denominó económica, pues comprendía los costos de la cadena de suministros. Se analizaron ambas metas como de igual prioridad; es decir, se aplicó el caso conocido como sin prioridad en las metas.
Las funciones objetivo de costos y emisiones de carbono, al aplicar la programación por metas, se convierten en restricciones. Además de las restricciones antes indicadas, se tienen las siguientes:
Restricción del costo total
Costo total - s1 + = monto definido como meta del costo
Restricción de las emisiones totales
Emisión total - s2 + = monto definido como meta de las emisiones
Donde
s1 + = la cantidad en la que se excede la meta de costo en la configuración
s2 + = la cantidad en la que se excede la meta de emisiones en la configuración
Como valores meta del costo total y de las emisiones, se utilizaron los valores mínimos obtenidos al optimizarlos separadamente. La formulación de la función objetivo para aplicar la programación por metas es la siguiente (cabe señalar que se busca su minimización):
Función objetivo = s1 + + s2 +
Para demostrar la utilidad del modelo se presenta su aplicación al caso de la cadena de suministros de un producto.
Caso de estudio
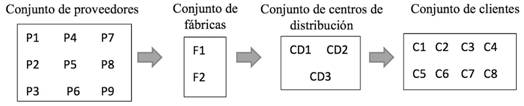
La cadena en estudio es la de un refresco que se fabrica y comercializa en Costa Rica. La fabricación requiere principalmente de tres materias primas con precios desde los 1850 hasta los 3750 $/t, y varios posibles proveedores de un total de nueve. La producción anual es de 250 toneladas. Los clientes demandantes del producto en el periodo del estudio se ubicaban en ocho localidades (aglomerados). Fue de interés investigar la conveniencia de crear centros de distribución, por lo que se evaluó la posibilidad de abrir tres, con iguales capacidades y características, en distintas ubicaciones, permitiendo prescindir de ellos. Igualmente, interesaba analizar el beneficio de operar más de una fábrica, por lo que se propusieron dos ubicaciones con iguales condiciones de tecnología de producción, costos operativos y capacidad, y se admitió la posibilidad de selección de una sola o de ambas. La Figura 1 muestra el esquema de configuración de la cadena de suministros del caso.
El transporte hacia las fábricas y desde ellas se realiza en camiones con capacidad (carga neta) de cuatro toneladas mientras que la capacidad de los camiones que distribuyen desde los centros de acopio hasta los clientes es de dos toneladas. El consumo de combustible (diésel) variaron según la ruta de conexión entre los eslabones de la cadena; para el transporte hacia las fábricas, entre 3 y 6 km/l, y desde los centros de distribución, entre 5 y 7 km/l. Los factores de emisión de carbono utilizados fueron del Instituto Meteorológico Nacional IMN (2014): en el caso de la energía eléctrica, 0,13 kg CO2/kWh, y en el del diésel, 2,69 kg CO2/l. Los Cuadros 1 y 2 muestran las distancias entre proveedores y fábricas, y desde ellas y los centros de distribución hasta los clientes.
Cuadro 1 Matriz de distancias de proveedores a fábricas (km).
| - | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 240 | 30 | 30 | 482 | 1408 | 16 | 432 | 1408 | 16 |
| F2 | 10 | 215 | 215 | 338 | 1315 | 270 | 338 | 1315 | 270 |
Cuadro 2 Matriz de distancias desde fábricas y centros de distribución hasta los clientes (km).
| - | CD1 | CD2 | CD3 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 17 | 31 | 70 | 9 | 31 | 167 | 132 | 20 | 220 | 210 | 70 |
| F2 | 265 | 220 | 280 | 242 | 220 | 385 | 387 | 270 | 155 | 272 | 315 |
| CD1 | - | - | - | 25 | 46 | 144 | 117 | 5 | 290 | 141 | 87 |
| CD2 | - | - | - | 23 | 7 | 184 | 167 | 49 | 192 | 97 | 90 |
| CD3 | - | - | - | 69 | 90 | 95 | 270 | 146 | 276 | 115 | 6 |
Resultados y discusión
Para la solución del modelo se utilizó el Analytic Solver de Frontline Systems, Inc. que se ejecuta sobre Excel®. El Cuadro 3 muestra los resultados de la optimización, primero de la función de los costos solamente y luego de la función de emisiones de carbono.
Cuadro 3 Resultados de la optimización de los costos y de las emisiones de carbono.
| - | Optimización de costos | Optimización de emisiones |
|---|---|---|
| Costos ($) | 545 998 | 627 391 |
| Emisiones (kg CO2e) | 85 339 | 43 718 |
| Configuración | Una fábrica (F1) y ningún centro de distribución. Los materiales 2 y 3 se adquieren de los proveedores P2 y P3. El material 1 se adquiere del proveedor P7. | Dos fábricas y un centro distribución. Los materiales 1 y 2 se adquieren de los proveedores P1 y P2. El material 3 se adquiere de P3 una parte y otra de P6. |
| Indicador kg CO2e/t | 341 | 175 |
Al optimizar los costos, se determina una configuración que tiene un costo en el periodo (anual) de $545 998 y genera unas emisiones de 85 339 kg CO2e. Al optimizar solo las emisiones se obtiene una configuración con menos emisiones, 43 718 kg CO2e, pero de mayor costo, al igual que se reportó en [9] y [11]. En consecuencia, optimizar únicamente las emisiones resulta poco atractivo desde el punto de vista económico. Cabe subrayar que también hay variaciones entre la optimización de los costos y la optimización de las emisiones de carbono en las instalaciones que deben operar y en la selección de los proveedores de los materiales.
Posteriormente se resolvió el modelo mediante la programación por metas. Se establecieron como metas los resultados obtenidos individualmente, para el costo $ 545 998 y para las emisiones 43 718 kgCO2e. El cuadro 4presenta la configuración de la cadena de suministros, con las emisiones y costos que determina el modelo propuesto.
Al optimizar la configuración para cumplir con la meta ambiental y la económica simultáneamente, no fue posible cumplir ninguna de ellas a cabalidad, pues los valores finales para ambas resultaron ser mayores que los definidos como meta. Mediante la programación por metas, sin embargo, se logró determinar una configuración de la cadena de suministros con emisiones cercanas a las mínimas posibles (3% mayores), a un costo de operación también cercano al mínimo posible (1,4% mayor). Además, el indicador de emisiones de carbono disminuyó de 341 a 181 kg CO2e/t. Un comportamiento similar se reportó en [11] al utilizar la programación por metas.
Cuadro 4 Resultados de la optimización por metas.
| - | Meta | Resultado final | Diferencia con respecto a la meta (incremento) |
|---|---|---|---|
| Costos de la configuración ($) | 545 998 | 553 751 | 7753 |
| Emisiones (kg CO2e) | 43 718 | 45 124 | 1407 |
| Configuración | Una fábrica (F2) y ningún centro de distribución. El material 1 se adquiere del proveedor P1, el material 2 de P2 y el material 3 de P3. | ||
| Indicador kg CO2e/t | 181 | ||
Cabe destacar que el modelo desarrollado en esta investigación incorpora el desglose de los requerimientos de materias primas, así como la posible participación de centros de distribución o almacenes en la distribución de productos, mientras que los presentados en las referencias [9], [10] y [11] no lo hacen. Además, la estructura del modelo posibilita su aplicación a distintos casos de cadenas de suministros, no solo de productos alimenticios como en el caso estudiado. Además, se demostró que optar por la programación por metas para su solución permitió lograr un acuerdo beneficioso tanto para el objetivo económico como para el ambiental.
Conclusiones
Se ha desarrollado este modelo de programación lineal entera mixta en apoyo a las acciones para mitigar el cambio climático. Se considera que el modelo específicamente contribuye en la valoración de los costos que implica la reducción de las emisiones de gases de efecto invernadero asociadas a las decisiones sobre la configuración de la cadena de suministros. Se demuestra así que los métodos y modelos de la investigación de operaciones son un área de conocimiento que puede contribuir considerablemente en la búsqueda de un desarrollo sostenible.
El modelo desarrollado es versátil y puede ser aplicado a diversos productos. Al abarcar desde el inicio de la cadena, los proveedores, incluyendo los materiales requeridos de ellos, así como sus emisiones y las de sus traslados; la conveniencia de almacenamiento en centros de distribución y las emisiones debidas a los traslados hasta los clientes, permite valorar con mayor profundidad las decisiones en torno a la configuración de la cadena de suministros. Estos aspectos se encontraron en los modelos revisados en la literatura, pero no reunidos todos en un mismo modelo.
La aplicación del modelo en el caso de estudio demuestra el beneficio de contar con modelos comprensivos de los distintos componentes, que permitan ponderar los efectos de las decisiones que se toman en torno a la configuración de la cadena de suministros en búsqueda del equilibrio en su impacto ya no solo económico, sino también ambiental. Los resultados numéricos en el caso de estudio, demuestran que la programación por metas lleva a opciones que, aunque no corresponden a las óptimas, representan mayor balance entre los objetivos económicos y ambientales para la cadena de suministros.